目前,我国的CZ-3A、CZ-2E运载火箭均使用弹道修正补偿的方法进行减载控制[4]。弹道修正补偿的方法是指将预先测量的高空平稳风以及切变风信息引入控制系统,以补偿风载对运载火箭的影响。这种减载补偿方法原理简单,较易实现,可靠性强,同时不影响原控制系统的结构。但是,射前的高空风补偿法的准确度依赖于所装订的高空风信息的精度[5],对风载的实时不确定性抑制能力较差。因此,主动减载控制技术的发展成为了运载火箭飞行减载技术的重要研究内容[6]。所谓主动减载控制技术就是在伺服控制系统中引入减载控制,使用实时测量或计算的攻角信息进行飞行补偿,使火箭朝气流影响的方向飞行。
George[5]在减载控制系统报告中系统地给出了飞行环境中风场建模与分析方法、被动弹道修正法以及攻角与横向载荷反馈下的主动减载方法。Blanchet和Bartos[7]针对德尔塔运载火箭提出了一种精确的风载模型,提高了被动修正的精度。Sharp[8]分析设计了土星系列运载器飞行减载控制系统。这些方法从工程中解决了飞行减载的问题,但都是基于高精度风载建模下的传统减载方案,并未在方法上进行改进。李效明等[4]在改进弹道模型的基础上,提出了一种攻角和侧滑角的工程近似方法,从而进行攻角、侧滑角的反馈补偿。所建模型中多数参数使用标准弹道代替,计算精度难以满足实时计算的需求。Renault和Saunois[9, 10]使用减载网络进行飞行减载仿真,但出现振荡现象。宋征宇[11]结合已有的测量数据,对弹道修正法等减载技术进行仿真,并分析了主动减载控制方法,同时指出自抗扰控制器(Active Disturbance Rejection Controller,ADRC)抗干扰性强,但减载能力较差。随着自抗扰控制技术的发展以及在飞行控制系统中的应用[12, 13, 14],自抗扰控制为飞行减载技术提供了了新的研究方向。
本文针对现有运载火箭的主动减载技术进行了仿真,同时,深入地研究了ADRC在运载火箭减载控制的作用,解决了无法区分干扰组成的难题,推导得出了自抗扰控制律设计方法,有效地改善了ADRC的减载作用。
1 运载火箭俯仰通道动力学模型对于使用液体推进剂的运载火箭而言,其飞行动力学特性必须要考虑各个贮箱推进剂的晃动以及弹性振动对姿态运动的影响[15]。
质心动力学方程:
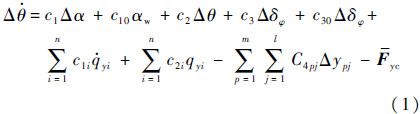
式中:θ为弹道倾角;α和αw分别为飞行攻角以及风攻角产生的附加攻角;δφ为发动机摆角;qyi为第i阶广义弹性振动位移;ypj为第p个贮箱的第j阶晃动;Fyc为干扰力;c1,c2,…,c2i,C4pj均为动力系数。
定义Δωz=Δ
(φ为俯仰角),则绕质心转动动力学方程: 
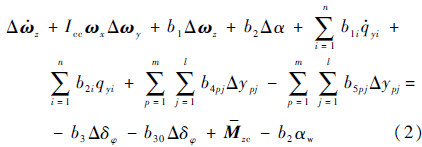
式中:ωx、ωy和ωz分别为俯仰、偏航和滚转角速度;Mzc为干扰力矩;b1,b2,…,b5pj为动力系数；Icc为侧向通道转动惯量。
运载火箭各阶弹性振动方程:
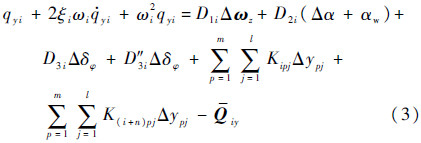
式中:ξi和ωi为第i阶弹性振动阻尼和频率;Qiy为第i阶弹性振动受到的广义干扰力;D1i、D2i、D3i、D″3i、Kipj和K(i+n)pj为动力系数。
推进剂晃动方程:
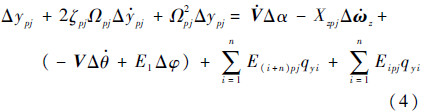
式中:ζpj和Ωpj分别为第p个贮箱第j阶晃动的阻尼和频率;V为速度;Xzpj为火箭质心至晃动质量质心距离;E1、E(i+n)pj和Eipj为动力系数。
测量方程:
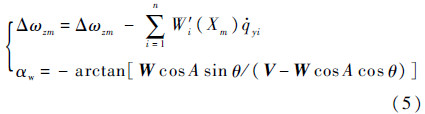
式中:W′i(Xm)为第i阶振动在传感器位置Xm处振型斜率;ωzm和ωzm为考虑与未考虑弹性时,传感器测的俯仰角速度信号;A为风速与发射平面的夹角;W为风速。
2 运载火箭主动减载控制运载火箭的主动减载控制中,风干扰的测量以及计算是进行伺服控制系统补偿外干扰的关键。主动减载方法包括基于攻角反馈的飞行减载控制以及基于加表反馈的飞行减载控制。
2.1 基于攻角反馈的飞行减载控制基于攻角反馈的飞行减载控制包括使用攻角传感器的直接测量法,以及使用攻角近似的间接计算法。攻角反馈下的减载控制框图如图 1所示。图中:a0、a1为静态、动态增益;WΔφ(Δα+αw)为俯仰角对输入攻角的传递函数。
 |
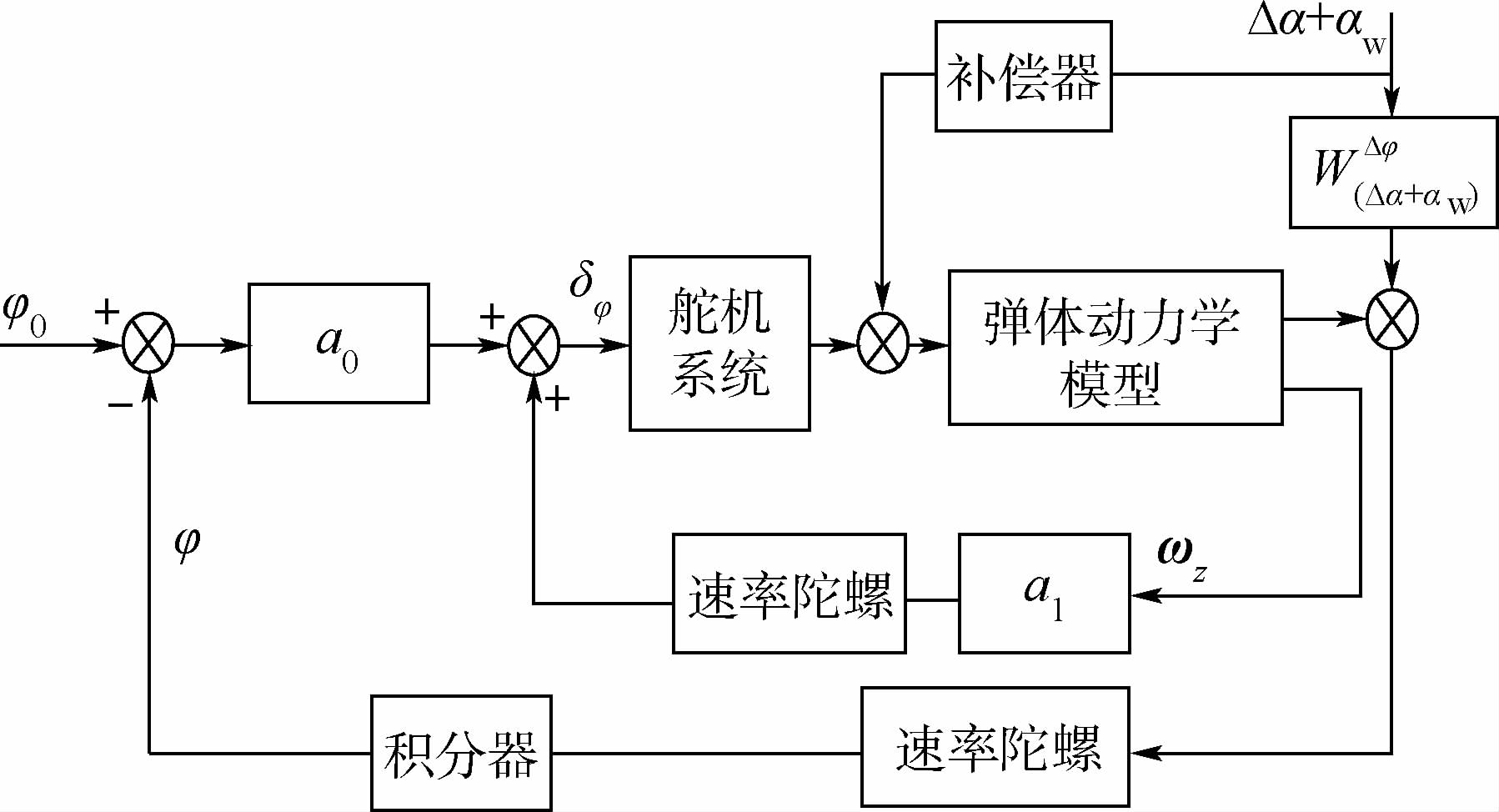| 图 1 攻角补偿模型Fig. 1 Attack angle feedback model |
| 图选项 |
攻角传感器的测量值包含2个部分:一部分是由于风干扰形成的附加攻角αw,一部分是由于弹体自身速度与姿态形成的攻角Δα。原系统控制方程的表达式为式(6)。引入攻角传感器后,反馈控制系统的控制方程表达式变为式(7)。
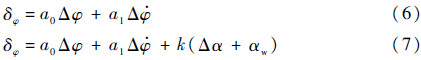
式中:k为攻角反馈增益。
将式(6)代入式(2)中,考虑弹性振动与推进剂晃动,忽略动态项可以得到
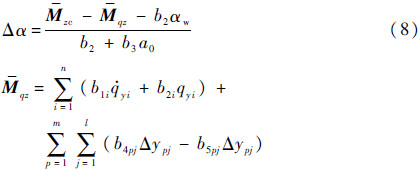
由于攻角传感器会将全部的气动载荷作为干扰进行补偿,因此,合并刚性弹体的姿态运动方程中(Δα+αw)项,作为整体进行反馈控制系统分析,若要消除气动力以及气动力矩对运载火箭的影响,记俯仰角对发动机摆角的传递函数为Wδφ,补偿器G1可取为
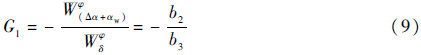
2.2 基于加表反馈的飞行减载控制利用弹体上的加速度表进行飞行减载控制的原理是加表测量的横向过载中隐含攻角信息,引入横向过载反馈也就同时抑制了横风形成的附加攻角。加表的测量信号Δε可以表示为
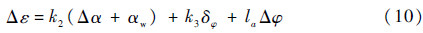
引入加表反馈后,控制方程变为
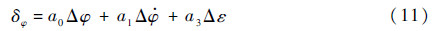
将控制方程代入刚性飞行器动力学方程中,并忽略动态项,可以得到引入加表反馈对运载火箭减载的作用。
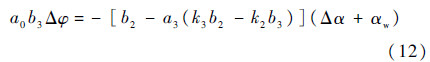
显然,适当地选择反馈控制律a3,可以达到运载火箭的减载飞行作用,当a3取式(13)时,可以消除高空风载对运载火箭飞行控制系统的影响。
加表反馈较易安装实现,同时对运载火箭有良好的飞行减载能力。但是加速度表的引入,改变了系统的结构,降低了飞行控制系统的稳定性,因此减载效果受到限制。
3 基于自抗扰的飞行减载技术运载火箭的主动飞行减载技术包括:以引入攻角传感器为代表直接测量方法,以加表反馈为代表的等效间接抑制方法,以及实时近似计算攻角和侧滑角的补偿控制方法。这些控制技术依赖于风模型测量或计算的精确性。随着自抗扰控制技术的发展,给运载火箭的飞行减载技术带来了新的思路,将风模型看作标准模型的扰动量,利用ADRC自身的抑制干扰的优点进行高空风减载。
3.1 自抗扰控制器自抗扰控制技术综合了现代控制理论中状态观测的思想,巧妙地将经典控制理论与现代控制理论相结合。ADRC通过状态观测器估计运载器状态变量,同时,观测器将飞行器中的模型不确定部分、干扰力、干扰力矩以及高空风认为是系统的总扰动,对系统进行补偿。
ADRC主要由跟踪微分器(TD)、扩张状态观测器(ESO)以及非线性状态误差反馈(NLSEF)3个部分组成[12],如图 2所示。图中:u(t)为输入;y(t)为输出;z1(t),z2(t),…,zn(t)为状态估计量;e1(t),e2(t),…,en(t)为误差;b为补偿因子;w(t)为干扰信号;v(t)为设定值;v1(t),v2(t),…,vn(t)为安排过渡过程以及其微分。
 |
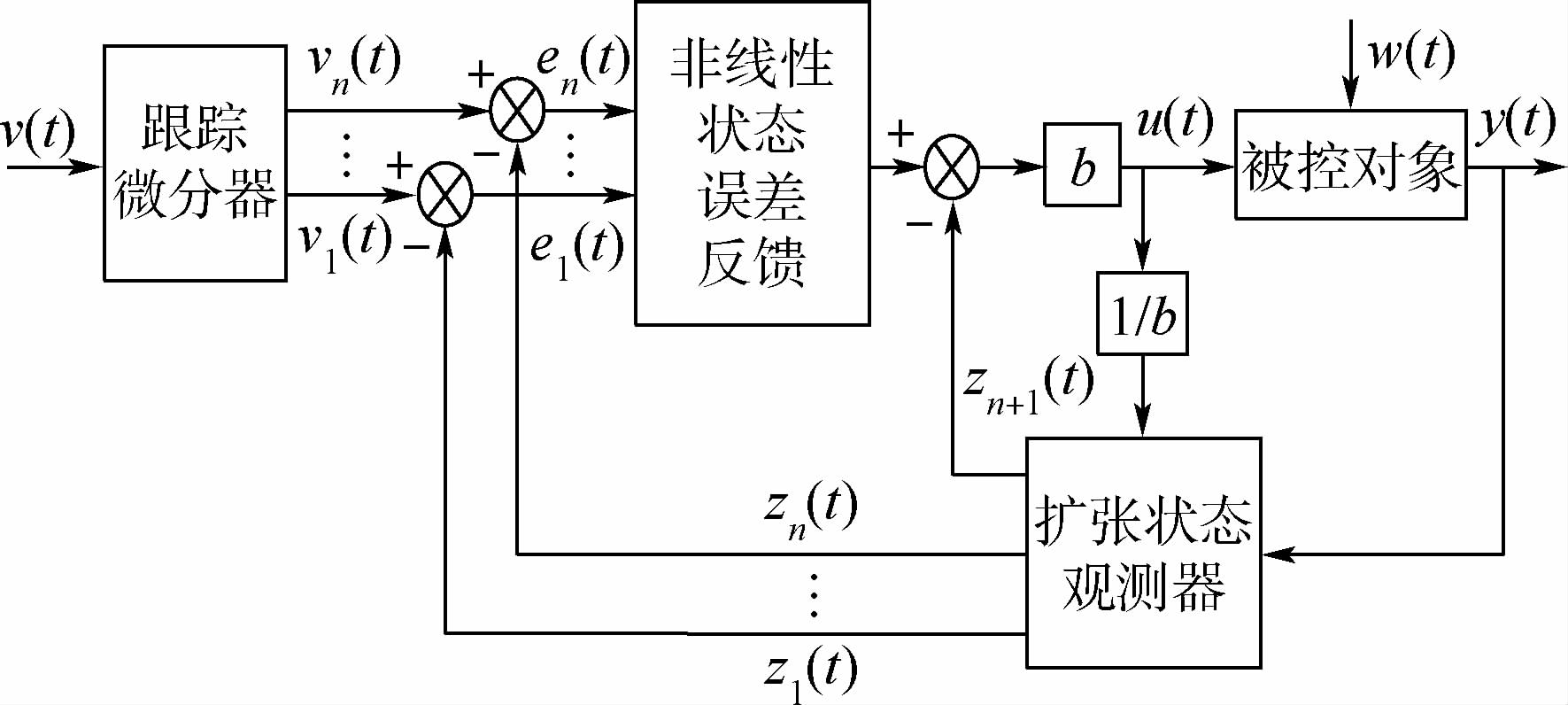| 图 2 ADRC结构图Fig. 2 Structure diagram of ADRC |
| 图选项 |
1) 跟踪微分器
ADRC的设计中,跟踪微分器的主要作用是快速无超调地跟踪输入信号,二阶离散形式的最速跟踪微分器的形式为
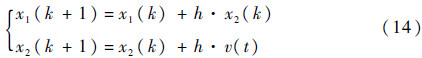
式中:h为步长；v(t)=fhan(x1(k)-v(k),x2(k),r,h0)，h0为步长初始值，r为速度因子，fhan结构[13]如式(15)所示：
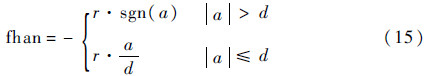
式中：a和d为跟踪微分器特征参量。
2) 扩张状态观测器
由于飞行器模型未知,扩张状态观测器将飞行动力学模型看成包含不确定扰动的积分串联环节。扩张状态用于表征观测不确定扰动项,并将其引入控制回路进行补偿。同时,观测器可以输出状态观测量以及其微分值,用于闭环反馈。
扩张观测器的微分方程形式如下:
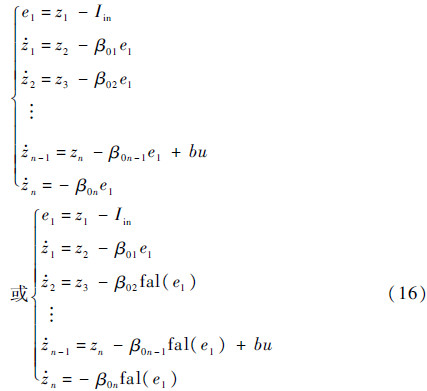
式中:Iin为观测器输入信号;zi为状态观测值以及状态微分;β0i为状态观测器中所调参数;fal[13]为具有较好性能的非线性函数,其表达式为
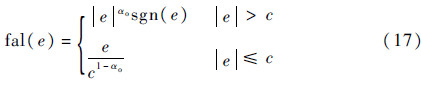
式中：αo为观测器常数因子；c为线性段区间的长度。
3) 非线性状态误差反馈
ADRC中的误差反馈控制部分,不但可以使用PID调节器中的线性组合进行控制,同时还可以选取非线性组合进行控制,其表达形式为
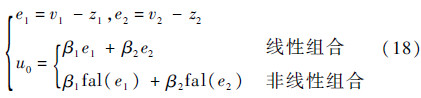
3.2 基于ADRC的飞行减载控制方法选取俯仰角为观测对象设计ADRC,使用二阶最速跟踪微分器安排过渡过程,同时使用线性PD反馈以方便推导运载火箭减载控制方程。其伺服控制系统框图如图 2所示。
设计控制器时,考虑各阶弹性以及晃动的影响时,运载火箭的姿态角动力学方程为
构造三阶扩张状态观测器形式为
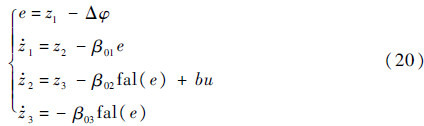
式中:用z1跟踪俯仰角偏差Δ
;z2跟踪俯仰角速度偏差Δφ;z3表征飞行器建模的不确定性以及随机风的干扰。ADRC中使用线性控制器,形式为
由图 2,引入自抗扰减载控制器后,运载火箭的控制方程变为
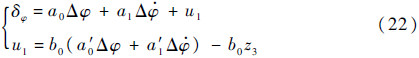
3.3 ADRC的飞行减载控制的改进方法由运载火箭的扰动运动方程式(19),结合自抗扰扩张观测器表达式(20)表明,不确定扰动z3包含b1Δ
,b2Δφ,Mzc,b2αw以及弹性振动和晃动项Mqz。由于扩张观测器并不能区分干扰中的高空风干扰部分和其余干扰,同时,扩张观测器将飞行动力学模型看成包含不确定扰动的积分串联环节,这就使各种不确定项抵消了减载效果。因此,此种形式的自抗扰减载控制器仅具有较强的抗干扰能力,减载效果仅仅在高空风占主导作用时较为明显。
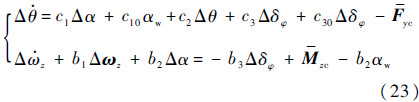
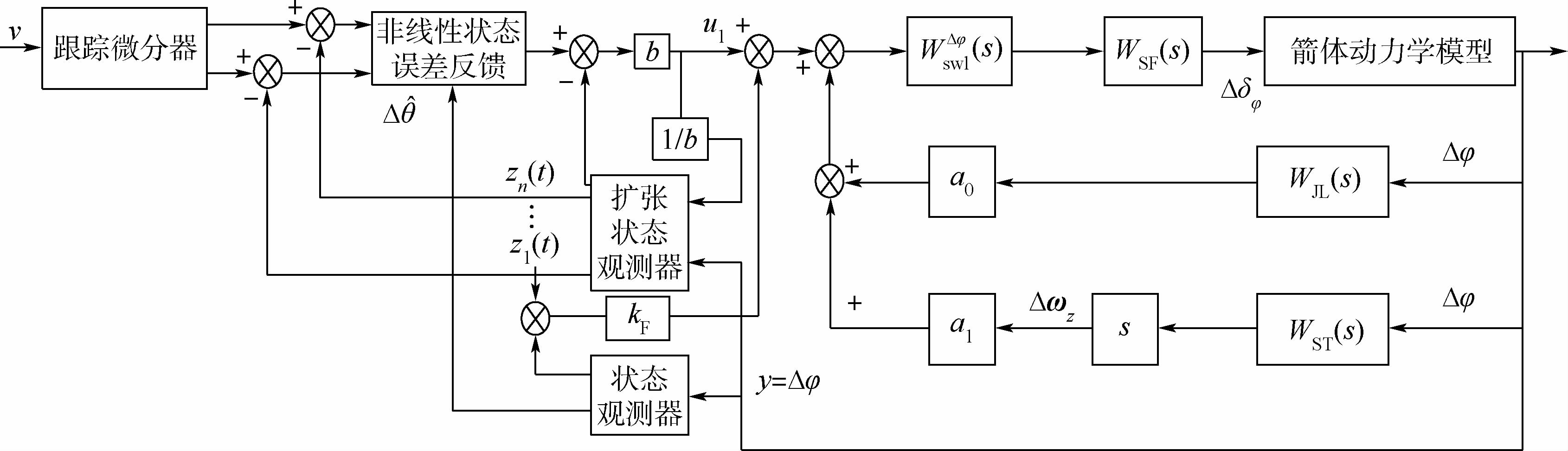
一般情况下,运载火箭的飞行动力系数c1》c10(本次试验c1>10c10),弹道倾角偏差Δθ受附加攻角αw的影响远小于俯仰角偏差Δφ受到附加攻角αw的影响。因此,设计刚体状态观测器式(24),忽略附加攻角αw对弹道倾角偏量Δθ的作用,将弹道倾角Δθ的观测误差看作干扰力Fyc的作用,并对俯仰角偏差Δφ中的误差进行补偿,以改进减载作用,WJL(s)、WST(s)、WSF(s)和WswlΔφ(s)为捷联惯导、速率陀螺、伺服和网络传递函数。减载控制框图如图 3所示。图中:kF为补偿信号增益;u0为自抗扰控制中控制方案;u1为自抗扰控制的整体输出控制律。
 |
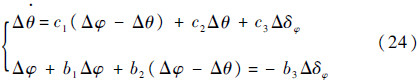
| 图 3 基于改进ADRC的运载火箭减载控制框图Fig. 3 Improved launch vehicle load relief control block diagram based on ADRC |
| 图选项 |
经过扰动补偿后,ADRC输出的俯仰角偏差控制量u1以及控制方程δφ变为
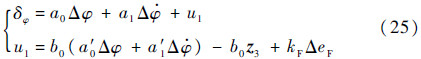
对于ADRC减载控制器设计而言:一方面可以对观测误差进行补偿以加强减载效果；另一方面可以改进ADRC中的控制方程以增强运载火箭飞行减载能力。
不妨假设ADRC中使用线性控制器,同时控制器参数为观测器输出参数,ADRC中线性控制器的形式可以由式(21)变为
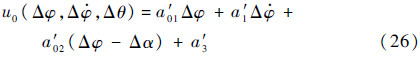
令a′0=a′01+a′02,a′2=－a′02,式(26)变为
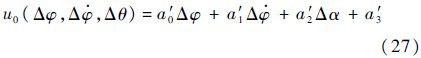
结合图 3,此时ADRC输出的俯仰角偏差控制量u1以及控制方程δφ变为
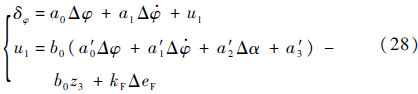
将式(28)合并同时代入式(2),得到考虑振动与晃动影响时,运载火箭在ADRC与PID联合控制作用下的俯仰角偏差方程为
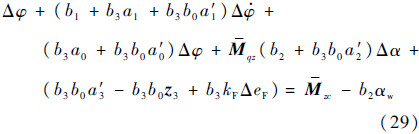
忽略动态项,并考虑Δφ=Δα代入得到
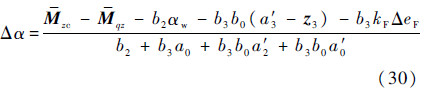
经过推导,得到基于ADRC的运载火箭减载控制后的攻角偏差Δα(式(30)),对比未经减载的原控制系统的攻角偏差Δα(式(8))。得到结论:在满足控制系统稳定性的前提下,当所选择的增益参数大于0,同时满足a′3大于不确定扰动量的范数,即a′3>z3时,攻角偏差受干扰力矩以及风载的作用减小,满足减载要求。
4 运载火箭减载效果评估与分析本文以某型号液体运载火箭为例,系统地研究运载火箭的主动减载控制技术。分析经典方法存在的问题,然后使用本文所提出的ADRC控制器设计理论进行仿真研究。
4.1 风的模型根据历年高空风测量数据,将液体运载火箭在高空时受到的高空风划分为平稳风以及切变风2类,平稳风由实验测试数据给出,切变风采用三角波形式。运载火箭发射后50~80 s时刻所受到的高空风以及产生的附加攻角如图 4、图 5所示。
 |
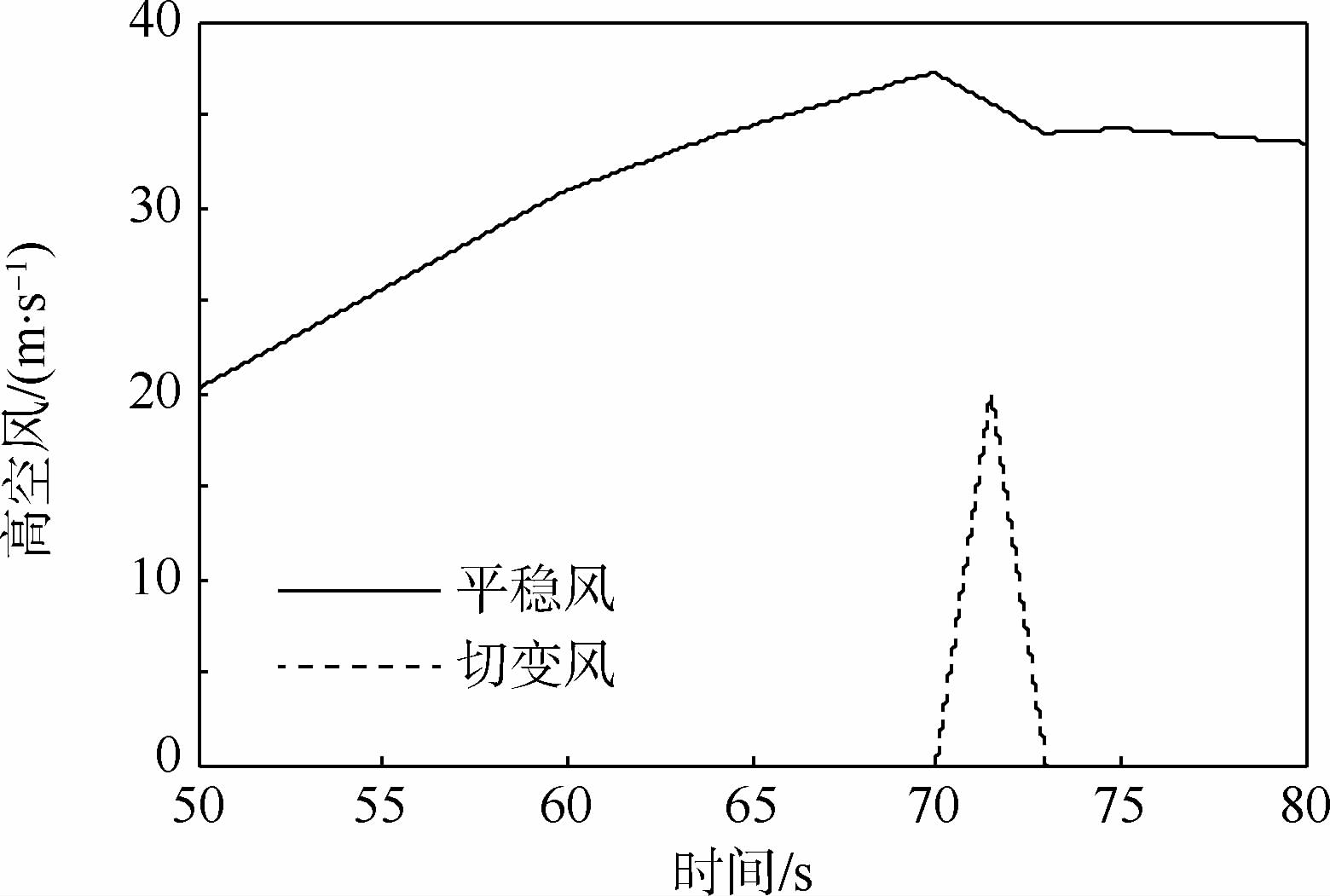| 图 4 运载火箭所受到的高空风模型Fig. 4 Wind aloft model acting on launch vehicle |
| 图选项 |
 |
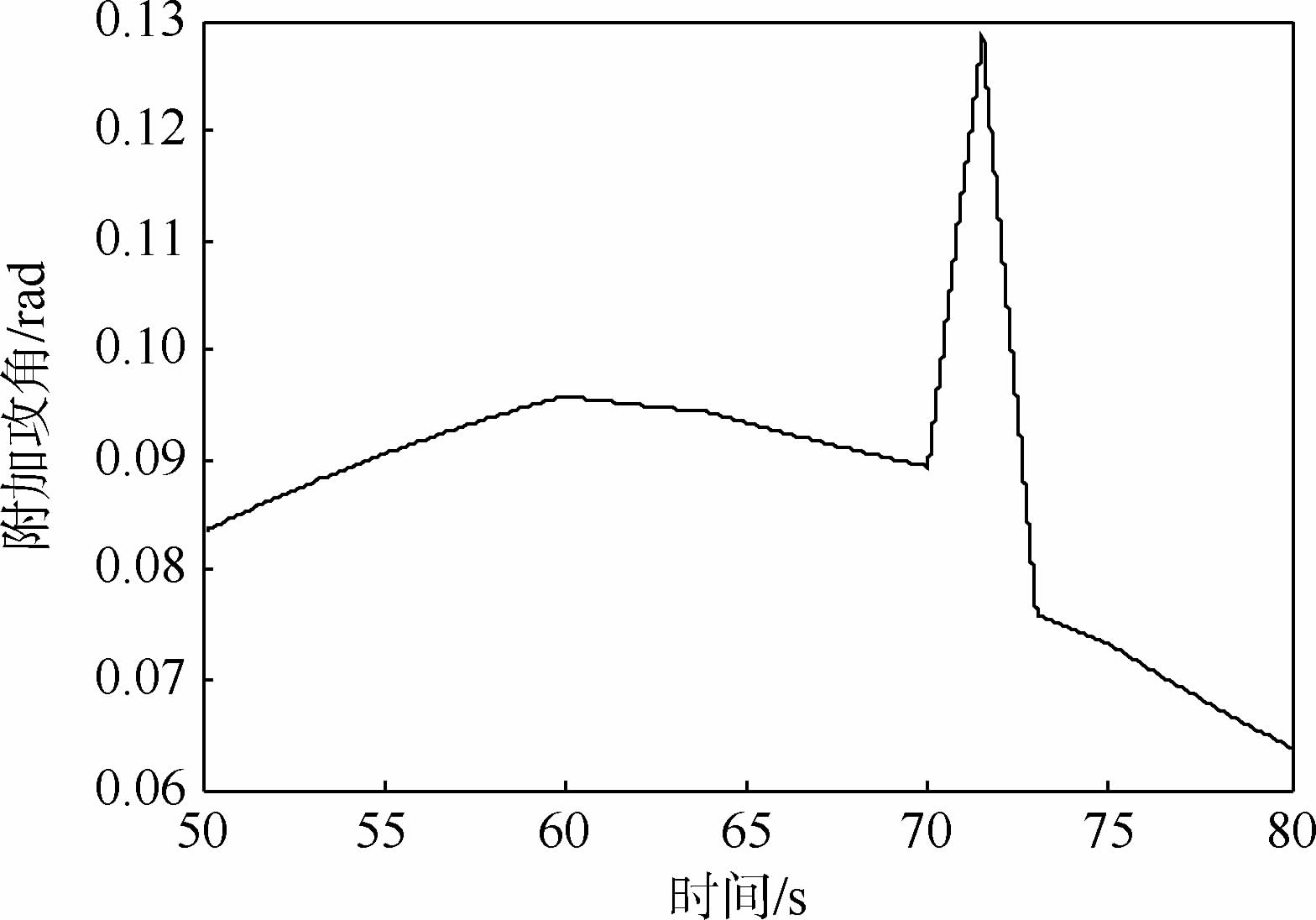| 图 5 在高空风作用下的附加攻角Fig. 5 Accessional attack angle under wind aloft |
| 图选项 |
4.2 攻角与加表反馈作用下的飞行减载控制针对液体运载火箭,考虑弹体的六阶弹性振动,4个贮箱中各个贮箱的前2阶晃动,同时考虑刚性弹身由于受到气动弹性以及液体晃动而形成的耦合。选取PID参数,其中静态增益a0=1.2,动态增益a1=0.8,攻角反馈系数k=0.233,校正网络如式(31)所示:
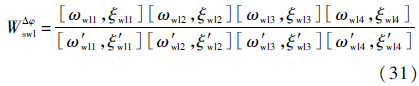
式中:[m,n]=(1/m)2s2+2n(1/m)s+1。
选取飞行时刻为50~80 s,分别对液体运载火箭在未减载情况、基于攻角反馈以及基于加表反馈3种情况下进行仿真,得到的俯仰角偏差曲线如图 6所示。引入加表反馈后,反馈系数a3对控制系统的影响如图 7所示。
 |
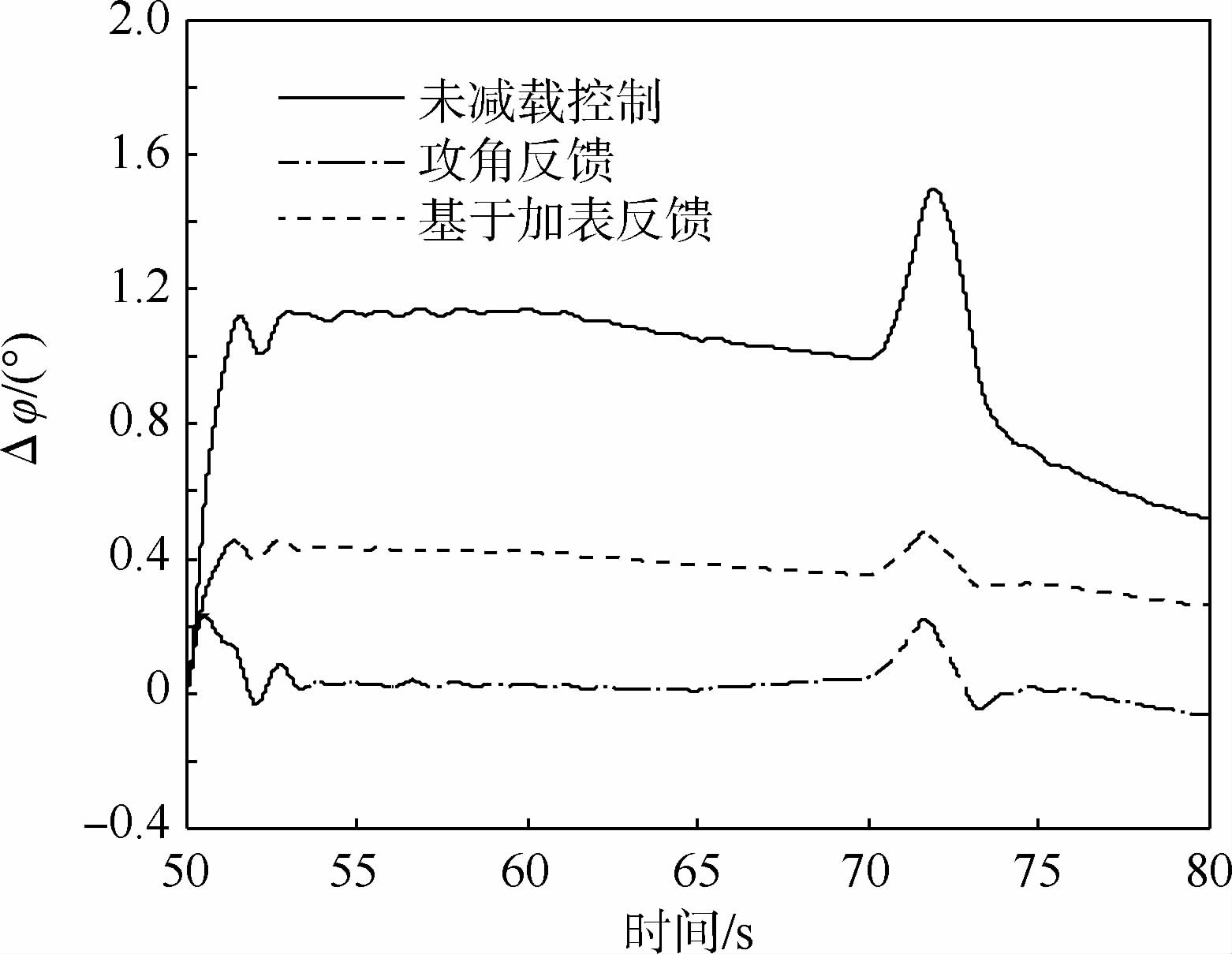| 图 6 在高空风作用下的俯仰角偏差曲线Fig. 6 Pitch angle deviation curves under wind aloft |
| 图选项 |
 |
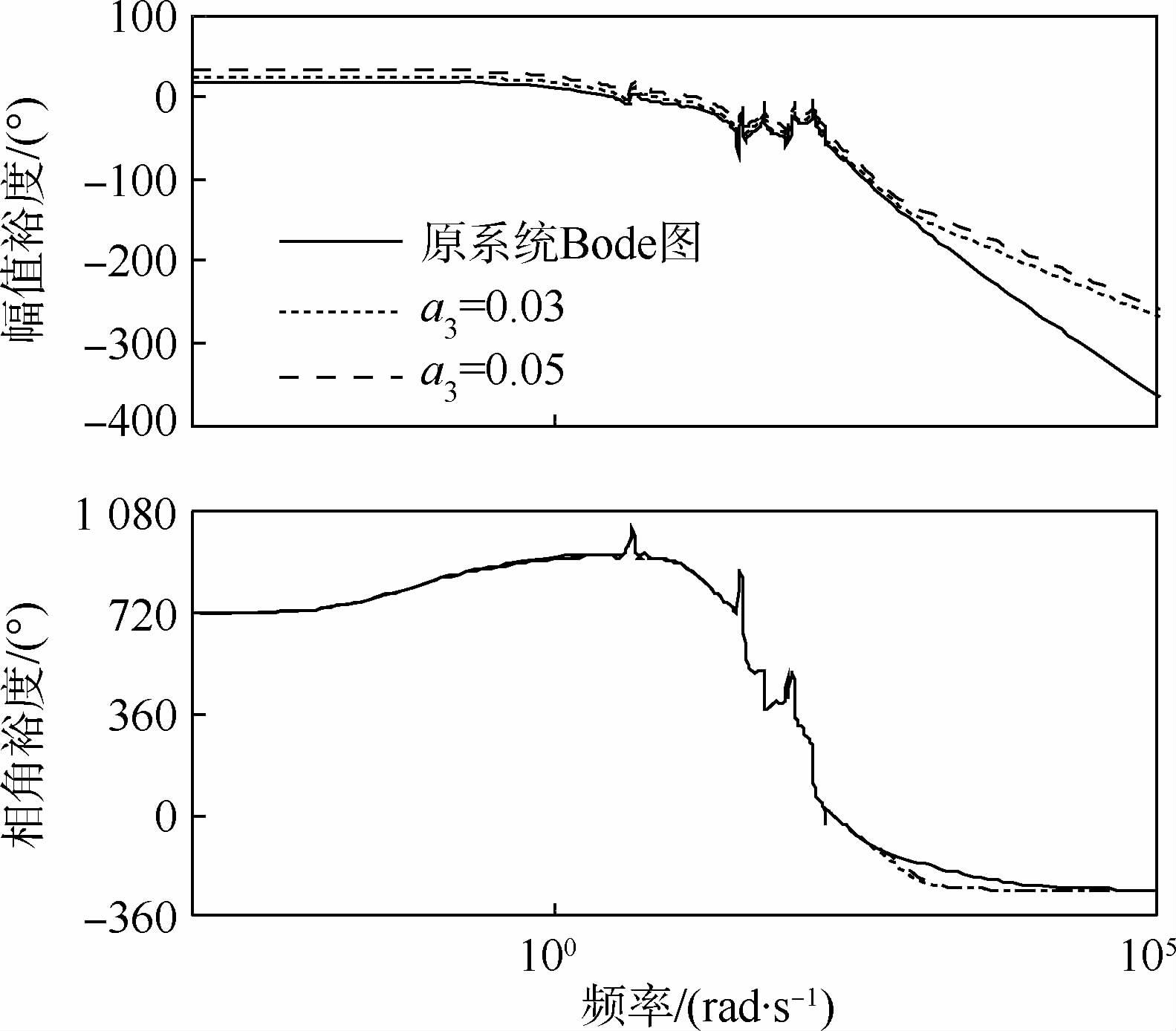| 图 7 加表反馈对伺服控制系统的影响Fig. 7 Accelerometer feedback effect on servo control system |
| 图选项 |
仿真结果表明:相比较于原控制系统,使用攻角补偿反馈技术以及使用加表反馈技术所设计的减载控制器具有明显的减载作用。使用攻角反馈控制进行飞行减载时,姿态角偏差减少95.18%,基本可以完全抵消高空风载的干扰作用。同时,使用加表反馈时,姿态角偏差也可以减少73.36%。但是采用攻角反馈严重依赖攻角传感器的测量精度,就目前而言,攻角传感器很难精确测量飞行攻角,故难以使用。
图 7表明,原飞行控制系统的幅值裕度为10.1 dB,相角裕度为31°,伺服控制系统稳定。引入加表反馈后,随着反馈系数a3的增大,当a3=0.03时,对数幅值曲线被抬高,穿越频率增大,幅值裕度下降到4.71 dB,相角裕度下降到21.2°。当a3=0.05时,相角裕度为-28.9°,飞控系统失稳。这就限制了加表反馈作用下运载火箭的减载控制效果。
4.3 ADRC作用下的飞行减载控制针对所使用的液体运载火箭飞行控制系统模型,使用自抗扰控制理论以及本文提出的改进方法对液体运载火箭主动减载技术进行仿真。
选取PID参数。其中静态增益a0=1.2,动态增益a1=0.8,校正网络仍使用式(31)。
选取ADRC参数。其中跟踪微分器选取最速跟踪微分器,形式如式(14)所示:r=0.1,h=0.01,h0=10。扩张状态观测器形如式(20)所示,其中:β01=5,β02=20,β03=5。控制组合参数形如式(21)所示,其中:a′0=－5,a′1=－4.5。状态观测器系数由飞行动力系数得到。干扰力矩补偿系数kF=0.18。
使用本文所提出的基于ADRC的运载火箭的飞行减载技术设计理论进行液体运载火箭的飞行仿真。同时,对比了经典的飞行减载控制技术以及未加改进的ADRC飞行减载技术。其中,俯仰角偏差Δφ、俯仰角速度偏差Δω、攻角偏差Δα、|qα|以及1号和2号贮箱一阶晃动(Δy11、Δy21)的仿真结果分别如图 8~图 13所示。
 |
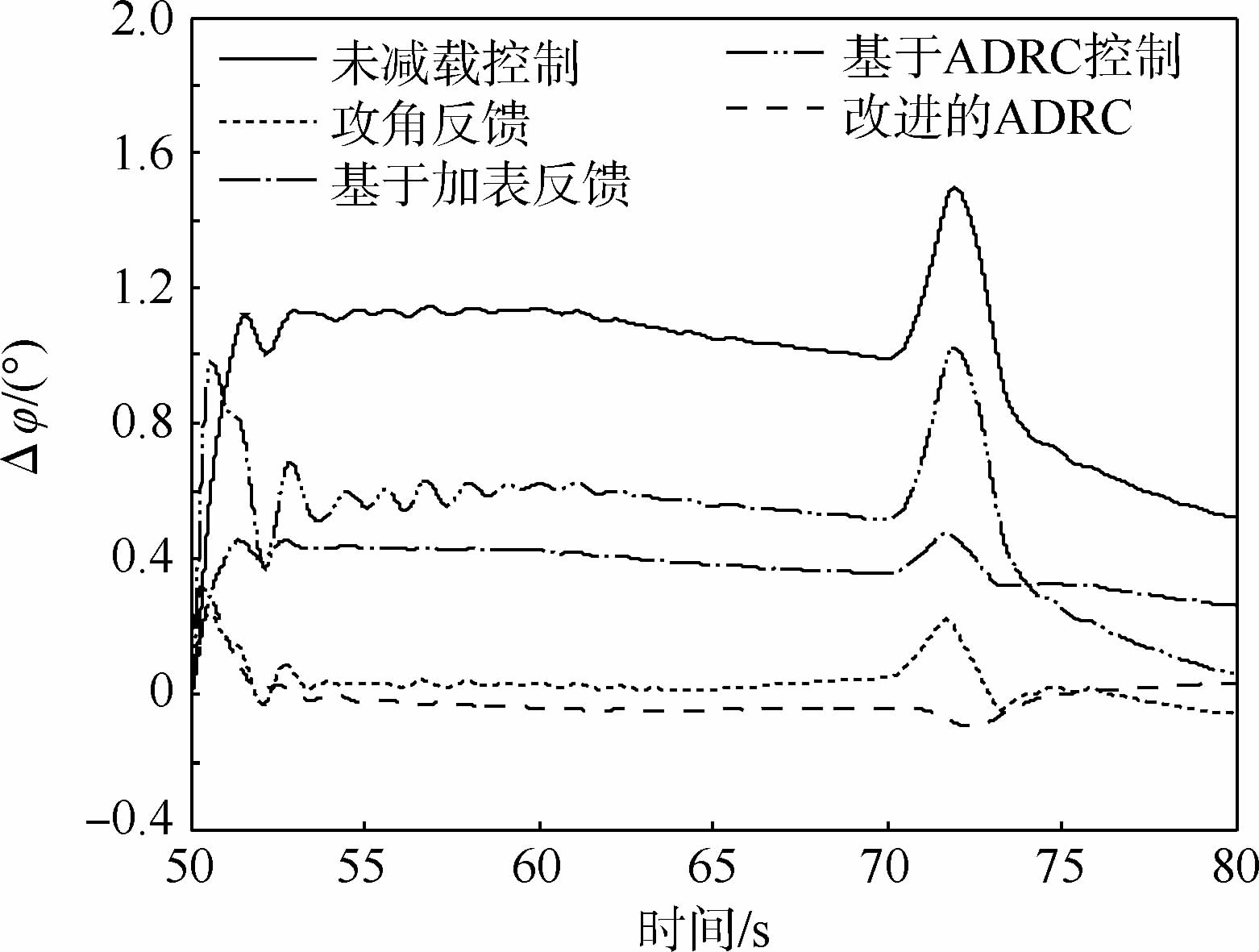| 图 8 俯仰角偏差随时间的变化Fig. 8 Time history of pitch angle deviation curves |
| 图选项 |
 |
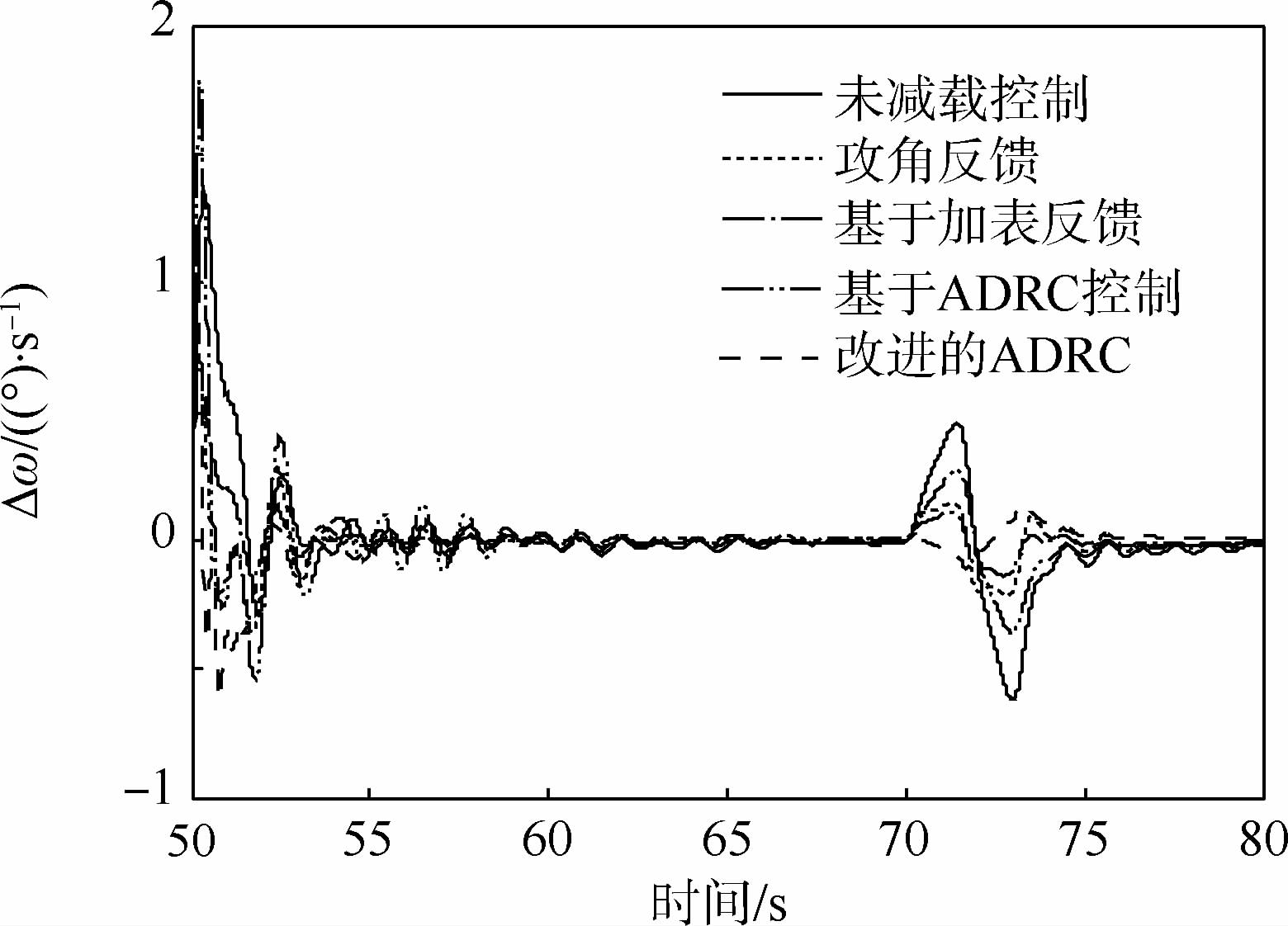| 图 9 俯仰角速度偏差随时间的变化Fig. 9 Time history of pitch angle rate deviation curves |
| 图选项 |
 |
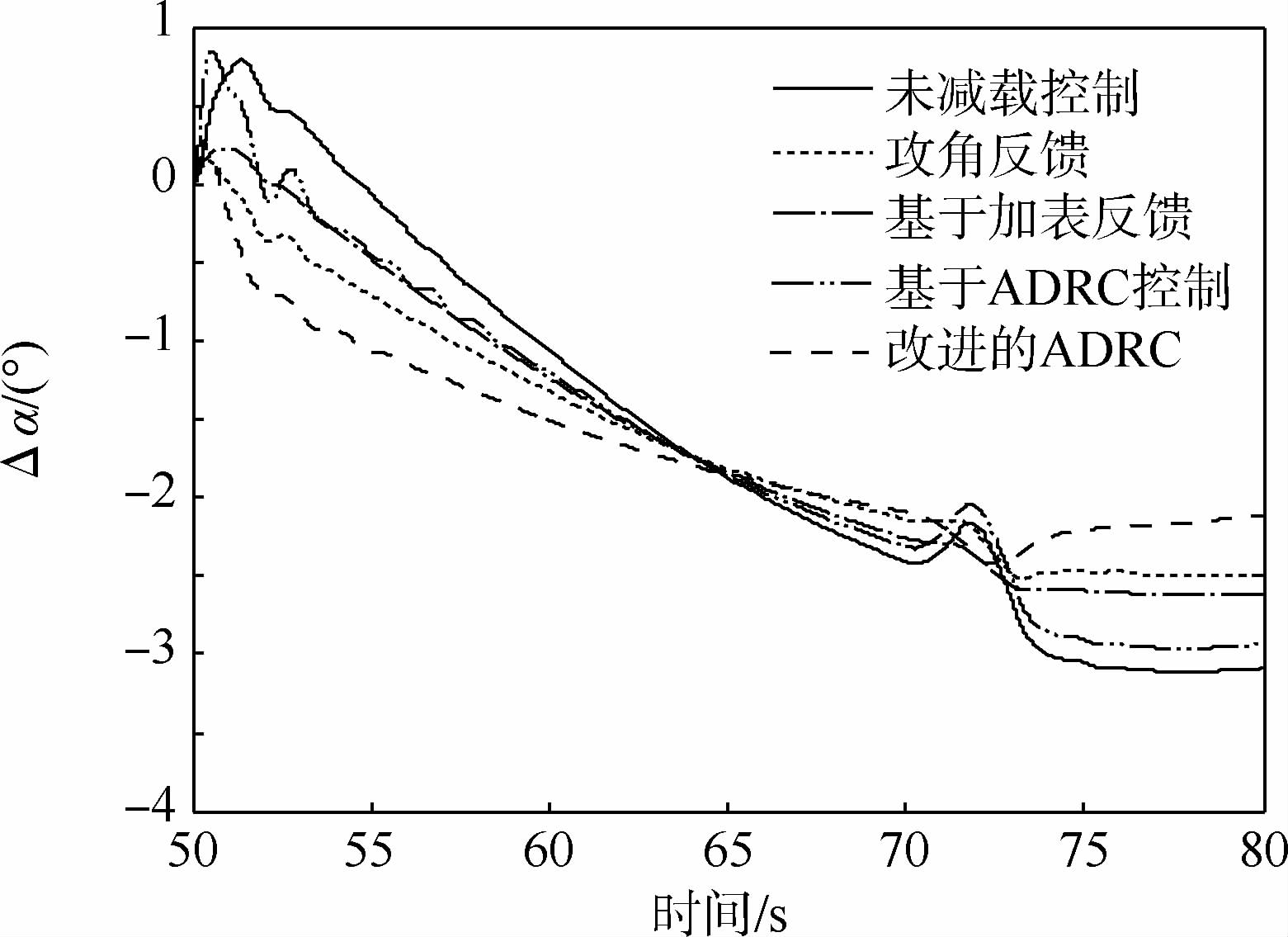| 图 10 攻角偏差随时间的变化Fig. 10 Time history of attack angle deviation curves |
| 图选项 |
 |
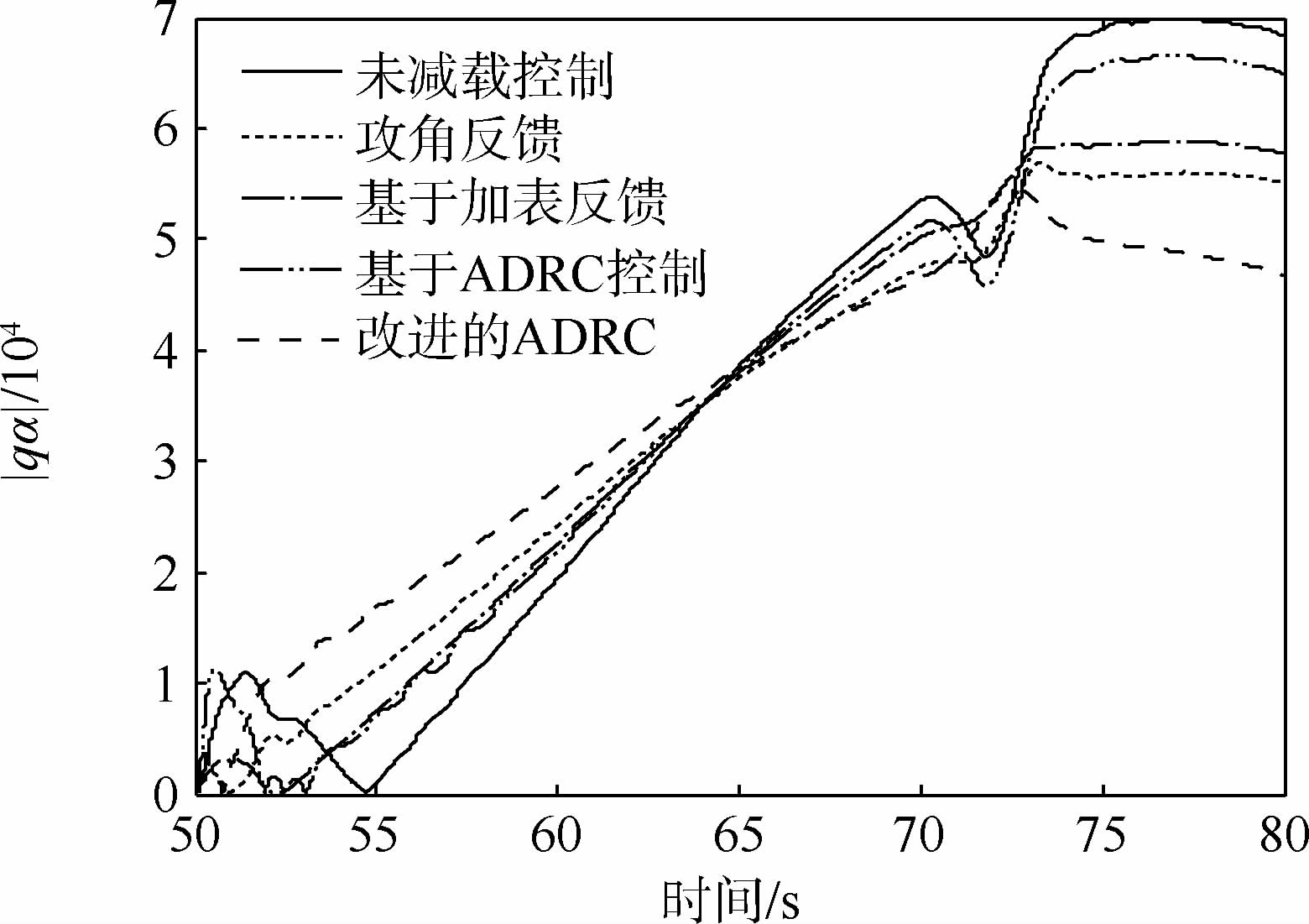| 图 11 qα随时间的变化Fig. 11 Time history of dynamic pressure qα curves |
| 图选项 |
 |
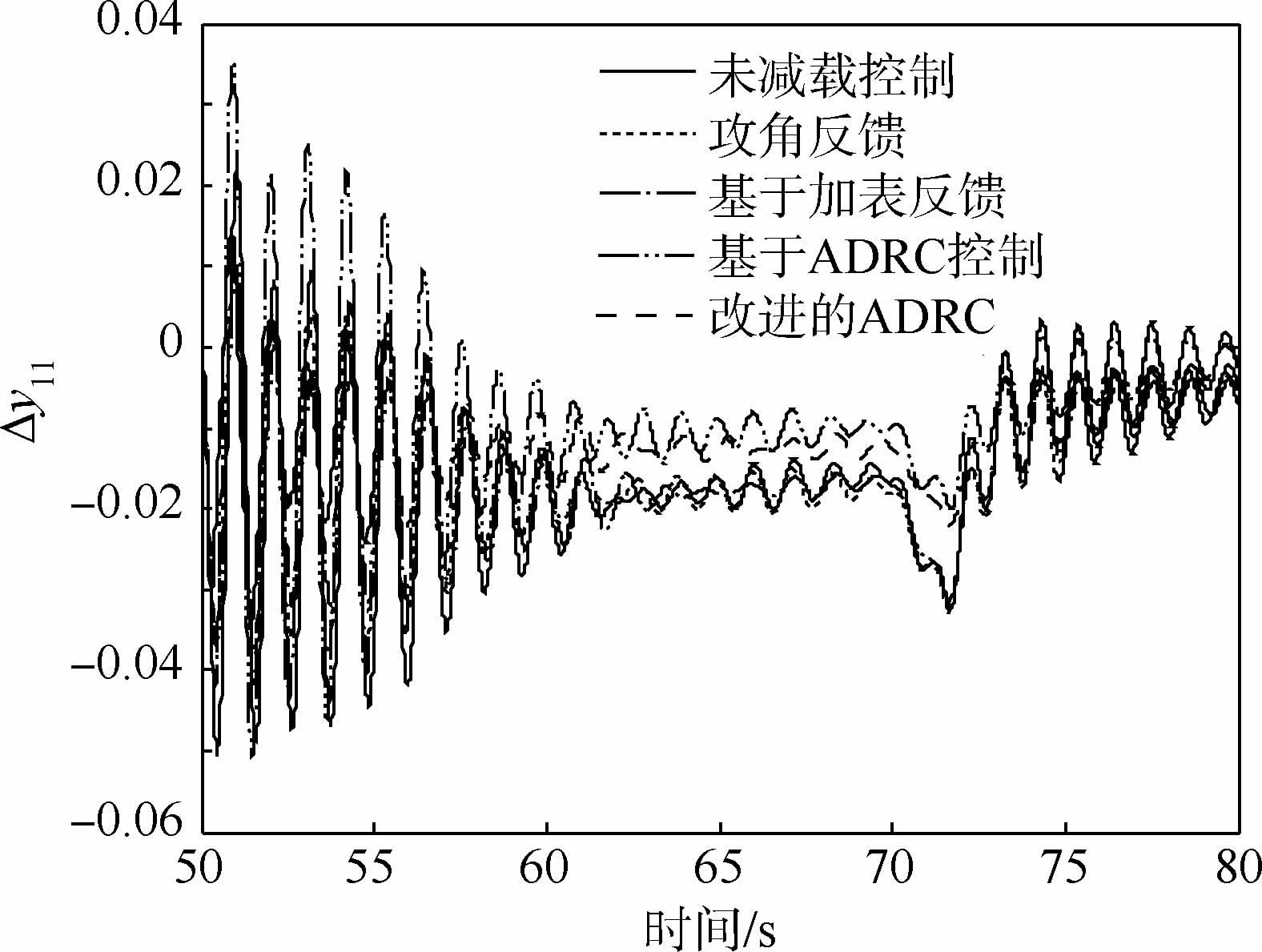| 图 12 1号贮箱一阶晃动随时间的变化Fig. 12 Time history of first order sloshing curves of the first tank |
| 图选项 |
 |
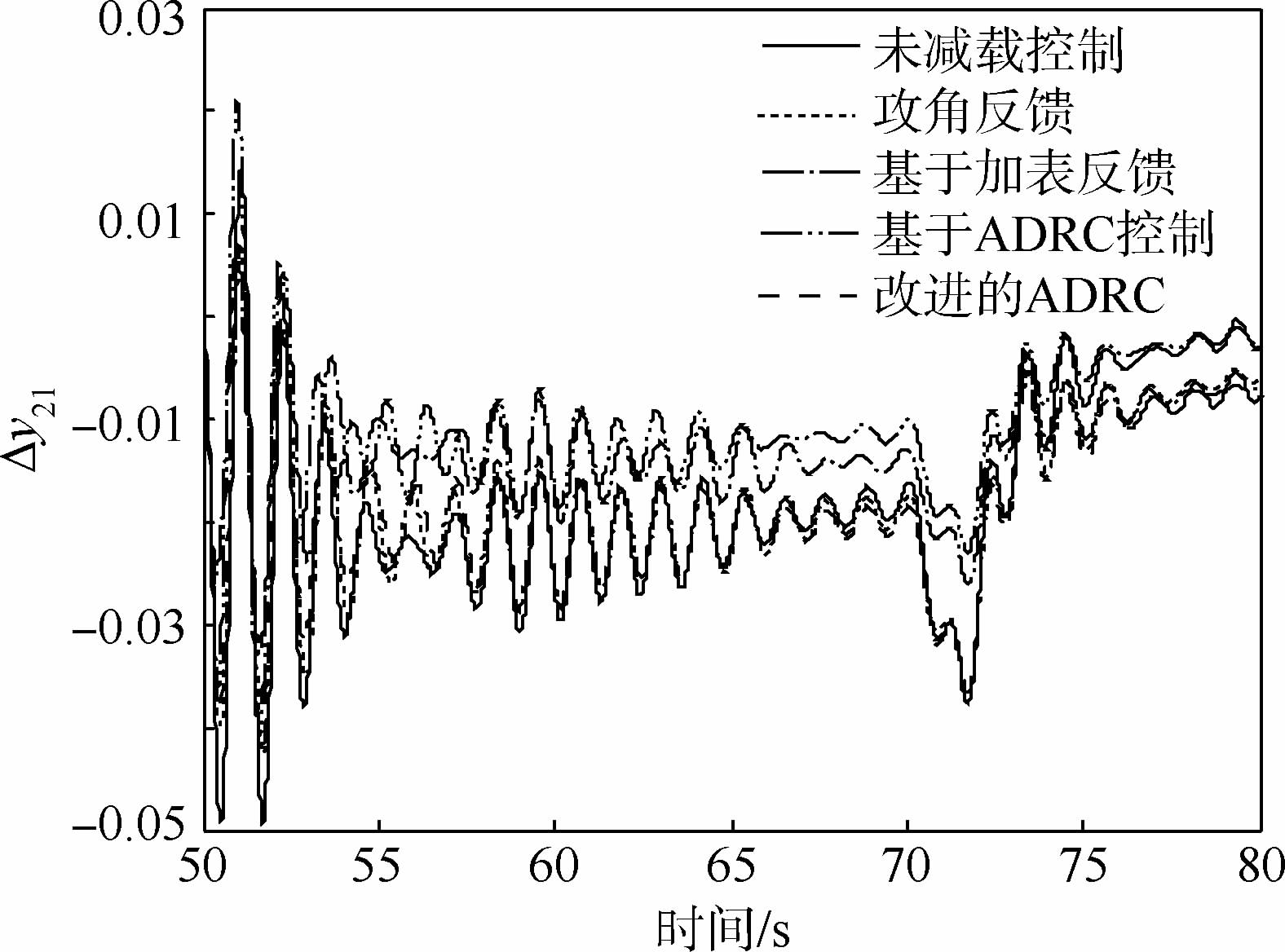| 图 13 2号贮箱一阶晃动随时间的变化Fig. 13 Time history of first order sloshing curves of the second tank |
| 图选项 |
仿真结果表明:使用ADRC进行液体运载火箭的飞行减载控制时,由于扩张状态观测器估计的误差包含了状态参数以及风载外的其他参数,飞行减载效果较差。经过改进后的ADRC控制器可以补偿干扰力矩等不确定因素的影响,稳定裕度由10.1 dB与31°分别变为11 dB与39.3°,满足鲁棒性裕度指标。同时,所设计的减载控制方程可以有效地抑制干扰作用,大幅度地提高了姿态角偏差的控制能力以及减载效果。
若定义控制系统对风载的补偿效果为:
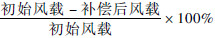,补偿效果如表 1所示。表 1 各种减载控制方法的补偿效果Table 1 Compensation effects under different load relief methods
| 减载方法 | 攻角反馈 | 加表反馈 | ADRC | 改进ADRC |
| 补偿效果/% | 19.41 | 13.57 | 5.06 | 22.41 |
表选项
5 结论1) 基于攻角传感器的飞行减载控制补偿效果达到19.41%,但受到测量精度及器件安装的影响,无法满足实际工程需求。采用加表反馈控制的运载火箭减载控制效果受到系统的稳定性的限制,仅能达到13.57%。
2) ADRC的发展为飞行减载控制提供了新的思路。但由于ADRC无法分辨观测误差的组成,同时并没有适应于减载的控制律,风载补偿效果仅为5.06%。
3) 使用本文所提出的控制器设计方法,一方面,扩展状态观测器与刚性状态观测器的配合使用不但增强了系统的抗干扰能力,还补偿了由于误差组成不确定性带来的干扰。另一方面,所推导设计的减载控制律大大增强了控制系统的减载控制能力,补偿效果由5.06%提高到22.41%。
参考文献
| [1] | EDINGER L D,SKELTON G B,STONE C R.Design of a load relief control system:NASA contractor report CR-61169[R].Washington,D.C.:NASA,1967:13-20. |
| [2] | DEATON A W,KELLY P B.Structural load reduction of the space shuttle booster/orbiter configuration using a load relief guidance technique:NASA technical report TM-X-64738[R].Washington,D.C.:NASA,1973:1-20. |
| [3] | 盖斯勒,成楚之.风对发射飞行器的影响[M].北京:国防工业出版社,1976:133-170. GEISSLER E D,CHENG C Z.Wind effects on launch vehicles[M].Beijing:National Defence of Industry Press,1976:133-170(in Chinese). |
| [4] | 李效明,许北辰,陈存芸.一种运载火箭减载控制工程方法[J].上海航天,2004,21(6):7-12. LI X M,XU B C,CHEN C Y.An engineering method on the control of decreasing load for a launch vehicle[J].Aerospace Shanghai,2004,21(6):7-12(in Chinese). |
| Cited By in Cnki (1) | Click to display the text | |
| [5] | GEORGE C.Design of a load relief control system:Honeywellreport 12013-QR2[R].Minnesota:Marshall Space Flight Center,1965:1-30. |
| [6] | MAUFFREY S,MEUNIER P.H∞ control for the Ariane 5 plus launcher[C]//52nd International Astronautic Congress.Toulouse:IAA,2001:1-9. |
| [7] | BLANCHET P,BARTOS B.An improved load relief wind model for delta launch vehicle[C]//39th Aerospace Sciences Meeting and Exhibit.Reston:AIAA,2001:1-8. |
| [8] | SHARP J.Attitude control system for load relief of Saturn-class launch vehicles:NASA contractor report CR-61375[R].Washington,D.C.:NASA,1971:13-17. |
| [9] | RENAULT C,SAUNOIS P.Launchers control architecture and synthesis with analytical loop shaping[C]//7th International ESA Conference on Guidance,Navigation,Control Systems.Tralee:GNC,2008:1-7. |
| [10] | SAUNOIS P.Comparative analysis of architectures for the control loop of launch vehicles during atmospheric flight[C]//European Conference for Aerospace Sciences (EUCASS).Toulouse:European Aeronautic Defence & Space Company,2005:1-8. |
| Click to display the text | |
| [11] | 宋征宇.运载火箭飞行减载控制技术[J].航天控制,2013,31(5):3-9. SONG Z Y.Load control technology in launch vehicle[J].Aerospace Control,2013,31(5):3-9(in Chinese). |
| Cited By in Cnki | |
| [12] | 韩京清.自抗扰控制技术[J].前沿科学,2007,1(1):24-31. HAN J Q.Auto disturbances rejection control technique[J].Frontier Science,2007,1(1):24-31(in Chinese). |
| Cited By in Cnki | Click to display the text | |
| [13] | 韩京清.自抗扰控制技术[M].北京:国防工业出版社,2008:183-280. HAN J Q.Active disturbance rejection control technique[M].Beijing:National Defence of Industry Press,2008:183-280(in Chinese). |
| [14] | BALAS M J,FROST S A.Robust adaptive control with disturbance rejection for linear infinite dimensional systems[C]//AIAA Guidance,Navigation,and Control Conference.Reston:AIAA,2012:1-10. |
| Click to display the text | |
| [15] | 徐延万.控制系统(上)[M].北京:宇航出版社,1989:430-470. XU Y W.Control system design[M].Beijing:Aerospace Press,1989:430-470(in Chinese). |
