经过自然界长期进化[2],蜘蛛织造的牵引丝是已知最强韧的材料,其强度和韧性远高于一般的生物材料,如骨头、筋腱、木材[3]。与高强度钢、芳纶、碳纤维等人造材料比,牵引丝的强度虽不及它们,但延展性却是它们的几倍,使得牵引丝的韧性也远大于一般的人造材料[4]。蜘蛛织造的另一种粘丝刚度极小,但延展率极高,最大应变可达300%[5]。牵引丝和粘丝都具有较大的粘滞效应,一个循环加载过程中的能量耗散高达65%[6, 7]。大部分蜘蛛圆网中,高强度和高韧性的牵引丝构建了网的径线和骨架,保证网不被轻易冲破;而易延展极柔顺的粘丝构建了网的周线,利于缠绕和容纳猎物[8]。2种丝线又都具有较强的能量耗散作用,能使猎物尽快静止下来。因此,2种丝线相互作用,使蜘蛛网的捕猎功能发挥至最大[9]。
可见,蜘蛛网是自然界中一种优良的拦阻结构,其轻质、简单的特点可启发设计新型柔性阻拦网,应用于轻型飞机的回收,飞船在太空中的防护和高空坠物的拦截等领域。然而前人更多地从进化和生态学的角度研究蜘蛛网[9, 10, 11],对于阻拦过程的力学问题却关注较少。Lin[12]和Ko[13]等曾分别利用OASYS DYNA和ABAQUS软件对蜘蛛网进行过有限元建模,研究了网在冲击作用下的响应,但没有给出网内丝线的应力-应变状态和能量耗散。Alam等[14, 15]利用ABAQUS软件对蜘蛛网进行有限元分析,给出了静态载荷下网内单元的应力状态,但没有涉及冲击载荷问题。
本文中,首先建立单根丝线受横向冲击时的力学模型,给出其动力学响应的理论解,同时采用LS-DYNA软件进行数值模拟,验证有限元方法的可靠性。然后,利用有限元方法对蜘蛛网阻拦猎物的过程进行模拟,揭示了阻拦过程中网内丝线的应力-应变状态和能量耗散问题,为今后仿生阻拦结构的设计提供借鉴和指导。
1 蜘蛛丝力学模型的建立蜘蛛丝只能受拉,Liu等[16]进行了径线在拉伸和循环加载下的实验,其应力-应变曲线如图 1所示。丝线的韧性T为单向拉伸时曲线下的面积:

式中:A1和A2分别如图 1所示,而丝线的粘滞效应H为循环载荷中丝线耗散的能量所占的比例:

如图 1所示,径线被拉伸时,初始段ab接近于直线,粘滞效应接近于0。当拉伸超过屈服点b后,应力应变曲线呈J型,如bc段所示。本文的目的是研究蜘蛛网的能量吸收,更关心丝线的韧性和粘滞效应,为简化分析,以极限应变为终点,将径线的应力-应变曲线拟合成斜率为E1和E2的2条直线,如图 1所示,保证直线E1、E2与原曲线abc底下面积相同,即保证接近拉伸极限时的韧性相同。径线重新加载时的路径与卸载路径相差很小,Denny[17]的实验也证明第2次循环加载丝线的粘滞效应明显下降,因此用同一条斜率为E3的直线来表示卸载和重新加载,保证粘滞效应相同,如图 1所示。当丝线重新加载超过卸载点后,应力-应变曲线与单调拉伸时重合,因此假定当重新加载至卸载点c后,将按照E2路径继续加载[18]。
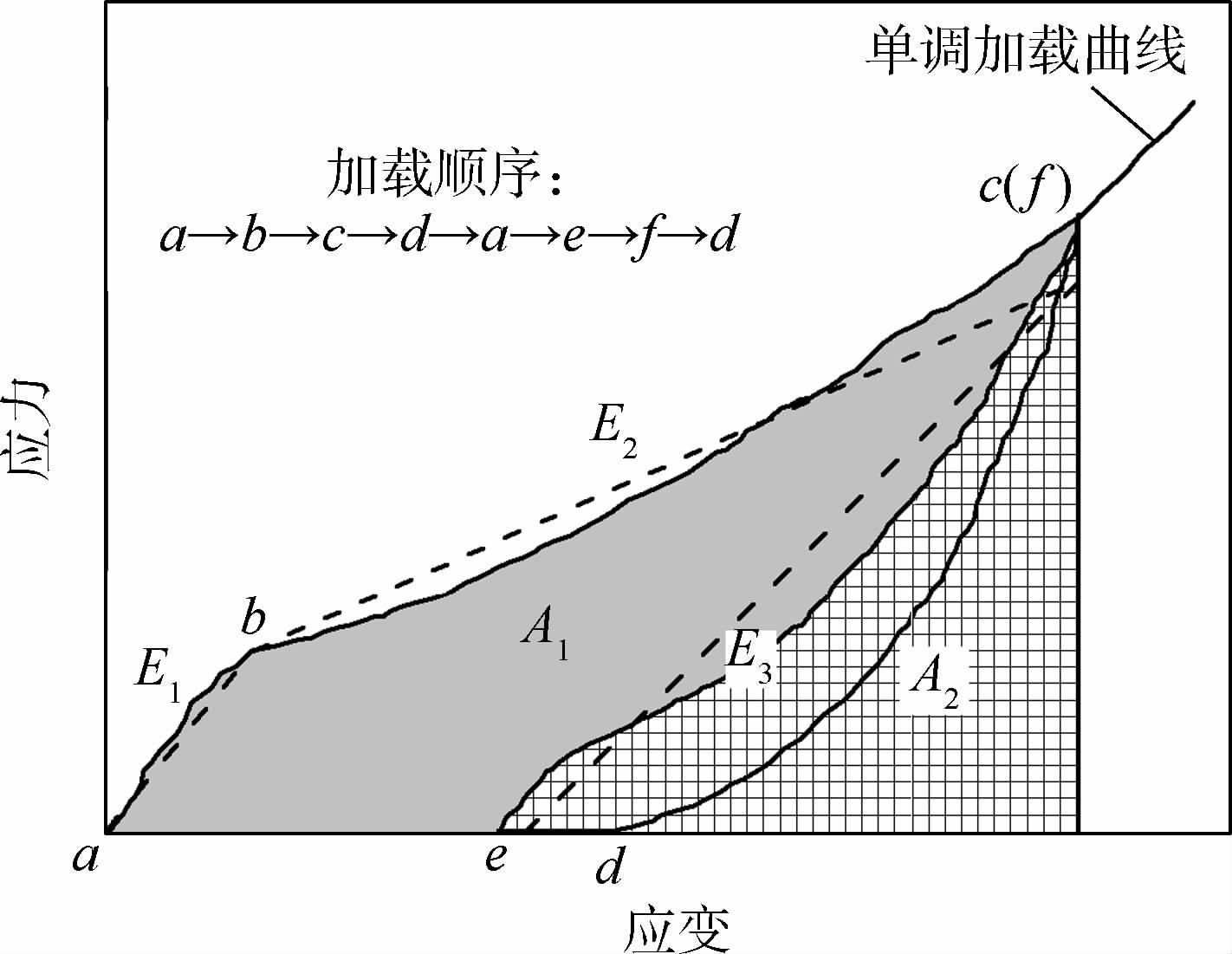 |
| 图 1 循环加载下径线的应力-应变曲线[16] Fig. 1 Stress-strain curves of radial silk under cyclic test[16] |
| 图选项 |
基于Gosline等[8]提供的十字园蛛径线的力学参数,如表 1所示,可给出径线应力-应变关系的拟合表达式:

式中:σ为材料应力;ε为材料应变;εy为材料屈服应变。
表 1 十字园蛛径线和周线拉伸时的力学参数[8] Table 1 Tensile mechanical parameters of Araneus diadematus silk[8]
| 力学 属性 | 初始刚度/ GPa | 极限强度/ GPa | 极限 应变 | 韧性/ (MJ·m-3) | 粘滞效应/ % |
| 径线 | 10 | 1.1 | 0.27 | 160 | 65 |
| 周线 | 0.003 | 0.5 | 2.7 | 150 | 65 |
表选项
周线的应力-应变曲线呈J形,可采用多项式幂函数拟合[12, 19]: σ=a(ε+bεn) 0 <ε<2.7(5)
基于表 1的数据,可确定式(5)中的参数,加载时:a=3,b=0.033 6,n=8.55;卸载时:a=3,b=22.97,n=10.83。
由于实验中均采用工程应力和工程应变[8, 16],式(3)~式(5)中的σ和ε均代表工程应力和工程应变。依据式(3)~式(5)建立的径线与周线的应力-应变关系如图 2所示。
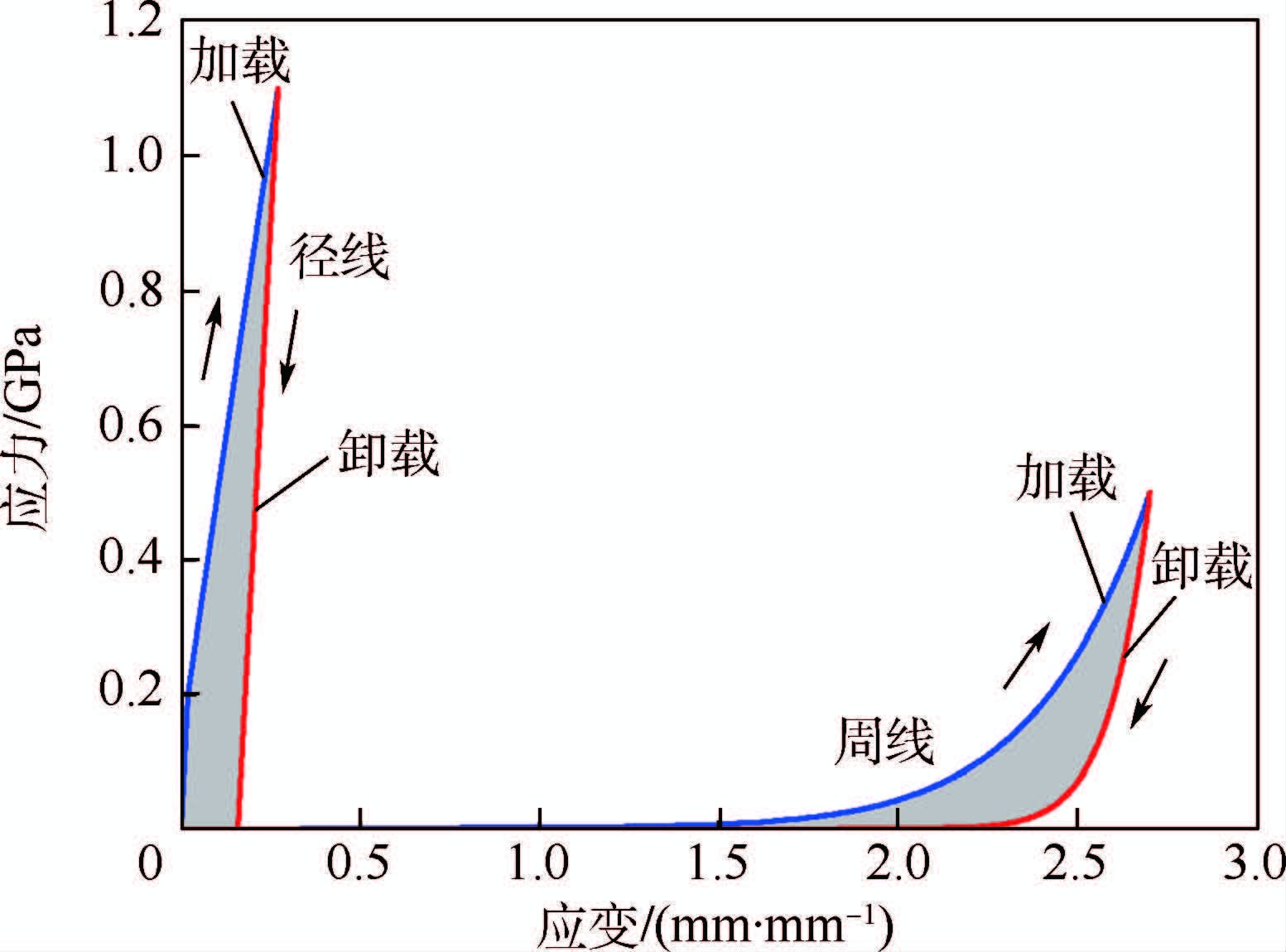 |
| 图 2 径线与周线的应力-应变关系 Fig. 2 Stress-strain relationships of radial and spiral silks |
| 图选项 |
2 单根丝线受横向冲击2.1 力学模型一根横截面积为As、线长为2L的径线蜘蛛丝受到质量为m的昆虫,以初速度v0的对称撞击,丝的两端固定,如图 3所示。通常情况下,猎物触网后会被粘附并随网振荡,因此将昆虫等效为一个质量为m的质点以初速度v0撞击丝的中点,随后粘附在中点一起振荡。
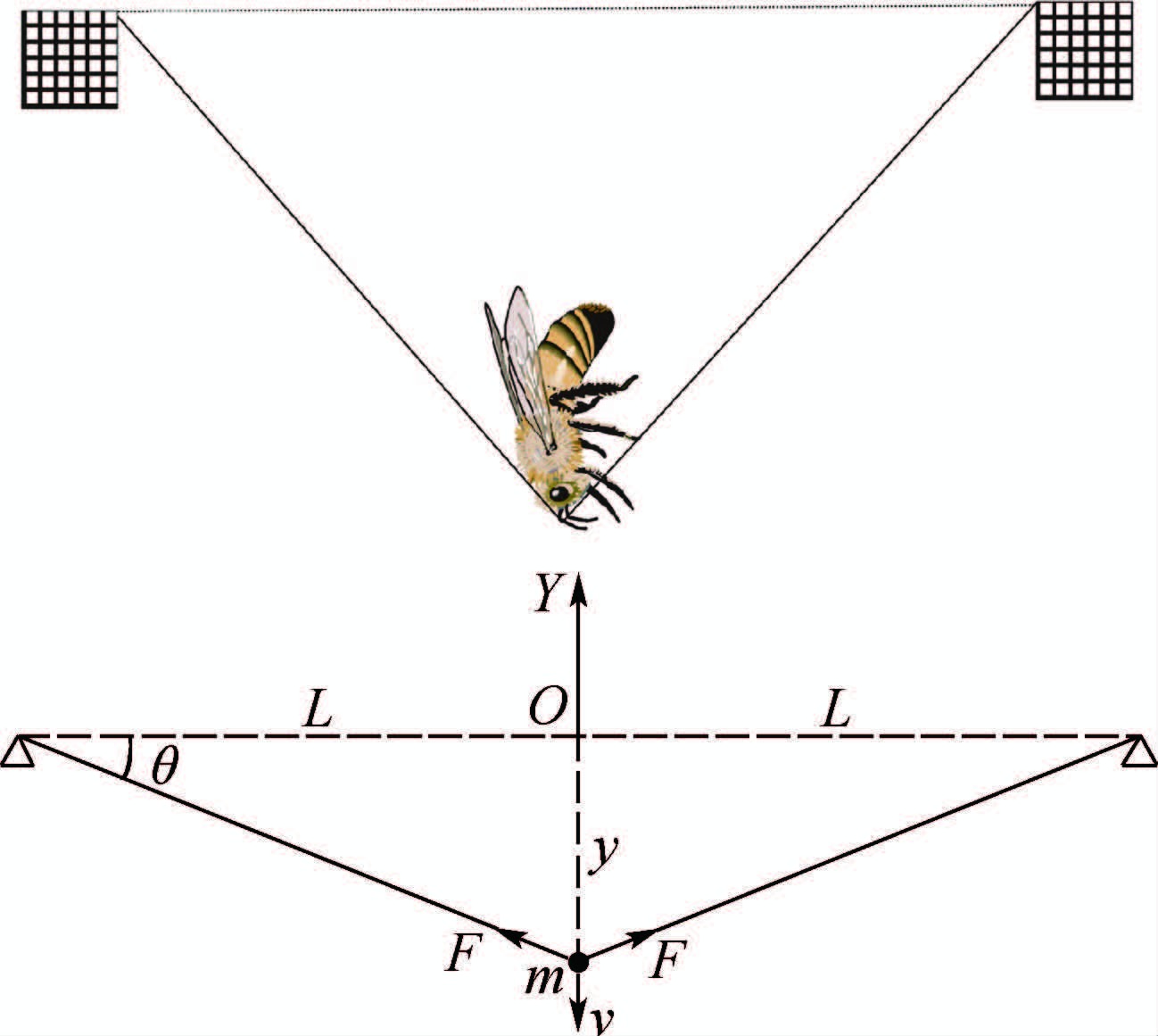 |
| 图 3 单根丝线受昆虫横向撞击模型 Fig. 3 Model of a single silk thread subjected to transverse insect impact |
| 图选项 |
坐标系如图 3所示,由几何分析可知

式中:y为质点竖直位移;θ为丝线与水平线的夹角(顺时针为正)。
丝线长度的改变量为

因此,丝线的应变为

径线的本构关系如式(3)和式(4)所示,可见无论加卸载,丝线的应力和应变总是呈线性关系,因此丝线的应力σ可统一表示为

式中:E和S为常数,根据不同的加卸载状态确定。
将表达式(8)代入式(9),得

式中:B=S-E。
忽略重力和丝线的质量,丝线的动力学方程为

以角度θ为变量时,得到微分方程:

2.2 理论求解现求解方程式,首先作变量替换:

则有
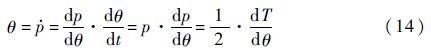
因此,方程式(12)变为以θ为自变量的一阶线性微分方程:
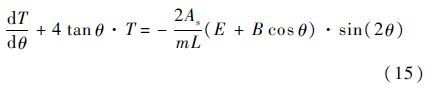
可解出:
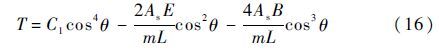
联系变量替换式(13),可得时间t为
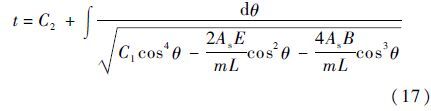
式(17)是单根径线受横向冲击时的理论解,其中微分方程解中的常数C1和C2由初始条件决定。单根径线受横向冲击的动力学响应会经历不同的阶段(见第2.3节),该问题的初始条件y=0,y·=v0仅适用于第1阶段,之后阶段的初始条件由前一阶段结束时的状态决定。
2.3 动力学响应分析单根径线受冲击后的动态响应如图 1所示,其可分为3个阶段。
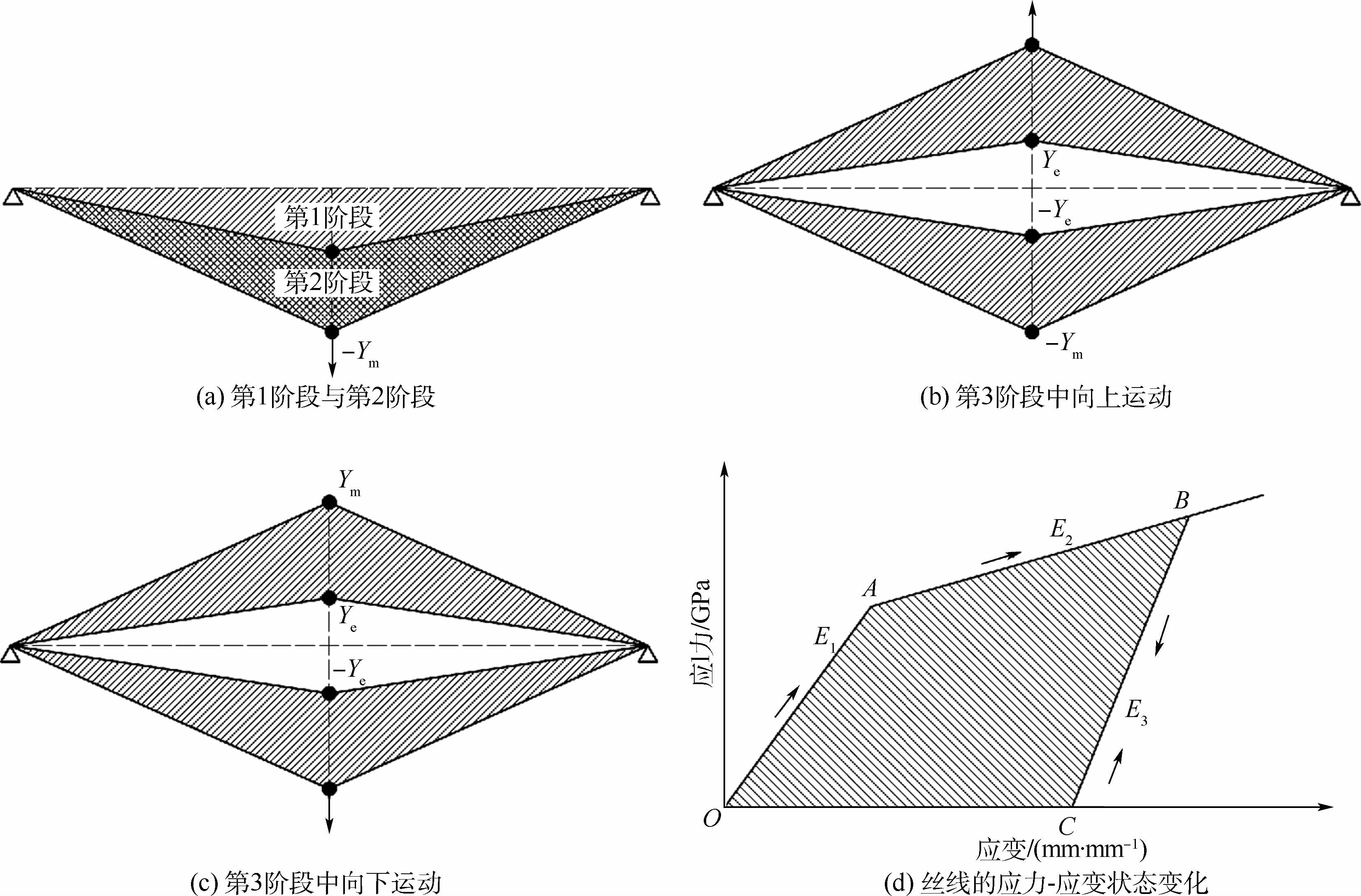 |
| 图 4 单根径线在横向冲击下的动态响应 Fig. 4 Dynamic response of a single radial silk under transverse impact |
| 图选项 |
第1阶段:质点向下运动,丝线沿应力-应变曲线E1段被拉伸,直至到达屈服点A,如图 4(a)和图 4(d)所示。
第2阶段:质点继续向下运动,丝线沿E2段被拉伸,直至到达点B,此时质点速度减为0,位置为-Ym,准备反向运动,如图 4(a)和图 4(d) 所示。
第3阶段:质点向上运动,丝线沿E3段卸载,直至卸载到C点,此时质点位置设为-Ye,之后丝线处于无应力状态,如图 4(b)和图 4(d) 所示。质点继续向上运动至对称位置Ye,丝线从C点开始沿E3段重新加载,直至质点速度再次降为0。然后,质点将再次向下运动,经历与向上运动类似的过程,系统处于持续振荡状态,如图 4(c)所示。第3阶段中丝线不断地加载和卸载始终沿着E3段,且由于没有外界能量输入,丝线的拉伸状态将不会超过初始卸载点B,这意味着振荡过程中不再产生新的能量耗散,质点的向上最大位置与向下最大位置保持对称,如图 4(b)和图 4(c)中的Ym与-Ym。
2.4 有限元求解对于该问题,同时采用有限元软件进行数值模拟,计算工况均与第1节的理论模型一致。考虑到丝线只能受拉的特性,使用LS-DYNA中的Seatbelt单元对丝线建模。Seatbelt单元是专为汽车安全带设计的计算单元,只能产生拉应力,并考虑了卸载。质点位移响应的理论预测值与有限元数值解结果对比如图 5所示。可以看二者吻合得很好,验证了有限元方法的可靠性。响应后期略有差异,可能是Seatbelt单元固有的粘性造成的。
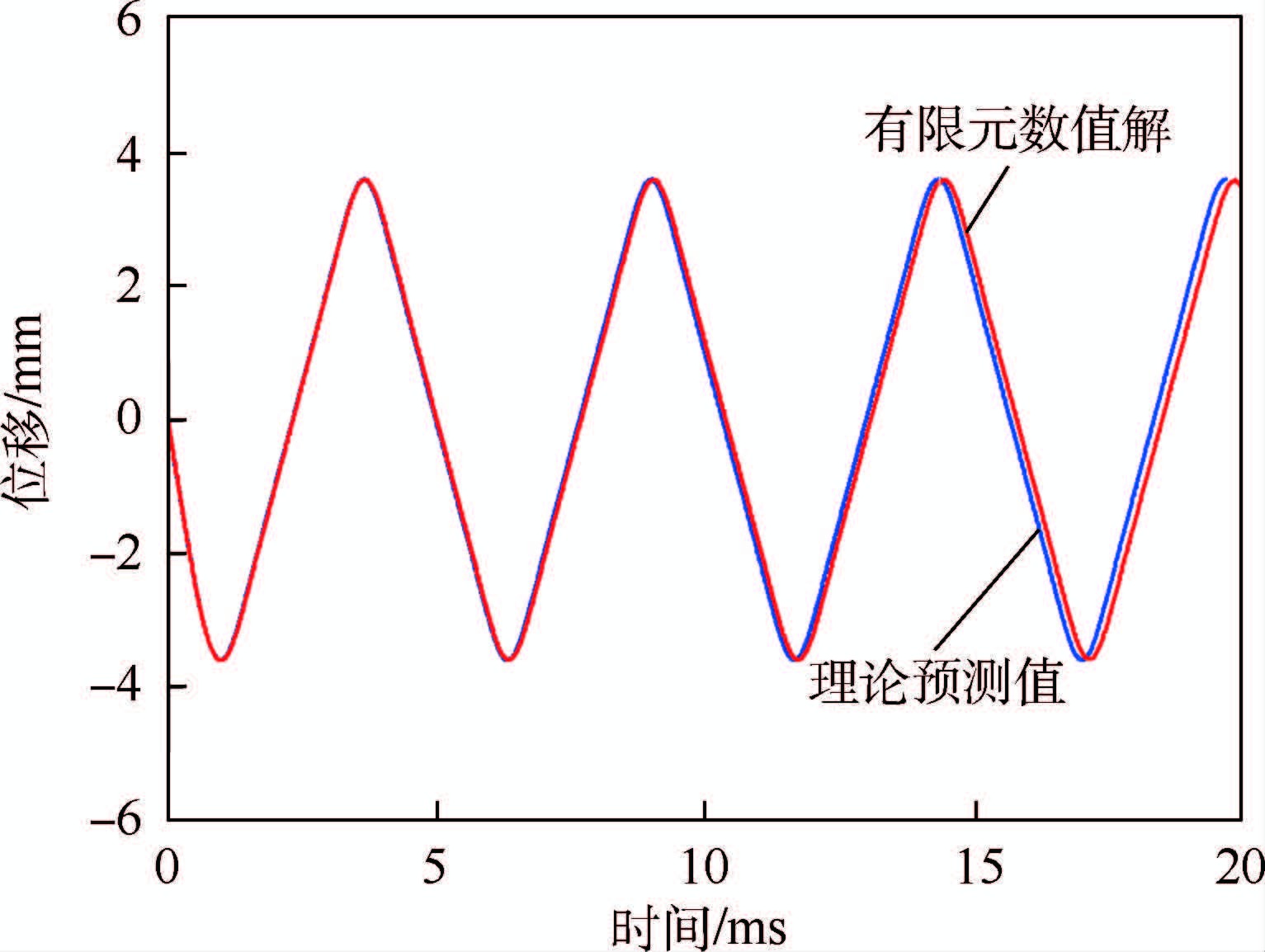 |
| 图 5 质点撞击单根径线时的位移 Fig. 5 Displacements of a single radial silk under concentrated mass impact |
| 图选项 |
3 蜘蛛网整网模型基于前面的有限元方法,本节中将模拟蜘蛛网受冲击载荷时的动态响应,有限元模型如图 6所示,圆网直径21 cm,径线16 根,周线15根,周线间距5 cm,丝线直径约5 μm,所有径线在网的中部汇聚成一点,另一端采用固定约束。径线与周线使用Seatbelt单元建模,其材料力学性质如图 2所示。网的几何参数和丝的力学性质与已有实验一致[20],在该实验中,松木块以180 μJ的初始动能撞击圆网并随网振荡,撞击时松木块仅与一条径线和一条周线相碰。为了模仿该过程,有限元中使用一个质量为90 mg的集中质量以2 m/s的速度横向撞击网内的节点,如图 6所示,随后粘附在该点并随网振荡。
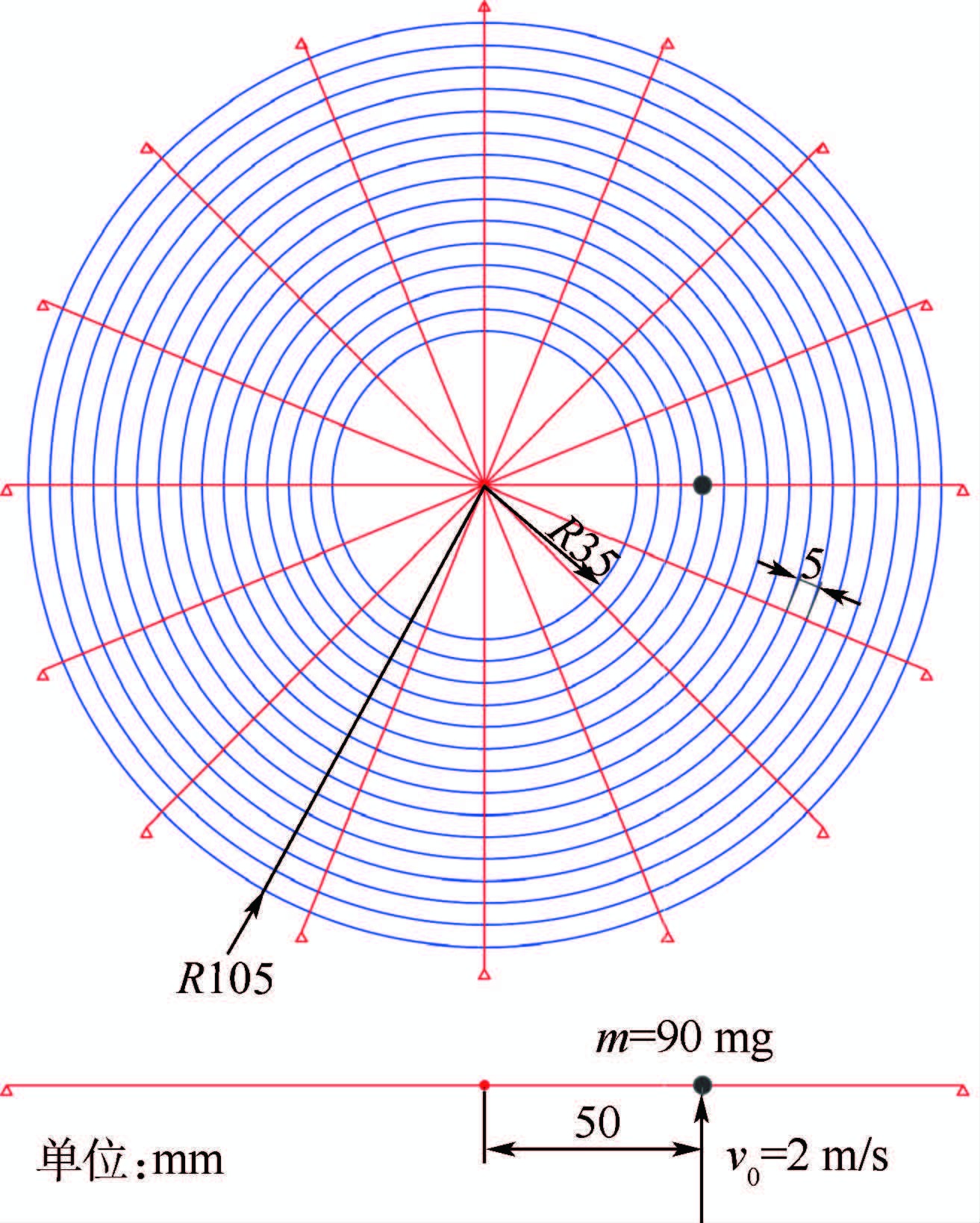 |
| 图 6 蜘蛛网的有限元模型 Fig. 6 Finite element model of spider web |
| 图选项 |
3.1 应力和应变网内丝线的最大应力和应变出现在撞击点处的丝线内,其应力-应变历程如图 7所示。可以看出,周线的应变大于径线,但应力却远小于径线,这是因为周线的延展率极好,初始阶段的刚度比径线小3个数量级,因此应力水平很低。对于网内丝线的最大应变,有限元结果与实验结果基本一致[20],如表 2所示,证明了有限元整网模型的准确性。
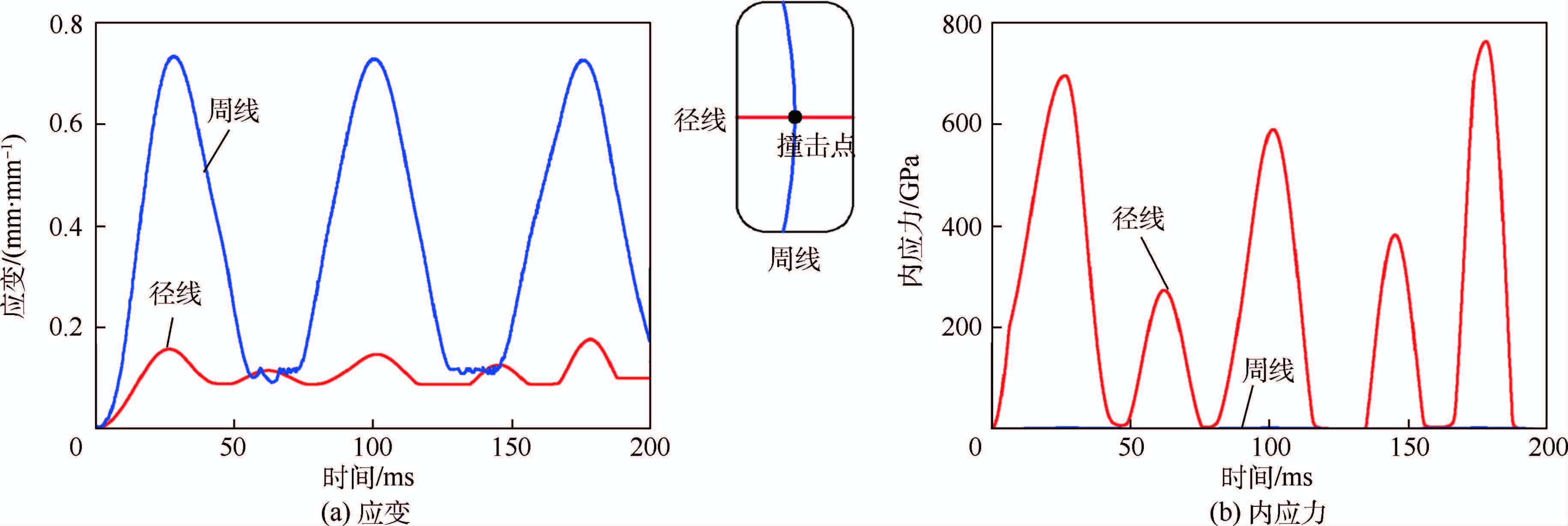 |
| 图 7 撞击处的径线和周线内应力和应变的时间历程曲线 Fig. 7 Time-history curves of internal stress and strain in radial and spiral silks at impact point |
| 图选项 |
表 2 网内丝线最大应变Table 2 Maximal strain of silks in web
| 计算方法 | 网内丝线最大应变/(mm·mm-1) | |
| 径线 | 周线 | |
| 实验 | 0.120 | 0.800 |
| 有限元 | 0.176 | 0.734 |
表选项
分别以撞击点处的径线和周线内的最大应力为基本单位,设为1.00,对撞击点相邻径线和周线内的应力进行无量纲化,如图 8所示,可见与撞击点相邻的径线应力较小,而相邻的周线应力较大。这说明冲击对径线的影响被局限在撞击点处的径线内,撞击点周围的径线不易破损,而周线受冲击的影响范围相对较大,周围的周线容易破损。这有利于蜘蛛网的修复,因为径线与外部相连,是维持网形状的骨架,不易修复,而周线仅连接径线,修复难度小。基于冲击对周围丝线的影响,预测撞击时物块接触的径线越多,蜘蛛网的吸能能力就越强,但接触的周线数增加对网的吸能能力影响不大,这也与前人的实验结果相符[20]。
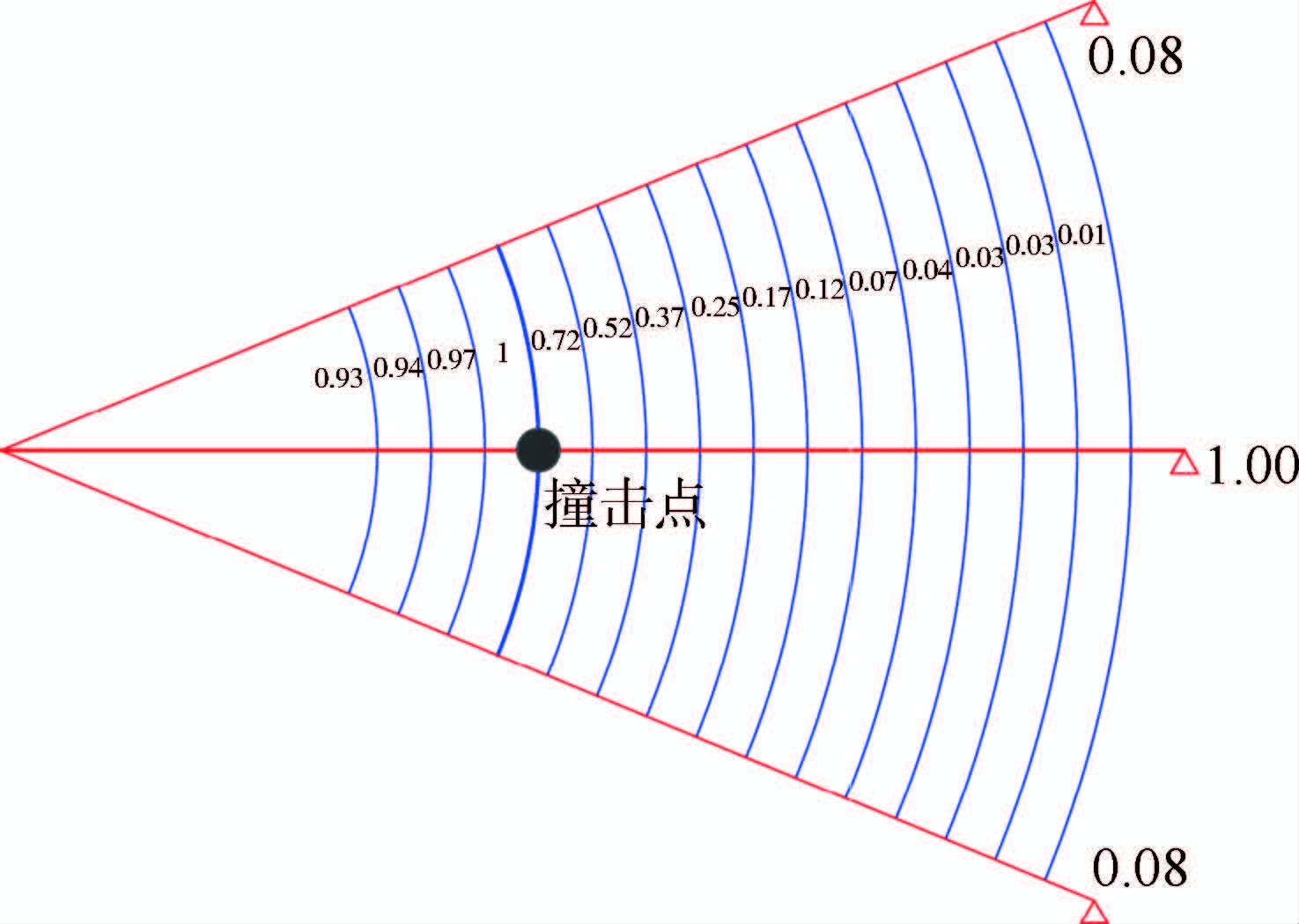 |
| 图 8 撞击点周围丝线与撞击点处丝线应力水平的 无量纲化比较 Fig. 8 Comparison of normalized stress in silks around and at impact point |
| 图选项 |
3.2 能量耗散有限元结果中,撞击物的动能、径线和周线的耗能和已有的实验结果相比[20],变化趋势是一致的,数值大小是基本吻合的,如图 9(a)所示。可以看出,阻拦猎物过程中,径线占据能量耗散的主导地位,周线耗能所占比例较小,这一点也与实验结果一致[20]。仿真中,撞击物动能大于实验结果且波动较大,是因为有限元模型中未考虑空气阻力的作用;而周线耗能总是小于实验结果,是因为实验中物块在网内会被柔顺的周线缠绕,在大变形情况下周线的粘滞效应将会显著增强,将物块等效成集中质量后无法考虑这一因素。
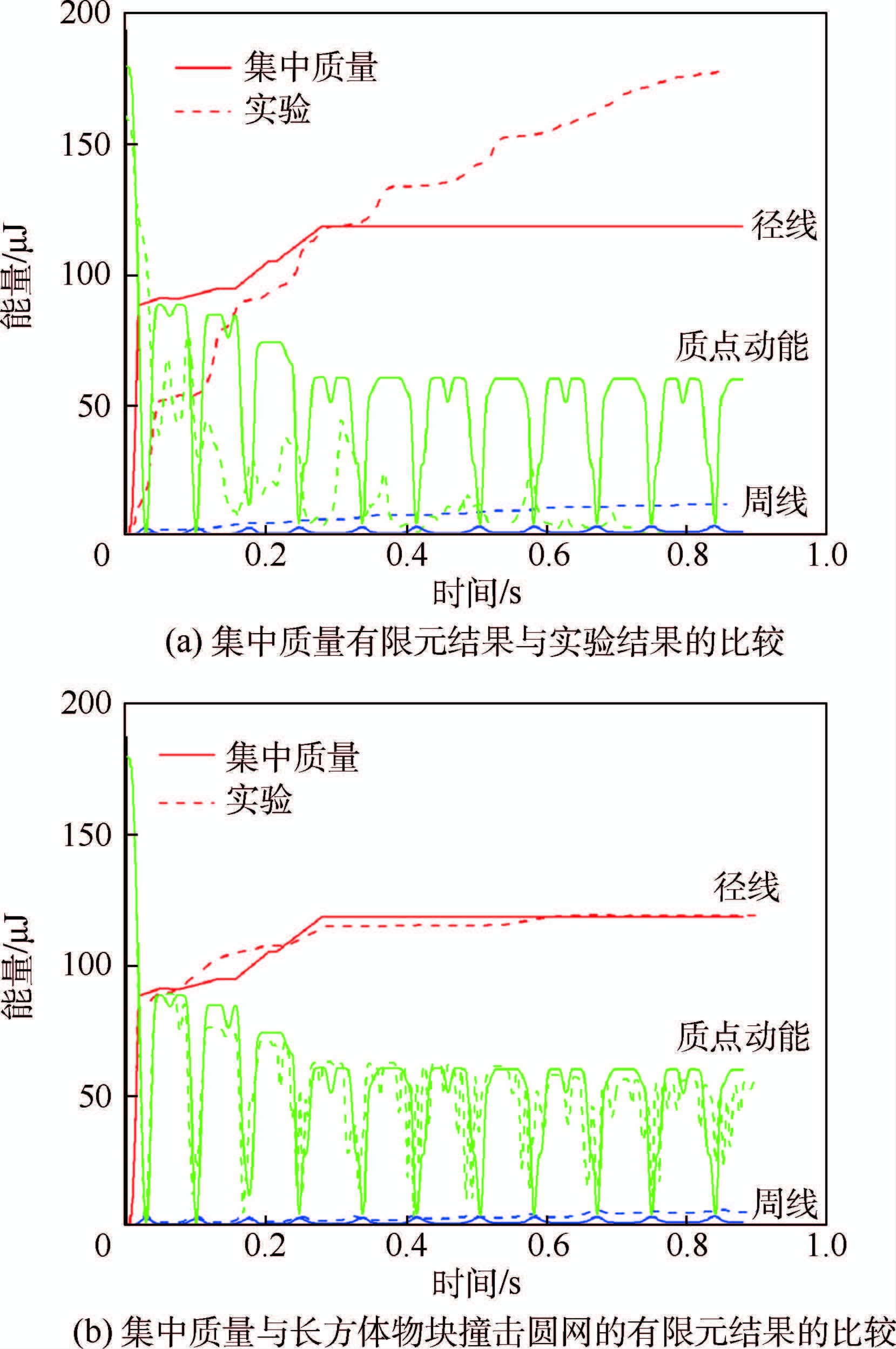 |
| 图 9 网内能量的时间历程曲线 Fig. 9 Time-history curves of energy in web |
| 图选项 |
为考察撞击物尺寸对能量耗散的影响,使用有限元方法模拟16 mm×6 mm×2.5 mm的长方体以相同的初始动能撞击相同的位置,其结果如图 9(b)所示。与集中质量相比,长方体撞击时径线耗能的时间历程有微小变化,但总量相同,而周线耗能量稍有增加,这是因为仿真中会产生一定的缠绕。但该模型仍不足以完整地模拟出周线的缠绕现象,因此有限元预测仍低估了周线的耗能量。另外,材料应力-应变曲线拟合过程中参数的选取可能也会对此造成一定误差。
3.3 撞击位置撞击初始动能越大,网被冲破的危险就越大,将蜘蛛网临近被冲破时的撞击动能称为临界动能,在有限元模型中考察不同撞击位置对临界动能的影响。由于模型是中心对称的,仅考察撞击径线不同位置时的临界动能,如图 10所示。可以看出,径线中点附近的区域(图中阴影区域)有能力捕捉初始动能更大的猎物,而圆网外边界区域对猎物的阻拦能力有限,因此推测圆网沿径线的中间区域是蜘蛛网拦截猎物的主要区域。
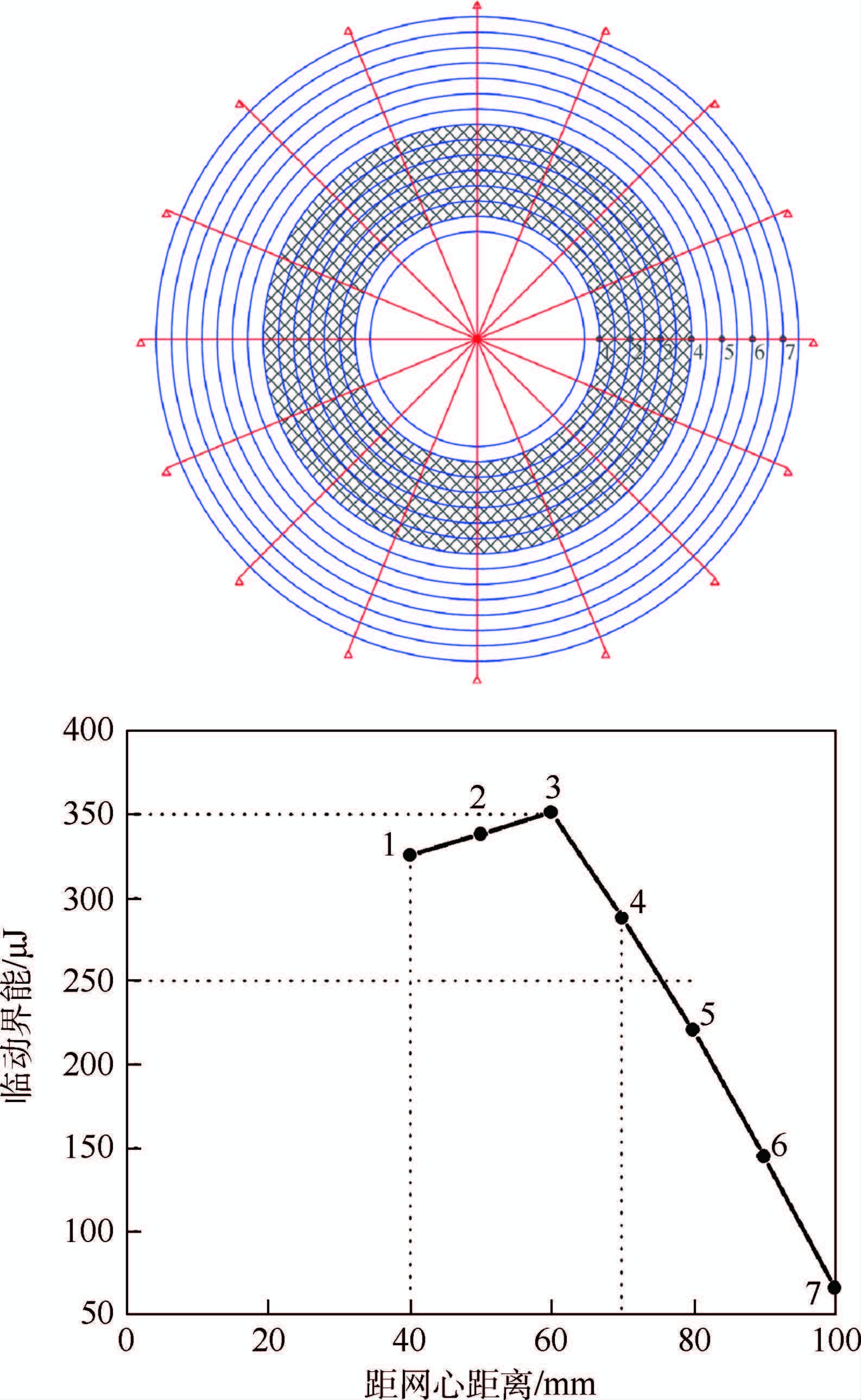 |
| 图 10 撞击位置对临界动能的影响 Fig. 10 Effects of impact position on critical kinetic energy |
| 图选项 |
4 结 论本文中的有限元模型是初步的,与实际情况还有一定差距,但该模型还是能较好地模拟蜘蛛网阻拦猎物的过程,结果表明:
1) 冲击过程中,径线的应力水平较高而周线应力水平较低,这与2种线不同的力学性质有关。猎物对网的冲击影响被局限在一定区域内,尤其对于径线,未被撞击的径线应力很小。
2) 径线在对猎物动能的耗散中占主导地位,周线在阻拦阶段对总耗能的贡献很小,这一点与已有实验结果相符。
3) 径线中点附近区域阻拦初始动能较大的猎物的能力最强,是蜘蛛网拦截和捕食的主要区域。
通过这一研究,揭示了蜘蛛网阻拦猎物过程的内在力学规律,可为新型柔性阻拦结构的设计提供指导。
参考文献
| [1] | FOELIX R F.Biology of spiders[M].2nd ed.New York:Oxford University Press,1996:330-332. |
| [2] | BLACKLEDGE T A,KUNTNER M,AGNARSSON I.The form and function of spider orb webs:Evolution from silk to ecosystems[J].Advances in Insect Physiology,2011,41:175-262. |
| Click to display the text | |
| [3] | GOSLINE J,LILLIE M,CORRINGTON E,et al.Elastic proteins:Biological roles and mechanical properties[J].Philosophical Transaction of the Royal Society B,2002,357(1418):121-132. |
| Click to display the text | |
| [4] | VOLLRATH F,PORTER D.Silks as ancient models for modern polymers[J].Polymer,2009,50(24):5623-5632. |
| Click to display the text | |
| [5] | SWANSON B O,BLACKLEDGE T A,HAYASHI C Y.Spider capture silk:Performance implications of variation in an exceptional biomaterial[J].Journal of Experimental Zoology,2007,307A(11):654-666. |
| Click to display the text | |
| [6] | OMENETTO F G,KAPLAN D L.New opportunities for an ancient material[J].Science,2010,329(5991):528-531. |
| Click to display the text | |
| [7] | KELLY S P,SENSENIG A,LORENTZ K A,et al.Damping capacity is evolutionarily conserved in the radial silk of orb-weaving spiders[J].Zoology,2011,114(4):233-238. |
| Click to display the text | |
| [8] | GOSLINE J M,GUERETTE P A,ORTLEPP C S,et al.The mechanical design of spider silk:From fibroin sequence to mechanical function[J].Journal of Experimental Biology,1999,202(23):3295-3303. |
| Click to display the text | |
| [9] | HARMER A M T,BLACKLEDGE T A,MADIN J S,et al.High-performance spider webs:Integrating biomechanics,ecology and behavior[J].Journal of Royal Society Interface,2011,8(57):457-471. |
| Click to display the text | |
| [10] | SENSENIG A,AGNARSSON I,BLACKLEDGE T A.Behavioural and biomaterial coevolution in spider orb webs[J].Journal of Evolutionary Biology,2010,23(9):1839-1856. |
| Click to display the text | |
| [11] | TARAKANOVA A,BUEHLER M J.The role of capture spiral silk properties in the diversification of orb webs[J].Journal of Royal Society Interface,2012,9(77):3240-3248. |
| Click to display the text | |
| [12] | LIN L H,EDMONDS D T,VOLLRATH F.Structural engineering of an orb-spider's web[J].Nature,1995,373(6510):146-148. |
| Click to display the text | |
| [13] | KO F K,JOVICIC J.Modeling of mechanical properties and structural design of spider web[J].Biomacromolecules,2004,5(3):780-785. |
| Click to display the text | |
| [14] | ALAM M S,JENKINS C H.Damage tolerance in naturally compliant structures[J].International Journal of Damage Mechanics,2005,14(4):365-384. |
| Click to display the text | |
| [15] | ALAM M S,WAHAB M A,JENKINS C H.Mechanics in naturally compliant structures[J].Mechanics of Materials,2007,39(2):145-160. |
| Click to display the text | |
| [16] | LIU Y,SHAO Z Z,VOLLRATH F.Elasticity of spider silks[J].Biomacromolecules,2008,9(7):1782-1786. |
| Click to display the text | |
| [17] | DENNY M. The physical properties of spider's silk and their role in the design of orb-webs[J].Journal of Experimental Biology,1976,65(2):483-506. |
| Click to display the text | |
| [18] | VEHOFF T,GLISOVIC A,SCHOLLMEYER H.Mechanical properties of spider dragline silk:Humidity,hysteresis and relaxation[J].Biophysical Journal,2007,93(12):4425-4432. |
| Click to display the text | |
| [19] | LIN L H,SOBEK I W.Structural hierarchy in spider websand spider web type systems[J].The Structural Engineer,1998,76(4):59-64. |
| [20] | SENSENIG A T,LORENTZ K A,KELLY S P,et al.Spider orb webs rely on radial threads to absorb prey kinetic energy[J].Journal of Royal Society Interface,2012,9(73):1880-1891. |
| Click to display the text |
