?三维编织复合材料作为一种以整体编织预成型件为承载体的材料,在制造过程中不需要二次加工,保证了内部承载纤维的连续性,具有较高的刚度、强度以及较好的抗冲击性和损伤容限,因此三维编织复合材料在航空航天等高技术领域的应用日益广泛。
针对三维编织复合材料力学性能的试验和理论研究早在20世纪80年代就已经展开,****们通过对细观编织结构的研究建立了一系列的理论预测模型^{[1, 2]},经过不断地改进和完善,这些模型目前已经能够对三维编织复合材料的弹性性能做出较为准确的预测^{[3, 4, 5]}。强度性能方面,目前主要是基于三维编织复合材料周期性单胞在细观层面上进行有限元预测^[6],研究者们基于单胞模型将复合材料损伤力学引入纤维纱线和树脂基体中^[7],通过对单胞进行非线性有限元模拟得到其在指定载荷条件下的极限应力^{[8, 9]}。但是通过单胞计算得到的细观强度性能并不能直接用于预测三维编织复合材料结构件的极限承载能力,对于非标准形状的三维编织复合材料结构件仍需建立一套宏观强度性能分析方法。对于宏观结构件强度性能的研究工作目前进行的较少,相比较于传统层合复合材料而言,尚未形成一个获得广泛认可的针对三维编织复合材料的强度准则。在单胞性能研究的基础上,Guo等^[10]对三维编织连接接头进行了有限元分析,对比了不同编织参数下的接头最大主应力和最大主应变。Zhou和Zhuang^[11]对三维编织复合材料T型结构件进行了强度性能分析,分析过程中引入了Tsai-Hill准则作为结构件的宏观材料强度准则。Wu等^[12]采用桥联模型和临界损伤面积理论对三维编织复合材料在弯曲载荷作用下的渐进失效过程进行了模拟,预测了宏观材料的极限承载能力。
复合材料连接技术尤其是机械紧固件连接技术是复合材料成为承载结构件的一项关键技术^[13]。传统的金属紧固件在与复合材料结构连接时会导致电化腐蚀、应力腐蚀、金属疲劳等并可能产生一定的电磁信号,在特定工作条件下会对结构件的抗疲劳和抗腐蚀性能造成很大的影响。复合材料机械连接紧固件相对于金属紧固件拥有更好材料匹配性,在一些特定的复合材料结构中已经得到了广泛应用^[14]。目前针对复合材料紧固件的研究主要集中在碳基以及陶瓷基复合材料为主的高温复合材料连接件上^{[15, 16, 17]},这些复合材料紧固件大都采用细编穿刺等工艺首先制备出毛坯,再通过机械加工最终成型,而三维编织工艺可以通过合理设计成型截面形成接近于圆柱形的预制件,再通过模具成型,无需二次机械加工成型,保证了试件内部纤维的连续性。
本文针对三维全五向编织复合材料圆柱销紧固件的双剪性能进行了试验和有限元模拟研究,在前期研究工作的基础上采用了Tasi-Hill强度准则并引入了连续介质损伤理论建立了针对三维编织复合材料的宏观强度性能分析方法,并使用该方法对三维编织复合材料圆柱销试件在双剪载荷作用下的极限承载能力和损伤演化过程进行了有限元数值分析模拟,通过与试验结果的对比,验证了三维编织复合材料强度分析方法和有限元模型的有效性,为三维编织复合材料圆柱销在实际工程中的运用提供了参考。
1 试 验1.1 试验件制备试验所使用的三维编织复合材料圆柱销直径为6 mm,纤维原料为玻璃纤维,固化树脂为以环氧TDE85为主体材料的树脂传递模塑(RTM)环氧树脂体系。试验件制备过程中首先采用三维全五向编织工艺将纤维束编织成横截面接近圆形的预制件,然后依靠RTM工艺进行模具成型,最终制成圆柱形试件。试验件工艺参数如表 1所示。
表 1 圆柱销试验件编织工艺参数Table 1 Braiding parameters of straight pin specimens

工艺参数	数值
纤维束k数/k	10
表面编织角β/(°)	30.8
内部编织角γ/(°)	50
花节长度h/mm	5
纤维体积含量/%	52

表选项


1.2 试验方案试验参考GJB 715.26A-2008《紧固件试验方法 双剪》相关标准^[18]进行试验件的剪切测试。试验过程中采用INSTRON 8801伺服液压测试系统进行加载,试验加载装置如图 1所示。三维编织复合材料圆柱销剪切强度计算式为
式中:D为圆柱销直径;F为圆柱销双剪试验载荷。

图 1 剪切试验加载装置 Fig. 1 Loading device of shear test

图选项

2 数值模拟分析2.1 几何模型三维编织复合材料内部编织结构具有周期性的特征,因此可以通过选取编织结构内部具有周期性分布特征的最小结构单元来表征三维编织复合材料的材料特性。三维全五向编织复合材料的周期性单胞如图 2所示,由图可知,三维全五向编织复合材料由轴向纱、编织纱以及树脂基体3部分构成,其中轴向纱和编织纱由纤维和树脂基体合成,可以看作具有横观各向同性性质的单向复合材料柱体,而树脂基体可以看作是各向同性材料。轴向纱主方向均沿编织方向而根据编织路径的不同,编织纱一共有4个主方向,根据三维全五向编织复合材料周期性单胞内部编织结构的几何关系,可以得到轴纱和不同主方向的编织纱在单胞中的体积分数分别为
式中:A为周期性单胞的单胞宽度;V_ia为轴向纱的体积分数;V_ib1、V_ib2、V_ib3和V_ib4为4个主方向编织纱的体积分数；S_a和S_b分别为轴纱和编织纱的截面面积。

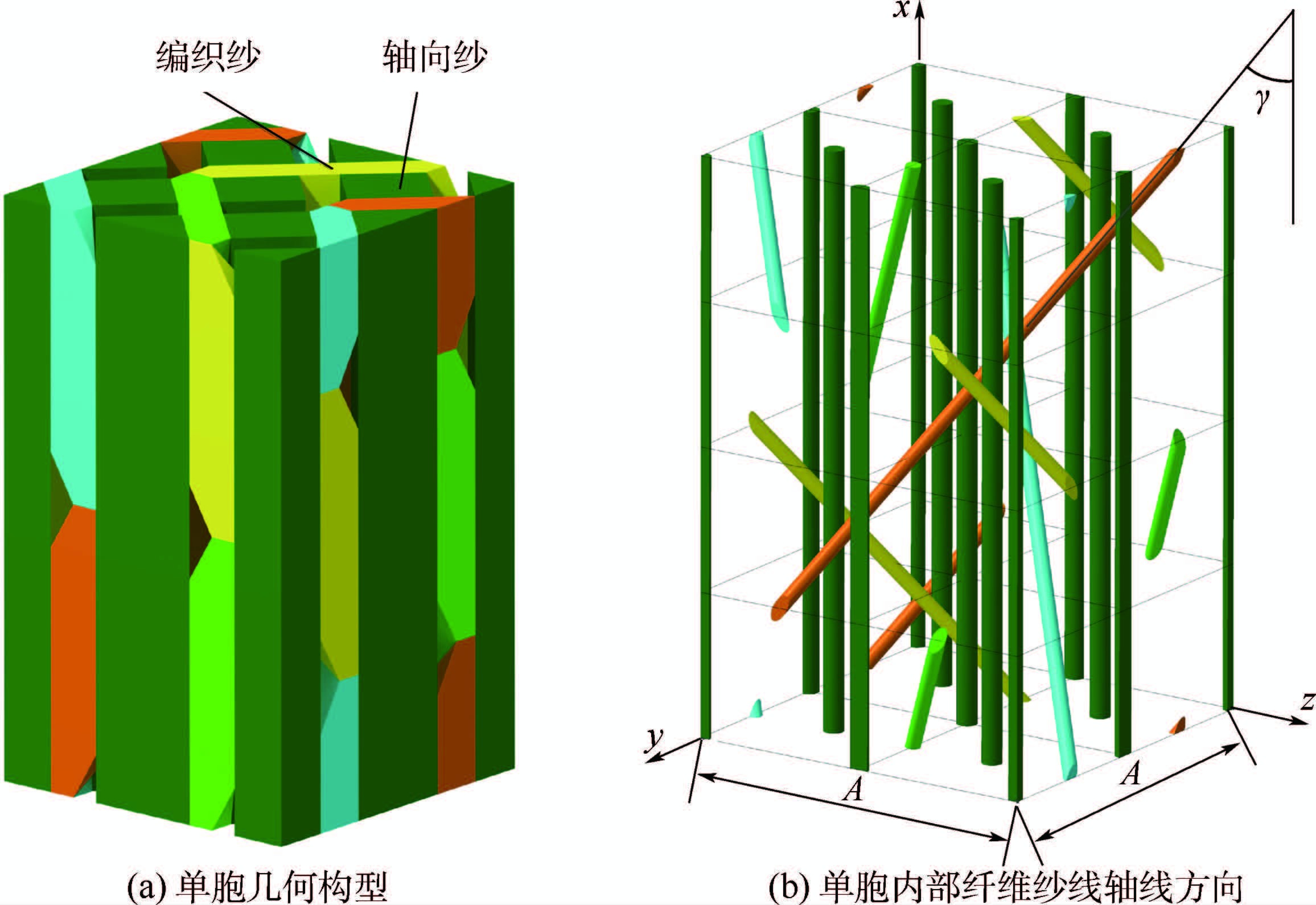图 2 三维全五向编织复合材料周期性单胞 Fig. 2 Periodic repeated cell of three-dimensional full five-directional braided composites

图选项

2.2 弹性性能计算三维编织复合材料弹性阶段的力学性能可以通过采用细观力学刚度均匀化方法对其周期性单胞的刚度矩阵进行计算进而得到:

式中:$\bar C$_total为单胞的总体刚度矩阵;V_n和$\bar C$_n分别为纱线和树脂基体在单胞中的体积分数和单胞总体坐标系下的刚度矩阵,其中$\bar C$_n可由式(5)得到:
式中:C_n为纱线和基体在其局部材料主方向坐标系下的刚度矩阵;T_σ,n为应力坐标转换矩阵:

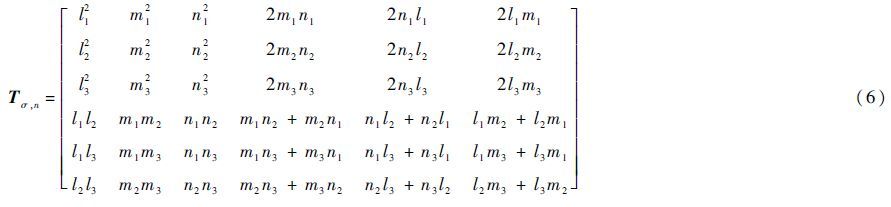
式中:l_i、m_i和n_i(i=1,2,3)为局部坐标系坐标轴与总体坐标系坐标轴之间的夹角余弦。由于轴向纱以及4个方向的编织纱局部坐标系各不相同,所以在合成单胞总体刚度矩阵的时候,这5种纱线在总体坐标系下的刚度矩阵须分别进行计算。
根据以上计算方法结合三维全五向编织复合材料周期性单胞的几何结构编制了弹性常数计算程序,通过输入相应的编织工艺参数可以得到三维全五向编织复合材料圆柱销试件的宏观弹性性能如表 2所示。
表 2 圆柱销试验件宏观弹性性能Table 2 Macroscopic elastic properties of straight pin specimens

弹性性能	Ex/GPa	Ey/GPa	Ez/GPa	Gxy/GPa	Gxz /GPa	Gyz/GPa	μxy	μxz	μyz
数值	80.97	13.26	13.26	11.55	11.55	9.32	0.42	0.42	0.3
注:Ex,Ey,Ez—x,y,z材料方向上的弹性模量;Gxy,Gxz,Gyz—xy,xz,yz材料平面内的剪切弹性模量;μxy,μxz,μyz—xy,xz,yz材料平面内的泊松比。

表选项


2.3 强度计算方法由于目前尚未建立起针对三维编织复合材料的宏观强度准则,在前期已有研究工作的基础上,采用Tsai-Hill各向异性强度准则对三维编织复合材料圆柱销的失效破坏进行预测,Tsai-Hill强度准则的具体表达形式为


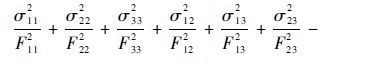
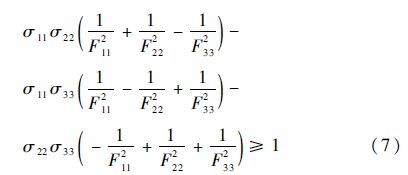
式中:{σ₁₁,σ₂₂,σ₃₃,σ₁₂,σ₁₃,σ₂₃}为三维编织复合材料的宏观应力分量;F₁₁、F₂₂和F₃₃分别为3个材料方向上的强度。由于Tsai-Hill强度准则在表达式中并未考虑三维编织复合材料拉压强度的不同,因此需要对其进行修正:
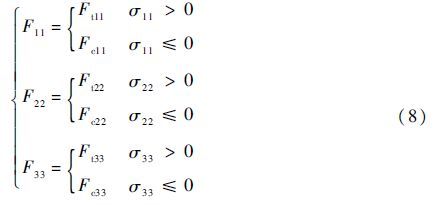
式中:F_tii和F_cii(i=1,2,3)分别为三维编织复合材料在3个宏观材料主方向上的拉伸和压缩强度。三维全五向编织复合材料各个材料方向上的宏观材料强度已经在文献^[19]中进行了试验研究,其中编织角为50°、纤维体积分数为50%情况下的具体试验结果如表 3所示。
表 3 三维全五向编织复合材料宏观强度性能Table 3 Macroscopic strength properties of three-dimensional full five-directional braided composites

材料方向	宏观强度/MPa
纵向(x方向)拉伸	980.5
纵向(x方向)压缩	321.4
横向(yz方向)拉伸	143.6
横向(yz方向)压缩	92.91
剪切	64.53

表选项


为了表征圆柱销局部材料达到强度破坏准则会后的损伤扩展状态,引入了损伤状态因子d来对出现损伤的材料进行刚度退化,即
式中:E_d为材料含损伤刚度;E₀为材料未损伤状态下的刚度；d可以通过材料的临界损伤面积A_d来表示:
式中:A₀为材料产生破坏前的临界面积。根据Cordebois和Sidoroff^[20]的断裂能理论材料损伤演化过程中释放的断裂能等于损伤区域的应变能:
式中:σ_e、ε_e和G分别为三维编织复合材料宏观等效应力、等效应变以及断裂能密度;l₀为损伤区域的等效长度,因此损伤状态因子可以表示为 d=A_eA₀=σ_eε_el₀2G(12)
2.4 有限元模型采用ABAQUS商业有限元软件建立有限元分析模型,如图 3所示,三维编织复合材料圆柱销试件采用C3D8R三维实体单元,双剪加载刀片采用离散刚体单元R3D4,网格总数为39 038。分析过程中加载刀片与圆柱销试件之间设置接触关系,下刀片固定,上刀片施加垂直向下的位移载荷,从而实现双剪载荷的加载。

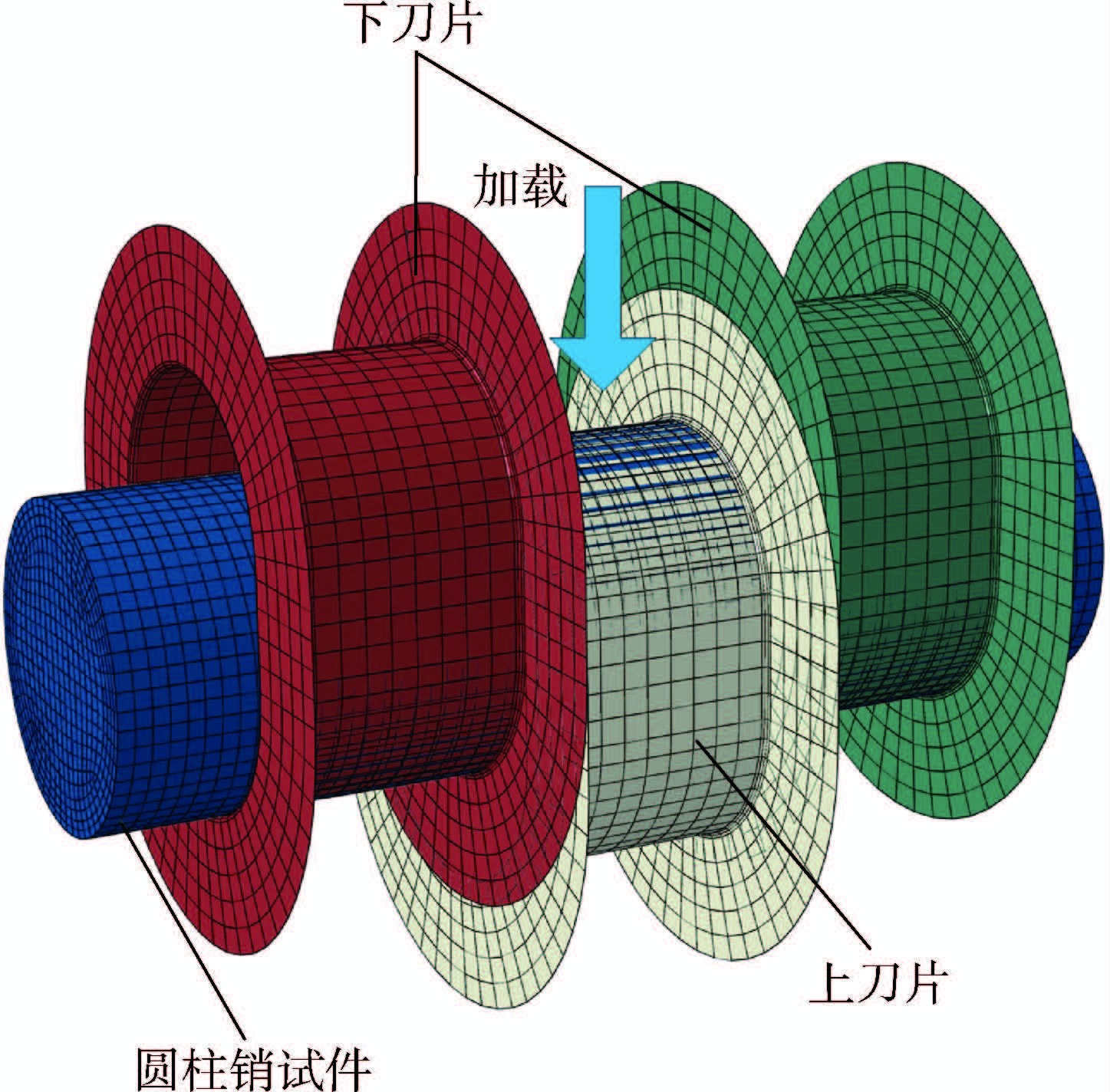图 3 圆柱销试件剪切模拟有限元模型 Fig. 3 Finite element model of straight pin specimens for shear simulation

图选项

ABAQUS有限元软件中只提供针对单向复合材料平面应力状态下的Hashin破坏准则,无法直接运用于三维编织复合材料的失效分析,为此,根据第2.3节提供的强度计算方法对ABAQUS有限元软件进行了二次开发,编制了相应的材料子程序以模拟三维全五向编织复合材料初始破坏和损伤演化过程。同时为了模拟损伤过后纤维和树脂基体的断裂,在分析过程中设置了单元生死,当局部单元的损伤状态因子数值达到0.99时就删除该单元。
3 试验与模拟分析结果讨论3.1 双剪极限强度试件双剪极限强度的试验与模拟分析结果如表 4所示。可以看出不同圆柱销试件之间的结果略有差异,2个试件的剪切强度分别达到了396.3 MPa和369.6 MPa,远高于使用细编穿刺等制备工艺制备的圆柱销试件^[17],这说明三维编织复合材料圆柱销在常温工作环境下具有很高的力学性能和工程应用价值。同时有限元模拟分析结果与试验结果之间的误差最大不超过5%,能够满足实际应用中的精度要求
表 4 圆柱销试件剪切极限载荷的试验与模拟结果Table 4 Test and simulation results of ultimate shear load for straight pin specimens

试件及有限元模拟	极限载荷/N	剪切强度/MPa
试件1	11 206	396.3
试件2	10 450	369.6
有限元模拟	10 765	380.7

表选项


3.2 载荷-位移曲线圆柱销试件双剪载荷-位移曲线有限元模拟计算结果与试验结果如图 4所示。受试件制备过程中材料的不均匀性以及气泡和纤维断裂等初始加工缺陷的影响,不同试件的试验结果之间存在一定的差异,但试件破坏失效全过程的载荷-位移曲线变化趋势仍然表现出较好的一致性。

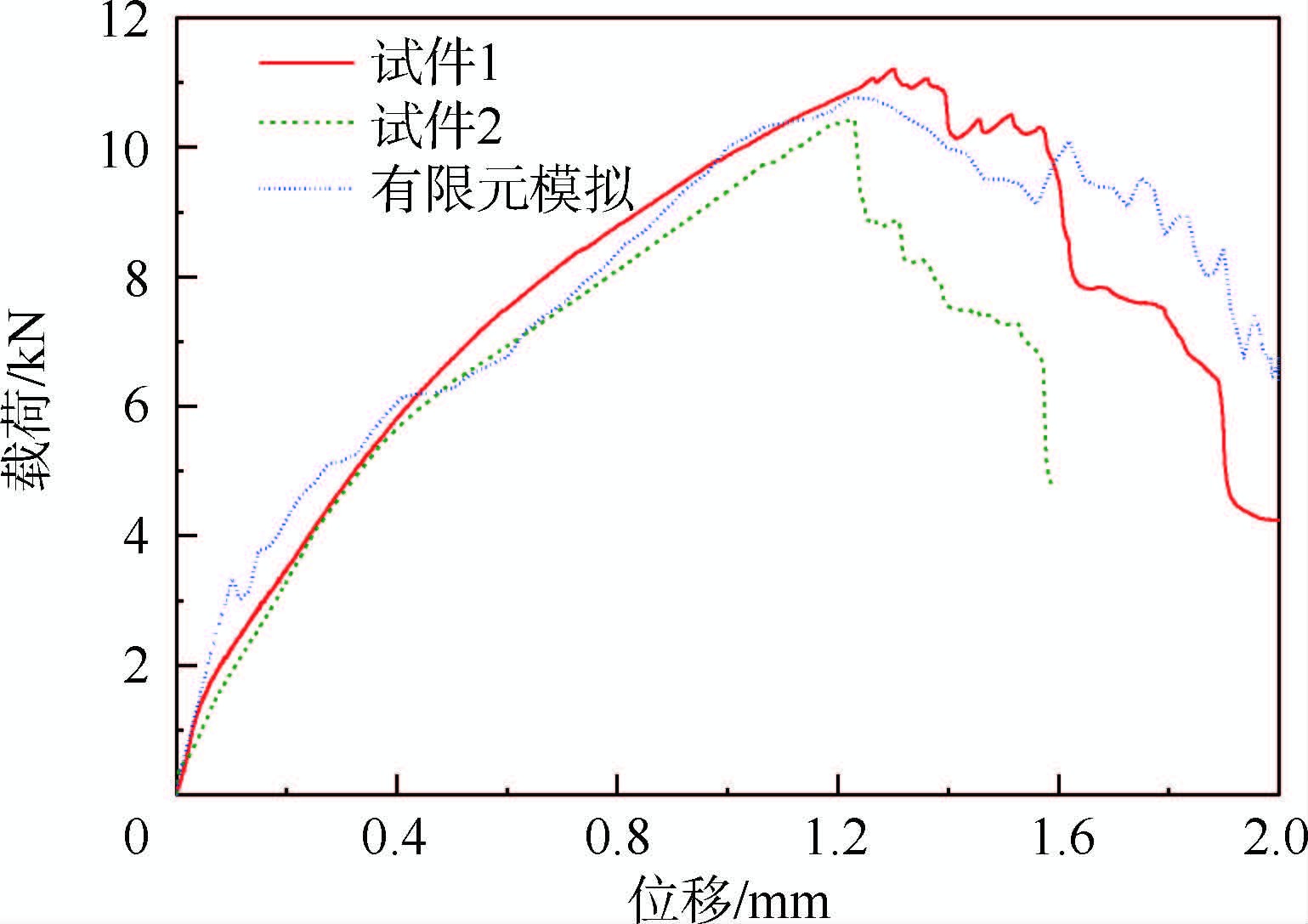图 4 载荷-位移曲线模拟与试验结果对比 Fig. 4 Comparison of load-displacement curves between simulation and test results

图选项

从载荷-位移曲线上可以看出,试件初始破坏发生在0.1 mm变形处,初始破坏产生之后,双剪载荷仍然会随着位移增加而继续增加,但是由于试件内部已经出现了损伤,载荷-位移曲线的上升斜率出现了较大幅度的减小。圆柱销试件的双剪载荷在1.25 mm变形处达到极值,之后开始随着载荷的增加而下降,最终失去承载能力。从圆柱销试件双剪载荷下的渐进失效全过程可以看出,试件在达到极限载荷之前会经历一个较长的非线性阶段,初始损伤的出现并不会使试件立即失去承载能力,只有当试件内部损伤累积到一定程度之后才能最终导致承载载荷的下降,这说明三维全五向编织复合材料圆柱销在双剪载荷作用下具有一定的塑性化特征。同时从有限元模拟预测曲线与试验曲线的比较上来看,数值模拟结果同试验结果在试件渐进失效各个阶段的变化趋势都基本吻合。
3.3 试件破坏断裂形貌试件剪切破坏断口形貌如图 5所示。从图中可以看出,圆柱销试件在加载刀口处形成了明显的断裂面,同时试件的损伤主要集中在中间区域,在该区域中出现了大量的树脂基体破碎和纤维断裂。

图 5 圆柱销试件破坏断裂形貌 Fig. 5 Damage morphology of straight pin specimens

图选项

圆柱销试件加载过程中损伤初始和扩展过程如图 6所示。由图可知在位移0.1 mm时试件在上刀片和下刀片刀口处首先产生初始损伤,随着位移的增加,损伤开始在试件内部沿着横向和纵向2个方向扩展,在位移为0.2 mm时,试件与上刀片接触的部位已经完全破坏,此时试件上部和底部的损伤区域相对独立,试件仍然具有一定的承载能力。当加载位移达到0.4 mm时,损伤开始贯穿整个试件截面并在试件中部区域不断扩展,圆柱销试件在位移为1.1 mm时在刀口处出现了断裂并沿着刀口所在截面纵向拓展,此时试件达到极限承载载荷,随着断裂面积的不但扩大,试件的承载能力逐步下降,载荷-位移曲线开始进入下降段。试件的损伤扩展过程模拟结果与试验结果之间表现出了良好的一致性,说明本文所采用的三维编织复合材料强度分析方法是有效可行的,能够满足实际工程应用的精度要求。

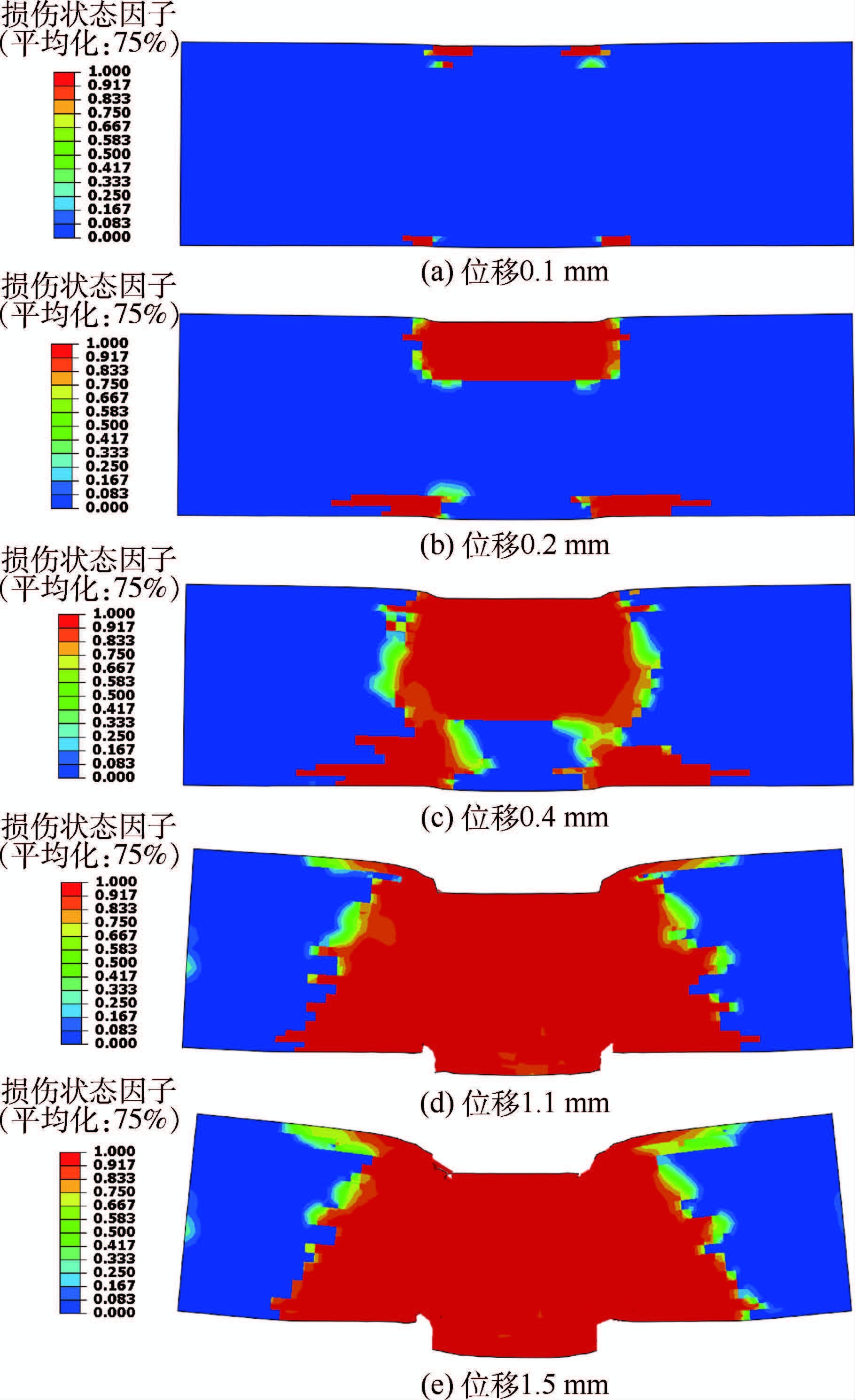图 6 圆柱销试件在剪切载荷下的损伤拓展过程 Fig. 6 Progressive damage process of straight pin specimen under shear loading

图选项

4 结 论1) 三维全五向编织复合材料圆柱销试件在剪切性能试验测试中表现出稳定的承载性能,说明采用三维编织工艺制备的树脂基复合材料紧固件具有广泛的工程应用前景。
2) 基于细观均匀化方法结合三维全五向编织复合材料周期性单胞的几何结构编制了弹性常数计算程序,有效预测了圆柱销试件的宏观弹性性能,为进一步的强度性能分析提供了初始输入参数。
3) 建立了三维编织复合材料结构件宏观强度性能计算方法,引入了Tsai-Hill各向异性强度准则和基于断裂能理论的材料性能损伤后退化方案,实现了对三维编织复合材料结构件渐进失效破坏全过程的数值模拟。
4) 采用本文建立的强度计算方法对三维编织复合材料圆柱销结构件宏观强度进行预测能够取得与试验测试一致性较好的结果,具有工程实用价值。
参考文献

[1]	YANG J M,MA C L,CHOU T W.Fiber inclination model of three-dimensional textile structural composites[J].Journal of Composite Materials,1986,20(5):472-484.
	Click to display the text
[2]	WANG Y Q,WANG A S D.Microstructure/property relationships in three-dimensionally braided fiber composites[J].Composites Science and Technology,1995,53(2):213-222.
	Click to display the text
[3]	SANKAR B V,MARREY R V.Analytical method for micromechanics of textile composites[J].Composites Science and Technology,1997,57(6):703-713.
	Click to display the text
[4]	SUN X,SUN C.Mechanical properties of three-dimensional braided composites[J].Composite Structures,2004,65(3):485-492.
	Click to display the text
[5]	SHOKRIEH M M,MAZLOOMI M S.A new analytical model for calculation of stiffness of three-dimensional four-directional braided composites[J].Composite Structures,2012,94(3):1005-1015.
	Click to display the text
[6]	ZENG T,WU L,GUO L.A damage model for 3D braided composites with transverse cracking[J].Composite Structures,2003,62(2):163-170.
	Click to display the text
[7]	ZENG T,WU L,GUO L.A finite element model for failure analysis of 3D braided composites[J].Materials Science and Engineering:A,2004,366(1):144-151.
	Click to display the text
[8]	FANG G D,LIANG J,WANG B L.Progressive damage and nonlinear analysis of 3D four-directional braided composites under unidirectional tension[J].Composite Structures,2009,89(1):126-133.
	Click to display the text
[9]	DONG J,FENG M.Asymptotic expansion homogenization for simulating progressive damage of 3D braided composites[J].Composite Structures,2010,92(4):873-882.
	Click to display the text
[10]	GUO Q,ZHANG G,LI J.Process parameters design of a three-dimensional and five-directional braided composite joint based on finite element analysis[J].Materials & Design,2013,46(4):291-300.
	Click to display the text
[11]	ZHOU L D,ZHUANG Z.Strength analysis of three-dimensional braided T-shaped composite structures[J].Composite Structures,2013,104:162-168.
	Click to display the text
[12]	WU L,GU B,SUN B.Finite element analyses of four-step 3D braided composite bending damage using repeating unit cell model[J].International Journal of Damage Mechanics,2015,24(1):59-75.
	Click to display the text
[13]	HAENSEL D,HALD H,RUEHLE F,et al.Development of a joining method for high temperature constructions[C]//European Conference on Spacecraft Structures,Materials and Mechanical Testing.Paris:European Space Agency,1999:333-338.
	Click to display the text
[14]	DOGIGLI M,HANDRICK K,BICKEL M,et al.CMC key technologies-background,status,present and future applications[C]//Hot Structures and Thermal Protection Systems for Space Vehicles.Paris:European Space Agency,2003:79.
	Click to display the text
[15]	李俊,矫桂琼,王刚,等.室温下C/SiC复合材料螺纹紧固件的拧紧特性[J].复合材料学报,2012,29(5):164-170. LI J,JIAO G Q,WANG G,et al.Tightening characteristic of C/SiC composite threaded fasteners at room temperature[J].Acta Materiae Compositae Sinica,2012,29(5):164-170(in Chinese).
	Cited By in Cnki (3)
[16]	MEI H,CHENG L,KE Q,et al.High-temperature tensile properties and oxidation behavior of carbon fiber reinforced silicon carbide bolts in a simulated re-entry environment[J].Carbon,2010,48(11):3007-3013.
	Click to display the text
[17]	王杰,李克智,郭领军,等.炭布叠层穿刺C/C复合材料螺栓连接件微观组织和力学性能[J].固体火箭技术,2012,35(2):248-252. WANG J,LI K Z,GUO L J,et al.Microstructure and mechanical properties of C/C composite bolts[J].Journal of Solid Rocket Technology,2012,35(2):248-252(in Chinese).
	Cited By in Cnki (7)
[18]	国防工业技术委员会.紧固件试验方法双剪:GJB715.26A-2008[S].北京:中国航空综合技术研究所,2008:1-6. The Commission of Science,Technology and Industry for National Defense of the PRC.Fastener test methods double shear test:GJB715.26A-2008[S].Beijing:AVIC China Aero-Polytechnology Establishment,2008:1-6.
[19]	黄雨霓.三维编织复合材料力学性能研究[D].北京:北京航空航天大学,2012:43-62. HUANG Y N.Research on the mechanical properties of three dimensional braided composites[D].Beijing:Beihang University,2012:43-62(in Chinese).
[20]	CORDEBOIS J P,SIDOROFF F.Damage induced elastic anisotropy[M]//Mechanical Behavior of Anisotropic Solids/Comportment Méchanique des Solides Anisotropes.Berlin:Springer Netherlands,1982:761-774.