双材料被广泛应用于如航空、航天和交通运输等领域,双材料界面处往往会出现裂纹等缺陷,这些缺陷会导致材料强度的降低,而且损伤通常开始于界面或界面附近区域,因此对双材料界面裂纹的研究至关重要。
研究人员已使用如有限元法、边界元法^[1]、扩展有限元法(Extended Finite Element Method,XFEM)^[2-6]等数值方法计算双材料界面裂纹的应力强度因子(Stress Intensity Factor,SIF)。有限元法在处理裂纹问题时需要在裂纹尖端划分很细的网格,不可避免地会出现几何形状比较差的单元,且随着裂纹增长网格需要重构,从而影响计算精度和计算效率。XFEM^[7-8]通过在单元位移场函数中增加富集函数来描述不连续问题,使得网格与结构内部细节或物理界面无关,从而克服了裂纹尖端等高应力区网格划分的困难,同时在模拟裂纹增长过程中无需对网格重构。但是XFEM在计算精度上并没有显著提高。文献^[9]结合广义有限元法(Generalized Finite Element Method,GFEM)和XFEM的优点提出广义扩展有限元法(Generalized Extended Finite Element Method,GXFEM)概念,并应用于各向同性材料的裂纹分析。文献^[10]分别用无网格伽辽金法和XFEM计算了双材料界面裂纹的应力强度因子,无网格伽辽金法因在其求形函数及其导数时常涉及到矩阵求逆及多个矩阵相乘,使得计算时间很长,并且其在XFEM中所用的界面富集函数往往会因为混合单元的存在,影响解的收敛性。文献^[11]基于XFEM提出一种新的界面富集函数,有效提高了解的收敛性。文献^[12]利用三角变换将裂纹尖端位移场富集函数由4项减少到2项,减少了计算量,但是其没有涉及到比较复杂的双材料裂纹尖端富集函数。文献^[13]用常规XFEM计算双材料界面裂纹的应力强度因子,没有引入界面的富集函数,计算精度并不高。
本文首先建立了分析双材料界面裂纹的GXFEM,其中引入界面富集函数改进界面单元,应用三角变换等手段将界面裂纹的裂纹尖端富集函数由12个减少到6个,然后采用偏移富集函数对混合单元的问题进行处理,对裂纹尖端和裂纹面的单元引入附加的结点广义参数来提高计算精度。最后通过数值算例验证本文GXFEM的合理性和有效性。
1 GXFEM的基本原理 1.1 位移逼近方程的建立 对于双材料界面裂纹,GXFEM的位移场由4个部分构成：常规有限元法的位移和反映裂纹面、裂纹尖端、材料界面存在的加强位移。

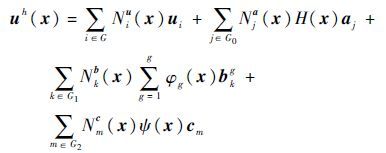(1)

式中：i、 j、 k和m为单元结点编号；G、G₀、G₁和G₂分别为常规单元、裂纹贯穿单元(空心圆)、裂纹尖端单元(实心圆)和材料界面单元(三角形)结点的集合；g为裂纹尖端富集函数的数目；x为高斯点的坐标向量；u^h为结点位移,h为空间维数；u_i为结点i的常规位移；a_j、b_k^g和c_m分别为贯穿裂纹结点j、裂纹尖端结点k和材料界面结点m的附加自由度向量；H(x)、φ_g(x)和ψ(x)分别为裂纹面、裂纹尖端和材料界面的富集函数；N_u、 N_j^a、N_k^b和N_m^c分别为常规单元、裂纹贯穿单元、裂纹尖端单元和材料界面单元的广义形函数,上标u为常规位移,a、b和c分别为裂纹贯穿结点、裂纹尖端结点、材料界面结点的附加自由度向量。

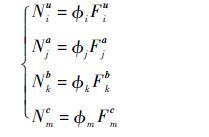(2)

式中：F_i^u、F_j^a、F_b^k和F_c^m分别为常规单元、裂纹贯穿单元、裂纹尖端单元和材料界面单元的结点位移插值函数，由于不同结点位移的插值函数之间的协调性没有强制要求,在理论上F_uⁱ、F_a^j、F_b^k和F_c^m可以随意选取；φ_m、φ_m、φ_m和φ_m为常规有限元的形函数。

(3)

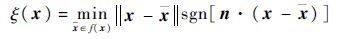(4)

(5)

式中：r和θ为以裂纹尖端为原点的极坐标；为间断面上离x距离最短的点；f(x) 为间断面函数；ξ(x)为最短距离函数；n为间断面在点处的外法向矢量；ε为裂纹尖端双材料参数。双材料界面裂纹裂纹尖端富集函数有12项。在GXFEM中裂纹尖端结点有74个自由度,约束式(1)的b_k¹=b_k²,b_k³=b_k⁴,b_k⁵=b_k⁶,b_k⁷=b_k⁸,b_k⁹=b_k¹⁰,b_k¹¹=b_k¹²,利用三角变换,且不考虑常数项系数,使式(5)变为

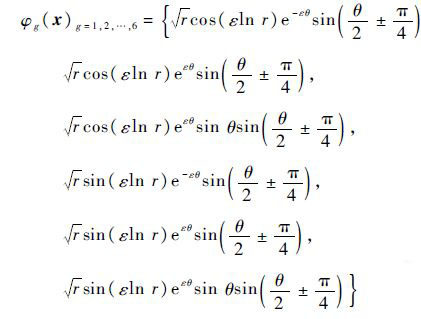(6)

经过变换,裂纹尖端的富集函数变为6项。式中：π/4前的符号应与θ的符号保持一致。引用式(6)作为裂纹尖端富集函数,裂纹尖端结点自由度为38个,大大减少了运算量。当ε=0时,裂纹尖端富集函数φ_g(x)为

(7)

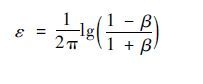(8)

双材料间的弹性不匹配可用Dundurs参数α和β来描述^[13] ：

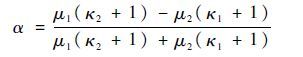(9)

(10)

式中：μ_i为材料i(i=1,2)的剪切模量；κ_i为Kolosov常数：

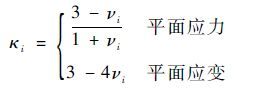(11)

式中：ν_i为材料i(i=1,2)的泊松比。
可以选择问题的已知解,问题本身所具有的物理特性或者部分解析解作为富集函数。文献^[14]为了模拟孔洞和夹杂问题,首次在XFEM中引入材料界面富集函数：

(12)

式中：ξ_m(x)为材料界面富集结点m在材料界面水平集函数中的值,其表达式见式(4)。但是由于混合单元存在使得解的收敛性不好。文献^[11]提出了新的改进方法,表达式为

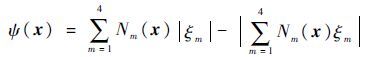(13)

富集单元的结点位移并不是真实的结点位移,为了使所有的结点都是真实的结点位移,需要对式(1)进行转基处理,变换为

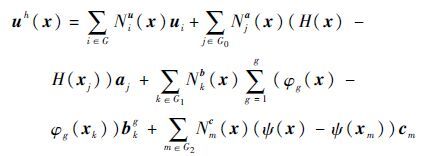(14)

式中：H(x_j)为单元结点j的Heaviside值；φ_g(x_k)为单元结点k的裂纹尖端单元富集函数值；ψ(x_m)为单元结点m的材料界面富集函数值；x_j、x_k和x_m分别为裂纹贯穿单元结点、裂纹尖端结点和材料界面结点坐标向量。
将式(2)代入式(14),位移模式可表示为

(15)

本文在常规结点和材料界面结点的结点位移插值函数取0阶,对应每个结点有2个自由度。结点的广义形函数为

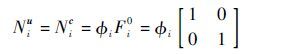(16)

式中：F_i⁰为0阶结点位移插值函数。
裂纹的贯穿单元结点和裂纹尖端单元结点的结点位移插值函数取1阶,即对应每个结点具有6个广义自由度。结点的广义形函数为

(17)

式中：F_i¹为1阶结点位移插值函数。
双材料界面裂纹模型的加强方式如图 1所示。

图 1 双材料界面裂纹的加强结点 Fig. 1 Enriched nodes for a bi-material interfacial crack

图选项

1.2 GXFEM离散方程的建立 和常规有限元法一样,将式(15)代入弹性体的虚功方程,可导出GXFEM的支配方程为

(18)

式中：δ为结点位移列阵；K和F分别为结构总刚度矩阵和结点载荷列阵,K按常规步骤由单元刚度矩阵组集而成。单元层次上的k和f分别为

(19)

(20)

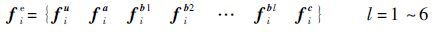(21)

式中：k^e_ij为刚度矩阵；B_i^r为单元应变转换矩阵；D为材料矩阵；B_j^s为单元应变转换矩阵；Ω为弹性体的区域；f_i^e为所有结点荷载力矩阵；f_uⁱ为常规结点荷载力矢量；f_aⁱ为裂纹贯穿结点荷载力矢量；f_i^b1,f_i^b2,…,f_i^bl为裂纹尖端结点荷载力矢量；f_i^c为材料界面结点荷载力矢量。单元结点荷载力矢量分量表示为

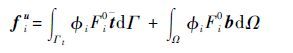(22)

(23)

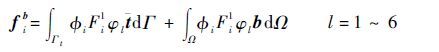(24)

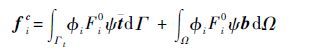(25)

式中：H为裂纹贯穿单元结点的富集函数；为表面力向量；b为体力矢量；Γ_t为表面力给定的表面；φ_g为裂纹尖端富集函数。
B_i^u、B_i^a、B_i^b和B_i^c分别为常规结点、裂纹贯穿单元结点附加、裂纹尖端单元结点附加和材料界面单元附加的应变转换矩阵,其定义如式 (26)～式(29)所示：

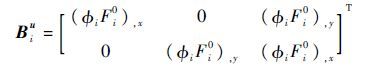(26)

(27)

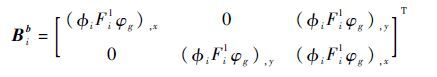(28)

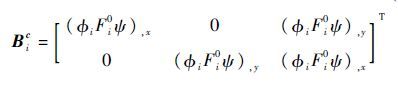(29)

式中：()_,x和()_,y分别为形函数对x求偏导和形函数对y求偏导。
2 双材料界面断裂力学 双材料界面裂纹尖端的应力场的形式为^[13]

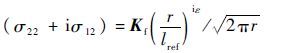(30)

式中:σ₁₂为剪切应力；σ₂₂为拉应力；K_f=K₁+iK₂为复应力强度因子,i为虚数单位；l_ref为参考长度。
3 双材料界面裂纹的区域积分 在复杂应力状态下,已经广泛应用从相互作用积分中提取应力强度因子。对于界面裂纹,相互作用积分可以表示为

(31)

式中：δ_1j为kronecker记号；u_i,1^aux、ε_ik^aux和σ_ij^aux分别为辅助位移对x方向求偏导、辅助应变和辅助应力；A为积分区域的面积； q_,j为权函数对x、y方向求偏导；σ_ij和σ_ik为真实应力。
相互作用积分与应力强度因子的关系可以表示为

(32)

式中：K₁^aux=1,K₂^aux=0,此时把I记为I₁,或者K₁^aux=0,K₂^aux=1,此时把I记为I₂,可以求得真实场作用下的K₁和K₂；E的定义为

(33)

式中：E₁为相对应下半平面的弹性模量；E₂为相对应的上半平面的弹性模量。
σ_ij 和ui,₁由广义扩展有限元算得,u_i,1^aux、ε_ik^aux和σ_ij^aux由辅助位移场求出：

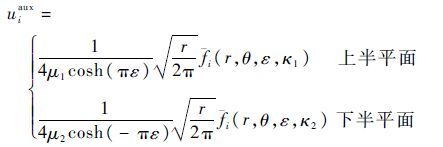(34)

当计算K₁时,辅助位移场函数为

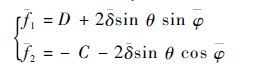(35)

当计算K₂时,辅助位移场函数为

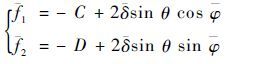(36)

式中：C和D定义参见文献^[13]。
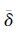
辅助应变为

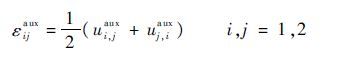(37)

由辅助位移函数可求得

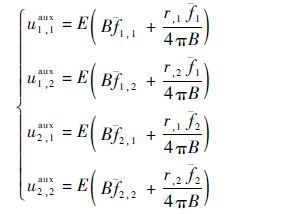(38)

式中：

利用胡克定律,辅助应力场σ_ij^aux可由辅助应变σ_ij^aux求得。
4 数值算例 4.1 中心界面裂纹 一个二维双材料正方形板上下边界受均匀拉应力σ=1MPa,模型中心有长度为2a=2mm的裂纹,板长为H_c=2L=60mm,E₁/E₂=2～1000,E₂=1MPa,ν₁=ν₂=0.3。模型是对称的,采用一半模型来模拟,其板内的界面裂纹如图 2所示。假设板处于平面应变状态,需要采取合适的边界条件消除刚体位移的影响。本问题可以看作是无限大板双材料界面裂纹问题。式(30)中l=1。令,裂纹尖端的应力强度因子K₁和K₂的解^[15]为

图 2 双材料板内的界面裂纹 Fig. 2 Interfacial crack in center of a bi-material plate

图选项

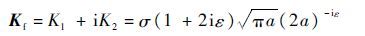(39)

本算例网格密度为151×75,计算结果列于表 1。从表 1可以看出：本文的GXFEM计算得到的应力强度因子和式(39)的结果近似,F₁和F₂的相对误差分别在0.2%和3%之内,说明本文的GXFEM可以准确地计算界面裂纹的应力强度因子。随着E₁/E₂的增大,F₁和F₂的绝对值随着增加。
表 1 双材料界面裂纹F_i结果比较 Table 1 Results for F_i of an edge interfacial crack bi-material plate

E1/E2	α	β	本文GXFEM(L/a=30)				Sukumar等[13](L/a=30)				准确结果(L/a=∞)
			F1	F1误差/%	F2	F2误差/%	F1	F1误差/%	F2	F2误差/%	F1	F1误差/%
2	0.333	0.095	1.0026	0.1	-0.0408	2.8	1.002	0.1	-0.0411	3.5	1.0011	-0.0397
4	0.600	0.171	1.0051	0.2	-0.0735	2.1	1.004	0.1	-0.0743	3.2	1.0035	-0.0720
8	0.778	0.222	1.0076	0.2	-0.0955	1.7	1.007	0.2	-0.0967	3.0	1.0059	-0.0939
20	0.905	0.259	1.0097	0.2	-0.1115	1.5	1.009	0.1	-0.1127	2.6	1.0081	-0.1098
40	0.951	0.272	1.0106	0.2	-0.1173	1.4	1.010	0.1	-0.1185	2.4	1.0090	-0.1157
100	0.980	0.280	1.0110	0.1	-0.1209	1.3	1.010	0	-0.1220	2.2	1.0096	-0.1194
1000	0.998	0.285	1.0108	0.1	-1.0229	1.0	1.010	0	-1.2396	1.9	1.0100	-0.1217

表选项






4.2 内部含副裂纹的单边界面裂纹 单边界面裂纹和副裂纹板如图 3所示。一个二维弹性双材料平板上边界和下边界受单向拉伸载荷σ=1MPa,在沿界面有长度为a₁=40mm的边缘主裂纹,板上还有a₂=10mm副裂纹。板尺寸为L×W,L=2W=200mm,E₂/E₁=2～100,E₂=100MPa,ν₁=ν₂=0.3。副裂纹的中心和主裂纹的右裂纹尖端水平距离为0,垂直移动副裂纹,计算主裂纹尖端的应力强度因子,求得的应力强度因子均通过进行无量纲化,并与文献^[10]的结果进行比较。

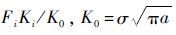
图 3 单边界面裂纹和副裂纹板 Fig. 3 Edge interfacial cracked with minor crack plate

图选项

本算例网格密度为19×39,图 4在不同的弹性模量比下,随着裂纹之间相互距离变化,主裂纹尖端无量纲应力强度因子(K_Ⅰ、K_Ⅱ)的变化。在同等的裂纹之间相互距离时,E₂/E₁=100比E₂/E₁=2的无量纲应力强度因子大一些。图中的无网格伽辽金法(EFGM)结果^[10]和本文的GXFEM结果符合的很好。

图 4 不同E2/E1下,无量纲应力强度因子随裂纹之间相互作用域的变化 Fig. 4 Normalized stress intensity factors changing with crack interaction domain for different E2/E1

图选项

5 结论 1) GXFEM结合了XFEM和GFEM的优点,不需要在裂纹尖端设置过密的网格,同时能够保证较高的计算精度。
2) 本文在运用GXFEM处理界面裂纹时,使用三角变换将裂纹尖端位移场逼近函数由12个减少到6个,在不损失精度的情况下大大减少了计算量；采用偏移富集函数对混合单元的问题进行了处理,提高了计算的收敛性；应用GFEM对裂纹尖端和裂纹面的元素通过增加结点广义位移参数,提高了计算精度。算例表明,采用本文的GXFEM计算双材料界面裂纹的应力强度因子是成功和有效的。
3) FEM、GFEM及XFEM均可以看作GXFEM在特定条件下的简化。在处理不连续问题时,只需要对不连续的区域增加富集函数、进行结点自由度广义化,对其他区域则采用FEM进行处理,从而可以减少建模的复杂性和工作量。

参考文献

[1]	MATSUMTO T, TANAKA M, OBARA R. Computation of stress intensity factors of interface cracks based on interaction energy release rates and BEM sensitivity analysis[J]. Engineering Fracture Mechanics,2000, 65(6): 683–702.
	Click to display the text
[2]	LIU Z L, MENOUILLARD T, BELYTSCHKO T. An XFEM/spectral element method for dynamic crack propagation[J]. International Journal of Fracture,2011, 169(2): 183–198.
	Click to display the text
[3]	CHENG K W, FRIES T P. Higher-order XFEM for cured strong and weak discontinuities[J]. International Journal for Numerical Methods in Engineering,2010, 82(5): 564–590.
	Click to display the text
[4]	MOUSAVI S E, GRINSPUN E, SUKUMAR N. Higher-order extended finite elements with harmonic enrichment functions for complex crack problems[J]. International Journal for Numerical Methods in Engineering,2011, 86(4-5): 560–574.
	Click to display the text
[5]	GRACIE R, WANG H W, BELYTSCHKO T. Blending in the extended finite element method by discontinuous Galerkin and assumed strain methods[J]. International Journal for Numerical Methods in Engineering,2008, 74(11): 1645–1669.
	Click to display the text
[6]	MOTAMEDI D, MOHAMMADI S. Dynamic analysis of fixed cracks in composites by the extended finite element method[J]. Engineering Fracture Mechanics,2010, 77(17): 3373–3393.
	Click to display the text
[7]	BELYTSCHKO T, BLACK T. Elastic crack growth in finite elements with minimal remeshing[J]. International Journal for Numerical Methods in Enginering,1999, 45(5): 601–620.
	Click to display the text
[8]	MO?S N, DOLBOW J, BELYTSCHKO T. A finite element method for crack growth without remeshing[J]. International Journal for Numerical Methods in Engineering,1999, 46(1): 131–150.
	Click to display the text
[9]	章青, 刘宽, 夏晓舟, 等. 广义扩展有限元法及其在裂纹扩展分析中的应用[J]. 计算力学,2012, 29(3): 427–432.ZHANG Q, LIU K, XIA X Z, et al. Generalized extended finite element method and its application in crack growth analysis[J]. Chinese Journal of Computational Mechanics,2012, 29(3): 427–432.(in Chinese).
	Cited By in Cnki (0) | Click to display the text
[10]	PATHAK H, SINGH A, SINGH I V. Numerical simulation of bi-material interfacial cracks using EFGM and XFEM[J]. International Journal of Mechanics and Materials in Design,2012, 8(1): 9–36.
	Click to display the text
[11]	MOES N, CLOIREC M, CARTRAUD P, et al. A computation approach to handle complex micro-structure geometries[J]. Computer Methods in Applied Mechanics and Engineering,2003, 192(28): 3163–3178.
	Click to display the text
[12]	江守燕, 杜成斌. 一种XFEM断裂分析的裂尖单元新型改进函数[J]. 力学学报,2013, 45(1): 134–138.JIANG S Y, DU C B. A novel enriched function of elements containing crack tip for fracture analysis XFEM[J]. Chinese Journal of Theoretical and Applied Mechanics,2013, 45(1): 134–138.(in Chinese).
	Cited By in Cnki (0) | Click to display the text
[13]	SUKUMAR N, HUANG Z Y, PRéVOST J H, et al. Partition of unity enrichment for bimaterial interface cracks[J]. International Journal for Numerical Methods in Engineering,2004, 59(8): 1075–1102.
	Click to display the text
[14]	SUKUMAR N, CHOPP D L, MOES N, et al. Modeling holes and inclusions by level sets in the extended finite element method[J]. Computer Methods in Applied Mechanics and Engineering,2001, 190(46): 6183–6200.
	Click to display the text
[15]	RICE J R. Elastic fracture mechanics concepts for interfacial cracks[J]. Journal of Applied Mechanics,1988, 55(1): 98–103.
	Click to display the text