目前,针对低速冲击下复合材料加筋板的试验和理论研究主要集中在冲击过程与响应[3, 4],冲击位置、冲击能量等影响因素[5, 6]以及低速冲击损伤对压缩性能的影响[7, 8, 9]等,对凹坑深度的关注则相对较少。目前在针对复合材料凹坑深度的理论预测中,利用接触定律[10, 11]是一类方法,但该方法仅适用于凹坑深度较小的情况,因此预测范围有限。一些****[12, 13]采用剪切非线性模型预测凹坑深度,但需要进一步的试验验证。Bouvet等[14]基于基体开裂形成“阻塞系统”的机理建立了特殊的单元对凹坑深度取得了较好的预测效果,但该方法无法对纤维断裂形成的较深凹坑进行预测。研究发现[2, 15],含BVID结构内部通常含有纤维断裂损伤,本文作者在前期工作中[16]基于引入纤维断裂损伤的各向异性弹塑性理论建立了一套凹坑深度模拟方法,对复合材料层板的凹坑深度-冲击能量关系进行了准确的预测,但并未在加筋结构中进行验证。
本文通过试验和数值模拟方法研究了冲击能量、蒙皮厚度和筋条厚度对低速冲击下复合材料加筋板损伤阻抗性能的影响,验证了低速冲击下复合材料加筋板永久凹坑深度的理论预测方法,为复合材料加筋结构设计提供参考。
1 试验对象及方法1.1 试验对象试验对象为复合材料加筋板,如图 1所示。加筋板尺寸为365 mm×308 mm,筋条高度为34 mm,筋条间距为77 mm。为了研究蒙皮厚度和筋条厚度的影响,共设计了2种不同形式的蒙皮(编号SK1和SK2)和2种不同形式的筋条(编号Ⅰ1和Ⅰ2)共计3组试验件,编号分别为SK1-Ⅰ1、SK1-Ⅰ2和SK2-Ⅰ1。其中SK2-Ⅰ1组含10件试验件,用于研究冲击能量的影响;SK1-Ⅰ1与SK1-Ⅰ2组各含3件试验件,用于与SK2-Ⅰ1对比研究筋条蒙皮厚度的影响。各组试验件的铺层如图 2和表 1所示。加筋板材料体系为T300/QY8911,单层厚度为0.12 mm,通过试验测得的材料属性如表 2所示。
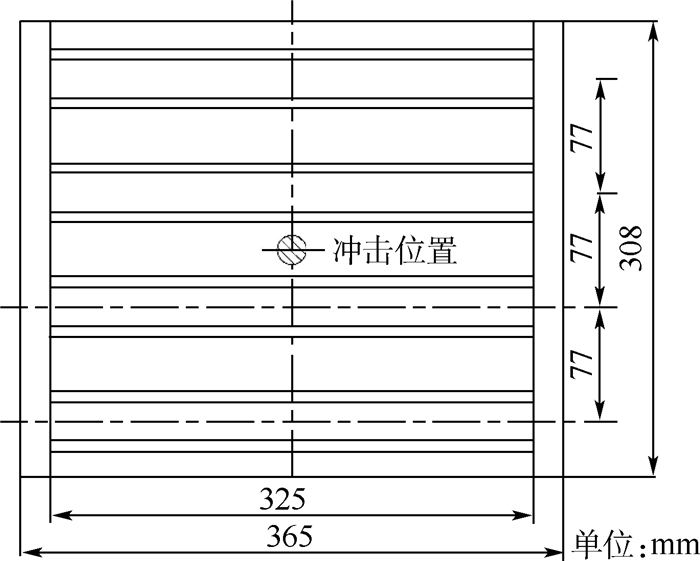 |
| 图 1 复合材料加筋板示意图 Fig. 1 Sketch map of stiffened composite panels |
| 图选项 |
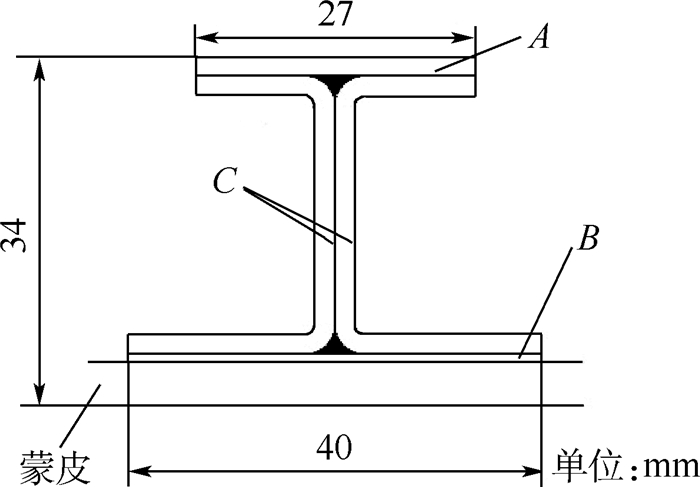 |
| 图 2 筋条铺层示意图 Fig. 2 Sketch map of stiffener’s plies |
| 图选项 |
表 1 复合材料加筋板铺层形式 Table 1 Ply sequences of stiffened composite panels
| 种类 | 试验件编号 | 铺层形式 |
| 蒙皮 | SK1 | [45/-45/0/45/-45/90/(-45/45/0)3/90/0/-45/45/0]s |
| SK2 | [45/-45/0/45/-45/90/(-45/45/0)2/-45/0/90/0/45/0]s | |
| Ⅰ1-A | [(45/-45/0/90)s(0/45/0/-45/0)s](由上到下) | |
| Ⅰ1-B | [45/-45/0/90]s | |
| 筋条 | Ⅰ1-C | [(45/-45/0/90)s(0/45/0/-45/0)s](由外到内) |
| Ⅰ2-A | [(45/-45/90)s(0/45/0/-45/0)s](由上到下) | |
| Ⅰ2-B | [(45/-45/90)s(0/45/0/-45/0)s](由外到内) | |
| Ⅰ2-C | [45/-45/90]s | |
| 注:A、B和C对应图2相应区域。 | ||
表选项
表 2 T300/QY8911复合材料单层板材料属性 Table 2 Material properties of T300/QY8911 unidirectional composite panels
| 材料属性 | E11/GPa | E22/GPa | ν12 | G12/GPa | XT/MPa | XC/MPa | YT/MPa | YC/MPa | S12/MPa |
| 数值 | 135 | 8.8 | 0.33 | 4.47 | 1 665 | 1 362 | 80 | 232 | 90.6 |
| 注:E11—纵向刚度;E22—横向刚度;ν12—泊松比;G12—纵横剪切刚度;XT—纵向拉伸强度;XC—纵向压缩强度;YT—横向拉伸强度;YC—横向压缩强度;S12—纵横剪切强度。 | |||||||||
表选项
1.2 试验方法通过FC落锤式冲击试验机[17]进行冲击试验,试验机系统如图 3所示。试验机由机械系统和数据测量处理系统组成。其中机械系统由机械钢架、落锤及提升机构和试样固定结构组成;数据测量处理系统由力采集系统、速度采集系统和试验软件系统组成。力采集系统中安装在冲头上的压电传感器采集频率为210 kHz,采集到的随时间变化的电信号经过电荷放大器放大后再经数据采集处理系统即可转换为随时间变化的接触力信号;速度采集系统中的红外传感器可以采集冲头落下接触试样和弹起瞬间的速度,经过计算即可得到冲头的冲击能量和回弹能量。参考ASTM试验标准[18],采用直径为16 mm、质量为5.36 kg的圆球型冲头进行试验。试验时将试验件筋条向下固定在水平试验台上,通过调整落锤高度对试验件中心(如图 1所示)进行不同能量的冲击。冲击后通过人工方式对落锤阻拦防止2次冲击。试验结束后立即使用精度为0.01 mm百分表对试验件冲击区域中心凹坑深度进行测量,采用进口PAC水浸超声C扫描无损检测(NDT)设备对试验件内部分层损伤进行检测。
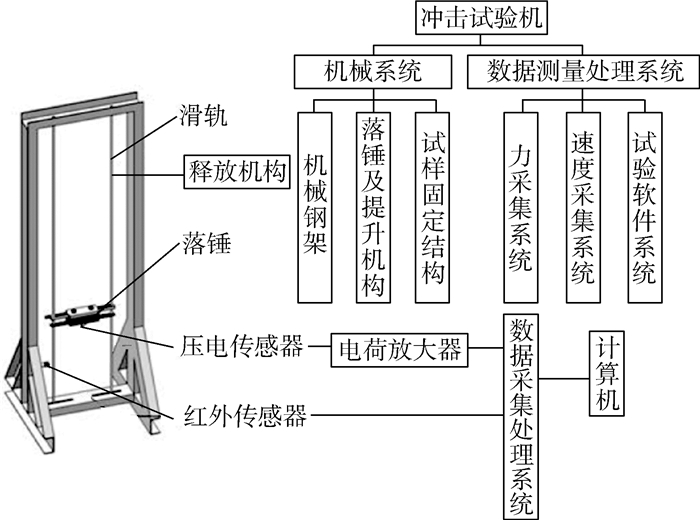 |
| 图 3 FC落锤式冲击试验机 Fig. 3 FC drop weight impact testing machine |
| 图选项 |
2 试验结果分析2.1 冲击能量的影响分析为确定冲击能量对复合材料加筋板低速冲击损伤阻抗性能的影响,采用第1.2节中所述方法选取不同能量对SK2-Ⅰ1组试验件进行冲击试验。
2.1.1 凹坑深度SK2-Ⅰ1组加筋板试验件凹坑深度随冲击能量的变化关系如图 4所示,可以得出,试验件的凹坑深度-冲击能量曲线存在一个明显的拐点。图 5给出了不同冲击能量下试验件冲击点及其背面区域的照片,可以得出,随着冲击能量的增大,冲击点附近区域的损伤越来越严重,在冲击能量大于25 J也即达到拐点之后,冲击点附近区域纤维断裂明显增多,与文献[2]中复合材料层板的相关结论一致。
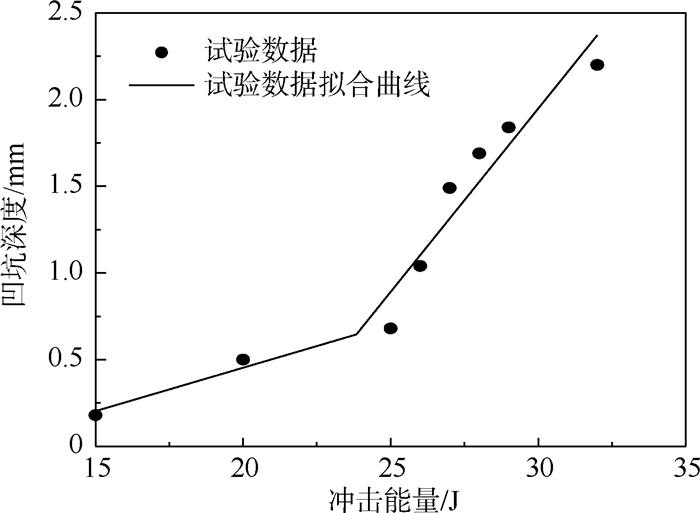 |
| 图 4 SK2-Ⅰ1组试验件凹坑深度-冲击能量关系 Fig. 4 Relationships between dent depth and impact energy of SK2-Ⅰ1 specimens |
| 图选项 |
 |
| 图 5 SK2-Ⅰ1组试验件不同冲击能量冲击区域照片 Fig. 5 Photos of impact locations on SK2-Ⅰ1 specimens under different impact energies |
| 图选项 |
2.1.2 接触历程与能量吸收SK2-Ⅰ1组加筋板试验件在20、25和27 J 3种冲击能量下的冲击接触力变化历程如图 6所示,其中冲击接触力-时间关系根据试验机传感器测量数据得到,冲击接触力-位移关系为
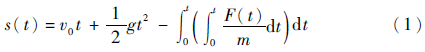
式中:s(t)为冲头位移;v0为冲头初速度;t为时间;g为重力加速度;m为冲头质量;F(t)为试验测得的随时间变化的冲击接触力。
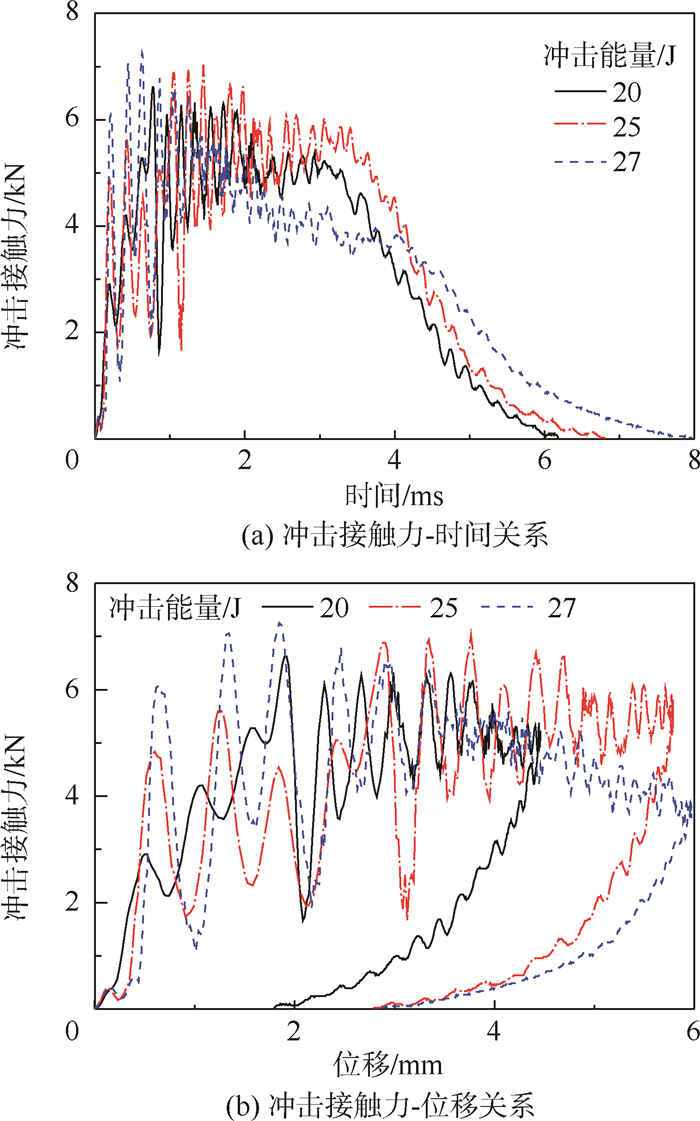 |
| 图 6 SK2-Ⅰ1组试验件不同冲击能量下的冲击接触力变化历程 Fig. 6 Impact force histories for SK2-Ⅰ1 specimens under different impact energies |
| 图选项 |
20、25和27 J冲击能量分别代表了试验件在拐点之前、拐点附近以及拐点之后3种情况下的试验结果,从图 6中可以分析得出,随着冲击能量的增大,冲击接触力的持续时间以及冲头最大位移都在不断增大。从图 6(a)中可以得出,20 J和25 J冲击能量下的冲击接触力随时间的变化趋势基本相同,而27 J冲击能量下的冲击接触力随时间的变化趋势则差别较大,主要体现在冲击接触力在越过峰值点并发生突降后到最终的反弹阶段之前经历了一段持续时间较长的平缓下降阶段,这也反映了拐点能量后试验件内部有较多纤维断裂发生。从图 6(b)中可以得出随着冲击能量的增大,损伤扩展阶段在不断变长。与冲击接触力-时间关系不同,20 J和25 J冲击能量下的冲击接触力-位移变化关系差别相对较大,25 J冲击能量下冲击接触力-位移关系中所反映的损伤扩展阶段明显变长,说明25 J冲击能量下试验件内部分层等损伤与20 J冲击能量相比有了明显的扩展。
试验得到的不同冲击能量下SK2-Ⅰ1组加筋板试验件的分层起始载荷与最大接触力随冲击能量的变化关系如图 7所示,其中分层起始载荷数值的确定方法参考文献[19]。从图中分析可以得出,试验件在各冲击能量下的分层起始载荷基本一致,平均值为6.07 kN。试验件的最大接触力稍大于分层起始载荷,且随着冲击能量的增大有不断增大的趋势。结果说明,随着冲击能量的增大,试验件分层所需载荷大小几乎不变,但不断增大的最大接触力会导致试验件内部出现更严重的损伤。
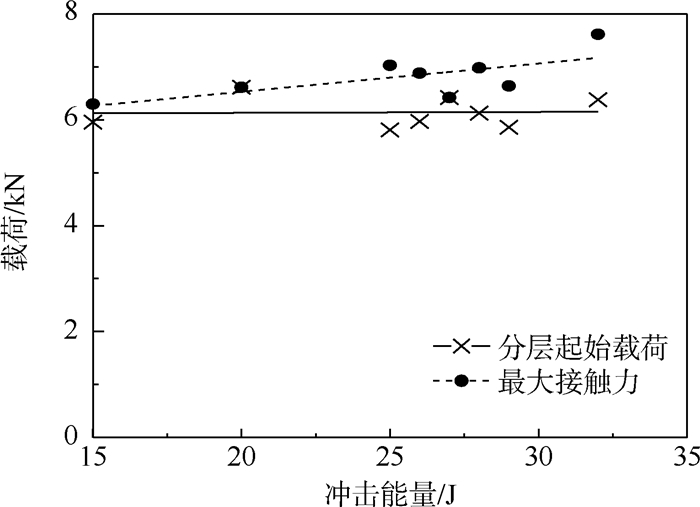 |
| 图 7 SK2-Ⅰ1组试验件分层起始载荷和最大接触力随冲击能量的变化 Fig. 7 Variation of delamination initiation load and maximum impact force with impact energy for SK2-Ⅰ1 specimens |
| 图选项 |
根据试验中测量得到的SK2-Ⅰ1组加筋板试验件冲击过程冲头下落能量和反弹能量,可以计算得到试验件吸收的能量,由此绘制出的能量剖面图如图 8所示。
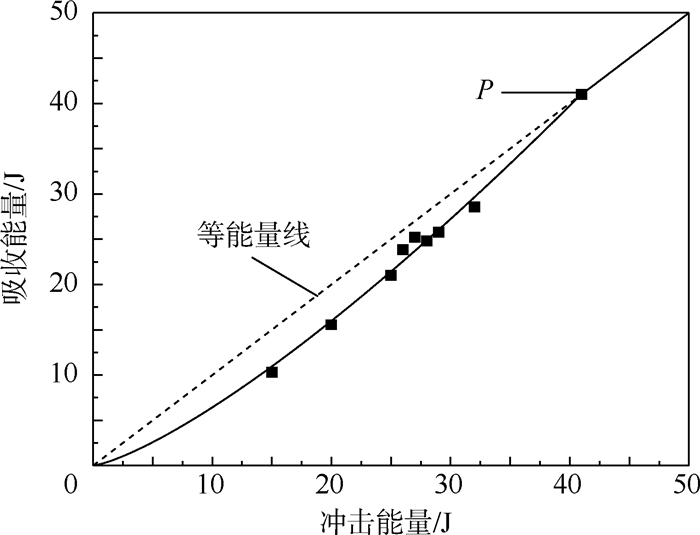 |
| 图 8 SK2-Ⅰ1组试验件能量剖面图 Fig. 8 Energy profile diagram for SK2-Ⅰ1 specimens |
| 图选项 |
图 8中等能量线上试验点对应的试验件所吸收的能量等于冲击能量,也即试验件发生了穿透损伤,冲击能量完全被试验件所吸收。与文献[20]中复合材料层板的试验结果类似,试验件的能量剖面曲线分为2段,包含原点到P点1段曲线和P点后与等能量线重合的直线。从原点到P点之间的1段曲线为吸收能量随冲击能量的增大的速率不断增大的凹曲线,曲线与等能量线之间的差值即为冲头的反弹能量,该段曲线反映了随着冲击能量的增大,试验件内部的主要损伤模式有基体开裂、分层到纤维断裂的逐步转化;P点表示试验件开始发生穿透损伤的能量点,对应的冲击能量为40.89 J,P点后试验件会发生穿透损伤,能量全部吸收。
2.1.3 分层面积试验中通过超声C扫描测得的SK2-Ⅰ1组加筋板试验件分层面积与冲击能量关系的试验结果如图 9所示,超声C扫描无损检测结果如图 10所示。
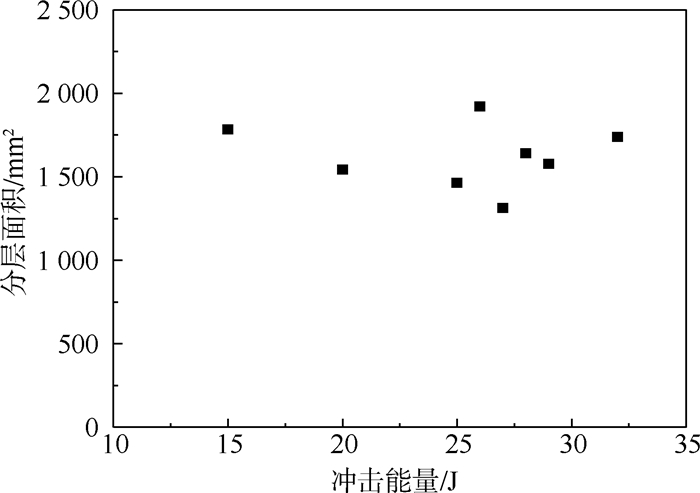 |
| 图 9 SK2-Ⅰ1组试验件分层面积试验结果 Fig. 9 Test results of delamination area for SK2-Ⅰ1 specimens |
| 图选项 |
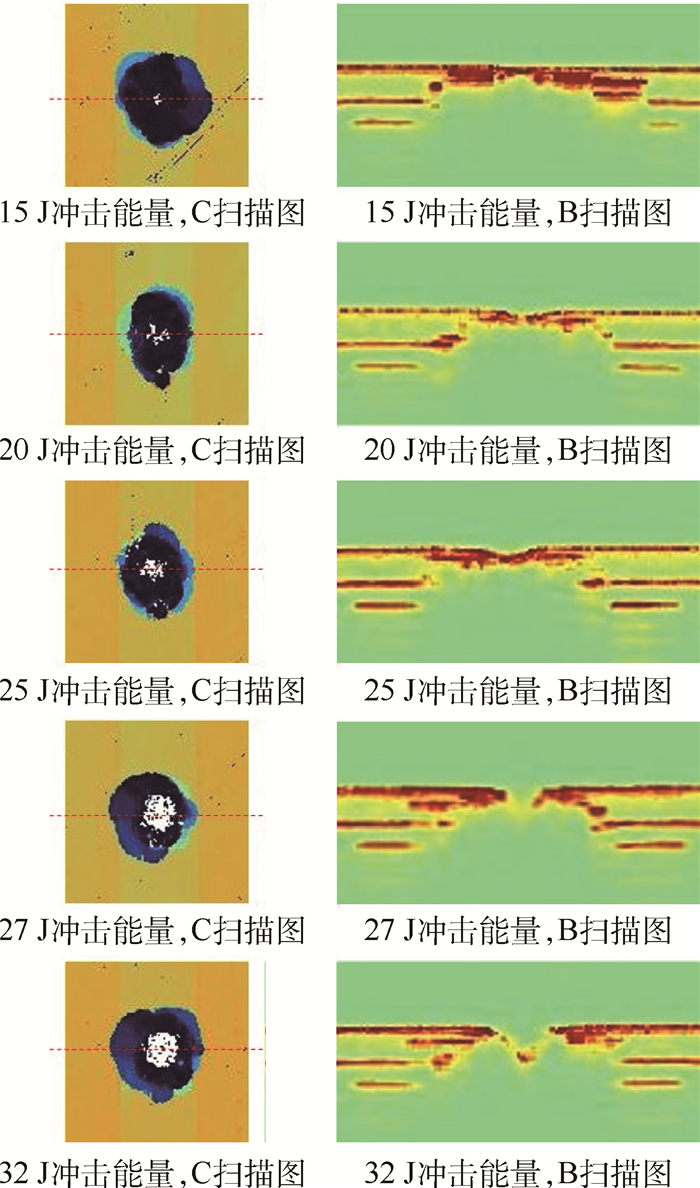 |
| 图 10 SK2-Ⅰ1组试验件不同冲击能量下NDT结果 Fig. 10 NDT results for SK2-Ⅰ1 specimens under different impact energies |
| 图选项 |
与文献[2]中层板的试验结果不同,无论是随着冲击能量还是凹坑深度变化,SK2-Ⅰ1组加筋板试验件的分层面积都变化不大。通过图 10中的C扫描图和B扫描图可以看出,不同冲击能量下试验件冲击点附近的损伤范围基本都被限制在了筋条之间的区域内。试验结果说明,除了分层面积试验结果的分散性外,筋条的限制作用导致了不同能量下大致相同的分层面积结果。
2.2 筋条、蒙皮厚度的影响分析为确定筋条、蒙皮厚度对复合材料加筋板低速冲击损伤阻抗性能的影响,采用第1.2节所述方法针对SK1-Ⅰ1和SK1-Ⅰ2组试验件进行低速冲击试验。
表 3给出了3组中含BVID损伤(凹坑深度1.5 mm左右)试验件的结果。从表 3中可以得出,在损伤大致相同的情况下,蒙皮SK1对应加筋板的冲击能量比蒙皮SK2对应加筋板提高了29.6%,其对厚度进行正则化后的比冲击能提高了约15%;筋条Ⅰ1对应加筋板的冲击能量比筋条Ⅰ2对应加筋板提高了6%。
表 3 3组含BVID试验件试验结果 Table 3 Test results for 3 groups of specimens containing BVID
| 试验件编号 | 冲击能量/J | 凹坑深度/mm | 分层面积/mm2 | 分层起始载荷/kN | 最大接触力/kN |
| SK1-Ⅰ1 | 35 | 1.51 | 1.707 | 7.764 | 9.448 |
| SK1-Ⅰ2 | 33 | 1.52 | 1.609 | 7.813 | 8.716 |
| SK2-Ⅰ1 | 27 | 1.47 | 1.721 | 6.079 | 7.251 |
表选项
图 11给出了3组含BVID试验件冲击接触力变化历程,分别包括冲击接触力随时间和位移的变化历程。3组试验件的分层起始载荷和最大接触力如表 3所示。可以得出,随着蒙皮厚度的增加,加筋板弯曲刚度的增大,加筋板的分层起始载荷、最大接触力以及冲头最大位移均不断增大。随着筋条厚度的增加,加筋板弯曲刚度的增大,最大接触力和冲头最大位移均不断增大,而分层起始载荷则变化不大。试验结果说明,在产生相同程度损伤的情况下,弯曲刚度大的加筋板试验件所需接触力较大,损伤扩展过程也较长;分层起始载荷的变化与仅与蒙皮厚度相关,与筋条厚度关系不大。
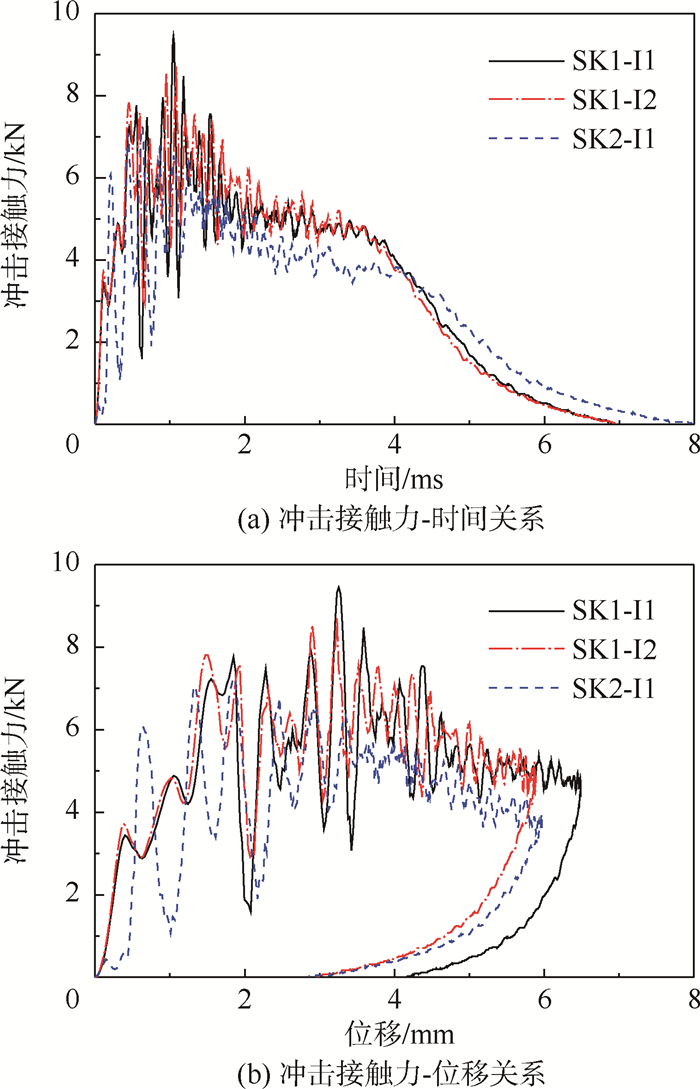 |
| 图 11 3组含BVID试验件的冲击接触力变化历程 Fig. 11 Impact force histories for 3 groups of specimens containing BVID |
| 图选项 |
3 有限元分析3.1 永久凹坑深度预测方法3.1.1 复合材料层内损伤模型根据第2节所述试验结果,含BVID复合材料加筋板试验件内部出现了纤维断裂损伤,因此采用引入纤维断裂损伤的各向异性弹塑性理论方法[16]建立复合材料层内损伤模型。
各向异性弹塑性理论中关键的部分为所采用的关于应力分量二次函数的屈服函数:
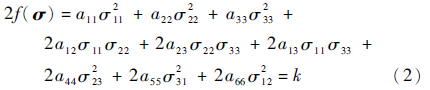
式中:σij为材料坐标系下各方向的应力;9个常数aij为描述各向异性塑性行为的系数;k为与塑性应变相关的表征塑性状态的变量,每一次塑性计算后都会更新;σ为应力。
根据关联流动准则,塑性应变增量为

式中:dλ为比例因子;f为式(2)中的屈服函数。弹塑性计算采用增量理论,在进行数值计算时,应变增量可分为弹性应变增量与塑性应变增量:

式中:dεe为弹性应变增量。
根据塑性增量理论,应力增量仅与弹性应变增量相关:
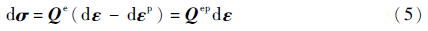
式中:Qe为材料的弹性矩阵;Qep为弹塑性矩阵。
结合式(3),单位体积内的塑性功增量可以表示为

定义有效应力、等效塑性应变增量以及塑性模量分别为

由式(3)~式(9)可得塑性应变增量和弹塑性矩阵表达式分别为
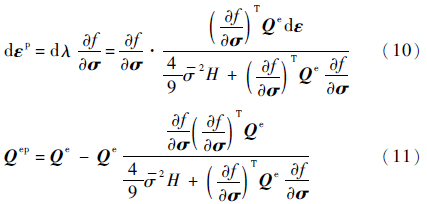
在进行弹塑性计算时,除屈服函数外,还需要用到硬化准则,这里硬化准则采用的是幂函数的形式:

基于该理论进行弹塑性计算的流程图如图 12所示。
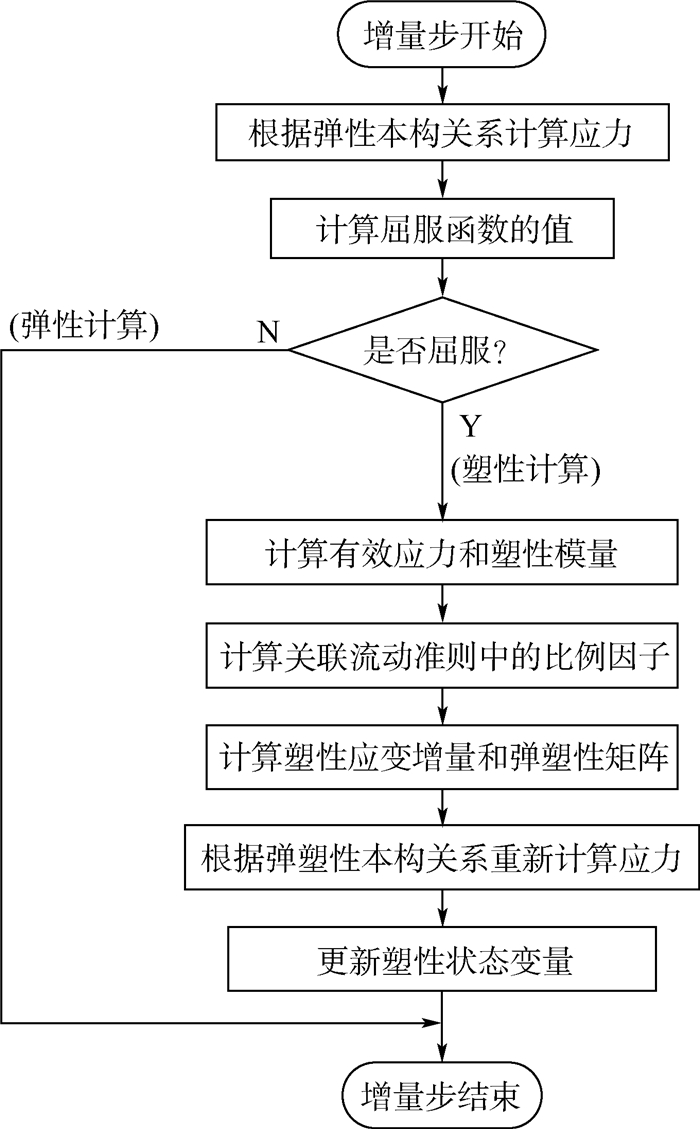 |
| 图 12 弹塑性数值计算流程图 Fig. 12 Flowchart for numerical elasto-plastic calculation |
| 图选项 |
在进行塑性计算前,先要确定屈服面方程中的9个系数aij和硬化准则中的系数A。采用文献[16]中的方法来计算以上系数,该方法主要基于细观有限元(Finite Element,FE)模型在几种单轴加载情况下的有限元分析结果处理得到。细观模型中,纤维为横观各向同性线弹性材料,基体为各向同性塑性材料。
定义塑性泊松比为

式(13)为i方向单轴加载下的定义(i,j=1,2,3),且此式右端并非对重复指标求和,后面类似的表达式也有同样的约定。
由式(3)和式(13)可以得到屈服函数中的系数:
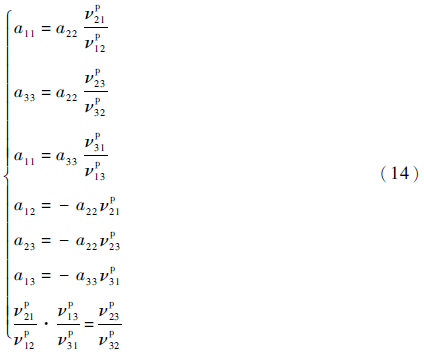
为不失一般性,令a22=1,通常可以认为复合材料单层在2、3方向材料性能相同,于是
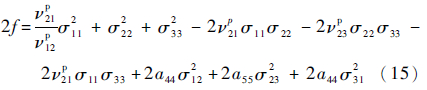
由式(6)~式(8)可以推导出:
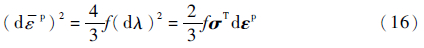
由式(15)和式(16)可以得出等效塑性应变增量和塑性应变增量之间的关系为
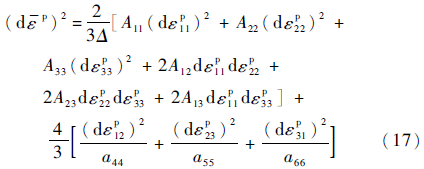
式中:
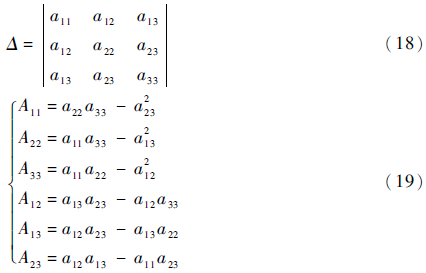
因此在施加单轴正应力σii情况下,由有效应力的定义(式(7))可得

由关联流动准则的表达式(式(3))可得

再由式(17)可以得到

同理,在施加单轴切应力σij情况下,可得

于是由不同的加载情况都可以得到硬化准则σ-εp关系,并且原则上不同加载情况下所得到的硬化准则都应相同。由于屈服函数中前3项的系数已知,于是通过试错法对arr(r=4,5,6)进行调整并与施加正应力情况下得到的硬化准则进行比较可最终得到arr(r=4,5,6)的值,并且也可以得到最终的硬化准则σ-εp关系。计算流程图如图 13所示。
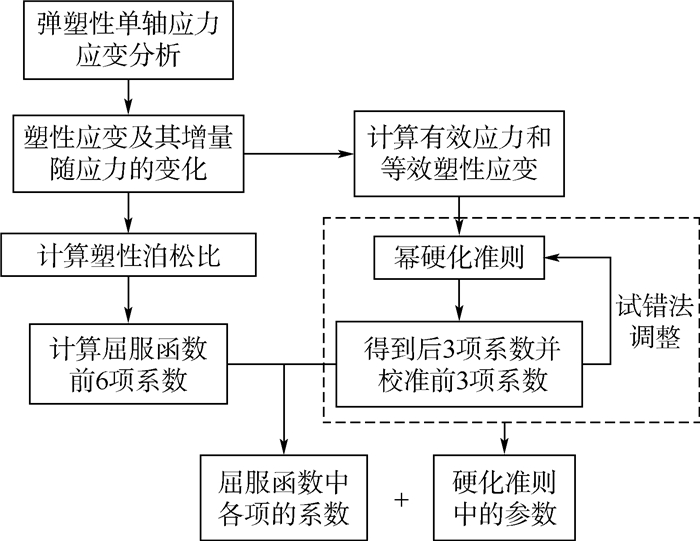 |
| 图 13 宏观塑性参数计算确定流程图 Fig. 13 Flowchart for determination of plasticity parameters in macroscopic model |
| 图选项 |
在模型中,纤维断裂通过最大应力准则来判断,在发生纤维断裂后,对材料性能进行较大程度的退化以模拟结构抵抗冲击能力的大幅度降低,包括弹性性能和塑性性能2个方面。其中,纤维断裂后的宏观塑性参数确定方法与纤维断裂前类似,即通过细观模型的有限元分析得到,不过此时细观模型中组分材料纤维和基体的性能同样进行了折减以形成较强的材料塑性,从而对纤维断裂后凹坑深度随冲击能量的急剧增大进行模拟。
通过上述方法得到的T300/QY8911材料体系纤维断裂前后的宏观塑性参数如表 4所示。
表 4 T300/QY8911宏观塑性参数 Table 4 Macroscopic plasticity parameters for T300/QY8911
| 纤维状态 | 屈服函数中的系数 | 硬化准则中的参数 | 弹性常数 |
| 纤维断裂前 | a22=a33=1,a23=-0.5 a44=a66=4.6,a55=6.2 | A1=2.5×10-8MPa-1.5,A2=1.5×10-6MPa-1.3 n1=1.5,n2=1.3,σt=100 MPa | |
| 纤维断裂后 | a11=a22=a33=0.667 a12=a13=a23=0.333 a44=a55=a66=1 | A1=5×10-3MPa-1.8,A2=0.5 MPa-0.6 n1=1.8,n2=0.6,σt=0.31 MPa | E11=E22=E33=30 MPa ν12=ν13=ν23=0.001 G12=G13=G23=15 MPa |
表选项
3.1.2 复合材料层间损伤模型参考文献[16],本文利用ABAQUS中的界面单元COH3D8对分层进行模拟,损伤起始同样采用二次应力准则,而与文献[16]不同的是损伤演化采用了基于能量释放率的BK准则:
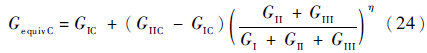
式中:GⅠ、GⅡ和GⅢ分别为法向和2个切向能量释放率的值;下标C表示对应的临界值。计算时,将式(6)右端各方向临界能量释放率的值替换为当前值则得到等效临界释放率的当前值,当等效临界释放率的当前值达到临界值时,界面单元发生完全破坏。表征界面不同受载方向的混合度的参数η取值为1.45[12]。
界面单元的刚度和强度值利用文献[21]所介绍的方法确定,其中推荐的界面单元刚度的计算公式为

式中:α=50;h为界面单元所连接复合材料层板子层中的小厚度值。若K为界面单元在法向的刚度Knn;E对应于复合材料单层在厚度方向上的模量E33;若K为界面单元在2个切向上的刚度Kss和Ktt,则E分别对应于复合材料单层在2个纵向的剪切模量G12和G13。
在给定网格尺寸下界面单元的强度计算公式为

式中:Ne0为裂纹尖端胶层区域所应包含的单元数,其值大于等于2;le为单元长度;GC为临界能量释放率。
而最终的界面强度取值如下:

式中:τ0为最大的界面强度值。与刚度计算类似,式(26)中的弹性模量E取复合材料单层对应方向的弹性模量,而式(26)中的Gc和式(27)中的界面强度τ0则分别取界面在对应方向的值。模型中的界面参数如表 5所示。
表 5 T300/QY8911界面参数 Table 5 Interface parameters for T300/QY8911
| 模型 | 界面刚度/(GPa·mm-1) | 界面强度/MPa | 能量释放率/(N·mm-1) |
| Ⅰ | 1 222 | 27.87 | 0.2 |
| Ⅱ | 621 | 44.45 | 1 |
| Ⅲ | 621 | 44.45 | 1 |
表选项
3.2 有限元模型的建立有限元模型使用ABAQUS软件建立。参考文献[22],复合材料加筋板有限元模型由2个部分组合而成,如图 14所示,2个部分模型之间利用绑定约束(tie constraint)进行连接。根据试验结果,加筋板试验件损伤均在冲击点附近60 mm×60 mm的矩形区域内,因此在该区域内建立了较为细致的模型,其中蒙皮和筋条缘条分别采用了三维实体单元和连续壳单元并划分了较密的网格,各层实体单元以及筋条蒙皮界面之间插入了界面单元以对分层进行模拟;复合材料各单层采用的是考虑了纤维断裂的各向异性弹塑性模型,
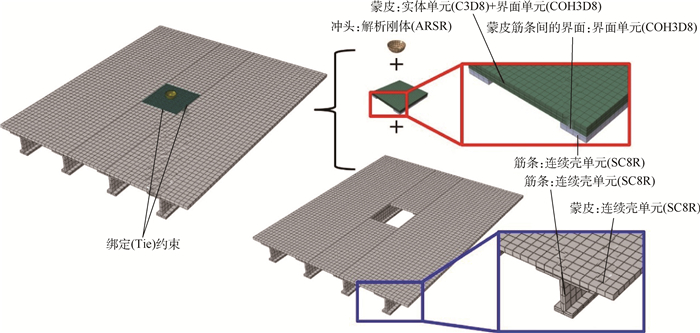 |
| 图 14 复合材料加筋板试验件低速冲击FE模型 Fig. 14 FE model of stiffened composite panel specimen under low-velocity impact |
| 图选项 |
各层界面单元则采用了粘聚区模型。加筋板有限元模型的余下部分则均采用连续壳单元建立,并划分了较为稀疏的网格;为节约计算成本,该部分模型的材料属性被赋予的仅是各对应材料的弹性性能,而没有考虑损伤、塑性等材料的非线性行为。加筋板模型中不包含两端部灌封部分,在两端面施加固支约束。
模型中采用了解析刚体壳模型对冲头进行简化,冲头的质量则以集中点质量的形式施加在代表冲头刚体模型的参考点上。对冲头参考点施加了不同的沿冲击方向的初始速度以模拟不同的冲击能量,而对其他的各方向则进行了约束。
采用ABAQUS/Explicit中的通用接触算法来模拟加筋板中的各类接触问题。加筋板有限元模型中加入了Rayleigh阻尼来消除冲击过程结束后加筋板残余的持续振荡,阻尼参数的取值参考文献[16]。
3.3 计算结果分析SK2-Ⅰ1组加筋板试验件凹坑深度-冲击能量关系有限元模拟与试验结果的对比如图 15所示。可以得出,基于引入纤维断裂的各向异性弹塑性理论建立的复合材料加筋板有限元分析模型可以较好地预测凹坑深度随冲击能量的变化趋势。拐点前后2个冲击能量(20 J和27 J)下加筋板试验件的纤维断裂范围如图 16所示,图中红色区域为纤维断裂损伤区域。从计算结果中可以得出,拐点后试验件冲击位置表面出现纤维断裂,从而导致凹坑深度急剧增大,与试验结论一致。
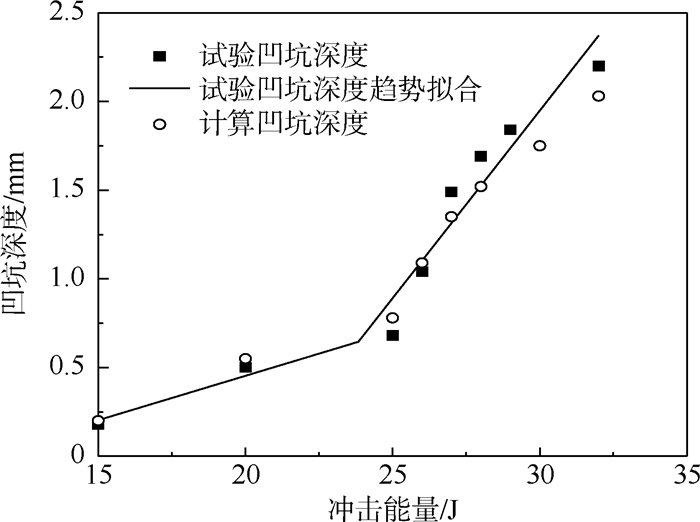 |
| 图 15 SK2-Ⅰ1组试验件凹坑深度计算结果 Fig. 15 Calculation results of dent depths for SK2-Ⅰ1 specimens |
| 图选项 |
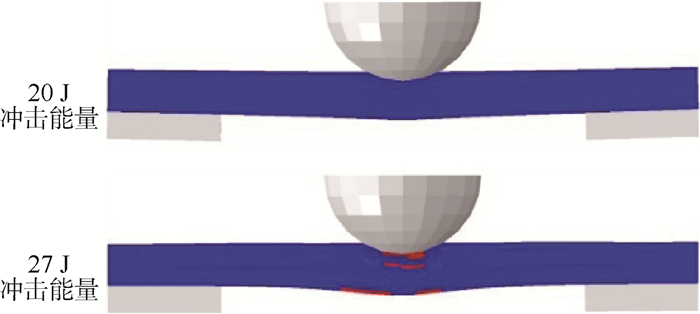 |
| 图 16 拐点前后SK2-Ⅰ1试验件数值计算结果对比 Fig. 16 Comparison of numerical results for SK2-Ⅰ1 specimens before and after knee point |
| 图选项 |
表 6列出了3组含BVID试验件凹坑深度试验和数值计算结果对比,从表中可以看出,数值计算结果与试验结果吻合较好,该有限元模型可以对不同尺寸的加筋板低速冲击后形成的永久凹坑深度进行有效地模拟预测。
表 6 凹坑深度试验结果与数值计算结果对比 Table 6 Comparison of dent depths between test results and numerical results
| 试验件编号 | 冲击能量/J | 凹坑深度 | ||
| 试验结果/mm | 计算结果/mm | 相对误差/% | ||
| SK1-Ⅰ1 | 35 | 1.51 | 1.66 | 9.9 |
| SK1-Ⅰ2 | 33 | 1.52 | 1.59 | 4.6 |
| SK2-Ⅰ1 | 27 | 1.47 | 1.35 | 8.2 |
表选项
图 17所示为SK2-Ⅰ1组加筋板试验件在冲击能量为20 J和27 J情况下分层损伤有限元模拟与试验结果的对比,其中试验结果为对应试验件在冲击点附近的C扫描结果,有限元模拟结果则与此相应地给出了冲击区域附近各界面分层在面内投影的叠加图。由图 17可以看到,分层损伤面积的有限元模拟结果与试验结果大致相同。
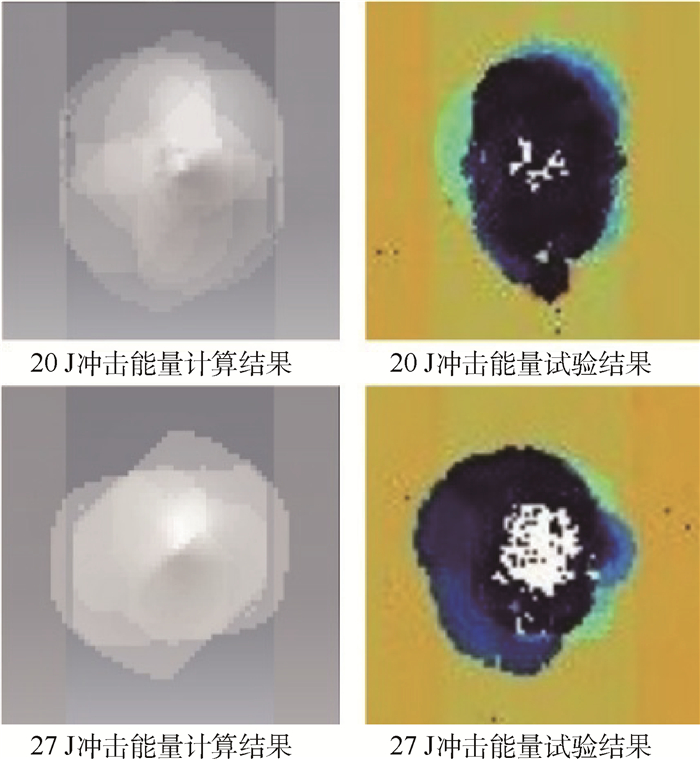 |
| 图 17 SK2-Ⅰ1组试验件分层数值模拟与试验结果对比 Fig. 17 Comparison between numerical results and test results of delamination for SK2-Ⅰ1 specimens |
| 图选项 |
图 18为SK2-Ⅰ1组加筋板试验件在冲击能量为20 J和27 J情况下筋条蒙皮界面分层损伤模拟结果,可以得出随着冲击能量的增大,筋条蒙皮间界面损伤几乎没有扩展,说明筋条对损伤的扩展起到限制的作用,与试验结论一致,也证明了模型建立时忽略筋条分层损伤的假设是合理的。
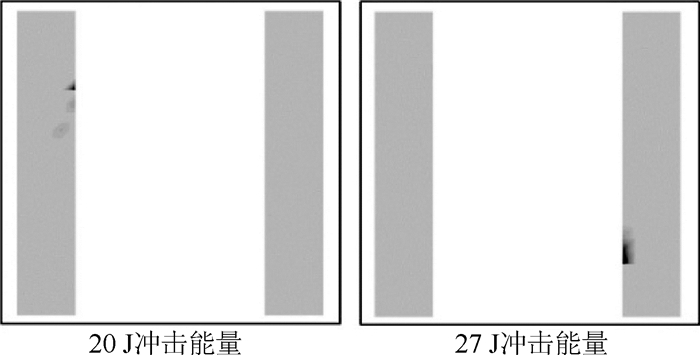 |
| 图 18 SK2-Ⅰ1组试验件筋条蒙皮间界面分层FE结果 Fig. 18 FE results of delamination on interface between skin and stiffener for SK2-Ⅰ1 specimens |
| 图选项 |
4 结 论本文对3组不同尺寸的工型筋条复合材料加筋板低速冲击损伤阻抗性能进行了试验和数值模拟研究,确定了冲击能量、蒙皮厚度以及筋条厚度的影响,结果表明:
1) 复合材料加筋板低速冲击后凹坑深度随冲击能量变化曲线存在一个明显的拐点,表面冲击部位纤维断裂的出现是拐点后凹坑深度急剧增大的主要原因。
2) 随着冲击能量的增大,复合材料加筋板的分层起始载荷变化不大,而最大接触力不断增大且冲头最大位移不断增大,从而导致结构内部损伤不断增加。
3) 随着冲击能量的增大,复合材料加筋板的分层损伤基本被限制在筋条之间的范围内,只有很少面积的损伤扩展至筋条与蒙皮界面,分层面积变化不大。
4) 同样含BVID的复合材料加筋板冲击最大接触力和冲头最大位移随着筋条和蒙皮厚度的增加而增大;而分层起始载荷仅随蒙皮厚度增加而增大,与筋条厚度的变化关系不大。
5) 基于引入纤维断裂损伤的各向异性弹塑性理论建立的有限元模型可以对复合材料加筋板冲击后凹坑深度进行有效的模拟预测。
参考文献
| [1] | 孙侠生. 民用飞机结构强度刚度设计与验证指南(第三册)[M].北京:航空工业出版社,2012:277-280. SUN X S.Guidelines for strength and stiffness design and verification of civil aircraft structures (Vol.3)[M].Beijing:Aviation Industry Press,2012:277-280(in Chinese). |
| [2] | 沈真,杨胜春, 陈普会.复合材料层压板抗冲击性行为及表征方法实验研究[J].复合材料学报,2008,25(5):125-133. SHEN Z,YANG S C,CHEN P H.Experimental study on the behavior and characterization methods of composite laminates to withstand impact[J].Acta Materiae Compositae Sinica,2008,25(5):125-133(in Chinese). |
| Cited By in Cnki (846) | |
| [3] | GREENHALGH E, BISHOP S M,BRAY D,et al.Characterization of impact damage in skin-stringer composite structures[J].Composite Structures,1996,36(3-4):187-207. |
| Click to display the text | |
| [4] | 赵秀峰. 复合材料加筋板冲击损伤及损伤容限研究[D].西安:西北工业大学,2007:29-48. ZHAO X F.Damage behavior of the stiffened plates subjected to the low-velocity impact[D].Xi'an:Northwestern Polytechnical University,2007:29-48(in Chinese). |
| Cited By in Cnki (828) | |
| [5] | 饶辉,许希武, 朱炜垚,等.复合材料加筋板低速冲击损伤的数值模拟[J].复合材料学报,2013,30(4):211-218. RAO H,XU X W,ZHU W Y,et al.Numerical simulation of low velocity impact damage on stiffened composite panels[J].Acta Materiae Compositae Sinica,2013,30(4):211-218(in Chinese). |
| Cited By in Cnki (407) | |
| [6] | WIGGENRAAD J F M, ZHANG X, DAVIES G A O.Impact damage prediction and failure analysis of heavily loaded,blade-stiffened composite wing panels[J].Composite Structures,1999,45(2):81-103. |
| Click to display the text | |
| [7] | GREENHALGH E, SINGH S,HUGHES D,et al.Impact damage resistance and tolerance of stringer stiffened composite structures[J].Plastics Rubber and Composites,1999,28(5):228-251. |
| Click to display the text | |
| [8] | 邵青,何宇廷, 张腾,等.复合材料加筋板低速冲击损伤及剩余强度试验研究[J].复合材料学报,2014,31(1):200-206. SHAO Q,HE Y T,ZHANG T,et al.Experimental research on low-velocity impact and residual compressive strength of composite stiffened panels[J].Acta Materiae Compositae Sinica,2014,31(1):200-206(in Chinese). |
| Cited By in Cnki (221) | |
| [9] | SUH S S, HAN N L,YANG J M,et al.Compression behavior of stitched panel with a clearly visible stiffener impact damage[J].Composite Strutures,2003,62(2):213-221. |
| Click to display the text | |
| [10] | 刘德博,田甜,关志东. 复合材料低速冲击永久凹坑深度预测方法[J].航空制造技术,2011(19):87-90. LIU D B,TIAN T,GUAN Z D.Prediction of permanent indentation depth if laminate subjected to low-velocity impact[J].Aeronautical Manufacturing Technology,2011(19):87-90(in Chinese). |
| Cited By in Cnki (122) | |
| [11] | SWANSON S R. Contact deformation and stress in orthotropic plates[J].Composites Part A:Applied Science and Manufacturing,2005,36(10):1421-1429. |
| Click to display the text | |
| [12] | SHI Y, SWAIT T,SOUTIS C.Modelling damage evolution in composite laminates subjected to low velocity impact[J].Composite Structures,2012,94(9):2902-2913. |
| Click to display the text | |
| [13] | FANTERIA D, LONGO G,PANERTTIERI E.A non-linear shear damage model to reproduce permanent indentation caused by impact in composite laminates[J].Composite Structures,2014,111:111-121. |
| Click to display the text | |
| [14] | BOUVET C, RIVALLANT S,BARRAU J J.Low velocity impact modeling in composite laminates capturing permanent indentation[J].Composites Science and Technology,2012,72(16):1977-1988. |
| Click to display the text | |
| [15] | GUAN Z D, HE W,CHEN J,et al.Permanent indentation and damage creation of laminates with different composite systems:An enperimental investigation[J].Polymer Composites,2014,35(5):872-883. |
| Click to display the text | |
| [16] | HE W,GUAN Z D, LI X.Prediction of permanent indentation due to impact on laminated composites based on an elasto-plastic model incorporating fiber failure[J].Composite Structures,2013,96:232-242. |
| Click to display the text | |
| [17] | 关志东,赵伟. FC落锤式冲击试验机的研制及T300/QY8911层合板低速冲击损伤试验研究[J].复合材料学报,2005,22(Suppl.):27-31. GUAN Z D,ZHAO W.FC impact testing machine and the research of low velocity impact damage of T300/QY8911 composite plates[J].Acta Materiae Compositae Sinica,2005,22(Suppl.):27-31(in Chinese). |
| Cited By in Cnki (153) | |
| [18] | American Society for Testing and Materials Committiee.Standard test method for measuring the damage resistance of a fiber-reinforced polymer matrix composite to a drop-weight impact event :ASTM D7136/D7136M-12[S].Philadelphia:ASTM,2012:10. |
| [19] | SHOEPPNER G A, ABRATE S.Delamination threshold loads for low velocity impact on composite laminates[J].Composites Part A:Applied Science and Manufacturing,2000,31(9):903-915. |
| Click to display the text | |
| [20] | AKATAS M, ATAS C,ICTEN B M.An experimental investigation of the impact response of composite laminates[J].Composite Structures,2009,87(4):307-313. |
| Click to display the text | |
| [21] | TURON A, DÁVILA C G,CAMANHO P P,et al.An engineering solution for mesh size effects in the simulation of delamination using cohesive zone models[J].Engineering Fracture Mechanics,2007,74(10):1665-1682. |
| Click to display the text | |
| [22] | FAGGIANI A, FALZON B G.Predicting low-velocity impact damage on a stiffened composite panel[J].Composites Part A:Applied Science and Manufacturing,2010,41(6):737-749. |
| Click to display the text |
