EIDI是一种电动-机械除冰方式,由线圈产生的电磁力作用于表面附有冰层的蒙皮上,使其产生振动,破坏冰层结构,达到去除冰层的目的。对EIDI系统的研究主要包括电磁场研究、结构动力学研究和除冰效果预测3步。电磁场研究主要解决“发生电路—线圈—蒙皮”除冰模型在电流激励下产生脉冲力的问题,包括对脉冲力造成影响的各种因素的研究等;结构动力学研究分析由脉冲力所产生的结构变形及振动特性;除冰效果预测根据结构变形及振动的动力学特性,建立一套预测除冰的评价准则。
电磁场研究是EIDI系统研究中的重要组成部分,是蒙皮结构动力学分析及除冰效果预测的基础。EIDI系统需要获得电磁脉冲力来进行性能分析,由线圈产生的脉冲力大小及其在蒙皮上的分布情况来确定各种电路参数、部件几何形状及结构因素等对脉冲力的影响规律。尤其是运行电路(电容器的电容、电容器的初始电压和线圈电流等)及线圈的静态参数(几何尺寸、电导率和匝数等),它们是整个EIDI系统设计的核心要素。因此需要建立计算模型,对EIDI系统的电磁场进行仿真。
国外对EIDI系统的研究源于20世纪80年代。美国国家航空航天局(NASA)的Lewis[6]运用汉克尔以及拉氏变换,采用有限差分方法解决电磁场磁矢位问题;Henderson[7]建立了电磁场的汉克尔空间传递模型;威奇塔州立大学的Bernhart和Schrag[8]首次运用有限元的思想分析电磁场,建立了Bernhart-Schrag模型,通过计算线圈与试验蒙皮的电感来求得磁感应强度,进而求出蒙皮受到的电磁力大小。国内对EIDI系统的研究起步较晚且研究成果较少,所见研究方法基本与Zumwalt[3]和Schrag[8]等保持一致。
目前的研究中,进行EIDI系统电磁场仿真时,线圈中的电流多采用等效的正弦波或既定输入[9],即先计算出电流波形再将其作为电磁场仿真的激励。此过程未考虑EIDI系统其他部分对电路参数的反馈,如忽略了线圈与蒙皮之间存在的互感会影响线圈电感值等,这与真实情况存在一定区别。求解电磁力分布时,未关注蒙皮厚度方向上涡电流密度、电磁力密度的变化,仅将蒙皮厚度方向视作一层求解其受力,也会产生误差。
本文在求解电磁力分布时,使用有限元方法对电磁场进行仿真研究,考虑系统其他部分对电路的影响,获得了更精确的电磁力随时间变化的趋势;在求解电磁力分布时,考虑趋肤效应的影响,在蒙皮厚度方向上进行了更详细的分析。使用有限元方法进行仿真采用了更少的假设条件,使求解电磁力分布不仅限于平板线圈之间,还可以进行机翼蒙皮的电磁力分布求解,利于工程应用。
1 EIDI系统组成及仿真方法1.1 系统组成飞机EIDI系统的原理示意图见图 1。在飞机蒙皮的下方安装用铜导线绕制的脉冲电感线圈。当有除冰需求时,启动控制系统以导通脉冲除冰电路,供能电容器向脉冲电路放电,电感线圈短时间内流过上千安的脉冲电流,这一变化电流在线圈周围激发出磁场,使蒙皮中形成感应涡电流,从而在蒙皮上产生巨大的电磁力,该瞬态电磁脉冲力引起了蒙皮小振幅高加速度的振动,以此除掉蒙皮表面的冰层。
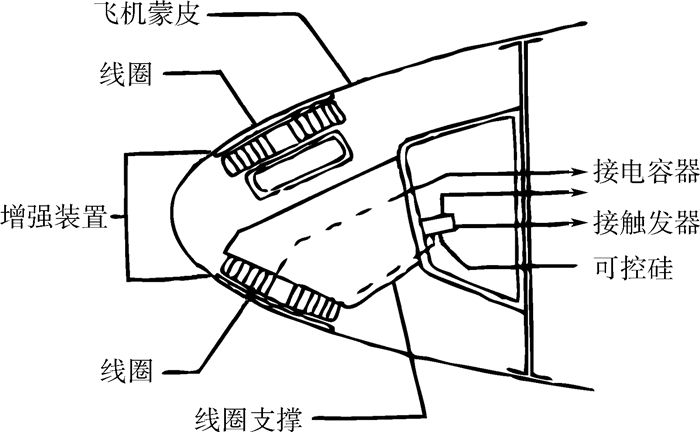 |
| 图 1 EIDI系统原理示意图Fig. 1 Schematic of EIDI system principle |
| 图选项 |
1.2 脉冲力求解原理与方法本文通过麦克斯韦方法来完成脉冲力的求解,微分形式的麦克斯韦方程组为[10]
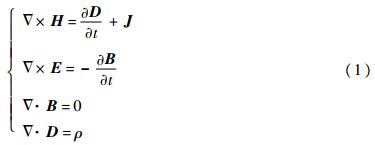
式中:H为磁场强度;D为位移电流;J为电流密度;E为电场强度;B为磁感应强度;ρ为电荷密度。
式(1)表达了求解域内每点处的电磁场状态。在求解麦克斯韦方程组时,还需要用到如下本构关系:

式中:ε、μ和σ为材料本身的物理属性。ε为介电常数(电容率),代表了电介质响应外电场而产生电极化的程度,ε=εrε0,ε0为真空介电常数,εr为相对介电常数。类似地,μ为磁导率,其表示在磁场中导通磁力线的能力,μ=μ0μr,μ0为真空磁导率,μr为相对磁导率。σ为电导率,在介质中其与电场强度之积等于传导电流密度,电导率的值与同种材料的电导率与电阻率互为倒数。
图 2所示为电磁场中的某一个单元(立方体),其电流密度J与流经此处电流I的关系为:I=J·S,其中,S为立方体上与电流密度J垂直面的截面积。
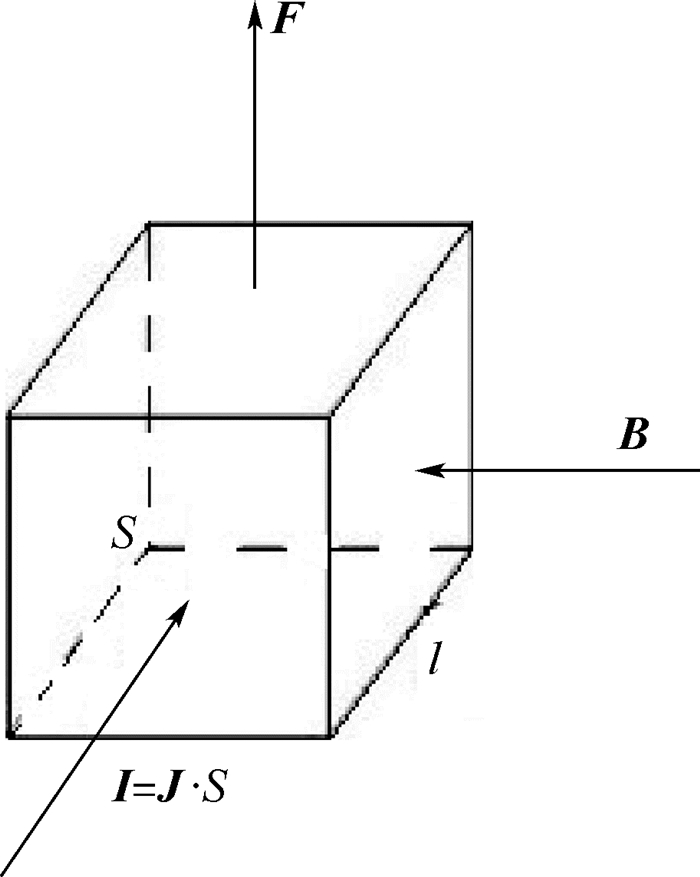 |
| 图 2 单元电流密度、磁感应强度及受力示意图Fig. 2 Schematic of current and magnetic flux density with force of an element |
| 图选项 |
根据磁场对电流的作用,电磁脉冲力的表达式为

因此,对于小立方体有
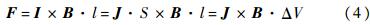
式中:l为J方向上的立方体长度;ΔV=Sl为立方体的体积。由此可知,如果已知某一立方体处的电流密度J、磁感应强度B,即可得到此立方体所受到的电磁力。平板上的电流密度与磁感应强度矢量的外积决定了电磁力F的方向垂直于平板。
使用麦克斯韦方法对EIDI系统进行电磁场分析时,分别将系统中的线圈、蒙皮以及其周围的空间进行单元划分,将其分成有限个立方体(有限元,尺寸形状不一定相同)。EIDI系统工作时,线圈的每一个有限元都是一个小电流元,根据麦克斯韦方程,电流元的电场在空间内激发产生磁场,并在不远处的蒙皮中感生出涡电流,涡电流本身也可以分解为一个个小电流元(用该点处的电流密度J表示)。利用这点处的磁感应强度及电流密度,由式(4)可以求出该点处受到的电磁力。对蒙皮上各点的受力情况进行积分便可得到整个蒙皮上的受力情况。
2 麦克斯韦电磁场有限元求解2.1 电磁力随时间变化的计算为便于说明电磁力的计算原理,先将蒙皮与线圈的组合简化成平板与线圈的形式,见图 3。
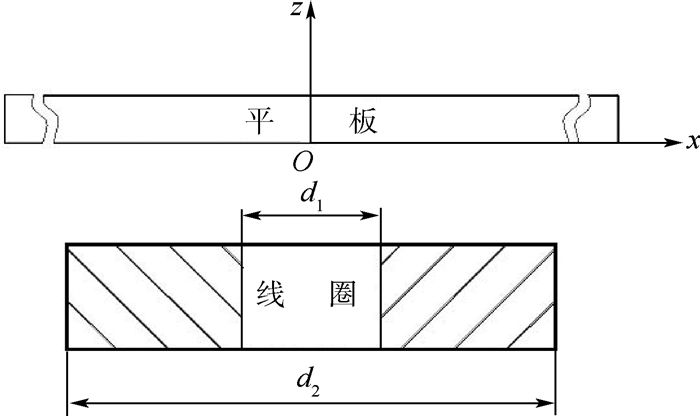 |
| 图 3 平板与线圈组成的EIDI系统电磁场分析几何模型Fig. 3 Geometric model of EIDI system electromagnetic field analysis made up of plate and coil |
| 图选项 |
由于EIDI系统在工作时,平板中感生出的涡电流可以等效为多个半径不同的同轴圆环[11],因此线圈与平板之间存在互感M。在EIDI系统的电路中,线圈与平板的相对位置情况类似于2个串联的电感L1、L2,其等效总电感值为Leq=L1+L2±2M,其中,当2个电感器产生的磁场方向相同时,取“+”,反之,取“-”。易知,当电路中电流值增大时,线圈磁感应强度增大,此时平板中感生出的电磁场与线圈电磁场反向,因此取“-”,此时电路中的等效电感Leq要小于线圈自身的电感L;反之,在电流值减小时,平板感生出的电磁场与线圈电磁场同向,因此取“+”,此时电路中的等效电感Leq要大于线圈自身的电感L。
由式(1)中的∇×E=-∂B/∂t可知,线圈中电流激励通过激发的电场对磁感应强度的变化率产生影响,电路中电感值变小会导致电路响应时间变短。图 4为有、无平板在线圈旁时仿真得到的电路响应。在有平板存在时,等效电感减小,导致电路中的感抗减小,电路电流峰值变大,而等效电感的减小也会导致电路频率升高,峰值提前到来。由于EIDI系统的发生电路中等效电阻值很小,因此该电路属于RLC电路中的欠阻尼情况[11],电路中的电流会随时间产生振荡,其振荡频率为

式中:L、C分别为电路中的总电感、电容值。
 |
| 图 4 仿真过程中电路电流、线圈电感随时间的变化Fig. 4 Current and coil inductance time history in simulation process |
| 图选项 |
图 5为本文加载的激励电流与文献数据的对比。可知,在峰值与实验电流相同的基础上,使用本文方法仿真的电流波形与实验中线圈产生的电流波形更为接近。
 |
| 图 5 线圈中的电流随时间的变化Fig. 5 Time history of current in coil |
| 图选项 |
2.2 平板电磁力在空间的分布电磁力为体积力,其密度会在平板的x方向及z方向(见图 3)上均有变化。x方向上的变化是由线圈尺寸、位置不同而产生的,一般距线圈中心x=(d1+d2)/2处附近的电磁力密度最大;在z方向上,由于导体有趋肤效应,距离线圈较近的一侧平板内涡电流密度会比另一侧大,同时这一侧磁感应强度也较大,因此产生的电磁力较大,反之,远离线圈一侧的平板产生电磁力较小。
通常,用趋肤深度对导体趋肤效应进行度量,其表达式为

从式(6)可知,发生电路的频率越高,平板的趋肤深度越浅。图 6中的J1、J2分别为2种不同电路参数下的平板上下表面电流密度随位置的变化曲线。仿真设定的平板厚度为2 mm,J2所对应的发生电路初始参数为L=30 μH,C=200 μF,平板的电导率和真空磁导率分别为3.8×107 S/m和4π×10-7 H/m。由式(5)、式(6)计算出这种条件下平板的趋肤深度约为1.8 mm,小于平板厚度,平板上的电流密度随离线圈距离的增加而降低,因此在远离线圈一侧的感生涡电流密度下降明显。而J1所对应的发生电路的初始参数为L=30 μH,C=800 μF,计算得到其趋肤深度约为2.55 mm,大于平板厚度,因此平板的z方向各处电流密度变化不明显。需要注意在J1条件下,根据毕奥-萨伐尔定律,平板上下表面的磁感应强度的差异依然存在,因此2个表面上的电磁力密度大小仍然有明显区别。
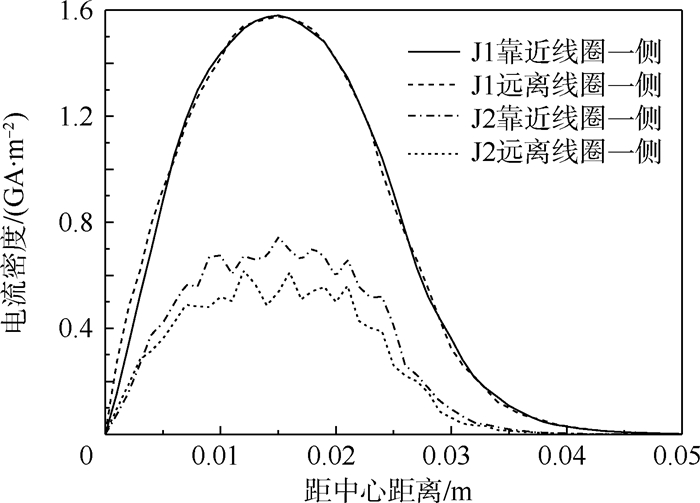 |
| 图 6 电流峰值时刻平板上下表面电流密度随位置变化Fig. 6 Current density on both sides of plate changes with position at peak current |
| 图选项 |
图 7为平板上下表面的磁感应强度随位置变化的分布。随着平板与线圈间距离增大,空间中感生磁场的磁感应强度下降明显,远离线圈一侧的磁感应强度远小于靠近线圈一侧。
 |
| 图 7 电流峰值时刻平板上下表面磁感应强度随位置变化Fig. 7 Magnetic flux density on both sides of plate changes with position at peak current |
| 图选项 |
为了更充分地利用平板的厚度产生电磁力,可以对电路静态参数(电容C、电感L)进行调整,以此改变电路响应频率f,从而使趋肤深度与平板厚度匹配。
图 8清晰展示了在图 6的J2参数条件下,平板上下表面电磁力密度的差别,上下表面间的电磁力密度介于图中实线与虚线之间。在距中心x处不同的厚度位置上,z方向上电磁力密度的变化并不一致(见图 9)。因此,选择平板任何一层上的电磁力乘以一个系数来代替整体受力都会造成误差。
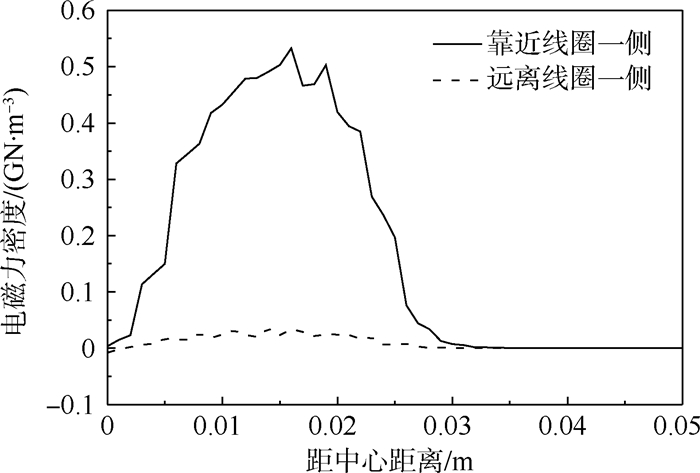 |
| 图 8 峰值时刻平板上下表面电磁力密度随位置变化Fig. 8 Electromagnetic force density on both sides of plate changes with position at peak current |
| 图选项 |
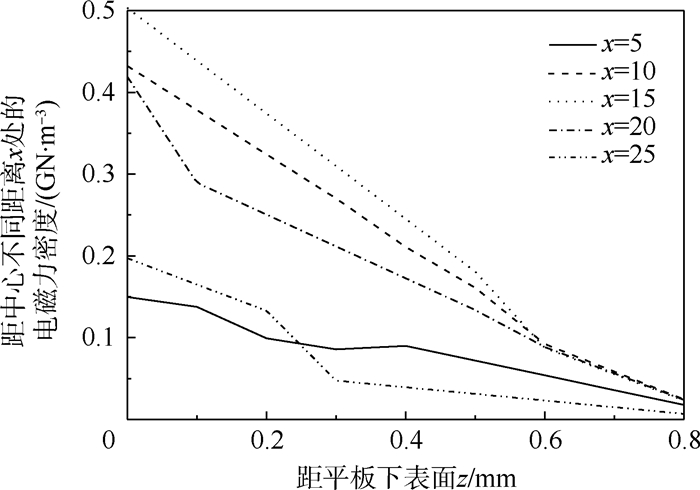 |
| 图 9 电磁力密度随z坐标变化Fig. 9 Electromagnetic force density changes with z coordinate |
| 图选项 |
3 仿真结果与分析3.1 计算模型验证取相同状态的矩形平板为对象进行分析,将本文计算得到的电路及电磁场响应随时间变化结果与文献[12]结果进行比较。图 10显示了本文方法与文献[12]中电磁力随时间的变化结果对比。可见,2种仿真方法的结果响应时间比较一致,本文得到的电磁力比文献[12]中的略小。电磁压力空间分布结果计算出的压强与文献[13]结果的比较见图 11。可见,本文结果与文献[13]的值吻合较好。本文结果在平板中心位置偏大。通过电磁力随时间变化、空间分布的比较可知,本文计算模型具有较好的计算精度。
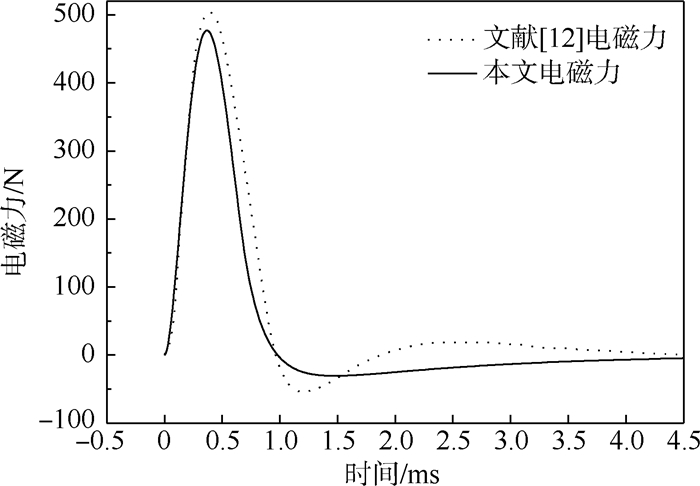 |
| 图 10 2种不同方法求解随时间变化的电磁力Fig. 10 Calculated electromagnetic force time history in two different ways |
| 图选项 |
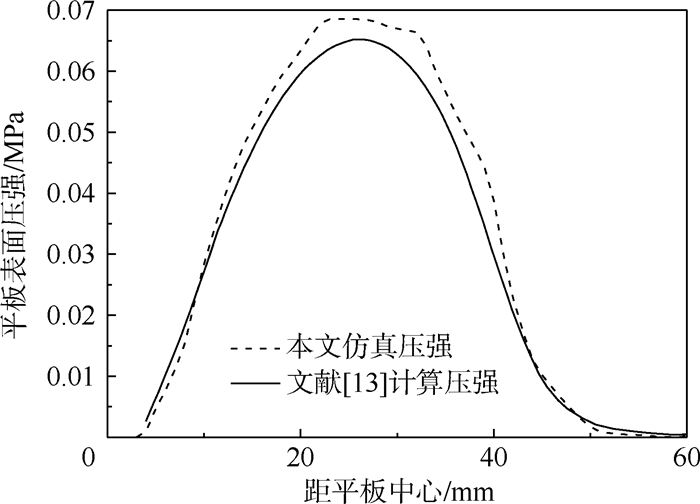 |
| 图 11 2种不同方法平板上的电磁压强对比Fig. 11 Contrast of electromagnetic pressure on plate in two different ways |
| 图选项 |
3.2 平板电磁力分布结果后处理通过仿真可以得到电磁力密度在时间、空间上的分布,分析时需要对仿真结果进行后处理[14, 15]。在平板表面各区域内,不同颜色代表不同电磁力密度(单位为N/m3),见图 12,整理成表 1。d为该处距平板中心的距离,Pmax为平板表面最大电磁力密度转化成的压强。将结果表示成压强随时间的变化规律(见表 2,为0.1Pmax对应区域),加载到平板上进行结构动力学分析。
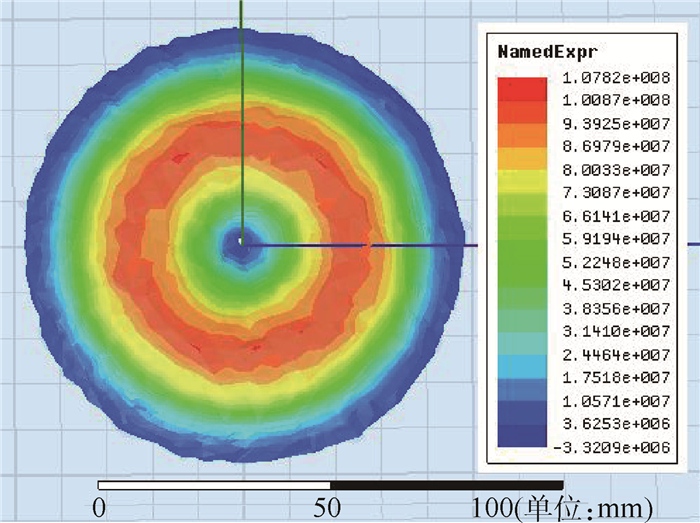 |
| 图 12 电磁力密度在平板上的分布Fig. 12 Distribution of electromagnetic force density on plate |
| 图选项 |
表 1 平板上随区域变化的压强Table 1 Pressure on plate changes with zone
| d/mm | p |
| 7~12 | 0.3Pmax |
| 12~17 | 0.5Pmax |
| 17~22 | 0.7Pmax |
| 22~27 | 0.9Pmax |
| 27~32 | 0.7Pmax |
| 32~37 | 0.5Pmax |
| 37~42 | 0.3Pmax |
| 42~47 | 0.1Pmax |
表选项
表 2 平板上压强随时间的变化Table 2 Pressure on plate changes with time
| t/s | p/MPa |
| 0.000 05 | 0.162 921 |
| 0.000 10 | 0.483 311 |
| 0.000 15 | 0.802 171 |
| 0.000 20 | 1.006 672 |
| 0.000 25 | 1.043 409 |
| 0.000 30 | 0.917 433 |
| 0.000 35 | 0.698 893 |
| 0.000 40 | 0.521 213 |
| 0.000 45 | 0.385 084 |
| 0.000 50 | 0.280 305 |
| 0.000 55 | 0.199 474 |
| 0.000 60 | 0.137 065 |
| 0.000 65 | 0.088 894 |
| 0.000 70 | 0.051 771 |
| 0.000 75 | 0.023 249 |
| 0.000 80 | 0 |
表选项
3.3 带曲率的蒙皮算例结果使用求解麦克斯韦方程组进行仿真的优点之一是在计算时未假设线圈与平板间距离一致,因此可以将在平板上使用的方法直接推广到带有曲率的蒙皮上。按照图 13建立仿真模型,黄色是线圈,外径为58 mm,内径为40 mm,厚度为7 mm,匝数为32;蓝色是蒙皮,在x、y方向上的投影长度分别为245 mm、260 mm,线圈与蒙皮之间的最大距离为10.16 mm。电路参数设置为:线圈等效电感为62 μH,电路等效电阻为0.5 Ω,电容为200 μF,初始放电电压为1 000 V。
 |
| 图 13 蒙皮仿真几何模型示意图Fig. 13 Schematic of skin geometry model for simulation |
| 图选项 |
图 14(a)为某时刻蒙皮上的磁感应强度分布,单位为T;图 14(b)为某时刻蒙皮上的电磁力密度分布,单位为N/m3。可以看到,与平板不同,有曲率蒙皮表面的磁感应强度、电磁力密度并没有呈规则圆环分布。原因在于平板上以板中心为圆心,任意半径的圆上各点距线圈中心的距离都相同,因此磁感应强度等物理量会以圆环形式分布;但在带有曲率的蒙皮表面上,距线圈中心等距离的各点并未分布在同一平面内,因此物理量会出现未以圆环形式分布的状态。图 14(a)中,红色区域代表磁感应强度绝对值较大处,这是与线圈距离较小造成的。同理,图 14(b)中,相同位置出现了电磁力密度的极大值,也是由于此处与线圈距离小。
 |
| 图 14 蒙皮磁感应强度分布和电磁力密度分布Fig. 14 Distribution of magnetic flux density and electromagnetic force density on skin |
| 图选项 |
4 结 论1) 使用有限元分析方法对EIDI系统的电磁场进行研究,考虑系统工作时其他部分对线圈电感的影响,并对电流响应进行了优化,分析趋肤效应对蒙皮电磁力求解的影响,并对电磁力分布进行了计算与分析。
2) 使用的有限元分析方法解决了曲面上电磁力等物理量分布的计算问题,对求解真实蒙皮上电磁力分布有重要意义。
3) 求解蒙皮上全部各有限元的电磁力仿真时间较长,为提高效率,需要对求解进行简化;在仿真中未考虑蒙皮在受力时发生的形变,这会对电磁力的求解产生影响,今后研究中需要考虑结构与电磁力的耦合作用。
参考文献
| [1] | THOMAS S K,CASSONI R P,MACARTHUR C.Aircraft anti-icing and deicing techniques and modeling:AIAA-1996-0390[R].Reston:AIAA,1996. |
| [2] | 何舟东.飞机电脉冲除冰系统参数设计[J].航空科学技术,2014,25(6):33-37. HE Z D.Parameter design of electro-impulse de-icing[J].Aeronautical Science & Technology,2014,25(6):33-37(in Chinese). |
| Cited By in Cnki | |
| [3] | ZUMWALT G.Electromagnetic emissions from an electro-impulse deicing system in a composite wing equipped with lightning protection:DOT/FAA/CT-TN90/32[R].Cambridge:FAA,1991. |
| [4] | LI Q Y,ZHU C L,BAI T.Numerical simulation and experimental verification of the electro-impulse de-icing system:AIAA-2012-1992[R].Reston:AIAA,2012. |
| [5] | LABEAS G N,DIAMANTAKOS I D,SUNARIC M M.Simulation of the electro-impulse de-icing process of aircraft wings[J].Journal of Aircraft,2006,43(6):1876-1885. |
| Click to display the text | |
| [6] | LEWIS G J.The electro-dynamic operation of electro-impulse de-icing systems:AIAA-1986-0547[R].Reston:AIAA,1986. |
| [7] | HENDERSON R A.Theoretical analysis of the electrical aspect of the basic electro-impulse problem in aircraft de-icing application[D].Wichita:Wichita State University,1986:11-20. |
| Click to display the text | |
| [8] | BERNHART W D,SCHRAG R L.Electro-impulse de-icing electro-dynamic solution by discrete elements:AIAA-1988-0018[R].Reston:AIAA,1988. |
| [9] | 李清英,朱春玲,白天.电脉冲除冰系统除冰激励的简化与影响因素[J].航空学报,2012,33(8):1384-1393. LI Q Y,ZHU C L,BAI T.Simplification of de-icing excitation and influential factors of the electro-impulse de-icing system[J].Acta Aeronautica et Astronautica Sinica,2012,33(8):1384-1393(in Chinese). |
| Cited By in Cnki (5) | |
| [10] | 邹澎,周晓萍.电磁场与电磁波[M].北京.清华大学出版社,2008:20-26. ZOU P,ZHOU X P.Electromagnetic field and electromagnetic wave[M].Beijing:Tsinghua University Press,2008:20-26(in Chinese). |
| [11] | 李广超.电脉冲除冰系统建模与实验研究[D].北京:北京航空航天大学,2014:32-58. LI G C.Electro-impulse de-icing system modeling and experimental research[D].Beijing:Beihang University,2014:32-58(in Chinese). |
| [12] | 李清英.电脉冲除冰系统的实验、理论与设计研究[D].南京:南京航空航天大学,2012:55-66. LI Q Y.Research on the experiments,theories,and design of the electro-impulse de-icing system[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2012:55-66(in Chinese). |
| Cited By in Cnki | |
| [13] | 李清英,白天,朱春玲.电脉冲除冰系统除冰激励的仿真研究[J].系统仿真学报,2011,23(12):2799-2804. LI Q Y,BAI T,ZHU C L.Simulation of deicing excitation of electro-impulse deicing system[J].Journal of System Simulation,2011,23(12):2799-2804(in Chinese). |
| Cited By in Cnki | |
| [14] | 蒋大青.瞬变电磁法全程正演模拟研究[D].重庆:重庆大学,2012:31-41. JIANG D Q.The whole course forward modeling for transient electromagnetic method[D].Chongqing:Chongqing University,2012:31-41(in Chinese). |
| Cited By in Cnki (4) | |
| [15] | 刘国强,赵凌志,蒋继娅.Ansoft工程电磁场有限元分析[M].北京:电子工业出版社,2005:219-225. LIU G Q,ZHAO L Z,JIANG J Y.Ansoft finite elements analysis of electromagnetic field engineering[M].Beijing:Electronic Industry Press,2005:219-225(in Chinese). |
