壳体效应漂移影响因素众多,根据其漂移原理主要分为以下4类:伺服电路零位和框架轴上干扰力矩、振动、温度和磁场。目前国内外对壳体效应的研究主要是分析其漂移值随航向角变化的瞬态特性,并据此设计标定补偿电路来保障壳体效应的使用精度[4, 5, 6, 7]。但对于具有“长期贮存、一次使用”的导弹平台惯导系统来说,长期贮存条件下的轴承刚度漂移、材料蠕变和润滑阻尼退化等因素对壳体效应的贮存稳定性影响很大,各因素间的相互作用、相互干扰和相应的变化规律及分析过程十分复杂[8, 9, 10],给贮存条件下平台惯导系统壳体效应漂移的标定和维护带来了极大困难,因此研究其贮存稳定性具有更重要的研究意义。
本文针对伺服电路零位和框架轴上干扰力矩这类影响因素,通过分析其引起壳体效应漂移的功能原理,给出了其漂移表达式,并通过理论和试验相结合的方法对漂移表达式中各参数的变化特性进行了分析,综合推导了平台惯导系统壳体效应漂移变化行为模型,并结合实际贮存环境剖面对其进行了长期漂移特性、加速性和稳定性分析,分析表明在现有贮存条件下伺服电路零位和框架轴上干扰力矩引起的壳体效应在X、Y和Z轴的长期漂移特性相近且无加速特性,与实际使用状态的影响特性不同,从而为合理安排标定维护资源提供了依据。
1 壳体效应漂移的影响因素1.1 研究对象图 1为本文所研究的平台惯导系统框架结构示意图,主要由方位环、俯仰环、横滚环及其连接结构组成,通过平台框架轴上的姿态角传感器为装置提供导弹姿态控制所必需的俯仰角、滚动角和航向角的测量值[11]。
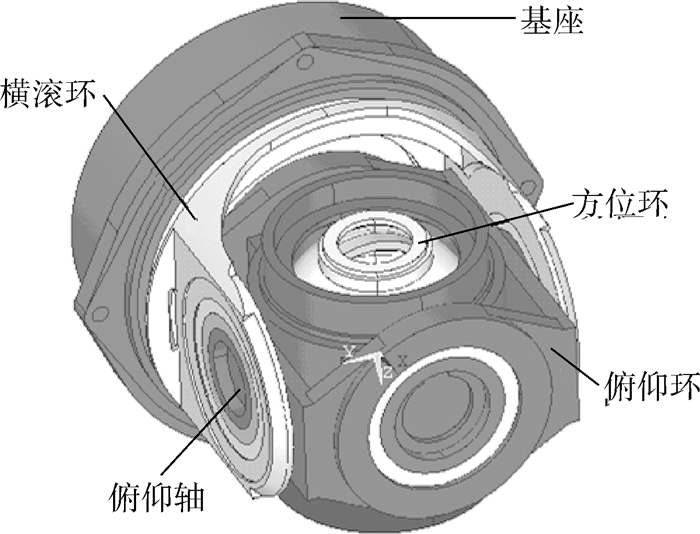 |
| 图 1 平台惯导系统框架结构示意图 Fig. 1 Schematic of frame structure of platform inertial navigation system |
| 图选项 |
在长期贮存条件下,当材料蠕变或平台航向姿态角改变时,图 1中所示平台惯导系统伺服电路零位和框架轴上干扰力矩会发生相应变化,从而使陀螺输出与航向姿态角变化有关的附加漂移[12]。
1.2 壳体效应计算三环三轴平台是靠横滚、俯仰和方位3条伺服电路隔离载体的角运动,使平台在惯性空间保持稳定和跟踪。文献[6, 7, 13]推导得到垂直陀螺稳定平台横滚和俯仰伺服电路、方位陀螺稳定平台方位伺服电路及其自锁回路,并在此基础上给出了伺服电路零位引起的壳体效应弹性漂移为
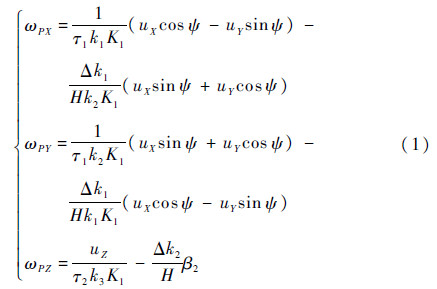
框架轴上干扰力矩引起的壳体效应弹性漂移为
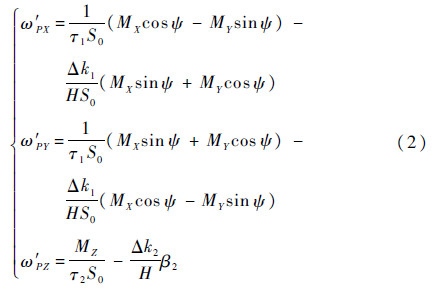
式中:τ1和τ2分别为垂直陀螺和方位陀螺时间常数;K1为前置放大器标度系数;H为陀螺角动量值;S00为伺服电路刚度系数;MX、MY和MZ分别为平台俯仰、横滚和方位轴上的干扰力矩;uX、uY和uZ分别为平台俯仰、横滚和方位伺服电路的零位电压;k1、k2和k3分别为垂直陀螺X轴、Y轴和方位陀螺Y轴传感器标度系数;β2为方位陀螺转子绕其Y轴的偏角;Δk1和Δk2分别为垂直陀螺和方位陀螺的剩余弹性系数;ψ为航向角。2 壳体效应变化行为模型工程经验表明,伺服电路零位主要是指解调器输入端的交流干扰和直流放大器的输入零位,均可折合到解调器的输入端进行分析,作用在平台上的框架轴上干扰力矩主要是轴承摩擦力矩[1, 14],所以本节通过深入分析解调器输入端零位和轴承摩擦力矩蠕变机理和变化行为特性,并对式(1)和式(2)中各模型参数进行变化行为特性分析,综合推导平台惯导系统壳体效应漂移的变化行为模型。
2.1 伺服电路零位变化行为分析平台惯导系统中,伺服电路中的零位电压漂移机理如图 2所示(以俯仰和横滚伺服电路为例描述)。
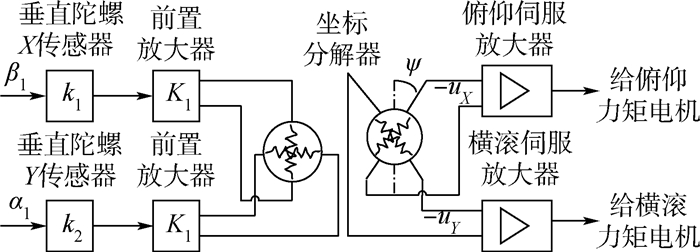 |
| β1—垂直陀螺转子绕其X轴的偏角;α1—垂直陀螺转子绕其Y轴的偏角。图 2 伺服电路零位产生原理 Fig. 2 Production mechanism of servo loop zero |
| 图选项 |
王芳和汤浩[14]指出环境温度的变化会引起伺服电路零位的变化,伺服电路中的零位电压uX、uY、uZ主要是指解调器输入端19.2 kHz交流干扰和直流放大器的输入零位等,这些参数都是模拟电路参数,其变化规律取决于电阻、电容和放大器退化特性。本文通过对试验分析伺服电路关键元件(前置放大器)随时间的变化规律,推导得到某平台惯导系统中伺服零位设计初值uX=uY=uZ=10 mV=0.01 V的变化行为模型为

式中:t为时间,h;T为温度,K。2.2 轴承摩擦力矩变化行为分析轴承摩擦力矩是指与轴承旋转有关的各种阻尼力矩,不仅涉及轴承结构、尺寸、材料及热处理性能等参数,还与工作载荷、润滑条件及环境等参数有关,各种因素相互作用,相互干扰,分析过程极其复杂[10, 11, 12]。
轴承摩擦力矩是当前的研究热点,其计算方法总的来说可分为基于Hertz弹性接触理论的拟静力学分析方法和基于动摩擦的工程经验公式两大类[15, 16, 17]。在长期贮存条件下,由于战备值班和测试标定等因素,某型平台惯导系统轴承摩擦力矩具有动摩擦特性,因此可根据经验计算公式,将轴承摩擦力矩分为无载荷时的摩擦力矩和由载荷引起的摩擦力矩两部分[16]:
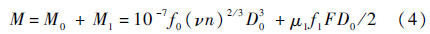
式中:M为轴承摩擦力矩,N·mm;M0为轴承无载荷时的摩擦力矩,N·mm;M1为由载荷引起的摩擦力矩,N·mm;f0为轴衬类型和润滑类型因数;ν为在工作温度下润滑剂基础油的润滑系数,mm2/s;n为轴承转速,r/min;D0=(d+D)/2为轴承平均直径,mm,d为轴承内径,mm,D为轴承外径,mm;μ1为摩擦系数;f1为反映载荷方向的因数;F=sqrt(Fr2+Fa2)为轴承载荷,N,Fr为轴承径向载荷,N,Fa为轴承轴向载荷,N。某型号平台惯导系统所用的滚子轴承使用结构参数值如表 1所示。
表 1 SKF密封球面滚子轴承使用结构参数 Table 1 Structure parameters of SKF sealed spherical roller bearing
| 结构参数 | 数值 |
| 平均转速/(r·min-1) | 5 |
| 轴承内径/mm | 60 |
| 轴承外径/mm | 95 |
| 轴向载荷/N | 150 |
| 径向载荷/N | 180 |
| f0 | 6 |
| f1 | 5×10-4 |
表选项
长期贮存环境下润滑系数和摩擦系数具有蠕变特性,对轴承摩擦力矩的变化影响很大。
1) 润滑系数蠕变规律
平台惯导系统轴承在贮存期内不能再加润滑剂,且要求其既不能缺油又不能有过多油积聚,在温度、时间等长期贮存应力作用下,润滑剂润滑系数发生蠕变,引起轴承摩擦力矩变化。
采用基于Hagen-Poiseuille定律的毛细管黏度测量方法,可得某型号平台惯导系统轴承4123#润滑油在贮存20~70℃温度范围内,不同温度下润滑系数随时间变化的蠕变规律如图 3所示。
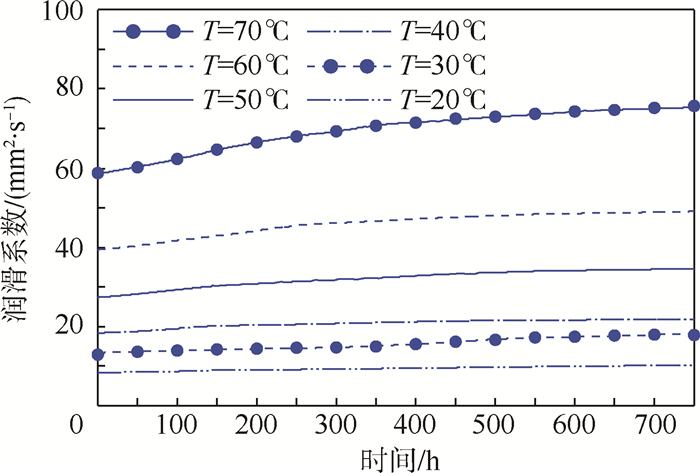 |
| 图 3 4123#润滑油润滑系数蠕变规律 Fig. 3 Creep principle of lubrication coefficients of lubricating oil 4123# |
| 图选项 |
通过系统辨识方法进行曲线拟合,可得图 3中润滑系数随温度、时间变化的蠕变规律为
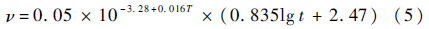
2) 摩擦系数蠕变规律
轴承摩擦系数受过盈量、材料表面微观组分和表面粗糙度等因素综合影响,机理复杂。
在表 1中所示轴向和径向载荷条件下,采用逐级加载轴承磨损试验,可得在常温贮存条件下某型号平台惯导系统滚子轴承摩擦系数随时间的蠕变规律如图 4所示。
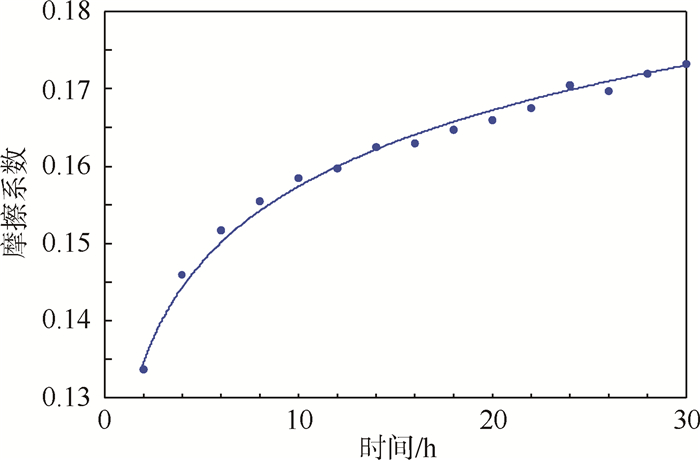 |
| 图 4 滚子轴承摩擦系数蠕变规律 Fig. 4 Creep principle of roller bearing friction coefficients |
| 图选项 |
通过曲线拟合,可得轴承摩擦系数随时间变化的蠕变方程为

结合式(4)~式(6)及表 1可得,轴承摩擦力矩蠕变机理模型为

从式(7)中可以看出,轴承摩擦力矩蠕变近似服从对数变化的规律,即摩擦系数近似单调增大,但增大的速率逐渐趋缓。这一结果表明随着时间的推移,轴承摩擦力矩蠕变对系统稳定性的影响将逐渐减小。
2.3 壳体效应漂移模型参数变化行为分析平台惯导系统中,伺服电路中的零位电压漂移机理如图 2所示(以俯仰和横滚伺服电路为例描述)。
伺服电路零位和框架轴上干扰力矩引起的壳体效应漂移表达式与K1、k1、k2、H、陀螺时间常数τ、剩余弹性系数Δk、β2和S0有关,下面依次对这些参数的变化特性进行研究。
1) 前置放大器标度系数
前置放大器标度系数的退化主要与电阻、电容的退化规律相同,根据电子产品加速变化模型特点,类推其加速模型符合阿伦尼斯模型,主要受温度载荷影响[18]。
通过试验测量分析前置放大器关键电阻变化特性,可得设计初值为K1=50的前置放大器标度系数变化行为模型为
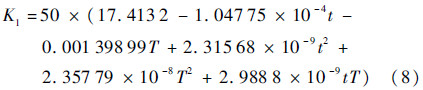
2) 传感器标度系数
传感器是一个测量系统,包括敏感元件和测量线路,传感器有多种形式,国内外动力调谐陀螺仪多采用变磁阻电感式传感器[19]。
变磁阻电感式传感器系数表达式为[13]

式中:Kp为传感器的标度因数;U为电压;δ0为初始时刻铁芯与磁导环之间的起始间隙。工程经验表明传感器标度系数的变化主要与铁芯与导磁环间隙、传感器铁芯中心半径等参数漂移有关,其主要受温度作用下热膨胀系数的影响,但温度作用下热膨胀系数不具有变化特性,所以本文对传感器系数取设计初值为k1=k2=2.5 mV/(′)。
3) 陀螺角动量
陀螺的动量矩表达式为[13]

式中:Jz为陀螺转子极轴转动惯量;ω=πf/30为陀螺转子的旋转角速度,rad/s,f为陀螺转子的转速,r/min。可以看出,陀螺角动量主要取决于设计参数,不随时间和温度变化,故取设计初值H=74.088 kg·m2/h。
4) 陀螺时间常数
时间常数计算公式为[13]

式中:ξ为转子气体阻尼系数;δ1为挠性接头内耗阻尼系数;λ为正交阻尼弹性系数。从上述参数可知,陀螺时间常数主要受材料阻尼影响,因此可以用材料阻尼系数退化规律来反映陀螺时间常数的退化规律。本文通过引入等效黏性阻尼的概念,将陀螺阻尼折算为等价的黏性阻尼(折算的方法是认为其他阻尼与黏性阻尼在振动一周内所消耗的能量相等),并将其作为陀螺时间常数的加速系数,试验测量分析可得某型平台惯导系统设计初值τ1=1/60 h的陀螺时间常数变化行为模型为
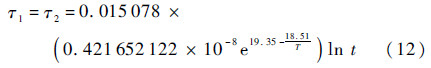
5) 剩余弹性系数
剩余弹性系数的定义为[13]
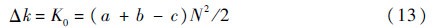
式中:K0为陀螺仪弹性刚度系数;a、b和c为中间平衡环绕x、y和z轴的转动惯量;N为陀螺仪自转角速度。通常,在挠性支撑结构参数已经确定后,可供调整的参数主要是a、b、c和N,因此剩余弹性系数变化特性主要与陀螺材料的刚度特性有关系。通过对动力调谐陀螺仪的材料刚度特性进行试验分析,可得剩余弹性系数退化轨迹辨识模型为

6) 方位陀螺绕X轴的偏角
方位陀螺的X轴通过自锁电路作用于台体,因此β2仅取决于自锁电路的零位和输出等,不随航向角变化。陀螺仪多余轴锁定回路原理方框图如图 5所示[13]。
 |
| 图 5 陀螺仪多余轴锁定回路原理方框图 Fig. 5 Principle block diagram of excessive axis lock loop for gyroscope |
| 图选项 |
陀螺传感器将陀螺仪多余输出轴的转角变成电信号,送给锁定放大器,锁定放大器输出与信号成比例的电流给相应的力矩器,力矩器产生力矩使陀螺仪进动,直到陀螺仪的H轴回到零位。
因此方位陀螺绕转子X轴的偏角与伺服电路零位的变化行为相同,根据式(3)可得设计初值为β2=1.5×10-6rad=(270/π)×10-6(°)的方位陀螺绕X轴偏角的变化行为模型为

7) 伺服电路刚度系数
伺服电路刚度的表达式为[20]

式中:φ(s)为s的函数;θ(s)为转角;Kg=H/C,C为黏性阻尼系数;Km为电机力矩系数;R为力矩电机总电阻;K′aF(s)为伺服放大器传递函数,K′a为伺服放大器的总放大倍数,F(s)为网络传递函数;J为力矩电机绕输出轴的总转动惯量;MD为陀螺力矩。从式(16)中可以看出,伺服电路刚度的加速规律取决于锁定回路的变化特性,因此与伺服电路零位的退化规律相同,参照式(3),可得设计初值S0=5×107 g·cm/rad=(50π/18)kg·m/(°)的伺服电路刚度系数变化行为模型为

2.4 平台惯导系统壳体效应漂移变化行为模型通过将式(3)~式(17)代入伺服电路零位和框架轴上干扰力矩引起的壳体效应漂移表达式(1)和式(2),并设MX0=MY0=MZ0,并将各参数单位统一,且为了更形象地描述伺服电路零位和框架轴上干扰力矩引起的壳体效应变化行为模型,本文采用响应面曲面辨识方法,得到伺服电路零位和框架轴上干扰力矩引起的壳体效应变化行为辨识模型为


式中:g为重力加速度。3 壳体效应贮存行为分析对式(18)进行仿真计算,设贮存条件下航向角为0,得到不同温度下平台惯导系统壳体效应在10 a内的漂移值,如图 6所示。
 |
| 图 6 平台惯导系统X、Y和Z轴壳体效应变化规律 Fig. 6 Heading sensitive drift behavior change law of platform inertial navigation system in X-axis, Y-axis and Z-axis |
| 图选项 |
长期漂移特性分析:从图 6中可以看出,在长期贮存条件下壳体效应漂移在X、Y和Z轴方向的大小和规律相近,这与实际使用条件下X、Y轴方向的漂移明显大于Z轴的规律不同[1]。
加速特性分析:从图 6中可以看出,温度变化对壳体效应漂移的影响不大,但长期温度应力作用下壳体效应漂移变化很明显,说明温度对壳体效应漂移无加速特性。
贮存稳定性分析:某平台惯导系统在库房贮存时的平均温度为20℃,贮存周期为每隔12个月标定测试一次,测试温度为70℃,测试时间为48 h,每个周期后仿真计算平台惯导系统壳体效应累积漂移量,分析其稳定性水平,结果如表 2所示。
表 2 平台惯导系统壳体效应稳定性分析结果 Table 2 Analysis results of heading sensitive drift behavior stability of platform inertial navigation system
| 贮存周期/a | X轴稳定性 | Y轴稳定性 | Z轴稳定性 |
| 1 | 0.143 043 78 | 0.142 997 68 | 0.143 023 47 |
| 2 | 0.143 492 20 | 0.143 446 08 | 0.143 471 88 |
| 3 | 0.143 702 90 | 0.143 656 80 | 0.143 682 58 |
| 4 | 0.143 852 62 | 0.143 806 48 | 0.143 832 30 |
| 5 | 0.143 988 08 | 0.143 941 94 | 0.143 967 75 |
| 6 | 0.143 993 76 | 0.143 946 62 | 0.143 972 44 |
| 7 | 0.144 002 42 | 0.143 956 29 | 0.143 982 10 |
| 8 | 0.144 018 50 | 0.143 972 31 | 0.143 998 13 |
| 9 | 0.144 034 53 | 0.143 988 39 | 0.144 014 21 |
| 10 | 0.144 050 28 | 0.144 004 14 | 0.144 029 95 |
表选项
将表 2中X、Y和Z轴的壳体效应累积漂移量拟合成曲线如图 7所示。从表 2和图 7中可以看出,在没有考虑振动、温度和磁场等影响因素的条件下,伺服电路零位和框架轴上引起的壳体效应稳定性虽能满足现有工程规定中1 a的稳定性水平为0.2℃/h的阈值要求(最大漂移差值≤0.2℃/h),但仍具有较大漂移值,在壳体效应漂移的资源优化配置中应作为重点考虑因素。
 |
| 图 7 平台惯导系统壳体效应累积漂移曲线 Fig. 7 Heading sensitive drift behavior accumulation drift curves of platform inertial navigation system |
| 图选项 |
4 结 论本文研究内容和结论对指导惯性平台标定以及维护资源配置具有重要的理论意义和实用价值。主要贡献与创新点包括:
1) 首次将轴承刚度漂移、材料蠕变和润滑阻尼退化等因素考虑到贮存条件下的壳体效应漂移研究中,为具有“长期贮存、一次使用”特点的导弹平台惯导系统壳体效应变化行为分析提供了理论支持。
2) 通过将轴承摩擦力矩蠕变机理和壳体效应漂移模型参数的逐层分析,推导了平台惯导系统壳体效应漂移变化行为模型,并通过系统辨识方法形象地展现了壳体效应随温度和时间长期漂移的行为。
通过分析壳体效应漂移贮存行为,可知伺服电路零位和框架轴上干扰力矩引起的壳体效应漂移无加速特性,长期温度应力对其漂移影响很大,但仍满足长期稳定性要求,对指导实际平台惯导系统标定、维护资源提高战备质量具有重要意义。
参考文献
| [1] | 胡平华. 动力调谐陀螺稳定平台航向效应漂移研究[D].北京:中国运载火箭技术研究院,2000:50-62. HU P H.Heading DTG stable platform drift effects research[D].Beijing:China Academy of Launch Vehicle Technology,2000:50-62(in Chinese). |
| [2] | NADEAU F. The CIGTF connection:A story of precision testing at the central inertial guidance test[C]//Proceedings of the 51st Annual Meeting of the Institute of Navigation(1995).Manassas,VA:ION,1995:283-292. |
| [3] | ZHANG D R, YE B.Flight-test performance analysis of the platform inertial navigation system[C]//Proceedings of 2010 International Symposium on Inertial Technology and Navigation.Beijing:CSIT,2010:349-354. |
| [4] | 王东升,林晓彬, 刘玉峰,等.陀螺输出中的1N交流成分对平台航向效应的影响[J].中国惯性技术学报,2007,15(1):44-50. WANG D S,LIN X B,LIU Y F,et al.Influence of 1N alternating components of DTG's output on platform heading sensitivity[J].Journal of Chinese Inertial Technology,2007,15(1):44-50(in Chinese). |
| Cited By in Cnki (2) | Click to display the text | |
| [5] | 李方锁,季德成, 陈柳静.惯导平台航向效应的标定与补偿[J].战术导弹技术,2002,37(2):23-27. LI F S,JI D C,CHEN L J.Calibration and compensation of inertial platform heading effect[J].Tactical Missile Technology,2002,37(2):23-27(in Chinese). |
| Cited By in Cnki | |
| [6] | 胡平华,杜祖良. 正交弹性漂移补偿电路对平台航向效应漂移的补偿作用[J].中国惯性技术学报,2001,9(1):31-35. HU P H,DU Z L.Compensation of quadrature spring rate amplifier for platform heading sensitive drift[J].Journal of Chinese Inertial Technology,2001,9(1):31-35(in Chinese). |
| Cited By in Cnki (4) | |
| [7] | 胡平华,杜祖良. 伺服电路零位对平台航向效应漂移的影响与补偿[J].战术导弹控制技术,2003,42(3):34-38. HU P H,DU Z L.Effect and compensation of servo loop zero to the drift of platform heading-effect[J].Control Technology of Tactical Missile,2003,42(3):34-38(in Chinese). |
| Cited By in Cnki | |
| [8] | KANATSU M, OHTA H.Running torque of ball bearings with polymer lubricant (running torque foumulas)[J].Transactions of the Japan Society of Mechanical Engineering(Part C),2005,71(1):272-279. |
| Click to display the text | |
| [9] | LEBLANCE A, NELIAS D.Ball motion and sliding friction on a four-contact point ball bearing[J].Journal of Tribology,2007,129(4):801-808. |
| Click to display the text | |
| [10] | 郑传统,徐绍仁,杨德卿,等. 球轴承摩擦力矩的研究现状与发展[J].轴承,2009(8):52-56. ZHENG C T,XU S R,YANG D Q,et al.State and development on research of friction torque of ball bearings[J].Bearing,2009(8):52-56(in Chinese). |
| Cited By in Cnki (27) | Click to display the text | |
| [11] | 陈永冰,钟斌. 惯性导航原理[M].北京:国防工业出版社,2007:103-106. CHEN Y B,ZHONG B.Principles of inertial navigation[M].Beijing:National Defense Industry Press,2007:103-106(in Chinese). |
| [12] | 林士鄂. 动力调谐陀螺仪[M].北京:国防工业出版社,1988:60-61. LIN S E.Dynamic tuned gyroscope[M].Beijing:National Defense Industry Press,1988:60-61(in Chinese). |
| [13] | 潘荣霖. 飞航导弹惯性器件[M].北京:中国宇航出版社,1990:420-425. PAN R L.Cruise missile inertial devices[M].Beijing:China Astronautic Publishing House,1990:420-425(in Chinese). |
| [14] | 王芳,汤浩. 伺服电路零位对惯导航向效应影响的研究[C]//信号与信息处理技术第三届信号与信息处理全国联合学术会议论文集.雅安:中国体视学学会图像分析分会,2004:290-293. WANG F,TANG H.Study of servo-loop zero drift's effect on inertial navigation heading effect[C]//Proceedings of the 3rd National United Academic Conference on Signal and Information Processing.Ya'an:China Society for Stereology-Image Analysis Branch,2004:290-293(in Chinese). |
| [15] | SZUMIŃ SKI P, KAPITANIAK T.A model for the determination of the resisting torque of the rolling bearing cage motion of slow-speed kinematic pairs[J].Meccanica,2005,40(1):35-47. |
| Click to display the text | |
| [16] | 李梦甦. 多工位制笔机床小动力头系统轴承摩擦力矩的分析[J].东华大学学报(自然科学版),2008,34(4):471-474. LI M S.Friction moment analysis of bearings in small power unit system of bali-pen machine with multi-station[J].Journal of Donghua University(Natural Science),2008,34(4):471-474(in Chinese). |
| Cited By in Cnki | Click to display the text | |
| [17] | 朱江红. 低速球轴承摩擦力矩的分析研究[J].导弹与航天运载技术,2000,248(6):20-25. ZHU J H.The research of the friction moment of low speed ball bearing[J].Missiles and Space Vehicles,2000,248(6):20-25(in Chinese). |
| Cited By in Cnki (43) | Click to display the text | |
| [18] | 张伦东,潘献飞,吴美平. 机抖激光陀螺检测电路前置放大器的设计与分析[J].光电子技术,2006,26(2):110-114. ZHANG L D,PAN X F,WU M P.Design and analysis of pre-amplifier for detection circuit of mechanically dithered ring laser gyroscope[J].Optoelectronic Technology,2006,26(2):110-114(in Chinese). |
| Cited By in Cnki (7) | Click to display the text | |
| [19] | 金超武,徐龙祥. 磁悬浮轴承用位移传感器测量误差[J].南京航空航天大学学报,2009,41(5):626-632. JIN C W,XU L X.Measurement error of displacement sensors for active magnetic bearings[J].Journal of Nanjing University of Aeronautics and Astronautics,2009,41(5):626-632(in Chinese). |
| Cited By in Cnki (1) | Click to display the text | |
| [20] | 郭富强. 论惯导平台中的振动诱导漂移[J].西北工业大学学报,1995,13(1):92-97. GUO F Q.On the vibration induced drift of the inertial navigation platform[J].Journal of Northwestren Polytechnical University,1995,13(1):92-97(in Chinese). |
| Cited By in Cnki (6) | Click to display the text |
