然而运载火箭整体多学科设计模型包含的参数较多,极大地增加了MDF方法的计算复杂度,使得优化过程相当的耗时,导致该方法难于被应用于大规模的工程系统中。为了提高优化过程的效率,学科协调一致性要求，满足文献[8]提出一种含序贯策略的改进协同优化方法,以改进系统优化中存在的大量迭代甚至无解现象。而文献[9]则是将火箭总体设计和多级固体发动机设计分成系统级总体优化和并行的子系统的优化,采用物理规划的思想进行套嵌循环,这样可以缩减每一个子系统的寻优的规模,以提高效率。文献[10]以液体运载火箭为研究对象进行横向分解,单独建立每一级火箭的多学科优化模型,并针对液体运载火箭的特点对学科建模和约束进行了一定简化,提出了一种能够较好地解决液体运载火箭多学科优化问题的方法。
基于以上方法,本文提出将分级优化策略与固体运载火箭的总体优化设计结合,以固体运载火箭为研究对象,对其几何外形学科、气动学科、推进学科、质量学科、弹道/制导学科进行建模[11, 12],并分成若干子系统,通过级间飞行状态连续性条件连接到一起,以起飞质量最轻为目标函数,分别采用并行、串行2种分级优化的方法对三级固体火箭进行优化设计。由于固体运载火箭具有推力不可调、耗尽关机等特点,其推力时间曲线约束严格,飞行过程相对复杂,导致总体优化计算效率低,总体优化设计技术难度更高。本文考虑了上述固体运载火箭特有的约束并通过将约束与目标函数组合的方式,在不影响优化结果的前提下,消除约束,简化了优化算法。与MDF方法相比,采用分级优化的多级运载火箭,其每一个子级都相当于一个单级运载火箭的MDF设计优化,减少了总体多学科建模的工作量,得到了更好的优化结果。
1 多级运载火箭学科模型对运载火箭的多学科建模是优化的基础,本文以美国MINOTAUR IV火箭为研究对象进行建模分析。MINOTAUR IV是以和平卫士洲际弹道导弹为基础研制的新型四级固体运载火箭,其构型如图 1所示,采用惯性制导,地基发射,具有保守设计余量、结构系统先进、组装和测试简便、电子设备模块化等特点,性能可靠[13]。
 |
| 图 1 MINOTAUR IV运载火箭外形示意图Fig. 1 Schematic of shape of MINOTAUR IV launch vehicle |
| 图选项 |
1.1 几何外形学科建模几何外形学科采用CATIA进行建模,如图 1所示。
运载火箭整流罩采用直径为Df的OGIVE外形,将几何外形进行参数化,给定具体的参数即可完全确定运载火箭的形状。本文选取的外形参数为直径Df,整流罩长度Lf,运载火箭每一级长度Li。
为了减少设计变量,本文固定其火箭长度,选取直径为设计变量。
1.2 质量学科建模运载火箭各部件的质量大小与部件设计有关,在设计过程中,质量会随之变化。本文在进行运载火箭质量的计算时将其质量分成2类:一类是不随时间变化的质量,称其为固定质量;一类是随时间变化的质量,称其为非固定质量,如图 2所示。
 |
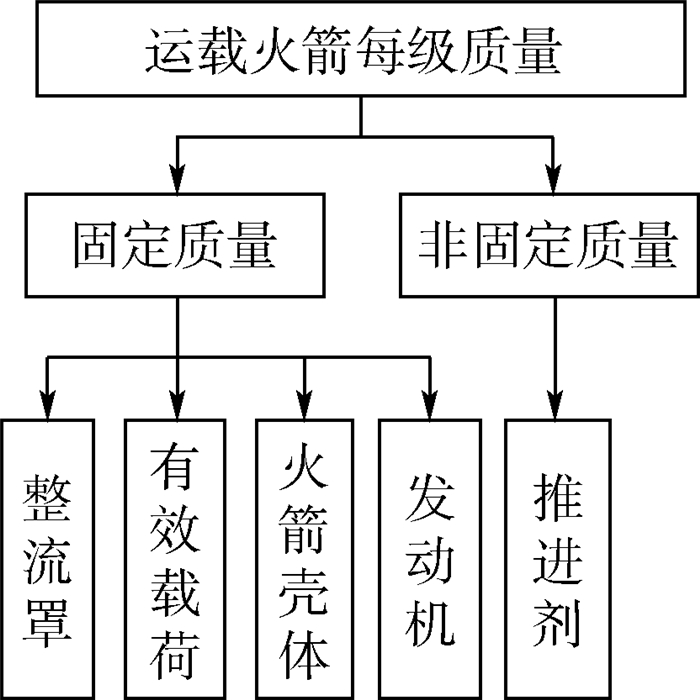| 图 2 质量分类Fig. 2Classification of mass |
| 图选项 |
有效载荷和每一级发动机为给定集中质量,火箭壳体视为薄壁圆筒,质量计算为
式中:ρi为壳体密度;Si为壳体表面积，Si=πDfLi;e为火箭壳体厚度。
整流罩的表面积表达式为
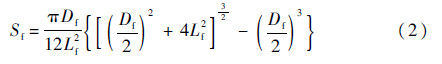
整流罩的质量计算公式为
式中:ef为整流罩厚度(与火箭壳体厚度相等);ρf为整流罩密度。
推进剂的总体质量为设计变量,推进剂质量随着工作时间而变化。
经过上述简化建模,减少了不必要的变量和参数,降低了总体优化的复杂程度,能有效提高计算效率。
1.3 气动学科建模气动计算一直都是运载火箭多学科设计优化的瓶颈之一。运载火箭飞行环境复杂并且多级火箭每一次级间分离导致几何外形的改变,给运载火箭的气动计算带来很大的困难。在本文中采用专用导弹空气动力估算软件MISSLE DATCOM进行气动阻力系数的计算。
本文考虑飞行高度在80km以下,攻角范围为0°～18°,马赫数范围为0~7,建立阻力系数与攻角、马赫数的三维插值表。
图 3是运载火箭第一级在海平面阻力系数随攻角和马赫数变化的示意图。
 |
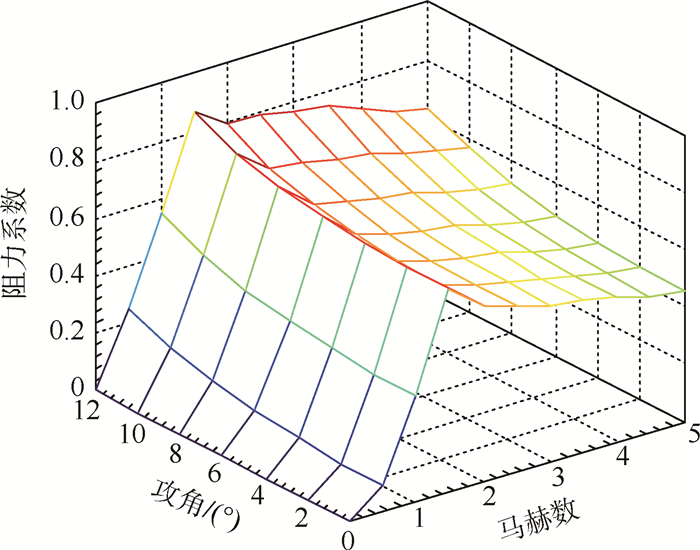| 图 3 阻力系数Fig. 3 Drag coefficients |
| 图选项 |
1.4 推进学科建模MINOTAUR IV前三级均采用固体火箭发动机,本文采用理想固体火箭发动机[14],如图 4所示。
 |
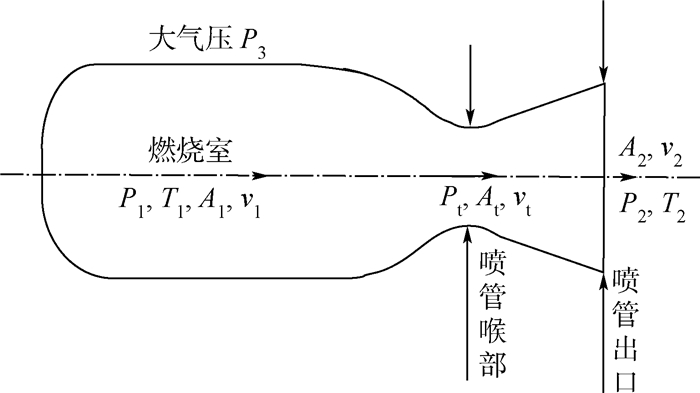| P1 ，T1,A1,v1—发动机燃烧室压强、温度、面积和气流速度；P2 ，T2,A2,v2—喷管出口压强、温度、面积和气流速度；P3—外部大气压强；Pt,At,vt—喉道压强、面积和气流速度。图 4 理想火箭发动机构型Fig. 4 Constitution of ideal rocket engine |
| 图选项 |
发动机推力的表达式为
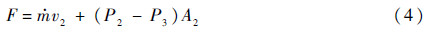
式中:
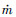为推进剂质量流量。发动机秒流量可以计算为
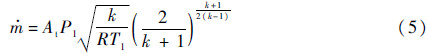
式中:k为燃烧产物比热比;R=8314为气体常数。特征排气速度可以表示为
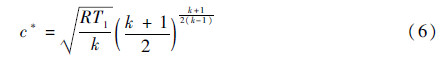
由式(4)、式(5)可以得出
对于比热比为常数的情况下,有喷管出口的速度:
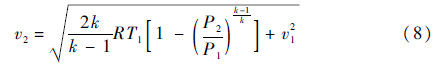
当燃烧室温度即喷管进口温度时,在等熵条件下它与滞止温度T0或(对于化学火箭)燃烧温度差别很小,因此可以简化排气速度的表达式为
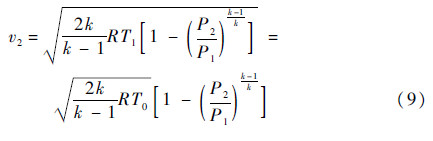
滞止温度和马赫数之间的关系可以表示为
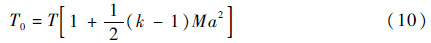
式中:Ma为马赫数。
由式(9)得出修正后的推力公式为
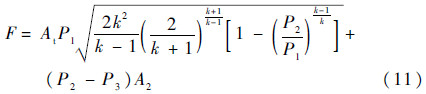
由于固体运载火箭是耗尽关机,且推进剂的燃烧速度由装药截面尺寸和形状等决定,推力不可调节,其推力时间曲线是固定的。相比于推力可调的液体运载火箭,固体运载火箭的总体优化难度高,具体的处理方式在后文介绍。
1.5 弹道/制导学科建模出于对运载火箭飞行高度的考虑,将地球视为圆球,采用极坐标系对运载火箭进行建模,如图 5所示。
 |
| θ—弹道倾角;α—攻角;γ—俯仰角;L—升力;D—阻力;F—推力;v—飞行速度。图 5 运载火箭动力学模型Fig. 5 Dynamic model of launch vehicle |
| 图选项 |
弹道微分方程[15]为
式中:r为飞行半径;m为飞行质量;g为重力加速度,随高度变化,且有
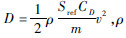,ρ为空气密度，Sref为飞行器的参考面积，CD为飞行器的阻力系数。纵向过载表达式为
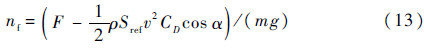
文中运载火箭制导方式采用方案制导,选择程序角输入,在运载火箭飞行的总时间t中,选择10个节点ti,将火箭俯仰角离散到这10个点上,见图 6。整个飞行过程的俯仰角由插值得到。
 |
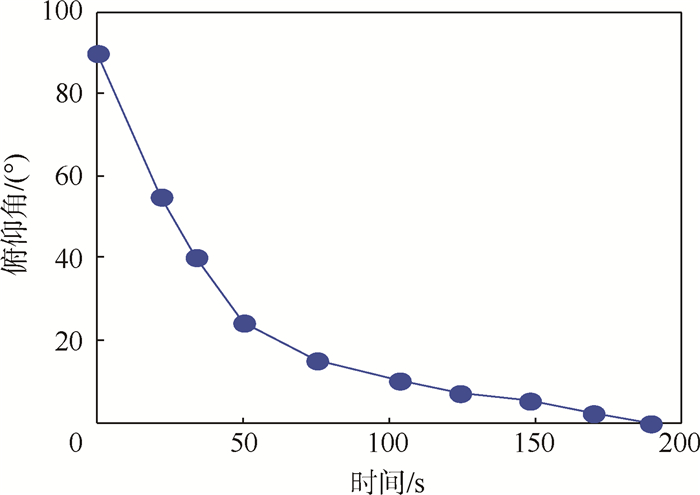| 图 6 俯仰角指令曲线Fig. 6 Profile of pitch angle command |
| 图选项 |
该运载火箭的目标轨道为740km×740km圆轨道,入轨方式选择为Hohmann转移,如图 7所示。
 |
| 图 7 Hohmann转移Fig. 7 Hohmann transfer |
| 图选项 |
运载火箭的目标轨道为半径为r2的圆轨道,中间经过椭圆转移轨道,长半轴为
飞行半径为r1的圆轨道速度为
运载火箭在椭圆轨道r1处的速度为
式中:μ=GM,万有引力常量G=6.67×10－11 N·m2/kg2,地球质量M=5.976×1024 kg。
本文将计算飞行终点高度与飞行终点速度关系,使其满足进入转移轨道约束。
2 多学科分级优化应用于运载火箭最传统的多学科设计优化方法是MDF,本文采用分级优化的方法,按照多级运载火箭飞行阶段进行分段,对每一段火箭单独使用MDF方法进行优化,通过飞行状态参数的连续性条件让各段“拼接”起来,从而得到整体的优化结果。
2.1 分级优化思想2.1.1 经典多学科方法——MDFMDF是解决MDO问题中的最普遍、最经典的方法,它包括多学科分析(MDA)与系统优化器。MDA是多学科分析的过程,它用来分析各学科之间的耦合关系。在每一次迭代过程中都需要调用一次MDA,这样如果增加该系统学科的复杂度,会使MDA过程相当地耗时,极大地增加了MDF的计算复杂度。在系统优化器中经常采用遗传算法进行优化计算。
图 8是MDF流程示意图,可是看出在MDA中集合了多级火箭多学科的耦合分析,工程庞大。
 |
| MGLOW—运载火箭起飞质量; Mpi—各级推进剂质量;Mengine—发动机质量。图 8 MDF流程图Fig. 8 Process of MDF |
| 图选项 |
2.1.2 分级优化方法采用运载火箭分级优化就要将所有的参数按照级数进行分解,其中最主要的是状态变量的分解。
1) 飞行过程分段
对于多级运载火箭而言,整条弹道分成了不同的飞行阶段,而又被级间分离状态连续条件约束着,所有的状态变量中只有质量不是连续变化的。
对固体运载火箭进行分段处理后,每一段是一个子优化问题,可以单独使用MDF方法进行优化,在保证飞行程序的可行性和连续性的前提下,有效简化了运载火箭飞行程序,在一定程度上克服了总体多学科优化变量多、耦合性强的缺点。
状态变量按照不同的飞行阶段分解如图 9所示。图 9中tfi为第i级飞行阶段结束的时间,z为设计变量,u(z,t)为制导规律,xi0(同ui0)为状态变量第i级飞行阶段的初始条件,xi(tfi)(同ui(tfi))为状态变量在第i级飞行阶段的终止结果。为了保持弹道的连续性,在每一级计算中都要满足飞行状态变量连续,包括飞行高度、飞行速度、飞行弹道倾角以及质量突变。
 |
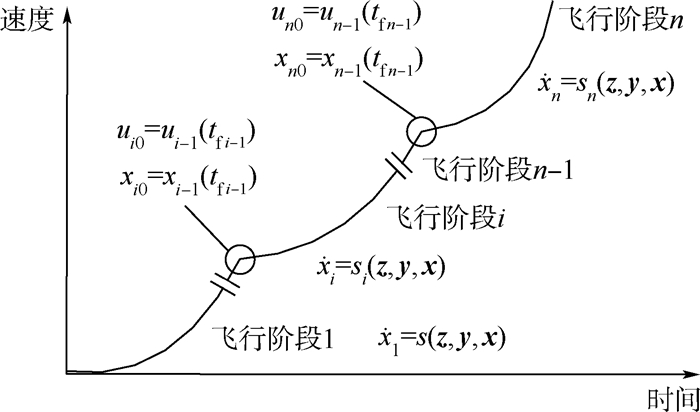| 图 9 多级运载火箭飞行过程分段Fig. 9 Flight process division of multi-stage launch vehicle |
| 图选项 |
2) 优化算法
分级优化分为2个不同层次的优化器,用于系统级优化的为主优化器,其他各学科内部的优化在子优化器中优化。本文中主优化器即系统级优化过程中采用遗传算法,遗传算法在多学科优化设计中应用最为广泛。在子优化器即子级优化过程中采用SQP方法,这是较快解算含有非线性约束条件的最有效的方法之一。
2.2 MDF方法在三级固体运载火箭中,MDF优化方法数学建模如下。
目标函数:
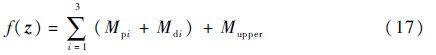
式中:Mdi为推进剂以外的其他质量,包括结构质量、发动机、燃料储箱等;Mupper为上面级质量(包括有效载荷、整流罩等)。
设计变量:
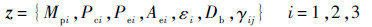
式中:Pci为燃烧室压强;Pei为喷管出口压强;Aei为喷管出口面积;εi为发动机喷管出口面积与喉部面积比;Db为运载火箭弹体直径;γij为每一级的俯仰角。
值得说明的是,弹体长度是根据推进剂装药量、弹体直径、长细比等求得的,是一个间接的优化变量。
约束条件:
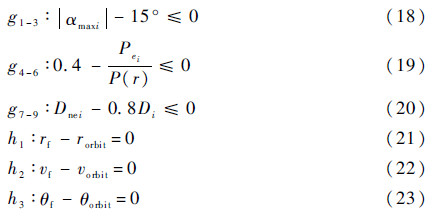
式中:αmax为最大攻角;P(r)为不同高度处的大气压强;Dnei为各级发动机喷管出口直径;rf、vf和θf分别为终端的飞行极半径、飞行速度和弹道倾角;rorbit、vorbit和θorbit分别为入轨极半径、速度和弹道倾角。
同时由于固体运载火箭耗尽关机的特点,还应满足:
即当火箭当前质量Mi等于该级燃料耗尽时的剩余质量Mirest时,立即结束该级飞行程序并分离。
在应用遗传算法进行优化时,等式约束难以满足,于是将等式约束换算到目标函数中,这样目标函数就变为
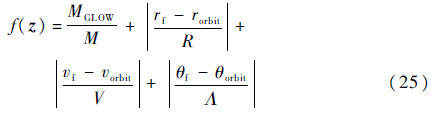
式中:M、R、V和Λ为各参数不同的归一系数。
2.3 分级优化方法在三级固体运载火箭中,本文采用2种分级优化方式：并行计算方式和串行计算方式。
2.3.1 并行方式在三级固体运载火箭中,并行分级方式流程如图 10所示。
 |
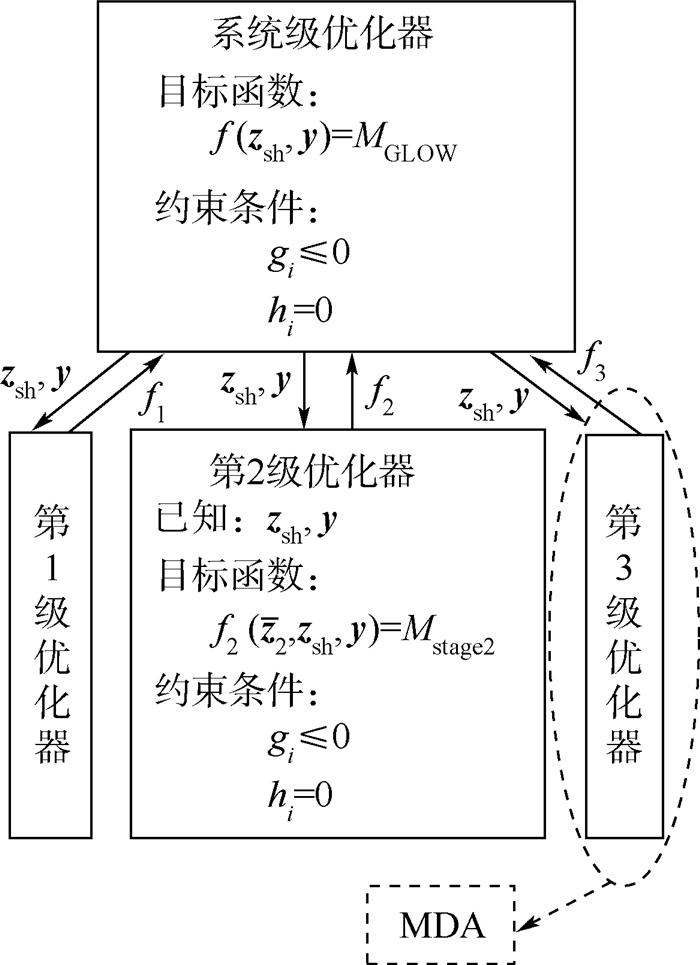| 图 10 并行方式分级优化流程图Fig. 10 Parallel stage-wise optimization process |
| 图选项 |
该方式优化方法数学建模如下[2]。
1) 系统级
目标函数:
设计变量:
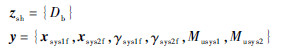
约束条件:
式中:zsh为所有的对其他飞行阶段有影响的设计变量,即多级共用设计变量；y为耦合变量；xsysif={rsysif,vsysif,θsysif,Msysi},包括各级终端飞行极半径、速度、弹道倾角和质量,需要在系统级进行估计;γsys1f和γsys2f为系统级飞行俯仰角；Musys1和Musys2为系统级有效载荷质量；Mu1*和Mu2*为系统级有效载荷质量的上限。
2) 第i子系统级
已知:
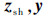
目标函数:
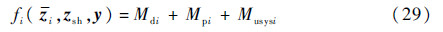
设计变量:
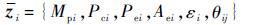
约束条件:
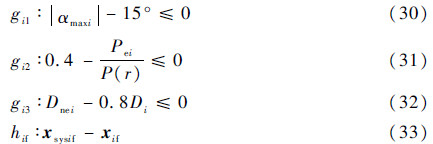
其中最后一级子系统要满足火箭入轨条件。在系统级中存在等式约束,在子系统级中飞行阶段状态变量的末值难以满足等式约束,于是在优化过程中将等式约束消除,改变其目标函数。
由于分级优化的每个子系统都相当于单级运载火箭以起飞质量为目标函数的MDO问题,根据这一特点,将子系统设计在MATLAB中设计成通用的模块。
同理,在具体优化算法实现过程中将系统级目标函数改变为
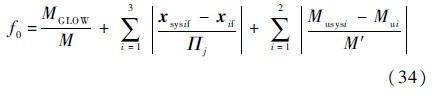
式中:M、Πj和M′为各参数不同的归一系数。
子系统级目标函数变为
该分级优化是并行计算方式,然而在优化过程中需要处理等式约束,这样就导致了优化的误差,为了改变这一状况,将子系统优化给以一定的顺序,变为串行分级优化方式。
2.3.2 串行方式与并行方式不同,串行方式不再将每一级的起飞质量作为系统级的设计变量,而是根据多级运载火箭的特点,按照一定的顺序对子级进行优化。如图 11所示,从第3级到第1级依次进行优化,并将上一级的优化结果作为下一级的已知量。
 |
| 图 11 串行方式分级优化流程图Fig. 11 Serial stage-wise optimization process |
| 图选项 |
下面对该方式分级方法进行数学建模。
1) 系统级
与并行方式不同在于设计变量中没有Musys1和Musys2。
2) 子系统级
for i=3:1
已知:
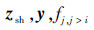
子级优化中与并行方式相同,目标函数中的Musysi由fj,j>i代替。
end
同理,系统级目标函数变为
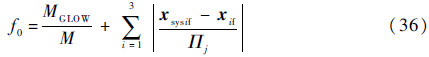
子系统级目标函数变为
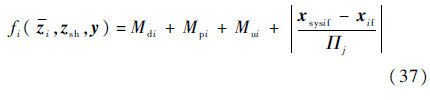
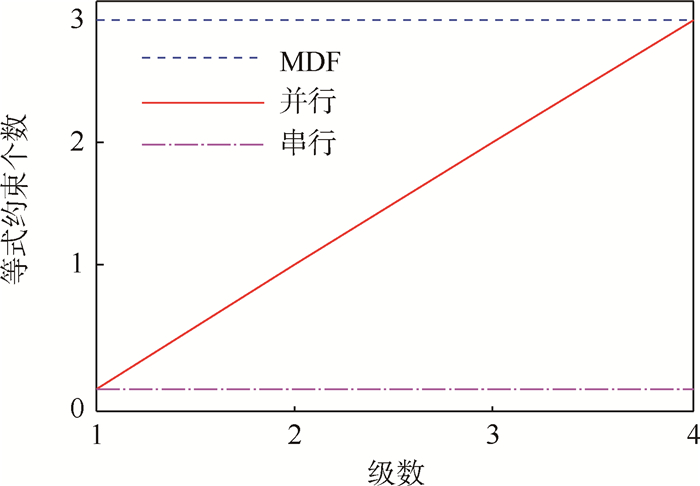
3 优化方法对比及结果分析3.1 设计优化规模本文评判运载火箭设计优化规模包括设计变量个数、不等式约束个数和等式约束个数随运载火箭级数增加的变化。在分级优化中,考虑系统优化级的规模。
图 12~图 14是MDF和分级优化设计变量个数、不等式约束个数和等式约束个数随着运载火箭级数变化的情况。
 |
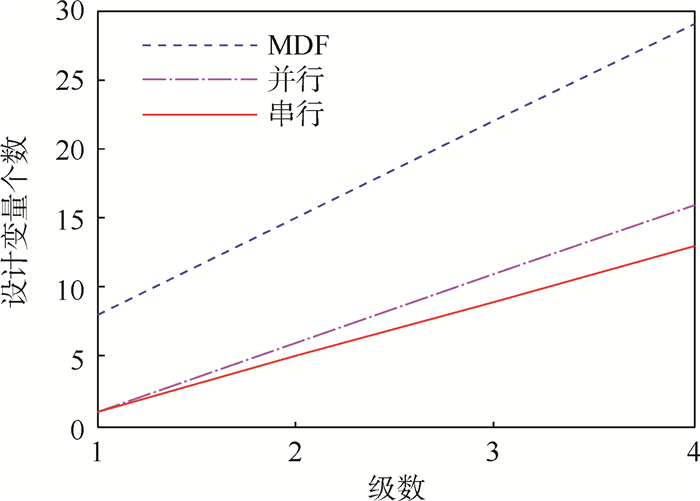| 图 12 设计变量个数随运载火箭级数变化Fig. 12 Number of design variable changing with stages of launch vehicle |
| 图选项 |
 |
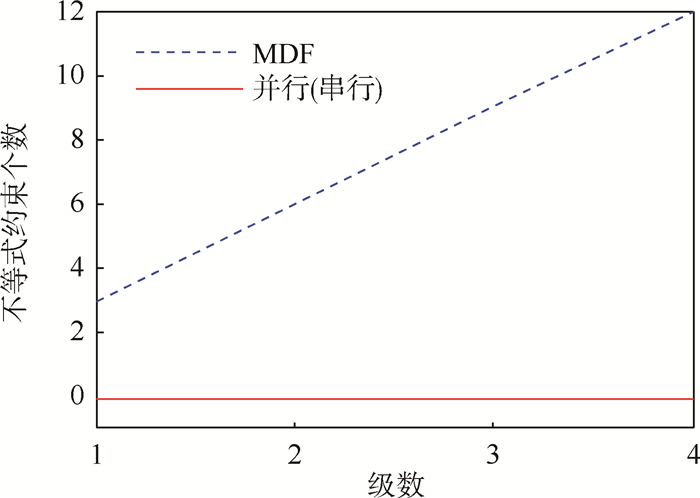| 图 13 不等式约束个数随运载火箭级数变化Fig. 13 Number of inequality constraints changing with stages of launch vehicle |
| 图选项 |
 |
| 图 14 等式约束个数随运载火箭级数变化Fig. 14 Number of equality constraints changing with stages of launch vehicle |
| 图选项 |
通过对运载火箭的分级,系统级的规模缩小,设计变量的搜索空间相应减小,这样使得其设计变量相互影响程度相对MDF小,而MDF在系统级要控制所有的变量,设计规模相应要大一些。而串行的分级优化在设计规模上有了进一步的提高。总之,随着运载火箭级数的增加,分级优化器在MDF上的优越性体现得更加明显。
3.2 优化结果对比MDF和分级优化结果如表 1所示。可以看出分级优化起飞质量比MDF小,有效地降低了运载火箭的起飞质量,尤其对起飞质量较大的固体运载火箭意义重大。而且,结果中的状态变量的连续误差都在5%以内,在运载火箭设计的初级阶段是可以被接受的。
表 1 MDF和分级优化结果对比Table 1 Results comparison between MDF and stage-wise optimization
| 优化方法 | 目标函数 | |
| 达到目标函数最优迭代次数 | 起飞质量/kg | |
| MDF | 97 | 87299.16 |
| 并行 | 47 | 86635.79 |
| 串行 | 34 | 86203.01 |
表选项
由于分级优化设计规模减小,目标最优值的迭代次数比MDF少。由于条件限制,分级优化并行方式是在一台电脑上完成,若采用多台电脑则可以提高计算效率。
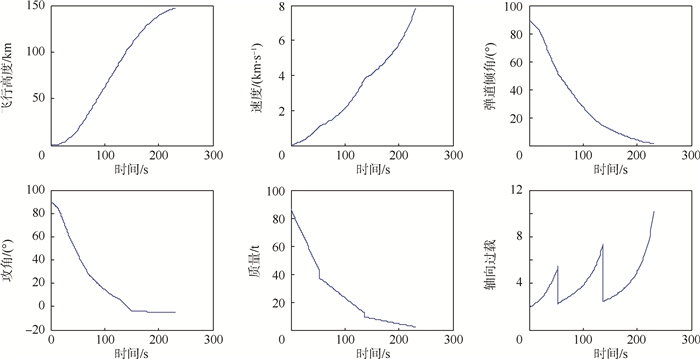
图 15是分级优化的弹道示意图,这里未给出MDF和串行分级优化方式的结果弹道,MDF优化主动段结束时飞行高度比较低,在85km左右,这样就需要足够大的速度来满足进入Hohmann转移的要求,这样就需要比较大的发动机推力,同时增加了上面级发动机压力。而分级优化并行方式飞行高度在150km左右,串行方式飞行高度在250km左右,降低了发动机推力要求。
 |
| 图 15 分级优化结果弹道Fig. 15 Trajectory results of stage-wise optimization |
| 图选项 |
通过以上的对比表明,分级优化将运载火箭按照质量突变分段,减少了设计规模,提高了效率,尤其体现在多级运载火箭的多学科优化应用中。将分级优化并行方式改为串行计算之后,稍稍降低了效率,但是根据火箭级与级之间的特点,减少了约束条件,提高了精度。2种分级优化方式都体现了其优越性。
4 结 论本文结合固体火箭的特点,针对MINOTAUR IV固体运载火箭的前三级完成了多学科建模,分别用MDF和并行、串行2种分级优化方式对其进行了设计优化,将几种方法进行了设计规模和优化结果的对比,证明了分级优化的可行性和应用在多级固体运载火箭上的优越性,为固体运载火箭总体优化提供了一种有效的新方法。
不同级数的运载火箭应用分级优化从设计变量个数、约束条件个数与传统的MDF相比有所减小,以运载火箭起飞质量为目标函数,由于分级优化级与级之间连接的飞行状态变量在系统级统一控制,所以存在一些可以接受的误差。由此可见,将多级运载火箭按照质量突变进行分级的方式可以很好地应用于运载火箭的多学科设计优化中。
参考文献
| [1] | 甘楚雄. 弹道导弹与运载火箭总体设计[M].北京:国防科技图书出版社,1993:53-54. GAN C X.Design of ballistic missile and launch vehicle[M].Beijing:National Defense Science and Technology Press,1993:53-54(in Chinese). |
| [2] | 吴魁,华楠, 弓川锦,等.运载火箭总体多学科协同优化平台方案研究[J].宇航学报,2009,30(6):2072-2076. WU K,HUA N,GONG C J,et al.A MDO platform resolution for launch vehicle system design[J].Journal of Astronautics,2009,30(6):2072-2076(in Chinese). |
| Cited By in Cnki (3) | Click to display the text | |
| [3] | 许林,陈小前, 王振国.飞航导弹总体设计MDO问题表述研究[J].弹箭与制导学报,2008,28(6):1-10. XU L,CHEN X Q,WANG Z G,Research on MDO formulation of cruise missile design[J].Journal of Projectiles,Rockets,Missiles and Guidance,2008,28(6):1-10(in Chinese). |
| Cited By in Cnki (1) | Click to display the text | |
| [4] | 王振国,陈小前. 飞行器多学科设计优化理论与应用研究[M].北京:国防工业出版社,2006:32-33. WANG Z G,CHEN X Q.Research on the theory and application of multidisciplinary design optimization of flight vehicles[M].Beijing:National Defence Industry Press,2006:32-33(in Chinese). |
| [5] | 龚春林,顾振芳, 赵吉松,等.基于整体级概念的多级固体运载火箭设计与优化[J].固体火箭技术,2009,32(1):1-5. GONG C L,GU Z F,ZHAO J S,et al.Design and optimization of multi-stage solid launch rocket based on integrated stage concept[J].Journal of Solid Rocket Technology,2009,32(1):1-5(in Chinese). |
| Cited By in Cnki (1) | |
| [6] | BAYLEY D J. Design optimization of space launch vehicles using a genetic algorithm[D].Alabama:the Graduate Faculty of Auburn University,2007:15-20. |
| Click to display the text | |
| [7] | 龚春林,谷良贤, 栗华.亚轨道重复使用运载器总体多学科优化方法[J].固体火箭技术,2012,35(1):5-10. GONG C L,GU L X,LI H.Multidisciplinary design optimization method for suborbital reusable launch vehicle[J].Journal of Solid Rocket Technology,2012,35(1):5-10(in Chinese). |
| Cited By in Cnki (7) | Click to display the text | |
| [8] | 杨希祥,张为华. 基于改进协同优化方法的固体运载火箭多学科设计优化[J].固体火箭技术,2011,34(6):671-676. YANG X X,ZHANG W H.Multidisciplinary design optimization of solid launch vehicles based on collaborative optimization[J].Journal of Solid Rocket Technology,2011,34(6):671-676(in Chinese). |
| Cited By in Cnki (8) | Click to display the text | |
| [9] | 宣颖,张为华, 张育林.基于物理规划的固体运载火箭多学科设计优化[J].宇航学报,2009,30(2):669-674. XUAN Y,ZHANG W H,ZHANG Y L.Physical programming based multidisciplinary design,optimization of solid launch vehicle[J].Journal of Astronautics,2009,30(2):669-674(in Chinese). |
| Cited By in Cnki (4) | Click to display the text | |
| [10] | BALESDENT M, BÉREND N,DÉPINCÉ P.Optimal design of expendable launch vehicles using stage-wise MDO formulation[C]//Proceedings of AIAA/ISSMO Multidisciplinary Analysis Optimization Conferences.Reston:AIAA,2010:9324-9341. |
| [11] | CASTELLINI F, LAVAGNA M R,RICCARDI A,et al.Multidisciplinary design optimization models and algorithms for space launch vehicles[C]//Proceedings of AIAA/ISSMO Multidisciplinary Analysis Optimization Conferences.Reston:AIAA,2010:9086-9109. |
| [12] | CASTELLINI F, RICCARDI A,LAVAGNA M,et al.Global and local multidisciplinary design optimization of expendable launch vehicles[C]//Proceedings of Structures,Structural Dynamics,and Materials Conferences.Reston:AIAA,2011:1901-1916. |
| [13] | 世界航天运载器大全编委会. 世界航天运载器大全[M].北京:中国宇航出版社,2007:117-121. The World Encyclopedia of Aerospace Vehicle.The world launch vehicles[M].Beijing:China Aerospace Press,2007:117-121(in Chinese). |
| [14] | 萨顿G P,比布拉兹O. 火箭发动机基础[M].洪鑫,等, 译.北京:科学出版社,2003:256-312. SUTTON G P,BIBLARZ O.Rocket engine base[M].HONG X,et al,translated.Beijing:Science Press,2003:256-312(in Chinese). |
| [15] | BALESDENT M, DÉPINCÉ P,BÉREND N.Optimisation multidisciplinaire de lanceurs[J].Journées des Thèses,2010,19(2):225-237. |
| Click to display the text |
