传统的航迹优化方法一般视飞机为质点[5, 6, 7, 8, 9, 10, 11],不仔细考虑其力矩的平衡问题。飞机在实际飞行时,需通过偏转舵面以保持外力矩处于平衡状态[12, 13],以保证实现稳定飞行与性能要求。舵面配平将引起飞机的全机升阻比发生变化。由于飞机的续航性能与其升阻特性密切相关,因此,基于飞机质点假设的传统航迹优化方法存在一定的计算误差;此外,多操纵面布局飞机具有多种舵面组合配平方式,不同的方式对全机升阻比的影响不同,因而对续航性能的影响也不相同。
针对上述问题,本文分析了舵面的力与力矩效应对飞机续航性能的影响;在此基础上,提出了基于舵面配平的续航飞行航迹优化方法。通过在传统航迹优化方法中引入舵面配平,一方面可以实现航迹的精确优化;另一方面,对于多操纵面布局飞机,可以确定其最优的舵面组合配平规律,从而最大限度地发挥飞机的续航性能。
1 基于总能量原理的航迹优化方法基于总能量原理的航迹优化方法[14, 15]是本文的研究基础。根据总能量原理,飞机单位重量的动能与势能之和为等效能量,其表达式为

式中:E、h和V分别为等效能量、飞行高度和飞行速度。
飞机的总航程由上升段、巡航段与下降段3个飞行阶段的水平飞行距离组成,如图 1所示。
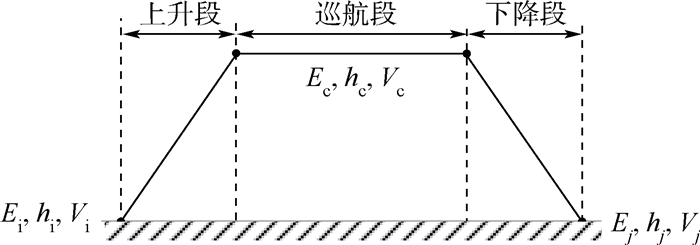 |
| 图 1 飞机纵向飞行剖面 Fig. 1 Vertical flight profile of airplane |
| 图选项 |
从能量的角度来看,在上升段,飞机加速爬升,推力大于阻力,因此等效能量从初始值Ei递增至Ec;在巡航段,飞机定直平飞,推力等于阻力,因此等效能量Ec保持不变;在下降段,飞机减速下滑,推力小于阻力,因此,等效能量从Ec递减至最终值Ej。
根据式(1)与飞机的纵向质点运动方程[12],可得到飞机的质点能量运动模型:

式中:x、γ、mf和Wf分别为水平飞行距离、航迹倾角、耗油量和发动机燃油流量。
对式(2)中的飞行距离方程进行积分,可得到飞机在上升段与下降段的航程。因此,以航程最大为性能指标的航迹优化问题可以表示为

式中:JR为图 1中3个飞行阶段的总航程;mfc为飞机在巡航段的耗油量;λ-为巡航段的平均燃油里程,燃油里程指飞机消耗单位燃油所获得的航程。
如图 1所示,巡航段航迹决定了上升段航迹的最终状态与下降段航迹的起始状态。因此,全飞行剖面航迹优化的第1步是优化巡航段航迹。在此基础上,分别完成上升段与下降段航迹的优化。
根据最小值原理,航迹优化问题最终可以转换为式(4)所示的代数函数的点态极值问题(pointwise extremization problem)[15]:
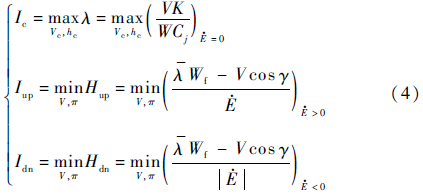
式中:下标c、up和dn分别为巡航段、上升段和下降段;λ为巡航段的燃油里程;Hup与Hdn分别为上升段与下降段的哈密顿函数;K、W、Cj和π分别为升阻比、飞机重量、发动机单位时间单位推力的燃油流量和发动机油门位置。
受飞行状态的影响,飞机在各飞行阶段的燃油经济性不同,即飞机在上升、巡航与下降过程,消耗相同的燃油所产生的航程不同。令飞机在上升段增加、在下降段减少单位等效能量时获得的航程分别为ΔRup与ΔRdn,若这个过程的耗油量用于巡航,将产生的航程为ΔRc,则分别定义ΔRc-ΔRup、ΔRc-ΔRdn为飞机的上升成本与下降成本。
令飞机在整个飞行过程中总的上升成本与下降成本分别为Cup与Cdn。若飞机所有的燃油都用于巡航段时所产生航程为Rc,则飞机的实际总航程为Rc-Cup-Cdn。Rc越大,Cup与Cdn越小,飞机的总航程则越大。
式(4)中,λ越大,表示Rc越大;上升段与下降段的哈密顿函数Hup与Hdn可以统一表示为
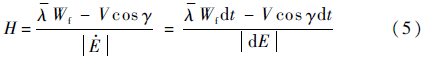
如式(5)所示,Vcosγdt表示飞机在上升段增加(或下降段减少)单位等效能量时所获得的航程,λ-Wfdt表示这个过程消耗的燃油若用于巡航时将产生的航程,因此,哈密顿函数H即为飞机的上升(或下降)成本。H越小,飞机的总航程将越大。
综上所述,如式(4)所示,巡航段航迹优化是以燃油里程λ为性能指标、?=0为约束条件、飞行速度与飞行高度为控制变量,通过控制变量寻优,使λ达到最大; 上升段航迹优化是以上升成本Hup为性能指标、? > 0为约束条件、飞行速度与油门位置为控制变量,通过控制变量寻优,使Hup达到最小;下降段航迹优化是以下降成本Hdn为性能指标、? < 0为约束条件、飞行速度与油门位置为控制变量,通过控制变量寻优,使Hdn达到最小。
2 舵面配平对飞机续航性能的影响 2.1 舵面配平对全机升阻比的影响本文以某型飞机为研究对象,为了提高升阻比,该飞机采用了大展弦比且机身相对较短的气动构型。对于这种特殊的气动布局,需要采用多组纵向操纵面来保证可控性,因而具有多种舵面配平方式。其纵向操纵面包括前翼升降舵与后翼升降舵,在飞行过程中,前翼升降舵与后翼升降舵可以单独或组合偏转,为飞机提供配平力矩。
舵面偏转将改变飞机的气动特性,且不同的舵面配平方式对飞机气动特性的影响也不同。对于本文的研究对象,当飞机定直平飞(h=12 km,Ma=0.8)时,其前翼升降舵单独配平(前翼配平)、后翼升降舵单独配平(后翼配平)以及前翼升降舵与后翼升降舵组合配平(组合配平)所引起的全机升阻比变化如图 2所示。
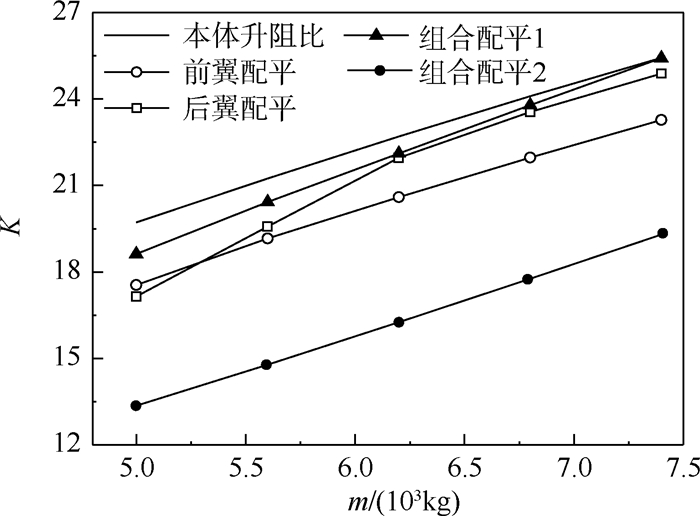 |
| 图 2 舵面配平对全机升阻比的影响 Fig. 2 Effects of control surface trimming on lift-drag ratio of aircraft |
| 图选项 |
飞机保持定直飞行时需要满足切向力平衡、法向力平衡与外力矩平衡3个条件。根据飞机的纵向运动方程[12],求解相应的配平迎角、配平舵面与配平油门,可以使飞机满足上述3个平衡条件。在同一飞行条件下,对于单一舵面配平方式,只存在唯一的配平解;对于舵面组合配平方式,则存在多组配平解。因此,图 2中给出了舵面组合配平方式下的2条升阻比曲线,分别对应最大与最小的全机升阻比。如图 2所示,舵面配平将明显地改变飞机的全机升阻比。此外,通过组合舵面配平,飞机可以获得比单一舵面配平更大或更小的全机升阻比。
2.2 升阻比对续航性能的影响通过航迹优化能够提高飞机的续航性能,如式(4)所示,影响航迹优化结果的因素包括性能指标与控制变量。因此,升阻比对飞机续航性能的影响可以从升阻比对性能指标与控制变量寻优范围的影响2个方面进行分析。
2.2.1 升阻比对性能指标的影响对于巡航段,如式(4)中第1个式子所示,性能指标λ与升阻比K成正比。对于上升段与下降段,由于飞机非急剧机动时的航迹倾角通常不大(γ < 15°)[16],因此,如式(5)所示,性能指标H的分子近似为λWf-V,其值仅由飞行速度V与发动机油门位置π决定,不受K影响;分母为等效能量变化率的绝对值|?|,?即为飞机单位重量的剩余功率,其表达式为?=(Ta/W-1/K)V[12],Ta为可用推力,对于上升段,? > 0,即 ?随K增大而增大;对于下降段,? < 0,即?随K增大而减小。
因此,巡航段的性能指标λ随K增大而增大;上升段与下降段的性能指标H亦随K改变而变化,其变化规律由性能指标H的符号决定。
2.2.2 升阻比对控制变量寻优范围的影响飞机在某一重量与飞行高度下,最大可用飞行速度Va.max、最小可用飞行速度Va.min、最大可用推力Ta.max、最小可用推力Ta.min以及平飞需用推力TR如图 3所示。
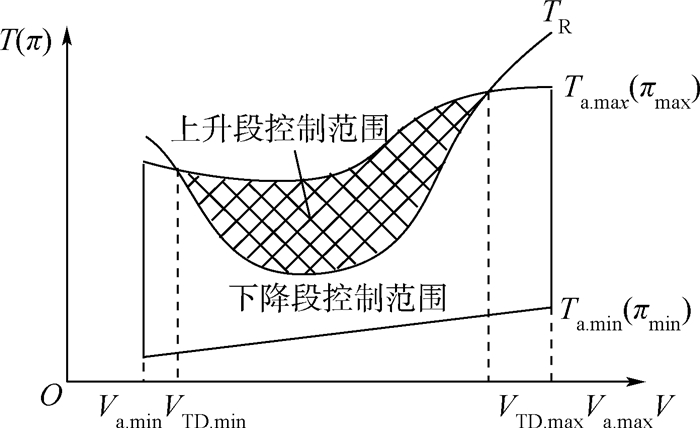 |
| 图 3 控制变量寻优范围 Fig. 3 Search range of control variable |
| 图选项 |
对于巡航段,控制变量为飞行速度与飞行高度。飞机巡航时应满足Ta=TR,因此,Ta.max与TR的交点决定了巡航速度的可用范围[VTD.min,VTD.max]。由飞机平飞需用推力的计算式TR=W/K可知[12],飞机重量不变时,图 3中平飞需用推力曲线随K增大而向下平移,使Ta.max与TR的交点所对应的速度VTD.min变小、VTD.max变大,即巡航速度的寻优范围扩大。
对于上升段与下降段,控制变量为飞行速度与油门。如图 3所示,最大可用飞行速度Va.max、最小可用飞行速度Va.min、最大可用推力Ta.max(对应最大油门)以及最小可用推力Ta.min(对应最小油门)构成了飞机总的飞行速度与油门可用范围。由于飞机上升时应满足Ta > TR,下降时应满足Ta<TR,因此,在整个飞行速度与油门可用范围内,Ta.max与TR所包络的区域即为上升段的飞行速度与油门可用范围,Ta.max与TR所包络之外的区域即为飞机下降时的飞行速度与油门可用范围。由于图 3中的平飞需用推力曲线随K增大而向下平移,因此,增大K将使上升段的控制变量寻优范围扩大,减小K将使下降段的控制变量寻优范围扩大。
综上所述,舵面配平将使飞机的全机升阻比发生改变,并最终影响航迹优化的结果。根据第1节,对于巡航段,同时增大性能指标与控制变量寻优范围,能够使航迹优化获得更优解;对于上升段与下降段,减小性能指标、增大控制变量寻优范围,能够使航迹优化获得更优解。因此,若舵面配平所引起的升阻比变化能够同时对性能指标与控制变量寻优范围产生有利影响,则将提高飞机的续航性能;若同时对性能指标与控制变量寻优范围产生不利影响时,则将降低飞机的续航性能;若仅对性能指标与控制变量寻优范围中的二者之一产生有利影响,则不能直接判断升阻比变化对航迹优化结果的影响,还需从飞行原理进一步分析舵面配平对飞机续航性能的影响。
3 基于舵面配平的航迹优化方法传统的航迹优化方法并不仔细考虑飞机的力矩平衡问题,因此,性能指标的解算、控制变量寻优范围的确定都忽略了舵面气动效应的影响。在传统航迹优化方法的基础上,通过在控制变量中引入舵面偏度,并以力矩平衡作为附加的约束条件,可以得到基于舵面配平的飞机续航飞行航迹优化方法:
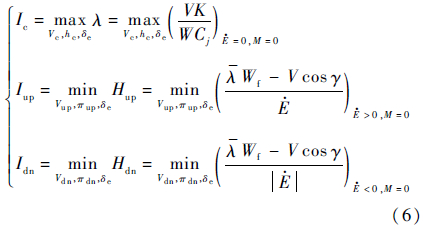
式中:δe为飞机的各纵向操纵面;M为力矩。如第1节所述,全飞行剖面航迹优化首先是优化巡航段航迹,再优化上升段与下降段航迹。在巡航段,飞机的等效能量保持不变,重量随着燃油消耗而逐渐减小,因此航迹优化是针对飞机的每一重量状态,在控制变量寻优范围内,求解满足约束条件且使性能指标λ达到最大的最优控制变量,在此基础上,解算其他状态参数;在上升段与下降段,飞机的等效能量E分别递增与递减,因此航迹优化是针对飞机每一等效能量状态,在控制变量寻优范围内,求解满足约束条件且分别使性能指标Hup与Hdn达到最小的控制变量,在此基础上,解算其他状态参数。因此,上升段、巡航段与下降段的航迹优化流程如图 4所示。
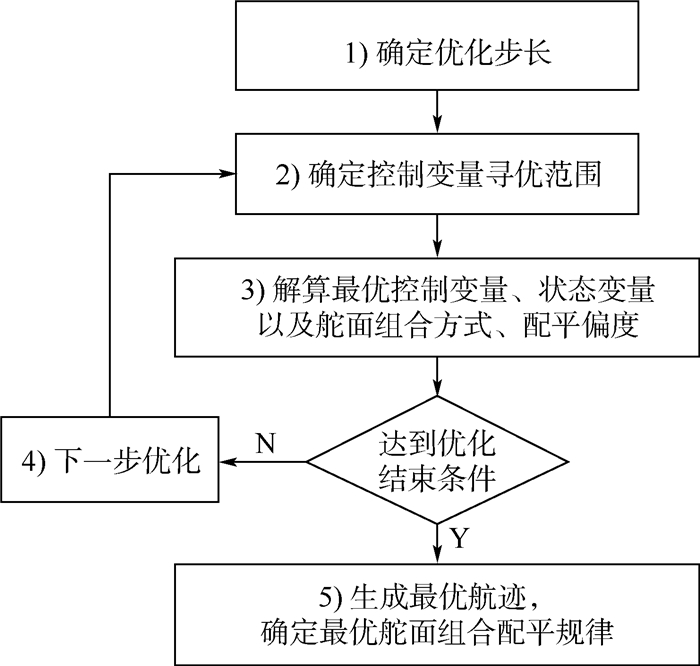 |
| 图 4 航迹优化流程 Fig. 4 Trajectory optimization flow |
| 图选项 |
以巡航段为例,图 4所示的优化流程中主要步骤的具体说明如下:
1) 将飞机的重量范围分割成若干计算点。
2) 确定当前计算点对应的飞行高度、飞行速度以及舵面偏转的容许范围。
3) 以?=0、M=0作为约束条件,分别解算使性能指标达到最大的最优控制变量、状态变量以及舵面组合方式与配平偏度。
4) 针对下一重量计算点,重复步骤2)与步骤3)。
5) 由步骤3)确定每一计算点的最优状态变量以及舵面组合方式与配平偏度,即可得到飞机在整个飞行过程的最优航迹与舵面配平规律。
4 算 例以第1.2节所述的研究对象为算例,在航迹优化过程中,飞机载油2 400 kg,巡航高度范围为10~12 km,巡航马赫数范围为0.6~0.8,上升段初始飞行状态和下降段最终飞行状态均为h=0.1 km、Ma=0.2。在上述条件下,算例飞机在无配平 (即传统航迹优化方法)、前翼配平、后翼配平以及最优组合配平4种方式下的航迹优化结果如图 5所示。
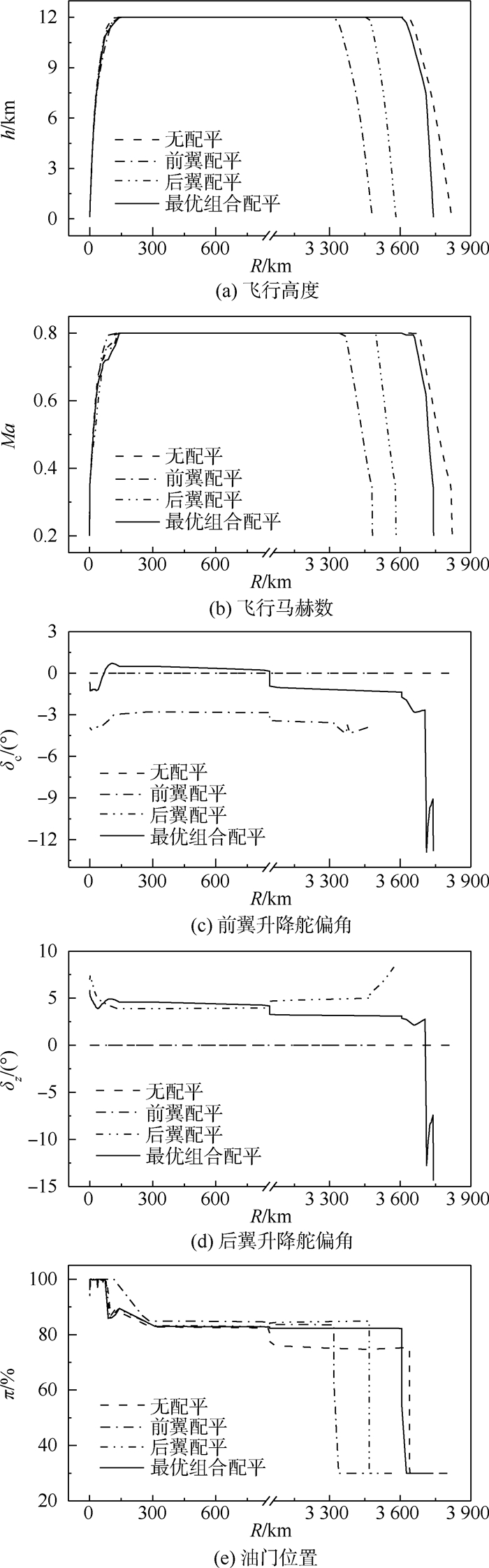 |
| 图 5 飞行航迹优化结果 Fig. 5 Flight trajectory optimization results |
| 图选项 |
图 5(e)中,π=100%和π=30%分别表示发动机均处于最大推力和慢车状态。由图 5(a)和图 5(b)可知,4种方式下的飞行航迹均明显呈现上升段、巡航段及下降段3个飞行阶段,巡航段均为主要的飞行阶段。最优巡航高度均为巡航高度范围的上边界(hopt=12 km),最优巡航马赫数均为巡航马赫数范围的上边界(Maopt=0.8)。 根据上述4种方式下的航迹优化结果,算例飞机的续航性能如表 1所示。
表 1 算例飞机的续航性能 Table 1 Endurance performance of example airplane
| 方式 | 耗油量/kg | 总航程/km |
| 无配平 | 2 400 | 3 821 |
| 前翼配平 | 2 400 | 3 482 |
| 后翼配平 | 2 400 | 3 583 |
| 最优组合配平 | 2 400 | 3 742 |
表选项
如表 1所示,3种舵面配平方式下的航程均小于无配平方式下的航程。这是由于飞机在实际飞行时,需要偏转舵面以保持外力矩处于实时平衡状态。而飞机本体的气动特性通常经过优化设计,当舵面偏转时,往往会降低飞机本体的升阻特性,如图 3所示。此外,对于算例飞机,巡航段是主要的飞行阶段,巡航段续航性能与飞机的全机升阻比正相关。因此,相比于无舵面配平,考虑舵面配平时的航程计算结果更小,但这更接近于飞机实际的续航性能。
在航迹优化过程中,算例飞机在前翼配平、后翼配平以及最优组合配平下的性能指标与升阻比分别如图 6与图 7所示。
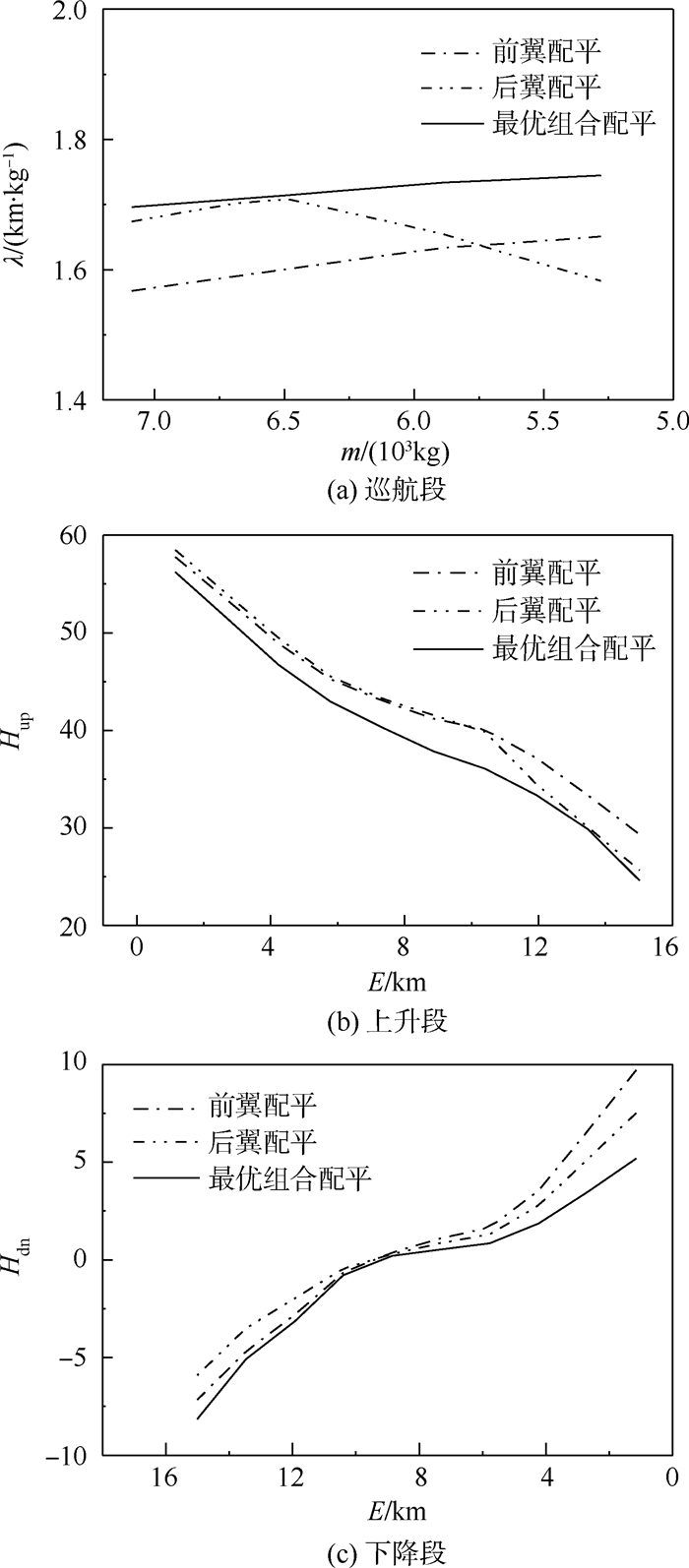 |
| 图 6 3种配平方式下的性能指标 Fig. 6 Performance indexes under three trimming modes |
| 图选项 |
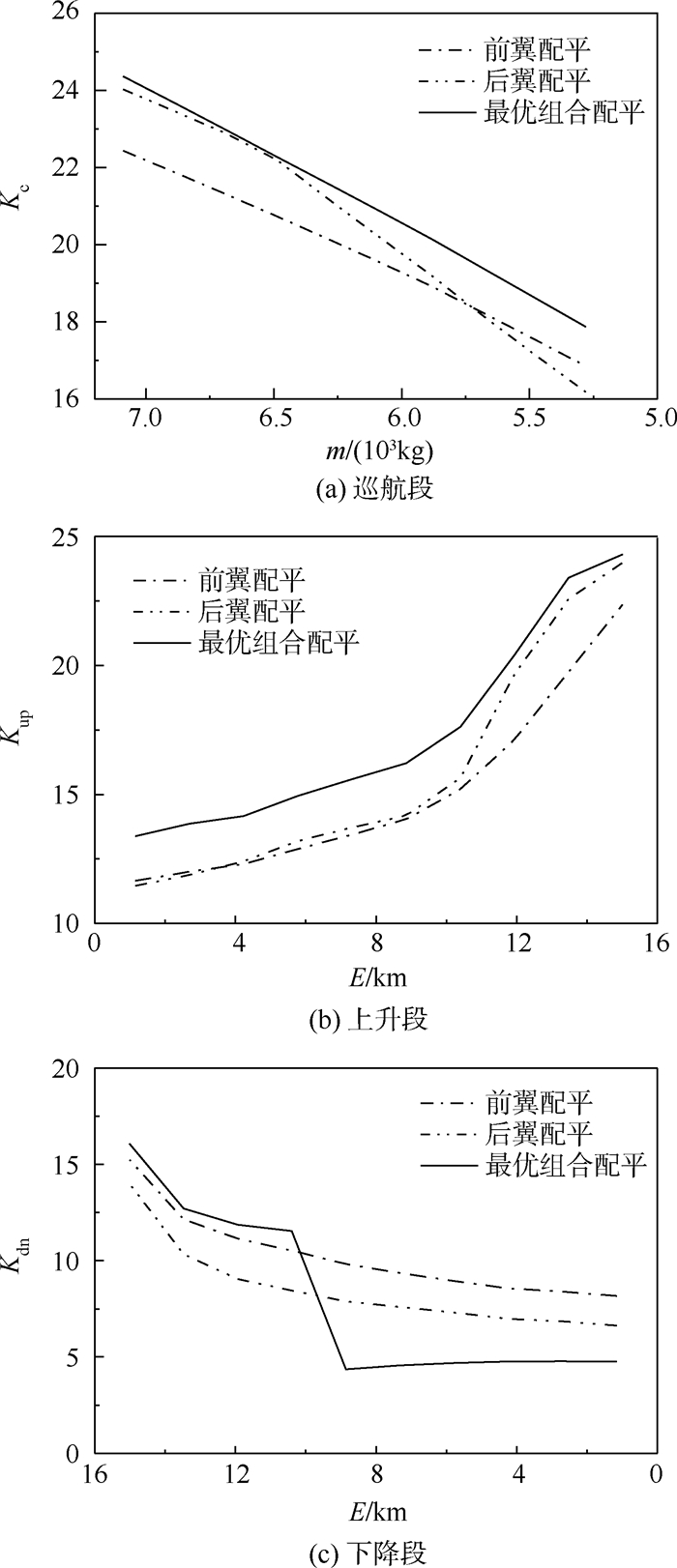 |
| 图 7 3种配平方式下的升阻比 Fig. 7 Lift-drag ratios under three trimming modes |
| 图选项 |
在航迹优化过程中,巡航段以质量为步长,上升段与下降段以能量为步长。因此,在仿真结果中,巡航段横坐标为飞机质量m,如图 6(a)、图 7(a)所示;上升段与下降段横坐标为飞机等效能量E,如图 6(b)、(c)与图 7(b)、(c)所示。
从图 6可以看出,在3种舵面配平方式中,最优组合配平方式下的巡航段性能指标λ最大,上升段性能指标Hup与下降段性能指标Hdn均最小,即通过最优组合配平,算例飞机能够在巡航段获得最大的燃油里程,同时在上升段与下降段付出最小的成本。如表 1所示,相比于单一舵面配平,最优舵面组合配平能够使算例飞机的总航程分别提高7.5%与4.4%。
对比图 7中3种配平方式下的升阻比可知,最优舵面组合配平方式下,飞机在上升段、巡航段、下降段前期的全机升阻比均最大,在下降段后期的全机升阻比最小。这是由于:
对于巡航段,如第2.2节所述,增大升阻比K能够同时增大性能指标λ与控制变量寻优范围,从而使航迹优化获得更优解,提高飞机的续航性能。
对于上升段,性能指标Hup大于零,如图 6(b)所示。如第2.2节所述,Hup的分子不受K影响,分母随K增大而增大,且控制变量寻优范围随K增大而增大。因此,增大K能够同时对性能指标与控制变量寻优范围产生有利影响,使航迹优化获得更优解,从而提高飞机的续航性能。此外,从飞行原理的角度,根据第1节,上升段的性能指标即为飞机的上升成本,其值由飞机在上升段与巡航段的燃油经济性决定。为了获得最佳的巡航性能,飞机通常是在燃油经济性最高的飞行状态下进行巡航。因此,相比于上升段,巡航段的燃油经济性更高,即巡航段对飞机的续航性能更为有利。上升段是飞机的等效能量从初始值Ei递增至Ec的过程,等效能量变化率?将影响飞机完成上升过程的飞行时间与耗油量。如第2.2节所述,在上升段,?随K增大而增大,因此,增大K可以使飞机更快地完成上升过程,为对巡航性能更有利的巡航段节省更多的可用燃油,从而提高飞机的续航性能。
在下降段前期,性能指标Hdn小于零,如图 6(c)所示。如第2.2节所述,Hdn的分子不受K影响,分母随K增大而减小,即性能指标随K增大而减小。然而,K增大将导致控制变量寻优范围也减小。因此,K的变化仅能够对性能指标与控制变量寻优范围中的二者之一产生有利影响,此时无法仅通过分析升阻比对航迹优化结果的影响来判断其对续航性能的影响。但是,从飞行原理的角度来看,飞机在下降段前期具有较高的能量储备,此时通过直接利用势能转换为动能,能够使飞机以相对较低的油耗继续保持较高的飞行速度,如图 8所示,从而获得比巡航段更高的燃油经济性。因此,相比于巡航段,下降段前期对飞机的续航性能更为有利。与上升段类似,下降段的等效能量变化率的绝对值|?|将影响飞机下降过程的长短。如第2.2节所述,在下降段,|?|随K增大而减小,因此,在下降段前期增大K可以延长这一飞行过程,从而提高飞机的续航性能。
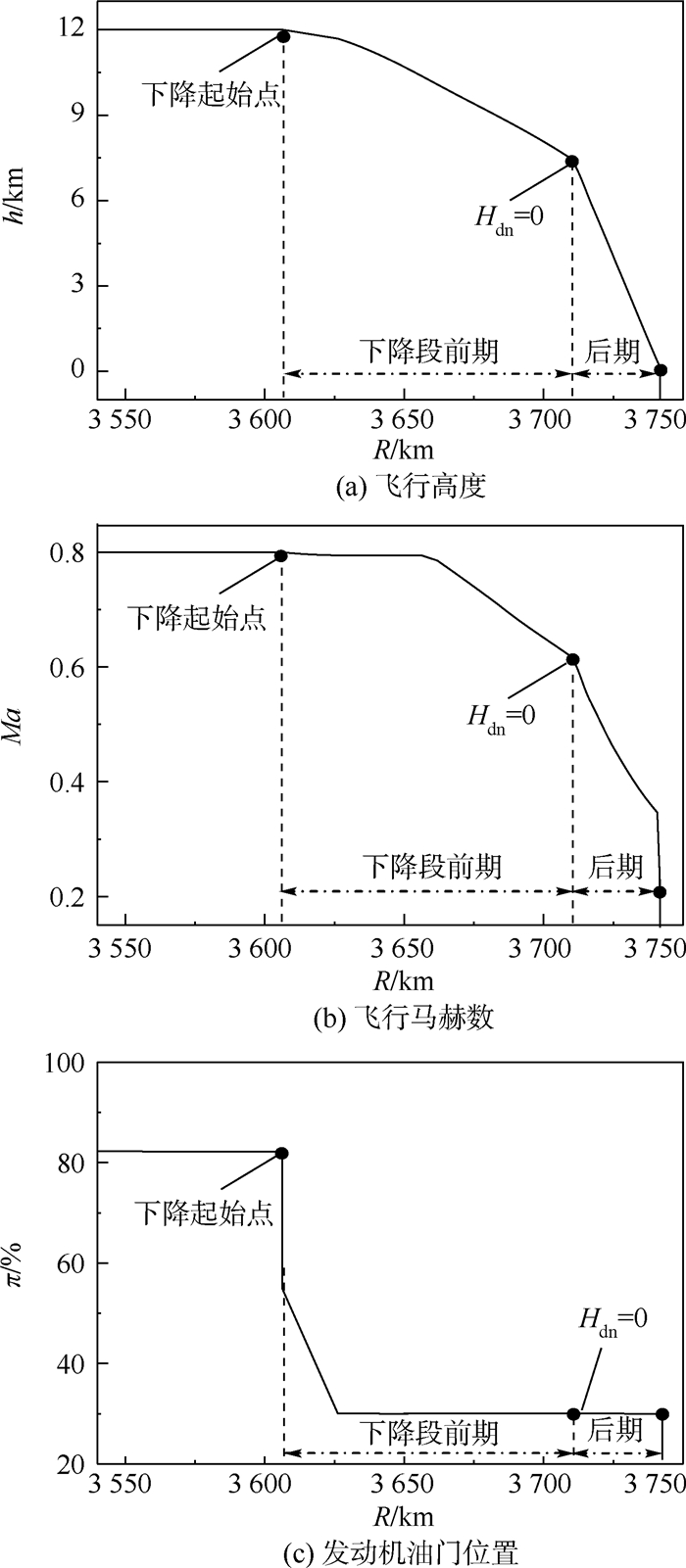 |
| 图 8 最优组合配平下的飞行航迹局部视图 Fig. 8 Local views of flight trajectory under optimum combined trimming mode of control surfaces |
| 图选项 |
在下降段后期,性能指标Hdn大于零,如图 6(c)所示。由于Hdn的分子不受K影响,分母随K减小而增大,且控制变量寻优范围随K减小而增大,因此,减小K能够同时对性能指标与控制变量寻优范围产生有利影响,使航迹优化获得更优解,从而提高飞机的续航性能。此外,从飞行原理的角度来看,在下降段后期,随着飞机的等效能量逐渐降低,此时飞机虽然依然可以保持相对较低的油耗状态,但已经无法利用能量转换使飞机获得较高的飞行速度,如图 8所示。因此,与上升段类似,下降段后期的燃油经济性将低于巡航段的燃油经济性,即相比于下降段后期,巡航段对飞机的续航性能更为有利。此时通过减小K,能够使飞机更快地完成下降段后期的飞行过程,为对巡航性能更有利的巡航段节省更多的可用燃油,从而提高飞机的巡航性能。如图 8(a)所示,相比于下降段前期,飞机在下降段后期的航迹明显变陡,即更快地下降。
综上所述,通过舵面组合配平,使飞机在上升段、巡航段、下降段前期的升阻比增大,在下降段后期的升阻比减小,能够提高飞机的续航性能。
5 结 论1) 通过分析舵面配平对飞机续航性能的影响,提出了基于舵面配平的飞机续航飞行航迹优化方法。该方法能够获得更接近于发挥飞机实际潜力的最优航迹与最大航程。
2) 算例飞机的优化结果表明:对于多操纵面布局飞机,通过该方法能够确定其最优的舵面组合配平规律。相比于单一舵面配平,采用最优舵面组合配平能够使算例飞机的总航程最大提高7.5%。
3) 在上升段、巡航段及下降段前期增大全机升阻比,在下降段后期减小全机升阻比,有利于提高飞机的续航性能。
参考文献
| [1] | HUANG G Q,LU Y P,NAN Y.A survey of numerical algorithms for trajectory optimization of flight vehicles[J].Science China Technological Sciences,2012,55(9):2538-2560. |
| Click to display the text | |
| [2] | RIVAS D,FRANCO A,VALENZUELA A.Optimization of unpowered descents for commercial aircraft:AIAA-2011-7019[R].Reston:AIAA,2011. |
| Click to display the text | |
| [3] | CHERN J S,LIU Y C,CHEN C S.Investigation of maximum range cruise flight for B787:AIAA-2010-7809[R].Reston:AIAA,2010. |
| Click to display the text | |
| [4] | SHAPIRA I,BEN-ASHER J.Range maximization for emergency landing after engine cutoff[J].Journal of Aircraft,2005,42(5):1296-1306. |
| Click to display the text | |
| [5] | LI X,NAIR P B,ZHANG Z G.Aircraft robust trajectory optimization using nonintrusive polynomial chaos[J].Journal of Aircraft,2014,51(5):1592-1603. |
| Click to display the text | |
| [6] | NG H K,SRIDHAR B,GRABBE S.Optimizing aircraft trajectories with multiple cruise altitudes in the presence of winds[J].Journal of Aerospace Information Systems,2014,11(1):35-47. |
| Click to display the text | |
| [7] | 陈晓,王新民,周健.无人飞行器纵向剖面轨迹优化[J].控制理论与应用,2013,30(1):31-36. CHEN X,WANG X M,ZHOU J.Optimization of vertical profile trajectory for unmanned aerial vehicle[J].Control Theory & Applications,2013,30(1):31-36(in Chinese). |
| Cited By in Cnki (1) | Click to display the text | |
| [8] | FLANZER T C,BOWER G C,KROO I M.Robust trajectory optimization for dynamic soaring:AIAA-2012-4603[R].Reston:AIAA,2012. |
| Click to display the text | |
| [9] | MUELLER R.Multi-objective optimization of an aircraft trajectory between cities using an inverse model approach:AIAA-2012-4489[R].Reston:AIAA,2012. |
| Click to display the text | |
| [10] | VALENZUELA A,RIVAS D,FRANCO A.Cruise optimization using trajectory patterns:AIAA-2010-9140[R].Reston:AIAA,2010. |
| Click to display the text | |
| [11] | SACHS G,LENZ J,HOLZAPFEL F.Trajectory optimization for maximizing the range of powered sailplanes with retractable propeller:AIAA-2009-5626[R].Reston:AIAA,2009. |
| Click to display the text | |
| [12] | 方振平,陈万春,张曙光.航空飞行器飞行动力学[M].北京:北京航空航天大学出版社,2005:26-30,34,43. FANG Z P,CHEN W C,ZHANG S G.Aircraft flight dynamics[M].Beijing:Beihang University Press,2005:26-30,34,43(in Chinese). |
| [13] | WANG G,HU Y,WU C,et al.Improving performance of flying wing UAV with propeller thrust involved trimming the pitching moment:AIAA-2013-4421[R].Reston:AIAA,2013. |
| Click to display the text | |
| [14] | 周堃,王立新.大型军用运输机的飞行航迹优化[J].北京航空航天大学学报,2010,36(6):654-658. ZHOU K,WANG L X.Vertical flight trajectory optmization of heavy military airlift aircraft[J].Journal of Beijing University of Aeronautics and Astronautics,2010,36(6):654-658(in Chinese). |
| Cited By in Cnki (3) | Click to display the text | |
| [15] | WU S F,GUO S F.Optimum flight trajectory guidance based on total energy control of aircraft[J].Journal of Guidance,Control and Dynamics,1994,17(2):291-296. |
| Click to display the text | |
| [16] | CAVCAR A.Climb performance of piston-propeller airplane with cambered wing and variable propeller efficiency[J].Journal of Aircraft,2011,48(5):1701-1707. |
| Click to display the text |
