She和Pecht[5]及Amari等[2]针对单元寿命独立同分布且服从指数分布的n中取k温储备系统的可靠性进行了研究,推导了系统可靠度的显式表达式。Peng等[6]为温储备单元构造一种新的二分决策图(Binary Decision Diagram,BDD)表示,进而给出了基于BDD的(n+1)中取1温储备系统可靠度计算方法。该方法可用于单元寿命服从任意分布的系统。Zhai等[7]将该方法推广到(n+k)中取k温储备系统,但系统BDD仅显式给出失效单元的组合,而每一组合可能对应多种失效次序,因此该方法并不完整。Tannous等[8]针对温储备系统提出一种序贯BDD,但该方法并不规范,难以编程实现。
Zhai等[9]针对更为一般的基于需求的温储备系统,以系统中的故障而非系统的单元为对象,提出基于多值决策图(Multi-valued Decision Diagram,MDD)的温储备系统可靠性建模方法。该方法可以给出系统可靠度的解析表达式,但该表达式是不同维度积分的混合,在计算给定时刻处的系统可靠度时需要人工整理,以进一步利用数值积分求解。这就使得系统可靠度的计算无法完全地程序化实现。
为解决该问题,本文进一步发展了这一方法。在原方法基础上,通过“系统级MDD分解”,按故障数将系统级MDD分解为一系列子图,系统可靠度可分解为所有子图发生概率的加和。每一子图的发生概率对应于一个特定区域上的积分,积分区域仅依赖于任务时间T,因此可以将积分算子与被积函数分离。通过对子图中边的概率重新赋值,根据子图获得相应的被积函数,进而可以利用数值积分方法求解。这样便形成了一套完整的基于MDD的温储备系统可靠性建模方法。
1 温储备系统模型与MDD1.1 基于需求的温储备系统基于需求的温储备系统是n中取k温储备系统的推广[10]。系统中包含n个单元A1,A2,…,An,单元的寿命分布本身是独立的,且分布类型可以是任意的。假设单元Ai在正常工作状态下的寿命分布为Fio(t),温储备状态下的寿命分布为Fis(t)。其中,上标“o”与“s”分别表示正常工作与温储备;若无上标则表示正常工作状态。
单元Ai(1≤i≤n)在正常工作时有一名义效能Ci>0,而系统的整体效能则是系统中所有工作单元的效能之和。系统的整体效能需要满足某一额定需求d,否则认为系统失效。
在零时刻,单元A1,A2,…,Ak正常工作,而其他单元处于温储备状态,即假设
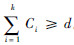。每当系统中的正常工作单元故障时,一个或多个温储备单元会切换到正常工作状态,以保证系统的整体效能满足给定的需求d。温储备单元的切换顺序是给定的:如果单元Ai未失效,则单元Aj不会先于Ai切换到正常工作状态,k<i<j≤n。1.2 MDDMDD是BDD的一种推广,最初用于多状态系统的可靠性分析[11, 12, 13, 14]。在MDD中,每一节点代表一个多状态单元,而每一分支对应单元的一种可能状态。具体地,一个k状态单元A对应的节点有k个分支,如图 1所示。其中,终值“1,2,…,k”分别表示A处于相应的状态。
 |
| 图 1 MDD中一个k分支节点表示 Fig. 1 A node with k branches in MDD |
| 图选项 |
2 MDD的构造Zhai等[9]给出了基于MDD的温储备系统可靠性建模方法。该方法包括MDD的构造与系统可靠度的计算2个部分,而MDD构造部分则包括故障级MDD的构造与系统级MDD的构造2步。从系统可靠度的数值计算出发,本文提出在获得系统级MDD后,按故障数对系统级MDD进行分解。因此,MDD构造部分共包括3步:
1) 故障级MDD的构造。
2) 系统级MDD的构造。
3) 系统级MDD按故障数进行分解。
2.1 故障级MDD的构造在Zhai等[9]给出的故障级MDD的迭代构造方法中,MDD的节点为系统中的故障,而MDD中的边则是相应故障发生后的可能结果。第1个故障对应的MDD表示如图 2所示[9],其中,节点FF表示第1个故障,从左至右n个分支分别表示第1个故障的单元是A1,A2,…,An,而最右分支则表示第1个故障没有发生(即系统中没有故障)。左侧n个分支中,每一分支的终值均为一个二元组(Wi,1,Wi,2),表示当相应单元失效后系统损失的实际效能(Wi,1)与可用效能(Wi,2)。最右分支的终值为一个三元组(S1,S2,N),分别表示第1个故障不发生时系统的实际效能(S1)、可用效能(S2)与故障数(N)。可见,这一决策图明确地表示了系统发生第1个故障时的所有可能与后果。
 |
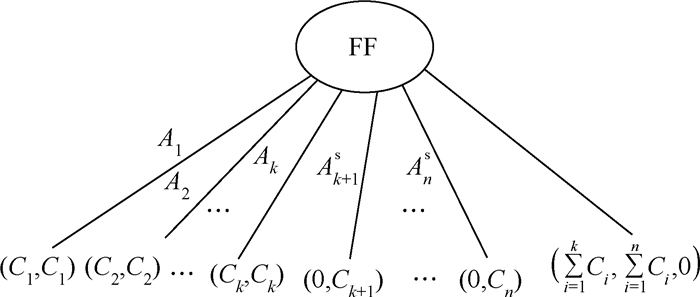| 图 2 第1个故障对应的MDD表示[9] Fig. 2 MDD representation for the first failure[9] |
| 图选项 |
通过裁剪、修改第1个故障的决策图,可获得第2个故障的MDD。对应于第1个故障的MDD中的第i(1≤i≤n)个分支,相应的第2个故障的MDD可根据下面4个步骤得到:
1) 移除第i个分支。
2) 更新最右分支的终值S1=S1-Wi,1,S2=S2-Wi,2。若S1<d,则从左到右依次将Wj,1=0的分支的Wj,1变为对应的单元的名义效能Cj,并令S1=S1+Wj,1,直到S1≥d。这一过程对应于系统中的温储备单元的切换过程。设在这一过程中温储备单元(Aj1s,Aj2s,…,Ajrs)(1≤r≤n-k),切换至正常工作状态以替换失效的Ai。为显式地表示这一过程,可将该MDD的节点用“Ai→(Aj1s,Aj2s,…,Ajrs),(t0,t1)”表示。其中:t0为Ai的起始工作时间;t1为Ai的失效时间。相反地,如果S1≥d,则无需温储备单元切换,节点直接表示为“Ai,(t0,t1)”。
3) 针对MDD中的每一分支(不包括最右分支),计算S2-Wi,2。若此值小于d,则将该分支移除。
4) 更新最右分支的终值:N=N+1。
通过以上4步,针对第1个故障的MDD中的每一分支(不包括最右分支),可构造相应的第2个故障的MDD。同样地,可以迭代构造第3个故障的MDD,……,第n-1个故障的MDD。这里,在根据第m-1个故障的MDD构建第m个故障的MDD时,节点中故障单元的起始工作时间与故障时间可按如下更新:
1) 若该故障对应于某一已切换至正常工作状态的温储备单元,则需向上遍历找到该单元从温储备切换至正常工作的时间,并将其作为其在正常工作状态下的起始工作时间;否则,起始工作时间为t0。
2) 故障时间更新为tm-1。
2.2 系统级MDD的构造系统级MDD的构造实际上是与故障级MDD的构建同时进行的。具体的构造步骤如下:
1) 构建第1个故障的MDD,m=1。
2) 根据第m个故障的MDD构造第m+1个故障的MDD并将其添加到相应的分支。如果第m+1个故障的MDD仅包含一个分支,即最右分支,简便起见,将该分支的终值(S1,S2,N)替换为N。
3) m=m+1。
4) 如果m≥n或所有第m个故障的MDD都只包含一个分支,则迭代停止并获得系统的MDD,否则回到步骤2)。
2.3 系统级决策图的分解根据第2.2节步骤获得的系统级MDD中,汇节点N对应于相应路径上出现的失效单元个数。从计算系统可靠度的角度,需要按下面步骤,根据汇节点N将系统级MDD分解为一系列子决策图DN(1≤N≤Nmax,其中:Nmax为系统中最多可能的故障数):
1) 仅保留汇节点N并删除其他汇节点。
2) 自下而上遍历每一节点,并删除所有不包含子节点的节点。
3) 通过合并相同子树进一步简化所得MDD。
3 基于MDD的系统可靠度计算子决策图DN(1≤N≤Nmax)包含了系统发生N个单元故障时仍能完成任务的所有可能情形。通过计算所有子决策图DN对应情形的发生概率,可以获得系统的可靠度。
3.1 MDD中边的概率密度对于子决策图DN,为计算其发生概率,首先需要定义MDD中的边的概率。除顶节点(FF)与汇节点外,MDD中其他节点具有如下标准形式:
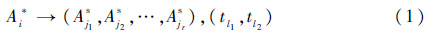
表示单元Ai*在tl1时开始工作,在tl2处发生故障,随后温储备单元Aj1s,Aj2s,…,Ajrs切换到正常工作状态。其中,上标“*”可以为“o”、“s”或为空。指向该节点的边的概率密度定义为
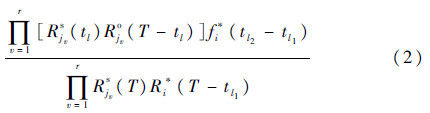
式中:f(·)与R(·)分别为概率密度函数与可靠度函数。显然,当式(2)中r=0时,即Ai*失效后并无温储备单元接替其工作,则相应边的概率密度为
另外,定义指向汇节点的边的概率为1。
3.2 子决策图的发生概率当MDD中所有边的概率密度指定后,根据MDD的性质,可以通过下面的递推公式计算得到顶节点(也即该子决策图)的概率密度:
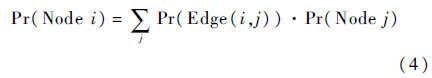
式中:i和j均为节点编号,Edge(i,j)为连接节点i与节点j的边,j取遍节点i的所有子节点。对于子决策图DN,可以证明,其发生概率可表示为
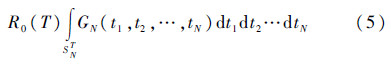
式中:
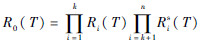为一基本项；积分区域SNT={(t1,t2,…,tN)|0<t1<t2<…<tN<T}为一个N维单纯形；N维被积函数GN(t1,t2,…,tN)则是由式(4)得到的顶节点的概率密度。这样,子决策图DN的发生概率即为一个N维单纯形上的积分,由于被积函数与积分区域均已知,因此该积分可以通过数值方法求解[15, 16]。3.3 温储备系统的可靠度当获得所有子决策图DN(1≤N≤Nmax)的发生概率后,给定时刻T处系统可靠度则可以由式(6)获得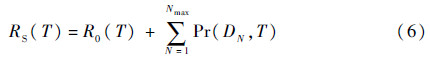
当考虑故障级不完全覆盖效应时[17, 18],即系统中第j个故障以概率cj被覆盖,且任一未被覆盖的故障均会导致系统失效,则系统的可靠度为
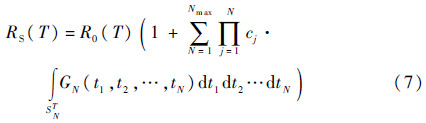
综上,基于MDD的温储备系统可靠度计算方法的总体流程如图 3所示。
 |
| 图 3 基于MDD的温储备系统可靠度计算方法 Fig. 3 MDD-based system reliability evaluation procedure for warm standby systems |
| 图选项 |
4 算法演示本节以Zhai等[9]的三单元温储备系统为例,着重说明系统级MDD的分解以及随后可靠度的计算。该温储备系统中3个单元A1、A2和A3的效能分别为1、2和3,而对系统的总需求为d=3(例如,一个电站共有3台发电机,其功率分别为1、2和3 MW,对电站的总功率需求是3 MW)。A1和A2为初始工作单元,A3为温储备单元。Zhai等[9]给出了该温储备系统的系统级MDD表示,如图 4所示。
 |
| 图 4 一个三单元温储备系统的MDD Fig. 4 MDD of a three-component warm standby system |
| 图选项 |
根据汇节点的值可见,系统中可能出现1或2个故障,或者无故障。根据第2.3节中的步骤,可以将该系统级MDD进行分解,得到2个子决策图D1和D2,如图 5所示。其中,MDD中各边的概率密度由式(2)获得,已在图中标注。
 |
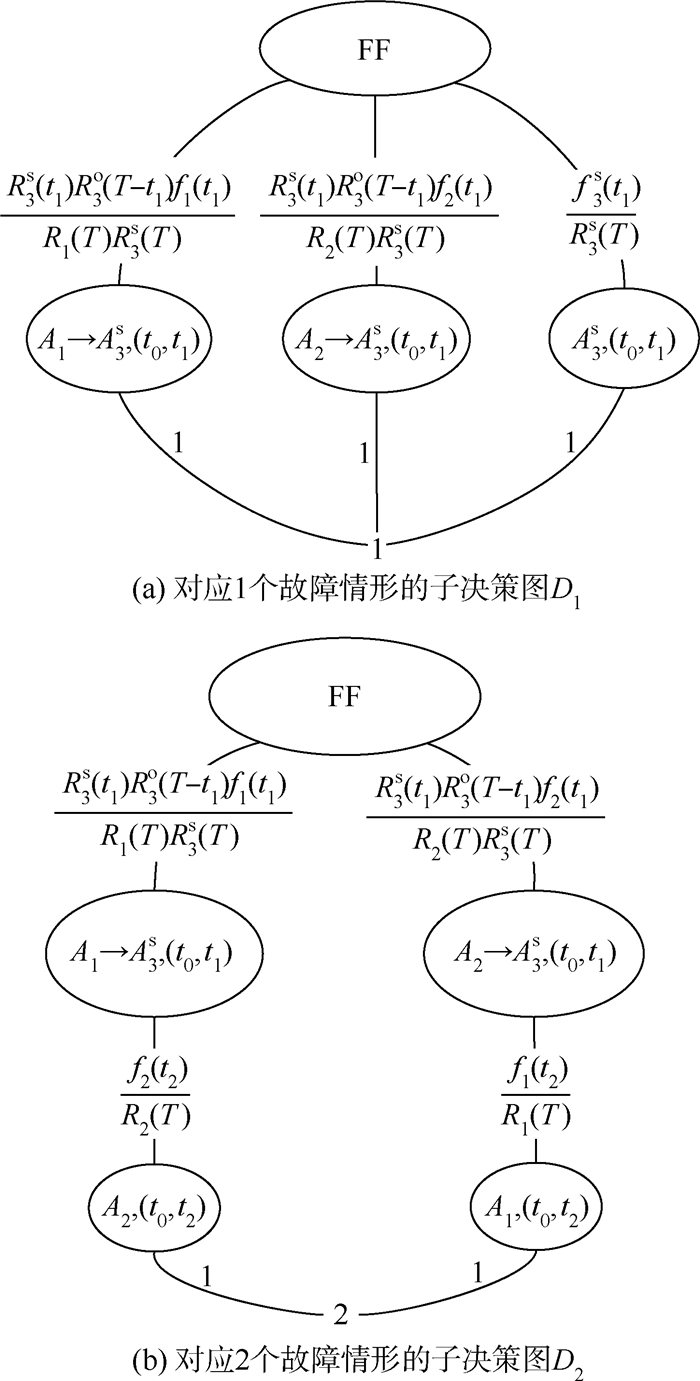| 图 5 三单元温储备系统系统级MDD分解后的2个子决策图 Fig. 5 Two child MDDs derived from system MDD of three-component warm standby system |
| 图选项 |
根据式(4)中的迭代公式,可分别得到2个子图中顶节点的概率密度:
由式(5)可以得到每一子决策图的发生概率Pr(D1,T)与Pr(D2,T),进而据式(6)、式(7)可以获得系统的可靠度。
5 结 论本文针对温储备系统的可靠性建模问题,对已有的基于MDD的系统可靠性建模方法进行了进一步发展:
1) 在构建系统级决策图后,提出依照故障单元个数对系统级MDD进行分解,每一子决策图的发生概率对应一个特定单纯形上的积分。
2) 针对子决策图中的节点,对指向节点的边的概率密度进行了重新赋值,使得子决策图发生概率对应的积分中的被积函数可表示为顶节点的发生概率密度。
3) 每一子决策图的发生概率可由数值积分算法获得,进而可得到给定时刻的系统可靠度。
4) 本文发展的方法关注给定时刻处系统可靠度的计算,可利用计算机编程实现。
参考文献
| [1] | AMARI S V, DILL G.A new method for reliability analysis of standby systems[C]//Proceedings of Annual Reliability and Maintainability Symposium (RAMS2009).Piscataway,NJ:IEEE Press,2009:417-422. |
| Click to display the text | |
| [2] | AMARI S V, PHAM H,MISRA R B.Reliability characteristics of k-out-of-n warm standby systems[J].IEEE Transactions on Reliability,2012,61(4):1007-1018. |
| Click to display the text | |
| [3] | TANNOUS O, XING L.Efficient analysis of warm standby systems using central limit theorem[C]//Proceedings of Annual Reliability and Maintainability Symposium (RAMS2012).Piscataway,NJ:IEEE Press,2012:1-6. |
| Click to display the text | |
| [4] | PAPAGEORGIOU E, KOKOLAKIS G.Reliability analysis of a two-unit general parallel system with (n-2) warm standbys[J].European Journal of Operational Research,2010,201(3):821-827. |
| Click to display the text | |
| [5] | SHE J, PECHT M.Reliability of a k-out-of-n warm-standby system[J].IEEE Transactions on Reliability,1992,41(1):72-75. |
| Click to display the text | |
| [6] | PENG R, ZHAI Q,XING L,et al.Reliability of 1-out-of-(n+1) warm standby systems subject to fault level coverage[J].International Journal of Performability Engineering,2013,9(1):117-120. |
| Click to display the text | |
| [7] | ZHAI Q, PENG R,XING L,et al.BDD-based reliability evaluation of k-out-of-(n+k) warm standby systems subject to fault-level coverage[J].Proceedings of the Institution of Mechanical Engineers,Part O:Journal of Risk and Reliability,2013,227(5):540-548. |
| Click to display the text | |
| [8] | TANNOUS O, XING L,DUGAN J.Reliability analysis of warm standby systems using sequential BDD[C]//Proceedings of Annual Reliability and Maintainability Symposium (RAMS2011).Piscataway,NJ:IEEE Press,2011:1-7. |
| Click to display the text | |
| [9] | ZHAI Q, PENG R,XING L,et al.Reliability of demand-based warm standby systems subject to fault level coverage[J].Applied Stochastic Models in Business and Industry,2015,31(3):380-393. |
| Click to display the text | |
| [10] | KUO W, ZUO M J.Optimal reliability modeling:Principles and applications[M].Hoboken:John Wiley & Sons,2003:231-280. |
| [11] | AKERS J, BERGMAN R,AMARI S V,et al.Analysis of multi-state systems using multi-valued decision diagrams[C]//Proceedings of Annual Reliability and Maintainability Symposium (RAMS2008).Piscataway,NJ:IEEE Press,2008:347-353. |
| Click to display the text | |
| [12] | XING L, DAI Y.A new decision-diagram-based method for efficient analysis on multistate systems[J].IEEE Transactions on Dependable and Secure Computing,2009,6(3):161-174. |
| Click to display the text | |
| [13] | SHRESTHA A, XING L,COIT D W.An efficient multistate multivalued decision diagram-based approach for multistate system sensitivity analysis[J].IEEE Transactions on Reliability,2010,59(3):581-592. |
| Click to display the text | |
| [14] | AMARI S V, XING L,SHRESTHA A,et al.Performability analysis of multistate computing systems using multivalued decision diagrams[J].IEEE Transactions on Computers,2010,59(10):1419-1433. |
| Click to display the text | |
| [15] | BERNTSEN J, ESPELID T O.Error estimation in automatic quadrature routines[J].ACM Transactions on Mathematical Software (TOMS),1991,17(2):233-252. |
| Click to display the text | |
| [16] | GENZ A, COOLS R.An adaptive numerical cubature algorithm for simplices[J].ACM Transactions on Mathematical Software (TOMS),2003,29(3):297-308. |
| Click to display the text | |
| [17] | MYERS A F. k-out-of-n:G system reliability with imperfect fault coverage[J].IEEE Transactions on Reliability,2007,56(3):464-473. |
| Click to display the text | |
| [18] | AMARI S V, MYERS A F,RAUZY A,et al.Imperfect coverage models:Status and trends[M]//MISRA K B.Handbook of performability engineering.London:Springer,2008:321-348. |
