基于退化轨迹和退化量分布2种建模技术使用最早且较为成熟,但因其将产品性能退化描述为确定性过程,未考虑产品个体随时间发生退化的随机性,使其工程应用范围受限。以Wiener过程为代表的随机过程模型,充分考虑了产品在正常工作或试验环境中所发生性能退化的随机性和动态性,可以较好地描述产品的真实退化过程,成为当前加速退化建模的重要技术手段。
Wiener过程是一种具有平稳、便于计算与分析特性的随机过程模型,具有广泛的应用前景。当产品的性能退化过程总体均匀变化,而个体差异随时间增加而逐步增大时,都可用Wiener过程来描述[6, 7]。目前,基于Wiener过程的加速退化建模的重点及难点主要在于以下2点:
1) 如何处理非线性数据。主要解决方法是进行坐标变换,将非线性数据组变换为线性数据组。Whitmore和Schenkelberg[8]最早提出2类时间尺度变换模型来解决Wiener过程在非线性退化数据建模中的问题,实例表明了模型具有较好的实用性。在此基础上,文献[9, 10, 11]采用时间尺度变换模型,进一步开展了基于非线性Wiener过程的加速退化数据建模与应用研究。
2) 如何考虑个体之间的性能退化差异。由于产品在制造、材料及环境中受随机因素的影响表现出个体之间退化速率不一,存在一定差异性,因此需要研究个体差异对产品寿命评估的影响。主要方法是对Wiener过程的系数进行随机化处理。文献[12, 13]对Wiener过程的2个系数都进行随机化处理,假定扩散系数服从逆伽马分布的前提下漂移系数服从正态分布,但假定的分布类型未经分布假设检验,通过最大期望(Expectation Maximization,EM)算法估计参数,计算复杂,难以推广;文献[14, 15]仅将Wiener过程的漂移系数看作服从正态分布的随机变量,给出了考虑个体差异的产品寿命模型,模型拟合性好,便于计算。
基于此,本文在步进应力加速退化试验场合下,采用时间尺度变换模型将非线性退化数据转换为线性数据,将Wiener过程的漂移系数随机化处理,建立考虑个体差异的加速退化数据模型,采用两步极大似然估计法确定模型中的未知参数,较EM算法更适合处理加速退化场合下的退化数据。
1 基于Wiener过程的退化模型假设产品的性能退化过程X(t)可以用Wiener过程进行描述:

式中:λ为漂移系数;σB为扩散系数;B(t)为标准布朗运动。
由于X(t)符合齐次马尔可夫过程,X(t)的均值和方差都是时间的线性函数,因此,Wiener过程一般用于描述产品线性退化过程,即退化量X(t)与时间t呈线性关系。
设产品退化失效的阈值为l。当X(t)首次达到l时,认定产品失效,则产品寿命T满足:

经推导可知,首次达到l时的寿命服从逆高斯分布,则产品的可靠度和概率密度函数分别为
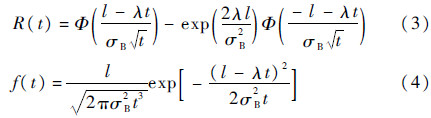
式中:Φ(·)为标准正态分布函数。
2 步进应力加速退化试验2.1 试验假设1) 试样在一组加速应力(即温度)作用下性能发生退化且退化过程不可逆。
2) 试样在各加速应力下的退化失效机理、模式都保持不变。
3) 试样在各加速应力下的性能退化参数仅有一个且测量间隔和次数相同。
4) 某时刻试样的剩余寿命仅与该时刻已累计退化失效水平和当时应力有关。
2.2 试验过程根据试验方案,预先确定一组高于正常应力S0的加速应力S1 < S2 < … < Sn,试验初期,将若干试样放置在初始应力S1下进行试验并记录相关性能退化参数,达到时刻t1后将应力提高至S2下继续试验,达到时刻t2后将应力提高至下一应力,如此进行,直到将应力提高至Sn下完成试验,其中,ti-1(i=1,2,…,n)为应力Si-1到Si的转换时刻。试验应力施加过程如图 1所示。
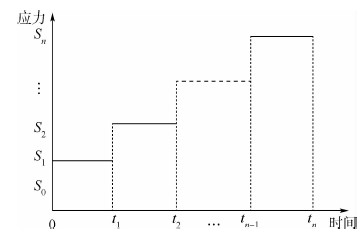 |
| 图 1 步进应力加速退化试验载荷历程Fig. 1 Step-stress accelerated degradation test loading process |
| 图选项 |
2.3 试验数据已知现有m个样本在n个加速应力下进行步进应力加速退化试验,每个应力水平下各测量K次性能退化参数,则在应力Si下第j个试样第k次测量时刻为ti,kj,性能退化量为X(ti,kj)。
经步进应力加速退化过程分析可知(见图 2),第j个试样在应力Si下的性能退化量初始值是前一步应力下性能退化量的末尾值,即X(ti,0j)=X(ti-1,kj),则基于Wiener过程的步进应力加速退化数据建模如下:
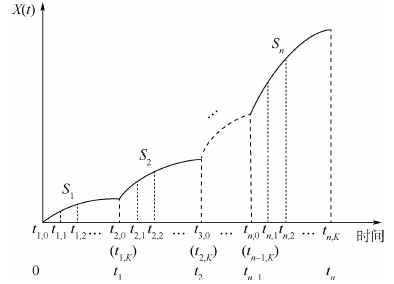 |
| 图 2 步进应力加速退化过程Fig. 2 Step-stress accelerated degradation process |
| 图选项 |
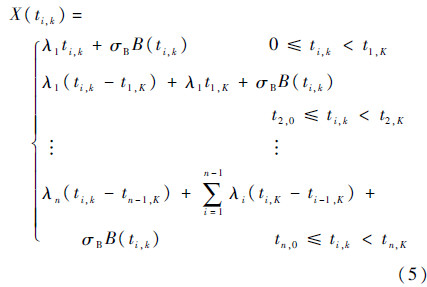
在应力Si下第j个试样第k次测量的性能退化量较第k-1次测量的性能退化量增加了ΔX(ti,kj)=X(ti,kj)-X(ti,k-1j),时间增量为Δti,kj=ti,kj-ti,k-1j,则根据Wiener过程性质可知:

3 非线性退化数据建模3.1 可靠度函数对于非线性退化数据,可采用时间尺度变换模型,将其转换为线性数据。Whitmore和Schenkelberg[8]首次提出了时间尺度变换模型应为时间t的非负单调递增函数,常见函数为
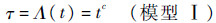
式中:c为非负待定常数。当0 < c < 1时,样本退化趋势为凸型;当c>1时,样本退化趋势为凹型。上述退化数据都呈现出非线性特征;当c=1时,样本的退化趋势为线型,都是线性数据。随着样本中出现非线性数据,c值开始偏离1。非线性数据越多,c值越偏离1,说明时间尺度变换模型可以处理非线性数据与线性数据并存的情况。
本文采用时间尺度变换模型,将非线性数据组[t,X(t)]转换为线性数据组[τ,Y(τ)],则可将式(1)改写为

则产品变换后的可靠度和概率密度函数分别为
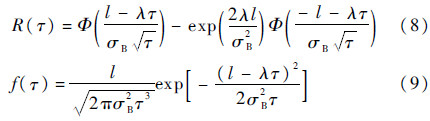
令τ=Λ(t),Y(τ)=X(t),则产品的寿命可靠度和概率密度函数分别为
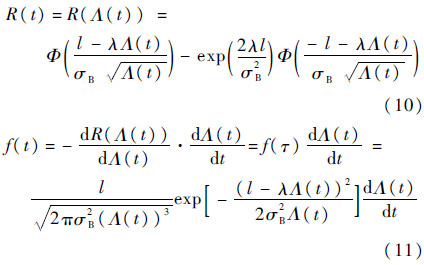
为了体现出试样个体之间的差异化,将漂移系数λ随机化处理,即假定λ服从正态分布N(μλ,σλ2),可将式(8)改写为
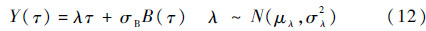
则考虑个体差异的产品可靠度和概率密度函数为
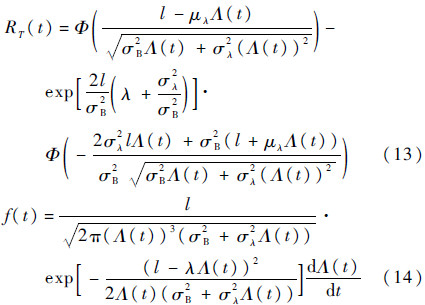
3.2 加速退化模型对于步进应力加速退化试验而言,一般认为Wiener过程的漂移系数λ与应力S有关,而扩散系数σ与应力S无关,则加速退化模型一般可表示为[16]

式中:a、b为待定常数;φ(S)为应力S的函数,对于温度应力的Arrhenius模型,φ(S)=1/S,对于电应力的逆幂律模型,φ(S)=lnS。
则温度应力下的步进应力加速退化模型为

式中:i=1,2,…,n;Si为第i步温度应力;λi为温度应力Si下的漂移系数。
分析式(16)可知,同一温度应力作用下的试样退化速度并无差异。而考虑到试样个体之间的差异客观存在,应采用基于随机变量的Arrhenius模型来描述试样个体之间的退化差异性,则在应力Si下第j个试样的加速退化模型可表示为

令a~N(μa,σa2),则应力Si下的考虑了个体差异的漂移系数λi可表示为
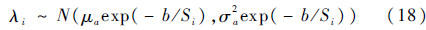
若不考虑个体差异,令σa2=0,则式(17)变为传统的Arrhenius模型。
3.3 两步极大似然估计针对经时间尺度变换模型变换后的、考虑个体差异的线性退化数据[τ,Y(τ)],由式(6)可知:
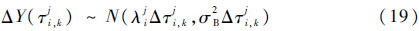
式中:
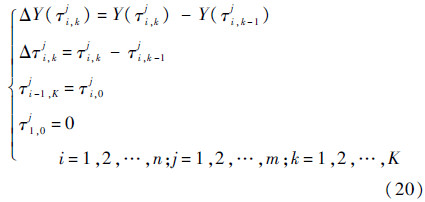
其中:Δτi,kj为应力Si下第j个试样第k次测量时间增量变换值;ΔY(τi,kj)为对应的性能退化增量。
根据式(19)、式(20),建立极大似然估计函数:

采用时间尺度变换模型Ⅰ,将τ=tc、ΔY(τi,kj)=ΔX(ti,kj)与式(17)代入式(21),可得
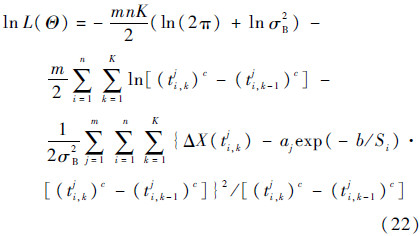
式中:Θ={aj,b,c,σB2}(j=1,2,…,m)为未知参数集合;lnL(Θ)为fminsearch函数所取的最大值。
分别令式(22)关于aj、σB2的1阶偏导数为零,即

则
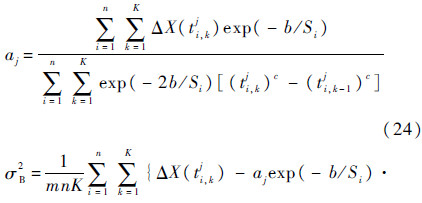
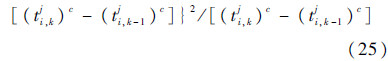
理论上,根据收集到的数据组[ti,kj,X(ti,kj)]及所建的模型,可以解出式(24)、式(25),求出aj、σB2。但进一步分析可知,式(24)、式(25)的求解其实依赖于b、c的取值。因此,采用两步极大似然估计法来求解未知参数Θ。
第1步 估计b、c。采用MATLAB软件中的fminsearch函数可解决上述问题。以b、c为变量,lnL(Θ)为优化函数,分别先给b、c赋初值b0、c0,然后进行二维遍历搜索,直到函数lnL(Θ)取得最大值时停止搜索,此时所返回的b、c值即为所求的b、c。
第2步 估计aj(j=1,2,…,m)、σB2。将第1步中所确定的b、c代入式(24)、式(25)中,即可求出aj、σB2。同时,μa、σa2估计公式如下:
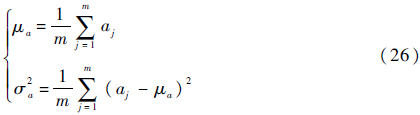
4 实例分析将文献[17]进行步进应力加速退化试验激光器的数据信息记为真实值,经仿真得到的性能退化数据见表 1,性能退化轨迹见图 3。已知激光器以电流为其性能特征参数,在工作过程中受温度应力影响较为敏感,其性能退化速度与温度之间的关系符合Arrhenius模型。激光器的正常工作温度为25℃,现有12个试样进行步进应力加速退化试验,步进温度应力分别为25、50和75℃,每个温度应力下分别测量5次数据,每次测量时间间隔为150h。当激光器工作电流增加量达到规定阈值(l=10mA)时,可认定其退化失效。
表 1 激光器仿真退化数据Table 1 Simulation degradation data of lasermA
| 试样 | 25℃退化量 | 50℃退化量 | 75℃退化量 | ||||||||||||
| 150h | 300h | 450h | 600h | 750h | 900h | 1050h | 1200h | 1350h | 1500h | 1650h | 1800h | 1950h | 2100h | 2250h | |
| 1 | 0.296 | 0.636 | 0.954 | 1.240 | 1.500 | 2.152 | 2.954 | 3.811 | 4.329 | 5.057 | 6.542 | 7.726 | 9.014 | 10.219 | 11.213 |
| 2 | 0.489 | 1.018 | 1.653 | 1.994 | 2.551 | 3.447 | 4.488 | 5.386 | 6.417 | 7.277 | 8.974 | 10.598 | 12.382 | 13.776 | 15.415 |
| 3 | 0.156 | 0.534 | 0.718 | 1.142 | 1.456 | 2.061 | 2.539 | 3.325 | 3.904 | 4.589 | 5.803 | 7.253 | 8.492 | 9.734 | 10.924 |
| 4 | 0.386 | 0.898 | 1.169 | 1.737 | 1.842 | 2.459 | 3.391 | 4.288 | 5.094 | 5.762 | 7.013 | 8.473 | 9.640 | 11.096 | 12.214 |
| 5 | 0.344 | 0.600 | 0.798 | 1.238 | 1.443 | 2.291 | 2.795 | 3.553 | 4.329 | 4.962 | 6.206 | 7.535 | 8.779 | 9.820 | 11.272 |
| 6 | 0.411 | 0.827 | 1.069 | 1.455 | 1.785 | 2.442 | 3.042 | 3.965 | 4.438 | 5.081 | 6.084 | 7.039 | 8.277 | 9.153 | 10.224 |
| 7 | 0.361 | 0.767 | 1.204 | 1.500 | 2.186 | 2.872 | 3.629 | 4.291 | 4.841 | 5.526 | 6.596 | 7.687 | 8.962 | 10.181 | 11.413 |
| 8 | 0.117 | 0.432 | 0.658 | 0.883 | 1.331 | 1.754 | 2.172 | 2.624 | 3.167 | 3.603 | 4.363 | 5.327 | 5.860 | 6.587 | 7.236 |
| 9 | 0.522 | 0.832 | 1.336 | 1.521 | 2.110 | 2.853 | 3.417 | 3.927 | 4.646 | 5.044 | 6.382 | 7.572 | 8.555 | 9.893 | 11.212 |
| 10 | 0.428 | 0.453 | 0.720 | 1.127 | 1.489 | 2.116 | 2.769 | 3.317 | 3.806 | 4.446 | 5.350 | 6.332 | 7.247 | 8.393 | 9.638 |
| 11 | 0.111 | 0.302 | 0.520 | 0.755 | 0.990 | 1.661 | 2.243 | 2.875 | 3.484 | 4.221 | 5.034 | 6.221 | 7.468 | 8.878 | 9.971 |
| 12 | 0.280 | 0.285 | 0.554 | 1.021 | 1.392 | 2.180 | 2.899 | 3.589 | 4.184 | 4.628 | 5.946 | 6.967 | 8.130 | 9.170 | 10.073 |
表选项
 |
| 图 3 步进应力加速退化轨迹Fig. 3 Step-stress accelerated degradation trajectories |
| 图选项 |
1) 判断标准
将本文提出的考虑个体差异且可处理非线性数据的方法记为M1;将文献[14]提出的考虑个体差异且只适用于线性数据的方法记为M2;将文献[18]提出的未考虑个体差异且只适用于线性数据的方法记为M3。
依据赤池信息量准则(Akaike Information Criterion,AIC)和总体均方误差(TMSE)判断各方法的优劣[14]。当AIC或TMSE的值越小时,说明方法的拟合程度越好,计算公式如下:

式中:p为Θ中未知参数的个数。
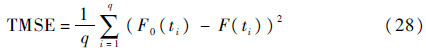
式中:q为所取的测量点个数;F0(ti)为ti处的寿命分布函数真实值;F(ti)为ti处的寿命分布函数的模型估计值。
2) 两步极大似然估计
令Arrhenius模型中参数b的初值为2600,时间尺度变换模型Ⅰ中参数c的初值为1,采用MATLAB软件中的fminsearch函数进行遍历搜索,再将所返回的b、c值代入式(24)~式(26),求得未知参数Θ,见表 2。
表 2 两步极大似然估计结果Table 2 Two-step maximum likelihood estimation results
| 方法 | μ a | σa 2 | b | c | ln L(Θ) |
| 真实值 | 12.54 | 7.723 | 2600 | 1.000 | |
| M1 | 12.91 | 7.183 | 2390 | 1.035 | 200.3 |
| M2 | 11.44 | 4.689 | 2505 | 197.2 | |
| M3 | 10.19 | 2516 | 162.4 |
表选项
由表 2可知,当c取1.035时,可将非线性退化数据转换为线性退化数据。同时,采用CvM检验法[19],对转换前后的性能退化增量数据,进行显著水平为0.05的正态分布假设检验,结果表明,仅有转换后的数据接受假设,进一步验证了对非线性退化数据进行转换的必要性。
3) 评估结果
根据本文所建模型,计算出Wiener过程的漂移系数、扩散系数、产品寿命的点估计值(MTTF)和置信度为95%的区间估计(CI),见表 3。
表 3 不同方法的评估结果Table 3 Assessment results of different methods
| 方法 | μ λ/10 -4 | σλ 2 /10 -7 | σB 2 /10 -4 | MTTF/h | CI(95%)/h |
| 真实值 | 2.037 | 2.039 | 1.094 | 4909 | [3338,8843] |
| M1 | 2.097 | 1.976 | 0.778 | 4766 | [3293,8179] |
| M2 | 1.859 | 1.238 | 1.024 | 5379 | [3809,8752] |
| M3 | 1.641 | 1.924 | 6092 | [4903,7485] |
表选项
4) 模型优劣判断
分别计算出不种方法的AIC值(见表 4),发现M1的AIC最小,说明M1的模型拟合性更好。在时间0~10000h内分别取10、100、1000个测量点,计算不种方法的TMSE的值(见表 4),发现M1的TMSE值始终最小,说明M1的寿命估计值更接近真实值。
表 4 不同方法的TMSE和AIC值Table 4 TMSE and AIC of different methods
| 方法 | TMSE/10 -3 | AIC | ||
| q=10 | q=100 | q=1000 | ||
| M1 | 0.59 | 0.59 | 0.59 | -392.6 |
| M2 | 5.35 | 5.37 | 5.38 | -388.4 |
| M3 | 38.32 | 38.51 | 38.53 | -318.8 |
表选项
另外,从可靠度曲线(见图 4)可以看出,M1可靠度曲线早期几乎与真实值曲线重合且低于M2和M3可靠度曲线;中期低于真实值、M2和M3可靠度曲线;末期略低于真实值和M2曲线,略高于M3可靠度曲线,说明M1的模型拟合性较好且可靠性评估略保守,与工程实践做法相符。
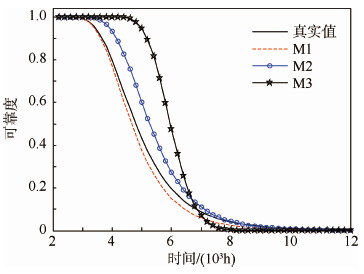 |
| 图 4 不同方法的可靠度曲线Fig. 4 Reliability curves of different methods |
| 图选项 |
从概率密度曲线(见图 5)可以看出,M1概率密度曲线较M2概率密度曲线更接近于真实值曲线,而M3概率密度曲线较真实值曲线偏差较大,与3种方法所计算出的TMSE值相符,说明3种方法的模型拟合优劣排序为:M1,M2,M3,M1最优。
 |
| 图 5 不同方法的概率密度曲线Fig. 5 Probatility density curves of different methods |
| 图选项 |
5 结 论1) 考虑了个体退化差异,将Wiener过程中的漂移系数随机化处理并假定为正态分布,这种处理方法较传统未考虑个体差异和未进行漂移系数随机化处理的方法更优。
2) 采用两步极大似然估计法,对模型中未知参数进行估计,可以较好地克服传统极大似然估计法的局限性,求解未知参数的最优值。
3) 优先采用时间尺度变换模型对非线性退化数据进行线性化处理,使得处理后的数据更符合Wiener过程特性。
4) 实例分析中,从3种不同方法的AIC值、TMSE值、可靠度曲线以及概率密度曲线进行对比分析,验证了本文所提出的方法的优势,具有一定的工程应用价值。
参考文献
| [1] | TANG S, GUO X,YU C,et al.Accelerated degradation tests modeling based on the nonlinear Wiener process with random effects[J].Mathematical Problems in Engineering,2014,201(4):1-11. |
| [2] | WANG X. Wiener processes with random effects for degradation data[J].Journal of Multivariate Analysis,2010,101(2):340-351. |
| Click to display the text | |
| [3] | 贾占强,蔡金燕, 梁玉英,等.基于步进加速退化试验的电子产品可靠性评估技术[J].系统工程理论与实践,2010,30(7):1279-1285. JIA Z Q,CAI J Y,LIANG Y Y,et al.Reliability assessment technology for electronic equipment based on step-up-stress accelerated degradation testing[J].Systems Engineering-The-ory & Practice,2010,30(7):1279-1285(in Chinese). |
| Cited By in Cnki (16) | |
| [4] | XIA X T. Forecasting method for product reliability along with performance data[J].Journal of Failure Analysis and Prevention,2012,12(5):532-540. |
| Click to display the text | |
| [5] | TSAI C C, TSENG S T,BALAKRISHNAN N.Mis-specification analyses of gamma and Wiener degradation processes[J].Journal of Statistical Planning and Inference,2011,141(12):3725-3735. |
| Click to display the text | |
| [6] | 潘正强,周经伦, 孙权.基于Wiener过程的步进应力加速退化建模[J].系统工程与电子技术,2011,33(4):963-968. PAN Z Q,ZHOU J L,SUN Q.Step-stress accelerated degradation modeling based on Wiener process[J].Systems Engineering and Electronics,2011,33(4):963-968(in Chinese). |
| Cited By in Cnki (5) | Click to display the text | |
| [7] | TANG J, SU T S.Estimating failure time distribution and its parameters based on intermediate data from a Wiener degradation model[J].Naval Research Logistics,2008,55(3):265-276. |
| Click to display the text | |
| [8] | WHITMORE G A, SCHENKELBERG F.Modeling accelerated degradation data using Wiener diffusion with a time scale transformation[J].Lifetime Data Analysis,1997,3(1):27-45. |
| Click to display the text | |
| [9] | SI X S, WANG W B,HU C H,et al.Remaining useful life estimation based on a nonlinear diffusion degradation process[J].IEEE Transactions on Reliability,2012,61(1):50-67. |
| Click to display the text | |
| [10] | 王小林,郭波, 程志君.基于非线性漂移Wiener过程的产品实时可靠性评估[J].中南大学学报(自然科学版),2013,44(8):3203-3209. WANG X L,GUO B,CHENG Z J.Real-time reliability evaluation for product with nonlinear drift-based Wiener process[J].Journal of Central South University(Science and Technology),2013,44(8):3203-3209(in Chinese). |
| Cited By in Cnki (2) | Click to display the text | |
| [11] | 王浩伟,徐廷学, 张鑫.基于步进加速退化试验的某型电连接器可靠性评估[J].电光与控制,2014,21(9):104-107. WANG H W,XU T X,ZHANG X.Reliability assessment for a certain type of electrical connector based on step-stress accelerated degradation test[J].Electronics Optics & Control,2014,21(9):104-107(in Chinese). |
| Cited By in Cnki (1) | Click to display the text | |
| [12] | WANG X L, BALAKRISHNAN N,GUO B.Residual life estimation based on a generalized Wiener degradation process[J].Reliability Engineering & System Safety,2014,124:13-23. |
| Click to display the text | |
| [13] | 王小林,郭波, 程志君.融合多源信息的维纳过程性能退化产品的可靠性评估[J].电子学报,2012,40(5):977-982. WANG X L,GUO B,CHENG Z J.Reliability assessment of products with Wiener process degradation by fusing multiple information[J].Acta Electronica Sinica,2012,40(5):977-982(in Chinese). |
| Cited By in Cnki (12) | Click to display the text | |
| [14] | 唐圣金,郭晓松, 周召发,等.步进应力加速退化试验的建模与剩余寿命估计[J].机械工程学报,2014,50(16):33-40. TANG S J,GUO X S,ZHOU Z F,et al.Step stress accelerated degradation process modeling and remaining useful life estimation[J].Journal of Mechanical Engineering,2014,50(16):33-40(in Chinese). |
| Cited By in Cnki | |
| [15] | TANG S J, YU C Q,WANG X,et al.Remaining useful life prediction of Lithium-ion batteries based on the Wiener process with measurement error[J].Energies,2014,7(2):520-547. |
| Click to display the text | |
| [16] | 姜同敏. 可靠性试验技术[M].北京:北京航空航天大学出版社,2012:202-204. JIANG T M.Reliability test technology[M].Beijing:Beihang University Press,2012:202-204(in Chinese). |
| [17] | MEEKER W Q, ESCOBAR L A.Statistical methods for reliability data[M].Hoboken:John Wiley & Sons,1998:56-63. |
| [18] | PENG C Y, TSENG S T.Mis-specification analysis of linear degradation models[J].IEEE Transactions on Reliability,2009,58(3):444-455. |
| Click to display the text | |
| [19] | 孙权,周星,冯静,等. 寿命分布的参数Bootstrap拟合优度检验方法[J].国防科技大学学报,2014,36(3):112-116. SUN Q,ZHOU X,FENG J,et al.Goodness-of-fittest for life distributions based on parametric Bootstrap[J].Journal of National University of Defense Technology,2014,36(3):112-116(in Chinese). |
| Cited By in Cnki |
