在过去的研究中,协同standoff跟踪已经取得一定的成果.Lawrence[2]第一次提出将李雅普诺夫矢量场用于standoff跟踪,Frew等[3]对李雅普诺夫矢量场进行扩展,其提出速度控制和航向角控制双层控制结构,将协同standoff跟踪分成相对独立的距离控制和角间距控制.Summers等[4]通过信息结构进一步扩展李雅普诺夫矢量场,通过设计可变空速控制器来实现多车辆协同控制中期望角间距控制.Chen等[5]第一次结合切向矢量场和李雅普诺夫矢量场形成复合控制结构,用以弥补切向矢量场控制当UAV在standoff圆内切线不存在的问题.除李雅普诺夫矢量场控制以外,Oh等[6]提出了一种基于微分几何方法的standoff跟踪导引律设计方法,通过引入目标速度项来提高跟踪精度.Ma和Hovakimyan[7]通过添加附加项的方式,结合角间距形成平衡圆编队用以实现协同standoff跟踪.此外,Oh等[8]通过航路构造的方法实现协同standoff跟踪;王树磊等[9]对参考点制导(RPG)法进行改进,提高UAV的整体跟踪效果.针对仅有角度测量的UAV,Ponda等[10]针对不同测量方式,对于距离误差和角度误差给出详细分析.Lee等[11]提出多UAV仅考虑一步信息量的反馈导引律设计实现最大化目标估计信息.Kim等[12]运用非线性模型预测控制(NMPC)实现协同standoff跟踪,将standoff距离和期望角间距引入性能指标,获得很好的跟踪效果.
目前standoff跟踪问题研究主要集中在控制律设计,但对UAV不同空间位置关系对目标位置估计精度的影响少有考虑.或者,尽管分析了UAV几何构型与目标位置估计精度之间的关系,但如何实现UAV最优构型下的控制律设计却很少涉及.
针对standoff跟踪过程中如何实现UAV的最优观测问题,本文提出了一种新的导引律设计思路.首先建立UAV协同观测空间构型与目标位置估计误差之间的关系;然后通过优化空间构型进而实现目标状态的最优估计.
1 目标跟踪问题描述1.1 无人机动力学模型假设所有无人机都拥有飞行控制系统可以有效跟踪控制指令,仅考虑在二维水平平面上的控制律设计,对应无人机运动学模型如下:
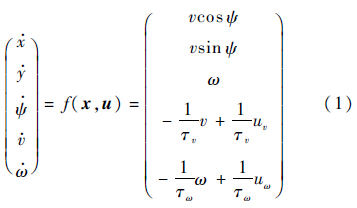
式中:x=[x y ψ v ω]T为无人机状态,(x,y)为惯性坐标系位置,ψ为航向角,v为速度,ω为偏航角速率;(τv,τω)为时间常数表征执行机构时延;u=[uv uω]T为速度和偏航角速率控制输入.基于无人机运动学模型,考虑如下约束[13]:
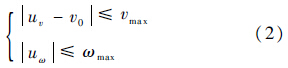
式中:v0为无人机的名义速度;vmax和ωmax分别为速度和偏航角速度的最大变化范围.
1.2 目标运动模型由于地面运动目标可以通过调整速度和方向进行任意机动,所以一般的匀速运动模型无法准确表示目标的运动状态.因此本文中采用加速度模型[14]来表示目标运动方程如下:
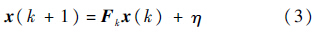
式中:x(k)=[xk $\dot x$k $\ddot x$kyk $\ddot y$k $\ddot y$k]T为目标状态,对应为目标的位置、速度、加速度信息;Fk为目标的状态转移矩阵;η为均值为0、方差为σa2的高斯白噪声用以表征加速度噪声.
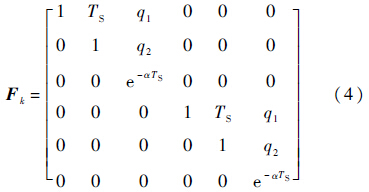
式中:${q_1} = \left( {{e^{ - \alpha Ts}} + \alpha Ts - 1} \right)/{\alpha ^2};{q_2} = \left( {1 - {e^{ - \alpha Ts}}} \right)/\alpha ;{T_s}$为采样时间;α为目标运动模型相对因子,α小则对应目标缓慢运动,反之对应目标快变运动.
1.3 传感器测量模型假设UAV对目标跟踪测量采用定高飞行,传感器模型为方位角测量传感器,模型如下:
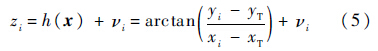
式中:(xi,yi)为第i架UAV的位置信息;(xT,yT)为目标的位置信息;νi为均值为0、方差为σi2的高斯白噪声作为测量噪声.假设不同UAV之间的测量噪声彼此不相关.
1.4 扩展信息滤波考虑式(5)的传感器观测模型为非线性模型,采用扩展信息滤波[15]对目标状态进行估计,扩展信息滤波包括预测过程和估计过程[16].
预测过程:
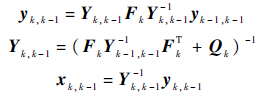
估计过程:
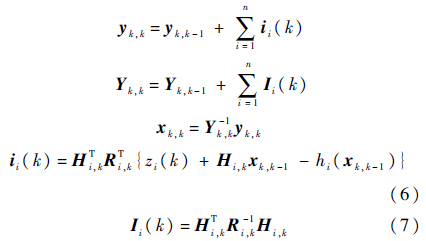
式中:${y_{k,k + 1}}$和${Y_{k,k - 1}}$分别为预测信息和预测信息矩阵;${y_{k - 1,k - 1}}$和${Y_{k - 1,k - 1}}$为$k-1$时刻的信息状态和信息状态矩阵;${Q_k}$为测量噪声协方差矩阵;${H_{i,k}}$为第$i$架UAV测量方程Jacobian矩阵;${R_{i,k}}$为测量协方差矩阵;${z_i}\left( k \right)$为角度测量信息;${\hat x_{k,k - 1}}$为预测目标状态;${h_i}\left( * \right)$为传感器测量方程.目标状态估计信息${\hat x_{k,k}}$作为非线性模型预测控制的状态输入信息用以最优化控制输出.
2 目标位置估计精度分析2.1 均方根误差模型
如图 1所示,两架UAV跟踪地面运动目标,通过方位角测量传感器可以实现目标定位.由于角度测量传感器存在噪声,因此目标定位中存在位置误差.两架UAV的角度测量信息如下:
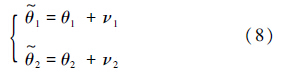
式中:(θ1,θ2)为真实方位角;($\tilde \theta $1,$\tilde \theta $2)为测量方位角;(ν1,ν2)为测量噪声.
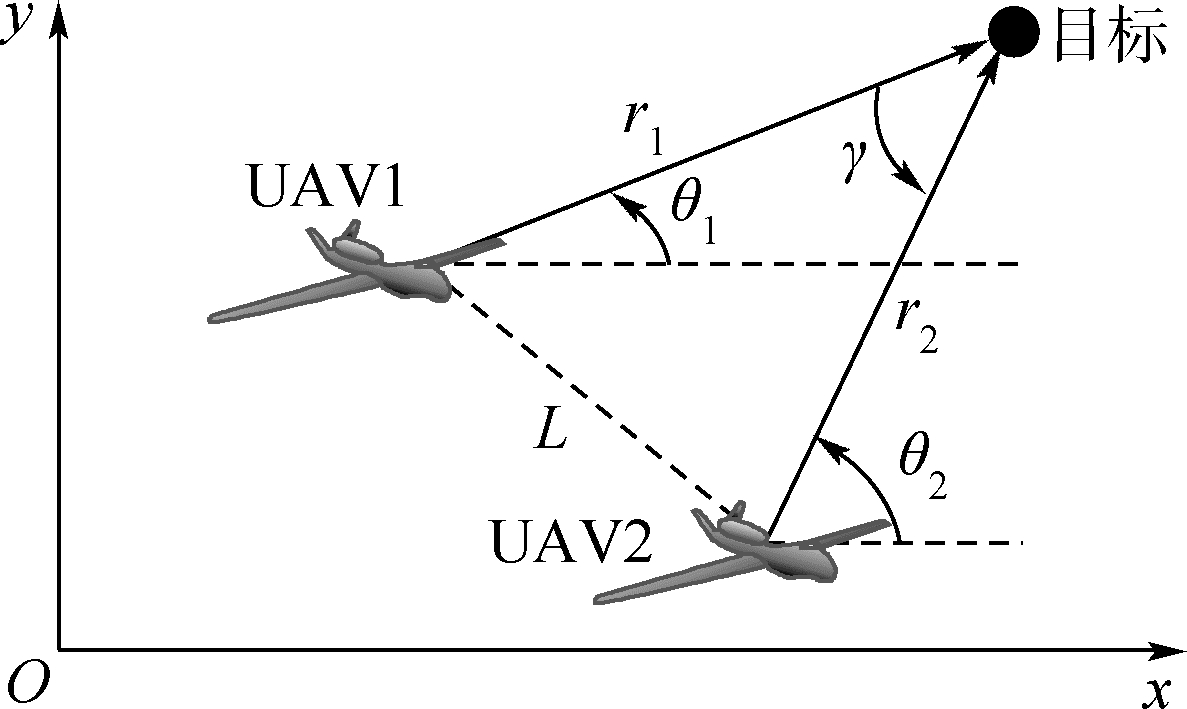 |
| 图 1 角度测量下的协同目标观测Fig. 1 Only bearing measurement cooperative target observation |
| 图选项 |
设(x1,y1)和(x2,y2)分别为两架UAV真实位置,($\tilde x$T,$\tilde y$T)为含有误差的目标位置信息.由式(8)可以获得以下结果:
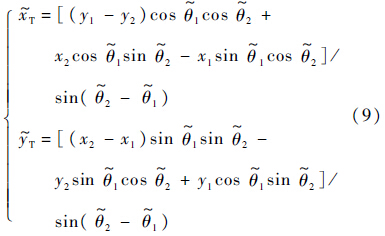
将式(9)表示为式(10)的函数形式,在(θ1,θ2)处进行泰勒展开并忽略二阶以上高阶项,可近似得到位置误差表达式:
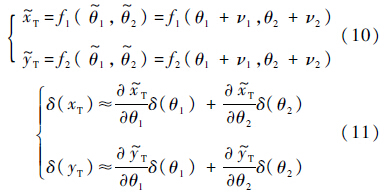
由图 1可得UAV和目标的距离可表示为
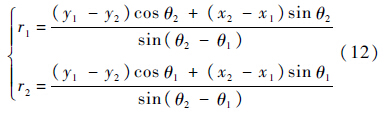
结合式(11)和式(12)可得目标位置误差:
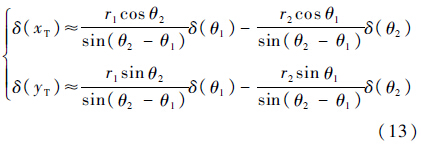
目标位置估计误差为
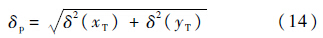
取均方根误差作为目标位置估计精度的参考准则[17],其定义如下:
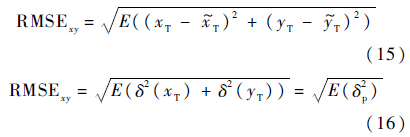
式中:RMSExy为目标位置估计的均方根误差,其值越小,目标位置估计越准确,估计精度越高.设无人机角度测量噪声均值为0、方差为$\sigma _{\theta i}^2\left( {i = 1,2} \right)$.位置误差平方的期望值如下:
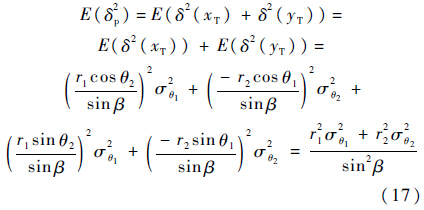
式中:$\left( {\sigma _{\theta 1}^2,\sigma _{\theta 2}^2} \right)$为UAV方位角测量方差.
将式(17)的结果代入式(16)中可得
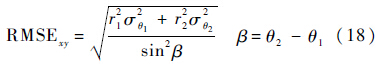
可知目标位置估计均方根误差RMSExy与ri、$\sigma _{\theta i}^2$、β有关,即δp与ri、$\sigma _{\theta i}^2$、β直接相关.
2.2 standoff跟踪问题UAV协同跟踪过程中,ri总会有一定的距离约束Rmin,称为standoff距离(rd),即ri≥Rmin=rd.分析可知:当$\sigma _{\theta i}^2$一定时,ri=Rmin=rd,且β=θ2-θ1=90°时RMSExy最小,对应目标位置误差δp越小,目标定位越准确.依据式(18)可知standoff跟踪最优观测构型如下:
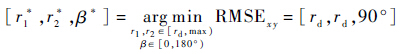
3 非线性模型预测控制基于第2节的分析,通过优化UAV的空间观测几何构型可实现对目标最优跟踪.文献[12]考虑standoff距离和UAV之间的角间距实现协同standoff跟踪.而本文则将目标位置估计均方根误差RMSExy作为目标跟踪评价指标,采用非线性模型预测控制实现对UAV几何观测位置构型优化:
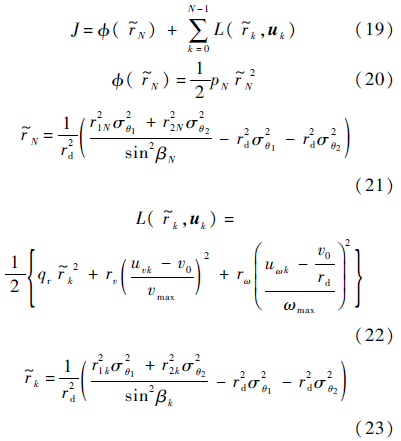
式中:pN和qr分别为第N步和第k步非线性模型预测性能指标函数相关系数;r1k和r2k为k时刻UAV与目标之间的距离.
式(21)和式(23)反映了standoff跟踪过程中当前实际构型对应跟踪误差与最优期望构型对应跟踪误差之间的差值.
为避免复杂的角度计算,考虑做如下变换:
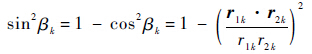
对应式(21)和式(23)可以变为
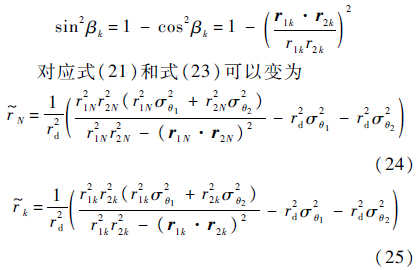
式中:r1k和r2k为UAV当前位置指向目标位置向量(k=0,1,…,N,N为预测步长).从性能指标中可以看出,期望的UAV运动模式为在随机运动目标周围做协同standoff跟踪,即与目标距离尽可能保持r≥Rmin=rd,并尽可能接近Rmin,两架UAV的观测夹角保持90°,即使目标位置估计均方差误差RMSExy尽可能小,实现最优目标位置估计.
考虑UAV动力学模型,有如下等式约束:
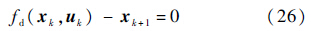
考虑控制输入限幅,机间防撞,安全距离限制Rmin,在非线性模型预测中以不等式约束代入:
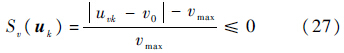
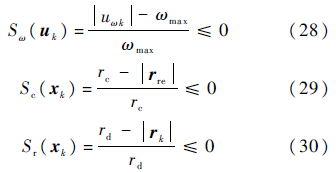
式中:${S_v}\left( {{u_k}} \right)$为第k步非线性模型预测速度控制量不等式约束函数;${S_\omega }\left( {{u_k}} \right)$为第k步非线性模型预测角速度控制量不等式约束函数;${S_c}\left( {{u_k}} \right)$(xk)为第k步非线性模型预测机间防撞不等式约束函数;${S_r}\left( {{u_k}} \right)$为第k步非线性模型预测当前UAV与目标距离不等式约束函数;rc为机间防撞距离;|rre|为两机之间距离;|rk|为当前UAV与目标之间的距离.相应改进的性能指标如下:
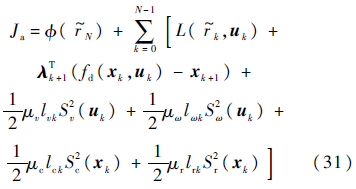
式中:μv、μω、μc和μr为非线性模型预测的不等于约束函数相关系数.
在式(31)的性能指标中对应有
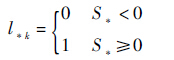
由性能指标式(31),定义Hamiltonian函数:
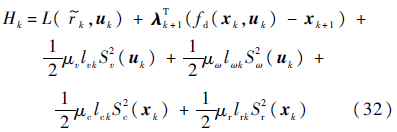
对改进性能指标Ja求偏导数,可得到
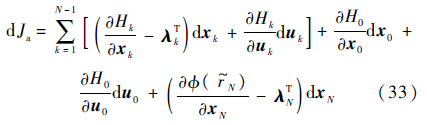
由于等式约束的存在,所以λk可以任意选择.故可以选择:
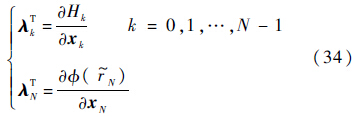
将式(34)代入式(33)中,dJa可以表示为
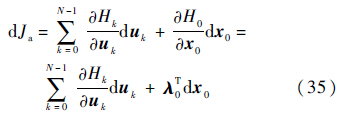
(35)
式(34)中的λ的计算公式为
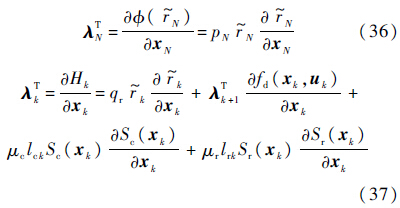
在式(36)、式(37)中对应项的计算公式为
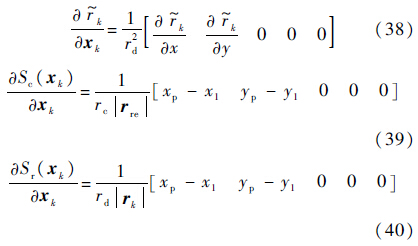
式中:(xp,yp)为相对于本机另外一架UAV k时刻对应的位置信息.
采用基本的梯度理论最小化Hamiltonian函数Hk,每个迭代周期的控制命令更新如下:
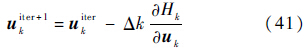
式中:Δk为可变步长,k=0,1,…,N-1.
式(41)对应的计算项有如下表示公式:
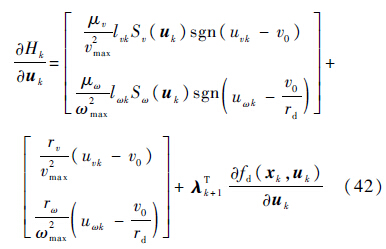
式中:sgn为符号函数,对应的非线性模型预测控制运行步骤如下所示[18, 19, 20]:
WhileΔJ>ε do
利用扩展信息滤波获得的目标估计状态作为原始状态输入,结合UAV运动方程式(1)计算控制输入序列(u0,u1,…,uN-1)作用下无人机的状态传播{xk},k=0,1,…,N.
基于拉格朗日乘子的计算公式(36)和式(37)后向计算出{λk},k=N,N-1…,1.
基于每个{xk,uk,λk+1}集,计算Hamiltonian函数对于控制输入偏导数$\left\{ {\frac{{\partial {H_k}}}{{\partial {u_k}}}} \right\}$,k=0,1,…,N-1.
计算性能指标改进程度ΔJ=Jiter-Jiter-1.
If ΔJ<0
利用梯度方法更新控制序列{uk}.
Else减少Δk来确保性能指标改善.
End If
迭代次数iter+1;
End While
在每一个UAV结点上分别运行非线性模型预测控制算法,实现控制性能在线优化,比较集中式优化结构,分布式控制有效降低了计算量,提高了算法的实时性.假设无人机彼此通信没有延迟且不存在丢包现象,每一个控制周期内,每一架UAV都可以获得所有飞机的状态信息,用以优化性能指标并更新控制序列.每次优化出的控制命令作为当前的周期的控制输入,而下一周期的控制序列输入设定如下:
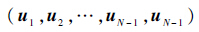
4 仿真结果与分析采用两架UAV跟踪一个地面随机运动目标,采用非线性模型预测控制优化控制输入序列.目标初始状态及估计值为
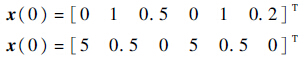
目标运动存在均值为0、均方差为0.02 m/s2的加速度噪声.两架UAV分别从(-1 500 m,0 m)、(0 m,-1 500 m)出发,对目标进行协同standoff跟踪,两架UAV的方位角测量噪声为均值为0、均方差分别为1.0°和0.7°的角度测量噪声.在仿真过程中两架UAV可以获取彼此相应的状态信息,用于非线性模型预测优化相应控制输出.具体的仿真结果参如图 2~图 6所示,具体仿真参数设置如表 1所示.
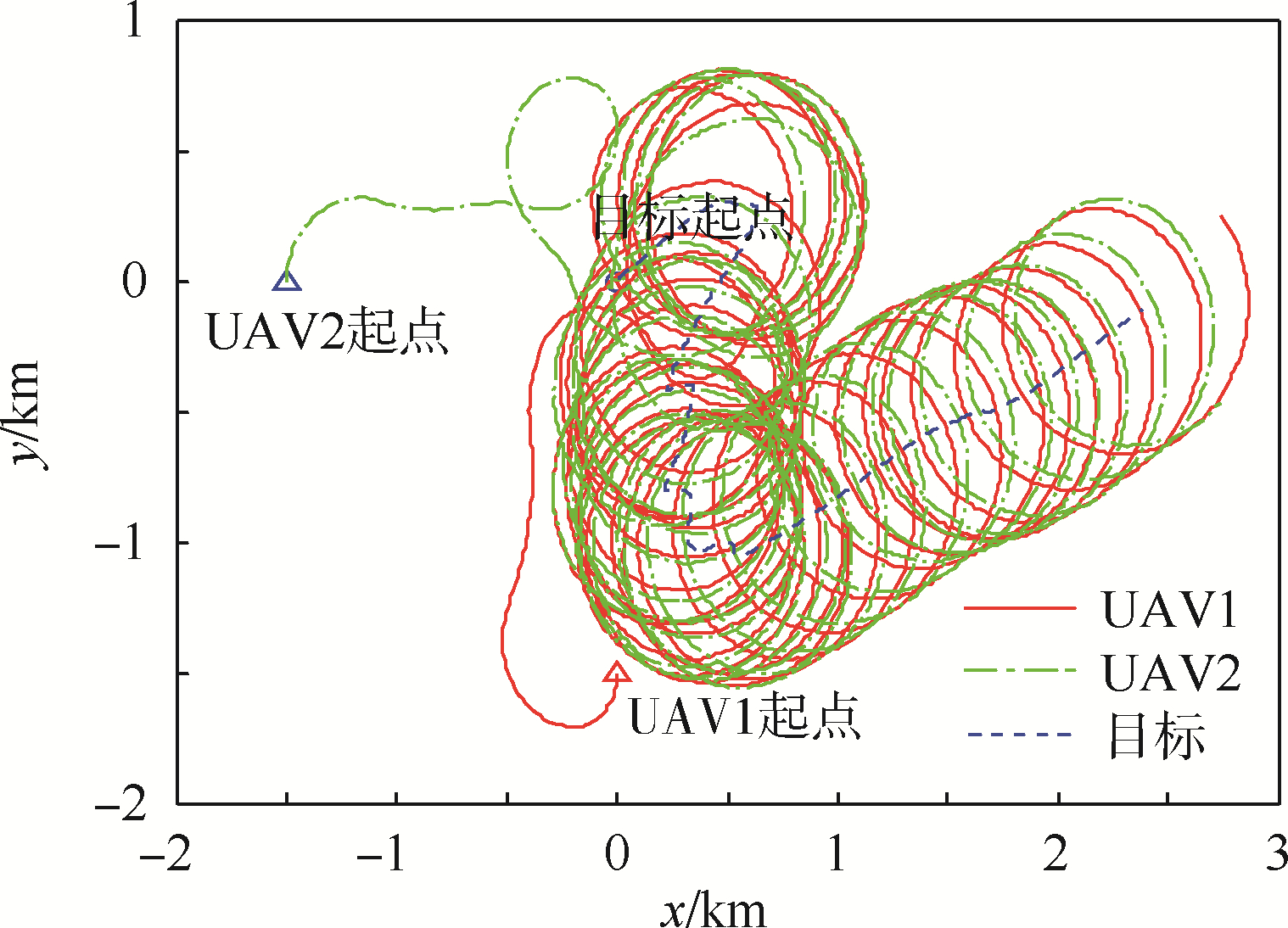 |
| 图 2 两架UAV与随机运动目标的绝对航迹Fig. 2 Absolute trajectories of two UAVs and random moving target |
| 图选项 |
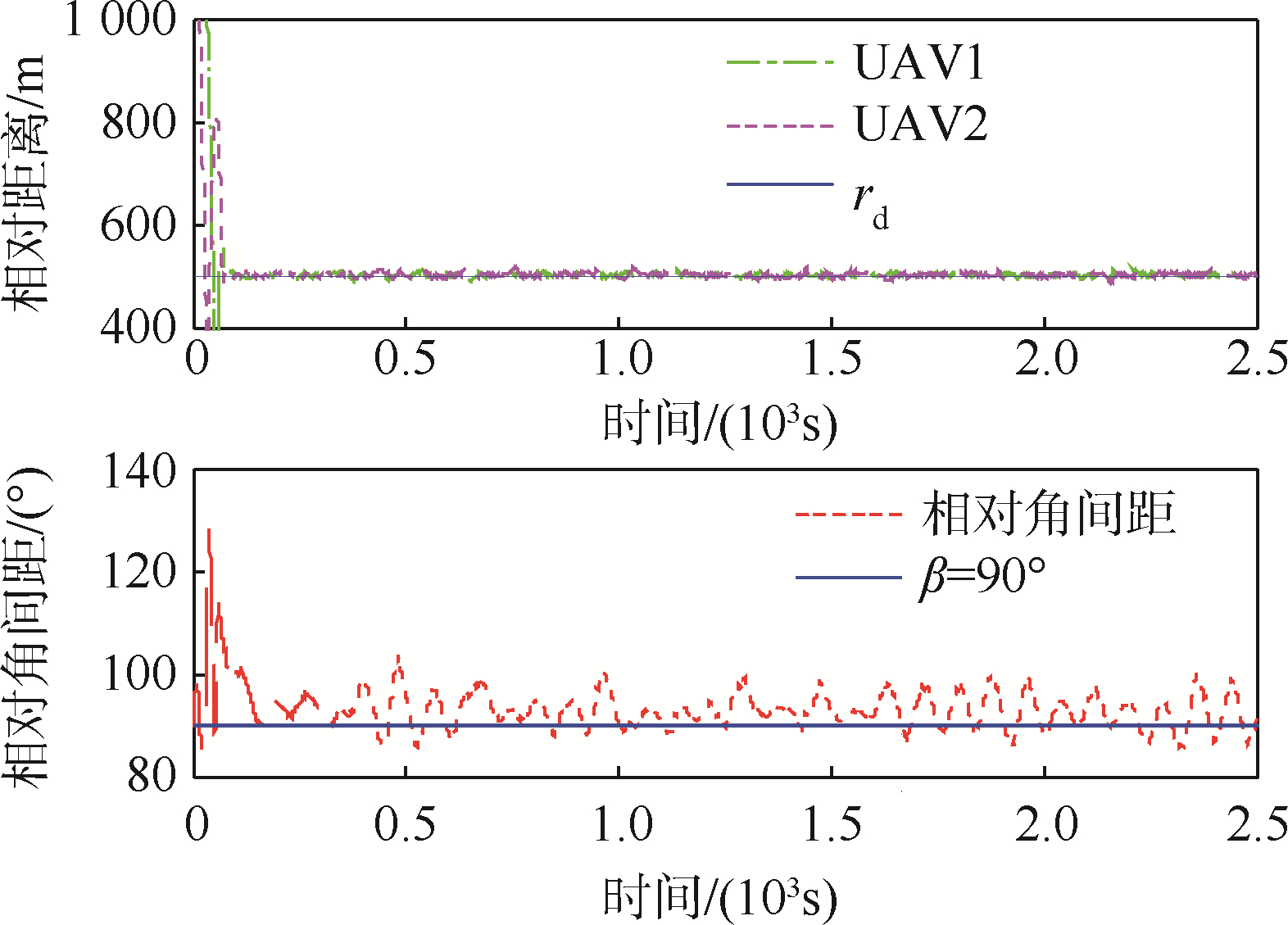 |
| 图 3 UAV与随机运动目标相对距离和相对角间距Fig. 3 Relative distances and angle spacing between UAV and random moving target |
| 图选项 |
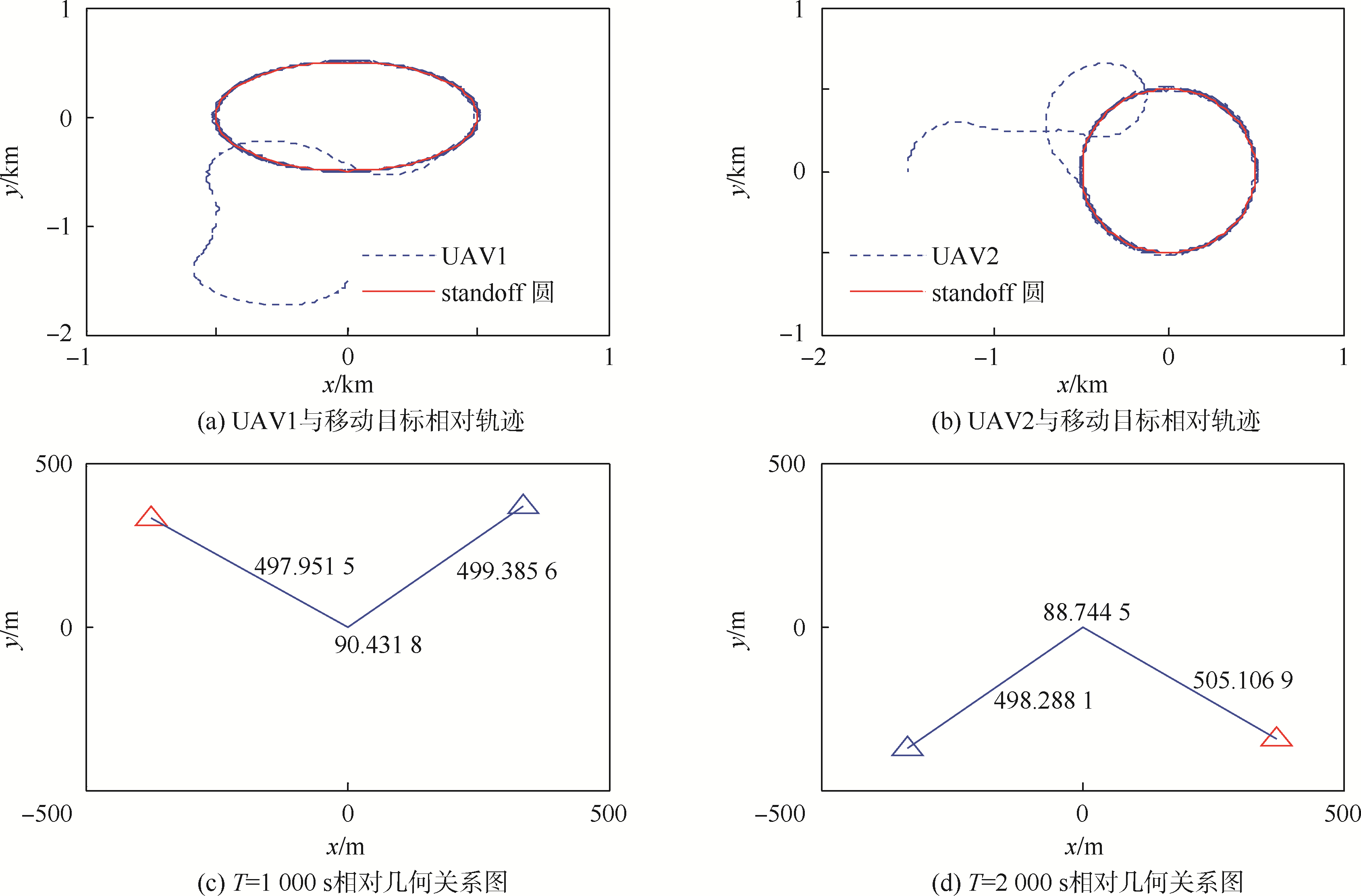 |
| 图 4 UAV与目标的瞬时相对轨迹和几何关系Fig. 4 Relative trajectories between UAV and target and their instantaneous geometric relationships |
| 图选项 |
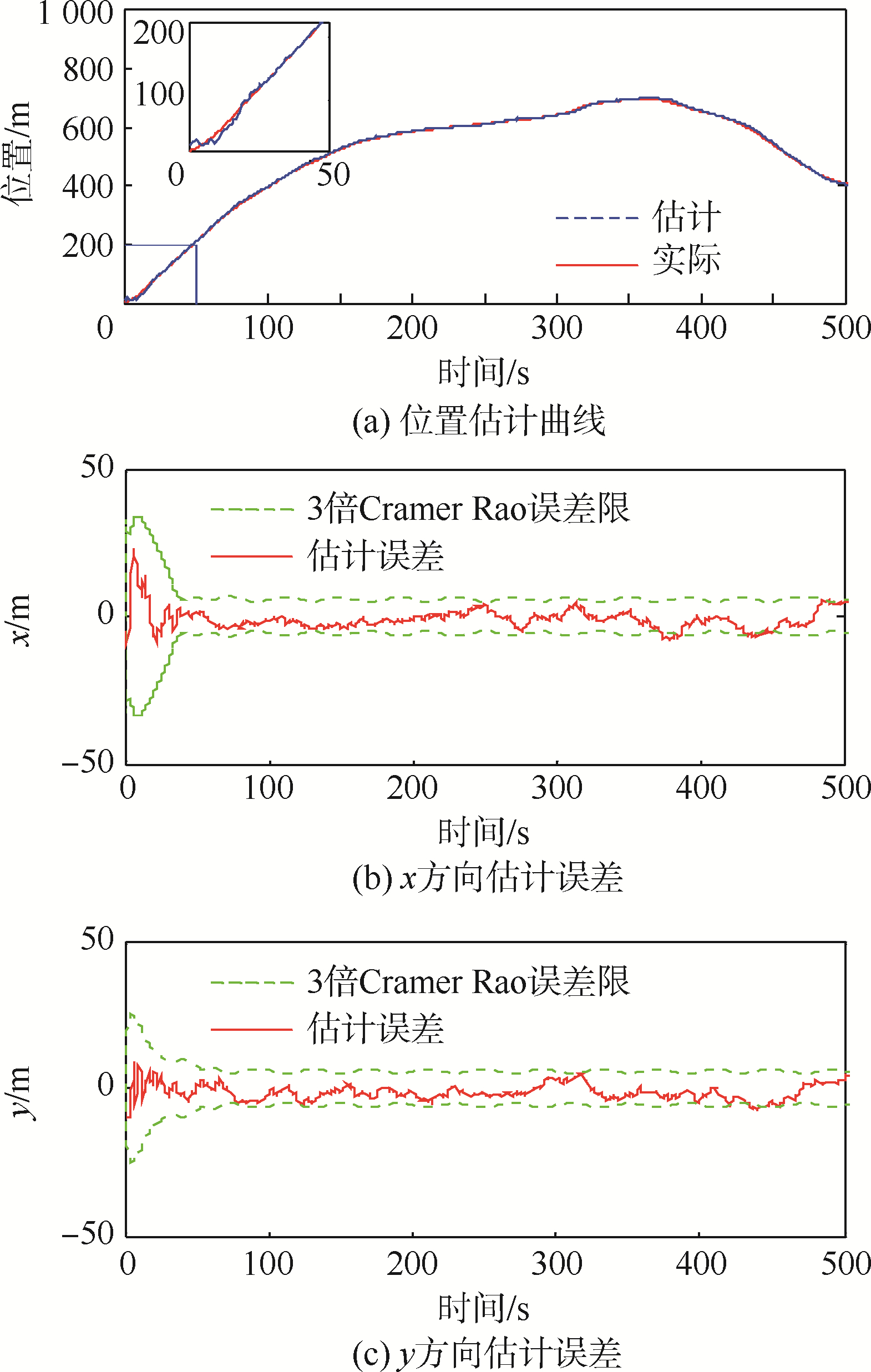 |
| 图 5 运动目标位置估计Fig. 5 Position estimation of moving target |
| 图选项 |
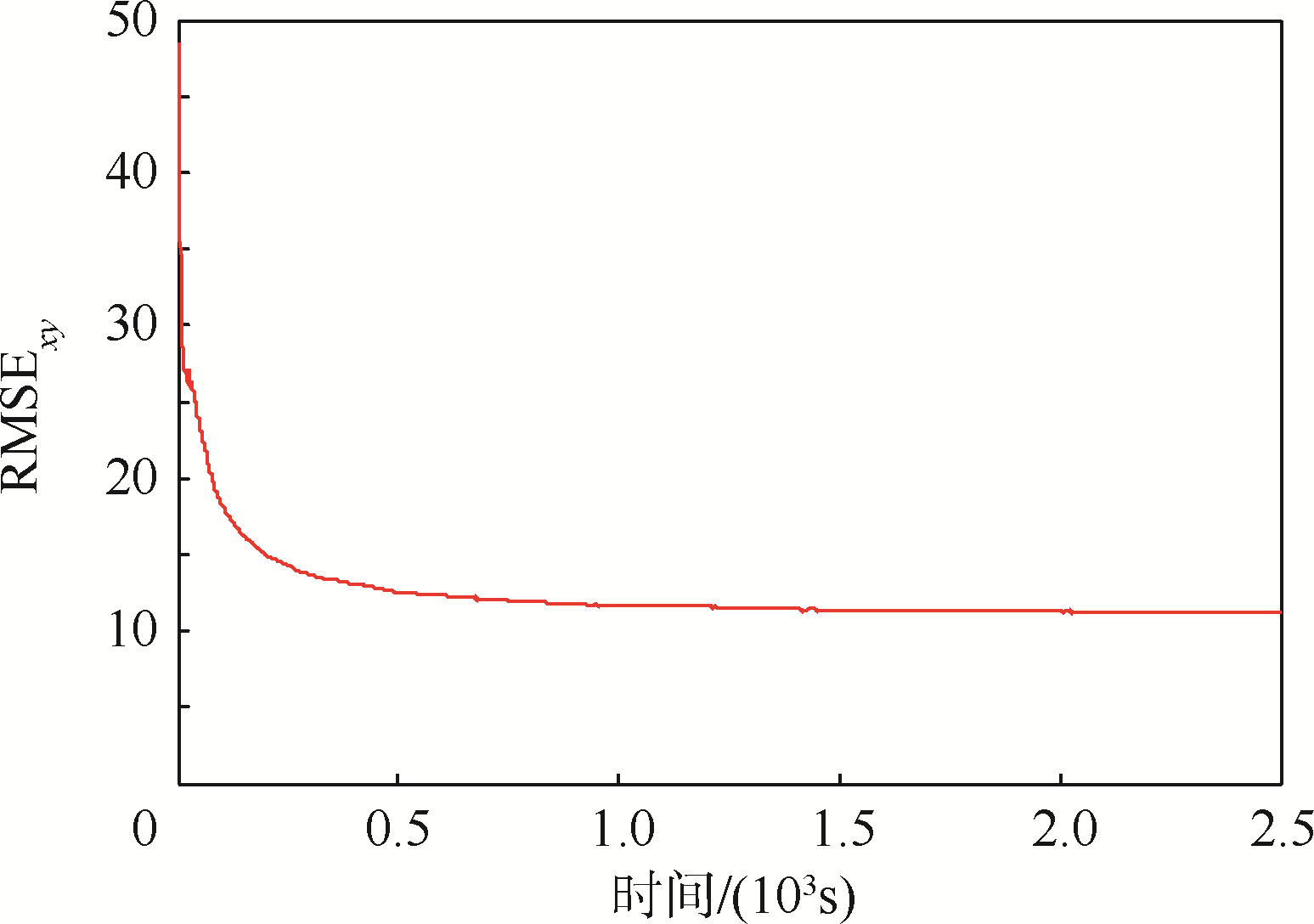 |
| 图 6 目标位置估计的均方根误差Fig. 6 Root mean square error of target position estimation |
| 图选项 |
表 1 仿真参数设置Table 1 Simulation parameters settings
| 参数 | 数值 |
| TS/s | 0.5 |
| N | 4 |
| 仿真时长/s | 2 500 |
| rd/m | 500 |
| α/(m·s-2) | 0.3 |
| vmax/(m·s-1) | 10 |
| ωmax/(rad·s-1) | 0.15 |
| τv,τω/s | 0.33 |
| v0/(m·s-1) | 40 |
| Δk | 0.2 |
| rc/m | 40 |
| 误差限ε | 0.8 |
| 优化参数μv,μw,μc,μr | 1.0×10-3 |
表选项
UAV与目标之间绝对和相对运动轨迹分别如图 2~图 4所示,可以看出:两架UAV实现了对随机运动目标的协同standoff跟踪,两架UAV与目标相对距离都收敛于standoff距离(rd=500 m).两架UAV实际角间距都收敛到期望角间距90°.双机为实现稳定协同standoff跟踪需动态调整与目标之间的距离和相对角间距.由于动态调整,在过渡阶段可能会出现较大波动,但很快会收敛到最优观测构型(即r1=r2=rd,β=θ2-θ1=90°),从而形成稳定双机协同standoff跟踪.稳定协同standoff跟踪过程中两架UAV与目标相对距离和角间距都在期望值附近小幅波动,分析其原因主要是由于目标随机运动的不确定性所造成.
从图 5可以看出,图 5(a)为目标实际运动曲线与利用扩展信息滤波得到的位置估计曲线图,图 5(b)和图 5(c)中的虚线代表 3倍Cramer Rao误差限,实线为x和y方向的估计误差.可以看出:随着两架UAV逐渐趋近期望构型,位置误差也逐渐减小,并且95%以上都处于3倍Cramer Rao曲线范围内,此时具有很好的位置估计效果[21].利用扩展信息滤波可以较好地估计出目标的位置信息,并作为非线性模型预测的初始状态输入,提高两架UAV协同standoff跟踪性能.
图 6为目标位置估计的均方根误差图,可以看出随着两架UAV在standoff跟踪中达到期望的构型,对应的目标位置估计的均方根误差逐渐减小并趋于平稳.
仿真结果表明:两架UAV的观测构型收敛于期望的最优构型,即UAV与目标的距离收敛于standoff跟踪距离rd,两架UAV的角间距收敛于90°,此时目标位置估计误差也达到最小.证明了所建立的目标位置估计误差与UAV几何观测构型之间关系模型的正确性,以及分布式非线性模型预测控制方法的有效性.
为考察本文所提出算法的实时性和有效性,利用MATLAB优化工具箱求解本文提出的问题,并与本文提出的方法进行对比,结果如表 2所示.本文提出的方法虽然牺牲了一定的控制精度(平均跟踪距离误差、平均跟踪角间距误差),但有效提高了算法执行速度,具有较好的实时性.
表 2 算法性能对照Table 2 Performance comparisons of algorithm
| 方法 | 平均跟踪距离误差/m | 平均跟踪角间距误差/(°) | 运行时间/s |
| 本文方法 | 16.107 | 3.803 | 39.87 |
| fmincon优化函数 | 12.258 | 2.017 | 1 371.2 |
表选项
协同standoff跟踪能实现对目标传感器全覆盖,在最优观测构型下最小化跟踪误差.而相应的rd、v0、vmax和ωmax等参数设置与UAV自身机动能力和传感器性能有关,并且与跟踪任务需求相关.显然UAV自身能力越强,standoff跟踪效果越好,形成稳定最优观测构型所需时间越短,反之亦然.
5 结 论主要针对仅有角度测量的UAV随机运动目标协同standoff跟踪问题进行研究.结论如下:
1) UAV仅有角度测量时,最大化目标位置估计精度对应的UAV最优观测空间构型为:保持设定的standoff距离同时保持90°的观测视线角间距.
2) 分布式非线性模型预测控制算法能够实现UAV之间的综合最优控制,在满足各种约束和控制性能的前提下有效提高对随机运动目标的协同standoff跟踪性能.
多机协同目标跟踪的最优空间构型分析以及无人机的协同最优控制问题是今后需要研究的问题.
参考文献
| [1] | Yang K, Kang Y, Sukkarieh S.Adaptive nonlinear model predictive path-following control for a fixed-wing unmanned aerial vehicle[J].International Journal of Control, Automation and Systems, 2013, 11(1):65-74. |
| Click to display the text | |
| [2] | Lawrence D A.Lyapunov vector fields for UAV flock coordination[C]//2nd AIAA Unmanned Unlimited Conference, Workshop, and Exhibit.Reston:AIAA, 2003. |
| Click to display the text | |
| [3] | Frew E W, Lawrence D A, Morris S.Coordinated standoff tracking of moving targets using Lyapunov guidance vector fields[J].Journal of Guidance, Control, and Dynamics, 2008, 31(2):290-306. |
| Click to display the text | |
| [4] | Summers T H, Akella M R, Mears M J.Coordinated standoff tracking of moving targets:Control laws and information architectures[J].Journal of Guidance, Control, and Dynamics, 2009, 32(1):56-69. |
| Click to display the text | |
| [5] | Chen H, Chang K, Agate C S.UAV path planning with tangent-plus-Lyapunov vector field guidance and obstacle avoidance[J].IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2):840-856. |
| Click to display the text | |
| [6] | Oh H, Kim S, Shin H S, et al.Rendezvous and standoff target tracking guidance using differential geometry[J].Journal of Intelligent & Robotic Systems, 2013, 69(1-4):389-405. |
| Click to display the text | |
| [7] | Ma L, Hovakimyan N.Cooperative target tracking in balanced circular formation:Multiple UAVs tracking a ground vehicle[C]//American Control Conference (ACC).Piscataway, NJ:IEEE Press, 2013:5386-5391. |
| Click to display the text | |
| [8] | Oh H, Turchi D, Kim S, et al.Coordinated standoff tracking using path shaping for multiple UAV[J].IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(1):348-363. |
| Click to display the text | |
| [9] | 王树磊,魏瑞轩,郭庆,等.面向协同standoff跟踪问题的无人机制导律[J].航空学报, 2014, 35(6):1684-1693. Wang S L, Wei R X, Guo Q, et al.UAV guidance law for coordinated standoff target tracking[J].Acta Aeronautica et Astronautica Sinica, 2014, 35(6):1684-1693(in Chinese). |
| Cited By in Cnki (1) | |
| [10] | Ponda S S, Kolacinski R M, Frazzoli E.Trajectory optimization for target localization using small unmanned aerial vehicles[C]//AIAA Guidance, Navigation, and Control Conference.Reston:AIAA, 2009:10-13. |
| Click to display the text | |
| [11] | Lee W, Bang H, Leeghim H.A cooperative guidance law for target estimation by multiple unmanned aerial vehicles[J].Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering, 2011, 225(12):1322-1335. |
| Click to display the text | |
| [12] | Kim S, Oh H, Tsourdos A.Nonlinear model predictive coordinated standoff tracking of a moving ground vehicle[J].Journal of Guidance, Control, and Dynamics, 2013, 36(2):557-566. |
| Click to display the text | |
| [13] | Zhu S, Wang D.Adversarial ground target tracking using UAV with input constraints[J].Journal of Intelligent & Robotic Systems, 2012, 65(1-4):521-532. |
| Click to display the text | |
| [14] | Mehrotra K, Mahapatra P R.A jerk model for tracking highly maneuvering targets[J].IEEE Transactions on Aerospace and Electronic Systems, 1997, 33(4):1094-1105. |
| Click to display the text | |
| [15] | 葛泉波,李文斌,孙若愚,等.基于EKF的集中式融合估计研究[J].自动化学报, 2013, 39(6):816-825. Ge Q B, Li W B, Sun R Y, et al.Centralized fusion algorithms based on EKF for multisensor non-linear systems[J].Acta Automatica Sinica, 2013, 39(6):816-825(in Chinese). |
| Cited By in Cnki (15) | |
| [16] | Gasparri A, Pascucci F.An interlaced extended information filter for self-localization in sensor networks[J].IEEE Transactions on Mobile Computing, 2010, 9(10):1491-1504. |
| Click to display the text | |
| [17] | Purvis K B, Astrom K J, Khammash M.Estimation and optimal configurations for localization using cooperative UAV[J].IEEE Transactions on Control Systems Technology, 2008, 16(5):947-958. |
| Click to display the text | |
| [18] | Sutton G J, Bitmead R R.Performance and computational implementation of nonlinear model predictive control on a submarine[M]//Nonlinear Model Predictive Control.Berlin:Springer, 2000:461-472. |
| Click to display the text | |
| [19] | Shin J, Kim H J.Nonlinear model predictive formation flight[J].IEEE Transactions on Systems, Man and Cybernetics, Part A:Systems and Humans, 2009, 39(5):1116-1125. |
| Click to display the text | |
| [20] | Shin H S, Thak M J, Kim H J.Nonlinear model predictive control for multiple UAV formation using passive sensing[J].International Journal of Aeronautical and Space Science, 2011, 12(1):16-23. |
| Click to display the text | |
| [21] | Raol J R.Multi-sensor data fusion with MATLAB?[M].London:CRC Press, 2009:157-159. |
