删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

基于降维算法和Edgeworth级数的结构可靠性分析

本站小编 Free考研考试/2021-12-25
结构可靠性[1, 2, 3]是工程领域内研究的重点内容之一。结构中的几何参数、材料属性、强度和载荷等都可视为结构的基本随机变量。失效概率Pf是结构可靠性分析的重要指标之一。现今已有很多方法用于求解失效概率,例如传统的一次二阶矩方法(First-Order Reliability Method,FORM)[4]和二次二阶矩方法(Second-Order Reliability Method,SORM)[5]、蒙特卡罗模拟(Monte Carlo Simulation,MCS)方法[6]以及响应面方法(Response Surface Method,RSM)[7]等。在利用上述方法计算时,MCS法简单易行、精度高,对求解没限制,但计算量相当大,耗时过长;FORM和SORM存在迭代收敛慢甚至不收敛,对功能函数为隐式的问题计算困难,难于求解变量的导数;RSM法对于非线性程度较高的工程实际问题则需要进行多次迭代,而且固定的函数形式也会影响其逼近精度。
Rahman[8]和Cho[9]等提出的降维算法(Dimension Reduction Method,DRM)避免了对功能函数梯度与矩阵的逆以及迭代最可能失效点(Most Probable failure Point,MPP)的求解,大大降低了计算工作量;Youn等[10]指出在基于矩的积分法时,随积分点的增多,导致线性方程组的系数矩阵出现奇异性、条件数和数值结果不稳定等。
因此,本文结合单变量降维算法和Edgeworth级数展开法[11]进行结构的可靠性分析。采用降维算法,将功能函数分解为n个一维函数叠加的形式,再利用变量转换和Gauss-Hermite数值积分得到各一维函数的原点矩,由所得各原点矩信息获得功能函数的中心矩,再将其前四阶中心矩应用到Edgeworth级数展开式中,该级数无需通过参数的分布类型进行拟合,仅需通过矩信息就可拟合累积分布函数计算。
1 降维算法假设由n维向量X=[x1 x2 … xn]T来表达任意一个连续、可微的实值响应函数g(X),n维函数g(X)的降维表达式[12]为

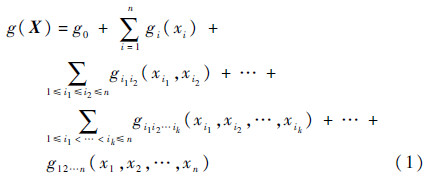
式中:g0为常数;函数gi(xi)为变量xi单独对响应的一阶表达式;函数gi1i2(xi1,xi2)为变量xi1和xi2对函数g(X)的共同影响的二阶表达式;gi1i2…ik(xi1,xi2,…,xik)则体现着前k阶项共同对g(X)的影响;最后一项g12…n(x1,x2,…,xn)包含了所有变量共同对响应函数的影响。选取随机变量空间中的任意一个参考点c=(c1,c2,…,cn),若只考虑式(1)中的一阶项。由式(1)可得到下列分量函数的关系式：

式中:gi=g(c1,c2,…,ci-1,xi,ci+1,ci+2,…,cn)。文献[12]研究表明参考点c的最佳选择为变量的均值,因此令c=(μ1,μ2,…,μn),则单变量降维表达式可写为
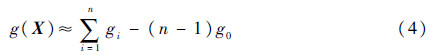
由二项式展开定理和统计矩定义知,n维函数g(X)的k阶原点矩公式[13]为

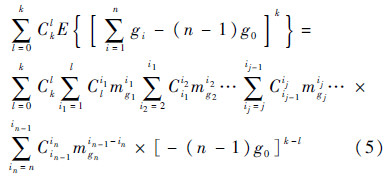
式中: 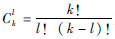为式(5)的二项式展开系数;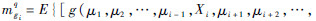 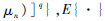为期望算子,q为原点矩的阶数。当随机变量xi的概率密度函数为f(xi)时,一维函数gi(X)的原点矩可以表示为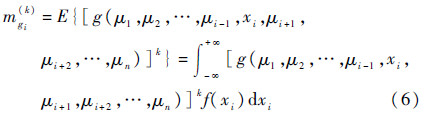

2 变量转换由于直接用积分计算式(6)会导致较大误差且为提高其计算精度,一维函数的积分表达式,通常可以运用传统的数值积分公式进行计算求解,但积分结果有误差。本文中将各变量均转换为服从N(0,0.5)(均值为0,方差为0.5)的正态分布的变量。基于等概率变换原理,将一组任意分布类型且相互独立的向量X=[x1 x2…xn]T转换成一组服从正态分布的向量U=[u1 u2…un]T。经转换后可得

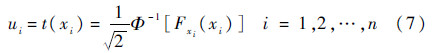
式中:Φ-1[·]为标准正态分布的累积分布函数;Fxi(xi)为随机变量xi的累积分布函数。转换后的概率密度函数fUi(ui)和累积分布函数FUi(ui)的公式分别为
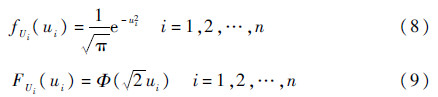
将式(7)和式(8)代入到式(6)中,利用Gauss-Hermite数值积分,则一维函数gi(xi)=g(μ1,μ2,…,μi-1,xi,μi+1,μi+2,…,μn)的原点矩表达式可表示为

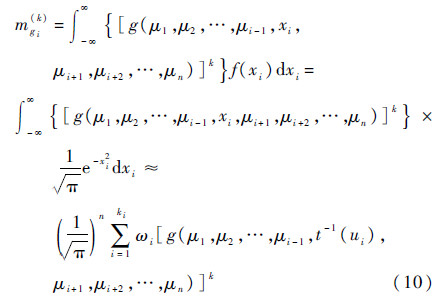
式中:ωi为高斯权重。由式(6)得到一维函数的各阶原点矩,再将其代入式(5),可计算出n维函数g(X)的各阶原点矩。3 Edgeworth级数式(5)得到功能函数的统计矩后,可根据矩信息拟合功能函数的累积分布函数。相应的方法有:Pearson系统[14],鞍点近似法[15],增广β和λ分布等。由于Pearson系统在拟合过程中因分布类型的区别在区域边界取值不同,导致数值解不稳定;鞍点近似法计算在数值过程中存在奇异性;增广β和λ分布仅适用于中低度可靠性水平的单峰概率密度函数的近似,且不能准确估计失效概率小于0.01的情况在鞍点近似的数值过程中存在奇异性等[12]。因而本文采用Edgeworth级数,其仅通过功能函数的矩信息,便可拟合其分布函数。
由Edgeworth级数展开法知,功能函数的累积分布函数F(g)可表示为

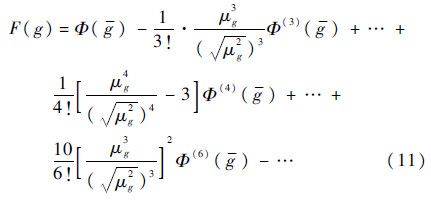
式中: g为已标准化的功能函数;Φ(g)和Φ(i)(g)分别为标准正态分布函数及其i阶偏导函数；μg2、μg3和μg4分别为n维函数g(X)的第2、第3和第4阶中心矩:
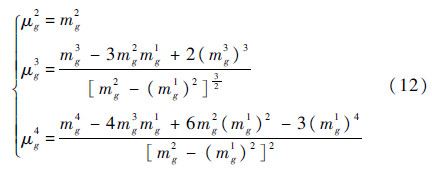
式中:mg2、mg3和mg4分别为功能函数的第2、第3和第4阶原点矩,g为功能函数。将式(12)代入式(11)便可通过计算得到结构的失效概率。其算法流程如图 1所示。
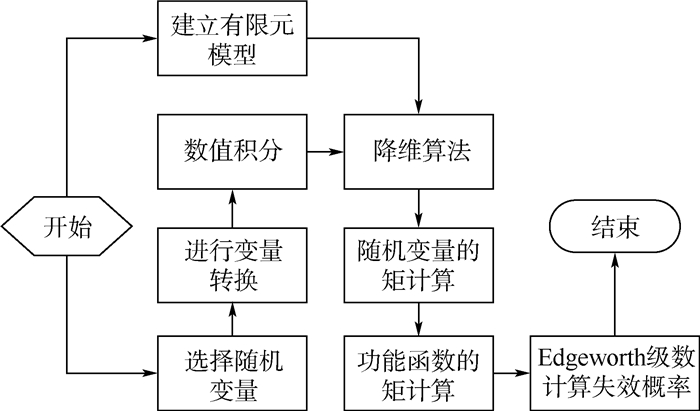图 1 结构失效概率计算流程图 Fig. 1 Calculation flowchart of structural failure probability
图选项


4 数值算例4.1 算例1已知非线性极限状态方程g=567fr-0.5H2,f和r服从正态分布,f～N(0.6,0.078 62),r～N(2.18,0.285 582),随机变量H服从对数正态分布,其均值为32.8,变异系数为0.03,计算极限状态方程的失效概率。
表 1为算例1的失效概率计算结果。由表 1可知,应用本文方法计算的结果与MCS方法吻合较好,具有较高的计算精度。功能函数无需对随机变量进行梯度求解,本文方法的相对误差为7.3%,体现了本文方法的正确性和高效性。
表 1 算例1的失效概率计算结果 Table 1 Calculation results of failure probability for Example 1
方法失效概率相对误差/%样本数
MCS0.028 0107
FORM0.023 020.139
SORM0.025 212.515
本文方法0.026 77.39

表选项


4.2 算例2平面十杆桁架结构如图 2所示。泊松比μ=0.3;弹性模量E=2.1×1011Pa;材料密度ρ=7.8×103 kg/m3;许用应力[σ]=160 MPa;P1=750 kN,P2=950 kN,P3=950 kN,杆①~杆⑥各杆件长度均为3.6 m,面积均为A1=0.03 m2;杆⑦~杆⑩面积均为A2=0.02 m2。节点5和节点6处施加平面约束,在节点4处施加竖直向下载荷P1,节点2处同时施加竖直方向载荷P2和水平方向载荷P3,参数统计特征列于表 2。节点2处的垂直位移Δ≤0.008 m,可得到功能函数为

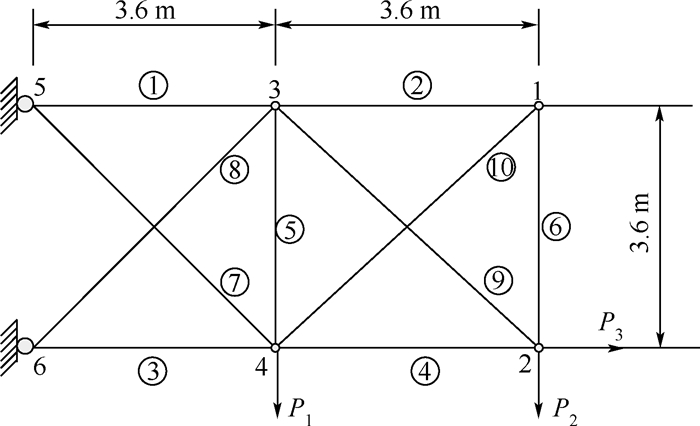图 2 平面十杆桁架结构 Fig. 2 Structure of ten plane truss
图选项


表 2 十杆桁架参数统计特征 Table 2 Parametric statistical characteristics of ten truss
随机变量 参数统计特征
分布类型均值/kN变异系数偏态系数峰度系数
P1对数正态7500.100.301 43.163 1
P2对数正态9500.120.362 53.235 1
P3正态9500.1103

表选项


依据图 1所示的算法流程,首先明确随机变量的分布类型,对其进行变量转换,选取高斯点的个数,该算例中3个随机变量,每个变量选用3个高斯点,再调用桁架结构的有限元程序,即获得节点2处垂直方向的最大位移的9个样本,利用样本计算出3个一维函数的原点矩,进而得到功能函数的前4阶原点矩,通过式(12)可得功能函数的前4阶中心矩,将中心矩作为系数代入式(11),可得节点2处垂直方向最大位移累积分布函数和最终的失效概率。该算例方法实现简单,仅通过9个样本来拟合隐式功能函数的累积分布函数(CDF),图 3为本文方法与MCS法对比的累积分布函数图,体现该方法与MCS法吻合较好。
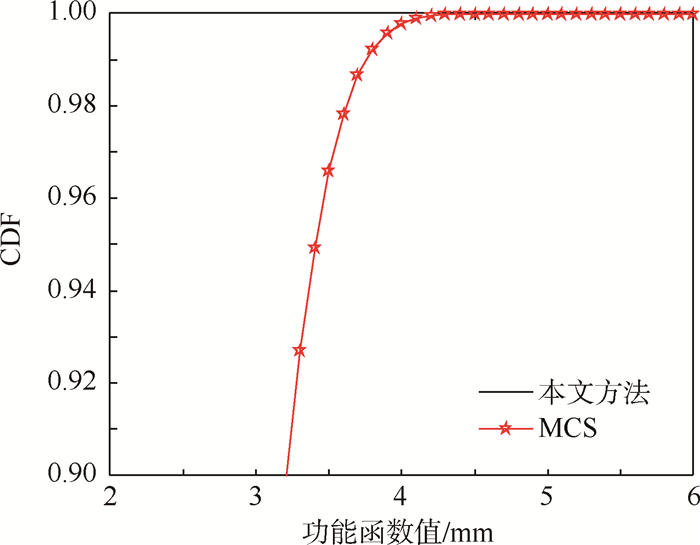图 3 功能函数的累积分布 Fig. 3 Cumulative distribution of performance function
图选项


计算结果列于表 3,与FORM和SORM相比,本文样本数为9,耗时仅用2.891 358 s;本文方法的相对误差仅为0.77%,明显低于FORM的8.77%与SORM的12.99%。验证了模型的正确性和高效性。
表 3 算例2的失效概率计算结果 Table 3 Results of failure probability for Example 2
方法失效概率Pf/10-4相对误差/%样本耗时/s
MCS6.000 0104310 440 000
FORM6.526 28.77156.338 395
SORM6.779 912.99154.697 708
本文方法6.046 30.7792.891 358

表选项


5 结 论本文提出了一种结合降维算法和Edgeworth级数的结构可靠性分析方法。
1) 运用降维算法使得高维积分运算的工作量大大减少,利用Edgeworth级数方法拟合功能函数的累积分布函数。
2) 解决了功能函数为隐式或高维非线性的复杂结构失效概率的计算问题。
3) 高效且稳定地降低了计算成本,算法流程简单,易于编程。具有收敛速度快、计算次数少和可以处理复杂结构可靠性分析问题等优点。

参考文献
[1] 马小兵,任宏道, 蔡义坤.高温结构可靠性分析的时变响应面法[J].北京航空航天大学学报,2015,41(2):198-202. MA X B,REN H D,CAI Y K.Time-varying response surface method for high-temperature structural reliability analysis[J].Journal of Beijing University of Aeronautics and Astronautics,2015,41(2):198-202(in Chinese).
Cited By in Cnki (1) | Click to display the text
[2] 许孟辉,邱志平. 结构模糊非概率混合可靠性分析方法[J].北京航空航天大学学报,2014,40(2):222-228. XU M H,QIU Z P.Reliability analysis of structures with fuzzy and non-probabilistic hybrid variables[J].Journal of Beijing University of Aeronautics and Astronautics,2014,40(2):222-228(in Chinese).
Cited By in Cnki (1) | Click to display the text
[3] MOJSILOVIĆ N, STEWART M G.Probability and structural reliability assessment of mortar joint thickness in load-bearing masonry walls[J].Structural Safety,2015,52:209-218.
Click to display the text
[4] HUANG X Y, ALIABADI M H.A boundary element method for structural reliability[J].Key Engineering Materials,2015,627:453-456.
Click to display the text
[5] LOW B K, PHOON K K.Reliability-based design and its complementary role to Eurocode 7 design approach[J].Computers and Geotechnics,2015,65:30-44.
Click to display the text
[6] CHOI M J, CHO H,CHOI K K,et al.Sampling-based RBDO of ship hull structures considering thermo-elasto-plastic residual deformation[J].Mechanics Based Design of Structures and Machines,2015,43(2):183-208.
Click to display the text
[7] SHI X, TEIXEIRA A P,ZHANG J,et al.Structural reliability analysis based on probabilistic response modelling using the maximum entropy method[J].Engineering Structures,2014,70:106-116.
Click to display the text
[8] RAHMAN S, XU H.A univariate dimension-reduction method for multi-dimensional integration in stochastic mechanics[J].Probabilistic Engineering Mechanics,2004,19(4):393-408.
Click to display the text
[9] CHO H, BAE S,CHOI K K,et al.An efficient variable screening method for effective surrogate models for reliability-based design optimization[J].Structural and Multidisciplinary Optimization,2014:50(5):717-738.
Click to display the text
[10] YOUN B D, XI Z,WANG P.Eigenvector dimension reduction(EDR)method for sensitivity-free probability analysis[J].Structural and Multidisciplinary Optimization,2008,37(1):13-28.
Click to display the text
[11] KONG C, SUN Z,NIU X,et al.Moment methods for C/SiC woven composite components reliability and sensitivity analysis[J].Science and Engineering of Composite Materials,2014,21(1):121-128.
Click to display the text
[12] LI G,ZHANG K. A combined reliability analysis approach with dimension reduction method and maximum entropy method[J] Structural and Multidisciplinary Optimization,2011,43(1):121-143.
Click to display the text
[13] ZHANG X F, PANDEY M D,ZHANG Y M.A numerical method for structural uncertainty response computation[J].Science China Technological Sciences,2011,54(12):3347-3357.
Click to display the text
[14] ANDREEV A, KANTOO A,MALO P.Computational examples of a new method for distribution selection in the Pearson system[J].Journal of Applied Statistics,2007,34(4):487-506.
Click to display the text
[15] SU G,YU B, XIAO Y,et al.Gaussian process machine-learning method for structural reliability analysis[J].Advances in Structural Engineering,2014,17(9):1257-1270.
Click to display the text


相关话题/计算 概率 结构 统计 信息
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 三维全五向编织复合材料细观结构实验分析
    ?20世纪80年代以来,三维(3D)编织技术及三维编织复合材料应用得到迅速发展[1]。三维编织复合材料不需缝合和机械加工,具有良好的综合性能指标,如高的比强度、比模量、高的损伤容限和断裂韧性,耐冲击、不分层、抗开裂和疲劳[2]。为了克服三维五向编织复合材料轴向性能上的缺陷,笔者[3]提出了一种新型的 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 基于小扰动理论的桨叶叶素气动载荷计算方法
    ?直升机依靠旋翼桨叶产生推进力、升力和操纵力,靠尾桨产生偏航力矩[1],可以垂直起降而不受地形限制,无需大面积机场,可以向任意方向进行机动飞行。由于旋翼的气动性能直接影响到直升机的整体飞行性能,因此气动性能的准确模拟就显得尤为重要。研究直升机旋翼的非定常气动特性,就是研究旋翼诱导速度场、非定常气动力 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 磁悬浮控制力矩陀螺热-结构耦合分析与研究
    ?磁悬浮控制力矩陀螺(MSCMG)是空间飞行器实现高精度姿态机动通常采用的惯性执行机构,具有转速高、输出力矩大以及寿命长等特点。磁悬浮控制力矩陀螺转子依靠磁轴承支承[1,2],并且在高速电机的驱动下持续高速旋转,陀螺在工作过程中电机与磁轴承会产生铁损与铜损,这些损耗最终转化为热量传递到陀螺其他结构部 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 确定飞机结构WFD平均行为的寿命升降法
    自1988年Aloha航空事故[1]以来,广布疲劳损伤(WidespreadFatigueDamage,WFD)问题引起了学术界和航空界的广泛关注。WFD是指多个相似或相同细节中同时出现尺寸和密度足够的裂纹,使结构的剩余强度不再满足美国联邦航空条例§25.571(b)的要求[2]。WFD包括2类情况 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 基于边缘信息的灰度目标跟踪算法
    ?目标成像跟踪作为近年来一个十分活跃的研究方向,在军事领域取得了广泛应用,如武器系统的末端制导、飞行器导引控制、光学和雷达图像侦察跟踪等.在军事领域中,灰度目标跟踪的目的是确定目标在图像序列中的位置和几何区域,以便于进一步实现目标识别或者目标拦截.灰度目标跟踪不同于彩色目标跟踪,主要原因在于这两种目 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 利用符号计算方法研究生物系统全时滞稳定性
    时滞微分系统的稳定性研究在理论和应用上都有其重要的意义,特别地,从控制理论的角度看,生物系统全时滞稳定即表明该系统对于时滞具有很好的鲁棒性和可靠性.长期以来,人们一直致力于寻找时滞微分系统全时滞稳定的代数判据,已取得了不少进展.秦元勋在文献[1]中第1次将单滞后多维系统的全时滞稳定判据由超越形式的检 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 结构偏差对二维连续地月载荷转移系统动力学影响
    绳系卫星作为一种新型的卫星概念,经过数十年的研究历程,在航天领域扮演着十分重要的角色.绳系卫星具有诸多特点[1,2]:能够实现动量(能量)的传递[3,4,5],能够借助于电动绳的原理为卫星系统提供可再生的能源,能够实现对太空垃圾的捕获等[6,7].动量交换作为绳系的一个重要功能,其基本思想就是通过系 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 航天员受银河宇宙线辐射的剂量计算
    空间中的质子、电子、重离子、中子和X射线等辐射是威胁航天员健康和安全的环境要素.近20年,国际和我国的载人航天事业均有了很大发展,更多航天员参与空间活动,航天员在空间停留的时间也更长,接受越来越多的空间辐射照射.不同于以X射线、γ射线和中子为主的地面辐射,空间辐射含有高传能线密度(LET)的银河宇宙 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 周期结构电磁特性在高频真空器件中的应用
    在行波类真空电子器件中,电子注和电磁波之间产生持续互作用的一个条件就是电磁波的相速小于光速,通常有两种方法来降低相速,一种是采用介质材料加载的波导,另一种就是采用周期性的金属或者介质结构.微波真空器件通常采用金属周期结构,其传输损耗比较小,可以维持较高的射频电场,还可以接收高频散焦等杂散电子注电流. ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 基于可编程控制网关的一体化网络体系结构
    随着Internet、移动通信和卫星通信技术的高速发展,涌现出了大量不同类型的通信网络,其中典型的网络有互联网、地面无线通信网络以及各种专用网络.其中互联网和地面无线通信网络以IP(InternetProtocol)技术为基础逐步走向融合.而非IP技术的专用网络,如战术数据链网络、基于国际空间数据系 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.