为了采用CIA进行机群结构的耐久性分析,首先应明确机群载荷谱的分散性。文献[8-10]对外场飞机进行了大量的载荷实测和统计分析,文献[11]对202架F-15飞机的载荷谱数据进行分析,得出了疲劳载荷谱的损伤可使用对数正态分布描述的结论,文献[12]指出中国某型飞机机群载荷谱损伤也服从对数正态分布,文献[13]进行了典型结构模拟试件在若干单机谱下的疲劳对比试验,进一步验证了机群载荷谱损伤可以用对数正态分布描述的结论。在阐明了载荷谱损伤分散后,文献[14]引入取值为1.5的额外分散系数以考虑机群载荷谱的分散,文献[15]在载荷谱损伤和结构特性均服从对数正态分布的基础上,推导得到机群寿命也服从对数正态,并得到机群寿命方差为载荷谱和结构损伤方差之和的结论,建立了机群安全寿命评估方法。
在明确载荷谱的分散后,需要综合考虑结构特性分散和载荷谱分散建立CIA。为此,本文在已有CIA进行的基础上,针对在考虑机群载荷谱分散时应关注的问题,进行了某型飞机某关键结构7B04 T74铝合金细节在3个反应不同严重程度单机载荷谱下的耐久性试验,对试验结果进行分析,提出了综合考虑载荷谱分散和结构特性分散的CIA,用于结构耐久性分析,并给出一个示例。
1 CIA概述 1.1 CIA原理 CIA[4]以结构细节裂纹达到经济修理极限ae对应的“裂纹萌生寿命”P-S-N曲线(存活率-应力-寿命曲线)族作为结构细节原始疲劳质量(IFQ)的表征,通过结构细节模拟试件的耐久性试验,确定结构细节裂纹萌生P-S-N曲线族参数,进而由谱载下寿命估算的线性累积损伤理论,建立损伤度p(i,t)随寿命t的函数关系,并预测经济寿命te。
1.2 CIA步骤[1] 1) 获取结构细节对应的一种应力比下三参数式P-S-N曲线族,其形式为
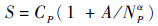 | (1) |
式中:A、α为形状参数;CP为对应可靠度P的疲劳极限,由结构细节模拟试件成组疲劳试验结果反推得到;S为应力水平;NP为指定存活率P下模拟试件在应力水平S下的安全裂纹萌生寿命。
为确定CP值,通常进行1~2种应力水平下结构细节模拟试件成组疲劳试验,获取对应经济修理极限的裂纹萌生寿命,假定裂纹萌生寿命服从对数正态分布LN(μ,σ2),μ为期望,σ为标准差。估计得到分布参数,确定各指定P对应的安全裂纹萌生寿命为tP=10μ+uPσ,uP为正态分布分位点。由线性累积损伤理论计算试验载荷谱下的寿命t,当t=tP时的CP即为反推得到的CP值。
按线性累积损伤理论,t的计算公式为
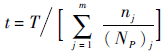 | (2) |
式中:T为载荷谱一个基本周期代表的寿命;nj为第j级应力水平循环数;(NP)j为第j级应力水平恒幅作用下的安全裂纹萌生寿命,利用等寿命曲线确定(NP)j值。等寿命曲线可采用Soderberg表达式:
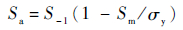 | (3) |
式中:Sa为交变应力幅值;S-1为应力比R=-1的疲劳极限;Sm为应力均值;σy为屈服极限。
将应力谱中的各级应力(Sj,Rj)等损伤折算为应力比为R*、最大值为Sj*的应力。
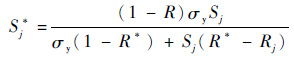 | (4) |
(NP)j由P-S-N曲线确定
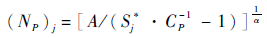 | (5) |
2) 指定应力区给定p(i,t)对应的t为存活率P=p(i,t)对应的安全裂纹萌生寿命。由应力区对应的结构细节名义应力谱和已知的指定应力比下结构细节裂纹萌生P-S-N曲线族及等寿命曲线,根据Miner线性累积损伤理论建立各应力区p(i,t)-t曲线。
3) 给定若干t值,由各应力区p(i,t)-t曲线确定p(i,t),进而确定细节群的裂纹超越数或裂纹超越百分数的平均值与上界,从而建立损伤度随时间的变化曲线,最后根据给定的耐久性要求(裂纹超越(百分)数和可靠度),由损伤度曲线预测经济寿命。
CIA分析流程见图 1。
 |
| 图 1 CIA分析流程 Fig. 1 Analysis process of CIA |
| 图选项 |
1.3 机群结构耐久性分析的关键问题 采用CIA分析机群结构耐久性,需要考虑2个关键问题:
1) 如何量化机群载荷谱分散。已有的分析方法建立在载荷谱给定的情况下,虽然可以考虑不同细节群应力水平的差异,但无法考虑机群内不同飞机载荷谱的差异,从而无法评估机群的可靠性寿命。
2) 载荷谱分散对原始疲劳质量的影响。结构细节的P-S-N曲线是依据试验寿命反推得到的,在考虑机群载荷谱分散时,即使机群内所有飞机按相同的使用要求(如飞行大纲和科目)进行使用,但不同飞机的载荷-时间历程存在明显的差异,对应的载荷谱也存在差别,这种差别是否会造成参数的不同,需要进行试验研究和分析。
2 多个谱下的耐久性试验 2.1 试 件 模拟某型飞机外翼关键部位,加工如图 2所示7B04 T74铝合金试件。
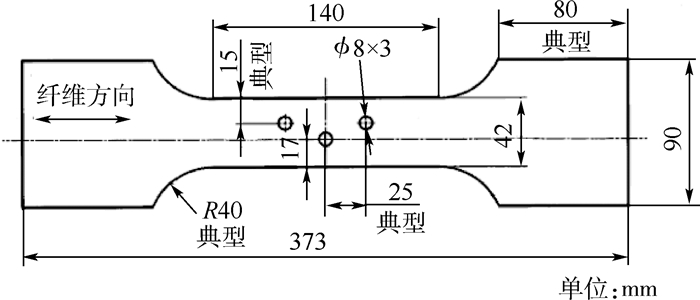 |
| 图 2 7B04 T74铝合金试件 Fig. 2 7B04 T74 aluminum alloy specimen |
| 图选项 |
试件材料为7B04 T74铝合金锻件,板厚8 mm,工作段宽42 mm,工作段交错排列有3个孔,孔径8 mm,螺栓孔加工至H9,并滚压强化。该铝合金材料的化学成分及基本力学性能分别如表 1和表 2所示。
表 1 7B04 T74铝合金化学成分 Table 1 Chemical composition of 7B04 T74 aluminum alloy
| 化学成分 | Cu | Mg | Mn | Cr | Zn | Fe |
| 含量/wt% | 1.4~2.0 | 1.8~2.8 | 0.2~0.6 | 0.1~0.25 | 5.0~6.5 | 0.05~0.25 |
表选项
表 2 7B04 T74铝合金化学成分 Table 2 Chemical composition of 7B04 T74 aluminum alloy
| 性能 | E/MPa | σy/MPa | σb/MPa | ν | KIC/(MPa·m1/2) | |
| 参数 | 69 | 536 | 598 | 0.3 | 26.28 | |
| 注:E—弹性模量;σb—强度极限;ν—泊松比;KIC—断裂韧度。 | ||||||
表选项
2.2 单机过载谱和载荷谱 1) 3个单机过载谱
使用文献[13]中所提到的3个机群载荷谱进行试验,经文献[13]的成组试验验证,上述3个谱对应的损伤严重程度分别为50%、70.323 9%和98.945 2%,即谱1为平均谱,谱2、谱3为重谱。
2) 载荷谱
载荷水平按净截面实测面积施加,对应的1g(g为重力加速度)应力水平为41 MPa。
2.3 试验结果 疲劳试验在MTS 880-500 kN疲劳试验机上进行,在室温大气环境下施加轴向拉-拉载荷,正弦波,试验频率f=6 Hz。试件数分别为:谱1共6件(1-1~1-6),谱2共7件(2-1~2-7),谱3共5件(3-1~3-5)。3种谱下的典型断口照片见图 3。
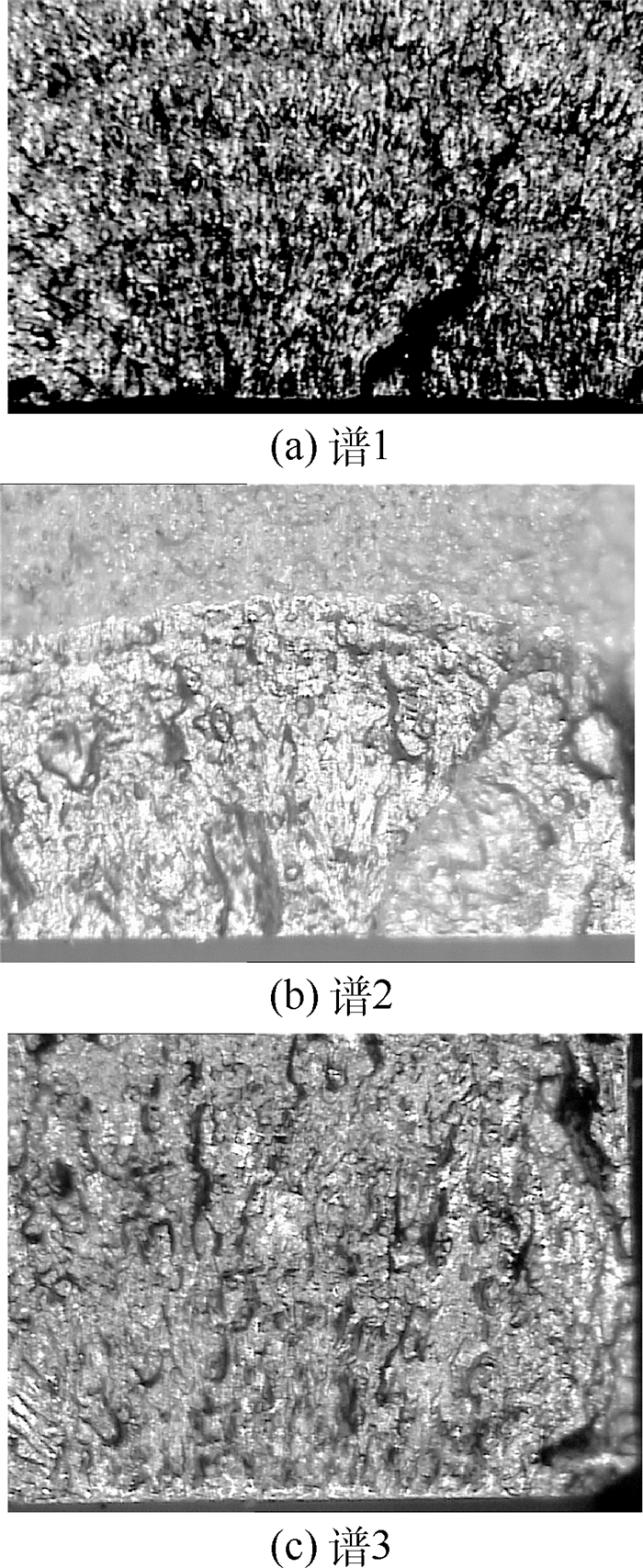 |
| 图 3 7B04 T74铝合金试件典型断口照片 Fig. 3 Typical fractograph of 7B04 T74 aluminum alloy specimen |
| 图选项 |
疲劳载荷在断口上留下了清晰的标识线,在带刻度尺的光学显微镜下进行断口判读,获得各谱下的沿孔径方向的裂纹扩展(a,t)数据集,a为裂纹长度,t为寿命,单位为飞行时间(fh)。当孔两侧均有裂纹产生时,取萌生较早的作为主裂纹,将主裂纹长度≤3 mm的(a,t)数据列入图 4中。
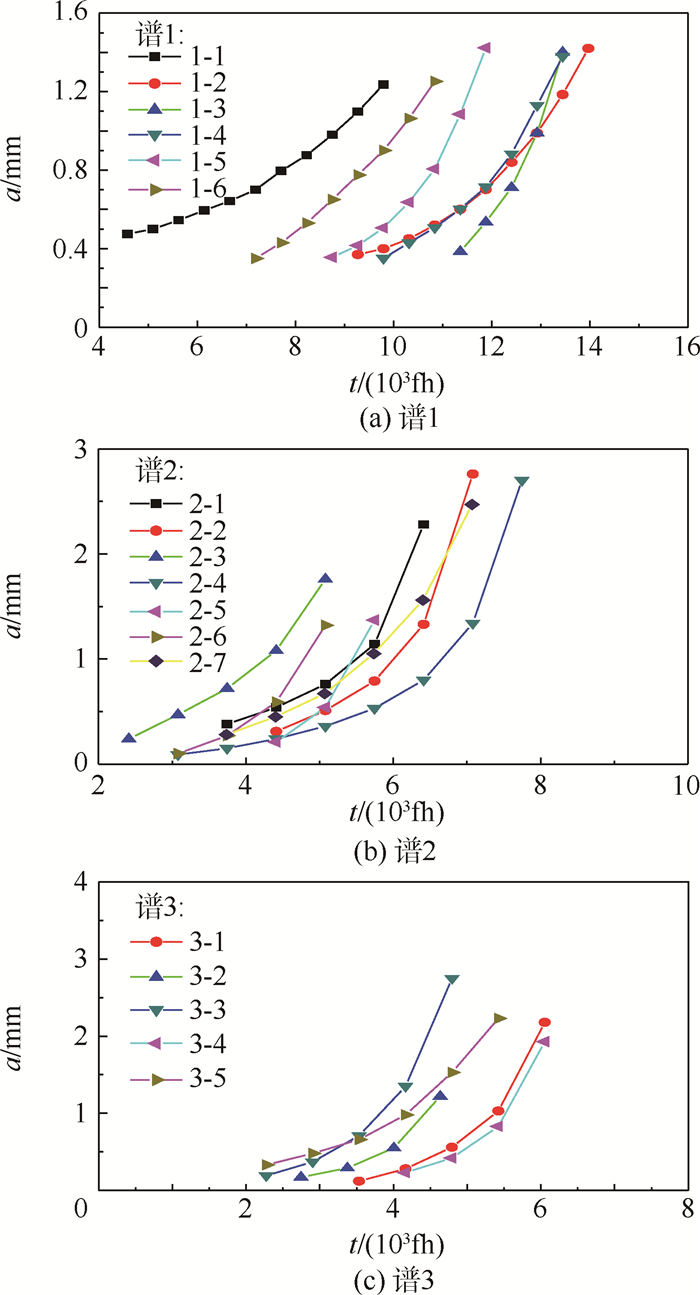 |
| 图 4 3个谱下的主裂纹扩展(a,t)数据 Fig. 4 Lead crack growth (a,t) data corresponding to three spectra |
| 图选项 |
取沿孔径方向的裂纹长度为0.8 mm,由(a,t)数据采用三点Lagrange插值确定每个谱下各试件的裂纹萌生寿命,假定裂纹萌生寿命服从对数正态分布,寿命分布特征参数见表 3,可估计得到的中值寿命和对数寿命标准差。
表 3 寿命分布特征参数 Table 3 Characteristic parameters of life distribution
| 载荷谱 | 试件数 | 中值寿命/fh | 对数寿命标准差 |
| 谱1 | 6 | 10 668 | 0.08 |
| 谱2 | 7 | 9 688 | 0.06 |
| 谱3 | 5 | 4 447 | 0.07 |
表选项
3 载荷谱差异对原始疲劳质量的影响 3.1 C值反推 采用式(1)描述结构细节的原始疲劳质量,参考材料性能手册,取本次试验细节三参数式P-S-N曲线的参数为应力比R=0.06下,应力集中系数Kt=3.0试件室温疲劳S-N曲线三参数式参数以保持参数的稳定性[5],其中:A=9 641.283 8,α=0.867 3,屈服强度σy=536 MPa。
由第2节中试验给出的每个谱下所有试件的裂纹萌生寿命分别反推得到3个谱下所有试件的C值依次为:
谱1 73.151 9,84.001 9,84.691 9,83.821 9,81.001 9,77.611 9 MPa;
谱2 77.556 4,79.046 4,80.106 4,82.976 4,75.456 4,82.846 4,83.406 4 MPa;
谱3 77.186 4,88.116 4,78.326 4,78.416 4,79.836 4 MPa。
3.2 C值对比 假定每个谱下的C值服从对数正态分布LN(μC,σC2),估计得到3个谱下C分布参数分别为:μC,1=1.906 36,σC,1=0.025;μC,2=1.903 9,σC,2=0.017;μC,3=1.904 62,σC,3=0.023;统计对比表明:3种谱下C具有方差齐性,中值无显著差异,表明载荷谱对原始疲劳质量基本无影响。综合所有的C值估计得到的参数为:μC=1.904 92,σC=0.020。
4 结构“当量”原始疲劳质量 4.1 载荷损伤分散性 根据2.2节3个谱严重程度50%、70.323 9%和98.945 2%,查表得到对应的正态分布分位点uP,下标P对应3个谱的严重程度,t50将(uP,t50)绘制在对数坐标纸上,见图 5。
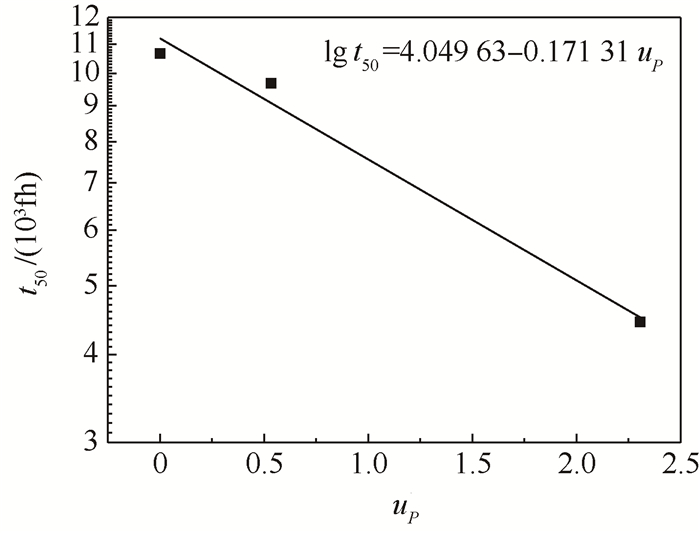 |
| 图 5 t50-uP关系曲线 Fig. 5 Relation curve of t50-uP |
| 图选项 |
从图中可以看出,(uP,t50)数据呈现良好的线性关系,表明载荷谱损伤分散也服从对数正态分布。(uP,t50)满足lg t50=k-σLuP,k为估计得到的截距,σL为载荷谱损伤标准差,由此估计得到载荷谱的对数损伤标准差为0.17。
4.2 机群对数寿命标准差 文献[15]假定结构特性和载荷谱损伤分散均服从对数正态分布,推导得到机群寿命分布特性为对数正态分布,其方差为载荷谱损伤方差和结构特性方差之和。
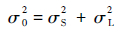 | (6) |
对表 3中3种谱下的对数寿命标准差进行统计对比,表明3种谱下的方差无明显差异,由此综合3种谱下的对数寿命标准差,估计得到反映结构特性的对数寿命标准差为σS=[(6-1)×0.082+(7-1)×0.062+(5-1)×0.072]/6+7+5-3=0.07,由此估计得到机群寿命对数标准差为
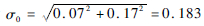
4.3 综合考虑载荷谱和结构特性分散的机群“当量”原始疲劳质量 结构原始疲劳质量P-S-N曲线参数是以给定谱下的可靠性寿命tP反推得到的,在计算tP时采用的是给定谱下结构寿命的对数寿命标准差σS,仅反映了结构特性的分散。为了反映机群载荷谱的分散性,本文提出机群“当量”原始疲劳质量的概念,即仍用P-S-N曲线描述结构原始疲劳质量,但在由tP反推CP时,计算tP的对数寿命标准差取综合考虑载荷谱和结构特性分散的机群寿命对数标准差σ0。
以平均谱下的寿命为基础,取中值寿命为10 668 fh,取结构对数寿命标准差和机群对数寿命标准差反推计算得到的典型CP值,见表 4。
表 4 典型CP值 Table 4 Typical values of CP
| 序号 | P/% | 结构CP/MPa | 机群“当量”CP/MPa |
| 1 | 50 | 80.66 | 80.66 |
| 2 | 90 | 75.80 | 67.01 |
| 3 | 95 | 74.46 | 63.27 |
| 4 | 99 | 71.92 | 56.37 |
| 5 | 99.9 | 69.40 | 49.63 |
| 6 | 99.99 | 69.18 | 49.05 |
表选项
5 裂纹超越概率和损伤度评估 给定p(i,t)对应的t值等于存活率P=1-p(i,t)对应的使用载荷谱下结构细节安全裂纹萌生寿命。根据指定应力区对应的应力谱和存活率P对应的结构细节裂纹萌生P-S-N曲线,由线性累积损伤理论,按式(2)计算对应的寿命。
在指定使用时间t预期超过规定的裂纹尺寸限制的耐久性关键件中结构细节数及标准差可用二项分布确定:
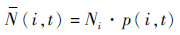 | (7) |
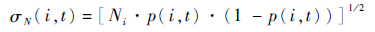 | (8) |
对应可靠度R′的裂纹超越数为
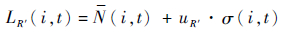 | (9) |
式中:uR′为对应R′的标准正态分位点。
6 示 例 1) 分析对象
设某型飞机机群有100架飞机,机群所有飞机该部位细节共3 800个,应力水平与试验应力水平相同。分析时取反映机群平均使用情况的载荷谱,为本次试验用谱1。
2) 关键参数
P-S-N曲线参数:A=9 641.283 8,α=0.867 3;σy=536 MPa。典型的CP值见表 4。
3) 经济修理极限
取经济修理极限为ae=0.8 mm。
4) 损伤度评估
计算得到的损伤度评估结果见图 6。
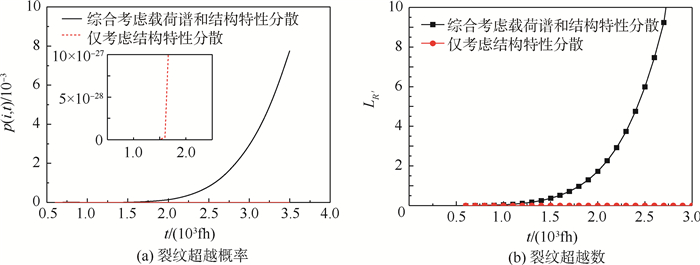 |
| 图 6 损伤度评估结果 Fig. 6 Assessment results of damage degree |
| 图选项 |
5) 经济寿命预测
取允许裂纹超越数[L95]=2,机群该结构的经济寿命te=2 050 fh。
7 结 论 进行了7B04 T74铝合金含孔试件在某型飞机3个单机谱下的耐久性试验,研究了载荷谱分散对结构原始疲劳质量的影响,建立了综合考虑载荷谱分散和结构特性分散的裂纹萌生(CIA)方法,得到:
1) 3个谱下的耐久性试验结果与分析表明,在采用三参数式P-S-N曲线描述结构的原始疲劳质量时,载荷谱的差异对结构原始疲劳质量基本无影响。
2) 提出了综合考虑结构特性和载荷谱分散的机群“当量”原始疲劳质量的概念,在反推三参数式P-S-N曲线CP值时,取对数寿命标准差为综合考虑载荷谱和结构特性分散的机群对数寿命标准差。
3) 通过评估机群载荷谱损伤分散性,建立了综合考虑载荷谱分散和结构特性分散的CIA。
参考文献
| [1] | 中国人民解放军总装备部.军用飞机强度规范:重复载荷,耐久性和损伤容:GJB 67.6A-2008[S].北京:中国人民解放军总装备部,2008. PLA General Armaments Department.Military airplane strength specification:Repeated loads,durability and damage tolerance:GJB 67A.6-2008[S].Beijing:PLA General Armaments Department,2008.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [2] | AN0N.Joint service specification guide:Aircraft structures (The second edition):SG-2006:1998[S].Washington,D.C.:Department of Defense of USA,2002. |
| Click to display the text | |
| [3] | ANON.Partment of defense standard practice for ASIP:MIL-STD-1530C[S].Washington,D.C.:Department of Defense of USA,2005. |
| Click to display the text | |
| [4] | 刘文珽, 郑旻仲, 费斌军. 概率断裂力学与概率损伤容限/耐久性[M].北京: 北京航空航天大学出版社, 1998: 182-194.LIU W T, ZHENG M Z, FEI B J. Probabilistic fracture mechanics and probabilistic damage tolerance and durability[M].Beijing: Beihang University Press, 1998: 182-194.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [5] | 刘文珽. 结构可靠性设计手册[M].北京: 国防工业出版社, 2008: 590-723.LIU W T. Design handbook for structural reliability[M].Beijing: National Defense Industry Press, 2008: 590-723.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [6] | SCHIJVE J. Statistical distribution functions and fatigue of structures[J]. International Journal of Fatigue,2005, 27(9): 1031–1039. |
| Click to display the text | |
| [7] | SCHIJVE J. Fatigue of structures and materials in the 20th century and the state of the art[J]. International Journal of Fatigue,2003, 25(8): 679–702. |
| Click to display the text | |
| [8] | DE JONGE J B.Load experience variability of fighter aircraft[C]//Australian Aeronautical Conference,1989:Research and Technology,the Next Decade.Barton,ACT:Institution of Engineers,1989:102-108. |
| Click to display the text | |
| [9] | ALAN M K.Statistical review of counting accelerometer data for navy and a marine fleet aircraft from 1 Jan 1962 to 30 Jun 1977:RCS NADC 13920-2[R].Washington,D.C.:Naval Air Systems Command Department of the Navy,1977. |
| Click to display the text | |
| [10] | ABELKIS P R,POTTER J M.Service fatigue loads monitoring,simulation and analysis:STP671-EB[S].Philadelphia,PA:American Society for Testing and Materials,1977. |
| Click to display the text | |
| [11] | LINCOLN J W, MELLIERE R A. Economic life determination for a military aircraft[J]. Journal of Aircraft,1999, 36(5): 737–742. |
| Click to display the text | |
| [12] | 王智, 刘文珽, 王磊. 单机疲劳分散系数研究[J]. 机械强度,2009, 31(1): 150–154.WANG Z, LIU W T, WANG L. Study on the fatigue scatter factor for individual aircraft structure[J]. Journal of Mechanical Strength,2009, 31(1): 150–154.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [13] | HE X F, SUI F C, ZHAI B, et al. Probabilistic and testing analysis for the variability of load spectrum damage in a fleet[J]. Engineering Failure Analysis,2013, 33(10): 419–429. |
| Click to display the text | |
| [14] | ANON.Design and airworthiness requirement for service aircraft:Defense Standard 00-970 Part 1 Issue 3[S].London:UK Ministry of Defense,2003. |
| Click to display the text | |
| [15] | 贺小帆, 董彦民, 刘文珽. 结构和载荷分散性分离的寿命可靠性分析方法[J]. 航空学报,2010, 31(4): 732–737.HE X F, DONG Y M, LIU W T. Reliability analysis on fatigue life with separated structural and load spectrum scatters[J]. Acta Aeronautica et Astronautica Sinica,2010, 31(4): 732–737.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
