早期对多轴疲劳的研究,一般是基于一维应力状态的疲劳数据而得出的经验公式,对于疲劳破坏机理却很少考察。研究者一般是将静强度理论推广到多轴疲劳中去,因此出现了等效应力和等效应变的概念,其中应用最广的是Von Mises准则与Tresca准则。多轴高周疲劳破坏准则一般是基于应力分析的;而多轴低周疲劳破坏准则一般基于应变分析。本文中所给出的对飞机某典型结构的多轴疲劳寿命分析是基于应变的比例多轴低周疲劳破坏准则。
近些年来,对多轴低周疲劳损伤累积和寿命分析方法的研究取得了很大的进展[3-11],提出了许多比较有效的多轴疲劳寿命预测模型[3-5, 7, 10],并对其工程应用进行了研究[9, 11-14],此外对于变幅载荷下的多轴疲劳问题同样开展了大量研究[6, 8]。当前对多轴低周疲劳破坏的损伤累积和寿命预测主要有3种方法:等效应变法、能量法和临界面法[3-4, 7]。
等效应变法是将某点处的各应变等效为一个应变值。等效应变可以是八面体剪应变、最大剪应变、Von Mises等效应变等。等效应变法在估算比例加载疲劳寿命方面比较一致,简单实用,易为工程接受。能量法认为塑性功的累积使材料产生了不可逆的损伤,该方法可以成功地处理一些试验数据,但塑性功是标量,不能反映多轴疲劳的破坏面;而且进行塑性功计算需要的精确本构关系很难得到;当塑性功较小时,也很难用于寿命分析。因此在工程实际中,能量法并不实用。Brown和Miller最早提出临界面法的概念[3-4],该方法是建立在裂纹萌生或扩展机理之上的,认为裂纹扩展第1阶段沿最大剪切面形成,第2阶段沿垂直于最大剪应变方向扩展,因此该方法有一定的物理意义,被普遍认为是分析多轴疲劳一种比较有效的方法。虽然临界面法的各计算模型中临界面的定义不同,但该方法在定义临界面后主要认为多轴载荷下裂纹的萌生扩展与3个参量有关,即临界面上的剪应变、正应变以及正应力。
本文选用3种临界面分析模型,对飞机典型机身框结构进行分析,并将分析结果与试验结果和基于单轴疲劳寿命分析方法的分析结果进行对比,研究临界面法在该类型飞机结构中的适用性,为该类结构疲劳寿命评定提供依据。
1 多轴疲劳寿命分析模型 1.1 Wang-Shang模型 Wang-Shang模型[3-4]利用最大剪应变幅平面上最大剪应变变幅Δγmax/2与最大剪应变相邻折返点之间正应变变程Δεmax来建立寿命预测模型,该模型的计算公式为
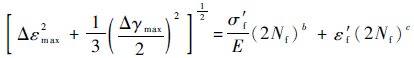 | (1) |
式中:Nf为疲劳寿命;σ′f、ε′f、b和c均为应变疲劳的材料常数,σ′f为疲劳强度系数,ε′f为疲劳塑性系数,b为疲劳强度指数,c为疲劳塑性指数;E为材料的弹性模量。
在完成结构细节有限元应力分析后,提取结构细节各危险点处的应力、应变值,根据材料力学知识即可计算得到各危险点处在各循环加载下的最大剪应变幅平面。由此计算得到各危险点处Δγmax/2与Δεmax。将各点处得到的参数代入Wang-Shang模型计算各点的Nf。
1.2 Smith-Watson-Topper模型 Smith-Watson-Topper (SWT)模型[3-4, 10]利用垂直于最大主应变平面的最大正应力与最大正应变变幅来建立疲劳寿命分析模型,该模型的计算公式为
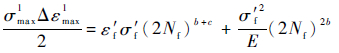 | (2) |
式中:Δεmax1为最大正应变变幅;σmax1为垂直于最大主应变平面的最大正应力。
计算方法同第1.1节中过程相同,计算得到各节点参数后代入计算模型得到疲劳寿命。
1.3 Morrow-Brown-Miller模型 Morrow-Brown-Miller模型[3-4]同Wang-Shang模型近似,是以Δγmax所在的平面作为临界平面,并将临界平面上所对应的正应变变幅Δεn作为参考参数来计算得到一个等效应变,代入Manson-Coffin方程进行疲劳寿命估算。其计算公式为
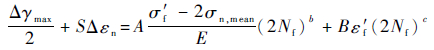 | (3) |
式中:S为正应变变幅影响系数;A=1.3+0.7S,B=1.5+0.5S;σn,mean为最大剪应变幅平面上的平均应力。
Morrow-Brown-Miller模型中考虑了最大剪应变幅平面上的平均应力σn,mean,并将其作为参数代入寿命预测模型。
2 某飞机典型结构疲劳寿命分析 2.1 结构概述 本文研究的对象为飞机机体结构典型的机身框腹板,它能够承受框平面内的弯矩和剪力,其上的大开孔通常为各类系统所需的通孔或减重所开的减轻孔,上下边的缺口为垂直面内方向构件通过所设计。本文的实例主要承受对称面上的集中载荷和由其产生的弯矩,由于开孔和缺口的存在,很多部位的应力状态表现出复杂的比例多轴状态。该结构的材料为7B04铝合金,其机械性能见表 1。
表 1 7B04铝合金的机械性能 Table 1 Mechanical properties of 7B04 aluminum alloy
| 性能参数 | E/GPa | σb/MPa | σp0.2/MPa | μ |
| 数值 | 70 | 490 | 449 | 0.3 |
| 注:σb—拉伸破坏强度;σp0.2—材料屈服强度;μ—泊松比。 | ||||
表选项
为方便试验,按等损伤的原则,将该部位的载荷谱简化为仅有4个峰谷值的载荷谱块,每一谱块的载荷历程见图 1。
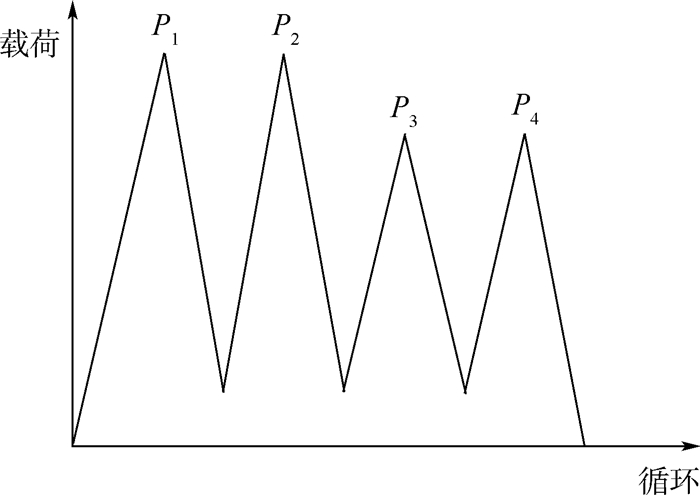 |
| 图 1 结构的载荷历程 Fig. 1 Load history of structure |
| 图选项 |
2.2 细节应力分析 为得到该结构破坏的可能危险部位,采用有限元法对结构进行细节应力分析[15]。该结构件左右对称,根据实际的受力特点,在建立有限元模型(FEM)时,对其两端进行固定约束,单元以六面体元为主,建立该结构件的有限元模型,将载荷谱最大一级的峰值载荷施加在结构件的对称轴线上。其模型和应力云图如图 2所示。
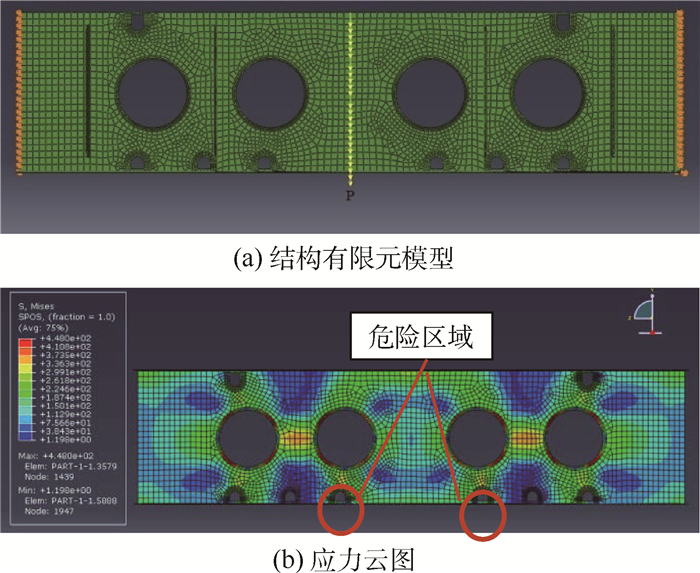 |
| 图 2 结构有限元模型及应力云图 Fig. 2 FEM of structural component and stress nephogram |
| 图选项 |
通过计算结果的应力云图可以看到,结构的危险区处于靠近中心对称线的小孔边,孔边放大的疲劳危险部位应力分布如图 3所示。通过进一步分析和查阅,孔边的几个节点均处于危险区域。为不遗漏所有的疲劳危险点,提取了孔边危险区域所有各节点处的应力、应变分量。在图 3中标出了应力最大点(危险点)位置。
 |
| 图 3 疲劳危险部位应力分布 Fig. 3 Stress distribution of fatigue critical site |
| 图选项 |
2.3 疲劳寿命分析结果 根据应力分析结果,可以判断该结构失效模式为拉伸失效,能够采用本文选取的3种不同的拉伸失效寿命预测模型对结构疲劳寿命进行预测。7B04铝合金材料的单轴疲劳材料常数如表 2所示。本节利用这些单轴材料参数进行多轴疲劳寿命分析,并分析了各材料参数对疲劳寿命分析结果的影响。
表 2 7B04铝合金材料的单轴疲劳材料常数 Table 2 Uni-axial fatigue constants of 7B04 aluminum alloy
| 参数 | σ′f/MPa | b | ε′f/(mm·mm-1) | c |
| 数值 | 916.0 | -0.080 3 | 0.231 6 | -0.873 4 |
表选项
2.3.1 Wang-Shang模型的预测结果 将各危险点处得到的应力、应变参数代入到Wang-Shang模型,计算各点的Nf,找出各节点中寿命最小的节点。计算得到最危险节点处疲劳寿命为10 216谱块。图 4为材料参数对疲劳寿命分析结果的影响。
 |
| 图 4 材料参数对疲劳寿命分析结果的影响 Fig. 4 Effects of material constants on fatigue life estimation results |
| 图选项 |
通过分析可知,在等效应变取5.872×10-3时(对应于P1载荷时的应变),当参数b增大时,结构疲劳寿命呈指数增加(见图 4(a)),其对预测的疲劳寿命的影响较大;参数c对疲劳寿命分析结果的影响与参数b对疲劳寿命的影响基本一致(见图 4(a));疲劳寿命结果与参数ε′f基本呈线性关系,且影响相对较小(见图 4(b)),疲劳寿命结果与参数σ′f的关系呈指数关系(见图 4(b)),且参数σ′f对疲劳寿命的影响很大。因此在测定单轴疲劳系数时,参数b、c以及σ′f需要精确地测得。图中三角符号表示本分析实例参数所处的位置,可以看出,所选择的参数均处于曲线变化的平缓段,其误差对本文的寿命预测结果不会产生显著的影响。
2.3.2 SWT模型的预测结果 计算方法与第2.3.1节的相同,计算得到各节点参数后代入计算模型,得到最危险点的疲劳寿命为23 453谱块。
为了分析各参数对预测结果的影响,同样将该模型等式左边项认为是“等效应变”。参数b、c、ε′f和σ′f对疲劳寿命分析结果的影响与Wang-Shang模型基本一致,b、c和σ′f值变化时会对预测结果产生较大的影响,ε′f影响较小。
2.3.3 Morrow-Brown-Miller模型的预测结果 计算方法与第2.3.1 节的相同,计算得到各节点参数后代入计算模型进行疲劳寿命分析,由于没有该材料的S值,因此,参考不锈钢材料S值的取值(1.5~2.0之间),本文取几个不同的S值计算得到了几组分析结果,见表 3。
表 3 Morrow-Brown-Miller模型疲劳寿命分析结果 Table 3 Results of fatigue life calculated on Morrow-Brown-Miller’s model
| S | 寿命/谱块 |
| 1.8 | 44 671 |
| 2.0 | 43 815 |
| 2.4 | 42 350 |
| 2.8 | 41 157 |
表选项
当用Morrow-Brown-Miller模型对结构寿命进行预测,随着系数S的增加,其寿命值减小。但是在用该模型对寿命进行预测时,由于其增加一个参数S,针对不同的材料可通过参数S修正预测结果,利于提高预测精度。由于该方法计算寿命时的公式与Wang-Shang模型相似,这里不再对其各参数的影响进行赘述。
2.4 单轴疲劳寿命分析方法的计算结果 为了更好地比较多轴载荷对结构件疲劳寿命的影响,此处给出单轴载荷时的疲劳寿命预测结果。利用单轴低周疲劳的Mason-Coffin方程对结构件疲劳寿命进行预测。Manson-Coffin方程是等温低周疲劳寿命计算的基础模型之一。Manson-Coffin描述ε-N曲线的公式为
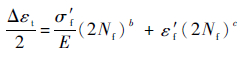 | (4) |
式中:Δεt为正应变变程。
同多轴低周疲劳寿命预测的过程相似,利用该方法对结构件进行疲劳寿命预测时,首先提取出危险点的应力应变,之后找到危险区各节点处最大的正应变变程Δεt,将其代入寿命预测模型,得到结构失效时所经历的谱块数为342 945。
3 与试验结果的对比分析 3.1 试验结果 试验件材料及构型与分析算例中相同,试验件通过特制的试验夹具安装在疲劳试验机上,见图 5。试验件上粘贴应变片,用于校验计算结果、有限元模型的修正、试验件安装是否对称和正确。根据测量得到的应变数据进行分析,试验件安装正确,结果有效。
 |
| 图 5 试验装置与试验件 Fig. 5 Test setup and specimen |
| 图选项 |
试验在INSTRON疲劳试验机上进行。施加的载荷谱(见图 1)与疲劳寿命分析使用的相同。
试验在室温大气环境下进行,采用正弦波,试验频率为6 Hz。试验结束后,在光学显微镜下对试验件的断口进行判读,以获取裂纹长度与循环谱块的成组(c,N)信息。经测量和断口判读得到试件的裂纹萌生寿命N0i和总寿命Nci,i=1,2,…,n,见表 4。
表 4 疲劳试验结果 Table 4 Results of fatigue testing
| 序号 | N0i/谱块 | Nci/谱块 |
| 1 | 13 200 | 19 300 |
| 2 | 10 100 | 13 000 |
| 3 | 6 700 | 8 200 |
表选项
假设试验件的裂纹萌生寿命服从对数正态分布,即可按式(5)由寿命样本N0i估计试验件中值寿命与对数标准差:
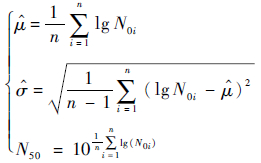 | (5) |
式中:
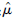
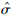
计算得到试验件裂纹萌生时N50=9 631谱块,
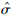
3.2 对比分析 以试验结果的9 631谱块为基准,对3种预测模型的寿命预测结果进行对比分析。结果显示,3种预测模型的计算值均偏大。其中Wang-Shang模型的预测结果较好,误差小于10%,SWT模型的误差为144%,而Morrow-Brown-Miller模型的误差最大,达到320%以上(S=1.8~2.8)。另按单轴低周疲劳的Mason-Coffin方程预测疲劳寿命为342 945谱块,其误差更大。
由以上的对比分析结果可以看到,若承受多轴载荷的结构件按单轴疲劳寿命分析方法进行寿命预测,计算得到的疲劳寿命误差远大于多轴计算模型的预测结果。
分析3种多轴疲劳寿命预测模型计算结果产生误差的主要原因有:
1) 缺少多轴疲劳的材料参数,计算中采用的单轴疲劳参数b、c及σ′f对预测结果有较大的影响,由分析可知,某些情况下,单轴疲劳参数测试结果的很小误差就可能会对多轴预测结果带来较大的变化。
2) 有限元模型简化带来的应力应变误差对疲劳分析结果也会有较大影响。
3) 试验件只有3件,疲劳试验结果的分散性也是产生误差的主要原因之一。
4 结 论 从疲劳寿命计算与试验结果对比分析后可以得出:
1) 对于该类型承受多轴载荷的结构件,若按单轴疲劳寿命分析方法对其进行疲劳寿命预测,其结果将会产生较大的误差。
2) Wang-Shang模型预测结果对于本文研究的这类结构是适用的,计算结果的精度在工程上是可以接受的,其结果好于SWT模型和Morrow-Brown-Miller模型。
3) 采用Morrow-Brown-Miller模型需要确定合适的S,才能得到较好的预测结果,对于本文的实例,S值的影响不大,但在材料参数缺乏情况下,不便于工程应用。
对于多轴疲劳寿命分析方法研究,在充分进行多轴疲劳理论分析与计算的同时,应加强试验研究,尤其是基础性的材料参数研究,同时也要加强单轴疲劳材料参数在多轴疲劳分析中的应用研究。
参考文献
| [1] | WANG C H, BROWN M W. Life prediction techniques for variable amplitude multi-axial fatigue-Part 2: Comparison with experimental results[J]. ASME Journal of Engineering Materials and Technology,1996, 118(1): 371–374. |
| Click to display the text | |
| [2] | 王雷, 王德俊. 一种随机多轴疲劳的寿命预测方法[J]. 机械强度,2003, 25(2): 204–206.WANG L, WANG D J. Life prediction approach for random multi-axial fatigue[J]. Journal of Mechanical Strength,2003, 25(2): 204–206.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [3] | 尚德广, 王德俊. 多轴疲劳强度[M].北京: 科学出版社, 2007: 118-129.SHANG D G, WANG D J. Multi-axial fatigue strength[M].Beijing: Science Press, 2007: 118-129.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [4] | DARRELL F S, GARY B M. Multi-axial fatigue[M].Warrendale: SAE Publication Press, 2000: 79-97. |
| Click to display the text | |
| [5] | 王英玉.金属材料的多轴疲劳行为与寿命估算[D].南京:南京航空航天大学,2005:4-9. WANG Y Y.Fatigue behavior and fatigue life prediction of metals under multi-axial cyclic loading[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2005:4-9.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [6] | WANG C H, BROWN M W. Life prediction techniques for variable amplitude multi-axial fatigue-Part1:Theories[J]. ASME Journal of Engineering Materials and Technology,1996, 118(1): 367–370. |
| Click to display the text | |
| [7] | 时新红, 张建宇, 鲍蕊, 等. 材料多轴高低周疲劳失效准则的研究进展[J]. 机械强度,2008, 30(3): 515–521.SHI X H, ZHANG J Y, BAO R, et al. Development of failure criterion on high-cycle and low-cycle multiaxial fatigue[J]. Journal of Mechanical Strength,2008, 30(3): 515–521.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [8] | 张莉, 唐立强, 付德龙. 基于损伤累积理论的多轴疲劳寿命预测方法[J]. 哈尔滨工业大学学报,2009, 41(4): 123–125.ZHANG L, TANG L Q, FU D L. An evaluation method of fatigue life under multi-axial loading based on damage accumulation theory[J]. Journal of Harbin Institute of Technology,2009, 41(4): 123–125.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [9] | 吴志荣, 胡绪腾, 宋迎东. 多轴载荷下缺口件的疲劳寿命估算方法[J]. 工程力学,2014, 31(10): 216–221.WU Z R, HU X T, SONG Y D. Estimation method for fatigue life of notched specimen under multi-axial loading[J]. Engineering Mechanics,2014, 31(10): 216–221.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [10] | 尚德广, 姚卫星. 基于临界面法的多轴疲劳损伤参量的研究[J]. 航空学报,1999, 20(4): 295–298.SHANG D G, YAO W X. Study on multiaxial fatigue damage parameters based on the critical plane approach[J]. Acta Aeronautica et Astronautica Sinica,1999, 20(4): 295–298.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [11] | 吴志荣, 胡绪腾, 宋迎东. 基于最大剪切应变幅和修正SWT参数的多轴疲劳寿命预测模型[J]. 机械工程学报,2013, 49(2): 59–66.WU Z R, HU X T, SONG Y D. Multiaxial fatigue life prediction model based on maximum shear strain amplitude and modified SWT parameter[J]. Journal of Mechanical Engineering,2013, 49(2): 59–66.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [12] | PARK J, NELSON D. Evaluation of an energy-based approach and a critical plane approach for predicting constant amplitude multiaxial fatigue life[J]. International Journal of Fatigue,2000, 22(1): 23–39. |
| Click to display the text | |
| [13] | 邱宝象, 高增梁, 王效贵, 等. 基于有限元法的16MnR缺口件疲劳寿命预测方法[J]. 工程力学,2010, 27(8): 21–26.QIU B X, GAO Z L, WANG X G, et al. A fatigue life prediction method for 16MnR steel notched components based on the finite element method[J]. Engineering Mechanics,2010, 27(8): 21–26.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [14] | 吴光强, 李运超, 盛云. 后悬架多轴疲劳寿命预测[J]. 同济大学学报,2010, 36(6): 881–884.WU G Q, LI Y C, SHENG Y. Multiaxial fatigue life prediction of rear suspension[J]. Journal of Tongji University,2010, 36(6): 881–884.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [15] | 张成成.复杂应力场下结构高周疲劳寿命分析[D].南京:南京航空航天大学,2010:60-71. ZHANG C C.Fatigue life prediction of structures in HCF region under complex stress field[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2010:60-71.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
