随着弹箭武器型号研制的可靠性要求越来越高,使得试验对于真实环境的模拟需求也日趋提升[2]。特别是飞行器上的管路系统,其职能特点决定了其在生产、运输、发射和飞行过程中同时承受多种恶劣的力学环境载荷[3]。目前,国内在管路力学环境试验过程中,尽可能考虑了其在预期使用过程中的环境因素如低温、位移和内压等作用[4, 5],这种努力的收效是值得肯定的,但大量的实践结果表明:试图通过改进实验室环境以达到消除环境条件与产品工作或使用过程中所处真实环境的差异并不能成为一个现实的解决思路,至少在费效比上如此。
环境试验中的所谓模拟,实际上是在相似性准则下将试验条件进行等效。其中“相似性准则”的制定需要解决2个方面的问题:①环境试验条件如何代表预期使用环境即试验的等效性;②环境试验条件与预期使用环境不一致造成的影响如何进行评估[3]。上述问题的解决必然是建立在对真实使用状态下的振动响应分布的了解以及结构动力学在时、频域和空间上分布规律特性认识的基础之上,即依赖于管路结构动强度(定量)的准确评估。
因此本文将从振动疲劳损伤分析的角度出发,首先将预期使用过程中的环境因素如位移、内压等作用作为预载荷,然后开展预载荷作用下管路结构动强度评估方法研究,最后通过实际算例分析了管路的动强度薄弱点以及剩余强度系数和疲劳寿命,该方法对于分析管路结构真实使用过程中的环境适应性以及可靠性提供了指导。
1 预载荷对动力学响应的影响预载荷或者预应力是由初始状态下的压力、重力或其他外力作用所产生的应力,也可以称其为一次应力,它是平衡外力所需的应力,随外力的增加而增加,没有自限性。例如当管路内塑性变形达到极限状态,即使外力载荷不再增加,管路仍将产生不可限制的塑性流动,直至破坏。
由工作条件中的热胀冷缩、端点位移等位移载荷的作用所产生的应力,可以称为二次应力。二次应力不直接与外力平衡,是为了满足位移约束条件和管路自身变形的连续要求所必须的应力,具有自限性,即局部屈服或小量变形就可以使位移约束条件和管路自身变形的连续要求得到满足,而变形不再继续增大。只要不反复加载,二次应力不会导致结构破坏,它引起的主要是疲劳破坏。
在动力学分析的时候需要考虑稳态静载荷(预载荷)的作用,初始静载荷对动力学响应分析主要包括2个方面的影响:①考虑静载荷引起的微分刚度的影响,需使用新的刚度矩阵来进行后续的动力学分析;②考虑静载荷作用对动力学稳态响应的贡献量,即在做动力学分析时必须要同时考虑静载荷和动态激励的影响,其实现方法需在动力学响应结果中叠加静态载荷结果。
此外,多数材料的疲劳数据都是在实验室里用对称载荷试验方法采集到的,工程上通过试验得到预载荷情况下材料的疲劳曲线成本是非常高的[6]。但由于大多数现场的服役条件都包含非零的平均应力,因此,就出现了表示交变应力幅和平均应力之间关系的经验公式,其中应用最为广泛的是Goodman曲线和Gerber曲线。其中:Goodman关系为[7]
Gerber关系为[7]
式中:Sa为非对称循环应力幅;Sm为平均应力;σb为材料的强度极限;σr为材料的疲劳极限。
2 预载荷作用下应力功率谱密度计算功率谱密度(Power Spectral Density,PSD)函数提供了有关随机过程统计学的大量信息,使用PSD的谱矩可以获得其他统计学特性,一个PSD的n阶谱矩定义为[7]
式中:G(f)为频率f(单位：Hz)处的单边PSD值,由此可得到多个重要的统计学特性参数。
峰值期望速率(单位时间内峰值数)为
根据Miner线性累积损伤理论,结构的疲劳损伤可表示为
式中:ni为第i级应力水平下的应力循环次数;Ni为应力水平为Si时的疲劳寿命。
对于连续应力状态,单位时间内在应力范围(Si,Si+ΔSi)内的循环次数为
式中:p(Si)为应力幅值概率密度函数,工程上常采用Dirlik[4]统计模型。
在航天工程实际应用中,所谓的随机振动疲劳通常都是在疲劳载荷谱作用下以及在预载荷所形成的准静态应力的基础上,同时叠加随机振动应力后所引起的疲劳破坏。随机载荷下应力功率谱密度的计算一般采用弹性模型,当存在预载荷时,应考虑静载荷引起的微分刚度的影响,使用新的刚度矩阵来进行频响函数及随机振动响应分析。
作为评估结构随机振动疲劳的输入条件时,与常规预载荷作用下动力学响应分析有所不同,计算应力功率谱密度时应不包含预应力的贡献量,而是将预应力视为平均应力,即在动应力谱归纳时,视静应力为平均应力Sm,而在平均应力Sm上叠加动应力。
如前所述,对于不对称应力(Sa,Sm)状态,即平均应力Sm≠0,动应力幅计算时可按第1节叙述的关系式进行转换,如果采用Goodman曲线,非对称循环应力幅Sa的等效对称循环应力幅SA为[8]
3 动强度评定由材料的S-N曲线得到[9]
式中:N为应力水平为S时的疲劳寿命;S为应力幅值; f(S)为应力水平为S下的频率;C和m为材料常数。
由式(6)~式(8)可得连续分布的应力状态下单位时间内的疲劳损伤为
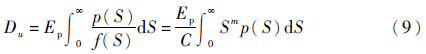
动应力的积分限为0~∞,在实际计算中应力幅的积分上限采用最大动应力Smax,下限一般采用0,即认为大大小小的随机动应力幅均对损伤做出贡献,或者采用常规的疲劳极限σr,即认为小于疲劳极限σr的动应力对疲劳损伤不做贡献,可依据实际情况进行选择[6]。
对各态历经随机应力过程,时间T内的疲劳损伤为
从工程使用要求偏保守的角度,以及考虑到各类误差因素的影响,建议考虑平均应力影响的管路疲劳寿命评估为
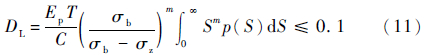
式中:根据有限元模型的简化程度,C和m取值要注意考虑缺口应力集中系数和表面加工系数等的影响;σz为综合应力。
4 算例与分析某运载器输送管路结构预载荷作用下的随机振动试验及其有限元模型如图 1所示。在振动试验过程中,输送管三通端固定;分支管固定端先施加位移x向-0.024 m,y向-0.01 m后与地面工装固支;分支管激振端连接振动台;输送管内压为1.1 MPa。
 |
| 图 1 输送管结构试验状态及其有限元模型 Fig. 1 Test status and finite element model of pipeline structure |
| 图选项 |
在上述位移、内压预载荷下,分别在x、y和z 3个方向将如图 2所示的加速度谱条件分别施加于分支管激振端,进行了3次随机振动试验。如图 1(a)所示为z向激振时的试验状态。3次随机振动试验的加速度测点位置相同,均为11个测点,见图 1(a),其中未标出的测量点位置2、4、7和9分别位于1、3、6和8号传感器的对称面相同位置。图 1(b)为输送管有限元模型。。
 |
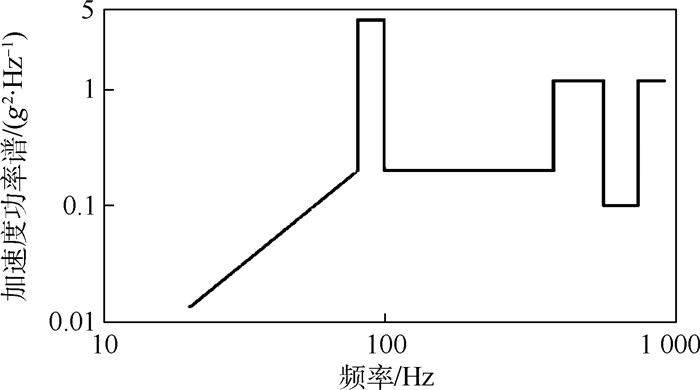| 图 2 随机激励输入加速度功率谱 Fig. 2 Acceleration power spectrum of random excitation |
| 图选项 |
利用前述有限元模型,计算了在上述位移、内压预载荷以及如图 2所示的加速度谱试验条件下,试验各测量点加速度功率谱密度。限于篇幅,这里仅列出了z向激励时,各试验测点位置的功率谱密度,如图 3所示。在频率为0～1 000 Hz范围内,仿真与试验加速度均方根值对比情况则如表 1所示。可见,仿真结果与试验结果基本一致,验证了有限元模型的准确性。
 |
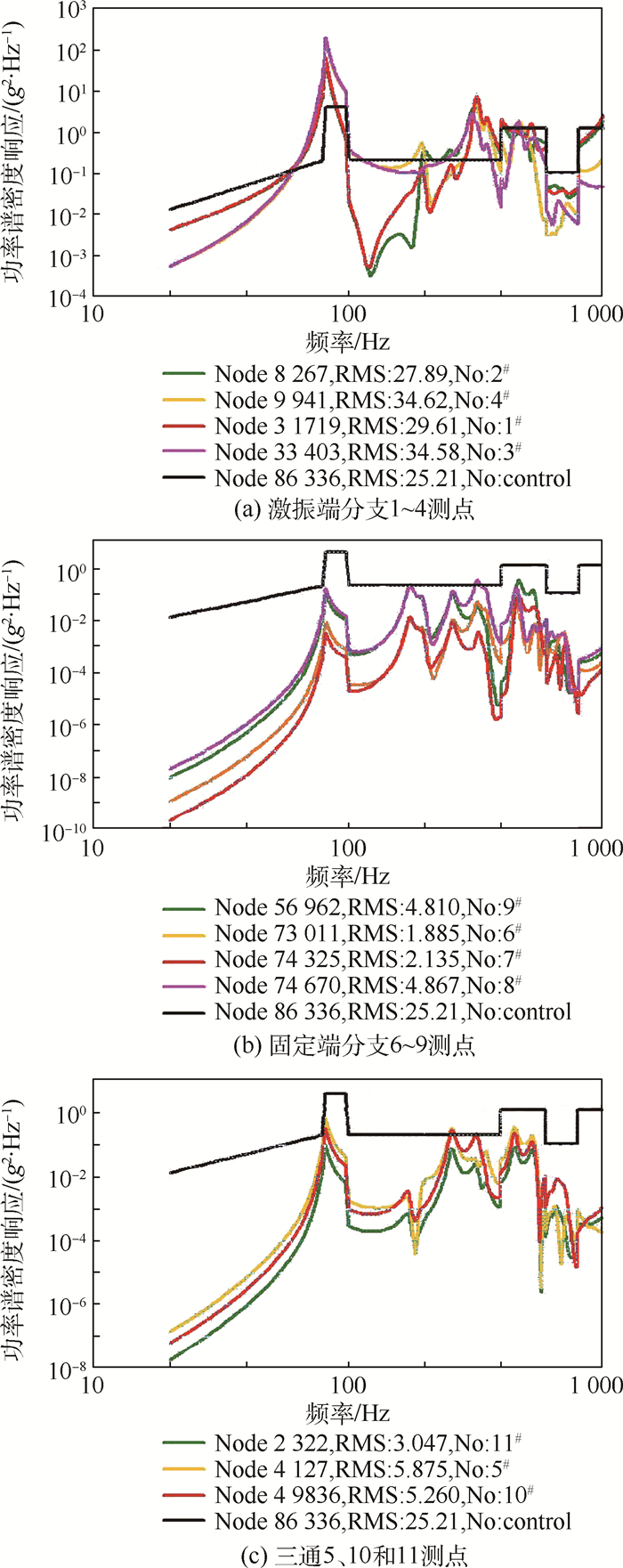| 图 3 z向激振随机振动试验,加速度测点功率谱密度响应 Fig. 3 Power spectral density response of acceleration measuring points under z-direction vibration of random vibration test |
| 图选项 |
表 1 随机振动鉴定级试验与仿真各测点均方根值对比 Table 1 Root mean square (RMS) contrast between identification of level random vibration test and simulation
| 测点 | x向激振/g | y向激振/g | z向激振/g | |||
| 试验 | 仿真 | 试验 | 仿真 | 试验 | 仿真 | |
| 1 | 83.065 | 76.02 | 42.380 | 42.11 | 34.439 | 29.61 |
| 2 | 69.697 | 73.45 | 36.771 | 46.36 | 35.044 | 27.89 |
| 3 | 98.760 | 88.73 | 35.243 | 28.24 | 31.714 | 34.58 |
| 4 | 97.140 | 95.73 | 34.755 | 28.05 | 34.306 | 34.62 |
| 5 | 4.977 | 3.81 | 6.176 | 4.92 | 4.358 | 5.85 |
| 6 | 1.802 | 2.66 | 4.310 | 3.58 | 3.777 | 1.89 |
| 7 | 1.724 | 2.73 | 5.058 | 3.60 | 3.925 | 2.14 |
| 8 | 1.097 | 3.35 | 3.095 | 4.92 | 8.112 | 4.87 |
| 9 | 1.198 | 5.72 | 7.257 | 4.94 | 8.453 | 4.81 |
| 10 | 3.824 | 3.01 | 6.547 | 4.49 | 4.076 | 5.26 |
| 11 | 1.583 | 1.68 | 1.349 | 1.45 | 1.620 | 3.04 |
表选项
从实际振动试验结果来看,各试验状态应变响应较大位置均处于波纹管上方区域,即主要集中在三通组件及其分支位置。鉴于上述考虑,这里仅对三通组件进行了动强度评估。利用此节的有限元模型,计算了在位移、内压2种预载荷及随机激励(见图 2)试验条件下,三通组件结构的Von Mises应力功率谱密度[10, 11]。
计算过程中考虑了静载荷引起的微分刚度的影响,即使用新的刚度矩阵来进行后续的频响函数及随机振动分析,但计算应力功率谱密度时没有计及预应力的贡献,而是将预应力视为平均应力处理[12]。
该输送管材料采用的是1Cr18Ni9Ti,其S-N曲线近似估计公式为SmN=C[13],m≈11.75,C≈4.59×1037[14]。利用本文理论,采用Dirlik模型,得到了激振频率在0～1 000 Hz范围内Von Mises应力累积均方根(
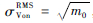,RMS为均方根值)和单位时间(per second)对数疲劳损伤(实际损伤以10为底的对数值)云图分别如图 4~图 6所示。  |
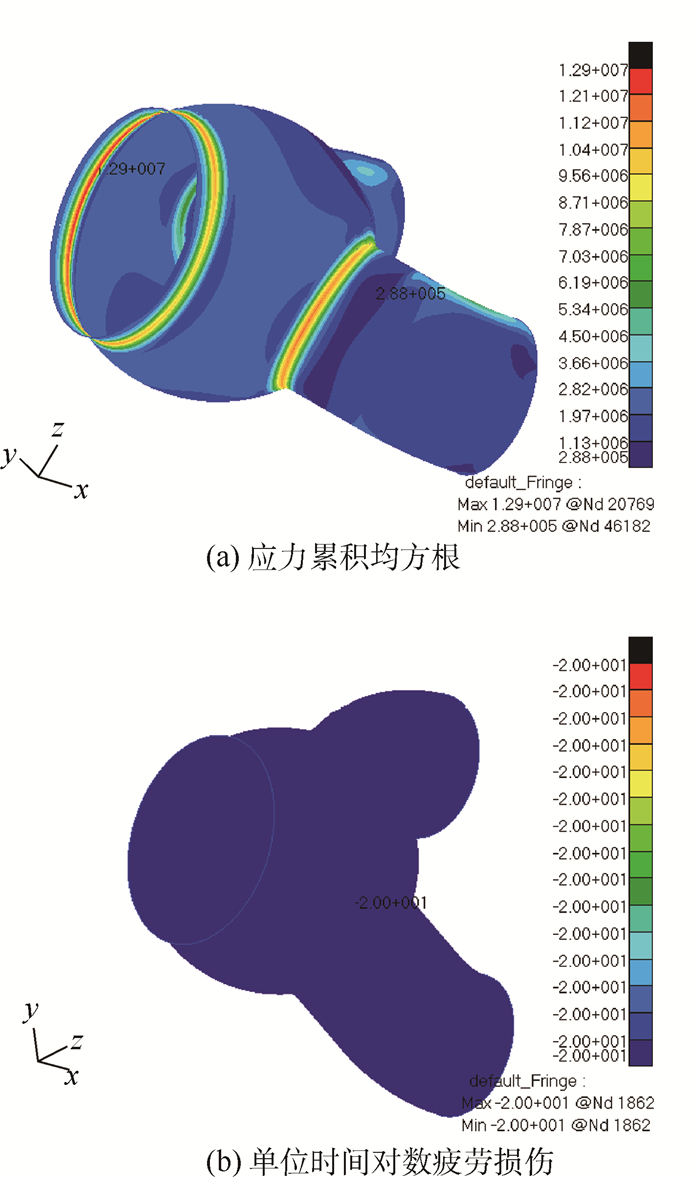| 图 4 x向激振随机振动试验三通结构疲劳损伤 Fig. 4 Fatigue damage of three-way structure under x-direction vibration of random vibration test |
| 图选项 |
 |
| 图 5 y向激振随机振动试验三通结构疲劳损伤 Fig. 5 Fatigue damage of three-way structure under y-direction vibration of random vibration test |
| 图选项 |
 |
| 图 6 z向激振随机振动试验三通结构疲劳损伤 Fig. 6 Fatigue damage of three-way structure under z-direction vibration of random vibration test |
| 图选项 |
从图 4~图 6的仿真结果可以看出:
1) 在该试验条件下,对于三通管路结构Von Mises应力累积均方根值较大部位出现位置:①A端与三通连接a处;②三通与下分支(激振分支)连接b处;③下分支波纹管上方弯曲c处。
2) x向激振时动力累积均方根最大值为12.9 MPa,位于a处;y向激振时应力动力累积均方根最大值为42 MPa,位于b处;z向激振应力动力累积均方根最大值为86 MPa,位于b处。
3) 对于三通管路结构单位时间对数疲劳损伤较大部位与上述相同,x向激振单位时间损伤为10-20,位于a处;y向激振时单位时间损伤为10-6.15,位于b处(见图 5);z向激振单位时间损伤为10-4.49,位于b处(见图 6)。说明工程中常利用应力响应均方根来定性地辨别动强度危险区域是可行的。
分析结果给出了在该位移、内压预载荷随机振动试验条件下管路的动强度薄弱点,并能获得结构的剩余强度和疲劳寿命。应该说明的是,应力考核点的选取及仿真结果的正确性是准确评估疲劳寿命的重要前提基础,但受限于数据匮乏,此处并未考虑结构表面处理、焊缝和应力集中等因素的影响。
5 结 论工程中,在管路结构破坏之处安置应变传感器的是少见的,此时只能应用理论分析手段进行动强度评估分析。本文针对管路结构在预载荷及随机振动条件作用下的疲劳损伤分析方法进行了研究。得出以下结论:
1) 明确了由预载荷引起的刚度、预应力对结构振动的影响,特别提出对结构随机振动响应、疲劳寿命分析时的区别及处理方法,对于结构响应、动强度仿真分析具有重要的参考价值。
2) 提供了预载荷作用下结构随机振动疲劳分析应力功率谱密度的处理方法、动应力幅值的概率密度计算方法,以及管路动强度评估方法。
3) 形成了一套适用于结构动强度评估的方法与流程,涵盖了存在预载荷作用时的处理办法,为确定结构(特别是为管路结构)的损伤及强度安全余量提供了一条可行的技术途径。
参考文献
| [1] | Department of Defense. Environment engineering consideration and laboratory tests:MIL-STD-810G[S].[S.l.]:Aeronautical Systems Center,2008:20-34,256-335. |
| [2] | 吴家驹,荣克林. 多维振动环境试验方法[J].导弹与航天运载技术,2003(4):27-32. WU J J,RONG K L.Multi-dimentional vibration environmental test method[J].Missiles and Space Vehicles,2003(4):27-32(in Chinese). |
| Cited By in Cnki (305) | |
| [3] | NASA. Dynamic environmental criteria:NASA-HDBK-7005[S].[S.l.]:NASA Standards Program Office,2001:75-86. |
| [4] | DIRLIK T. Application of computers in fatigue analysis[D].Coventry:University of Warwick,1985:127-145. |
| Click to display the text | |
| [5] | NATO International Staff-Defence Investment Division.Mechanical condition:AECTP-240(Edition 1)[S].[S.l.]:NATO Standardization Agency,2009:56-79. |
| [6] | 飞行器设计手册总编委会. 飞行器设计手册(第九册:载荷、强度和刚度)[M].北京:航空工业出版社,2001:26-67. Aircraft Design General Editorial Board.Aircraft design manual (Nineth volume:Load,strength and stiffness)[M].Beijing:Aviation Industry Press,2001:26-67(in Chinese). |
| [7] | 纽兰D E. 随机振动与谱分析概论[M].北京:机械工业出版社,1978:78-156. NEW LAND D E.An introduction to stochastic vibration spectrum analysis[M].Beijing:China Machine Press,1978:78-156(in Chinese). |
| [8] | SMITH K N, WATSON P,TOPPER T H.A stress-strain function for the fatigue of metals[J].Journal of Materials,1970,5(4) :767-778. |
| [9] | LIN Y K. Probalilisstic theory of structural dynamics[M].New York:McGraw-Hill Book Company,1976:106-178. |
| [10] | OCHI M K. Probability distribution of peaks and troughs of non-Ganssian random processes[J].Probabilistic Engineering Mechanics,1998,13(5):291-298. |
| [11] | SEGALMAN D J, FULCHER C W G,REESE G M,et al.An efficient method for calculating RMS Von Mises stress in a random vibration environment[J].Journal of Sound and Vibration,1970,230(2):393-410. |
| Click to display the text | |
| [12] | MADSEN H O. Extreme-value statistics for nonlinear stress combination[J].Journal of Engineering Mechanics,1985,111(9): 1121-1129. |
| Click to display the text | |
| [13] | 王帅,李佰灵,贾亮. 空间管路结构单多轴随机振动环境下的疲劳损伤研究[J].强度与环境,2012,39(6):36-41. WANG S,LI B L,JIA L.The fatigue damage research of space pipeline structures under uniaxial/multiaxial random vibration[J].Structure & Environment Engineering,2012,39(6):36-41(in Chinese). |
| Cited By in Cnki (72) | |
| [14] | 金奕山,李琳. 随机振动结构Von Mises应力过程峰值概率密度函数的研究[J].应用力学学报,2006,23(4):645-648. JIN Y S,LI L.Structure random vibration study on the peak probability density function of Von Mises stress process[J].Chinese Journal of Applied Mechanics,2006,23(4)645-648(in Chinese). |
| Cited By in Cnki (288) |
