在目前的研究中,基于频繁模式挖掘的活动识别是主要的方法[1, 2, 3, 4, 5],其优势在于:通过学习挖掘得到的活动模式全面准确,对相应环境中活动的识别效果好,并能识别一些只有在特定环境中能够进行的活动。Parisa等[1]通过机器学习方法挖掘人在智能环境中的频繁活动模式,并将监测结果应用于健康管理方面;Kevin等[3]在已有的识别方法基础上,提出了利用无源射频识别(RFID)技术进行活动识别。该方法仅依赖于空间信息,实现了对智能环境中对象的实时追踪,提高了活动识别的效率;Zhang等[4]将持续时间挖掘引入活动识别中,提高了识别的准确率。然而,这种方法存在以下两点不足之处:①空间局限性:模式挖掘和待识别活动必须在同一环境中进行,并要使用相同的传感器集合。一旦待识别活动来自于不同的环境或使用不同的传感器集合,则该方法的识别能力会下降。②时间开销大:频繁模式挖掘需要耗费较长的时间人工进行行为标注及活动信息采集,并对人在智能环境中的活动模式进行观察和学习。
为了克服基于频繁模式挖掘识别方法在空间局限性和时间开销大两方面的不足,研究人员提出基于迁移的识别方法[6, 7, 8, 9, 10, 11]。例如,Hu和Yang[10]提出利用少量的新标记数据去结合旧数据,从而为新数据构造出高质量的分类模型。但这种方法每次只能迁移来自一个环境中的数据,存在一定的迁移局限性。Francisco等[11]提出了基于贝叶斯推理的迁移识别算法。对于仅能提供无标签数据或少量有标签数据的智能环境而言,这种方法同样具有较好的活动识别效果。
总体而言,目前对基于迁移的识别方法的相关研究还不够深入。本文通过对活动信息模糊化,提取同类型活动具有的共同特征,提出了活动模式迁移学习框架,从而达到将活动模式快速迁移到新环境中,并应用于识别活动的目的。
1 活动描述 1.1 活动模型本文的活动模型中所用到的概念定义如下:M={m1,m2,…,mN}为传感器节点集合,其中:m1,m2,…,mN为传感器节点,N为节点的数目;S={s1,s2,…,sR}为行人在智能环境中活动时触发的传感器节点序列,即活动的轨迹,其中:si∈M,i=1,2,…,R,R为活动过程中被触发节点的数目;T={t1,t2,…,tR}为活动中节点触发持续时间序列,其中:t1,t2,…,tR为活动中被触发节点的触发持续时间。节点的触发持续时间为下一节点的首次触发时间减去该节点的首次触发时间。以ST={(s1,t1),…,(si,ti),…,(sR,tR)}表示一个活动,其中si∈S,ti∈T,此时R即为活动的长度。
按照节点所在的位置,将传感器节点的属性进行归类:

在本文所做的工作中,表 1中的符号将被使用到。
表 1 符号说明Table 1 Symbol description
| 符号 | 说明 |
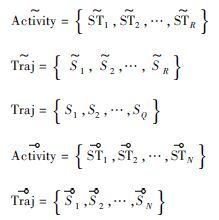 | 样板环境中的活动集 |
| 样板环境中的轨迹集 | |
| 备选轨迹集 | |
| 待识别的活动集 | |
| 待识别活动的轨迹集 |
表选项
1.2 活动模式在样板环境中,通过对大量活动的监测和学习,可以提取出
 ,过程在文献[4, 12]中已有详述。将
,过程在文献[4, 12]中已有详述。将 及其对应的活动类型称为活动模式集。在图 1中,图 1(a)作为样板环境,可以从中提取待迁移的活动模式。图 1(b)和图 1(c)作为2个新环境,其中的活动模式由图 1(a)中的活动模式经过迁移得到。例如,可以从图 1(a)中提取
及其对应的活动类型称为活动模式集。在图 1中,图 1(a)作为样板环境,可以从中提取待迁移的活动模式。图 1(b)和图 1(c)作为2个新环境,其中的活动模式由图 1(a)中的活动模式经过迁移得到。例如,可以从图 1(a)中提取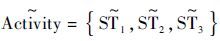 ,与活动类型构成活动模式集:
,与活动类型构成活动模式集:  |
| 图 1 智能环境结构图 Fig. 1 Layout of smart environment |
| 图选项 |

其中的每一个二元组表示经过学习和挖掘得到的活动模式。通过将活动模式迁移到新环境图 1(b)和图 1(c)中,可以实现对新环境中活动的识别。
1.3 活动模糊化由于新环境与样板环境的空间结构差异,造成同一类型的活动在轨迹及触发持续时间等方面的差异。例如在图 1(a)、图 1(b)以及图 1(c)中,
 、
、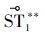 和
和  代表的活动类型均为“Go to sleep”,但三者分别记为
代表的活动类型均为“Go to sleep”,但三者分别记为 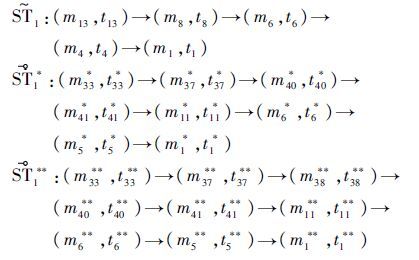
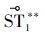 和
和 可以作为将
可以作为将 迁移到新环境之后的形式(*表示图 1(a)中的活动信息,**表示图 1(b)中的活动信息)。因此对活动模式的迁移定义如下:
迁移到新环境之后的形式(*表示图 1(a)中的活动信息,**表示图 1(b)中的活动信息)。因此对活动模式的迁移定义如下:定义1 对
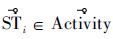 ,存在映射Φ,使得
,存在映射Φ,使得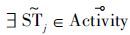 有
有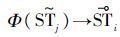 ,并且
,并且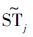 和
和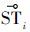 表示同一类型的活动,称Φ为活动模式的迁移。
表示同一类型的活动,称Φ为活动模式的迁移。由活动的定义可知,活动信息主要包括轨迹及触发持续时间2个方面,因此,活动模式的迁移可以分解为活动轨迹的迁移以及触发持续时间的迁移。
1.3.1 活动轨迹的模糊化在一项活动中,功能区域节点对活动的影响程度较大,而非功能区域节点对活动的影响程度则较小。例如在“Go to sleep”活动中,位置为bed的节点对该活动的影响程度最大,而Aisle(过道)处的节点的影响程度较小。针对活动中可能触发的3类传感器节点,用节点影响度来量化它们对于活动的影响程度,以便进行轨迹映射。定义如下:
定义2 以Node_imp表示节点影响度集,Node_imp={ωF,ωR,ωP}
其中:ωF>ωR>ωp,其分别表示活动中fNode、R_nfNode、P_nfNode对活动的影响程度。ω越大,影响程度越高。
1.3.2 触发持续时间的模糊化同类活动的判断标准不仅要基于轨迹,同时还要考虑节点的触发持续时间。本文采用模糊化方式来处理节点触发持续时间。将各节点处的活动持续时间ti划分为非常短、短、中、长、非常长5个等级,利用三角型隶属函数[13, 14]求得持续时间为非常短、短、中、长和非常长的概率分别为PVS_i、PS_i、PM_i、PL_i和PVL_i。
2 迁移算法将活动模式从样板环境迁移到新环境的过程包括3个阶段:
1) 在新环境中生成备选轨迹集,具体实现见第2.1节算法1。
2) 建立活动模式集中的活动轨迹与备选轨迹之间的映射,具体实现见第2.2节算法2。
3) 迁移触发持续时间,与映射后的备选轨迹及活动类型构成新的活动模式,具体实现见第2.3节算法5。
2.1 新环境中的备选轨迹集生成轨迹由一系列邻接节点构成。定义邻接节点如下:
定义3 行人从节点mi行至mj的过程中,仅触发这2个节点,而不会触发其他节点,则称mi和mj互为邻接节点。
以图 2(a)为例,将新环境中的所有节点整合成一张邻接节点表,如图 2(b)所示。
图 2(b)中(i,j)处的标识为“0”,表示节点mi和mj不是邻接节点;为“1”则表示节点mi和mj互为邻接节点。根据节点间的邻接情况及节点位置信息,可以找到环境中任意2个节点之间的最短轨迹,并提取出能够表示完整活动的轨迹,形成备选轨迹集。本文以经典的最短路径算法——Flod算法[15]为核心,提出算法1来实现阶段1。
算法1 备选轨迹集生成算法ATSG
Input: The node adjacency list of environment A,coordinate of every node;
Output: The alterative trajectory set Traj;
Initialization: Set alterative trajectory set Traj to NULL;
1: Flod (A);
2: add all trajectories to aset;
3: for i=1 to sizeof(aset) do
4: aset[i]→route;
5: if route[1].attribute is fNode and route[sizeof(route)].attribute is fNode
6: add route to Traj;
7: set route to NULL;
8: return Traj;
其中:sizeof()为求集合中轨迹数量的函数;A为新环境的邻接节点表;Flod (A)为提取新环境中各节点间最短路径的函数;aset为新环境中各节点间最短路径的集合。算法1第1行中,利用Flod算法得到环境中的各节点之间的最短轨迹;第3~第7行提取出能表示完整活动的轨迹。算法1的时间复杂度为O(N3),其中N为智能环境中的节点数量。
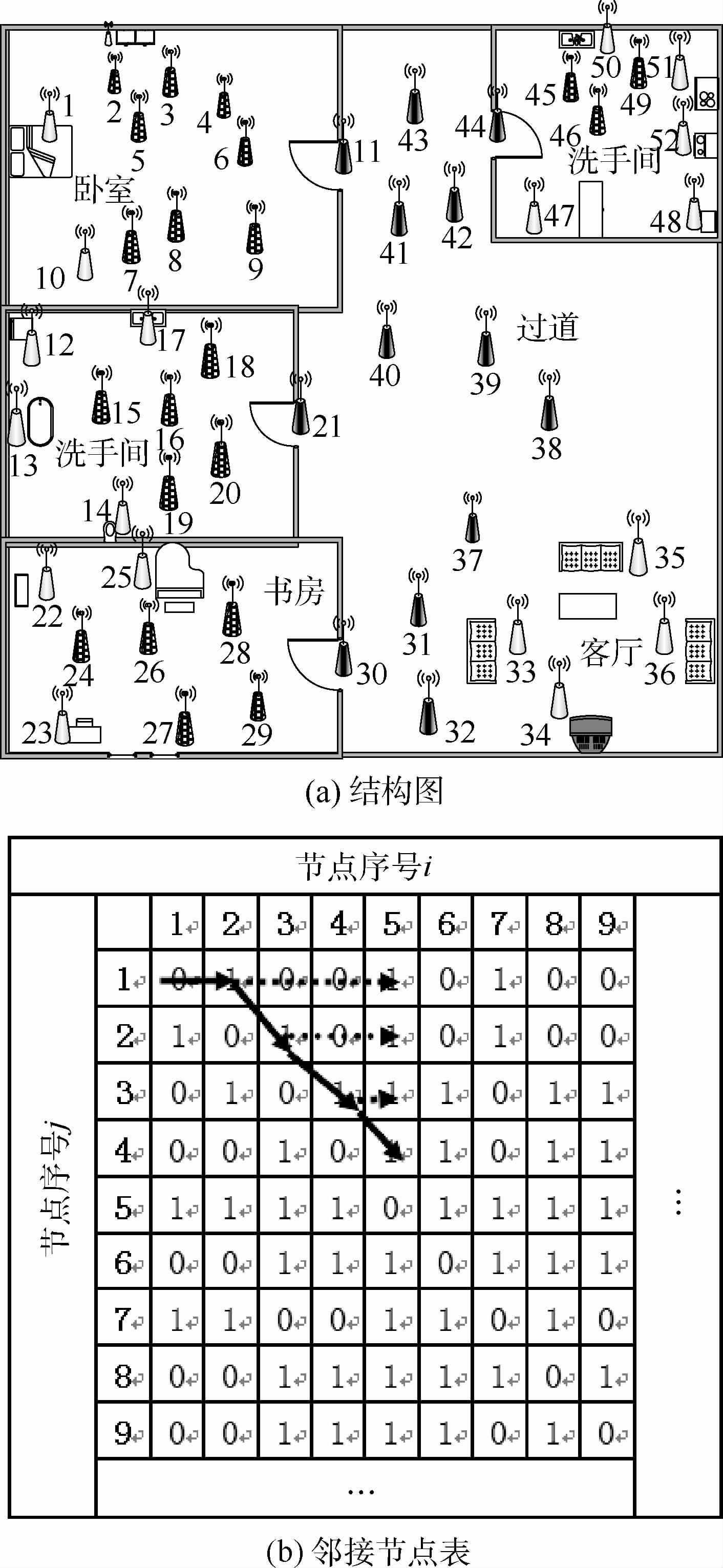 |
| 图 2 新环境的结构图及邻接节点表 Fig. 2 Layout and adjacency node list of new environment |
| 图选项 |
2.2 活动轨迹的迁移轨迹映射算法(Trajectory Mapping,TM)描述如下:
算法2 活动轨迹映射算法TM
Input: $\widetilde {{\rm{Traj}}}$ and $\widetilde {{\rm{Traj}}}$;
Output: Map-result set Result;
Initialization: 0→max;
1: for i=0 to sizeof (Traj) do
2: for j=0 to sizeof($\widetilde {{\rm{Traj}}}$) do
3: SC(Traj[i],$\widetilde {{\rm{Traj}}}$[j])→similarity;
4: if similarity≥max
5: similarity→max
6: $\widetilde {{\rm{Traj}}}$[j]→A
7: if max≥β
8: add (Traj[i],A) to Result;
9: return Result;
其中:β为轨迹相似度阈值,若轨迹间的相似度大于此阈值,则表明两轨迹表示同一类型活动; similarity为两轨迹间的相似度。该算法将活动模式集中的轨迹映射至备选轨迹,这种映射关系可通过轨迹之间的相似度来体现。算法2的第3行通过相似度计算算法(Similarity Computing,SC)计算活动模式集中的轨迹与备选轨迹之间的相似度,经第4~第6行得到最大相似度。若最大相似度满足第7行的阈值条件,则通过第8行记录映射结果。对第3行的算法SC描述如下:
算法3 相似度计算算法SC
Input: Trajectory Sequence S1and S2;
Output: Similarity between S1and S2;
Initialization: 0→r;
1: calculate effect degree of every node in S1 and S2;
2: STE (S1) and STE (S2);
3: extract the subset sub_ S1 and sub_ S2 whose positions correspond to S1.position ∩ S2.position;
4: for every item in sub_ S1 and every item in sub_ S2 do
5: if sub_ S1[i].position=sub_ S2[i].position
6: sub_ S1[i]→sub_S11[r];
7: sub_ S2[i]→sub_S22[r];
8: r+1→r;
9: extract effect degree of every node in sub_S11 and sub_S22;
10: calculate similarity between S1 and S2;
11: return similarity;
其中:r为两轨迹间相匹配的节点数量;sub_ S11为轨迹S1中能够与轨迹S2匹配的节点集合;sub_S22为轨迹S2中能够与轨迹S1匹配的节点集合。第2行将活动轨迹进行精简,减少轨迹中的冗余节点,以提高后续的轨迹迁移工作的准确性,算法描述见算法4;第10行对两轨迹间的相似度进行计算,计算公式为
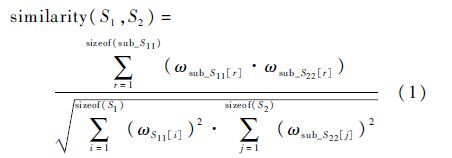
式中: ωsub_ S11[r]和ωsub_ S22[r]为集合sub_ S11和sub_ S22中第r个节点的节点影响度。
算法4 精简轨迹提取算法STE
Input: Trajectory sequence S;
Output: Streamlined trajectory sequence Sst
1: for every node in S do
2: if S[i].attribute=fNode
3: save this node’s all information,include its trigger duration,its position,its attribute,etc.;
4: else if S[i].attribute=R_nfNode
5: i→start;
6: while S[i+1].attribute=R_nfNode do
7: i++;
8: i→end;
9: combine these R_nfNodes between S[start]and S[end]into one node whose position is room_aisle;
10: else if S[i].attribute=P_nfNode
11: i→start;
12: while S[i+1].attribute=P_nfNode do
13: i++;
14: i→end;
15: combine these P_nfNodes between S[start]and S[end]into one node whose position is aisle;
16: update the processed S to Sst;
17: return Sst;
其中:Sst为轨迹S的精简轨迹。4~9行以及10~15行分别将轨迹中连续出现的R_nfNode和P_nfNode进行了合并处理,以简化活动轨迹,方便后续的迁移。该算法对轨迹的精简过程可以在O(sizeof(S))时间内完成。
因此,实现对轨迹的迁移所需时间为

接近于

从而实现了在短时间内完成轨迹的迁移。
2.3 触发持续时间的迁移对触发持续时间迁移算法(Trigger Duration Transfer,TDT)描述如下:
算法 5 触发持续时间迁移算法TDT
Input: Trajectory Sequence S1 and alterative trajectory S2 with mapping relationship;
Output: S2after transferred with trigger duration;
Initialization: 0→r
1: calculate trigger duration probability of every node in S1;
2: STE(S1) and STE(S2);
3: extract the subset sub_ S1 and sub_ S2 whose positions correspond to S1.position ∩ S2.position;
4: for every item in sub_ S1 and every item in sub_ S2 do
5: if sub_ S1[i].position=sub_ S2[i].position
6: calculate duration t2_i;
7: if there are nodes without duration in S2
8: Give the average of fNodes’ duration in S1 to fNode;
9: Give the average of R_nfNodes’ duration in S1 to R_nfNode;
10: Give the average of P_nfNodes’ duration in S1 to P_nfNode;
11: return S2;
其中:sub_S1和sub_S2为属于轨迹S1和S2的节点位置交集中的节点所构成的集合。第2行对活动轨迹进行了精简,精简过程在O(sizeof(S1)+sizeof(S2))时间内完成,详见算法4;第3行提取出轨迹S1和S2的交集,以便进行两轨迹间的节点匹配,该过程可以在O(sizeof(S1)·sizeof(S2))时间内完成;第5、6行完成两轨迹对应节点之间的触发持续时间迁移,其中第6行采用的触发持续时间迁移公式如式(2)所示。而对于未匹配的节点,则采用第7~10行的规则进行触发持续时间的迁移。
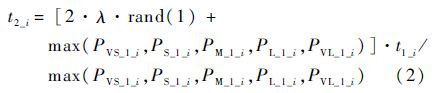
式中:t2_i为触发持续时间t1_i经过迁移后得到的值;λ为迁移扰动系数;rand(1)为从区间[0, 1]中生成一个随机数。
上述一系列算法构成的迁移学习框架可以使活动模式的获取在短时间内完成,相比于利用频繁模式挖掘获取活动模式,大幅度地减少了获取活动模式所需的时间开销,进而提高了活动识别工作的效率。
3 实验验证本文使用智能环境仿真系统(smart environment simulator tool)[5]对智能环境进行模拟。所要模拟的智能环境有2个:样板环境和新环境。样板环境用于获取待迁移的活动模式,而新环境则作为迁移目的地,并生成待识别的新活动。
3.1 实验参数设计1) 传感器节点数量
在样板环境中共设置35个传感器节点,其中,fNode共有17个,R_nfNode共有7个,P_nfNode共有11个。在新环境中共设置了52个节点,其中,fNode共有11个,R_nfNode共有21个,P_nfNode共有20个。2个环境中各个位置的节点数量如图 3所示。
 |
| 图 3 样板环境与新环境中的各位置节点数量示意图 Fig. 3 Number of nodes in different positions of template and new environment |
| 图选项 |
2) 轨迹数量
在样板环境中,设计了41条反映智能环境中的日常活动的轨迹,对应着行人可能进行的9种常规活动。其类型和数量如图 4所示。
 |
| 图 4 样板环境中的标准轨迹表示的活动类型和数量 Fig. 4 Activity types and quantities that template trajectories represent in template environment |
| 图选项 |
3) 触发持续时间
针对不同类型的传感器节点,本文设计了3类触发持续时间规则,分别为:①对于公共过道节点,由于行人的停留时间很短,设置的规则为{5 s,10 s,15 s,20 s};②对于房间过道节点,由于其在功能区域附近,行人的停留时间相比于公共过道节点要相对较长,因此设置的规则为{1.5 min,3 min,4.5 min,6 min};③对于功能区域节点,行人停留的时间较长,因此设置规则为{40 m,60 m,80 m,100 m}。
3.2 活动模式的迁移首先进行轨迹从样板环境到新环境的迁移。将迁移相似度阈值设置为0.8,对3种类型节点各自的节点影响度进行调整,迁移结果见表 2。
表 2 轨迹的迁移结果表Table 2 Results of trajectories’ transfer
| 3类传感器 节点的影响度 | 迁移得到的 轨迹数量 | 被迁移的 活动类型数量 | 平均相似度 |
| (3,2,1) | 43 | 7 | 0.859 |
| (4,2,1) | 57 | 8 | 0.882 |
| (5,2,1) | 60 | 8 | 0.903 |
| (5,3,1) | 58 | 8 | 0.876 |
| (6,2,1) | 60 | 8 | 0.918 |
| (6,3,1) | 60 | 8 | 0.894 |
| (7,2,1) | 64 | 8 | 0.921 |
| (7,3,1) | 60 | 8 | 0.909 |
| (7,4,1) | 60 | 8 | 0.887 |
| (8,2,1) | 65 | 8 | 0.925 |
| (8,3,1) | 64 | 8 | 0.912 |
| (8,4,1) | 60 | 8 | 0.901 |
| (8,5,1) | 58 | 8 | 0.883 |
| (9,2,1) | 66 | 8 | 0.928 |
| (9,3,1) | 64 | 8 | 0.920 |
| (9,4,1) | 60 | 8 | 0.911 |
| (9,5,1) | 60 | 8 | 0.893 |
| (9,6,1) | 57 | 8 | 0.880 |
表选项
从实验结果可以看到,不同的节点影响度对轨迹迁移结果会产生影响。fNode影响度与R_nfNode影响度的差距越大,则得到的新轨迹数量越少,并且新轨迹与原轨迹之间的相似度也会降低;而R_nfNode影响度与P_nfNode影响度的差距越大,得到的新轨迹数量越多,并且新轨迹与原轨迹之间的相似度越高。
在新环境中,分别用迁移和频繁模式挖掘的方式得到的活动模式类型对比如表 3所示。
表 3 基于迁移和基于频繁模式挖掘得到的 活动模式对比Table 3 Comparison of activity patterns obtained based on transfer learning and frequent pattern mining
| 活动类型 | 基于迁移 | 基于频繁模式挖掘 |
| Go to sleep | √ | √ |
| Go to toilet | √ | √ |
| Cook | √ | √ |
| Have a meal | √ | √ |
| Wash the clothes | ||
| Watch TV | √ | √ |
| Take a shower | √ | √ |
| Wash hands | √ | √ |
| Have a rest | √ | √ |
| Play the piano | √ |
表选项
从表 3中可知,有8种类型的活动轨迹被迁移到新环境中。由于新环境中没有‘washer’位置的节点,因此‘Wash the clothes’没有被迁移到新环境中,也无法在新环境中通过频繁模式挖掘得到。又由于样板环境中没有‘piano’这一功能区域的节点,使‘Play the piano’无法被迁移。由此可知,样板环境与新环境在空间结构上的差异会造成迁移的不完整性。
其次进行触发持续时间的迁移。实验采用上文设置的3类节点的触发持续时间规则,针对已经进行过轨迹迁移的新活动模式,利用TDT算法,迁移活动模式中的触发持续时间。
3.3 新活动的识别为分析迁移效果,在同一智能环境中利用迁移和频繁模式挖掘的方式得到2组活动模式集,并识别同一组待识别的活动,识别结果对比如下:
1) 基于迁移的识别结果
使行人在新环境中根据其所要完成的活动任务,随机选择行走路线。实验一共进行32次,共产生32个待识别的活动。活动中记录活动轨迹、各节点的触发持续时间以及实际的活动类型。对活动的识别采用文献[5]中提出的方法。首先利用基于迁移得到的活动模式进行识别。实验一共进行4次,分别设定不确定度阈值为0.4、0.6、0.8和1.0。针对环境中3种不同类型的节点,取18组不同的节点影响度组合,在每次实验中分别记录各组节点影响度组合的识别效果,得到各阈值条件下对新活动的识别情况,结果如图 5所示。
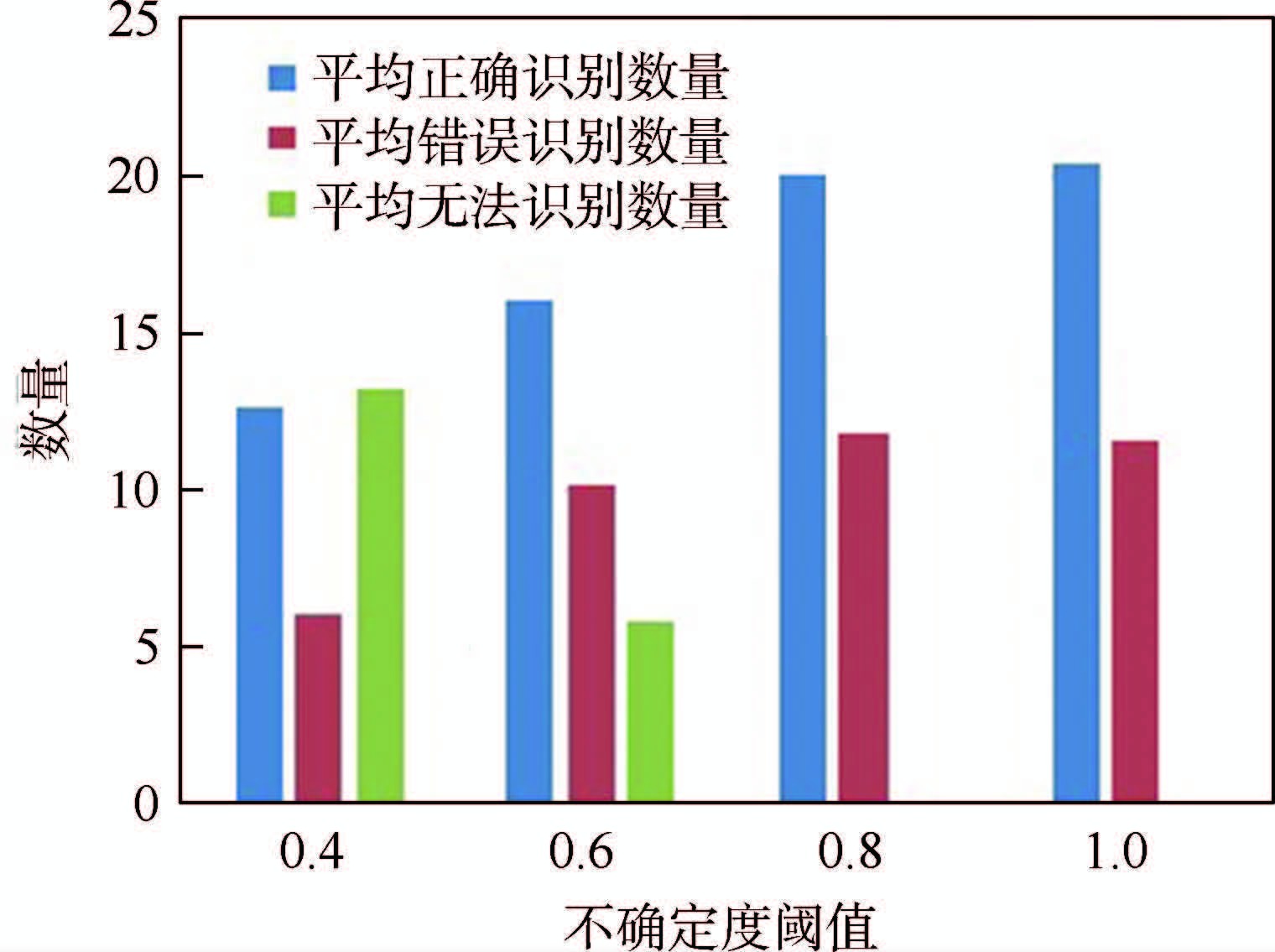 |
| 图 5 各不确定度阈值下基于迁移的平均识别数 Fig. 5 Average identification number under different uncertainty thresholds based on transfer learning |
| 图选项 |
从图 5可以看到,随着阈值的不断增大,系统整体的平均正确识别数逐渐提升,并趋于稳定。识别结果表明,不确定度阈值的设置会影响到基于迁移的识别结果。阈值设置得越宽松,则系统的识别能力越强,并最终趋于稳定。
2) 基于迁移与基于频繁模式挖掘的识别结果对比
为了对基于迁移的识别效果进行更为准确的评估,将其与基于频繁模式挖掘的识别效果进行对比。实验一共分为4组,分别设定不确定度阈值为0.4、0.6、0.8和1.0,对32项新活动进行识别。在每组实验中,针对智能环境中3种不同类型的节点,取表 2中的节点影响度组合,对正确识别数进行记录,实验结果如图 6所示。
 |
| 图 6 各不确定度阈值下的正确识别数对比 Fig. 6 Comparison of correct identification number under different uncertainty thresholds |
| 图选项 |
从图 6可以看到,基于迁移得到的活动模式可以取得较好的识别效果,当不确定度阈值设定为0.8及以上时,最多可以正确识别21项活动。但通过对比可以看到,基于频繁模式挖掘可以正确识别出27项活动,并且当不确定度阈值为0.4时就可以达到最佳的识别效果。但2种方式的识别正确数量差距并不大。对2种活动模式的识别差异进行分析可知:
首先,由于样板环境与新环境在功能区方面的差异,使基于迁移的活动模式无法识别新环境中的某些活动。由表 3可知,基于迁移无法识别新环境中的‘Play the piano’,而基于频繁模式挖掘则可以识别。
其次,不同类型活动之间的Overlapping和Crossover现象[12]导致了识别结果的偏差。例如,‘Wash hands’的活动模式匹配结果如图 7所示。
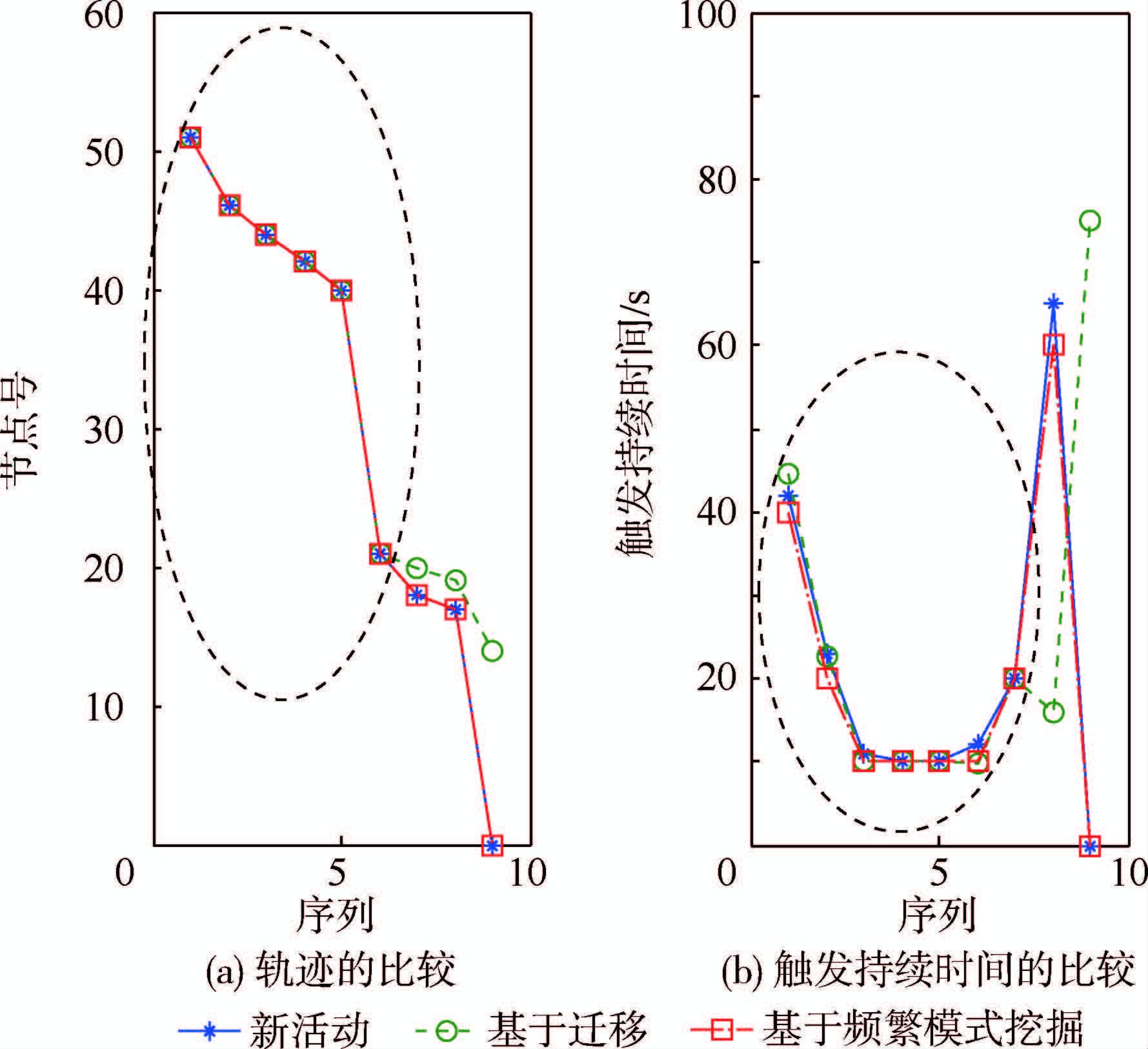 |
| 图 7 对 ‘Wash hands Ⅰ’的识别效果对比图 Fig. 7 Comparison of identification results on ‘Wash hands Ⅰ’ |
| 图选项 |
由于 ‘Wash hands’与‘Go to toilet’在轨迹和触发持续时间方面存在着明显的Overlapping现象,并且二者的不确定度为0.375,小于不确定度阈值,因此导致原本为‘Wash hands’的活动被识别为‘Go to toilet’。
另一组模式匹配结果如图 8所示,基于迁移的识别方法将 ‘Wash hands’识别为‘Take a shower’,而基于频繁模式挖掘的识别方法则可以准确识别。‘Wash hands’和‘Take a shower’的轨迹以及触发持续时间之间存在着明显的Overlapping现象,是导致错误识别的主要原因。
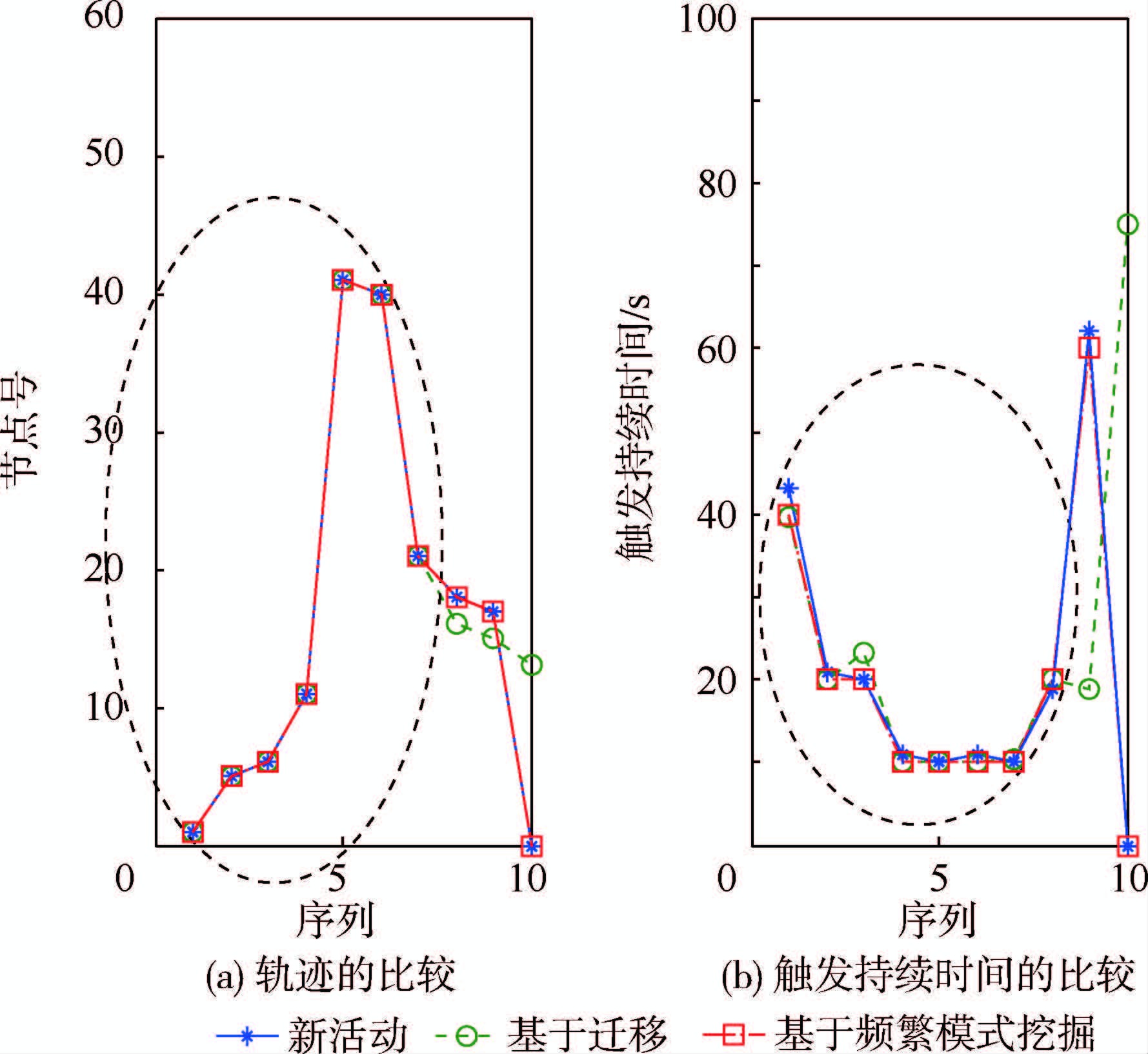 |
| 图 8 对‘Wash hands Ⅱ’的识别效果对比图 Fig. 8 Comparison of identification results on ‘Wash hands Ⅱ’ |
| 图选项 |
Overlapping和Crossover现象的出现,主要是因为环境中某些功能区域是相邻的,如‘closestool’和‘sink’,导致与这些功能区域相关的活动在轨迹和触发持续时间方面具有较高的相似性,使活动间的区别不显著。而活动模式的迁移依赖于轨迹相似度及触发持续时间迁移规则,因此,利用基于迁移得到的活动模式对Overlapping现象显著的活动进行识别时,容易产生偏差。
4 结 论1) 实现了将已有活动模式迁移到新环境中并应用于活动识别,提高了活动模式对不同环境的适应能力。
2) 利用本文方法获取活动模式,不必在新环境中耗费大量的时间进行模式挖掘,所需的时间开销小,从而显著提高了活动识别工作的效率。
3) 实验结果表明,利用本文方法获取活动模式并进行活动识别,取得了较好的识别效果,验证了方法的有效性和可行性。
未来研究将致力于解决如何在迁移过程中克服Overlapping和Crossover现象的干扰问题。
参考文献
| [1] | PARISA R,DIANE J C,LAWRENCE B H,et al.Discovering activities to recognize and track in a smart environment[J].IEEE Transactions on Knowledge and Data Engineering,2011,23(4):527-539. |
| Click to display the text | |
| [2] | FANG H Q,HU C.Recognizing human activity in smart home using deep learning algorithm[C]//201433rd Chinese Control Conference,CCC.Piscataway, NJ:IEEE Press, 2014:4716-4720. |
| [3] | KEVIN B,DANY F S,SEBASTIEN G,et al.Accurate RFID trilateration to learn and recognize spatial activities in smart environment[J].International Journal of Distributed Sensor Networks,2013,19(2):1-15. |
| Click to display the text | |
| [4] | ZHANG S,SALLY M,BRYAN S,et al.Using duration to learn activities of daily living in a smart home environment[C]//International Conference on Pervasive Computing Technologies for Healthcare.Piscataway,NJ:IEEE Press,2010:1-8. |
| [5] | WANG C L,ZHENG Q,PENG Y Y,et al.Distributed abnormal activity detection in smart environments[J].International Journal of Distributed Sensor Networks,2014,2014(3):1-15. |
| [6] | PAN S J L,YANG Q.A survey on transfer learning[J].IEEE Transactions on Knowledge and Data Engineering,2010,22(10):1345-1359. |
| Click to display the text | |
| [7] | BAYLOR W. Transfer learning in spatial reasoning puzzles[C]//IJCAI 2011-22nd International Joint Conference on Artificial Intelligence.California:International Joint Conference on Artificial Intelligence,2011:2864-2865. |
| [8] | HUANG P P,WANG G,QIN S Y.Boosting for transfer learning from multiple data sources[J].Pattern Recognition Letters,2012,33(5):568-579. |
| Click to display the text | |
| [9] | PARISA R,DIANE J C.Activity knowledge transfer in smart environment[J].Pervasive and Mobile Computing,2011,7(3):331-343. |
| Click to display the text | |
| [10] | HU D H,YANG Q.Transfer learning for recognition via sensor mapping[C]//IJCAI 2011-22nd International Joint Conference on Artificial Intelligence.California:International Joint Conference on Artificial Intelligence,2011:1962-1967. |
| [11] | FRANCISCO J O,GWENN E,PAULA D T,et al.In-home activity recognition:Bayesian inference for hidden Markov models[J].IEEE Pervasive Computing,2014,13(3):67-75. |
| Click to display the text | |
| [12] | WANG C L,DEBRAJ D,SONG W Z.Trajectory mining from anonymous binary motion sensors in smart environment[J].Knowledge-Based Systems,2013,37(2):346-356. |
| [13] | PROVOTAR A I,LAPKO A V,PROVOTAR A A.Fuzzy inference systems and their applications[J].Cyberbetics and Systems Analysis,2013,49(4):517-525. |
| Click to display the text | |
| [14] | THIERRY M.A Measurement-theoretic axiomatization of trapezoidal membership functions[J].IEEE Transactions on Fuzzy Systems,2007,15(2):238-242. |
| Click to display the text | |
| [15] | THOMAS H C,CHARLES E L,RONALD L R,et al.Introduction to algorithm[M].3rd ed.Cambridge,MA:Massachusetts Institute of Technology,2009:643-683. |
