?智能电表是指应用计算机技术、通讯技术等,形成以智能芯片(如CPU)为核心,具有电功率计量计时、计费等功能的电度表,是智能电网的智能终端.随着智能电表的市场化进程不断深入及多参数-多应力特性,使得如何分析、评价其可靠性和寿命成为了当前各智能电表生产厂家亟需解决的关键问题^{[1, 2, 3, 4, 5]}.
自智能电表进入电力市场以来,国内外在其可靠性和寿命方面开展了相关研究.Dissanayaka等^[6]通过在智能电表内应用ZigBee模块及其相关软件来监控电网电能消耗及其响应速度,实现了智能电网可靠性和寿命的改善,美国联邦能源管理委员会研发了一种具有双向通讯、自动波形记录和监控电压电流的智能电表,大大地提升其可靠性和寿命水平,Wang等^[7]采用历史数据和故障模式影响分析(FMEA)方法研究了智能电表敏感应力和薄弱环节,且通过强化试验初步探索了其失效模式和使用极限水平.上述研究一般将智能电表作为智能电网的一部分来进行其可靠性和质量分析,很少深入挖掘智能电表多参数-多应力作用下的失效机理及其可靠性水平.因此,本文的研究为智能电表单机的多应力-多参数特性,提供了可靠性和寿命分析、评估手段.
本文首先深入分析了在温度、湿度、电应力、振动和磁场等环境和工作条件下智能电表各类性能参数,采用故障模式、机理及影响分析(FMMEA),提炼了其可靠性和寿命关键性能参数及其敏感环境应力,然后通过合理的强化试验方案摸索了各关键性能参数响应行为,得到了关键性能参数应力极限条件范围内,并据此设计了加速寿命试验方案,采用智能电表综合测试系统分析了各关键性能参数试验数据,并对其进行了退化轨迹建模研究、多应力加速模型分析,综合得到了各置信水平下智能电表可靠性和寿命水平.本文提出了一种强化试验和加速寿命试验相结合的多应力-多参数智能电表可靠性和寿命评估方法,其研究思路和结论能为改善智能电表可靠性、提高其寿命水平提供理论支撑.
1 智能电表主机理及应力分析1.1 智能电表简介某智能电表系统结构框图如图 1所示.主要由电能计量单元、数据处理单元、供电系统和输入输出系统等4部分组成,其功能是先通过对用户供电电压和电流的实时采样,再采用专用的电能表集成电路,对采样电压和电流信号进行处理,并转换成与电能成正比的脉冲输出,最后通过单片机进行处理、控制,把脉冲显示为用电.

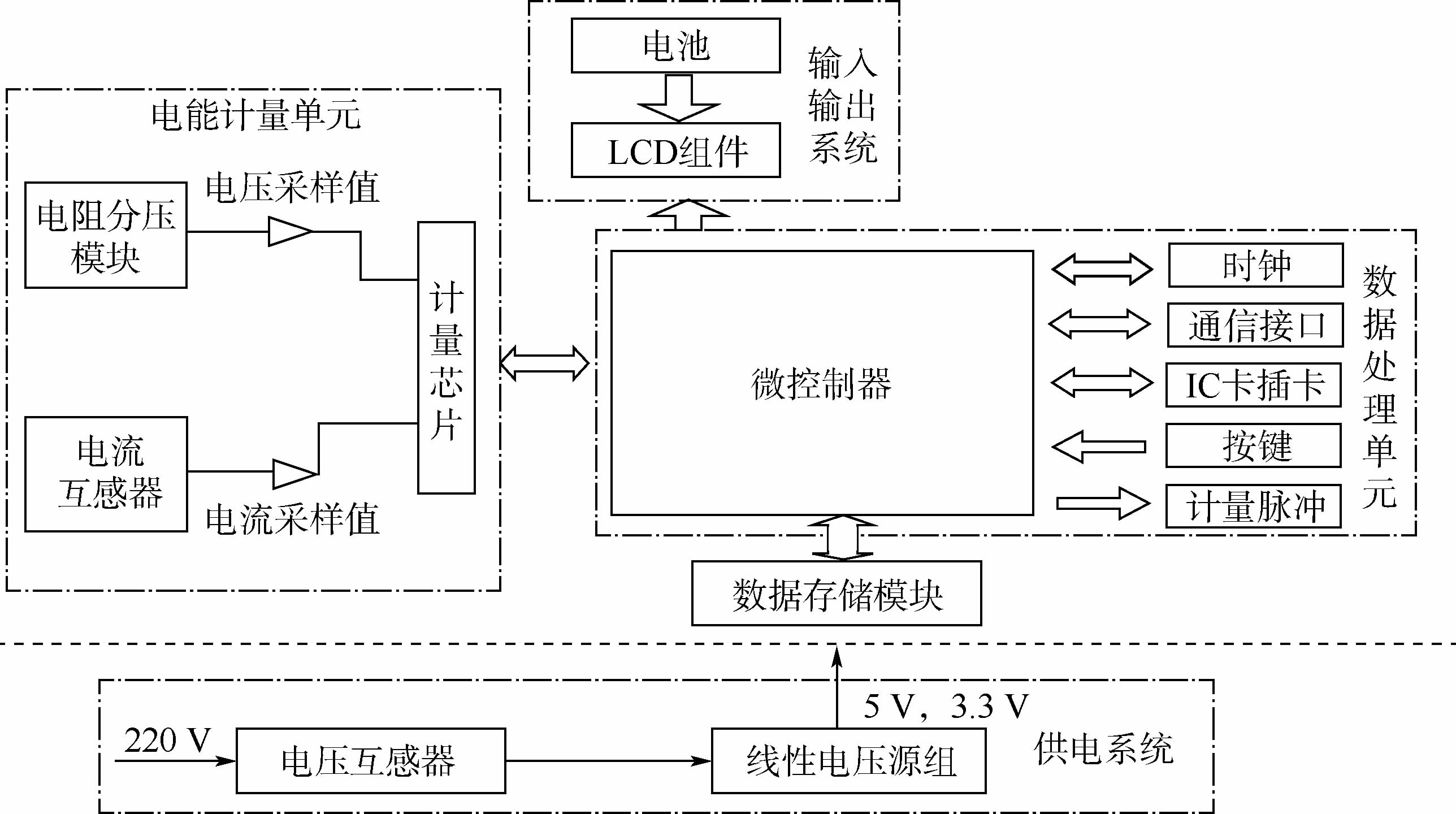图 1 智能电表系统结构框图Fig. 1 Structure diagram of smart meter system

图选项

1.2 智能电表性能参数及机理分析智能电表在使用过程中不可避免地受到设计、制造以及使用环境的影响,使其工作性能指标产生误差,下面深入分析了各环境因素对智能电表性能参数的影响机理.
1) 智能电表性能参数.
工程应用表明,智能电表性能参数主要为计量误差、日计时误差、电表常数.
计量误差:智能电表的计量误差表述为在智能电表的某个负载点下参考表的计量脉冲减去被测表的计量脉冲,再与参考表的计量脉冲相比，即
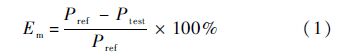
式中:E_m为根据测量结果计算的计量误差,一级表的失效判据为E_m≥1%;P_ref为参考表的计量脉冲;P_test为被测表的计量脉冲.
日计时误差:日计时误差主要取决于晶体振荡器的准确度及稳定度,而晶体振荡器的温漂是造成其准确度偏差的主要原因.
电表常数:表示智能电表记录的电能值与对应测试输出值之间关系的数值叫电表常数.也可用脉冲常数表示,即智能电表计量一度电时A/D转换器所发出的脉冲个数.智能电表测试输出与计量显示指示之间的关系应与铭牌保持一致,计算公式为
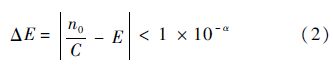
式中:n₀为计度器示值;C为智能电表脉冲常数;E为智能电表计度累计值;α为电能表计度显示的小数位数.
2) 智能电表主机理及应力分析.
下面主要分析温度、湿度、电应力、振动和磁场等多应力对智能电表性能参数的作用机理.
温度:温度升高使高锰铜电阻的电阻率变大,导致电表采样的电流值偏大,从而使锰铜分流器和电流互感器的精度和稳定性降低,进而影响电表计量误差;晶体振荡器偏离额定工作温度越大会使频率公差增大,相应的时钟准确度下降,引起振荡器振荡频率误差及信号传输过程产生失真,影响日计时误差;温度变化会通过失调温度系数、增益温度系数等引起A/D转换器的偏移误差和增益误差,影响电表常数误差.另外,长时间温度应力作用还会造成液晶盒材料变形、折射率改变、电阻值增大,导致液晶外流、光亮度减低、显示异常等现状.因此,温度是影响智能电表计量误差、日计时误差和电表常数的主要环境因素.
湿度:湿度对智能电表的影响主要表现在潮湿能透过芯片塑料封装从引脚等缝隙侵入芯片内部,产生芯片吸湿现象,在高温的环境中形成水蒸气,产生的压力导致芯片树脂封装开裂,并使芯片器件内部金属氧化,导致产品故障;高湿环境使液晶偏光片物理结构变性、铟锡氧化物电机慢性腐蚀、电阻值增大,造成液晶模组失效及铟锡氧化物图案线路损坏,容易导致液晶出现缺划甚至无显示内容,同时湿度还会使继电器绝缘电阻下降,这些影响最终体现为智能电表的计量误差、日计时误差和电表常数等性能参数的变化.
电应力:电表稳定的工作需要电表处于热稳定状态,而电流采样回路是表内的主要产热源,电应力过大会使电表内部热稳定失衡,温度升高,由于电表内置的各类元器件,对温升特别敏感,这样就会造成表内元器件电参数漂移,影响智能电表计量误差、日计时误差和电表常数等性能参数.同时,电应力过大导致长时间的过电应力会使液晶介电常数变化、静态电光转移特性改变、电介质的电老化及热老化,造成液晶电参数变化,最终影响计量误差、日计时误差和电表常数等性能参数.
振动:继电器一般采用与安装轴之间的轻微过盈配合而固定线圈.由于线圈骨架与定轴之间存在配合公差,在振动环境条件下可能导致线圈与固定轴之间产生转动以及轴向运动,导致在线圈引出线上附加一定外力．振动一段时间后会使线圈引出线产生疲劳断裂,从而影响日计时误差.
磁场:磁场通过影响铁芯的磁饱和度以及产生励磁电流,使互感器的变比及相位出现误差,即产生比差和角差,从而影响智能电表的计量误差.
在上述理论分析的基础上,结合工程使用经验,可总结出影响智能电表计量误差、日计时误差和电表常数等多参数的主要环境应力为温度、湿度和电应力.
2 智能电表强化试验设计及分析强化试验是一种激发性试验,采用加速应力环境快速激发产品潜在缺陷,暴露产品的主要故障模式.智能电表强化试验是指通过应力水平的步进施加并监测计量误差、日计时误差和电表常数3个性能参数,确定极限工作应力条件,并通过分析确定其主要故障模式和薄弱环节^{[8, 9]}.
2.1 智能电表强化试验方案设计智能电表强化试验实施方案如表 1所示.
表 1 智能电表强化试验测试项目Table 1 Enhancement test project of smart meter

序号	试验项目	试验目的	样本数
1	步进高温试验	确定电能表工作温度应力极限和主要故障模式	9
2	湿度循环试验	确定电能表工作湿度应力极限和主要故障模式	9
3	步进电应力试验	确定电能表电应力极限和主要故障模式	9

表选项


步进高温试验的起始温度点40℃,结束温度点120℃;在关键温度点70℃附近以5℃一个台阶变化,在其他温度点以10℃一个台阶变化.在每个温度台阶对电能表进行在线测试,而后将温度调节至固定温湿点(23℃,45%RH)条件下进行离线测试,智能电表步进高温试验剖面如图 2所示.

图 2 步进高温试验剖面Fig. 2 Step-stress test profile of high-temperature

图选项

湿度循环试验的起始湿度点定为45%RH,截止湿度定为98%RH,各湿度点的温度定为40℃,在各湿度点保持过程中进行在线测试后回到常温常湿点(23℃,45%RH)进行离线测试,智能电表湿度循环试验剖面如图 3所示.

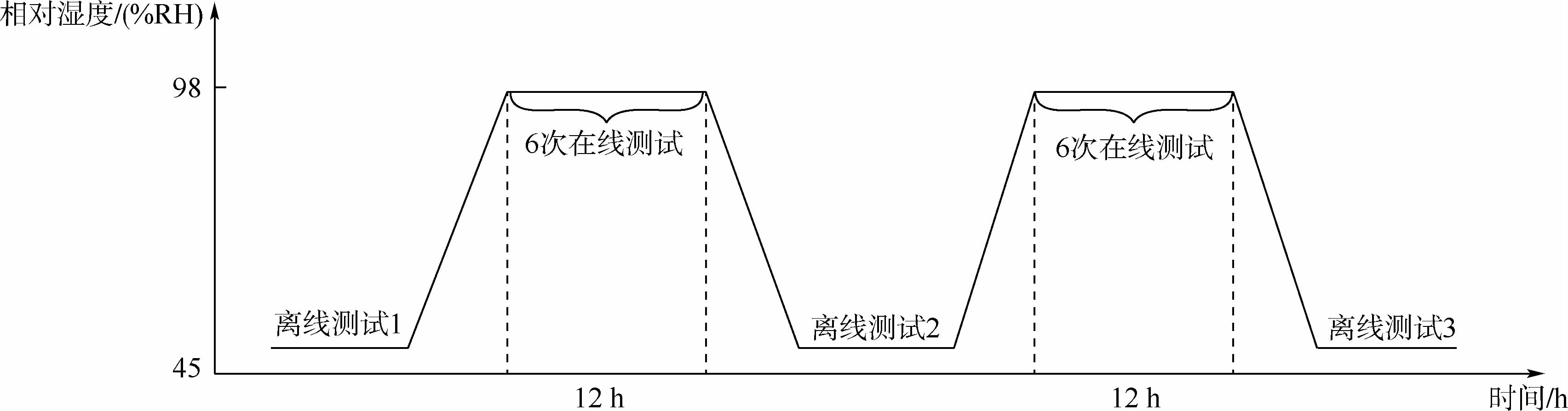图 3 湿度循环试验剖面Fig. 3 Test profile of humidity cycling

图选项

步进电应力试验采用电流应力强化,试验分成两组,一组是针对基本电流10 A,最大电流40 A的电能表,另一组是基本电流10 A,最大电流60 A的电流表.10(40)智能电表步进电应力试验剖面如图 4所示.

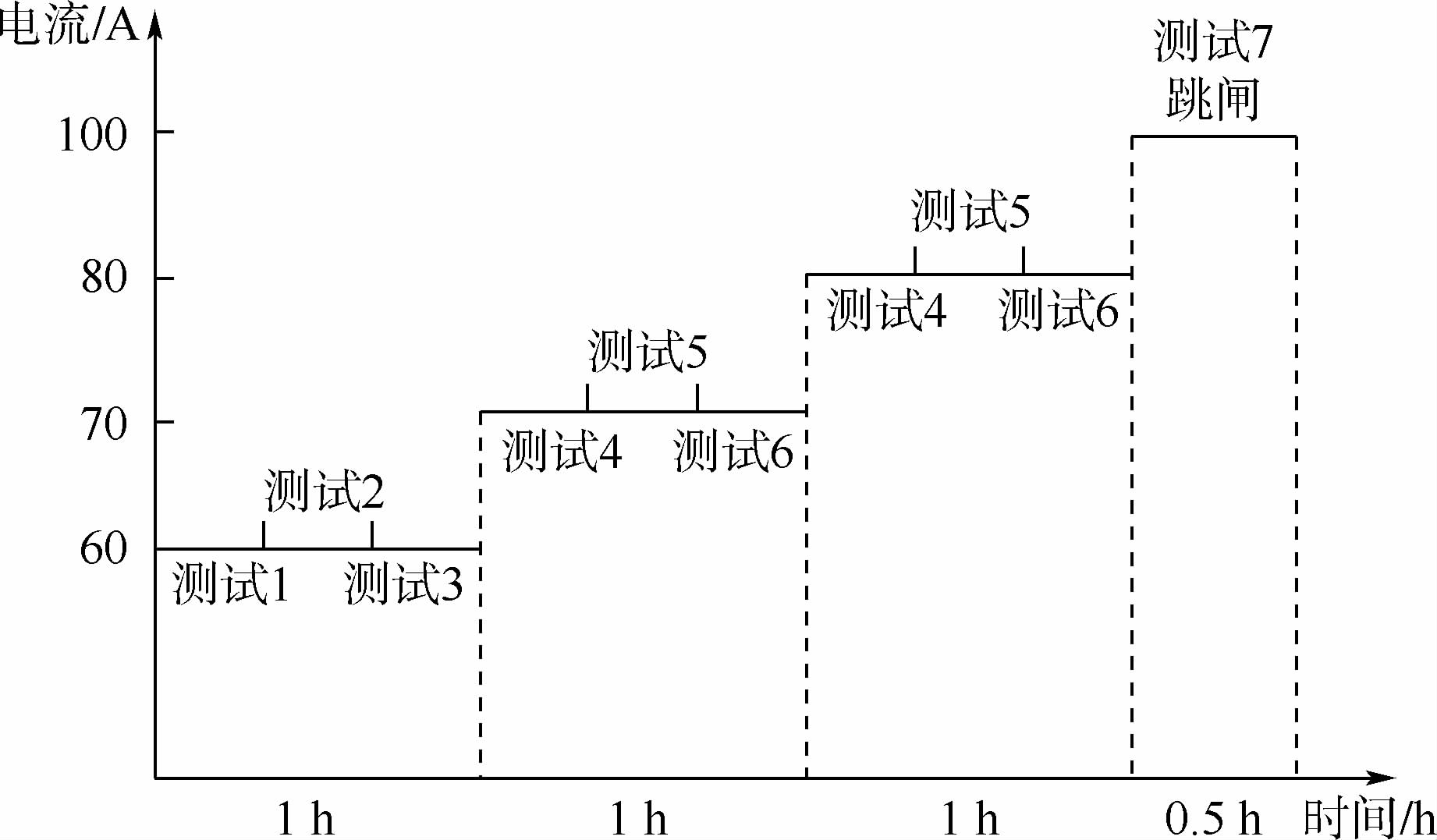图 4 步进电应力试验剖面Fig. 4 Step-stress test profile of electric stress

图选项

智能电表强化试验截止条件为:在线测试过程中电能表无任何输出信号(无计量数据输出、液晶不显示等).
2.2 智能电表强化试验结果分析依据第2.1节强化试验剖面开展试验,得到如下强化试验结果:
1) 计量误差离线测试值随温度、保温时间的增加基本无明显变化趋势;除个别智能电表在120℃离线测试出现超差外(110℃时正常),其他智能电能表在离线测试中没有出现超差.
2) 湿度应力对日计时离线误差有显著影响,但对智能电表计量误差、日计时在线误差和电表常数基本无影响.
3) 电应力对智能电表的计量误差有影响,电流标称值为10(40)的智能电表在电应力强化试验中100 A电流处发生跳闸,故障定位为继电器故障,重新更换继电器后电表恢复正常.
上述强化试验结果说明计量误差是智能电表的主要失效模式,且各应力功能极限水平试验结果为:温度为110℃、湿度为98%RH和电应力为60 A.
3 智能电表加速寿命试验评估根据第2.2节强化试验分析结果,确定温度、湿度及电应力工作极限范围,并在此限定内设计应力剖面组合,对智能电表计量误差进行恒加速寿命试验,建立智能电表计量误差与温度、湿度、电应力和工作时间之间的多应力加速寿命模型,分析智能电表在正常应力下的可靠性和寿命水平.
3.1 智能电表加速寿命试验方案根据温湿控制试验箱工作条件要求<80℃×95%RH,设计智能电表加速寿命试验方案如表 2所示.
表 2 智能电表加速寿命试验应力水平Table 2 Accelerated life test stress levels of smart meter

应力编号	温度T/℃	湿度/(%RH)	电流I/A	样本量
S1	80	80	60	56
S2	55	80	40	56
S3	55	95	20	56
S4	70	95	60	56
S5	70	95	40	56

表选项


在给定的可靠度R和置信度γ下,智能电表加速寿命试验每个应力水平下的样本量应满足以下条件:
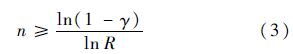
同时定义产品加速寿命试验过程中的失效数为f,试验样本量n应满足:
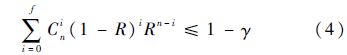
在失效数小于1且可靠度要求0.95的情况下,每个应力水平下智能电表的样本量取值56个.
试验截止条件为:失效试验表达到投入样本量的1/3以上或累积在线试验时间达到400 h.
综合得到智能电表加速寿命试验剖面如图 5所示.

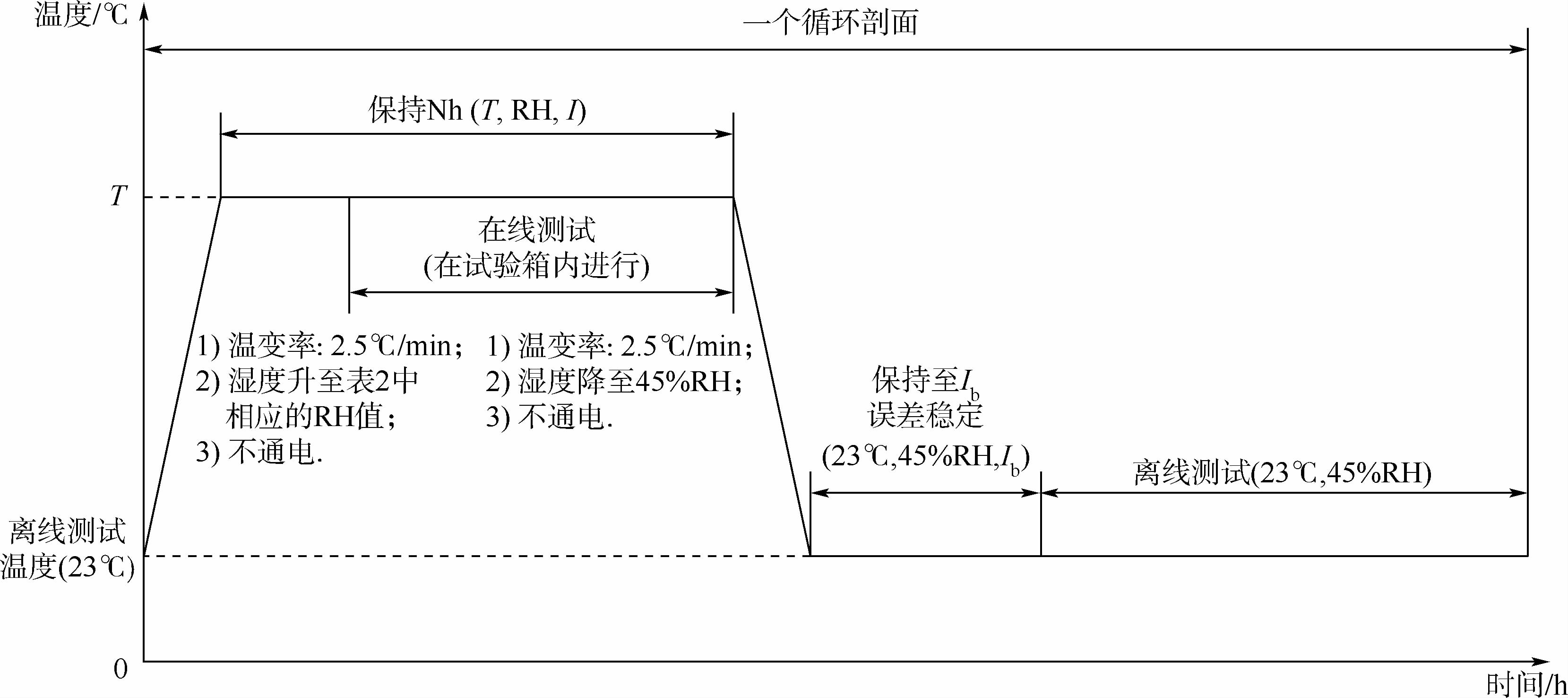图 5 智能电表加速寿命试验剖面Fig. 5 Accelerated life test profile of smart meter

图选项

根据上述加速寿命试验方案开展试验,并搭建智能电表性能指标综合测试系统^{[10, 11]},如图 6和图 7所示.

图 6 智能电表综合应力试验箱Fig. 6 Synthesized stress test chamber of smart meter

图选项

图 7 智能电表指标综合测试系统Fig. 7 Synthesized testing system of smart meter

图选项

3.2 智能电表加速寿命试验结果分析在测量得到的智能电表计量误差加速寿命试验数据,采用伪寿命估计方法对其分3步进行加速寿命分析如下:
1) 计量误差试验测试数据进行退化轨迹建模,给出各个智能电表的伪寿命估计.
2) 对同一应力水平下各个智能电表伪寿命估计值取最小值,得到各个应力水平下智能电表计量误差最小伪寿命.
3) 在最小伪寿命估计值基础上,建立多应力加速模型,确定模型参数.
通过分析智能电表计量误差随时间的变化规律,选取线性参数回归模型来建立智能电表计量误差退化模型:
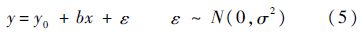
式中:y和y₀分别为计量误差测量值和初始值；b为退化模型常数；ε为模型误差；x=t.
设在第i个应力S_i(S₁2<…p)下进行q_i个智能电表的退化试验,y_i,j,k为应力S_i下第j个智能电表在第k个测试时刻t_i,j,k得到的参数值,i=1,2,…,p；j=1,2,…,q_i；k=1,2,…,n_ij.则应力S_i下第j个智能电表参数退化轨迹模型的y_0ij和b_ij的点估计可由下述诸式确定:
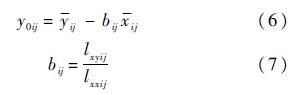
式中:
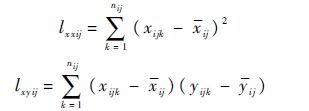
根据计量误差寿命的失效阈值J_LWCmax=1,结合式(5),可得智能电表计量误差伪寿命估计为
各智能电表计量误差伪寿命估计值如表 3所示.
表 3 不同应力水平对应的智能电表计量误差伪寿命数据Table 3 Pseudo life data of smart meter measurement error in different stress levels

S1		S2		S3		S4		S5
表号	伪寿命	表号	伪寿命	表号	伪寿命	表号	伪寿命	表号	伪寿命
1	0.442	57	2.353	113	0.326	169	0.309	225	0.560
2	0.363	58	1.486	114	0.350	170	0.670	226	0.358
3	0.304	59	2.835	115	0.207	171	0.392	227	0.483
4	0.284	60	1.459	116	0.299	172	0.409	228	0.319
5	0.335	61	0.868	117	0.506	173	0.341	229	0.351
6	0.305	62	1.445	118	0.348	174	0.373	230	0.460
7	0.451	63	1.575	119	0.280	175	0.739	231	0.472
8	0.293	64	1.356	120	0.243	176	0.498	232	0.416
9	0.389	65	1.255	121	0.337	177	0.365	233	0.307
10	0.587	66	0.928	122	0.208	178	0.416	234	0.510
11	0.426	67	0.953	123	0.806	179	0.568	235	0.304
12	0.369	68	1.350	124	0.351	180	0.389	236	0.308
13	0.433	69	2.015	125	0.251	181	0.745	237	0.405
14	0.531	70	1.321	126	0.473	182	0.257	238	0.372
15	0.351	71	0.811	127	0.424	183	0.261	239	0.482
16	0.344	72	1.141	128	0.339	184	0.654	240	0.311
17	0.648	73	1.113	129	0.358	185	0.250	241	0.390
18	0.421	74	1.470	130	0.429	186	0.307	242	0.384
19	0.510	75	0.933	131	0.338	187	0.330	243	0.377
20	0.317	76	1.056	132	0.280	188	0.673	244	0.334
21	0.446	77	1.302	133	0.316	189	0.162	245	0.454
22	0.482	78	1.220	134	0.905	190	0.420	246	0.443
23	0.326	79	0.635	135	0.503	191	0.496	247	0.411
24	0.455	80	1.156	136	0.418	192	0.929	248	0.342
25	0.572	81	1.271	137	0.565	193	0.424	249	0.497
26	0.782	82	1.182	138	0.242	194	0.425	250	0.416
27	0.525	83	1.985	139	0.580	195	0.516	251	0.494
28	0.401	84	0.271	140	0.416	196	0.690	252	0.300
29	0.206	85		141	0.462	197	0.386	253	0.389
30	0.425	86		142	0.299	198	0.311	254	0.409
31	0.292	87	0.471	143	0.451	199	0.231	255	0.588
32	0.514	88	1.125	144	0.319	200	0.109	256	0.409
33	0.356	89	1.498	145	1.013	201	0.338	257	0.397
34	0.343	90	0.387	146	0.471	202	0.365	258	0.316
35	0.536	91	1.544	147	0.326	203	0.201	259	0.384
36	0.477	92	0.914	148	0.357	204	0.664	260	0.365
37	0.386	93	1.695	149	0.330	205	0.686	261	0.544
38	0.385	94	1.984	150	0.333	206	0.679	262	0.347
39	0.468	95	0.952	151	0.373	207	0.333	263	0.366
40	0.369	96	1.043	152	0.413	208	0.323	264	0.302
41	0.705	97	1.645	153	0.480	209	0.584	265	0.373
42	0.411	98	1.186	154	0.287	210	0.313	266	0.423
43	0.441	99	1.274	155	0.280	211	0.217	267	0.337
44	0.488	100	1.307	156	0.407	212	0.393	268	0.391
45	0.497	101	1.383	157	0.344	213	0.520	269	0.419
46	0.596	102	1.983	158	0.361	214	0.298	270	0.404
47	0.457	103	0.920	159	0.385	215	0.365	271	0.303
48	0.379	104	1.417	160	0.354	216	0.380	272	0.347
49	0.323	105	1.132	161	0.382	217	0.297	273	0.499
50	0.573	106	0.914	162	0.383	218	0.410	274	0.634
51	0.603	107	0.964	163	0.293	219	0.542	275	0.726
52	0.658	108	0.778	164	0.348	220	0.549	276	0.648
53	0.480	109	1.582	165	0.321	221	0.711	277	0.495
54	0.752	110	1.227	166	0.334	222		278	0.556
55	0.712	111	1.373	167	0.390	223	0.552	279	0.378
56	0.503	112	1.466	168	0.308	224	0.550	280	1.125

表选项


经简化与等价变形后的电应力、温度寿命模型可分别由t=K·E^-n和t=A·e^B/T表示^[12],其中A、B为常数；E为电能表计度累计值.基于广义对数线性模型,可将综合应力加速寿命模型表示为
式中:X_j为加速应力；a_j为模型参数.在利用广义对数线性模型作为综合应力加速模型使用时,仅需将X_j用相应的变量(如温度、电应力及机械应力等)替换即可.根据智能电表温度、湿度、电应力3应力加速寿命试验特点及式(9),本文建立如下多应力加速寿命模型:
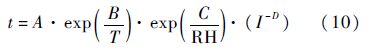
式中:C、D为常数^[12].
根据表 3中的伪寿命数据,采用拟合优度检验确定伪寿命服从最优分布为威布尔分布,并通过整体极大似然估计得到参数估计值^{[13, 14, 15]},最后求得可靠度为R的智能电表加速寿命模型如下:
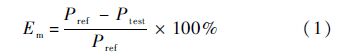
3.3 智能电表可靠性和寿命评估根据智能电表正常温度20℃、湿度为45%和电应力为10 A,可得其置信度γ为0.7、0.8、0.9.可靠度R为0.95下智能电表可靠寿命分别为29.02、26.62和23.61 a,满足工程上10 a的可靠寿命指标要求.
4 结 论1) 揭示了智能电表可靠性和寿命主要性能参数及其失效机理.通过分析智能电表计量误差、日计时误差和电表常数的物理含义,深入推导了各环境应力对各性能参数的影响机理,最后通过强化试验明确了计量误差为影响智能电表可靠寿命的主要性能参数及其各环境应力工作极限条件.
2) 建立了智能电表可靠寿命加速模型.在强化试验结论的基础上,设计加速寿命试验方案,并引入3应力加速模型和进行数据统计分析,得到了智能电表加速寿命试验,为评估正常工作条件下的智能电表可靠寿命奠定了基础.
3) 提出了一套评估多参数-多应力智能电表可靠性和寿命的方法体系.通过主机理及应力分析、强化试验分析和加速寿命试验分析,综合给出了一套智能电表可靠性和寿命评估方法,并最后得到了置信度γ=0.7、0.8、0.9，可靠度R=0.95下智能电表可靠寿命分别为29.02、26.62和23.61 a,满足工程要求.
参考文献

[1]	黄亮,王景存,康之讷,等.新型电能计量芯片RN8302在智能电表中的应用[J].电子设计工程,2013,21(3):93-95. Huang L,Wang J C,Kang Z N,et al.The application of a new type electric energy metering chip RN8302 in smart meter[J].Electronics Design Engineering,2013,21(3):93-95(in Chinese)
	Cited By in Cnki (1) | Click to display the text
[2]	郭宁辉,秦立军.智能用电系统的框架设计[J].企业技术开发,2013,3(3):6-7. Guo N H,Qin L J.A framework design of intelligent power system[J].Technological Development of Enterprise,2013,3(3):6-7(in Chinese)
	Cited By in Cnki
[3]	樊崇理,张进明.智能电表的发展现状及分析[J].现代科学仪器,2000(5):30-32. Fan C L,Zhang J M.The development situation and analysis of smart meter[J].Modern Scientific Instruments,2000(5):30-32(in Chinese)
	Cited By in Cnki (20)
[4]	Darby S J.Metering:EU policy and implications for fuel poor households[J].Energy Policy,2012,49:98-106
	Click to display the text
[5]	唐发荣.智能电表功能及其高级应用分析[J].价值工程,2012(23):28-30. Tang F R.Analysis of smart meters and advanced applications[J].Value Engineering,2012(23):28-30(in Chinese)
	Cited By in Cnki (2)
[6]	Dissanayaka D M L B,Fernando C T J,Abeyratne S G.Smart meter based inverter controlling network for demand response applications in smart grids[C]//2011 6th International Conference on Industrial and Information Systems,ICIIS 2011-Conference Proceedings.Piscataway,NJ:IEEE Press,2011:192-197.
[7]	Wang S T,Luo R R,Zhou H,et al.Research on reliability enhancement testing for single-phase smart meter[C]//2011 International Conference on Electrical and Control Engineering,ICECE 2011- Proceedings.Piscataway,NJ:IEEE Press,2011:3128-3131.
[8]	王根东.多用户电子式电能表的可靠性及其强化试验设计研究[D].重庆:重庆大学,2007. Wang G D.Study on multi-user electronic energy meter's reliability and it's RET[D].Chongqing:Chongqing University,2007(in Chinese)
	Cited By in Cnki (1)
[9]	刘宇宏.浅谈智能电能表可靠性[J].才智,2013(16):5-6. Liu Y H.The reliability of the intelligent electric energy meter[J].Intelligence,2013(16):5-6(in Chinese)
	Cited By in Cnki (1)
[10]	冯波,王俊龙,史轮,等.智能电能表用电信息采集方案分析与比较[J].河北电力技术,2013,32(3):39-41. Feng B,Wang J L,Shi L,et al.Analysis and comparison of smart meter power consumption information collection system[J].Hebei Electric Power,2013,32(3):39-41(in Chinese)
	Cited By in Cnki (2) | Click to display the text
[11]	牛春霞.电力用户用电信息采集[M].北京:中国电力出版社,2012:100-110. Niu C X.Power user electric energy data acquisition[M].Beijing:Chinese Power Press,2012:100-110(in Chinese).
[12]	李晓阳,姜同敏.加速寿命试验中多应力加速模型综述[J].系统工程与电子技术,2007,29(5):828-831. Li X Y,Jiang T M.Review of multiple-stress models in accelerated life testing[J].Systems Engineering and Electronics,2007,29(5):828-831(in Chinese)
	Cited By in Cnki (22) | Click to display the text
[13]	李向峰,宗建华.IEC62059标准在智能电能表可靠性预计与考核验证方法上的应用[J].电测与仪表,2010,47(1):75-81. Li X F,Zong J H.IEC62059 standards in smart meter dependability prediction and verification methods application[J].Electrical Measurement and Instrumentation,2010,47(1):75-81(in Chinese)
	Cited By in Cnki (17) | Click to display the text
[14]	Meeker W Q,Escobar L A,Lu C J.Accelerated degradation tests:Modeling and analysis[J].Technometrics,1998,40(2):88-89.
[15]	马小兵.基于伪寿命分布的退化数据可靠性评估方法[J].系统工程与电子技术,2011,33(1):228-232. Ma X B.Reliability assessment using constant stress accelerated degradation data based on pseudo life distribution[J].Systems Engineering and Electronics,2011,33(1):228-232(in Chinese)
	Cited By in Cnki (0) | Click to display the text