由于受卫星轨道限制、测量设备故障、通信链路中断及人为数据剔除等因素的影响,空间环境测量数据(包括太阳风参数、行星际磁场和高能粒子通量等)经常出现数据缺失现象,而很多分析过程及建模手段都需要连续的数据作为输入,因此,研究空间环境缺失数据插补方法有着重要的现实意义。
空间环境数据具有典型的非线性、非平稳特征,寻求能够适用于此类特征的数据插补方法已经受到越来越多的重视。作为一种非参数化、数据驱动和自适应的时间序列分析方法,奇异谱分析(Singular Spectrum Analysis,SSA)集成了经典时间序列分析、多元统计、动态系统和信号处理等方法的特点,尤其适合于从短时、噪声信号中提取有用信息^{[1, 2, 3]}。其基本思想是:通过将时间序列分解为一系列的模态项,如趋势项、周期项及噪声项,利用选取的主要模态重建原始信号,进而过滤掉噪声序列。由于模态项的分解过程对少数数据点并不敏感,可利用重建的数据序列插补原始缺失数据。
Schoellhamer^[4]于2001年首先提出了一种能够适应于缺失数据的SSA算法(S-SSA),通过忽略缺失数据,利用已知数据构建轨迹矩阵,设定嵌入窗口内缺失数据的比例,以此控制序列的重建过程。但此方法没有对缺失数据进行插补处理,为此,Shen等^[5]提出了一种改进的插补方案(I-SSA),将缺失数据的插补转换成关于主成分分量的矩阵方程近似解。I-SSA扩展了S-SSA算法的应用范围,但2种算法都是基于Toeplitz形式的轨迹矩阵,只适用于平稳时间序列的处理,且对SSA算法的2个关键性参数的选取没有讨论。
Golyandina和Osipov^[6]则利用Hankel轨迹矩阵的对称特性,基于SSA讨论缺失数据的插补方法,给出了算法的适用条件和数学证明。其主要问题在于适用条件过于严格,且最终整个数据序列都会发生变化,产生人为的失真。
Kondrashov和Ghil^[7]基于文献[8]中迭代经验正交函数法提出了一种2层循环结构的SSA数据插补算法(KG-SSA)。其中,内循环用于缺失数据的插补,外循环用于调整插补所用到的主要模态分量个数,最终利用交叉验证的方法实现对插补参数的评价与优选。Kondrashov等^{[9, 10]}将KG-SSA扩展到多元的情况,并利用地磁指数(K_p、Ds_t和A_E等)实现了不同时间尺度的太阳风参数缺失数据计算试验,得到了较好的结果。
KG-SSA算法中外循环采用的是遍历寻优的办法,计算效率较低。王辉赞^[11]和刘巍^[12]等针对此问题提出了一种区间四分法实现小波动情况下的参数快速寻优,但对嵌入窗口选择并未涉及。
本文对文献[7]中算法框架进行了改进,使得算法能够在一定程度上适应缺失数据的结构,同时考虑了嵌入窗口和主成分的选取问题。
1 SSA基本原理介绍SSA以奇异值分解为基础,包括分解和重构2个过程。分解过程利用原始序列生成一系列的时间经验正交函数和主成分分量,包括轨迹矩阵嵌入和奇异值分解2步;重构过程则实现对时滞矩阵的还原及时间序列的近似恢复,包括分组和对角化平均2步。
以一元SSA(U-SSA)为例,其过程简要描述如下^{[13, 14, 15]}。
1) 轨迹矩阵嵌入
设时间序列x₁,x₂,…,x_N,嵌入窗口为M,该步骤完成一维时间序列到高维相空间即时滞轨迹矩阵的映射,得到轨迹矩阵X=[x₁,x₂,…,x_K]_M×K,x_i=[x_i,x_i+1,…,x_i+M-1]^TT,i=1,2,…,K,K=N-M+1。X为一个具有反对角对称性的Hankel矩阵。
2) 奇异值分解
由轨迹矩阵X计算时滞协方差矩阵:

对C进行特征值分解,得到按降序排列的特征值λ_j及其对应的特征向量U_j即时间经验正交函数,此时奇异值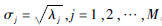。3) 分组
将特征值进行分组,代表不同特征的信号分量,比如取较大特征值表征有用信号,较小特征值表征噪声分量,此时有

式中:I为有用信号; 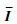为去除I后的噪声信号;d为时滞矩阵C的秩。原始信号可以表示成有用信号与噪声信号的和,即

式中: 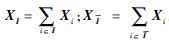。 4) 对角化平均
按照反对角元素求平均的步骤将信号矩阵还原成一维信号,得到重建后的信号。此时

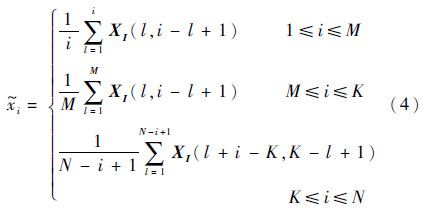
多元SSA(M-SSA)与此类似。注意当处理不同量纲的数据时,为了避免不同变量数据大小对结果的影响,一般要做标准化预处理。
2 SSA数据插补方法2.1 问题的提出Kondrashov和Ghil^[7]指出,缺失数据的分布、位置和数量对插补效果有很大的影响,但在其算法中并未充分体现缺失数据这种结构特性的影响。因此,本文的方法旨在解决如下2个问题:
1) 如何将缺失数据的结构特性考虑到插补方法中。
2) 如何有效地选取SSA的2个关键参数。
针对第1个问题,本文定义了描述缺失数据结构的分布数组F={F_i},i=1,2,…,N,有

式中:NaN表示无效值。
分布数组具有如下特性:设偏移量Δ∈Z,对F进行偏移,如果Δ>0,则向右移位Δ,如果Δ<0,则向左移位Δ。Δ>0时,移位过程中超出序列最大索引值的部分折回到序列的初始部分,实现循环移位;Δ<0时,同理,见图 1。其中X表示数据序列,F表示提取的分布数组,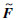表示移位后的分布数组,深色方框表示缺失数据,Δ=2表示向右移动2位,此时x₉处的缺失数据移动2位后超出序列最大长度,则循环到序列起始位置,x₈处缺失数据移动到x₁₀处,依次顺延。

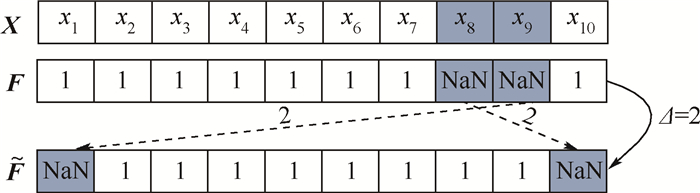图 1 缺失数据分布数组示意图 Fig. 1 Schema of distribution array of missing values

图选项

基于数组F实现数据插补的核心思路在于用F来构造测试数据集:首先用所有已知数据重构出原始缺失数据,此时所有数据为“已知”状态,然后按照交叉验证的思路,随机生成偏移项Δ,对F进行偏移,此时“已知”数据序列按照偏移后的F构造出缺失数据结构,即为所需要的测试数据集。与文献[7]不同的是,这里是先利用所有已知数据重构出缺失数据,然后用偏移后的测试数据集评价重构的精度,即重构参数的泛化能力。
上述插补方案并未涉及缺失数据在整个序列上分布的位置信息,这也是任何插补方法共有的、不可避免的问题,但最大程度地保留了缺失数据数量和相对位置的结构特性。
已有文献[16, 17, 18]对第2个问题进行了讨论,但只是给出了参数的选取范围,没有确定具体指标,且主要是针对全部数据已知的数据序列,对于缺失数据的情况其适应性有待进一步研究。本文将SSA参数的选取归结为参数的寻优问题,利用先进的群智能优化算法来寻找最优参数。
2.2 离散粒子群优化算法粒子群优化算法是一种群智能优化算法。由于其实现简单、寻优效率高,自提出以来便获得了广泛的应用和研究。粒子群优化算法中的每个粒子代表解空间中的一个解,用一个位置矢量来表示,粒子以一定的速度(具有方向和大小)在解空间中不断地运动以寻找更优的解。多个粒子形成的群体,称为种群。粒子能够从自身的经验和种群的信息交互中进行学习^{[19, 20]}。
离散粒子群优化算法是对标准粒子群优化算法适用于离散解空间的扩展,能够用于解决实际问题中的离散变量优化问题^{[21, 22]}。目前对离散粒子群优化算法的研究主要分为3类:基于二进制编码的方法、基于连续空间直接离散化的方法以及对算法动力学方程重新定义的方法^[23]。考虑到第2类方法易于理解,容易集成其他先验知识(约束问题),本文拟用其实现对SSA的参数寻优。
首先，将SSA的窗口长度和主分量个数编码为离散粒子群优化算法中的位置矢量z_i=(M_i,K_i),i=1,2,…,n,n为粒子种群规模。
然后,在离散粒子群优化算法迭代过程中,粒子按照如下方程更新其位置和速度。
粒子速度更新方程为

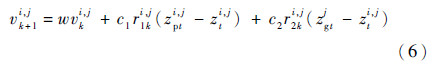
粒子位置更新方程为

式中:v_k+1^i,j为第k+1代粒子中第i个粒子的第j个维度的速度值;w为粒子继承上一代速度大小的惯性权重,通常以线性递减的形式表示，w=w_min+i_cur(w_max-w_min)/M_Iter,一般情况下取w_max=0.9,w_min=0.4,i_cur为当前迭代次数,M_Iter为最大迭代次数;c₁、c₂为粒子的加速因子,通常取c₁=c₂=2;r₁、r₂为[0,1]内服从均匀分布的随机数;z_pt^i,j为粒子自身经历的最好位置;z_gt^j为粒子种群经历的最好位置。式(7)中的ceil操作用来把连续型变量取整,使之成为离散型变量。针对不同的问题,取整策略会有所不同,如解空间是[10,20,30,40,…],则取整时需要进行相应的映射变换。本文中要处理的变量是连续的整数,故可以直接采用四舍五入的方法,简化了处理的流程。
为了防止粒子跳出参数的取值范围,通常定义粒子的位置的最大、最小值(z_max,z_min),并以此对粒子进行限定:

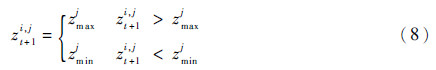
这样从优化的角度将SSA参数选取问题重新描述如下:
确定z^*=(M^*,K^*),使某种评价函数f(z)取最小值,满足

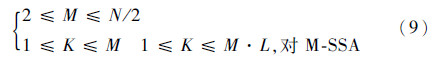
这是一个带有约束项的参数寻优问题,在更新粒子位置之后要判断其是否符合约束项。如果符合,则继续迭代过程;否则,对粒子位置进行必要的处理。本文处理方法为

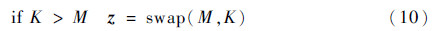
式中:swap()为交换算子,即交换两输入的位置。2.3 迭代插补算法本文提出的缺失数据插补方法以离散粒子群优化算法为基本框架,迭代SSA为计算核心,具体步骤如下:
1) 确定时间序列长度N。
2) 检测缺失数据结构,如果为简单型缺失数据,则可选择三次样条插值、线性插值等方案,插补结束;如果为复杂型缺失数据,则转步骤3)。简单型缺失数据可定义为连续缺失数据点数不超过τ个,且总的缺失数据比例小于某一阈值σ₀,定义简单缺失数据是为在线应用节省计算量。
3) 初始化算法参数,如n、w、c₁、c₂和M_Iter,并在约束范围内随机初始化粒子群位置z⁰=(z₁,z₂)和速度v⁰=(v₁,v₂)。
4) 按照速度更新公式(6)和位置更新公式(7)更新粒子速度和位置。
5) 判断粒子位置是否在约束范围内,如果不在,按式(10)进行相应处理。
6) 对各粒子按照评价函数f(z)进行适应度评价。
7) 更新粒子历史最优位置。
8) 更新种群历史最优位置。
9) 调整惯性权重、多样性参数等。
10) 若满足终止条件,输出全局最优粒子gBest对应的插补值序列,否则转至步骤4)。
以上插补算法中,主要的计算过程在于评价函数f(z)。本文评价函数取为迭代SSA插补结果与实际观测值之间的均方根误差,具体构造过程如下:
1) 从原始数据中提取缺失数据分布数组F。
2) 将原始数据做去中心化处理,并将缺失数据置0,得到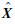,均值为X_ave。
3) 对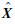进行SSA计算,按照指定的窗口长度和主成分个数重构得到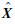′,用对应位置处的值替换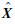中缺失数据位置处的值得到″。
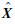4) 对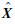″进行SSA计算,按照同样的参数重构得到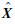''',如果前后2次重构序列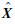′和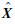'''的均方差满足一定条件,如R_ms<10^-3,则停止迭代,得到最终插补序列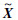=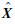″+X_ave,否则转至步骤3)进行循环迭代。
5) 随机生成一个偏移量Δ。
6) 对F进行Δ位偏移,得到新的缺失数据分布数组。
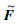7) 生成测试数据序列X_tes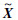t=^T·。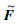
8) 对X_test重复步骤2)～步骤4),得到插补后的测试数据序列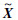_test。
9) 评价用的均方根误差输出为R_ms=rms(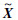-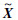_test)。
10) 重复步骤5)～步骤9)一定次数,取均值得到最终的评价函数输出。
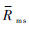3 插补试验为了评价所提算法的有效性,本文选取相关系数和均方根误差作为评价指标,对实际太阳风相关参数进行了测试验证。试验设计为:首先，对U-SSA插补方案进行横向对比,即与现有的插补工具进行对比试验,测试本文算法的有效性;其次，以SSA插补方案分别对太阳活动高年、太阳活动低年太阳风相关参数进行插补试验,检验算法对不同太阳活动周期的适应性;最后，在相同参数条件下,测试算法对缺失数据不同分布、不同数量的适应性。
3.1 U-SSA插补试验以2009年太阳风速度(V_el)为例,人为构造出一些随机的数据缺失点,包括离散点和连续区间,见图 2。太阳风数据取自美国宇航局地球物理数据设施网站(ftp://spdf.gsfc.nasa.gov/pub/data/omni)。为清晰起见,图 2及后续各图对坐标轴范围都进行了限定。图中横坐标表示一年中的天数,附近的黑色点线表示缺失数据的分布;S.M.SSA为台湾元智大学开发的SSA计算程序包spectral.methods计算所得结果。为便于比较,本文基于线性插值、样条插值和三次样条插值等方法对缺失数据进行了插补(未在图中标出),计算所得均方根误差R_ms和相关系数C_orr见表 1。

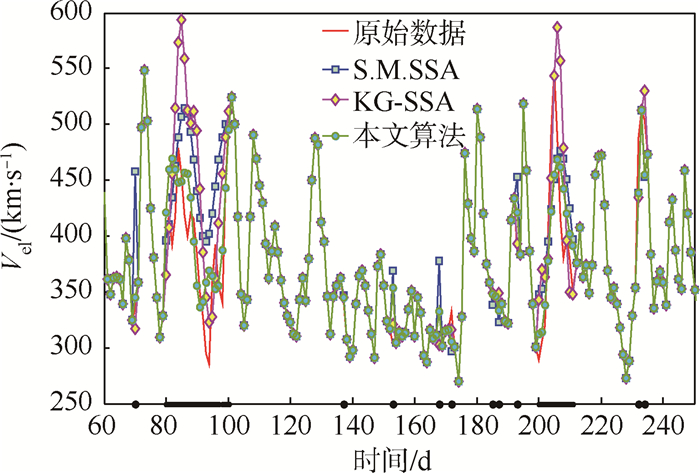图 2 基于U-SSA的太阳风速度插补结果 Fig. 2 Filling results of solar wind velocity based on U-SSA

图选项

表 1 不同方法插补结果对比 Table 1 Comparison of filling results based on different methods

方法	Rms	Corr
线性插值	71.776 0	0.380 1
样条插值	96.505 8	0.183 2
三次样条插值	82.875 1	0.308 9
I-SSA	59.557 4	0.779 5
S.M.SSA	62.258 9	0.632 2
文本算法	38.183 4	0.830 4

表选项


表 1中各项数据都是经过多次试验后的平均结果。由表中结果可知,传统的基于多项式的插值方法对于出现连续数据缺失的太阳风数据序列不再适用;此外,所提算法较其他方法无论从均方根误差或相关系数指标方面,都表现出较好的性能,说明方法的有效性。
3.2 M-SSA太阳活动高年数据插补试验太阳活动高年数据选取的是2000年太阳风参数和地磁指数日均值数据(2000年处在第23个太阳活动周峰值年份,共366组数据)。太阳风数据以太阳风速度(V_el)、粒子密度(D_en)为例;地磁数据取自世界地磁数据中心Tokyo站,选取行星际3 h磁情指数K_p、全球全日地磁扰动强度指数A_p和极区磁亚爆强度指数A_E。对于K_p指数,日均值计算过程为:对K_p指数的均值数据近似取整,然后取最邻近的K_p指数,详细描述可参考网站的说明文档。
多元插补方案中,以待插补太阳风参数和地磁指数为原始序列,构造时滞矩阵,分别测试不同参数条件下的插补效果。图 3、图 4分别为太阳风速度、太阳风密度的数据插补结果。表 2给出了多次计算试验后不同参数对应的均方根误差和相关系数均值结果。

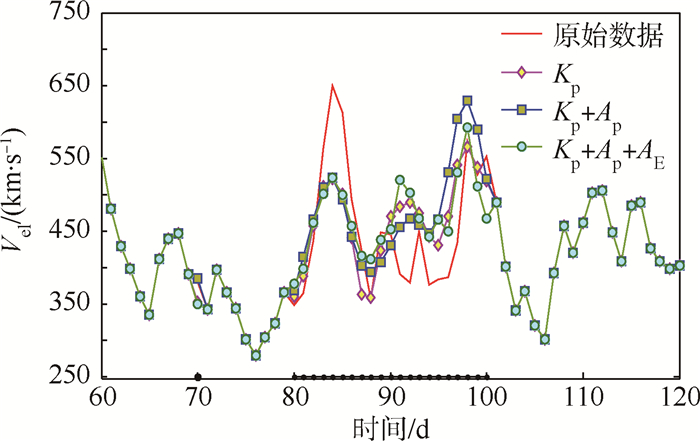图 3 基于M-SSA的2000年太阳风速度插补结果 Fig. 3 Filling results of solar wind velocity in 2000 based on M-SSA

图选项

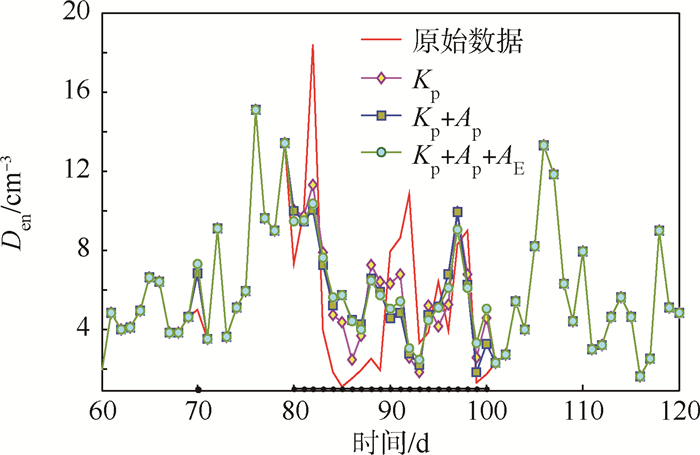图 4 基于M-SSA的2000年太阳风密度插补结果 Fig. 4 Filling results of solar wind density in 2000 based on M-SSA

图选项

表 2 2000年不同地磁指数下太阳风参数插补结果对比 Table 2 Comparison of filling results for solar wind parameters with different geomagnetic indices in 2000

参数	Vel		Den
	Rms	Corr	Rms	Corr
Kp	52.078 3	0.809 0	3.2212	0.630 7
Ap	61.587 2	0.737 4	3.489 2	0.538 8
AE	60.082 0	0.7300	3.465 3	0.548 3
Kp+Ap	59.156 8	0.756 9	3.464 9	0.568 9
Kp+AE	55.254 9	0.780 2	3.365 9	0.586 7
Ap+AE	59.660 1	0.750 6	3.439 9	0.560 8
Kp+Ap+AE	57.950 5	0.757 7	3.424 8	0.567 5

表选项


图 3、图 4显示,在太阳活动高年,本文的插补结果能够较好地跟踪太阳风参数的相位信息,但幅度上有所差异,尤其是在连续数据缺失时更为明显。由表 2中结果可知,对于2000年的太阳风速度和密度而言,K_p指数相对于其他地磁指数,能够更好地实现数据插补。
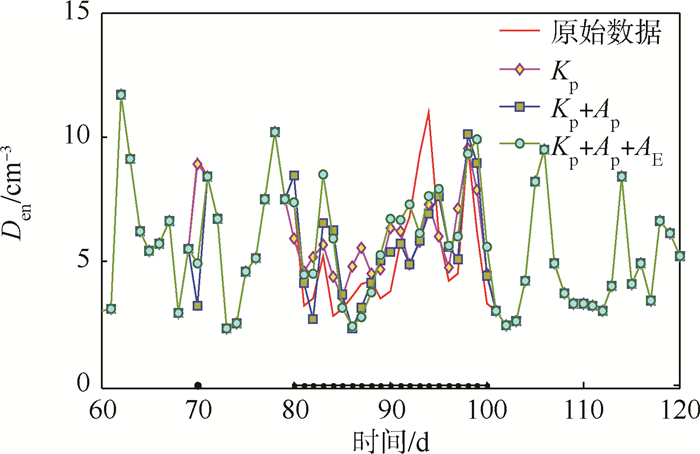
3.3 M-SSA太阳活动低年数据插补试验太阳活动低年各参量与高年情况一样,但选取的是2009年的数据,共365组。图 5、图 6为太阳风速度和密度的插补结果,表 3列出了多次计算后不同参数对应的均方根误差和相关系数均值结果。

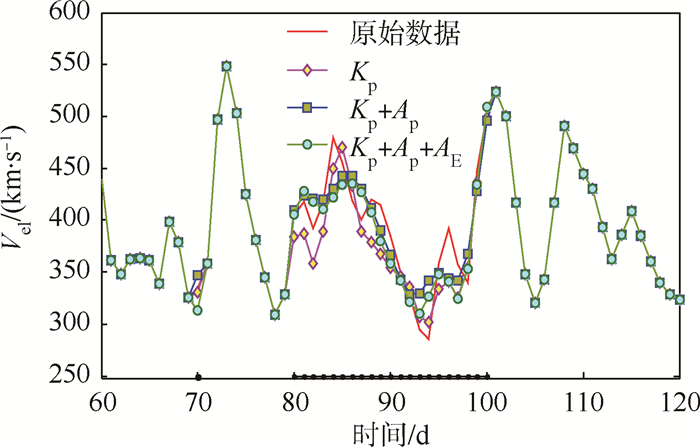图 5 基于M-SSA的2009年太阳风速度插补结果 Fig. 5 Filling results of solar wind velocity in 2009 based on M-SSA

图选项

图 6 基于M-SSA的2009年太阳风密度插补结果 Fig. 6 Filling results of solar wind density in 2009 based on M-SSA

图选项

表 3 2009年不同地磁指数下太阳风参数插补结果对比 Table 3 Comparison of filling results for solar wind parameters with different geomagnetic indices in 2009

参数	Vel		Den
	Rms	Corr	Rms	Corr
Kp	30.8736	0.9134	2.2976	0.7176
Ap	29.844 6	0.904 0	2.308 7	0.710 3
AE	32.511 9	0.891 8	2.520 1	0.648 7
Kp+Ap	27.863 1	0.918 3	2.302 9	0.733 6
Kp+AE	29.079 7	0.908 5	2.229 4	0.728 2
Ap+AE	29.054 6	0.905 0	2.342 8	0.701 2
Kp+Ap+AE	29.343 7	0.907 1	2.281 1	0.721 4

表选项


图 5、图 6显示,在太阳活动低年(2009年),本文的插补结果能够较好地跟踪太阳风参数的相位信息,而且插补结果幅度上有明显的改善。表 3中给出的均方根误差和相关系数进一步说明,总体上低年数据插补效果要明显好于高年的情况,且对于低年的太阳风速度和密度而言,K_p和A_p指数的组合相对于其他地磁指数,能够更好地实现数据插补。
3.4 不同比例缺失数据插补试验为了进一步验证本文所提算法对不同分布、不同数量缺失数据的插补效果,以2009年太阳风速度为例,地磁指数取K_p日均值数据,分别对缺失数据比例为10%、20%、30%、40%和50%的情况做多次计算试验,并取最后的平均值,结果见表 4。
表 4 太阳风速度不同比例缺失数据插补结果对比 Table 4 Comparison of filling results for different ratios of missing values for solar wind velocity

缺失比例/%	Rms	Corr
10	23.647 4	0.921 92
20	27.524 4	0.902 5
30	27.973 8	0.892 8
40	29.655 3	0.885 3
50	31.709 7	0.859 2

表选项


由表 4可知,随着缺失数据比例的增加,评价指标总体呈下降趋势,但总体插补效果仍然保持较好水平,所得数据可以为后续的建模、分析提供数据支撑。
4 结 论本文基于奇异谱分析迭代插补的思想设计了了一种新的空间环境缺失数据插补方法,该方法考虑缺失数据结构对插补结果的影响,并将奇异谱分析参数选取归结为参数寻优问题,应用群智能优化算法完成参数寻优,以提高计算效率。
通过对实际太阳风速度、行星际磁场以及不同比例缺失数据插补试验表明:
1) 本文算法能够适应不同太阳活动情况,但总体上太阳活动低年要比太阳活动高年效果好。
2) 多元插补方案也要优于一元插补方案,这是由于多元奇异谱分析利用了不同变量之间的相关信息。
3) 在多元插补方案中,不同输入变量对数据插补结果的贡献度不同,这同时提示可以由此来推断输入、输出之间的因果或相关关系。
本文算法能够拓展到地球物理领域涉及时间序列的数据插补问题中。后续工作将进一步完善本文算法,来满足实时数据对数据插补的需求,主要考虑:结合Korobeynikov^[24]的工作和并行计算思想,提高奇异值分解计算效率;采用更加高效的智能算法对参数进行寻优。

参考文献

[1]	BROOMHEAD D S, KING G P.Extracting qualitative dynamics from experimental data[J].Physica D,1986,20(2-3):217-236.
	Click to display the text
[2]	GHIL M, ALLEN R M,DETTINGER M D,et al.Advanced spectral methods for climatic time series[J].Reviews of Geophysics,2002:40(1):3.1-3.41.
	Click to display the text
[3]	ZHIGLJAVSKY A. Singular spectrum analysis for time series: Introduction to this special issue[J].Statistics and Its Interface,2010,3(3):255-258.
	Click to display the text
[4]	SCHOELLHAMER D H. Singular spectrum analysis for time series with missing data[J].Geophysical Research Letters,2001,28(16):3187-3190.
	Click to display the text
[5]	SHEN Y, PENG F,LI B.Improved singular spectrum analysis for time series with missing data[J].Nonlinear Processes in Geophysics,2014,1(2):1947-1966.
	Click to display the text
[6]	GOLYANDINA N, OSIPOV E.The “Caterpillar”-SSA method for analysis of time series with missing values[J].Journal of Statistical Planning and Inference,2007,137(8):2642-2653.
	Click to display the text
[7]	KONDRASHOV D, GHIL M.Spatio-temporal filling of missing points in geophysical data sets[J].Nonlinear Processes in Geophysics,2006,13(2):151-159.
	Click to display the text
[8]	BECKERS J M, RIXEN M.EOF calculations and data filling from incomplete oceanographic datasets[J].Journal of Atmospheric and Oceanic Technology,2003,20(12):1839-1856.
	Click to display the text
[9]	KONDRASHOV D, SHPRITS Y,GHIL M.Gap filling of solar wind data by singular spectrum analysis[J].Geophysical Research Letters,2010,37(15):1-6.
	Click to display the text
[10]	KONDRASHOV D, DENTON R,SHPRITS Y Y,et al.Reconstruction of gaps in the past history of solar wind parameters[J].Geophysical Research Letters,2014,41(8):2702-2707.
	Click to display the text
[11]	WANG H Z, ZHANG R,LI W.Improved interpolation method based on singular spectrum analysis iteration and its application in missing data recovery[J].Applied Mathematics and Mechanics,2008,29(10):1227-1236.
	Click to display the text
[12]	LIU W,JIN W D, WANG H Z,et al.An optimized atmospheric missed data recovery algorithm based on singular spectrum iteration[C]//Proceedings of IEEE Conference on Cybernetics and Intelligent.Piscataway,NJ:IEEE Press,2008:1129-1132.
	Click to display the text
[13]	GOLYANDINA N, NEKRUTKIN V,ZHIGLJAVSKY A.Analysis of structure of time series: SSA and related techniques[M].Boca Raton:The Chemical Rubber Company Press,2001:30-73.
[14]	CHENG D. Time series decomposition using singular spectrum analysis[D].Tennessee:East Tennessee State University,2014:12-14.
	Click to display the text
[15]	CLAESSEN D, GROTH A.A beginner's guide to SSA[EB/OL].Paris:Ecole Normale Supérieure,2010[2015-05-10].http:// www.environnement.ens.fr/IMG/file/DavidPDF/SSA_beginners_guide_v9.pdf.
	Click to display the text
[16]	WANG R, MA H,LIU G,et al.Selection of window length for singular spectrum analysis[J].Journal of the Franklin Institute,2015,352(2):1541-1560.
	Click to display the text
[17]	GOLYANDINA N. On the choice of parameters in singular spectrum analysis and related subspace-based methods[J].Statistics and Its Interface,2010,3(3):259-279.
	Click to display the text
[18]	MAHMOUDVAND R, ZOKAEI M.On the singular values of the Hankel matrix with application in singular spectrum analysis[J].Chilean Journal of Statistics,2012,3(1):43-56.
[19]	VALLE Y, VENAYAGAMOORTHY G K,MOHAGHEGHI S,et al.Particle swarm optimization:Basic concepts,variants and applications in power systems[J].IEEE Transactions on Evolutionary Computation,2008,12(2):171-195.
	Click to display the text
[20]	KENNEDY J, EBERHART R C.Particle swarm optimization[C]//Proceedings of the 1995 IEEE International Conference on Neural Networks.Piscataway,NJ:IEEE Press,1995:1942-1948.
[21]	CHOWDHURY S, TONG W,MESSAC A,et al.A mixed-discrete particle swarm optimization algorithm with explicit diversity-preservation[J].Structural and Multidisciplinary Optimization,2013,47(3):367-388.
	Click to display the text
[22]	BOUBAKER S, DJEMAI M,MANANANNI N,et al.Active modes and switching instants identification for linear switched systems based on discrete particle swarm optimization[J].Applied Soft Computing,2014,14:482-488.
	Click to display the text
[23]	郭文忠,陈国龙. 离散粒子群优化算法及其应用[M].北京:清华大学出版社,2012:13-16. GUO W Z,CHEN G L.Discrete particle swarm optimization algorithm and its application[M].Beijing:Tsinghua University Press,2012:13-16(in Chinese).
[24]	KOROBEYNIKOV A. Computationk- and space-efficient implementation of SSA[J].Statistics and Its Interface,2010,3(3): 357-368.
	Click to display the text