目前国内许多****已经提出了大量的基于微动特征的群目标分辨方法,文献[4]利用自适应chirplet变换对群目标回波信号进行拟合,消除交叉项干扰后,根据拟合结果判定群目标中子目标的数量,但这种方法仅针对单散射中心模型,不能有效反映弹道目标的整体特征。文献[5]利用B分布和Viterbi算法,在低信噪比(SNR)条件下,提取出振动多目标的微多普勒特征,进而实现了多目标分辨,但此类算法过分依赖于时频分析工具的好坏以及不太容易确定的门限Δ。文献[6]分析了低分辨雷达观测条件下目标与诱饵微多普勒谱的差异,并利用多次观测的回波数据提取真假目标的识别特征,包括微多普勒域熵和波形标准差,以实现真假目标识别,但该方法并不涉及群目标信号分离问题。文献[7]在不考虑微多普勒特征相互独立的情况下,利用欠定盲分离算法实现了多目标微多普勒特征的分离,但该方法需要雷达具有多天线体制以获得多路回波,这与实际观测条件不相适应。
为解决这些问题,文中在短时间内对群目标进行多次等间隔观测,观测时间间隔等于某一子目标的微动周期,该微动周期可由自相关法获得。然后利用群目标信号中各子目标回波不同的周期性变化特性,对多次观测得到的群目标信号分别进行双向延迟处理,延迟时间为所提取子目标对应的微动周期的倍数,从而实现群目标信号的时频域增强。再利用延迟信号在时频域上的稀疏性,采用基于全变差(Total Variation,TV)范数的数据融合方法对群目标信号进行高保真分离。
1 回波模型构建及微多普勒分析假设雷达发射窄带单频信号,目标回波经基带变换、平动补偿[8]后不难得到
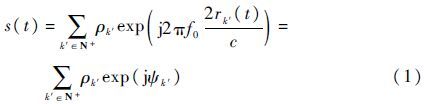
式中:ρk′为散射中心k′对应的散射系数;ψk′为相位项;rk′(t)为k′对应的微距离;f0为雷达载频;c为光速。在中段,群目标的微动形式主要包括弹头的进动、碎片及诱饵的翻滚、旋转等微运动。假设经平动补偿后,碎片及诱饵仅作旋转微运动。针对旋转目标模型[9],由于低分辨雷达的距离分辨率大于目标群中各子目标间的间距,即目标群在距离上不可分辨,此时目标群的回波集中于某一距离门内,则在该距离门内的回波s(t)可以近似表示为
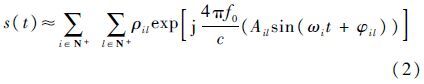
式中:ρil、Ail和φil分别为子目标i中第l个散射中心对应的散射系数、幅度和初相;ωi为子目标i的角频率。s(t)经相位求导后,得到多旋转目标回波的微多普勒频率为
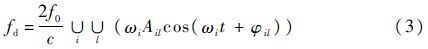
式中:∪(·)表示包含关系,角频率ωi为子目标固有属性,幅度Ail、初相φil由子目标的方位角、旋转轴指向以及子目标所含散射中心的相对位置决定。假若在相对较短的脉冲积累时间内,同一子目标的ωi近似保持不变。由于回波信号的周期性表征了中段目标的旋转周期性,且各子目标回波分量的周期性变化取决于各子目标本身的结构特征及质量分布等因素[10, 11],而碎片、诱饵及弹头的形状或质量分布通常存在较大差异[12],所以文中假设不同子目标对应的ωi值不同。文中采用自相关函数凸包算法[13],求取回波信号中不同子目标对应的微动周期Ti,微动周期的估计值具体表达式为
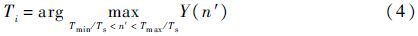
式中:Y(n′)=R(n′)-X(n′),0≤n′<Tmax/Ts,n′∈[0,N-1]为采样点,N为回波信号s(t)的总采样数;Ts为采样间隔;Tmax和Tmin为先验信息,分别表示Ti的上限和下限;R(n′)为雷达获取回波对应的离散自相关函数;X(n′)为离散自相关函数R(n′)的凸包,且满足[13]
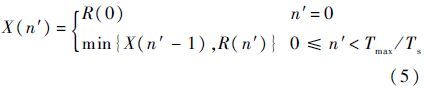
这种改进的自相关法对先验信息的要求不高,且适用范围广。当Tmin=0时,也可以取得较高的估计精度,具体性能分析见文献[13]。通过该方法,可以获得不同目标对应的高精度角频率ωi=2πTi,i∈[1,I]。其中,I为目标总量。
2 时频域增强处理在低分辨雷达观测下,由于目标群在距离和角度上可能均不可分,低分辨雷达观测到的回波信号中就会包含大量的子目标信息和噪声分量,这会使得单一子目标的信号淹没在噪声及其他子目标信号中。当采样率较低时,各子目标对应的回波分量在时频域上相互交织,单一子目标对应的微多普勒特征曲线的光滑性或连续性就会不足。此时若直接进行分离处理,就无法进一步分离出各子目标回波分量在时频域上的重叠区域,分离后的各子目标信号就会出现严重失真。因此,需要对群目标回波信号进行时频域增强处理。
由于不同子目标对应的微动周期不同,它的回波分量对应的微多普勒变化周期也会不同。因此,可将某一子目标对应的微动周期Ti作为观测时间间隔,在短时间内对群目标进行K次观测,每次观测时间为Ti。则多次观测信号可以表示为
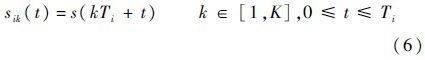
式中:K≥2。对于每次观测的回波数据而言,它都包含有子目标i在观测视角范围内一个微动周期的全部信息。为了增强单一子目标i时频特征的可分辨性和连续性,需对多次观测得到的回波数据进行双向延迟处理,延迟处理可以表示为
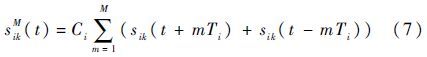
式中:M为时延总次数;Ci=exp(ωi)为扩展因子,用以提高群目标信号在时频域上的频率可分辨性,即稀疏性。同时,通过鉴相器得到延迟信号的相位信息,并乘以ωi。由于子目标i的时延信号分量在时频域上对应的能量分布及变化趋势一致,而其他子目标的时延信号分量不满足此条件,因此子目标i的回波分量在时频域上的能量强度得以增强。但是,这也会导致其他子目标的回波分量在时频域上的能量分布区域显著增加,使得各子目标间的交叉区域增多。因此,M值的选取不宜过大,只需满足可分辨条件即可。然后对时延信号进行时频变换,短时傅里叶变换(STFT)[14]是一种应用最为广泛的时频分析方法,它运算量低,能刻画信号的瞬时多普勒特性,适用于群目标信号的即时处理。经STFT变换后,延迟信号可以表示为
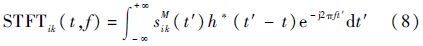
式中:h(t)为窗函数,此时信号的局部频谱特征被较好地刻画出。其中,STFTik(t,f)可以简写为Sik(t,f)。这样,就得到了时频域增强后的群目标信号对应的时频信息。
3 基于全变差的多次观测融合处理由第2节的分析可知,经时频域增强处理后,群目标信号中子目标i的时频域可分辨性明显增强。而对于其他子目标而言,由于微动周期与Ti不相等,经过双向延迟处理后,其他子目标对应的能量强度基本不变,只是能量分布区域得以扩大,此时子目标i的微多普勒变化趋势更加明显。然后利用群目标信号的梯度稀疏性和低分辨雷达的多次观测特性,运用基于全变差范数[15, 16]的数据融合理论,对群目标信号进行分离。
3.1 基于全变差范数的数据融合理论全变差像素级图像融合技术最先于2009年由Mrityunjay和Sarat[17]提出。由于信号的时频信息对应的能量强度分布类似于灰度图像的灰度值分布,因此可将此数据融合技术应用于群目标信号的时频分析中。群目标信号的全变差范数可写为
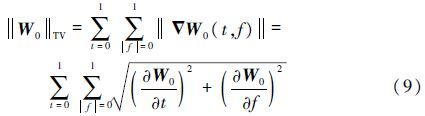
式中:W0为原始信号的时频信息;$\nabla $W0(t,f)为时频域中瞬时频点(t,f)处的梯度;‖·‖为2-范数,遍历整个时频域即可计算原始信号的全变差。设第k次观测的回波信号经时频域增强处理后对应的时频信息用Wk(t,f)表示,此时雷达受到的干扰噪声用Nk(t,f)表示。则满足如下等式关系:
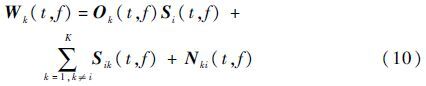
式中:Si(t,f)为子目标i对应的时频分量;Ok(t,f)为能量变化因子,表征为不同观测时间内回波信号能量强度微弱变化的度量。不难看出,融合的目的就是为了用多次观测的数据Wk(t,f)估计出不同的子目标i对应的时频分量Si(t,f),可利用全变差正则化的最小二乘法对Si(t,f)进行估计,具体过程见3.3节。为了方便表述,设多次观测的数据为W=(W1(t,f),W2(t,f),…,WK(t,f))T,多次观测的回波信号能量强度变化为O=(O1(t,f),O2(t,f),…,OK(t,f))T,多次观测的干扰分量为E=(E1(t,f),E2(t,f),…,EK(t,f))T。其中,Ek(t,f)满足如下条件:
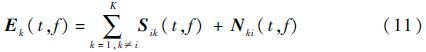
为了准确提取出W中子目标i的细节信息,发挥出各子目标回波分段平滑的特性,利用W在梯度域上的稀疏性对时频域进行最优化处理,该处理过程可以描述为
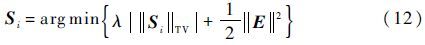
式中:|·|为绝对值符号;λ为滤波与细节保持之间的均衡参数。这样,群目标信号的分离问题就转化为基于全变差范数的数据融合问题。
3.2 估计能量变化因子由第2节的分析可知,不同观测时间内回波信号能量强度分布不同,这主要是由于其他子目标的时延信号分量对应的能量区域不一致造成的。因此,Ok(t,f)决定着数据融合的好坏。由式(10)可知,Ok(t,f)正比于Wk(t,f),即经时频域增强处理的多次观测信号Wk(t,f)之间的内在关系可以由能量变化因子Ok(t,f)来表示。反之,Ok(t,f)也可以由多次观测信号Wk(t,f)之间的相关性来进行说明。考虑到干扰分量E的能量强度较大,此时Si中会存在大量的干扰分量,严重影响数据融合的效果。为了有效降低干扰分量E的影响,这里将W分成多个局部子区域,通过W中不同观测时间各子区域之间的相关性,利用主分量分析方法有效地解决了E的影响。
以Wk中每一时频点gk(t0,f0)为中心,取a×a的窗口wgk。然后对该小窗口内的能量进行加权处理,加权表达式为
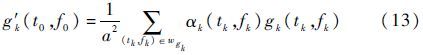
式中:(tk,fk)为窗wgk中的元素;gk(tk,fk)为(tk,fk)处的能量强度;αk(tk,fk)为窗wgk中各点的权系数。加权处理的目的在于在抑制干扰分量的同时不使时频曲线出现细节模糊,从而减小交叉干扰的影响。具体的加权处理规则如下。
Step 1 计算窗wgk内能量强度的均值Mk和方差ζk。主要是为了获得该窗内的统计特征,以计算出该窗的相关指标:
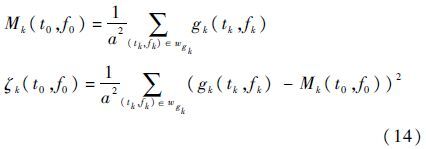
Step 2 瞬时频点之间相关度的确定。这里定义各瞬时频点之间的相关度为γk,且满足
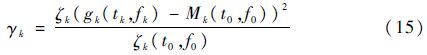
Step 3 权值的确定。

经加权处理后,时频曲线的干扰分量及细节模糊得到有效抑制。然后对多次观测的群目标信号进行相关处理,令
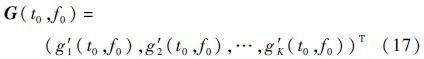
为了便于表述,G(t0,f0)简写为G。在式(17)的基础上,构造多次观测的相关矩阵为

根据主分量分析[18]的基本步骤,求出V的主特征向量η=(η1,η2,…,ηK)T,并使其满足ηηT=1。若ηk1≡ηk2,且k1≠k2;k1,k2∈[1,K],则令ηk≡1。由于所有主分量之间互不相关,因此利用主分量分析方法可以依次提取出不同观测时段的Wk(t,f)对应的能量变化因子Ok(t,f)。这样,就估计出能量变化因子O=η。
3.3 全变差正则项的最小二乘法由3.1节的分析可知,时频信息Wk(t,f)满足局部仿射变换,其映射关系为

由此可以推导出

若等式两边同时左乘(OTO)-1OT,则式(20)可改写为
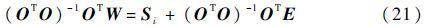
此时,子目标i对应的时频分量Si(t,f)满足最小二乘模型。因此,基于最小二乘估计的目标函数可以表示为
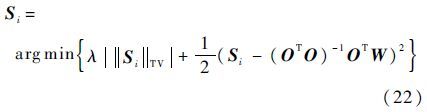
则由变分法可知,式(22)的Euler-Lagrange方程为
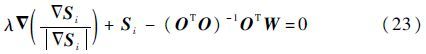
这样,就可以估计出滤波与细节保持之间的正则项参数λ,且λ>0。为了防止‖Si‖TV求偏导后为无穷大,这里引进一个微变参量ε,使得|$\nabla $Si|的值满足

最后,将式(22)的最优化问题应用于每一个滑动窗口,就可以实现对W的遍历融合。然后根据文献[17]的迭代算法求出最优解。具体迭代公式如下:
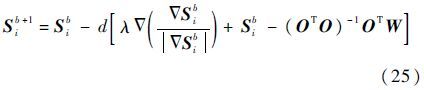
式中:b为窗口滑动的总次数;d为窗滑动的步长,且d≤a。然而,由于每一个滑动窗口相互重叠,这样会影响整个算法的计算量。因此,窗wgk不宜过大。利用广义STFT变换重构出对应的子目标i的信号分量,然后相位项乘以1/ωi。再根据式(7),通过乘以扩展因子的倒数exp(-ωi),逆推出原始子目标i的信号分量。当Wk(t,f)本身的数据量较大时,可以将W中的每一个元素均分为多个大小相等的固定窗口,然后对固定窗口直接进行数据融合处理即可。
4 仿真分析假设雷达载频为10GHz,采样率为2kHz。为了计算简便,假设空间中仅存在2个旋转目标,分别为目标1和目标2,目标1内含有2个旋转中心,坐标分别为(-0.6,0.5,0)m和(0.4,0,1.4)m,对应的旋转轴的视角为(65°,35°),旋转频率为f1=1Hz;目标2内也含有2个旋转中心,坐标分别为(0.5,0.8,0)m和(0,0.2,1.6)m,对应的旋转轴的视角为(75°,65°),旋转频率为f2=0.8Hz,且目标1和目标2所含散射中心的散射系数之比为4.5∶3.5∶3∶2。假设低分辨雷达的距离分辨率不足以分辨这2个速度一致目标,即这2个目标的雷达观测视线相同,这里均设为(45°,45°)。目标参数间变化关系见文献[9]。
在下述仿真中,文中用估计结果与理论值之间的相对误差(Relative Error,RE)来衡量参数的估计性能,并进行了100次Monte Carlo仿真。其中,信噪比在4~20dB的范围内变化,自相关算法的先验信息有:Tmax=3s,Tmin=0s。相对误差的具体表达式为
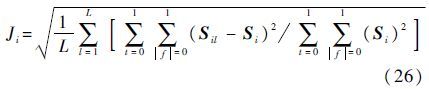
式中:L为总仿真次数;Sil=Sil(t,f)表示重构得到的子目标i的时频分量。不难看出,相对误差越小,则重构效果越好。
为了分析改进自相关法[13]的周期估计误差对重构效果的影响,这里引入了失配误差的概念,且失配误差δi=|Ti-Ti|/Ti。不同信噪比条件下微动周期的失配误差如表 1所示。
表 1 微动周期的失配误差Table 1 Mismatch errors of micro-motion period
| 信噪比/dB | 目标1失配误差δ1/10-3 | 目标2失配误差δ2/10-3 |
| 4 | 0.476 | 0.583 |
| 6 | 0.413 | 0.514 |
| 8 | 0.314 | 0.393 |
| 10 | 0.258 | 0.317 |
| 12 | 0.128 | 0.164 |
| 14 | 0.075 | 0.113 |
| 16 | 0.061 | 0.084 |
| 18 | 0.052 | 0.068 |
| 20 | 0.047 | 0.054 |
表选项
分析表 1结果可知,当信噪比为4dB时,微动周期的失配误差最大。此时,目标1、目标2作延时处理的周期偏差Δn′均约为1(四舍五入),且满足Δn′=δiTi/Ts。将该误差代入式(26),估计结果的相对误差与不考虑失配误差时的相对误差之间的偏差小于0.01。因此,当信噪比不小于4dB时,可暂不考虑失配误差对重构效果的影响。
当信噪比为10dB时,原始信号经延迟变换得到的时频图如图 1所示。可以看出,当原始信号按目标1的周期Ti延迟一个周期后,图 1(b)、图 1(c)中目标1对应的时频分量的分布区域与图 1(a)中目标1对应的时频分量的分布区域基本一致,而目标2对应的时频分量的分布区域存在较大差异,这验证了时频域增强的可行性。但此时图上包含多个散射中心的信息,交叉干扰比较严重。
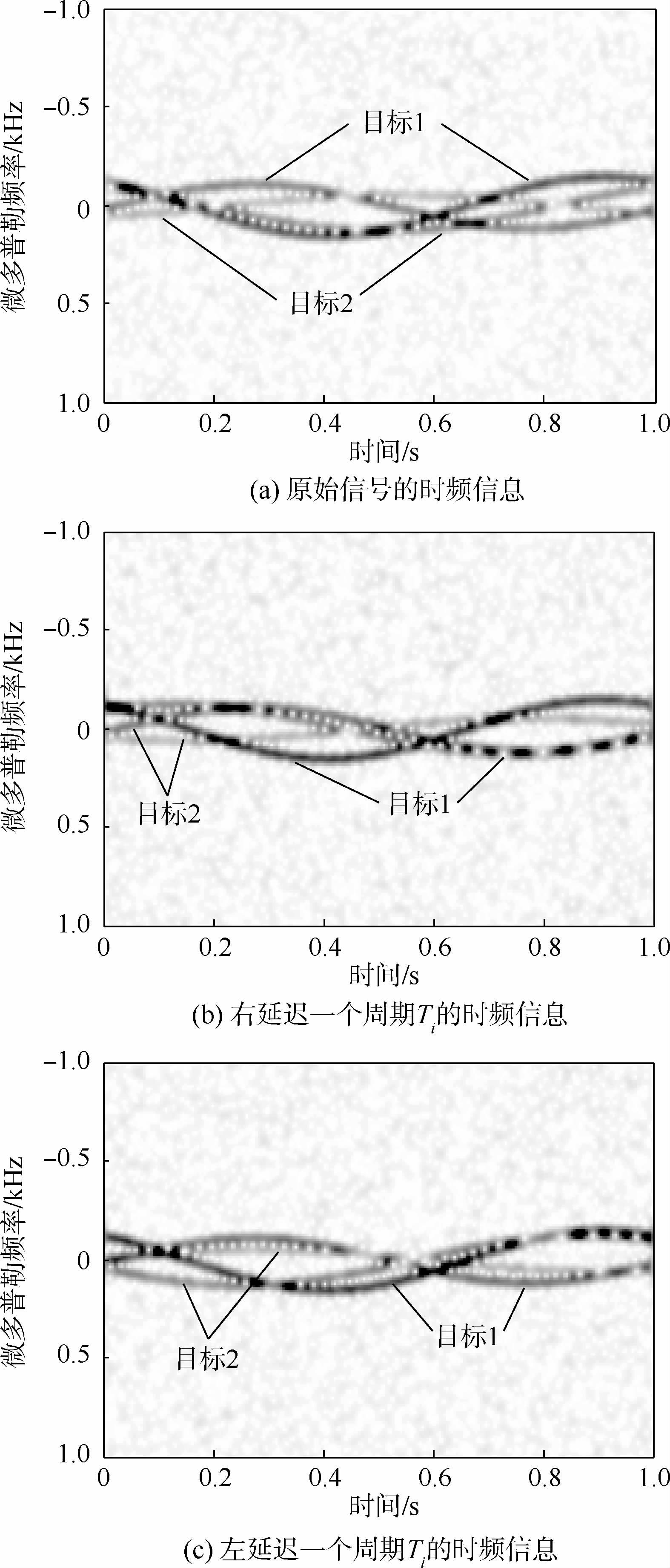 |
| 图 1 原始信号经延迟变换得到的时频信息Fig. 1 Time-frequency information of initial signal by delay processing |
| 图选项 |
经过时频域增强处理后,得到的多次观测的群目标信号对应的时频信息如图 2所示。其中,图 2(a)为0~1s观测时间段内的时频信息,图 2(b)为2~3s观测时间段内的时频信息,图 2(c)为4~5s观测时间段内的时频信息。可以看出,此时目标1的时频信息明显增强,且目标1的时频信息在图 2(a)~图 2(c)中分布区域相同,而目标2的时频信息在不同观测时段对应的分布区域各不相同。图 2中,4条浅色曲线表征目标2的微动特征。
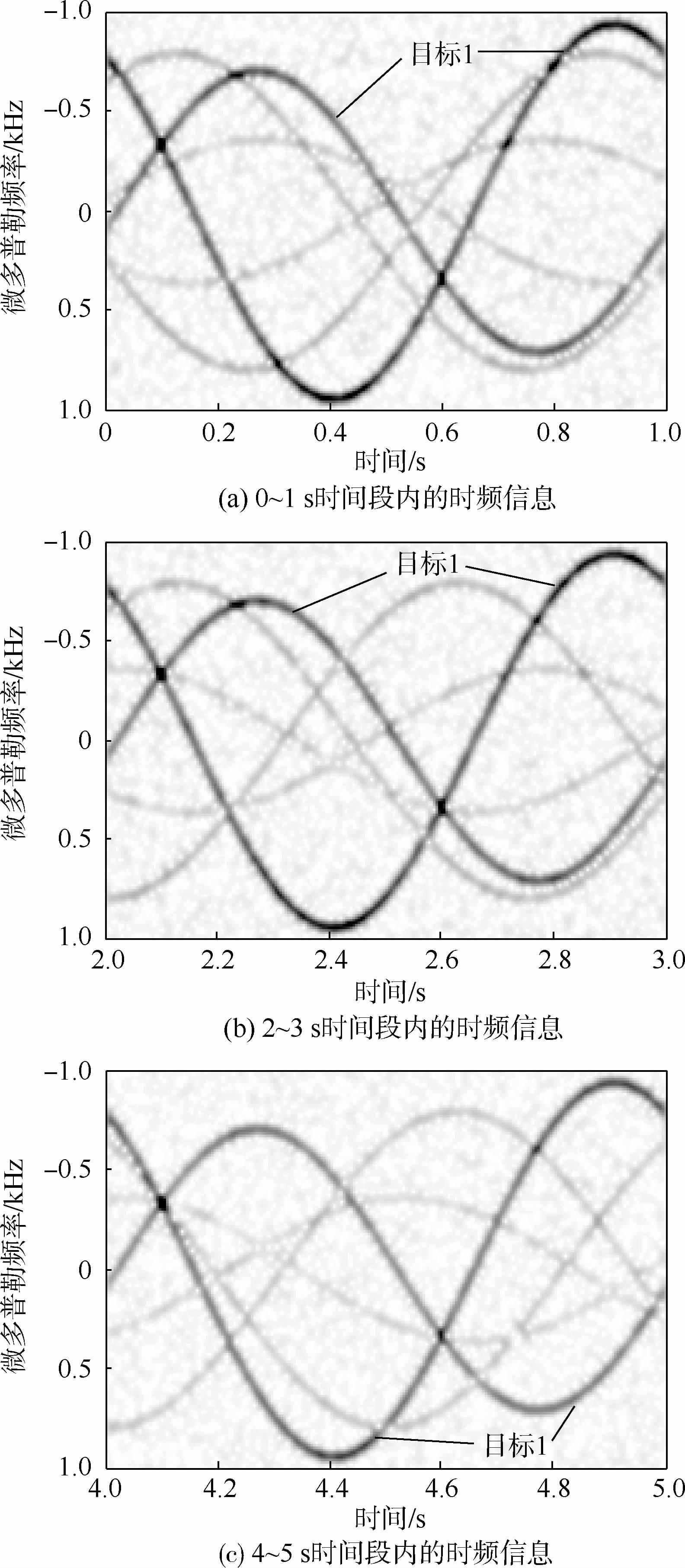 |
| 图 2 多次观测时间段内时频域增强信号对应的时频信息Fig. 2 Time-frequency information of multi-view signal by time-frequency enhancing |
| 图选项 |
最后通过基于全变差范数的多次观测融合处理方法,得到各子目标的重构信息。图 3(a)、图 3(b)分别表示本文方法得到的目标1、目标2对应的时频信息,图 3(c)、图 3(d)分别表示文献[17]中的TV融合方法得到的目标1、目标2对应的时频信息。可以看出,在仿真条件相同的条件下,本文方法的重构效果明显优于文献[17]的方法的重构效果。当采用文献[17]的方法进行融合重构时,强信号分量容易提取,而弱信号分量容易淹没在噪声和其他子目标分量中。当采用本文方法进行融合重构时,弱信号分量依然能被有效提取。
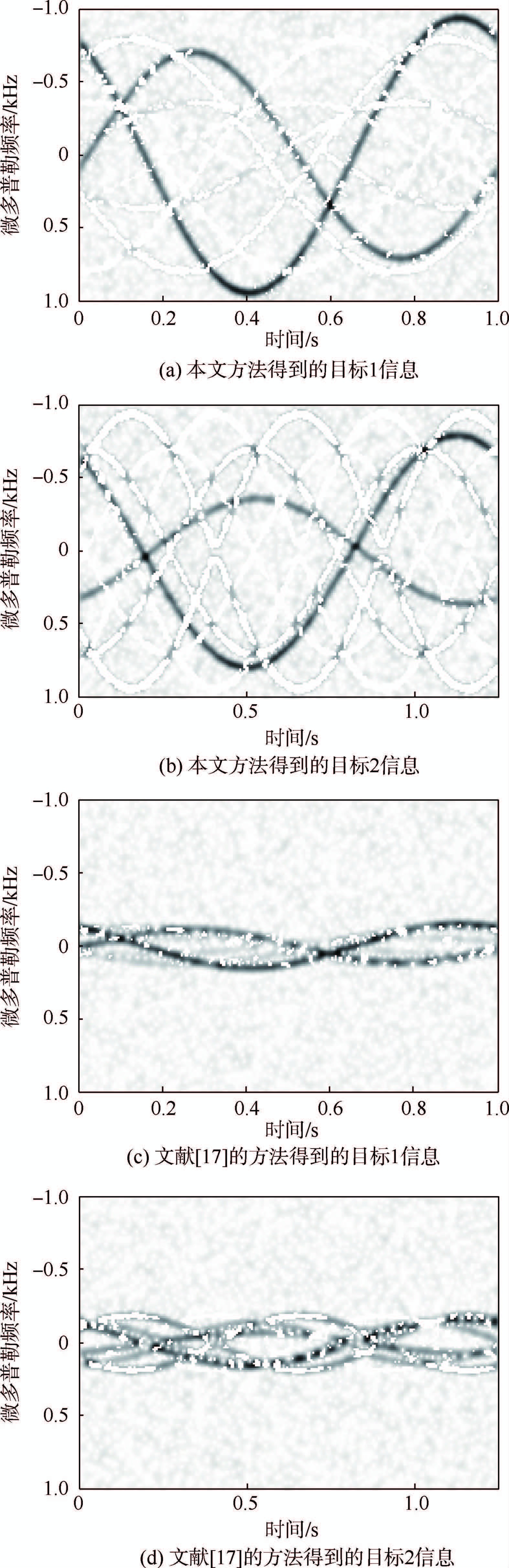 |
| 图 3 不同方法得到的各子目标对应的提取结果Fig. 3 Extracting results of each subsidiary target in different methods |
| 图选项 |
进一步分析不同融合方法的重构效果,本文在不同信噪比条件下对融合处理过程进行100次Monte Carlo仿真,不同方法对应的相对误差如图 4所示。
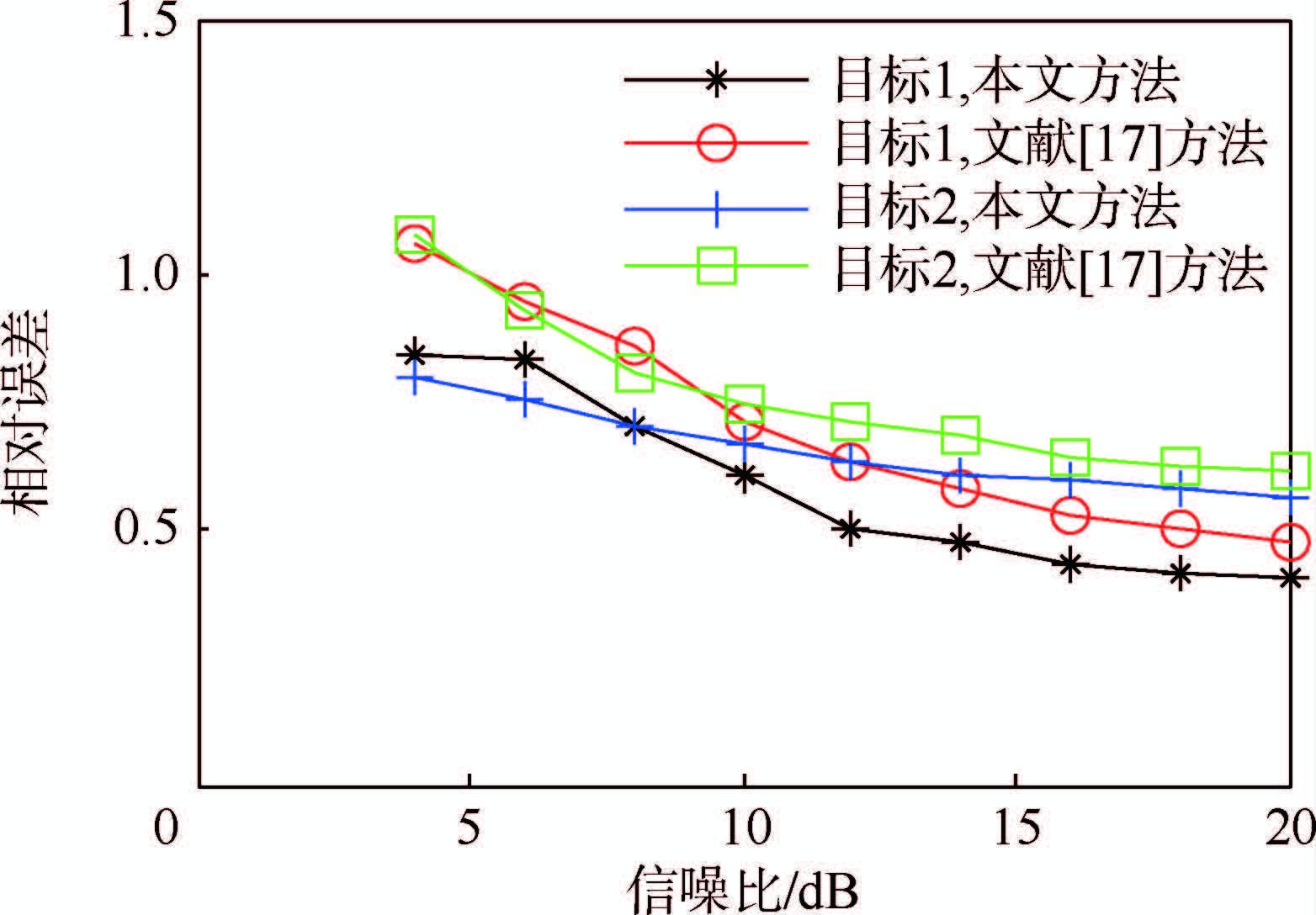 |
| 图 4 不同信噪比条件下本文方法与文献[17]的方法相对误差对比分析Fig. 4 Relative error comparative analysis between Ref.[17] and the proposed method in this paper under different SNR |
| 图选项 |
可以看出,本文方法明显优于文献[17]的方法,当信噪比小于或等于5dB时,文献[17]的方法容易出现错误;当信噪比大于5dB时,文献[17]的方法对应的相对误差明显大于本文方法对应的相对误差。而且,信噪比较低时,本文方法提取弱信号的能力明显优于文献[17]的方法。
5 结 论本文将群目标信号对应的时频信息的梯度稀疏性作为先验知识,提出了基于时频域增强和全变差的群目标信号分离方法。
1) 对于采样率较低的回波信号而言,各子目标对应的微多普勒特征曲线的光滑性或连续性相对不足。文中利用不同子目标对应的微动周期的差异性,对群目标回波信号进行时频域增强处理。
2) 在估计微动周期时,文中采用的自相关函数凸包算法会引入误差。经第4节的仿真分析,当信噪比不小于4dB 时,可以忽略失配误差对重构效果的影响。
3) 通过分析时频域增强处理得到的信号在时频谱上的能量强度分布,利用全变差范数的数据融合理论,实现了群目标信号的高保真分离,该算法适用于旋转类群目标或含旋转部件的目标。
4) 文中并没有分析平动分量对分离及重构效果的影响,是因为理想的平动补偿不会影响数据融合处理的分离效果,只需要在时频域增强处理过程中进行平动补偿即可。在下一步研究中,将利用暗室测量数据进行进一步验证。
参考文献
| [1] | DAVID R T.National missile defense:Policy issues and technological capabilities[M].Washington:SvecConway Priting Inc.,2000:1-21. |
| [2] | CHEN V C.Analysis of radar micro-Doppler signature with time-frequency transform[C]//Proceedings of the 10th IEEE Workshop on Statiscal and Array Processing.Piscataway,NJ:IEEE Press,2000:463-466. |
| Click to display the text | |
| [3] | HAN Y,SUN H Y,GUO H C.Analysis of influential factors on a space target's laser radar cross-section[J].Optics and Laser Technology,2014,56(1):151-157. |
| Click to display the text | |
| [4] | 黄小红,贺夏,辛玉林,等.基于时频特征的低分辨雷达微动多目标分辨方法[J].电子与信息学报,2010,32(10):2342-2347. HUANG X H,HE X,XIN Y L,et al.Resolving multiple targets with micro-motions based on time-frequency feature with low-resolution radar[J].Journal of Electronics & Information Technology,2010,32(10):2342-2347(in Chinese). |
| Cited By in Cnki (18) | |
| [5] | 关永胜,左群声,刘宏伟.高噪声环境下微动多目标分辨[J].电子与信息学报,2010,32(11):2630-2635. GUAN Y S,ZUO Q S,LIU H W.Micro-motion targets resolution in a high noise environment[J].Journal of Electronic & Information Technology,2010,32(11):2630-2635(in Chinese). |
| Cited By in Cnki (10) | Click to display the text | |
| [6] | 关永胜,左群声,刘宏伟.基于微多普勒特征的空间锥体目标识别[J].电波科学学报,2011,26(2):209-215. GUAN Y S,ZUO Q S,LIU H W.Micro-Doppler signature based cone-shaped target recognition[J].Chinese Journal of Radar Science,2011,26(2):209-215(in Chinese). |
| Cited By in Cnki (16) | |
| [7] | 郭琨毅,张永丽,盛新庆,等.基于欠定盲分离的多目标微多普勒特征提取[J].电波科学学报,2012,27(4):691-695. GUO K Y,ZHANG Y L,SHENG X Q,et al.An approach for extracting independent micro-Doppler characteristics of multiple targets based on underdetermined blind source separation[J].Chinese Journal of Radar Science,2012,27(4):691-695(in Chinese). |
| Cited By in Cnki (3) | |
| [8] | 杨友春,童宁宁,冯存前,等.弹道中段目标回波平动补偿与微多普勒提取[J].中国科学:信息科学,2013,43(9):1172-1182. YANG Y C,TONG N N,FENG C Q,et al.Translation compensation and micro-Doppler extraction of the echo from ballistic targets in midcourse[J].Science China:Informationis Science,2013,43(9):1172-1182(in Chinese). |
| Cited By in Cnki (2) | Click to display the text | |
| [9] | YOU P,LIU Z,WEI X Z,et al.Aliasing-free high resolution imaging of fast rotating targets with narrowband radar[J].Journal of Central South University,2014,21(5):1842-1851. |
| Click to display the text | |
| [10] | 王胜.动态目标雷达回波实时模拟技术及应用[D].长沙:国防科学技术大学,2011:163-167. WANG S.Moving target radar echo real-time simualtion:Technologies and application[D].Changsha:National University of Defense Technology,2011:163-167(in Chinese). |
| Cited By in Cnki (4) | |
| [11] | CHEN V C,LI F,HO S S,et al.Micro-Doppler effect in radar:Phenomenon,model and simulation study[J].IEEE Transactions on Aerospace and Electronic Systems,2006,42(1):2-21. |
| Click to display the text | |
| [12] | JAENISCH H.Discrimination via phased derived range measurements:MDA-02-003[R].Huntsville,AL:Missile Defense Agency Small Business Innovation Research Program,2002:1-3. |
| [13] | 肖立,周剑雄,何峻,等.弹道中段目标进动周期估计的改进自相关法[J].航空学报,2010,31(4):812-818. XIAO L,ZHOU J X,HE J,et al.Improved autocorrelation method for precession period estimation of ballistic target in midcourse[J].Acta Aeronautica et Astronautica Sinica,2010,31(4):812-818(in Chinese). |
| Cited By in Cnki (8) | |
| [14] | YIN Q B,SHEN L R,LU M Y,et al.Selection of optimal window length using STFT for quantitative SNR analysis of LFM signal[J].Journal of Systems Engineering and Electronics,2013,24(1):26-35. |
| Click to display the text | |
| [15] | ZHANG J,WEI Z H,LIANG X.A fast adaptive reweighted residual-feedback iterative algorithm for fractional-order total variation regularized multiplicative noise removal of partly-textured images[J].Signal Processing,2014,98(5):381-395. |
| Click to display the text | |
| [16] | 娄静涛,李永乐,谭树人,等.基于全变分的全向图像稀疏重构算法[J].电子学报,2014,44(2):243-249. LOU J T,LI Y L,TAN S R,et al.Sparse reconstruction for omnidirectional image based on total variation[J].Acta Electronica Sinica,2014,44(2):243-249(in Chinese). |
| Cited By in Cnki (3) | Click to display the text | |
| [17] | MRITYUNJAY K,SARAT D.A total variation-based algorithm for pixel-level image fusion[J].IEEE Transactions on Imaging Processing,2009,18(9):2137-2143. |
| Click to display the text | |
| [18] | MOUSAVI H,SHAHBAZIAN M,JAZAYERI-RAD H,et al.Reconstruction based approach to sensor fault diagnosis using auto-associative neural networks[J].Journal of Central South University,2014,21(6):2273-2281. |
| Click to display the text |
