理想情况下,在任一仿真接收历元时刻模拟器射频端口输出导航信号的码相位所对应伪距值应与模拟器所提供的该历元时刻的伪距记录值保持严格一致,两者之间的差值即为模拟器通道群时延.模拟器通道群时延是模拟器最重要的指标之一,目前关于模拟器通道群时延的标定方法尚未形成统一标准,甚至还存在较大争议.文献[1, 2]给出了一种利用高速示波器观测导航信号时域相位翻转点的方法,将翻转点与模拟器输出秒脉冲(One Pulse Per Second,1 PPS)信号上升沿间的时延作为模拟器通道群时延标定值.为了消除人眼判断相位翻转点的主观误差,文献[3]利用示波器的波形分析函数对导航信号进行平方运算和低通滤波得到翻转点附近的包络,取包络幅值的最小值为相位翻转点.文献[4]对翻转点附近波形进行采样并取平方后,用40阶多项式拟合出翻转点附近的包络,取包络最小值得到相位翻转点.文献[5, 6, 7]利用导航信号的相关域特性,将采集到的信号与本地伪码信号进行相关处理,找到相关峰相对于1 PPS上升沿的时延,进而计算出模拟器的通道群时延.以下将文献[1, 2, 3, 4]的方法称为翻转点法,将文献[5, 6, 7]的方法称为相关峰法.
文献[8]指出,翻转点法受导航信号体制的限制,且相位翻转点只是信号中的某个局部特征点,对于宽带导航信号,在通道传输特性非理想的情况下,它相对参考基准点的时延并不足以反映整个通道的群时延特性,因此不能简单地将其作为通道群时延的测量值.文献[9]分析了信号的相关峰时延与通道群时延间的关系,认为非理想的模拟器通道特性将导致相关曲线的非对称性,使得接收机延迟锁定环(Delay Locked Loop,DLL)的即时(punctual)支路锁定点与相关曲线的峰值点之间存在偏差.由于接收机是通过DLL环对导航信号做闭环跟踪,对模拟器通道群时延的标定最终是为了消除接收机测得伪距值中包含的偏差,因此通过相关峰最大值位置测得的模拟器通道群时延值仍有可能存在一定偏差.
本文在讨论传统的翻转点法和相关峰法测量原理的基础上,提出一种基于闭环伪距测量的模拟器通道群时延标定方法,着重探讨正常信号仿真场景下闭环伪距测量法标定模拟器通道群时延的性能;设计实现了模拟器群时延标定系统,并使用3种方法对两种商用模拟器的通道群时延分别进行了测量,实验结果表明闭环伪距测量法有效可行.
1 模拟器通道群时延传统测量方法模拟器通常应提供上升沿与所仿真基准系统时的整秒时刻保持严格一致的1 PPS信号供测试同步之用.这就意味着可以在1 PPS信号上升沿测得模拟器输出射频导航信号的码相位,将其对应伪距值与模拟器所记录该仿真历元时刻的伪距值求差,从而得到模拟器通道群时延标定值.
1.1 时域翻转点法导航信号的码相位对应着信号的发射时刻[10].当模拟器输出零伪距特殊仿真场景的射频导航信号且关闭各项误差源时,若模拟器通道群时延为零,则任一历元时刻信号的传播时间为零,即模拟器的1 PPS上升沿和导航信号中伪码序列的起始位置应严格对齐.实际信号中,由于模拟器通道群时延的存在,伪码序列起始位置和1 PPS上升沿之间存在时差,传统的时域翻转点法通过测量该时差作为模拟器通道群时延的标定值.以双相相移键控(Binary Phase Shift Keying,BPSK)调制的导航信号为例,其信号表达式为
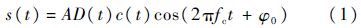
式中:A为信号幅度;D(t)为导航电文;c(t)为伪随机码;fc为载波频率;$\varphi $0为载波初相.为简化分析,假设A=1,D(t)≡1.可见,当两个相邻的伪码码片符号相反时,载波相位会在其交界处跳变180°,这个跳变点称为信号的相位翻转点,对应着伪码序列的码片起始,即码片内相位为零处.由于信号通道中滤波器有限带宽的限制,翻转点附近的时域波形如图 1所示,图中的包络零点即为相位翻转点[11],而包络幅值的过冲现象则是吉布斯效应的体现.
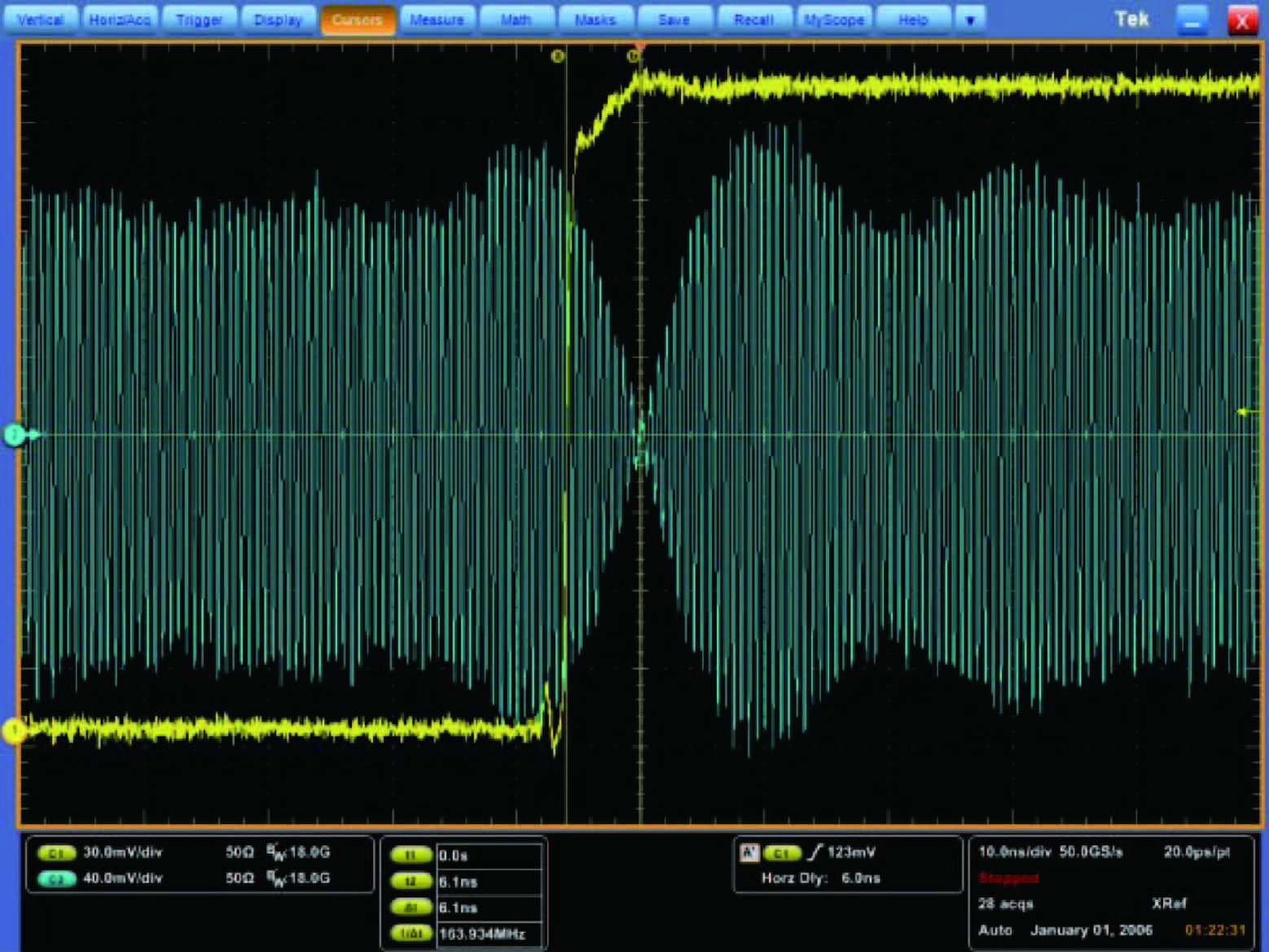 |
| 图 1 相位翻转点的时域波形Fig. 1 Time domain waveform at phase transition point |
| 图选项 |
文献[1, 2, 3, 4]将零伪距场景下的模拟器射频导航信号输出和1PPS输出分别接入高速示波器的两个通道,使用不同方法测量翻转点的位置和1PPS上升沿之间的时差,得到模拟器通道群时延的标定值.
正如文献[8]所指出的,翻转点法只利用了信号中局部特征点的信息,在通道特性非理想的情况下,其时延不足以反映整个通道的群时延特性,因而只适用于窄带信号;且翻转点位置的测量精度对示波器的采样率提出了很高要求.另外,当所模拟的通道发射带宽较宽时,信号时域波形的相位翻转点将不明显,翻转点位置的估计精度会随之下降甚至无法测量.
1.2 相关峰法与翻转点法通过时域波形判断伪码序列的起始位置不同,相关峰法利用导航信号的相关域特性对信号进行相关接收,从而找到相关峰相对于1 PPS上升沿的时延.对式(1)中的信号做相关接收,则经载波剥离和积分清除后的相关幅值P如式(2)所示[12]:
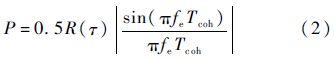
式中:R(τ)为伪随机码的自相关函数,τ为本地伪码与输入待测信号伪码的相位差;fe为本地载波与信号载波的频率差异;Tcoh为相干积分时间.从式(2)可知,当本地伪码与信号伪码的相位对齐时,相关幅值P达到最大.
目前公开文献中报道的相关峰法仍使用高速示波器采集数据,然而并未见给出关于相关峰位置估计方法的具体描述.实际上在模拟器通道传输特性非理想的情况下,由于信号失真引起相关曲线左右不对称,使得接收机DLL环所跟踪的码相位点(即DLL锁定点)与相关峰值点之间会有一定偏差,这一锁定点偏差的大小又与相关间距有关.因而一些文献中所述通过寻找相关峰最大值点的方法进行通道群时延标定是有失偏颇的,通过相关峰值点得到的通道群时延标定值在用于接收机测量校准的时候仍将引起未知的偏差.
为了避免这一问题,可以采用与DLL环类似的利用早迟相关值进行鉴相的方法测得相关器本地伪码相位与输入信号伪码相位的差异,进而得到信号伪码序列的起始位置相对于1 PPS上升沿的时延,作为模拟器通道群时延测量值.为了保证1 PPS上升沿的判定精度,要求采用很高的采样率.由于示波器的存储深度限制和初始信号码相位捕获误差的存在,传统信号跟踪环路无法在所采集数据时长内进入锁定状态,可采用开环估计的方法通过早迟相关值得到输入信号的码相位估计值.为了区别于前述估计相关峰值点位置的测量方法,本文将这种改进的方法称为相关域开环估计法.
2 基于闭环伪距测量的群时延标定除了上述问题外,传统测量方法多使用零伪距或固定伪距仿真场景下的特殊信号,而在导航接收机的测试校准中,模拟器输出正常星座动态和用户动态下的导航信号,这两种场景下模拟器的通道群时延性能也会存在差异.文献[13]指出,不同径向动态下模拟器所产生信号的精度可能是不一样的,模拟器产品手册中给出的射频信号精度指标应标明其所适用的信号动态范围.
为了解决上述问题,本文提出一种基于闭环伪距测量的模拟器通道群时延标定方法(简称闭环伪距测量法),利用高速直接射频采样系统对正常星座动态仿真场景下的导航信号和1 PPS信号同时进行记录,以1 PPS信号作为同步信号,通过高精度软件接收机的闭环跟踪和码伪距测量最终解算出模拟器的通道群时延.该方法适用于伪距随时间变化的正常动态下的各种调制信号仿真场景.
导航接收机在某一观测历元时刻解算的信号伪距为
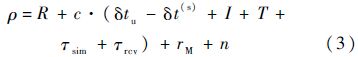
式中:R为接收机与卫星之间的真实距离,可从模拟器的数学仿真记录获取;c为光速;δtu为接收机钟差;δt(s)为卫星钟差;I和T分别为电离层和对流层引入的信号延时;τsim为模拟器通道群时延;τrcv为接收机通道群时延;rM为多径误差;n为噪声.标定模拟器的通道群时延时,关闭卫星钟差、电离层对流层效应和多径误差,此时伪距方程(3)变为式(4):
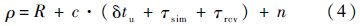
使用高保真度高速双通道采集存储系统对模拟器输出的射频导航信号和1 PPS信号同时进行直接采样,导航信号不经过下变频、滤波等处理,采集系统通道间时延偏差很小且可以通过标校进行补偿,因此τrcv=0.以模拟器输出1 PPS信号上升沿作为软件接收机观测历元时刻的同步信号,可消除接收机钟差的影响,因此δtu=0.此时伪距方程变为
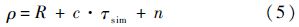
可见,软件接收机解算的伪距ρ和接收机与卫星之间的真实距离R存在偏差,该偏差为模拟器通道群时延所引入,τsim可由式(6)估算:

式中:〈·〉表示取均值.
图 2为闭环伪距测量法的实现框图.通过外接高稳定度频标(频率稳定度:2×10-13/s)的高性能频率综合器(附加相位噪声:-89dBc@1Hz,-114dBc@1kHz)产生采样时钟,可以消除采样时钟引入的额外误差;为了消除各设备内时基准确度和稳定度差异带来的测量误差,模拟器和矢量信号源应保证同源.衰减器可以使1 PPS信号的幅值匹配采集系统的输入电平,其引入的时延可以用矢量网络分析仪进行标定.
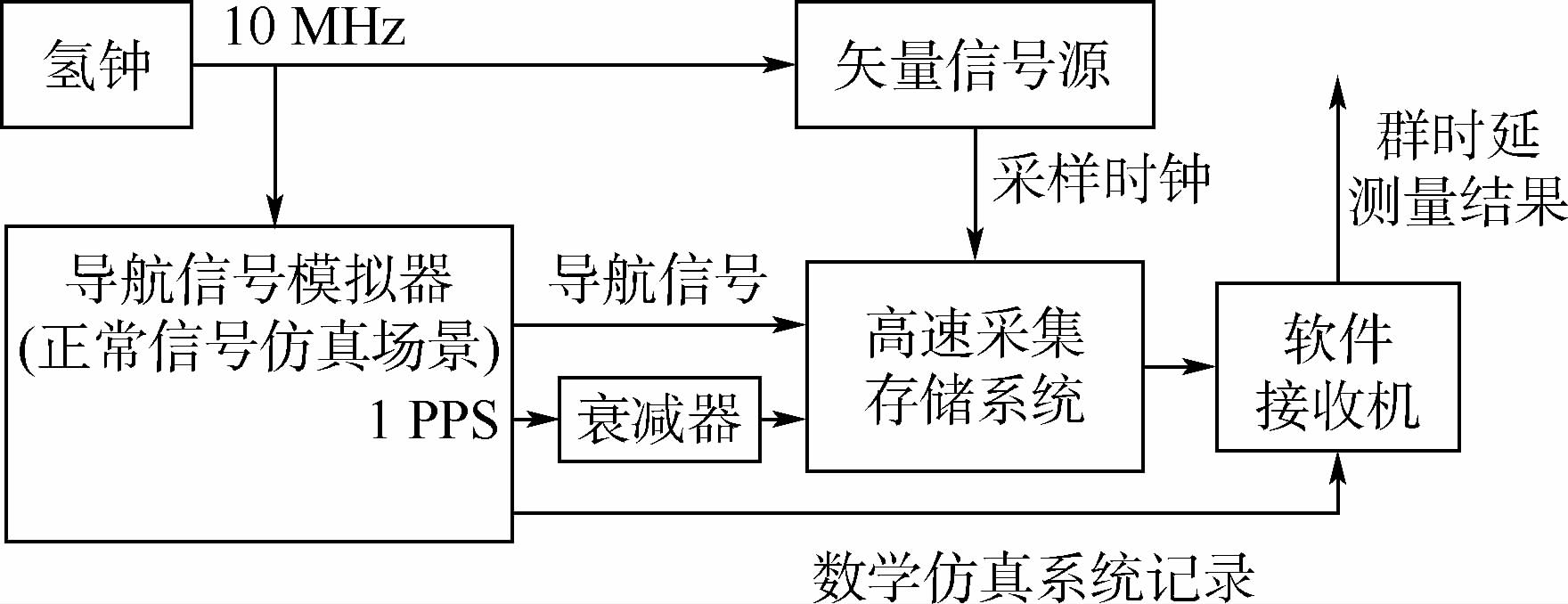 |
| 图 2 闭环伪距测量法框图Fig. 2 Block diagram of closed-loop pseudorange measurement method |
| 图选项 |
为了使软件接收机解算出信号的伪距和其对应的仿真历元时刻,采集的信号需要完整包含导航电文的一个子帧,以GPS为例,一个子帧长度[14]为6s,所以采集的信号长度应不低于12s.
软件接收机对采集的导航信号进行捕获跟踪,利用载波环辅助码环可基本消除码环的动态应力误差.待环路锁定后,以1 PPS上升沿作为码环伪距观测历元时刻的同步信号,上升沿对应的模拟器仿真历元时刻可从导航电文中的周内秒(Time of Week,TOW)获取.由式(6)知,将接收机解算的伪距和模拟器数学仿真系统记录的相应TOW时刻的伪距做数据比对和统计分析,即可测得模拟器的通道群时延值.
为了保证上升沿的判定精度,应使上升沿上至少有2个采样点(例如若1 PPS信号的上升时间在2ns内,则采样率应不低于1GHz),在此基础上本文通过三次样条内插提高上升沿的判定精度[15].图 3为1 PPS上升沿的采样和内插结果,以1 PPS高电平的50%作为触发电平,在三次样条内插曲线上判定上升沿的位置,可以大大提高上升沿的判定精度.
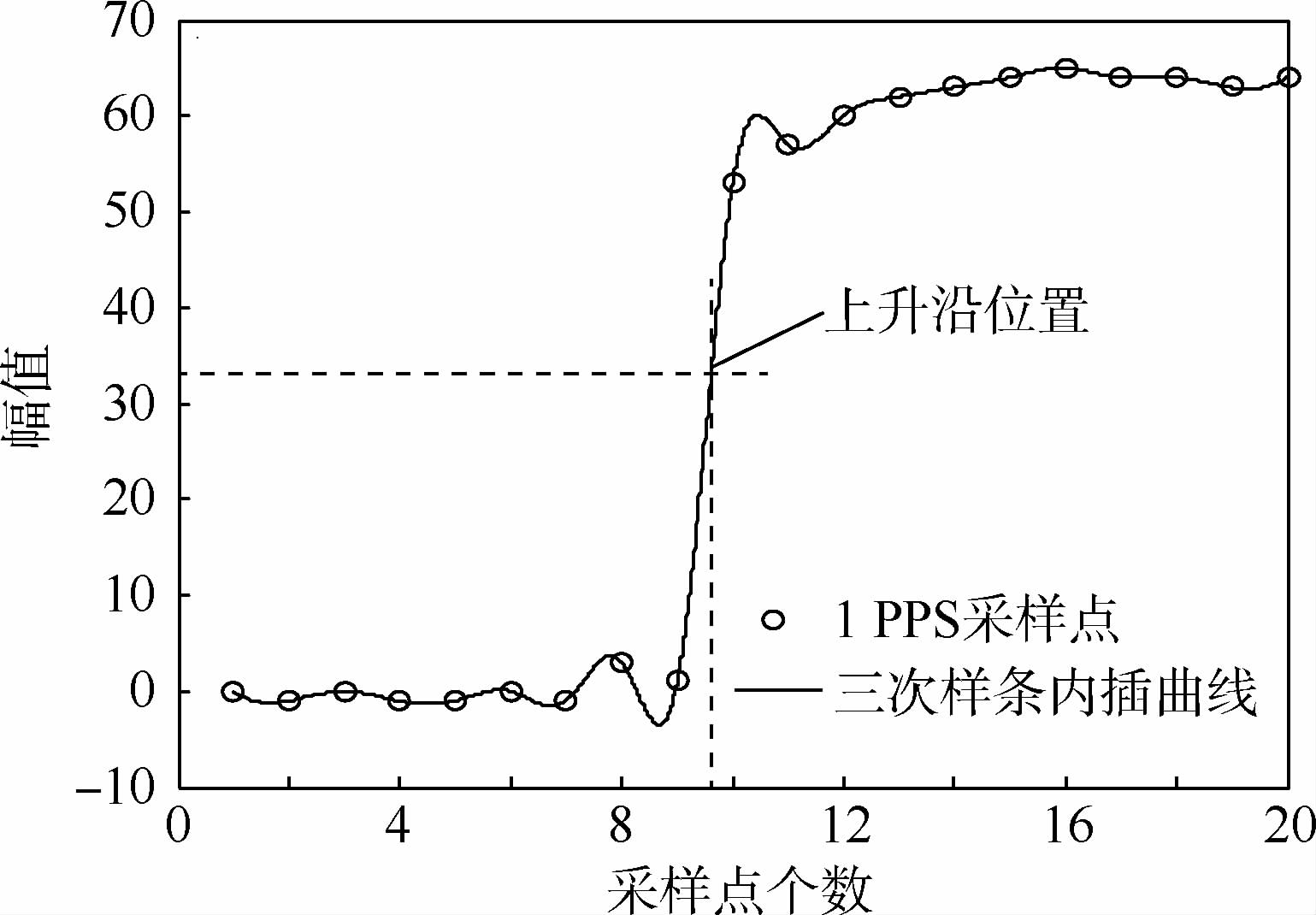 |
| 图 3 通过三次样条内插判定1 PPS上升沿位置Fig. 3 1 PPS rising edge determination using cubic spline interpolation |
| 图选项 |
3 实验分析使用传统方法和闭环伪距测量法对英国Spirent公司的GSS8000模拟器和长沙市卫导电子科技有限公司的NSS8000模拟器的通道群时延分别进行了标定.实验中设置模拟器输出GPS L1 C/A码信号,GSS8000输出导航信号的载噪比经实测为93.9dB·Hz,NSS8000输出导航信号的载噪比经实测为94.3dB·Hz.
3.1 时域翻转点法使用美国Tektronix公司的DSA72004示波器观测相位翻转点与1 PPS上升沿的时延作为模拟器的通道群时延.图 4(a)为GSS8000的单次测量结果,图 4(b)为NSS8000的单次测量结果,对10次观测结果取平均,测得GSS8000的群时延为3.08ns,NSS8000的群时延为6.10ns.
 |
| 图 4 两种模拟器群时延的时域翻转点法测量结果Fig. 4 Group delay measurement results of two simulators using time domain transition point method |
| 图选项 |
3.2 相关域开环估计法使用高速采集存储系统采集零伪距特殊仿真场景的信号,并使用开环相关域估计法解算模拟器通道群时延.利用零伪距特殊仿真场景中信号不存在多普勒频移的特点,设定本地载波频率为标称频率,本地伪码相位为捕获到的伪码相位,并使载波环和码环保持开环;为了消除本地载波初相误差带来的影响,对于码相位误差使用非相干鉴相方法[16, 17],即可测得本地伪码相位与信号伪码相位的差异,进而测得信号伪码序列的起始位置,得到模拟器通道群时延测量值.数据采集时的采样率为1GHz,采样分辨率为8bit,采集的信号长度为2s.模拟器通道群时延测量结果如图 5所示.
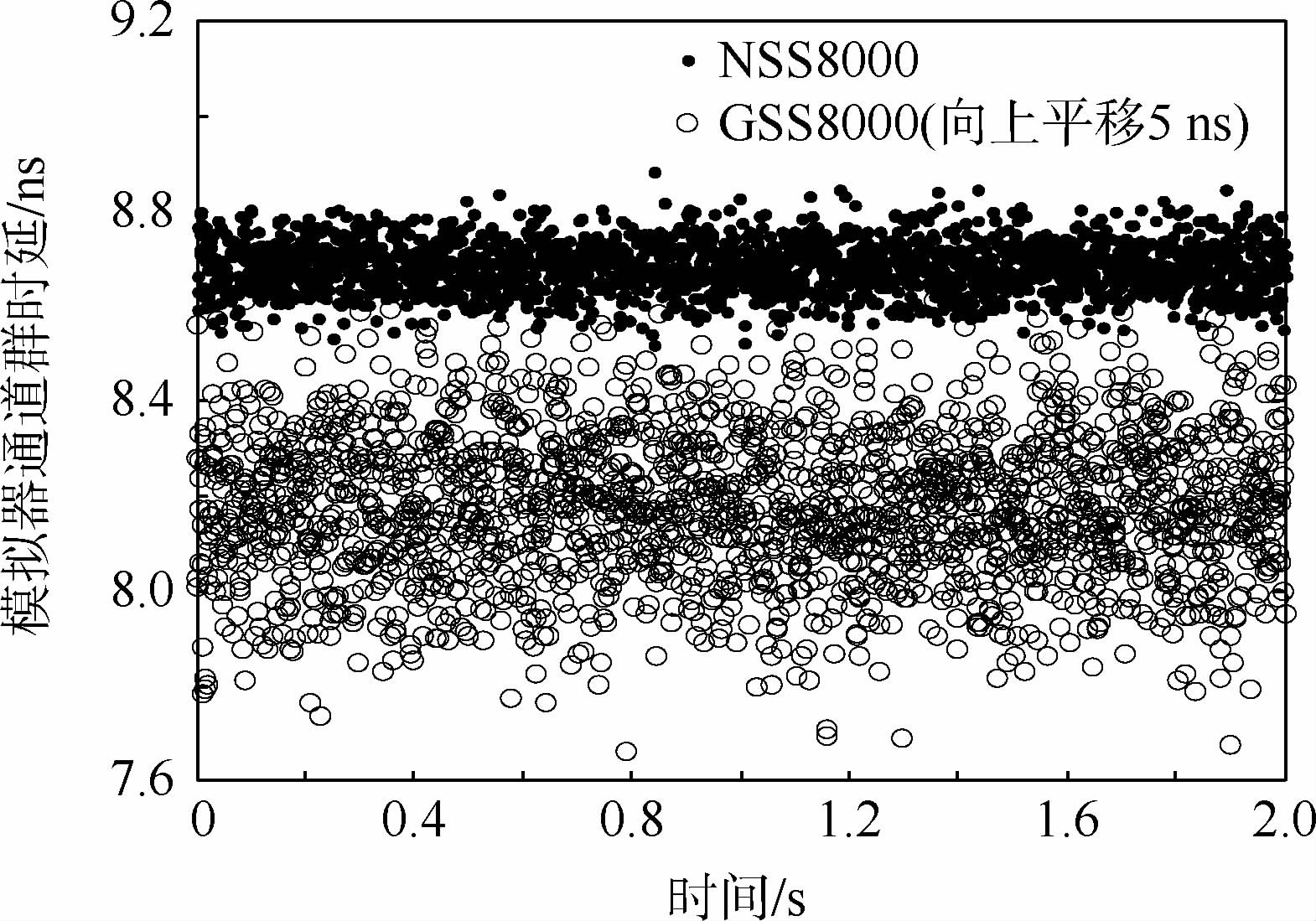 |
| 图 5 相关域开环估计法的群时延测量结果Fig. 5 Group delay measurement results using correlation domain open-loop estimation method |
| 图选项 |
图 5中每ms输出一个测量值,其中GSS8000的群时延和NSS8000的群时延相差约5.5ns,为了清晰比对二者的抖动情况,将GSS8000的群时延测量结果向上平移了5ns.模拟器通道群时延的统计结果如表 1所示.
表 1 相关域开环估计法的群时延统计结果Table 1 Statistical results of group delay measurement using correlation domain open-loop estimation method
| 模拟器 | 群时延/ns | |
| 均值 | 标准差 | |
| GSS8000 | 3.182 | 0.159 |
| NSS8000 | 8.684 | 0.054 |
表选项
3.3 闭环伪距测量法使用高速采集存储系统采集正常信号仿真场景下的信号,并使用闭环伪距测量法对GSS8000和NSS8000的群时延进行标定.数据采集时的采样率为1GHz,采样分辨率为8bit,采集的信号长度为13s,测量结果如图 6所示.
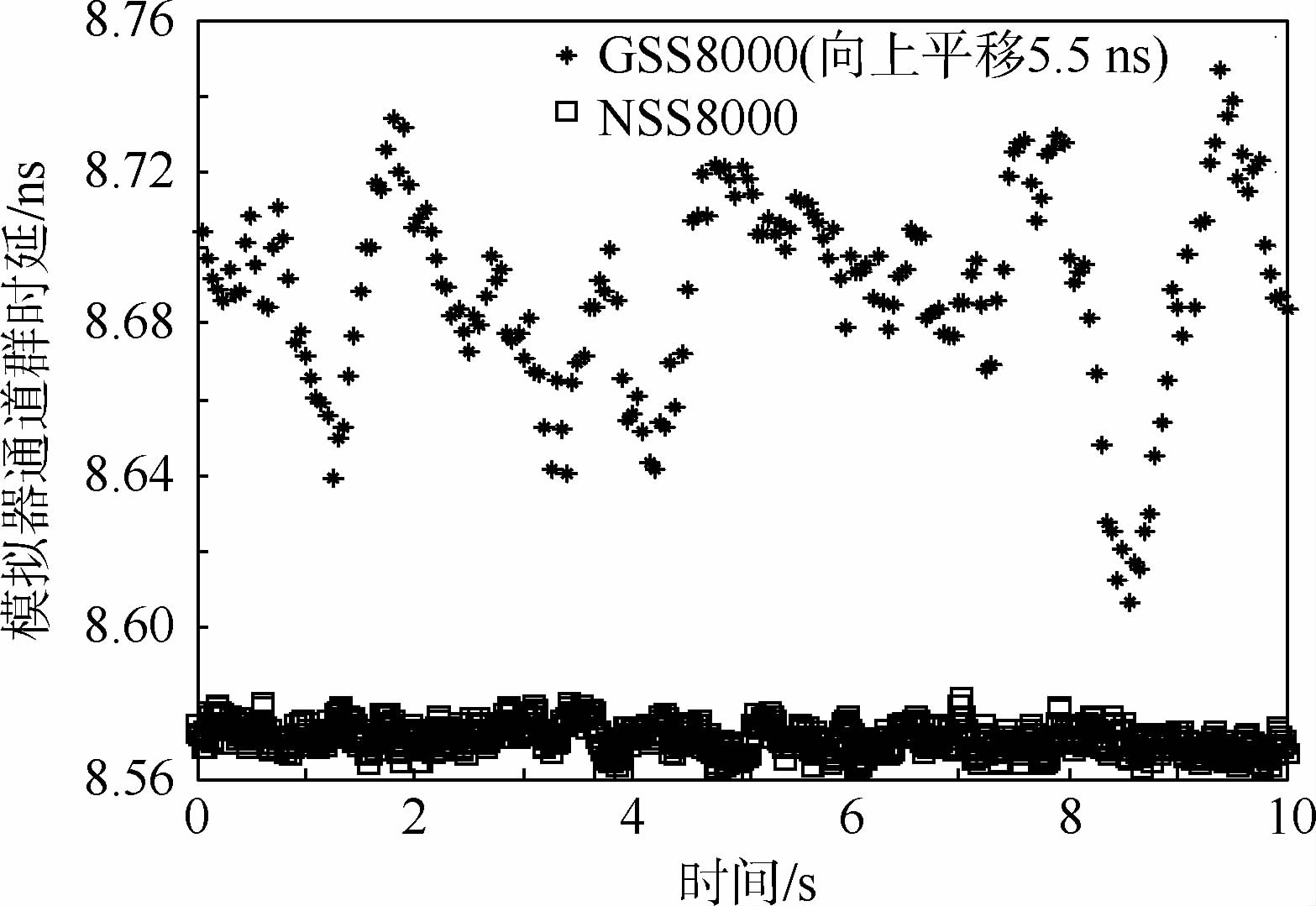 |
| 图 6 闭环伪距测量法的群时延结果Fig. 6 Group delay measurement results using closed-loop pseudorange measurement method |
| 图选项 |
实验中软件接收机的码环带宽为2.5Hz,早迟相关器间距为一码片,相干积分时间为1ms,接收机每ms输出一个伪距观测量.由于受被测模拟器数学仿真系统的伪距记录更新率限制,图 6中GSS8000的群时延测量结果每50ms输出一个,并向上平移了5.5ns,NSS8000的群时延测量结果每10ms输出一个.模拟器通道群时延的统计结果如表 2所示.
表 2 闭环伪距测量法的群时延统计结果Table 2 Statistical results of group delay measurement using closed-loop pseudorange measurement method
| 模拟器 | 群时延/ns | |
| 均值 | 标准差 | |
| GSS8000 | 3.188 | 0.027 |
| NSS8000 | 8.571 | 0.004 |
表选项
从以上测量结果可知,对于GSS8000,闭环伪距测量法和时域翻转点法的一致性在0.2ns内,而对于NSS8000,闭环伪距测量法和时域翻转点法的结果存在约2.5ns的偏差;两种模拟器群时延使用闭环伪距测量法和相关域开环估计法的测量结果均值差均在0.2ns内.从3种测量方法的原理可知,在模拟器通道特性非理想的情况下,闭环伪距测量法可以真实准确测得模拟器的通道群时延,而时域翻转点测量法的测量结果并不能真实反映模拟器的群时延值.
实际上,对模拟器通道群时延的标定最终是为了消除接收机通道群时延引入的伪距偏差,而接收机通过DLL环对正常仿真场景下的信号做闭环跟踪,因而利用闭环伪距测量法对模拟器的群时延进行标定,保证了信号仿真场景及测量原理和接收机群时延测量时的一致性,能够更好地达到测量模拟器通道群时延的目的.
值得注意的是,由于不同环境温度及相关间距下的模拟器通道群时延值可能不同,实用中应测得不同温度及相关间距下的模拟器通道群时延值提供用户使用.
3.4 性能分析由闭环伪距测量法的原理知,该方法不受导航信号体制的限制,对于增加二进制偏移载波(Binary Offset Carrier,BOC)调制的宽带信号仍然适用;该方法也不受零伪距或固定伪距仿真场景的限制,适用于伪距随时间变化的正常信号仿真场景.
在加性高斯白噪声(AWGN)背景下码环闭环跟踪可得到准最佳估计,其中相干DLL在相关间距趋于零时码相位估计误差标准差可达Cramer-Rao限,且闭环伪距测量法易于通过载波环辅助码环来消除视距动态引起的偏差;诚然开环估计也可采用最大似然等一系列最佳估计方法,但要达到闭环跟踪的精度其实现相对复杂.由表 1和表 2的群时延统计结果可知,本次实验中闭环伪距测量法测得结果的标准差小于相关域开环估计法,这是因为本文在开环估计法中直接利用了码环鉴相器输出作为估计结果,而在闭环伪距测量法中则对鉴相结果进一步利用环路滤波器抑制了噪声的影响且通过载波环辅助码环消除了动态应力误差,最后通过连续的闭环调整使得环路始终工作在鉴相曲线的过零点附近.
闭环伪距测量法的测量误差主要由1 PPS上升沿位置的判定、热噪声和线缆等引入.闭环伪距测量法中的数据采样率不低于1GHz,因此1 PPS上升沿位置的判定误差小于0.5ns.热噪声对测量精度的影响可以通过对码环跟踪性能的分析得到[18, 19, 20].当早迟相关器间距为一码片、码环带宽为2.5Hz、相干积分时间为1ms、射频前端带宽为20MHz时,码环跟踪误差的标准差在不同载噪比和伪码速率Rc下的变化情况如图 7所示.
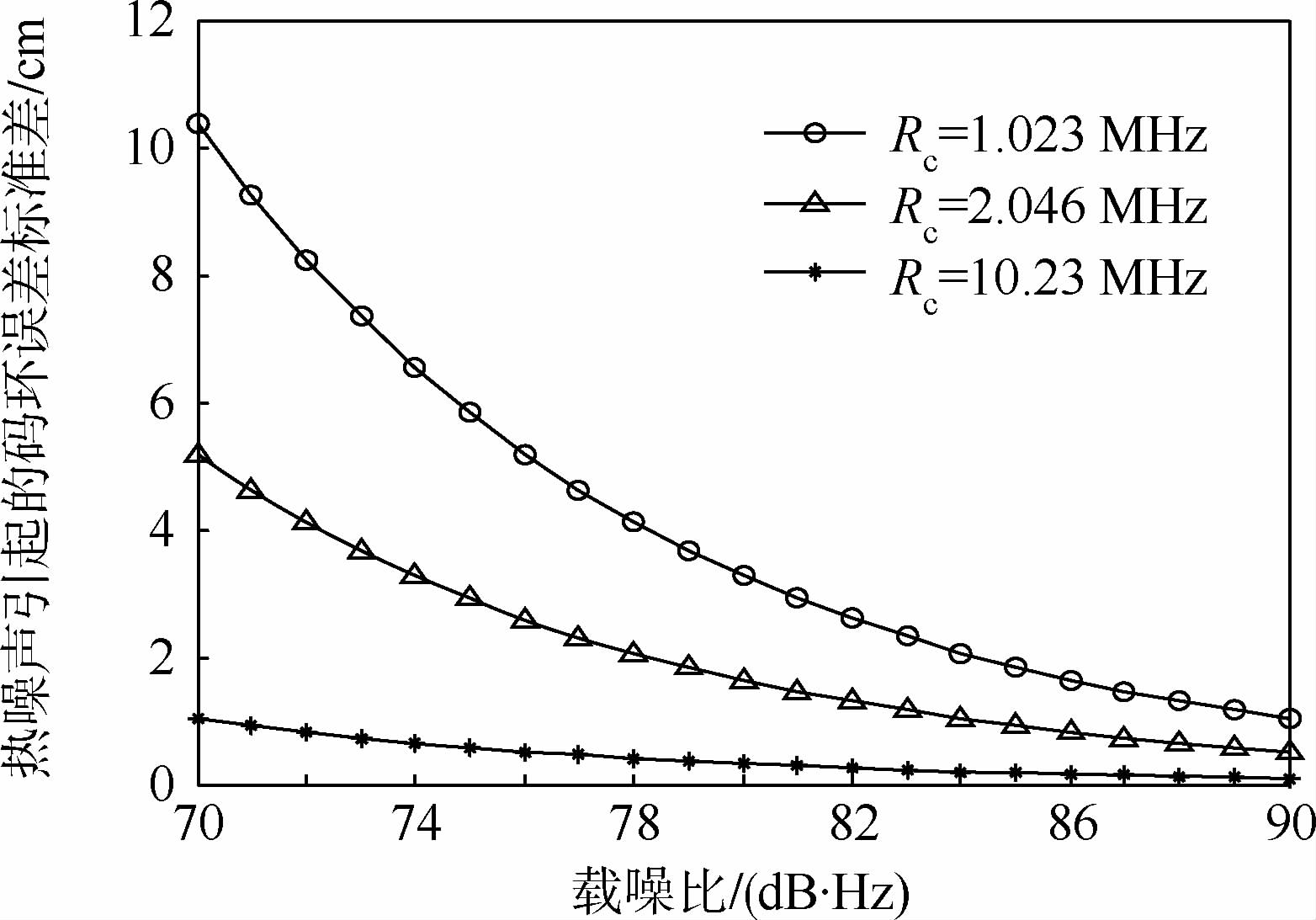 |
| 图 7 不同载噪比下的码环跟踪精度Fig. 7 Code tracking accuracy versus carrier noise ratio |
| 图选项 |
模拟器高功率口信号的载噪比可达80dB·Hz以上[21],此时在1.023MHz的伪码速率下,码环跟踪误差的标准差小于4cm,相应的码相位测量误差标准差小于0.15ns.闭环伪距测量法的各项不确定度来源如表 3所示,其中线缆、连接器、衰减器引起的不确定度参照文献[2, 5].由表 3可知,合成标准不确定度优于0.7ns.由表 3可见,闭环伪距测量法的测量不确定度主要受限于1 PPS上升沿判定的误差.
表 3 模拟器群时延标定的测量不确定度Table 3 Measurement uncertainty of simulator time delay calibration
| 不确定度来源 | 不确定度/ns |
| 线缆、连接器 | 0.3 |
| 衰减器 | 0.1 |
| 采集卡通道时延偏差 | 0.3 |
| 1PPS上升沿判定 | 0.5 |
| 码环跟踪误差 | 0.2 |
| 合成标准不确定度 | 0.7 |
表选项
4 结 论本文提出一种基于闭环伪距测量的模拟器通道群时延标定方法,并使用该方法对两种商用模拟器的群时延进行了标定,对实验结果和算法性能进行分析后,主要得到:
1) 本文方法使用的信号仿真场景及测量原理与接收机通道群时延测试时一致,可以真实准确地标定非理想通道特性下的模拟器通道群时延.
2) 本文方法利用码跟踪环的闭环高精度跟踪,容易实现比传统测量方法更高精度的通道群时延标定.
3) 本文方法可以对真实卫星动态、用户动态及各种导航信号体制下模拟器的通道群时延进行标定.
参考文献
| [1] | Landis G P,White J.Limitation of GPS receiver calibrations[C]//Proceedings of 34th Annual Precise Time and Time Interval (PTTI) Meeting.Manassas,VA:ION,2002:325-332. |
| Click to display the text | |
| [2] | Plumb J,Larson K M,White J,et al.Absolute calibration of a geodetic time transfer system[J].IEEE Transactions on Ultrasonics,Ferroelectrics,and Frequency Control,2005,52(11):1904-1911. |
| Click to display the text | |
| [3] | 冯富元.GPS信号模拟源及测试技术研究和实现[D].北京:北京邮电大学,2009. Feng F Y.GPS signal simulation source test technology research and implementation[D].Beijing:Beijing University of Posts and Telecommunications,2009(in Chinese). |
| Cited By in Cnki (10) | |
| [4] | Boulton P,Read A,Wong R.Formal verification testing of Galileo RF constellation simulators[C]//Proceedings of the 20th International Technical Meeting of the Satellite Division of the Institute of Navigation(ION GNSS 2007).Manassas,VA:ION,2007:1564-1575. |
| Click to display the text | |
| [5] | Grunert U,Thoelert S,Denks H,et al.Using of spirent GPS/Galileo HW simulator for timing receiver calibration[C]//Position,Locationand Navigation Symposium.New York:IEEE/ION,2008:77-81. |
| Click to display the text | |
| [6] | Proia A,Cibiel G.Progress report of CNES activities regarding the absolute calibration method[C]//Proceedings of the 42th Annual Precise Time and Time Interval (PTTI) Systems and Applications Meeting.Manassas,VA:ION,2010:16-18. |
| Click to display the text | |
| [7] | Proia A,Cibiel G,White J,et al.Absolute calibration of GNSS time transfer systems:NRL and CNES techniques comparison[C]//2011 Joint Conference of the IEEE International Frequency Control and the European Frequency and Time Forum(FCS).Piscataway,NJ:IEEE Press,2011:1-6. |
| Click to display the text | |
| [8] | 林红磊,牟卫华,王飞雪,等.卫星导航系统信号模拟器通道零值标定方法研究[J].导航定位学报,2013,1(4):61-64. Lin H L,Mou W H,Wang F X,et al.Research on calibration of GNSS signal simulator[J].Journal of Navigation and Positioning,2013,1(4):61-64(in Chinese). |
| Cited By in Cnki (0) | |
| [9] | Cartmell A.Considerations for calibration of frequency dependent delays[C]//Proceedings of the 13th International Technical Meeting of the Satellite Division of the Institute of Navigation(ION GNSS 2000).Manassas,VA:ION,2000:799-809. |
| Click to display the text | |
| [10] | Parkinson B W,Spilker J J.The global positioning system:Theory and applications.Volume I[M].Reston:AIAA,1996:410. |
| [11] | 吴海涛,李孝辉,卢晓春等.卫星导航系统时间基础[M].北京:科学出版社,2011:147-148. Wu H T,Li X H,Lu X C.Time base of GNSS[M].Beijing:Science Press,2011:147-148(in Chinese). |
| [12] | Ma C,Lachapelle G,Cannon M E.Implementation of a software GPS receiver[C]//Proceedings of the 17th International Technical Meeting of the Satellite Division of the Institute of Navigation(ION GNSS 2004).Manassas,VA:ION,2004:21-24. |
| [13] | Tetewsky A,Soltz A,Fuhry D,et al.Validating the validating tool:Defining and measuring GPS simulator specifications[C]//Proceedings of the 10th International Technical Meeting of the Satellite Division of the Institute of Navigation(ION GPS 1997).Manassas,VA:ION,1997:1681-1695. |
| Click to display the text | |
| [14] | IS-GPS-200G.Navstar GPS space segment/navigation user interfaces[S].CA:ARINC Research Corporation,2012:74-75. |
| [15] | 李庆扬,王能超,易大义.数值分析[M].5版.北京:清华大学出版社,2008:41-42. Li Q Y,Wang N C,Yi D Y.Numerical analysis[M].5th ed.Beijing:Tsinghua University Press,2008:41-42(in Chinese). |
| [16] | 谢钢.GPS原理与接收机设计[M].北京:电子工业出版社,2009:71-72. Xie G.Principles of GPS and receiver design[M].Beijing:Publishing House of Electronics Industry,2009:71-72(in Chinese). |
| [17] | van Dierendonck A J,Fenton P,Ford T.Theory and performance of narrow correlator spacing in a GPS receiver[J].Navigation,1992,39(3):265-283. |
| Click to display the text | |
| [18] | Betz J W,Kolodziejski K R.Extended theory of early-late code tracking for a bandlimited GPS receiver[J].Navigation,2000,47(3):211-226. |
| Click to display the text | |
| [19] | Kaplan E D,Hegarty C J.Understanding GPS principles and applications[M].2nd ed.Norwood,MA:Artech House,2006:173-178. |
| Click to display the text | |
| [20] | Kou Y H,Sui J T,Chen Y B,et al.Test of pseudorange accuracy in GNSS RF constellation simulator[C]//Proceedings of 25th International Technical Meeting of the Satellite Division of the Institute of Navigation 2012 (ION GNSS 2012).Manassas,VA:ION,2012:161-173. |
| Click to display the text | |
| [21] | Zhang H,Kou Y H.Single-SV timing in GNSS signal simulator and receiver closed-loop testing[C]//Proceedings of the 45th Annual Precise Time and Time Interval Systems and Applications Meeting.Manassas,VA:ION,2013:94-100. |
| Click to display the text |
