近年来,竞争故障预测问题已引起了国内外专家的广泛关注。Huang和Dietrich在文献[2]中基于威布尔分布建立了退化量的可靠性模型,Huang和Askin在文献[3]中运用串联模型分析了突发故障与退化故障不相关时的竞争故障建模方法。文献[4]基于竞争故障模型评估了舰船柴油机的可靠性。Bedford[5]在统计学相关理论的基础上分析了各竞争失效评估模型的适用性与特点。Lehmann[6]运用退化阈值冲击(Degradation-Threshold-Shock,DTS)模型分析了突发故障、退化故障以及环境因素之间的相互关系。Li和Pham[7]对多故障模式下复杂多态系统的可靠性评估问题进行了研究。文献[8]针对竞争故障问题,采用了线性退化模型的半更新过程设计了一种非参数估计方法。目前国内对于竞争故障相关领域的研究较少,赵建印等[9]运用参数回归模型对竞争故障问题进行了分析,苏春和张恒[10]利用退化量来表示突发故障的分布函数并建立了竞争故障可靠性评估模型,王华伟等[11]引入混合威布尔模型量化了退化故障对突发故障的影响,并由此实现了航空发动机的剩余寿命预测。
目前大部分文献在对竞争故障问题进行分析研究时,大都假设突发故障与退化故障不相关,且在建立竞争故障模型时仅考虑一种突发故障和单一退化量的单边退化,对于含有多元退化量的竞争故障问题少有涉及。通常,导弹随着性能退化程度的增加其发生突发故障的概率越来越大,因此有必要考虑突发故障与退化故障的相关性。导弹的性能退化过程是由多个退化量共同导致的,且多数退化量为双向退化,若仅考虑单一退化量建立导弹竞争故障预测模型则过于简单。针对上述问题,本文基于导弹退化特性建立了具有多元退化量的导弹竞争故障预测模型。在模型参数求解过程中,针对导弹性能退化数据分布参数存在小样本、非线性等特点,运用最小二乘支持向量机(Least Squares Support Vector Machine,LS-SVM)预测算法对性能退化数据的分布参数进行了预测;考虑退化量与突发故障的相关性,运用位置-尺度模型分析了退化量与突发故障的关系,进而求解出突发故障与退化量的相关参数。
1 导弹突发与退化竞争故障预测导弹在服役期间突发故障与退化故障均可能发生。通常,导弹在贮存伊始其性能就开始不断退化,该过程是必然的,而突发故障在导弹性能退化过程中则可能发生也可能不发生,因此导弹故障是突发故障与退化故障竞争的结果。
1.1 导弹竞争故障预测模型设导弹有n个退化特征参数,第i(i=1,2,…,n)个退化特征参数对应的退化量、退化上阈值和退化下阈值分别记为xi、Ui和Li。在t时刻对导弹进行了一次测试,其退化量xi(t)的分布函数为G(x,βi)(其中βi=(β1,β2,…,βk)为该分布的参数向量),对应的概率密度函数g(x,βi)可表示为
所有退化特征参数的退化量均由工业部门给出了阈值范围和标准值,若超出阈值则可判定为故障。记Tsi为第i个特征参数发生退化故障的时间,则第i个特征参数在t时刻的退化故障概率为
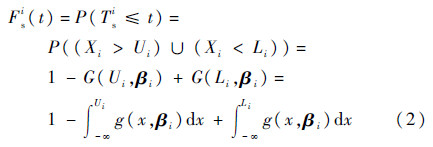
考虑到导弹具有n个退化特征参数,任一参数的退化故障均会引起导弹故障,因而导弹的退化故障可看做是由n个退化特征参数的退化故障竞争导致的。假设导弹各退化特征参数间相互独立,则导弹在t时刻的退化故障概率为
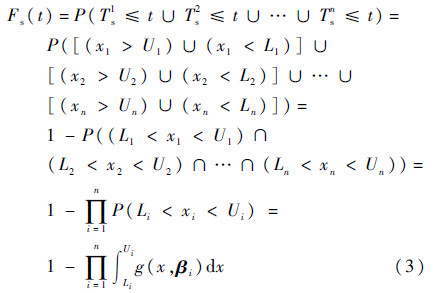
突发故障不仅与时刻t有关,还与t时刻某退化特征参数的退化量xi(t)相关。假设导弹所有退化量均与突发故障相关,只是影响突发故障的程度不同。
记Th为导弹发生突发故障的时间,λi(t,x)为与退化量xi(t)相关时Th的失效率函数,则Th的可靠度函数可表示为
导弹在t时刻的突发故障概率可表示为
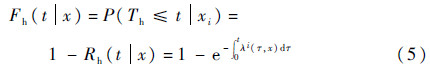
导弹故障是突发故障与退化故障竞争的结果,根据以上分析,导弹在t时刻的竞争故障概率可表示为
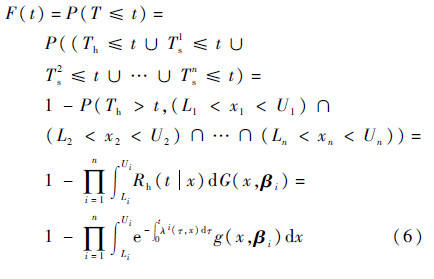
1.2 导弹竞争故障预测流程由1.1节可知,对贮存状态下的导弹进行竞争故障预测,首先要在一定置信度下对性能退化数据与突发故障数据进行统计分析,即通过分布类型假设、参数估计和分布拟合检验来确定性能退化数据与突发故障数据的分布规律;其次,利用LS-SVM预测算法对退化模型中的未知参数进行预测,得到未来某一时刻的分布函数,考虑突发故障与退化量的相关性,利用位置-尺度模型求解出突发故障模型的未知参数;最后利用式(6)建立导弹竞争故障预测模型,对导弹退化与突发竞争故障概率进行预测。导弹竞争故障预测建模流程如图 1所示。
 |
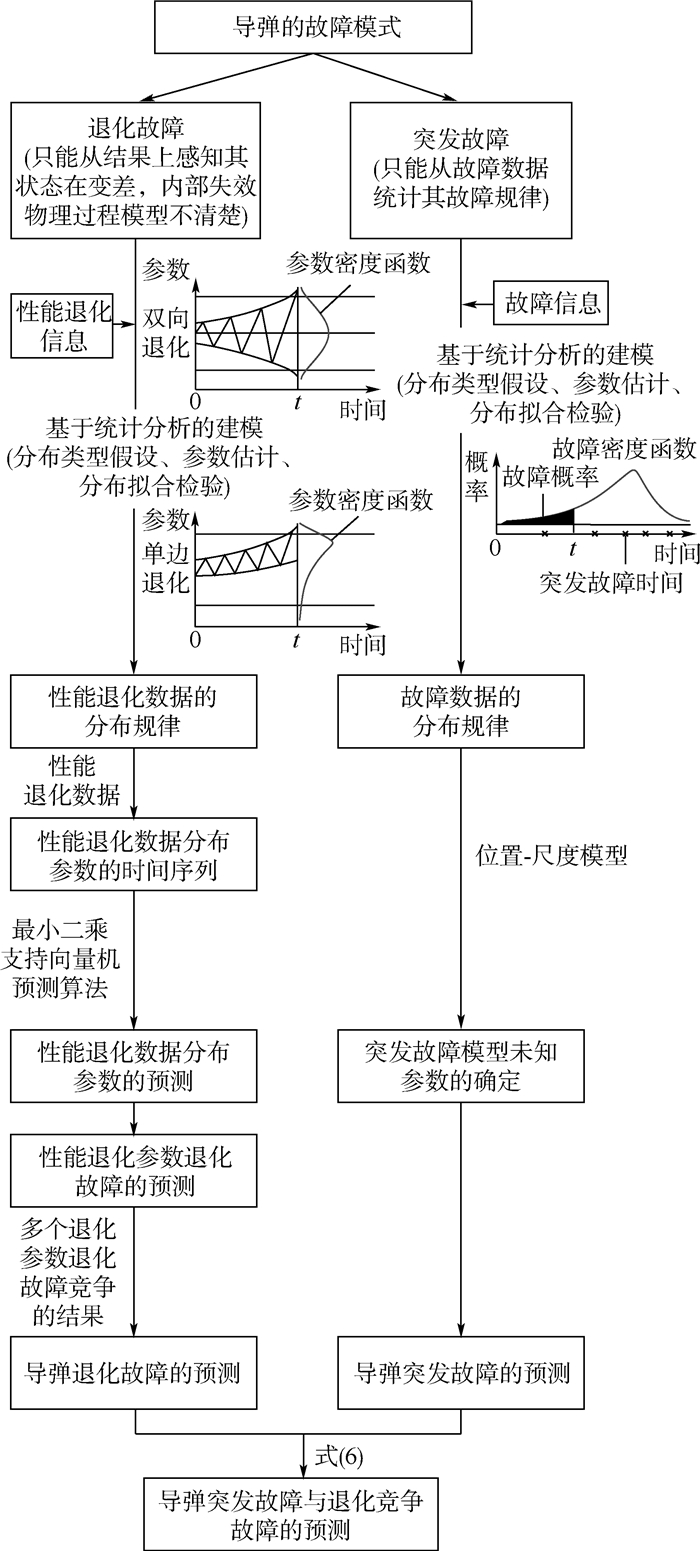| 图 1 导弹竞争故障预测流程Fig. 1 Flowchart of missile competing failure prediction |
| 图选项 |
2 数据分布类型的确定对于数据分布类型的确定,在概率论与数理统计中常采用分布拟合检验的方法,主要有χ2拟合检验、概率纸检验和Копмогоров检验等。概率纸检验方法主要依靠直观观察,大多为定性分析,判断结果往往因人而异,不够精确。Копмогоров检验当总体为一维且理论分布完全已知时相对于χ2检验更有优势。因而,本文采用Копмогоров检验方法对性能退化数据与突发故障数据的分布类型进行检验。
对于性能退化数据,假设其分布函数G(x,β)的分布类型与时间t无关,只是参数向量β随着时间t的变化而改变。显然,分布G(x,β)可看作β与时间t的函数,可记为G(x,β(t))。因此,若确定了G(x,β(t))的分布类型,又通过性能退化数据估计出了β(t)的估计值β,就可得出性能退化数据的分布函数G(x,β)。在确定G(x,β(t))的分布类型时,可首先根据工程经验假设其可能的分布类型,然后对其进行参数估计与分布拟合检验,最终确定出G(x,β(t))的分布类型。
双向退化与单边退化是导弹特征参数的2种主要退化趋势。双向退化是指随着时间的推移,特征参数的性能退化数据波动性变大,对应于性能退化数据的方差变大;单边退化是指随着时间的推移,特征参数的性能退化数据逐渐偏离标准值并有接近上阈值或下阈值的趋势,对应于性能退化数据的均值偏离标准值的程度变大。综合考虑这2种退化趋势,假定其性能退化数据服从正态分布N(x;μ,σ2),则分布密度函数为
式中:μ和σ2分别为t时刻性能退化数据的均值和方差。
若特征参数的性能退化数据服从正态分布,则其参数向量β=(μ,σ2)。设在某一时刻t,特征参数的性能退化数据X～N(μ,σ2),X1,X2,…,Xn是来自总体X的一个样本,则μ和σ2的无偏估计[12]可表示为
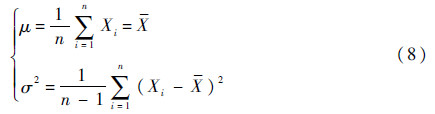
在工程上通常假定导弹的性能退化数据服从正态分布,对其进行的拟合检验为正态性检验,可利用样本{X1,X2,…,Xn}来检验总体分布是否服从N(μ,σ2)。N(μ,σ2)中含有未知参数μ和σ2,无法直接采用Копмогоров检验方法[13],为此本文利用其无偏估计量μ和σ2进行替换,则Копмогоров检验中的假设变为
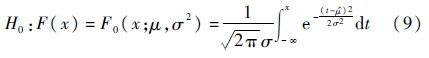
检验统计量为
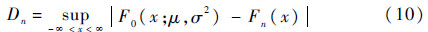
式中:Fn(x)为经验分布函数,其与F0(x;μ,σ2)均为x的单调非降函数,因此偏差F0(x;μ,σ2)-Fn(x)的上确界可在n个点X(i)处求得,即
检验统计量Dn的值即为n个di中的最大值,可表示为
在确定的显著性水平α下,检验规则为:若Dn>Dn,α,则拒绝H0,否则接受H0。Dn,α的值可通过查询临界值表获取。
威布尔分布是基于串联模型或最弱环原理提出的,近年来在装备可靠性领域得到了迅猛发展,其在表示产品故障方面具有很强的适应性与灵活性,常用来表征电子设备故障的指数分布即为威布尔分布的一种特殊形式。因而,本文根据相关工程经验假设突发故障数据服从威布尔分布,并采用Копмогоров检验方法对其进行验证,检验过程与性能退化数据分布类型的检验相类似,只是参数估计方法略有不同[14]。
3 模型参数的求解3.1 退化故障分布参数预测由导弹退化故障预测模型可知,导弹退化故障预测的实质是对性能退化数据分布函数的预测。由于假设性能退化数据的分布类型与时间无关,相关的仅为分布的参数向量,即性能退化数据分布函数预测的重点是对其分布参数的预测。采用第2节的方法可以确定出性能退化数据的分布类型,从而得出性能退化数据的分布参数。根据退化特征参数的历史性能退化数据求解其分布参数的历史值,并基于该历史值选用适当的预测算法预测未来某一时刻的分布参数,即可得到未来该时刻性能退化数据的分布函数,进而根据式(3)预测导弹的退化故障概率。
贮存状态下的导弹采取定期检测方式,通过测试获得的性能退化数据为一系列与时间相关的数值,相应的分布参数也随时间变化,因此可将其看作时间序列。通过上述分析,导弹的退化故障预测就转变为性能退化数据分布参数时间序列的预测。目前常用的时间序列预测方法主要有时间序列分析、神经网络、回归分析和支持向量机等[15]。导弹性能退化数据分布参数具有小样本、非线性等特点,而目前在处理小样本预测和估计问题时,统计学理论一般被认为是最佳理论。支持向量机(Support Vector Machine,SVM)以统计学理论的Vapnik-Chervonenkis(VC)维理论和结构最小化原则为理论基础,是一种新兴的机器学习算法。SVM利用结构最小化原则替代了传统统计学中的经验风险最小化原则,在处理小样本、高维数的非线性问题方面具有很强的适用性,并有效克服了局部极值和维数灾难等问题,目前在时间序列预测、函数拟合、模式识别等领域的应用取得了很好的效果[16, 17]。
SVM算法的实质是求解凸二次优化问题,能保证求得的极值解即为全局最优解,但算法的复杂度与样本量密切相关,随着样本量的增大,运算速度会显著降低。LS-SVM采用等式约束替代了SVM中的不等式约束,同时将风险由误差的一范数变为二范数[18],进而将二次优化问题的求解简化为一次方程组的求解,既减少了计算时间又有效降低了计算复杂度。因此,在预测性能退化数据的分布参数时间序列时,本文选用LS-SVM预测模型。
给定时间序列{xt}(t=1,2,…,N),采用前n(n <N)个数据来确定预测器的拓扑结构并估计模型的相关参数,剩余数据用来检验模型的预测效果。相空间重构前n个数据并得出嵌入维数m与输入输出样本对后,即可开始训练LS-SVM,进而得到其回归函数为
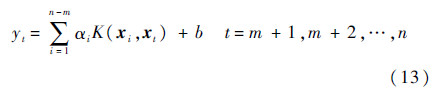
式中:αi为拉格朗日乘子;K为核函数;b⊂R为常数。由于xn-m+1={xn-m+1,xn-m+2,…,xn},则1步预测模型可表示为
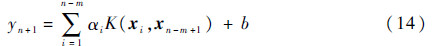
令yn+1=xn+1,将其加入原时间序列得到xn-m+2={xn-m+2,xn-m+3,…,xn,xn+1},则可得2步预测模型。依次类推,第k步LS-SVM预测模型可表示为
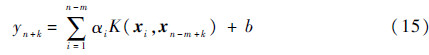
式中:xn-m+k={xn-m+k,…,xn+1,…,xn+k-1}。
3.2 突发故障分布参数求解突发故障不仅与时间有关,还与退化特征参数的退化量相关。为更好地表示突发故障时间与退化量间的关系,可将突发故障时间当作响应变量,退化量看作回归变量,则可在回归模型中对突发故障时间与退化量的关系进行明确表示。位置-尺度模型是回归分析中的一类重要模型[19],其在确定的退化量x的基础上对Y=lnT(T为突发故障时间)的分布进行研究,模型可表示为
式中:μ(x)为位置参数;σ>0为不变的尺度参数;e的分布与x无关。给定x、Y的可靠度函数形如
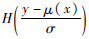,H(e)为e的可靠度函数。对于突发故障时间Th,利用Yh=lnTh的分布,则Th=expYh的可靠度函数可表示为
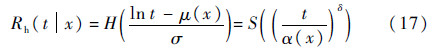
式中:α(x)=exp(μ(x));δ=1/σ;S(w)=H(ln(w))。利用该模型,式(6)可进一步表示为
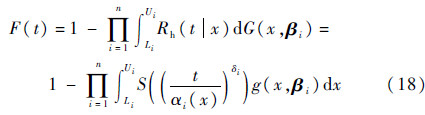
由第2节的分析可知,导弹突发故障时间Th服从威布尔分布。威布尔分布中含有尺度参数η和形状参数v,在运用位置-尺度模型分析突发故障时间与退化量关系时,通常假设形状参数v与退化量x不相关,而尺度参数是退化量x的函数η(x)。
现对给定退化量x下Yh=lnTh的分布进行分析,由于Th服从威布尔分布,则Yh=lnTh服从极值分布,其密度函数可表示为
式中:位置参数μ(x)=lnη(x)；尺度参数σ=1/v,若采用标准极值分布进行表示,则
e具有标准极值分布,其密度函数为exp(e-exp(e))。为满足大多数应用，μ(x)通常取线性形式,令
μ(x)=γ1+γ2·x
σ=γ3
则式(19)可表示为
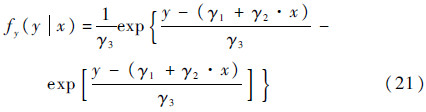
通过分析Z枚导弹突发故障数据可知,发生突发故障的导弹均伴随有一个突发故障时间tj(j=1,2,…,Z)和一个与其相对应的退化量xji(i=1,2,…,n),则基于突发故障数据的似然函数可表示为
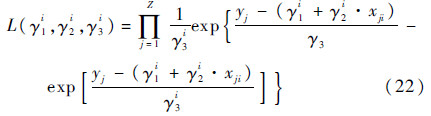
对式(22)取对数并求关于γ1i、γ2i和γ3i的偏导且令其为0,则可得
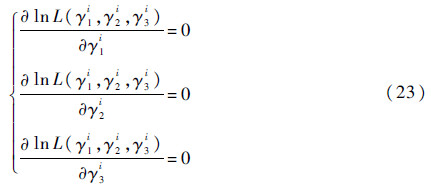
解方程组(23)可得到γ1i、γ2i和γ3i的估计值,但由于这是3个超越方程,难以得到解析解,只能采用数值解法,文献[20]对此进行了分析研究,本文采用极大似然估计法对其进行求解。
4 实例分析以某岸导部队贮存状态下整批导弹为研究对象,随机抽取10枚导弹作为样本进行故障预测。贮存状态下的导弹采取定期检测的方式,每年测试一次,其测试信息从2004年开始记录到2014年,测试信息主要包括性能退化数据与突发故障数据,因此可根据2004—2012年的测试信息预测导弹2013年和2014年的故障概率,并将预测结果与导弹实际故障情况进行对比,以检验本文设计方法的合理性与有效性。
4.1 数据的分布类型根据工程经验,可假设导弹某特征参数的性能退化数据服从正态分布。以抽取的10枚导弹某特征参数2004年的性能退化数据为例,采用第2节的方法对该性能退化数据进行分布拟合检验以确定其分布类型。
通过整理测试信息可知,抽取的10枚导弹某特征参数2004年测试时的性能退化数据分别为:10.21,11.37,9.79,11.13,10.23,10.74,11.66,11.00,10.90,12.84。设该性能退化数据为X,则检验X服从正态分布与否就变为检验假设H0:X~N(μ,σ2)是否成立,这是一个正态性检验。将X代入式(8)可得参数μ和σ2的无偏估计为
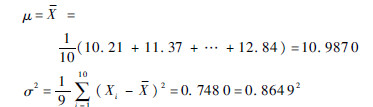
按升序排列性能退化数据,并对其进行Копмогоров检验,检验过程如表 1所示。其中：Φ(ui)为标准正态分布函数。
表 1 性能退化数据的正态性检验Table 1 Normality testing of performance degradation data
| i | X (i) | 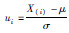 | Φ(u i) | 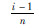 | 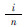 | 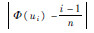 | 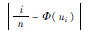 | d i |
| 1 | 9.79 | -1.3840 | 0.0832 | 0 | 0.1 | 0.0832 | 0.0168 | 0.0832 |
| 2 | 10.21 | -0.8984 | 0.1845 | 0.1 | 0.2 | 0.0845 | 0.0155 | 0.0845 |
| 3 | 10.23 | -0.8752 | 0.1907 | 0.2 | 0.3 | 0.0093 | 0.1093 | 0.1093 |
| 4 | 10.74 | -0.2856 | 0.3876 | 0.3 | 0.4 | 0.0876 | 0.0124 | 0.0876 |
| 5 | 10.90 | -0.1006 | 0.4599 | 0.4 | 0.5 | 0.0599 | 0.0401 | 0.0599 |
| 6 | 11.00 | 0.0150 | 0.5060 | 0.5 | 0.6 | 0.0060 | 0.0940 | 0.0940 |
| 7 | 11.13 | 0.1653 | 0.5656 | 0.6 | 0.7 | 0.0344 | 0.1344 | 0.1344 |
| 8 | 11.37 | 0.4428 | 0.6710 | 0.7 | 0.8 | 0.0290 | 0.1290 | 0.1290 |
| 9 | 11.66 | 0.7781 | 0.7817 | 0.8 | 0.9 | 0.0183 | 0.1183 | 0.1183 |
| 10 | 12.84 | 2.1424 | 0.9839 | 0.9 | 1.0 | 0.0839 | 0.0161 | 0.0839 |
表选项
由表 1可得,检验统计量D10=0.1344。若取显著性水平α=0.1,则通过查阅Dn的临界值表[12]可得D10,0.1=0.2390。由于D10<D10,0.1,因此在显著性水平α=0.1下接受H0,即可确定2004年测试时导弹某特征参数性能退化数据的分布类型为正态分布。
分别对抽取的10枚导弹某特征参数2005—2012年的性能退化数据进行正态性检验,检验结果表明这8年的性能退化数据均服从正态分布,由此可判定该特征参数的性能退化数据服从正态分布,只是其分布参数μ和σ2随时间的变化而改变。采用相同的方法可对导弹其余特征参数的性能退化数据进行正态性检验,检验结果表明在显著性水平α=0.1下,其余特征参数的性能退化数据的分布类型同样为正态分布。
同样,可根据工程经验假设导弹的突发故障数据服从威布尔分布。采用Копмогоров方法对其分布类型进行检验,该过程与性能退化数据的检验过程相类似,结果表明导弹的突发故障数据服从威布尔分布。
4.2 分布参数的预测与求解由4.1节分析可知,导弹性能退化数据服从正态分布,因此在预测性能退化数据的分布参数时,仅需预测均值μ和方差σ2即可。2004—2014年抽取的10枚导弹某特征参数的性能退化数据的均值和方差的时间序列分别记为:(10.9870,10.8220,10.7160,10.8160,10.7960,10.8240,10.7530,10.8000,11.0870,11.0020,10.9340)和(0.7480,0.6132,0.3534,0.3771,0.6871,0.5370,0.5003,0.4050,1.0234,0.5728,0.5980)。首先预测均值μ,根据最终预测误差(Final Prediction Error,FPE)准则[16],选取嵌入维数m=1,相空间重构均值时间序列的前9个数据,可得输入输出样本对为Xμ=[10.987010.822010.716010.816010.796010.824010.753010.8000]T、Yμ=[10.822010.716010.816010.796010.824010.753010.800011.0870]T。选取高斯径向基函数作为核函数,并采用交叉检验和网格搜索算法求解LS-SVM中的核函数宽度参数σ2与正则化参数γ,求得最优参数σ2=3.8279,γ=117.1561。利用LS-SVM训练输入输出样本对,可得均值μ的预测回归曲线如图 2所示。
 |
| 图 2 均值预测回归曲线Fig. 2 Regression curve of mean value prediction |
| 图选项 |
得到训练完毕的LS-SVM回归函数之后,即可开始预测输入样本Xμ*=[10.987010.822010.716010.816010.796010.824010.753010.800011.0870]T,预测结果如图 3所示,预测值和误差如表 2所示。同理,可预测性能退化数据的方差时间序列,其预测相关数值如表 3所示。
 |
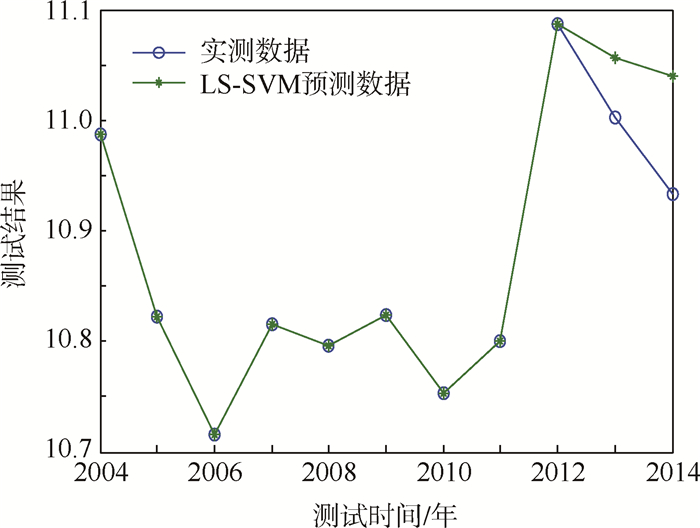| 图 3 LS-SVM均值预测结果Fig. 3 Result of LS-SVM mean value prediction |
| 图选项 |
表 2 均值预测与实测值对比Table 2 Contrast between mean value prediction and actual value
| 测试时间 | 预测值 | 实测值 | 绝对误差 | 相对误差 |
| 2013年 | 11.0561 | 11.0020 | -0.0541 | 0.0049 |
| 2014年 | 11.0405 | 10.9340 | -0.1065 | 0.0097 |
表选项
由图 2、图 3、表 2和表 3可以看出,LS-SVM预测模型具有较高的预测精度,可对性能退化数据相关分布参数进行较好的短期预测。采用LS-SVM预测模型对其余特征参数性能退化数据的分布参数进行预测,即可得到2013年和2014年导弹特征参数性能退化数据的分布函数。
表 3 方差预测与实测值对比Table 3Contrast between variance prediction and actual value
| 测试时间 | 预测值 | 实测值 | 绝对误差 | 相对误差 |
| 2013年 | 0.5184 | 0.5728 | 0.0544 | 0.0949 |
| 2014年 | 0.6374 | 0.5980 | -0.0394 | 0.0658 |
表选项
分析导弹2004—2012年的故障数据可以发现,抽取的10枚导弹在2005—2012年均有突发故障记录,其故障个数为1,1,1,1,2,2,2,2。由于导弹每年测试一次,因此若以年为时间单位,那么抽取的10枚导弹的突发故障时间可以表示为2,3,4,5,6,6,7,7,8,8,9,9。以某退化特征参数的退化量xi为例,其与突发故障时间的对应关系如表 4所示。
表 4 突发故障与相关退化量的对应关系Table 4 Correspondence relationship between sudden fault and related degradation data
| 导弹突发故障时间 | 退化量xi |
| 2 | 9.79 |
| 3 | 10.61 |
| 4 | 10.82 |
| 5 | 10.72 |
| 6 | 10.98 |
| 6 | 12.60 |
| 7 | 10.73 |
| 7 | 10.08 |
| 8 | 12.28 |
| 8 | 10.83 |
| 9 | 10.38 |
| 9 | 10.22 |
表选项
将表 4中的数据代入式(23),即可求得突发故障与退化量xi相关时的参数γ1i、γ2i和γ3i的估计值分别为10.3306、0.3568和0.7906,从而得到尺度参数ηi=exp(10.3306+0.3568x)和形状参数mi=1.2648。同理可求得导弹突发故障与其余退化量相关时的参数值。
4.3 预测结果分析确定了数据的分布类型以及相关参数后,即可根据式(18)对导弹在2013年的故障概率进行预测,结果为
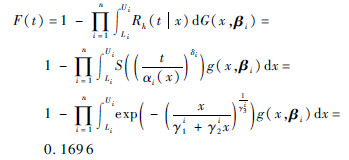
即该批导弹在2013年发生故障的概率为0.1696,同理可预测得到2014年的故障概率为0.1843。对该批导弹2013年和2014年的实际状态进行评估[21],可得该批导弹2013年和2014年的实际故障概率分别为0.1642和0.1765。实际评估结果与本文设计方法的预测结果基本一致,因此表明导弹竞争故障预测模型是合理的。
为了更好地检验本文设计方法的有效性,分别采用只考虑性能退化的故障预测方法、只考虑突发故障的故障预测方法、假设突发故障与退化故障相互独立的竞争故障预测方法和本文设计的方法对导弹2013年和2014年的故障概率进行预测,各方法预测结果对比如表 5所示。
表 5 各方法预测结果对比Table 5 Contrast results of each prediction method
| 预测方法 | 导弹故障概率预测值 | 导弹故障概率实际评估值 | 平均相对误差 | ||
| 2013年 | 2014年 | 2013年 | 2014年 | ||
| 只考虑性能退化 | 0.1367 | 0.1492 | 0.1611 | ||
| 只考虑突发故障 | 0.1496 | 0.1528 | 0.1116 | ||
| 0.1642 | 0.1765 | ||||
| 假设突发故障与退化故障相互独立 | 0.1723 | 0.1934 | 0.0725 | ||
| 本文方法 | 0.1696 | 0.1843 | 0.0385 | ||
表选项
由表 5可知,在只考虑性能退化或突发故障情况下对导弹故障概率进行预测时,虽然在对比结果中误差不大,但从表中可以看出,这2种方法对导弹故障概率的预测值均低于导弹故障概率的实际值,即存在着低估导弹故障概率的可能。对于导弹这类高可靠性的系统而言,一旦发生故障会造成严重的军事与经济损失,单纯考虑导弹贮存过程中的退化故障或突发故障,均会导致重大安全隐患。第3种方法忽略了突发故障与退化故障的相关性,假设突发故障与退化故障相互独立,此时竞争故障模型就变为可靠性分析中的串联模型。由于该方法未考虑性能退化对突发故障的影响,因此在对导弹故障概率预测时,相对于本文设计的方法可能会过高地估计导弹发生故障的概率,这将会对有效控制导弹维修成本与提高导弹利用率造成不利影响。通过比较各预测方法的平均相对误差,本文设计的方法预测精度更高且综合考虑了维修成本与故障风险,其预测结果更加合理有效。
5 结 论贮存状态下的导弹既具有突发故障模式也具有退化故障模式,其故障是由二者竞争引起的。本文通过分析导弹退化特性,在考虑突发故障与退化量相关性的基础上建立了具有多元退化量的导弹竞争故障预测模型,主要结论如下:
1) 利用数理统计的方法分别确定了导弹性能退化数据与突发故障数据的分布类型,其中性能退化数据服从正态分布,突发故障数据服从威布尔分布。
2) 在求解退化故障预测模型相关参数时,针对性能退化数据分布参数存在小样本、非线性等特点,应用LS-SVM预测算法对性能退化数据的分布参数进行了预测,预测结果表明该预测方法具有较高的拟合精度,可对相关参数进行较好的短期预测。
3) 对突发故障预测模型相关参数求解时,考虑了退化量与突发故障的相关性,并运用位置-尺度模型分析了退化量与突发故障的关系,进而求解出突发故障与退化量的相关参数。
4) 通过实例分析,并与其他预测方法进行对比,结果验证了本文设计方法的合理性与有效性。
参考文献
| [1] | 赵建印. 基于性能退化数据的可靠性建模与应用研究[D].长沙:国防科学技术大学,2005:61-64. ZHAO J Y.Reliability modeling and application study based on the data of performance degradation[D].Changsha:National University of Defense Technology,2005:61-64(in Chinese). |
| Cited By in Cnki (101) | |
| [2] | HUANG W, DIETRICH D L.An alternative degradation reliability modeling approach using maximum likelihood estimation[J].IEEE Transactions on Reliability,2005,54(2):310-317. |
| Click to display the text | |
| [3] | HUANG W, ASKIN R G.Reliability analysis of electronic devices with multiple competing failure modes involving performance aging degradation[J].Quality and Reliability Engineering International,2003,19(3):241-254. |
| Click to display the text | |
| [4] | BOCCHETTI D, GIORGIO M,GUIDA M,et al.A competing risk model for the reliability of cylinder liners in marine diesel engines[J].Reliability Engineering and System Safety,2009,94(8):1299-1307. |
| Click to display the text | |
| [5] | BEDFORD T. Competing risk modeling in reliability[M]//Modern statistical and mathematical methods in reliability.New Jersey:Word Scientific Publisher,2006:23-40. |
| [6] | LEHMANN A. Joint modeling of degradation and failure time data[J].Journal of Statistical Planning and Inference,2009,139(5):1693-1706. |
| Click to display the text | |
| [7] | LI W, PHAM H.Reliability modeling of multi-state degraded systems with multi-competing failures and random shocks[J].IEEE Transactions on Reliablity,2005,54(2):297-303. |
| Click to display the text | |
| [8] | BAGDONAVICIUS V, BIKELIS A,KAZAKEVICIUS V,et al.Analysis of joint multiple failure mode and linear degradation data with renewals[J].Journal of Statistical Planning and Inference,2007,137(7):2191-2207. |
| Click to display the text | |
| [9] | 赵建印,刘芳, 奚文俊.退化失效与突发失效共存下产品可靠性模型与评估方法研究[J].兵工学报,2011,32(9):1136-1139. ZHAO J Y,LIU F, XI W J.Reliability model and evaluation method of products in competing failure modes[J].Acta Armamentarii,2011,32(9):1136-1139(in Chinese). |
| Cited By in Cnki (4) | |
| [10] | 苏春,张恒. 基于性能退化数据和竞争失效分析的可靠性评估[J].机械强度,2011,33(2):196-200. SU C,ZHANG H.Reliability assessment based on performance degradation data and competiong failure analysis[J].Journal of Mechanical Strength,2011,33(2):196-200(in Chinese). |
| Cited By in Cnki (8) | Click to display the text | |
| [11] | 王华伟,高军, 吴海桥.基于竞争失效的航空发动机剩余寿命预测[J].机械工程学报,2014,50(6):197-205. WANG H W,GAO J,WU H Q.Residual remaining life prediction based on competing failures for aircraft engines[J].Journal of Mechanical Engineering,2014,50(6):197-205(in Chinese). |
| Cited By in Cnki (5) | Click to display the text | |
| [12] | 吴翊,李永乐, 胡庆军.应用数理统计[M].北京:国防科技大学出版社,2008:112-120. WU Y,LI Y L,HU Q J.Application mathematical statistic[M].Beijing:National University of Defence Technology Press,2008:112-120(in Chinese). |
| [13] | 丛林虎,徐廷学, 杨继坤,等.导弹退化故障预测方法研究[J].电光与控制,2014,21(5):78-82. CONG L H,XU T X,YANG J K,et al.A method for missile degradation fault prediction[J].Electronics Optics & Control,2014,21(5):78-82(in Chinese). |
| Cited By in Cnki (3) | Click to display the text | |
| [14] | 金良琼. 两参数Weibull分布的参数估计[D].昆明:云南大学,2010:6-16. JIN L Q.Two parameter estimation for Weibull distribution[D].Kunming:Yunnan University,2010:6-16(in Chinese). |
| Cited By in Cnki (13) | |
| [15] | 张广明,袁宇浩, 龚松建.基于改进最小二乘支持向量机方法的短期风速预测[J].上海交通大学学报,2011,45(8):1125-1129. ZHANG G M,YUAN Y H,GONG J S.A predictive model of short-term wind speed based on improved least squares support vector machine algorithm[J].Journal of Shanghai Jiao Tong University, 2011,45(8):1125-1129(in Chinese). |
| Cited By in Cnki (17) | Click to display the text | |
| [16] | 尉询楷,李应红, 张朴,等.基于支持向量机的时间序列预测模型分析与应用[J].系统工程与电子技术,2005,27(3):529-532. WEI X K,LI Y H,ZHANG P,et al.Analysis and applications of time series forecasting model via support vector machines[J].Systems Engineering and Electronics,2005,27(3):529-532(in Chinese). |
| Cited By in Cnki (72) | Click to display the text | |
| [17] | 洪杰,韩磊,苗学问, 等.基于支持向量机的滚动轴承状态寿命评估[J].北京航空航天大学学报,2010,36(8):896-899. HONG J,HAN L,MIAO X W,et al.Assessment based on support vector machine for rolling bearing grade-life[J].Journal of Beijing University of Aeronautics and Astronautics,2010,36(8):896-899(in Chinese). |
| Cited By in Cnki (10) | Click to display the text | |
| [18] | 唐杰明,刘俊勇,杨可,等. 基于灰色模型和最小二乘支持向量机的电力短期负荷组合预测[J].电网技术,2009,33(3):63-68. TANG J M,LIU J Y,YANG K,et al.Short-term load combination forecasting by grey model and least square support vector machine[J].Power System Technology,2009,33(3):63-68(in Chinese). |
| Cited By in Cnki (57) | |
| [19] | LAWLESS J F. 寿命数据中的统计模型与方法[M].茆诗松,译.北京:中国统计出版社,1998:40-50. LAWLESS J F.Statistical models and methods for lifetime data[M].MAO S S,translated.Beijing:China Statical Publishing House,1998:40-50(in Chinese). |
| [20] | 温艳清,刘保亮. 完全数据下Weibull分布参数的极大似然估计[J].应用数学,2008,21(增刊):67-70. WEN Y Q,LIU B L.Complete data parameters estimation under Weibull distribution[J].Mathematica Applicata,2008,21(S):67-70(in Chinese). |
| Cited By in Cnki (6) | Click to display the text | |
| [21] | 姚云峰,伍逸夫, 冯玉光.装备健康状态评估方法研究[J].现代防御技术,2012,40(5):156-161. YAO Y F,WU Y F,FENG Y G.Health condition assessment of equipment[J].Modern Defence Technology,2012,40(5):156-161(in Chinese). |
| Cited By in Cnki (9) | Click to display the text |
