经典的RCS起伏模型有Sweling Ⅰ~Ⅳ模型和Marcum模型。前者主要适用于典型的飞行器目标,后者的适用对象为非起伏目标(如金属球)[4]。在此基础上,Song等[5]通过对显性瑞利目标的分析,说明了Sweling Ⅲ、Ⅳ模型与赖斯分布的相似程度取决于模型参数s的大小。但是随着隐身目标、非良导体目标和高速飞行体等新型目标的出现,经典模型已难以精确表达各类目标的统计性能[6]。近年来,卡方分布、对数正态分布和勒让德多项式模型[7]等拟合精度较高的起伏模型陆续被提出。文献[8]针对隐身飞机RCS可能出现的对数中值比小于1的情况,提出了完备的对数正态分布模型。文献[9]利用经典起伏模型对典型隐身飞机的RCS统计特性进行拟合,所得的分布曲线可能存在对峰值估计过高的缺点。以上各种模型均有其适用范围,且存在一定的转换关系。但是现有文献多通过直接计算RCS的均值、平均中值比或者核密度函数等统计特征估计分布模型的参数。由于隐身飞机的整机RCS中存在较多的低值点,传统方法容易导致拟合的分布曲线偏离RCS真实分布曲线,从而产生较大拟合误差。
针对上述问题,本文提出采用贝叶斯-蒙特卡罗(Bayesian-Markov Chain Monte Carlo,Bayesian-MCMC)方法估计起伏模型的特征参数,从而提高模型的拟合精度。Bayesian-MCMC方法是一种动态的计算机模拟方法,能够解决高维度且形式复杂的未知参数后验概率估计问题[10]。采用Bayesian-MCMC方法估计模型参数时,首先利用贝叶斯理论推导卡方分布模型和对数正态分布模型参数的后验估计表达式;然后利用MCMC算法求解参数估计值;最后通过比较Bayesian-MCMC方法与传统方法所得曲线的拟合优度,说明本文方法能够较为准确地估计起伏模型的参数,且大幅提高RCS起伏模型的拟合精度。
1 模型参数的贝叶斯估计本节结合贝叶斯理论推导卡方分布模型和对数正态分布模型参数的后验估计表达式。
1.1 卡方分布模型的参数估计RCS随机变量σ的卡方分布概率密度函数(Probability Density Function,PDF)经典表达式为[8]
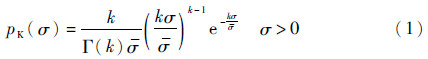
式中: σ为RCS的数学期望;k为双自由度,k值越大,拟合曲线起伏越缓和。采用式(1)对RCS建模时,通常先计算RCS的核密度函数,然后以均方差最小方法估计参数值k[6]。因为核密度函数并非精确表达式,参数k的估计值可能受低RCS特性影响,导致估计误差较大。将式(1)作以下替换:
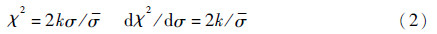
可得到卡方分布PDF的基本表达式为
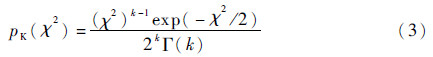
式中: χ2为自变量;k可以取非整数,以提高拟合精度。式(3)的形式便于使用Bayesian-MCMC方法对参数k进行估计。采用贝叶斯理论推导卡方分布模型的参数估计表达式时,首先把卡方分布的基本表达式(3)看作参数k的后验分布函数p(k|X),X为RCS的观测样本集合。根据贝叶斯理论[11],可计算出最大后验估计(MAP),即p(k|X)的最大值为
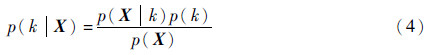
式中:
其中：p(k)为参数k的先验分布。通常假设p(k)与观测样本X相互独立,p(X)为p(k|X)的标准因子,且与k相互独立[12]。因此式(4)可简化为
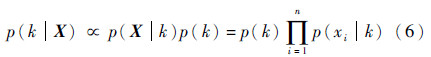
式中:xi为样本X中的元素;n为X的维数。因此,参数k的估计量为
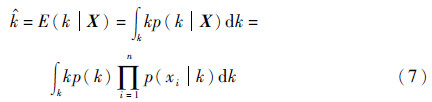
通常,卡方分布自由度k的先验分布服从伽马分布[10],即k～Γ(α,β),伽马分布的表达式为
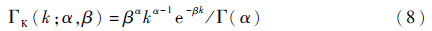
式中:α为形状参数;β为尺度参数。将式(3)和式(8)代入式(7),可得参数k的估计表达式为
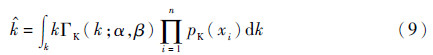
求解式(9)时,通过建立马尔可夫链得到k的估计值,可避免求取RCS样本的核密度函数。
1.2 对数正态分布模型的参数估计RCS随机变量σ的对数正态分布PDF的经典表达式为[8]
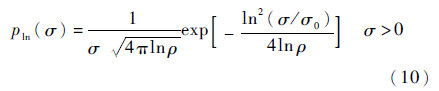
式中:σ0为随机变量σ的中值;ρ为σ的平均中值比,即σ/σ0,要求ρ值大于1。对于常规飞行器和大型舰船等传统目标,ρ值一般会大于1;隐身飞机与传统目标相比,其RCS中值相近,但是均值变小,可能会导致ρ值小于1。采用Bayesian-MCMC方法可以避免求取参数ρ。令μ和s分别为ln σ的均值和标准差,可得到对数正态分布模型PDF的基本表达式为
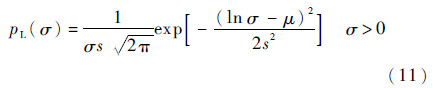
在估计参数μ时,可以固定参数s,反之亦然。μ和s的后验分布为式(11),对应的先验分布可取为正态分布和伽马分布[10],即μ～N(η,γ2),s～Γ(α,β)。则参数μ的先验分布为
式中:η为正态分布的期望;γ为正态分布的标准差。参数s的先验分布为
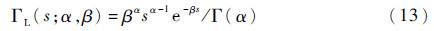
把式(11)~式(13)代入式(7),可得参数μ和s的估计表达式为
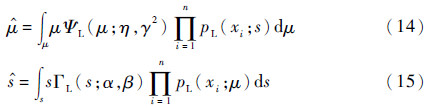
式中:pL(xi;s)和pL(xi;μ)分别为s和μ取固定值时对数正态分布PDF的表达式。传统方法通过直接计算RCS采样数据的统计特征估计起伏模型的参数,然后代入经典表达式(1)和式(10)求取2种分布的拟合曲线。由于隐身飞机的低RCS特性,可能会产生较大的参数估计误差和曲线拟合误差。采用Bayesian-MCMC方法拟合RCS分布曲线时,根据参数的后验估计表达式估计参数值,然后代入起伏模型的基本表达式(3)和式(11)对2种分布进行拟合,从而减小曲线拟合误差。
上述2种分布待估计参数的表达式均为高维度复杂形式,很难通过一般的数值方法求解,而MCMC算法能够很好地解决这类后验概率参数估计问题。
2 参数估计的MCMC实现利用MCMC算法进行模型参数估计的基本思想是:首先通过抽样实验来建立参数的马尔可夫链,使其极限分布为参数的后验分布。然后用所得的后验分布求取参数的估计值。如果合理定义初始值和迭代次数,MCMC算法总能得到一条或者几条收敛的马尔可夫链。在贝叶斯分析中,最为常用的2种MCMC算法是Gibbs采样算法和Metropolis-Hastings(M-H)采样算法[13]。为便于实现,本文采用M-H采样算法。
2.1 M-H采样算法下面以参数k的估计为例说明M-H采样算法的原理[10]。由第1节可知,X为RCS的采样数据集合,p(k|X)为参数k的后验分布。则M-H采样算法步骤如下:
1) 设定k的初始值为k(0)。
2) 令t=1,2,…,T,重复如下步骤:
① 令k=k(t-1)。
② 根据提议函数q(k′|k)产生新的备选参数值k′。其中,k的提议函数取以当前状态k(t)为均值,标准差为δ的正态分布,即q(k′|k)~N(k(t),δ2)。则备选参数值k′可表示为[14]
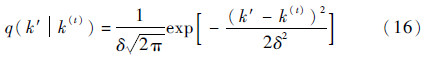
③ 计算接受概率ξ。
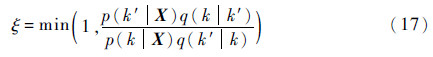
④ 是否更新第t个参数的标准如下:
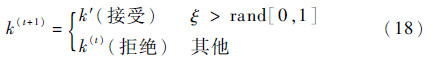
当判决状态为“接受”时,马尔可夫链状态值进行更新;否则,拒绝备选参数值,马尔可夫链保持不变,然后循环步骤2),直到目标分布p(k|X)趋于平稳。
3) 根据p(k|X)的平稳分布计算参数k的估计值。
需要说明的是,式(16)中提议函数的标准差δ的选取对算法效率的影响很大。标准差取值较小时,会得到很高的接受概率ξ,但是算法的收敛速度会变慢,导致收敛需要的迭代次数增加。因此在选取提议函数的标准差时,通常固定接受概率为20%~40%[10],通过多次实验的方法在一组标准差候选值中选择满足接受概率的候选值,详细的参数选择流程见文献[15]。
2.2 M-H采样算法收敛准则M-H采样算法的收敛准则基于边缘后验分布的Kolmogorov-Smirnov(K-S)统计函数D。实际的采样系统由2个平行运行、相互独立的M-H采样组成。每个参数的K-S检验函数表达式为[16]
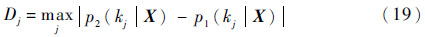
式中:p1(kj|X)和p2(kj|X)为2个平行运行样本的累积边缘分布函数。当Dj的最大值小于收敛误差门限值ε时,就可认为采样的结果收敛。Bayesian-MCMC方法的框图见图 1。
 |
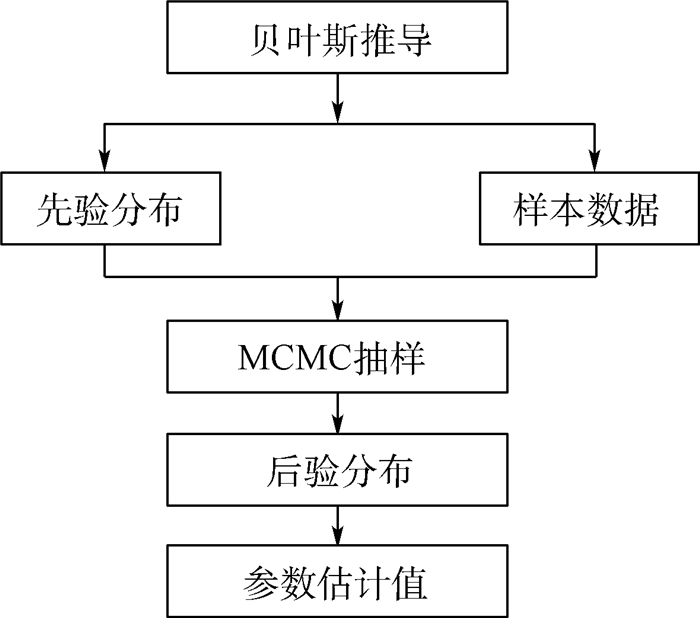| 图 1 Bayesian-MCMC方法框图 Fig. 1 Block diagram of Bayesian-MCMC method |
| 图选项 |
3 RCS数据拟合及检验为了验证Bayesian-MCMC方法对模型参数估计和曲线拟合的可行性及其精度,设计以下数值实验。
3.1 RCS数据获取将2种典型的隐身飞机目标作为研究对象(以下简称为Ⅰ型和Ⅱ型),由于隐身飞机的吸波材料结构复杂且电参数未知,本文仅考虑外形隐身技术对RCS数据的影响。隐身飞机的模型按照飞机真实尺寸在CAD中精确建立,然后导入电磁计算软件FEKO进行修模和网格剖分,采用多层快速多极子方法(MLFMM)实现了RCS的仿真计算。
2种隐身飞机的模型和姿态角定义如图 2所示。飞机迎头方向为:方位角φ=0°,俯仰角θ=0°。考虑到计算的规模和准确性,本文的仿真频率采用L波段的典型频点1 GHz,方位角采样间隔为0.1°(平飞状态,俯仰角为0°),极化方式采用水平极化。图 3为2种隐身飞机的RCS仿真数据。
 |
| 图 2 隐身飞机模型和机体坐标系 Fig. 2 Models and coordinate system of stealth aircraft |
| 图选项 |
 |
| 图 3 2种隐身飞机RCS随方位角变化 Fig. 3 RCS of two types of stealth aircrafts changing with different azimuth |
| 图选项 |
由图 3可知,2种飞机的整机RCS值都集中在-20~0 dB·m2,迎头±30°方向的RCS值集中在-20~-10 dB·m2,这与2种机型公开的RCS数据相符。图 3(a)中,由于Ⅰ型隐身飞机的外形由很多斜面组成,前机身和机翼融为一体且腹部扁平[17],其RCS样本中0 dB·m2以下的值占到采样总量的77.2%;图 3(b)中,Ⅱ型隐身飞机采用了相对传统的“平衡设计外形”,在强调隐身的同时兼顾了机动性,其RCS样本中0 dB·m2以下的值占到采样总量的69.5%。
由于所有起伏模型都是基于RCS的线性数据,因此需要将采样数据进行对数空间到线性空间的变换,变换关系如下[6]:
3.2 RCS分布拟合本节首先利用Bayesian-MCMC方法估计RCS分布模型参数,代入各模型的基本表达式得到拟合曲线;然后按照传统方法利用RCS起伏模型的经典表达式估计参数,得到RCS的拟合曲线;最后将两者进行比较。
进行Bayesian-MCMC仿真实验时,各参数的先验分布均由第1节给出,参照文献[10]设置每种先验分布合适的初值。每条马尔可夫链进行10 000次M-H迭代,初始接受概率ξ=20%,多次实验选取的提议分布标准差为δ=2,0.5,1(分别对应参数k,μ,s)。将前2 000次迭代结果舍去以保证收敛,收敛误差门限取为ε=0.05。Ⅰ型隐身飞机各参数的马尔可夫链和2种隐身飞机各参数的后验分布如图 4和图 5所示。
 |
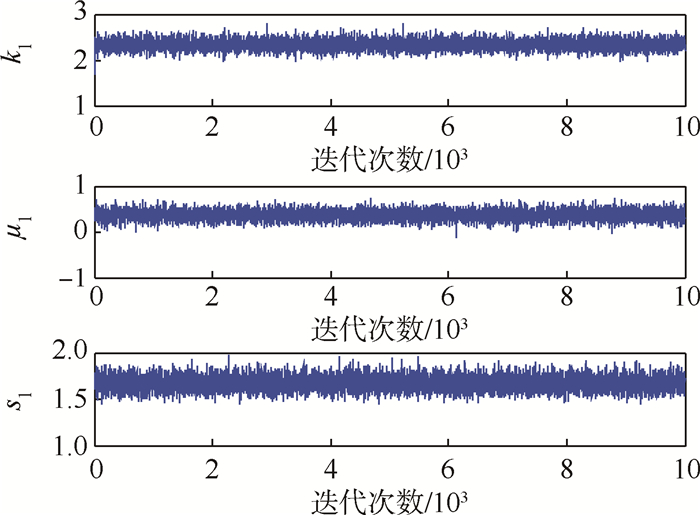| 图 4 Ⅰ型隐身飞机各参数的马尔可夫链 Fig. 4 Markov chain of parameters for type Ⅰ stealth aircraft |
| 图选项 |
 |
| 图 5 2种隐身飞机各参数的后验分布 Fig. 5 Posterior distribution of parameters for both types of stealth aircrafts |
| 图选项 |
图 4表明,随着迭代次数增加,各参数的马尔可夫链都能很快地收敛于其真实值,并在真实值附近振荡。图 5中各参数的后验分布都趋近于其先验分布(伽马分布的极限分布是正态分布),且后验分布的均值就是各参数的估计值。
表 1为采用Bayesian-MCMC方法对2种隐身飞机RCS数据的分布模型参数估计的结果。分析表 1可知,在相同迭代次数下,Bayesian-MCMC方法对2种分布的参数估计精度相当,且蒙特卡罗误差均远小于收敛误差门限,这说明该方法对2种模型均适用。将表 1中各参数的估计值代入各起伏模型的基本表达式进行拟合,与传统方法拟合结果进行对比,如图 6所示。
表 1 参数估计值与蒙特卡罗误差 Table 1 Parameter estimates and Monte Carlo errors
| 机型 | 估计值/蒙特卡罗误差 | ||
| k | μ | s | |
| Ⅰ型 | 2.33/1.3×10-3 | 0.36/1.0×10-3 | 1.67/7.9×10-4 |
| Ⅱ型 | 3.63/1.3×10-3 | 1.05/8.2×10-4 | 1.43/5.6×10-4 |
表选项
 |
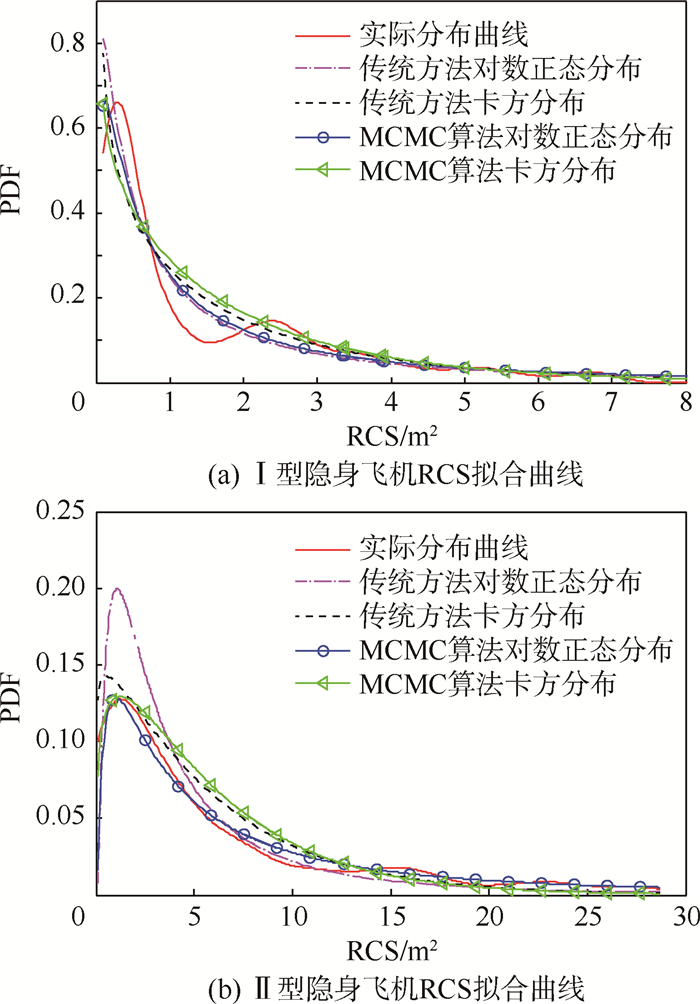| 图 6 2种隐身飞机RCS拟合曲线对比 Fig. 6 Comparison types of of RCS fitting curves for both types of stealth aircrafts |
| 图选项 |
2种类型隐身飞机的RCS分布特性及其拟合曲线特点如下:
1) 2种类型隐身飞机的RCS实际分布曲线的峰值均靠近纵轴且宽度较窄,反映了隐身飞机RCS的低值聚集特性,且Ⅰ型隐身飞机的低RCS特性更明显。
2) 传统方法的拟合曲线中,卡方分布对峰值拟合较好,对数正态分布存在对峰值估计过高的缺点,且RCS均值越小,拟合峰值越高,这是因为对数正态分布模型的包络项与自变量成反比。在曲线峰值后的RCS高值区域(RCS值大于1 m2的曲线部分),对数正态分布的拟合效果优于卡方分布。
3) 比较拟合曲线与实际分布曲线的吻合程度,Bayesian-MCMC方法比传统方法拟合的效果更好,且适用于2种起伏模型。这是由于传统方法通过直接计算原始采样数据的统计特征估计参数,而隐身飞机RCS的低值聚集特性会导致估计误差较大。Bayesian-MCMC方法通过构造马尔可夫链估计模型的参数值,避免直接计算核密度函数和参数ρ,使拟合曲线的峰值与真实的峰值比较接近。在曲线峰值后的RCS高值区域,2种方法拟合的效果相近。
下文通过拟合优度检验进一步比较分析2种方法的拟合精度。
3.3 拟合优度检验由于本文涉及卡方分布和对数正态分布的不同表达形式,因此采用文献[7]的非参数检验方法比较2种拟合方法的拟合精度,拟合误差公式为
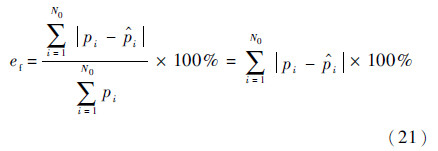
式中:pi为RCS数据的真实概率分布;
为各起伏模型估计的概率分布;N0为分布曲线被划分的段数,且 
。 检验结果如表 2所示,其中精度改善比例由2种方法的拟合误差之差除以传统方法拟合误差所得。分析表 2可知,就起伏模型而言,改善后的对数正态分布模型的拟合精度高于卡方分布模型,因为对数正态分布模型对峰值后曲线的拟合效果本就优于卡方分布模型,当峰值得到改善以后,综合效果会进一步提高拟合精度。就拟合方法而言,基于Bayesian-MCMC方法的曲线拟合误差均小于传统方法的拟合误差,对2种起伏模型的拟合精度的改善比例均为50%以上,且对于对数正态分布的拟合精度改善更明显。表 2 2种起伏模型的拟合误差 Table 2 Error-of-fit for both fluctuation models
| 机型 | 分布模型 | 拟合误差/% | 精度改善比例/% | |
| 传统方法 | MCMC算法 | |||
| Ⅰ型 | 卡方分布 | 6.83 | 2.04 | 70.13 |
| 对数正态分布 | 6.18 | 1.46 | 76.38 | |
| Ⅱ型 | 卡方分布 | 4.98 | 2.37 | 52.41 |
| 对数正态分布 | 12.59 | 1.29 | 89.75 | |
表选项
4 结 论本文研究了隐身飞机RCS起伏模型优化问题。在贝叶斯框架下重新推导了模型参数的后验估计表达式,并结合MCMC算法得到参数估计值。比较本文方法和传统方法的仿真结果,得出以下结论:
1) 本文方法对卡方分布模型和对数正态分布模型均适用,估计参数的蒙特卡罗误差比收敛误差门限低1~2个数量级。
2) 本文方法对2种模型峰值的拟合效果均优于传统方法,在曲线峰值后的RCS高值区域,2种方法的拟合效果相近。
3) 采用本文方法能够有效减小隐身飞机低RCS特性的干扰,对2种起伏模型的拟合精度均提高50%以上,且对于对数正态分布的改善更明显。
理论上,只要Bayesian-MCMC方法的迭代次数足够多,参数的估计值就可以逼近最优值,从而提高模型的拟合精度,这在起伏模型的实际应用中有一定参考价值。
参考文献
| [1] | CUI G, DE MAIO A,PIEZZO M.Performance prediction of the incoherent radar detector for correlated generalized Swerling-Chi fluctuating targets[J].IEEE Transactions on Aerospace and Electronic Systems,2013,49(1):356-368. |
| Click to display the text | |
| [2] | 岳奎志,孙聪, 姬金祖.双立尾对战斗机隐身特性的数值模拟[J].北京航空航天大学学报,2014,40(2):160-165. YUE K Z,SUN C,JI J Z.Numerical simulation on the stealth characteristics of twin-vertical-tails for fighter[J].Journal of Beijing University of Aeronautics and Astronautics,2014,40(2): 160-165(in Chinese). |
| Cited By in Cnki (6) | Click to display the text | |
| [3] | ZIKIDIS K, SKONDRAS A,TOKAS C.Low observable principles,stealth aircraft and anti-stealth technologies[J].Journal of Computations & Modeling,2014,4(1):129-165. |
| Click to display the text | |
| [4] | SWERLING P. Probability of detection for fluctuating targets[J].IRE Transactions on Information Theory,1960,6(2):269-308. |
| Click to display the text | |
| [5] | SONG X F, BLAIR W D,WILLETT P,et al.Dominant-plus-Rayleigh models for RCS:Swerling Ⅲ/Ⅳ versus Rician[J].IEEE Transactions on Aerospace and Electronic Systems,2013,49(3):2058-2064. |
| Click to display the text | |
| [6] | 黄培康,殷红成, 许小剑.雷达目标特征[M].北京:电子工业出版社,2010:112-117. HUANG P K,YIN H C,XU X J.Radar target characteristics[M].Beijing:Publishing House of Electronic Industry,2010:112-117(in Chinese). |
| [7] | XU X J, HUANG P K.A new RCS statistical model of radar targets[J].IEEE Transactions on Aerospace and Electronic Systems,1997,33(2):710-714. |
| Click to display the text | |
| [8] | 史伟强,徐乐, 史小卫,等.基于完备对数正态分布模型的隐形飞行器动态RCS统计特性研究[J].电子与信息学报,2013,35(9):2121-2125. SHI W Q,XU L,SHI X W,et al.Dynamic RCS statistic characterization of stealth aircraft using complete lognormal distribution[J].Journal of Electronics & Information Technology,2013,35(9):2121-2125(in Chinese). |
| Cited By in Cnki (5) | Click to display the text | |
| [9] | 陈世春,黄沛霖, 姬金祖.典型隐身飞机的 RCS 起伏统计特性研究[J].航空学报,2014,35(12):3304-3314. CHEN S C,HUANG P L,JI J Z.Research on radar cross section fluctuation characteristics of typical stealth aircrafts[J].Acta Aeronautica et Astronautica Sinica,2014,35(12):3304-3314(in Chinese). |
| Cited By in Cnki (2) | Click to display the text | |
| [10] | PAOLO G, GEOF H G,BANI K M.Bayesian modeling using WinBUGS[M].Hoboken:John Wiley & Sons,Inc.,2009:25-30. |
| [11] | LI Y,SONG S B. Bayesian estimation of parameters for pearson Ⅲ distribution[C]//IEEE International Symposium on Water Resource and Environmental Protection(ISWREP).Piscataway,NJ:IEEE Press,2011:630-632. |
| [12] | SHENG Z. The estimation of lower refractivity uncertainty from radar sea clutter using the Bayesian-MCMC method[J].Chinese Physics B,2013,22(2):029302. |
| Click to display the text | |
| [13] | GASEMYR J. The spectrum of the independent Metropolis-Hastings algorithm[J].Journal of Theoretical Probability,2006,19(1):152-165. |
| Click to display the text | |
| [14] | 马洪斌,马岩, 杨春梅,等.基于Metropolis-Hastings算法的 α 稳定分布参数估计[J].电机与控制学报,2012,16(12):94-98. MA H B,MA Y,YANG C M,et al.Parameter estimation of α-stable distribution using Metropolis-Hastings algorithm[J].Electrical Machines and Control,2012,16(12):94-98(in Chinese). |
| Cited By in Cnki (1) | Click to display the text | |
| [15] | 陈平,徐若曦. Metropolis-Hastings自适应算法及其应用[J].系统工程理论与实践,2008,28(1):100-108. CHEN P,XU R X.Metropolis-Hastings adaptive algorithm and its application[J].Systems Engineering-Theory & Practice,2008,28(1):100-108(in Chinese). |
| Cited By in Cnki (37) | Click to display the text | |
| [16] | 盛峥,黄思训,曾国栋.利用Bayesian-MCMC方法从雷达回波反演海洋波导[J].物理学报,2009,58(6):4335-4341. SHENG Z,HUANG S X,ZENG G D.Ocean duct inversion from radar clutter using Bayesian-Markov chain Monte Carlo method[J].Acta Physica Sinica,2009,58(6):4335-4341(in Chinese). |
| Cited By in Cnki (8) | Click to display the text | |
| [17] | 白振东,刘虎, 武哲.低可探测机身参数化造型与优化[J].北京航空航天大学学报,2007,33(12):1391-1394. BAI Z D,LIU H,WU Z.Parametric modeling and optimization of low observability fuselage in aircraft conceptual design[J].Journal of Beijing University of Aeronautics and Astronautics,2007,33(12):1391-1394(in Chinese). |
| Cited By in Cnki (10) | Click to display the text |
