人工神经网络(Artificial Neural Network,ANN)具有大规模并行运算、自组织性和自学习等特点,理论上可以任意精度拟合非线性模型,在模式识别领域有着非常成功的应用[6, 7, 8, 9, 10]。但与其他算法相比较,人工神经网络的分类准确率对初始权值的依赖程度高[11, 12];此外,原始数据一般含有冗长的无用信息且线性不可分[13, 14],所以有必要通过数据压缩技术提取原始数据的主要特征。本文以误差反向传播(Back Prorogation,BP)算法为理论基础,利用主成分分析(Principal Component Analysis,PCA)法对原始数据进行特征提取,并利用自动编码对权值进行初始化;设计了已知故障类型情况下的改进人工神经网络故障诊断学习系统。
1 系统流程及算法1.1 系统流程航天器信号检测时,数据采集速率快,每秒高达30 MB;种类繁多,如某航天器一共检测50路数据流。而其中某几路数据流才得到关注,却把其他数据存入Oracle数据库中以备后续研究。结合BP神经网络需要训练的特点,提出图 1所示的学习系统流程。可知,流程主要包括获取数据、电信号模式识别以及网络训练3个部分。整个过程可以实时进行网络训练,也可调用已经训练好的网络进行故障诊断,加入对网络参数合理性的判断环节,便可实现智能化的电信号模式识别。
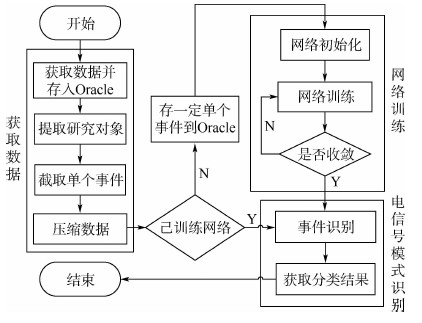 |
| 图 1 学习系统流程Fig. 1 Learning system flowchart |
| 图选项 |
1.2 算法1.2.1 网络结构人工神经网络不需要建立复杂的数学模型,只要选取合理的参数且通过足够数据的训练就能以任一精度拟合复杂的非线性问题。航天器信号诊断所采集的时域上的信号是高度非线性的,而且同一单个事件的信号相关性较高,所以适合用人工神经网络来进行信号诊断。本文用到的人工神经网络拓扑如图 2所示,该网络包括输入层、隐藏层以及输出层。输入层的神经元个数由数据特征数决定;隐藏层节点数可由经验公式得到,本文利用实验的方法获取;输出层为3个神经元。图 2中:Xn为训练样本;Wmn和Wkm为权值;Yk为输出;n为训练样本维数;m为隐藏层神经元的个数;k为输出层神经元的个数。隐藏层的激励函数选取Sigmoid函数,如式(1)所示:

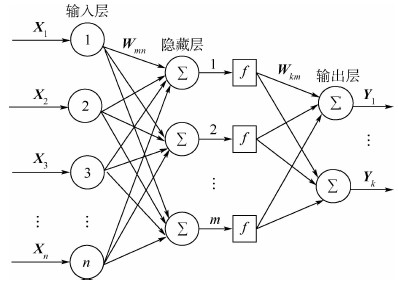 |
| 图 2 人工神经网络拓扑结构Fig. 2 Topology of artificial neural network |
| 图选项 |
1.2.2 网络训练Step 1获取在线或离线数据,滤波并提取单个事件的信号。
Step 2 随机产生小于1的初始权值。
Step 3 重复下述过程直至收敛(对各样本依次计算,其中j和i分别表示第j层和该层第i个神经元,其上限分别由神经网络总层数及每层神经元个数决定)。
正向计算各单元的输出值Outj:

对输出层计算中间变量σj:

对隐藏层计算中间变量σj:
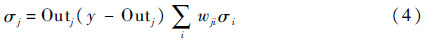
对各权值进行修正并保存第t次修正值Δwij(t):
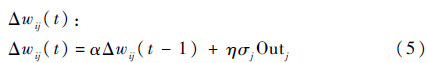
修正权值wij(t+1):
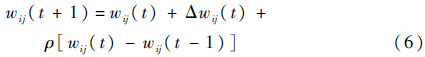
式中:ρ为动量学习率;α和η分别为惯性系数和步长。可以积累前训练经验,加快网络收敛过程。
1.3 算法改进人工神经网络算法本身决定了误差函数一般存在多个局部极小点[15]。算法能否快速收敛到全局最小值点在很大程度上依赖于网络初始权值。初始权值选择不合理将导致网络收敛至局部极小值点,使网络训练失败。在其他参数不变的情况下,随机产生200组初始权值对网络进行训练得到分类准确率随循环次数变化曲线,如图 3所示。可知,在其他参数不变的情况下,测试样本的分类准确率也会因为网络初始权值随机产生而发生明显且没有规律的变化,这样很难保证网络重新训练后分类准确率的改变保持在很小的范围内。因此,测试的分类准确率和网络初始权值之间的关系很难用数学模型描述。深度学习技术中的自动编码方法可以根据原始数据对网络权值进行初始化,使网络初始权值能更好地映射出原始数据中的关键特征。自动编码的基本思想是:将原始信号通过编码器编译成代码,再用译码器将代码转化成重构信号,最后用重构信号与原始信号的误差反向调整编码器与译码器的参数[16, 17]。根据该思想,对已有稀疏自动编码进行改进,提出适合浅层人工神经网络的自动编码算法,其流程和拓扑如图 4所示。图中:Xn为训练样本;Wmn为编码器权值;W1nm为译码器权值;Yn为译码数据;Om为编码器输出;ξ为惩罚因子。
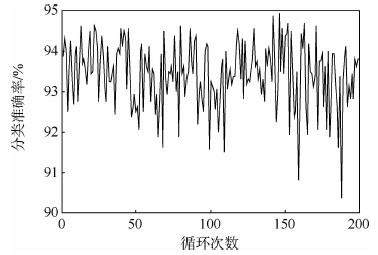 |
| 图 3 分类准确率随循环次数变化曲线Fig. 3 Curve of classification accuracy varying with cycle times |
| 图选项 |
由图 4(a)可知,编码器和译码器公式分别为

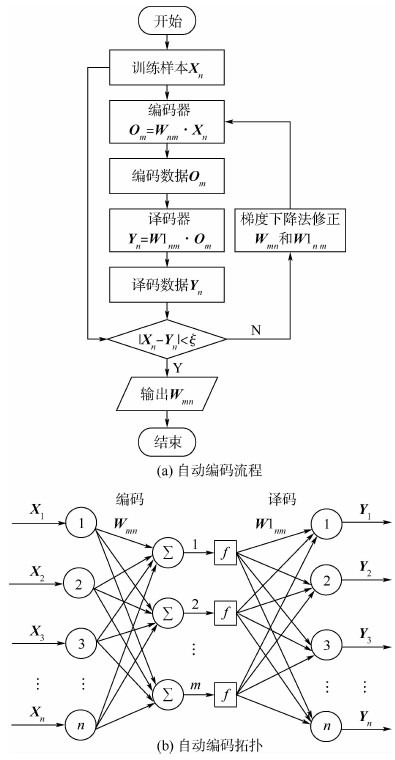 |
| 图 4 自动编码原理示意图Fig. 4 Schematic of auto-encoder principle |
| 图选项 |
可选择训练样本与重构数据的误差作为网络的惩罚函数:
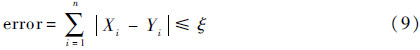
当总误差小于等于惩罚因子时,网络停止训练。
网络基本训练流程如下:
Step 1 训练样本作为自动编码的原始数据输入网络。
Step 2 通过编码器将训练样本的维度降至与隐藏层神经元个数相同的编码数据。
Step 3 通过译码器将编码数据转化为重构数据,重构数据的维数要与原始数据的维数相同。
Step 4 计算训练样本与重构数据的总误差,作为调整编码器和译码器权值的惩罚量。
Step 5 利用梯度下降法调整编码器和译码器的参数。
Step 6 重复Step 1~Step 5,使总误差达到能够容忍的程度。
Step 7 输出Wmn作为原人工神经网络输入层至隐藏层的初始权值。
2 仿真实验2.1 训练数据获取1) 用3种不同类型信号(分别表示航天器滚转、俯仰和偏航)作为原始数据,并俯仰和偏航信号模拟故障信号。分割成单个信号并打乱原有排序后共获取1 800个单事件信号,其中滚转、俯仰和偏航的分类编号分别为1、2和3。
2) 前1 000组数据用于训练,后800组数据用于测试。数据输入网络前用主成分分析法进行主成分提取。
2.2 隐藏层神经元个数抉择及训练循环次数估计对于不同的数据集合,隐藏层神经元个数的最优值往往不同;训练时,循环次数过少不能使网络收敛到稳定状态,过多又会增加训练时间。为此,选择122-15-3、122-20-3、122-30-3网络结构,分别在循环次数增加的情况下,得到如图 5所示的变化曲线。可以看出,神经元个数为20的隐藏层能很快收敛到稳定值,故选取122-20-3网络结构。在该网络结构下,循环次数大于15时,可以使网络收敛到稳定状态。为了保证每次训练都达到稳定,且又不延长训练时间,本系统选择的最大循环次数为25。
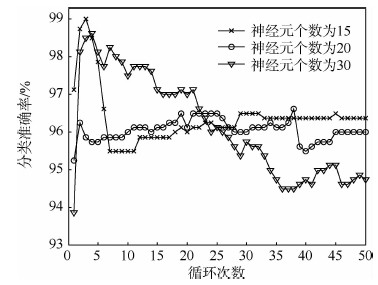 |
| 图 5 隐藏层神经元个数不同时分类准确率随循环次数变化曲线Fig. 5 Curves of classification accuracy varying with cycle times when number of hidden layer neurons changes |
| 图选项 |
2.3 学习率选择学习率对系统训练过程的稳定性影响很大。学习率过大,导致训练时网络权值修正量过大,进而使网络不能收敛;但学习率过小会使训练时间过长,并有陷入局部最小值的可能。为了获得最优的学习率,本文设计了在保证分类准确率大于98%的情况下,训练时间随学习率变化的实验,得到的曲线如图 6所示。
 |
| 图 6 训练时间随学习率的变化曲线Fig. 6 Curve of training time varying with learning rate |
| 图选项 |
由图 6可知,当学习率小于0.015或者大于0.150时,训练时间明显增加;学习率为0.050左右时,训练时间短且比较稳定。故本系统选取0.050作为学习率。
3 实验结果分析3.1 算法改进前后结果比对算法改进前后,得到分类总误差随循环次数的变化如图 7所示。可知,初始权值优化后,待网络达到稳定,虽然分类总误差增加(优化后分类总误差约为432,而未优化的网络分类总误差可以达到150以下);但与未优化前相比,网络能很快收敛到稳定状态(优化后只需不到100次循环就能使网络稳定,而未优化网络循环1 000多次还未能达到稳定)。
 |
| 图 7 算法改进前后分类总误差随循环次数变化Fig. 7 Classification total error changing with cycle times of original and improved algorithms |
| 图选项 |
因此,优化后的网络能使训练时间更短;而分类总误差只是作为权值修正的依据,网络稳定后的分类总误差大并不会导致分类准确率下降。本文设计如下实验进行验证:
分别用100组,每组1 800个单个事件的测试样本对优化前后且训练好的网络进行测试,结果如图 8所示。图中,横坐标表示分类准确率所在区间,纵坐标表示分类准确率在某区间的组数占总组数的百分比。可知,初始权值随机产生时,分类准确率集中在96%~100%范围内;而当初始权值用自动编码优化后,分类准确率范围缩小至97%~99%。网络优化前后分类准确率的平均值分别为98.18%和98.2%。因此,初始权值优化后网络的分类准确率没有下降,而稳定性和收敛速率显著提高。
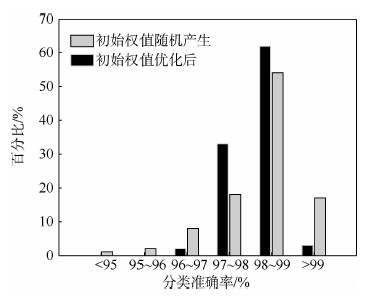 |
| 图 8 算法改进前后分类准确率分布Fig. 8 Classification accuracy distribution of original and improved algorithms |
| 图选项 |
3.2 算法比较除了稳定性和收敛速率,分类准确率是评价人工神经网络优劣的另一个重要标志。分别用K最近邻(K-nearest neighbor)、朴素贝叶斯(naive Bayesian)和本文提供的自动编码人工神经网络对200组,每组4 500个样本进行分类,得到的结果如图 9所示。图中,纵坐标表示分类准确率所在区间,横坐标表示分类准确率在某区间的组数占总组数的百分比。
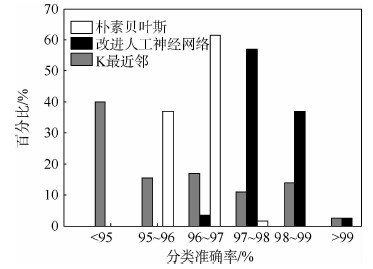 |
| 图 9 不同算法分类准确率分布Fig. 9 Classification accuracy distribution of different algorithms |
| 图选项 |
在稳定性方面:200组测试数据中,朴素贝叶斯分类准确率集中在95%~97%,分类准确率为97%~98%的只有7组;改进人工神经网络分类准确率则集中在97%~99%。因此,朴素贝叶斯和改进的人工神经网络稳定性比K最近邻略高。在分类准确率方面:改进人工神经网络、朴素贝叶斯及K最近邻的分类准确率平均值分别为97.87%、96.13%和95.1%,数据表明,改进人工神经网络的分类准确率更高。
4 结 论本文提出了对航天器信号进行诊断的一般流程;利用主成分分析提取原始数据的主要特征;并用自动编码对原人工神经网络算法进行了改进。实验数据表明:算法的稳定性、收敛速率及分类准确率都得到了提高。由于该算法仿真采用的是某航天器的原始数据,所以可直接运用于航天器信号分类识别。人工神经网络算法设计简便,在处理具体规则模糊的数据上有很大的灵活性和自适应性。对人工神经网络和其他算法融合做进一步研究,即可提高航天器故障信号识别准确率和实时性。本文设计的自动编码算法相对简单,还有很大的改进空间,后期可做进一步研究。
参考文献
| [1] | LI K,LIU W K, WANG J,et al.An intelligent control method for a large multi-parameter environmental simulation cabin[J].Chinese Journal of Aeronautics,2013,26(6):1360-1369. |
| Click to display the text | |
| [2] | LIU Y,LI K, SONG S,et al.The research of spacecraft electrical characteristics identification and diagnosis using PCA feature extraction signal processing[C]//International Conference on Signal Processing(ICSP).Piscataway,NJ:IEEE Press,2014:1413-1417. |
| Click to display the text | |
| [3] | LIU Y,LI K, HUANG Y,et al.Spacecraft electrical characteristics identification study based on offline FCM clustering and online SVM classifier[C]//Multisensor Fusion and Information Integration for Intelligent Systems(MFI).Piscataway,NJ:IEEE Press,2014:1-4. |
| Click to display the text | |
| [4] | LI K,LIU W K, WANG J,et al.Multi-parameter decoupling and slope tracking control strategy of a large-scale high altitude environment simulation test cabin[J].Chinese Journal of Aeronautics,2014,27(6):1390-1400. |
| Click to display the text | |
| [5] | 杨天社,杨开忠, 李怀祖.基于知识的卫星故障诊断与预测方法[J].中国工程科学,2003,5(6):64-67. YANG T S,YANG K Z,LI H Z.Research on knowledge-based method for satellite fault diagnosis and prediction[J].Engineering Science,2003,5(6):64-67(in Chinese). |
| Cited By in Cnki (11) | Click to display the text | |
| [6] | 韩立群. 人工神经网络[M].北京:北京邮电大学出版社,2006:20-66. HAN L Q.Artificial neural networks[M].Beijing:Beijing University of Posts and Telecommunications Press,2006:20-66(in Chinese). |
| [7] | 冯伟兴,梁洪, 王臣业.Visual C++数字图像模式识别典型案例详解[M].北京:机械工业出版社,2012:50-63. FENG W X,LIANG H,WANG C Y.Visual C++digital image pattern recognition detailed typical case[M].Beijing:China Machine Press,2012:50-63(in Chinese). |
| [8] | 秦振汉. 人工神经网络专家系统在卫星故障诊断中的应用研究[D].哈尔滨:哈尔滨工业大学,2005:8-12. QIN Z H.Application of neural network expert system in satellite fault diagnosis[D].Harbin:Harbin Institute of Technology,2005:8-12(in Chinese). |
| Cited By in Cnki (21) | Click to display the text | |
| [9] | HUANG H, ZHU Y W,YANG L P,et al.Stability and shape analysis of relative equilibrium for three-spacecraft electromagnetic formation[J].Acta Astronautica,2014,94(1):116-131. |
| Click to display the text | |
| [10] | KENIG S, BEN-DAVID A,OMER M,et al.Control of properties in injection molding by neural networks[J].Engineering Applications of Artificial Intelligence,2001,14(6):819-823. |
| Click to display the text | |
| [11] | 戴文战,娄海川, 杨爱萍.非线性系统人工神经网络预测控制研究进展[J].控制理论与应用,2009,26(5):521-530. DAI W Z,LOU H C,YANG A P,et al.An overview of neural network predictive control for nonlinear systems[J].Control Theory & Applications,2009,26(5):521-530(in Chinese). |
| Cited By in Cnki (1) | Click to display the text | |
| [12] | 姚健,纪志成,黄言平. 基于人工神经网络的非线性多模型自适应控制[J].控制工程,2014,21(2):172-177. YAO J,JI Z C,HUANG Y P.Nonlinear multi-model adaptive control based on neural networks[J].Control Engineering of China,2014,21(2):172-177(in Chinese). |
| Cited By in Cnki (1) | Click to display the text | |
| [13] | LEE C Y,LEE J J. Adaptive control for uncertain nonlinear systems based on multiple neural networks[J].IEEE Transactions on Systems,Man and Cybernetics-Part B:Cybernetics,2004,34(1):325-333. |
| Click to display the text | |
| [14] | VRABIE D, LEWIS F.Neural network approach to continuous-time direct adaptive optimal control for partially unknown nonlinear systems[J].Neural Networks,2009,22(3):237-246. |
| Click to display the text | |
| [15] | 林海明,杜子芳. 主成分分析综合评价应该注意的问题[J].统计研究,2013,30(8):25-31. LIN H M,DU Z F.Some problems in comprehensive evaluation in the principal component analysis[J].Statistical Research,2013,30(8):25-31(in Chinese). |
| Cited By in Cnki (64) | Click to display the text | |
| [16] | SCHÖLKOPF B, PLATT J,HOFMANN T.Greedy layer-wise training of deep networks[C]//Proceedings of the 2006 Conference, Advances in Neural Information Processing Systems. Cambridge:MIT Press,2007,19:153-160. |
| Click to display the text | |
| [17] | HINTON G E, OSINDERO S,TEH Y W.A fast learning algorithm for deep belief nets[J].Neural Computation,2006,18(7):1527-1554. |
| Click to display the text |
