乏信息是指测量数据具有的测量信息不完整和不充足,如概率分布已知,但只有少量数据可供分析;概率分布未知,测量数据也只有少量;趋势项未知等,都具有乏信息的特征^[1]。航空、航天运载系统、载人航天工程系统、战术导弹和飞行姿态控制等行业经常遇到更加复杂的乏信息问题^{[2, 3]}。
对于空间机械臂而言,振动会影响安装在机械臂上设备的工作精度,如北斗卫星要求接收天线对于机械臂的角度误差小于18″;空间机械臂视觉系统要求相机的图像误差小于1个像素^[4]。柔性机械臂减小臂杆的振动,提高末端的定位精度^[5]。因此,分析空间机械臂的振动信号是改善空间设备精度的重要前提。由于空间机械臂所处环境是复杂而未知的外太空,不利于稳定实验数据的获取,而且受实验操作困难、实验成本过高等因素影响,使得空间机械臂随机振动数据表现为样本量小且先验信息未知的特点。用传统的基于统计理论的数据归纳方法无法对其进行分析。
对于乏信息数据的估计,非统计理论显示出很大的优越性^[6]。近年来,自助法^{[7, 8]}、灰色系统理论^[9]、模糊理论和信息熵理论等方法在处理乏信息问题上得到了广泛的应用。文献[10]提出的灰色系统理论在乏信息数据中已得到具体应用^[11],但是灰色方法难以有效地检验置信区间。文献[2]将自助法应用到飞行振动数据的评估当中。文献[12]应用模糊数学理论实现了乏信息测量参数的有效估计。文献[13]利用最大熵理论实现了机床误差的概率分布。自助法是一种非参数估计方法^[14],虽然可用于区间估计^[15],但自助抽样的过程中产生了附加不确定度。文献[16]提出的灰自助方法将灰色系统理论和自助法的优点互补,可用于乏信息数据的估计,但对区间估计的评价还很不完善。
振动信号分为时域和频域2种。基于功率谱密度(Power Spectral Density,PSD)的频域分析方法由于计算简单、不需要循环计数等优点被广泛采用^[17]。振动功率谱密度的估计是航空航天设备安全性和可靠性的重要保障,传统的估计方法有极值包络法^[18]、统计容差法^[19]和改进的统计容差法^[20]等,但上述方法都是以统计理论为基础的,对乏信息数据给出的试验参数在量值及合理性方面尚缺乏严谨的理论依据。
本文将灰自助方法应用于乏信息空间机械臂振动功率谱密度的估计,提出相应的评价指标;并且将灰自助方法与灰色方法、自助法进行对比,验证了灰自助方法在乏信息随机振动信号估计中的优越性。
1 灰自助方法1.1 灰自助建模在动态振动试验中,设乏信息空间在总时间内得到的测量数据振动功率谱密度序列集合为

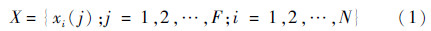
式中:x_i(j)为时刻i与频率j处的功率谱密度值;F为X的频率总点数;N为X在总时间内测量数据的个数。取频率j处的前m次测量得到的振动功率谱密度序列为

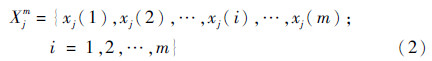
依据自助抽样原理^[21],在X_j^m中进行自助抽样,获得B个自助仿真样本:

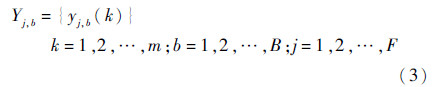
式中:y_j,b(k)为频率j处第b个自助样本中的第k个数据。根据灰色模型GM(1,1)^[22],设Y_j,b的一次累加生成序列为

均值生成序列为
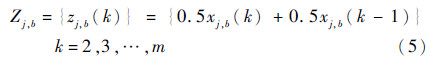
则在初始条件x_j,b(1)=y_j,b(1)下的最小二乘解为
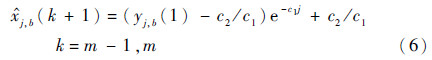
式中:

通过累减生成,第w=m+1次测量的预测值可以表示为

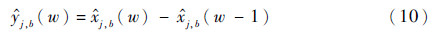
设在频率j处的第w=m+1次测量有B个数据,构成如下序列:

由于B很大,可以用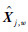建立关于属性x_j,m的频率函数:
式中:F_j,w为灰自助频率函数。可以看出,灰自助方法并未涉及原始数据序列的概率分布问题,这意味着灰自助方法不依赖于任何概率分布,因此弥补了统计理论在乏信息数据估计中的不足。灰自助方法通过自助抽样,在有限信息中充分挖掘更多的系统信息,供GM(1,1)进行累加生成和数据融合。因此,这种方法可以更加准确地对频域乏信息数据进行估计。
1.2 估计指标1) 真值估计
在频率j处的真值估计可以用加权平均值表示为

式中:X₀(j)为频率j处的估计真值;Q为分组数,即将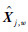分为Q组;x_mq为第q组中值;F_wq为对应于x_mq的灰自助频率。将在频率j处的真值估计误差定义为

式中:X(j)为频率j处的测量真值。在频率j处的真值估计相对误差定义为

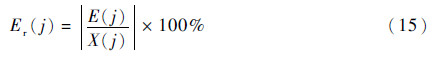
定义最小相对误差为

最大相对误差为

真值估计的平均相对误差定义为

估计误差E越小,真值估计的精度越高。
2) 区间估计
定义频率j处在置信度水平P下的区间估计为

式中:α=1-P为显著性水平;X_α/2(j)为对应于概率为α/2时的参数值x_m(j);X_1-α/2(j)为对应于概率为(1-α/2)时的参数值x_m(j);X_L(j)为区间估计的下限;X_U(j)为区间估计的上限。参数指标X_L(j)和X_U(j)分别描述了频率j处瞬时波动的极小值和极大值。
设当测量数据的个数为n时,有h个数据位于区间估计[X_L(j),X_U(j)]之外。定义置信度水平为P时区间估计的可靠度为

定义平均可靠度为

由上述定义可知,当置信度水平与可靠度越接近时,区间估计的质量越高。定义可靠度的偏差为

为说明区间估计的准确程度,定义区间估计准确度为

2 实例分析空间机械臂结构示意图如1所示。振动测量点为固结端和活动端。本文实验数据来源为太空真实实验数据,在太空进行随机振动数据测量,得到固结端、活动端和自由端的振动功率谱密度共80组测量数据。为体现乏信息的特点,取所测振动功率谱密度前m组数据作为原始样本。分别以空间机械臂固结端和活动端振动功率谱密度作为真值估计和区间估计,并以自由端振动功率谱密度来验证灰自助方法估计的有效性。

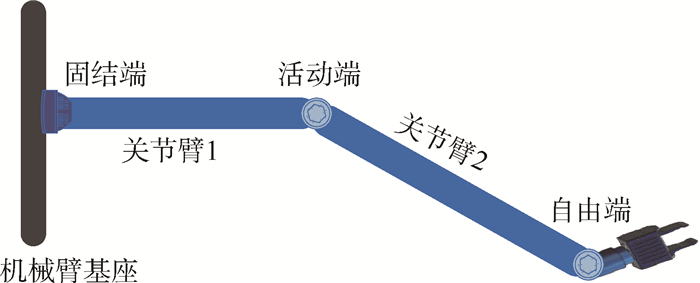图 1 空间机械臂结构示意图 Fig. 1 Schematic of space manipulator structure

图选项

2.1 实例评估 2.1.1 真值估计以空间机械臂固结端的振动功率谱密度为例。图 2为不同方法对固结端振动信号的真值估计和估计误差。其中频率测量范围为10～1 000 Hz,分辨力为5 Hz。图 2(a)给出了灰自助方法对固结端振动功率谱密度的真值估计(m=6,B=500,Q=10),图 2(b)和图 2(c)分别给出了相同条件下自助法和GM(1,1)的真值估计结果。

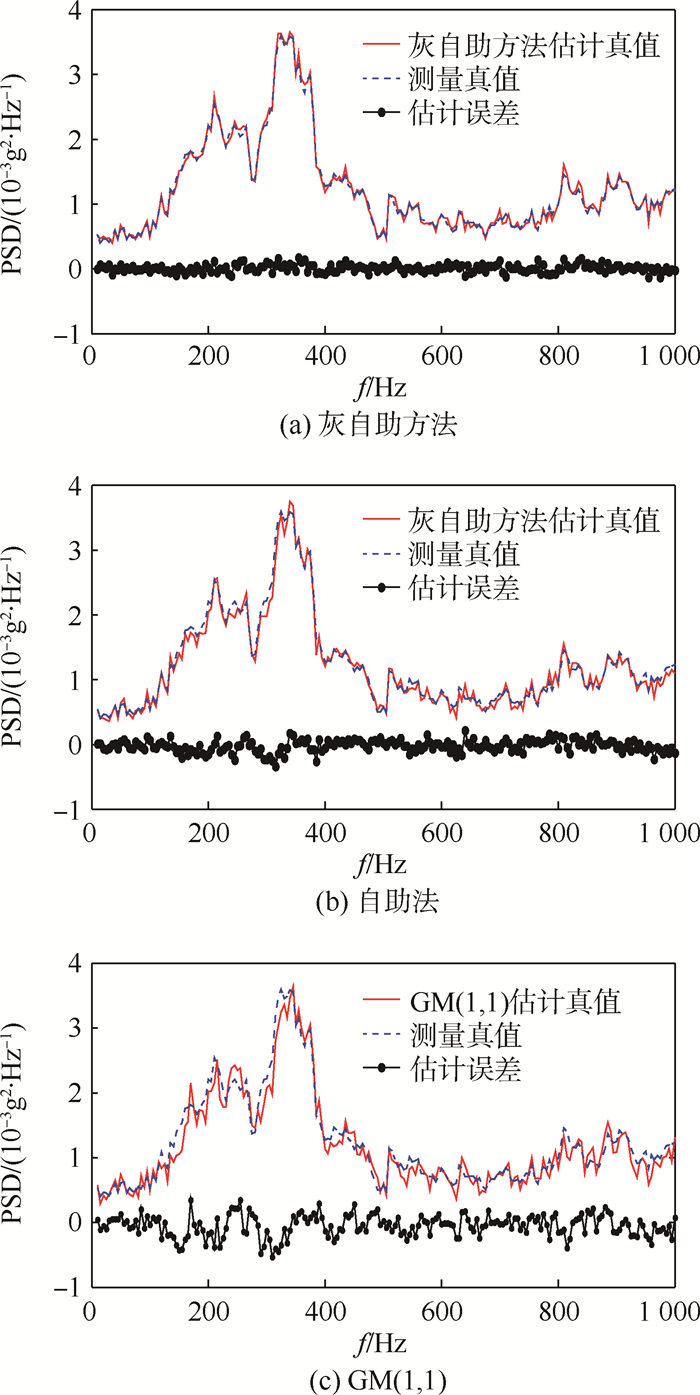图 2 不同方法对固结端振动信号的真值估计和估计误差 Fig. 2 Estimated values and estimated errors of fixed-end vibration signals by different methods

图选项

灰自助方法与自助法相比较,不仅具备自助法对数据的扩充能力,而且具备对数据预报的能力,因此数据信息挖掘得更加充分。由图 2可以看出,在乏信息条件下灰自助方法真值估计的效果最好,自助法真值估计误差比灰自助方法大,GM(1,1)真值估计的效果最差。
表 1给出了固结端振动信号真值估计相对误差的比较结果。可以看出,灰自助方法对全部测量真值估计的最大相对误差、最小相对误差和平均相对误差均为最小,且平均相对误差小于5%。因此,灰自助方法真值估计的准确性最高,自助法次之,GM(1,1)最差。
表 1 固结端振动信号真值估计相对误差比较 Table 1 Comparison of estimated relative errors using fixed-end vibration signals

%
方法	Emax	Emin	Erm
灰自助方法	15.84	0.11	3.83
自助法	17.01	0.25	6.45
GM(1,1)	38.22	1.69	13.56

表选项


2.1.2 区间估计以空间机械臂活动端振动功率谱密度为例。图 3给出了灰自助方法在不同置信度水平(80%,90%,95%,99%)下对活动端振动功率谱密度的区间估计(m=8,B=1 000,Q=12)。其中,频率分辨力为5 Hz,测量范围为10～1 200 Hz。为了说明灰自助方法在区间估计上的优势,将灰自助方法与自助法进行比较。同样的,取不同置信度水平(80%,90%,95%,99%)对活动端振动功率谱密度进行区间估计(m=8,B=1 000,Q=12)。自助法计算的区间估计[X_L,X_U]如图 4所示。

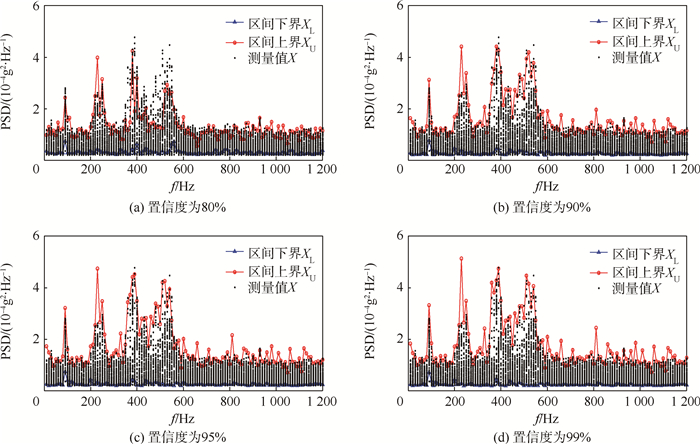图 3 灰自助方法计算得到的区间估计 Fig. 3 Estimated intervals calculated by grey bootstrap method

图选项

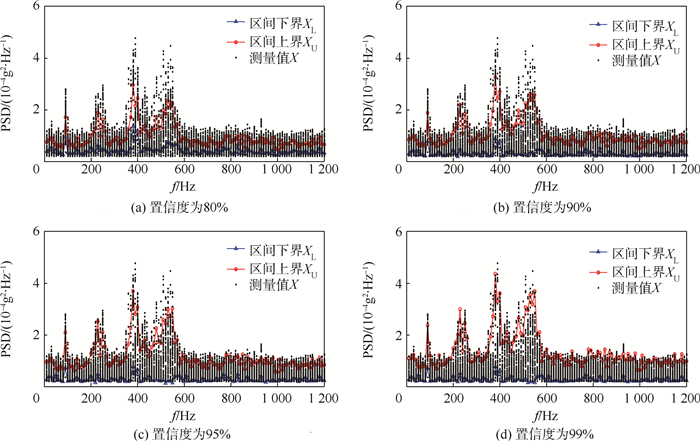图 4 自助法计算得到的区间估计 Fig. 4 Estimated intervals calculated by bootstrap method

图选项

图 3与图 4对比可以看出,在相同置信度水平下,灰自助方法的区间估计比自助法区间估计相对要宽,表明灰自助方法较自助法拥有更多的数据信息,数据挖掘能力更强。
图 5为灰自助方法与自助法在不同置信度水平下区间估计的可靠度偏差比较。图中:下面部分表示可靠度,上面部分表示可靠度偏差。可以看出,在不同置信度水平下,自助法区间估计可靠度偏差都很大,灰自助方法区间估计的可靠度偏差都很小。

图 5 灰自助方法与自助法区间估计的可靠度偏差比较 Fig. 5 Comparison of estimated interval reliability deviation by grey bootstrap method and bootstrap method

图选项

表 2给出了活动端振动信号估计区间准确度比较。可以看出,在不同置信度水平下,灰自助方法的区间估计准确度比自助法高,区间估计准确度高于97%。
表 2 活动端振动信号估计区间准确度比较 Table 2 Comparison of estimated interval accuracy using active-end vibration signals

P/%	Pr/%
	自助法	灰自助方法
80	67.58	97.99
85	69.87	98.11
90	73.98	98.89
95	75.12	97.92
99	75.01	97.47

表选项


2.2 实例验证为表明灰自助方法的有效性,以空间机械臂自由端振动功率谱密度为例,进行真值估计与区间估计。
图 6给出了不同方法对自由端振动信号的真值估计和估计误差(m=10,B=500,Q=10)。其中，频率的分辨力为3 Hz,测量范围为6～600 Hz。可以看出,对于自由端振动功率谱密度数据,灰自助方法真值估计效果较自助法要好,估计误差更小。

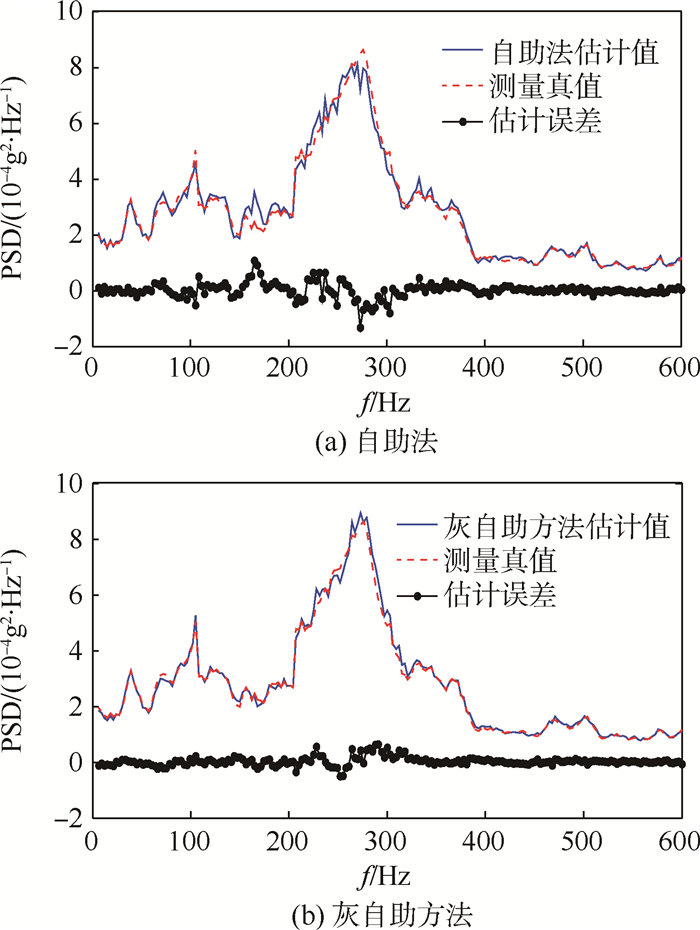图 6 不同方法对自由端振动信号的真值估计和估计误差 Fig. 6 Estimated values and estimated errors of free-end vibration signals by different methods

图选项

表 3给出了自由端振动信号真值估计相对误差比较。可以看出,对于自由端振动功率谱密度数据,灰自助方法估计效果也很好,平均相对误差只有3.08%,小于5%,验证了灰自助方法对乏信息空间机械臂随机振动信号真值估计的有效性。
表 3 自由端振动信号真值估计相对误差比较 Table 3 Comparison of estimated relative errors using free-end vibration signals

%
方法	Emax	Emin	Erm
灰自助方法	12.59	0.02	3.08
自助法	20.94	0.10	6.22

表选项


同样的,以空间机械臂自由端振动功率谱密度为例。表 4给出了在不同置信度水平下对自由端振动信号区间估计(m=10,B=1 000,Q=12)的准确度。可以看出,对于自由端振动功率谱密度,在不同置信度水平下,灰自助方法的区间估计准确度比自助法高,区间估计准确度高于97%,验证了灰自助方法对乏信息空间机械臂随机振动信号区间估计的有效性。
表 4 自由端振动信号估计区间准确度比较 Table 4 Comparison of estimated interval accuracy using free-end vibration signals

P/%	Pr/%
	自助法	灰自助方法
80	69.16	97.01
85	75.87	99.74
90	79.81	99.01
95	79.91	98.61
99	79.69	97.33

表选项


3 结 论1) 将灰自助方法应用于乏信息随机振动信号的分析中,构建了灰自助模型,拓展了随机振动信号估计方法,提出了相应的估计指标。利用灰自助方法对空间机械臂固结端振动功率谱密度进行真值估计,并与自助法和GM(1,1)比较,实例表明灰自助方法估计效果最好,在全频域真值估计的平均相对误差小于5%,验证了灰自助方法在真值估计中的优越性。
2) 利用灰自助方法对空间机械臂活动端振动功率谱密度进行区间估计,并与自助法比较说明其区间估计的特性,实例表明灰自助方法的区间估计准确度较自助法方法要好,区间估计准确度高于97%。
参考文献

[1]	王中宇,王倩, 付继华.乏信息多传感器压力数据自助模糊融合估计[J].北京航空航天大学学报,2013,39(11):1426-1430. WANG Z Y,WANG Q,FU J H.Pressure multi-sensor data fusion and estimation of poor information based on bootstrap-fuzzy method[J].Journal of Beijing University of Aeronautics and Astronautics,2013,39(11):1426-1430(in Chinese).
	Cited By in Cnki (2)
[2]	WANG Y, WANG Z,SUN J,et al.Gray bootstrap method for estimating frequency-varying random vibration signals with small samples[J].Chinese Journal of Aeronautics,2014,27(2):383-389.
	Click to display the text
[3]	WANG Z, WANG Y,WANG Q,et al.Fuzzy norm method for evaluating random vibration of airborne platform from limited PSD data[J].Chinese Journal of Aeronautics,2014,27(6):1442-1450.
	Click to display the text
[4]	谭启蒙,胡成威, 高升.空间机械臂视觉相机内参标定技术研究[J].航天返回与遥感,2013,34(6):74-80. TAN Q M,HU C W,GAO S.Research on calibration of intrinsic parameters for space manipulator camera based on 2D planar pattern[J].Spacecraft Recovery & Remote Sensing,2013,34(6): 74-80(in Chinese).
	Cited By in Cnki (1) | Click to display the text
[5]	徐文福,徐超, 孟得山.基于粒子群优化的刚柔混合机械臂振动抑制规划[J].控制与决策,2014,29(4):632-638. XU W F,XU C,MENG D S.Trajectory planning of vibration suppression for rigid-flexible hybrid manipulator based on PSO algorithm[J].Control and Decision,2014,29(4):632-638(in Chinese).
	Cited By in Cnki (2) | Click to display the text
[6]	GE L Y, WANG Z Y.Novel uncertainty-evaluation method of virtual instrument small sample size[J].Journal of Testing and Evaluation,2008,36(3):273-279.
	Click to display the text
[7]	XIA X, CHEN X,ZHANG Y,et al.Grey bootstrap method of evaluation of uncertainty in dynamic measurement[J].Measurement,2008,41(6):687-696.
	Click to display the text
[8]	EFRON B. Bootstrap methods:Another look at the Jackknife[J].The Annals of Statistics,1979,7(1):1-26.
	Click to display the text
[9]	王中宇,葛乐矣, 佟杰,等.乏信息材料布氏硬度测量误差的灰自助预报[J].北京航空航天大学学报,2010,36(5):524-528. WANG Z Y,GE L Y,TONG J,et al.Error predicting for material Brinell hardness measurement of poor information based on grey bootstrap method[J].Journal of Beijing University of Aeronautics and Astronautics,2010,36(5):524-528(in Chinese).
	Cited By in Cnki (2)
[10]	DENG J L. Introduction to grey system theory[J].Journal of Grey System,1989,1(1):1-24.
	Click to display the text
[11]	夏新涛,陈晓阳, 张永振,等.机械系统属性的灰假设检验[J].机械工程学报,2006,42(12):218-223. XIA X T,CHEN X Y,ZHANG Y Z,et al.Grey hypothesis testing for mechanical system attribute[J].Chinese Journal of Mechanical Engineering,2006,42(12):218-223(in Chinese).
	Cited By in Cnki (4)
[12]	WANG Q, FU J,WANG Z,et al.A seismic intensity estimation method based on the fuzzy-norm theory[J].Soil Dynamics and Earthquake Engineering,2012,40:109-117.
	Click to display the text
[13]	夏新涛,秦园园, 邱明.基于灰自助最大熵法的机床加工误差的调整[J].中国机械工程,2014,25(17):2273-2276. XIA X T,QIN Y Y,QIU M.Adjustment for the machining errors of machine tool based on grey bootstrap maximum entropy method[J].China Mechanical Engineering,2014,25(17):2273-2276(in Chinese).
	Cited By in Cnki
[14]	陈文华,李奇志, 张为鄂,等.产品可靠性的Bootstrap区间估计方法[J].机械工程学报,2003,39(6):106-109. CHEN W H,LI Q Z,ZHANG W E,et al.Method of bootstrap interval estimation for product reliability[J].Journal of Mechanical Engineering,2003,39(6):106-109(in Chinese).
	Cited By in Cnki (43) | Click to display the text
[15]	YATRACOS Y. Assessing the quality of bootstrap samples and of the bootstrap estimates obtained with finite resampling[J].Statistics & Probability Letters,2002,59(3):281-292.
	Click to display the text
[16]	XIA X T, CHEN X Y,ZHANG Y Z,et al.Grey bootstrap method of evaluation of uncertainty in dynamic measurement[J].Measurement,2008,41(6):687-696.
	Click to display the text
[17]	WANG Y Q, WANG Z Y,SUN J Y,et al.Dynamic uncertainty analysis for random vibration signals in flight test[J].Journal of Aircraft,2014,51(6):1966-1972.
	Click to display the text
[18]	航空工业部. 飞机飞行振动环境测量数据的归纳方法:HB/Z 87-84[S].北京:中国航空综合技术研究所,1985. Ministry of Aviation Industry.The inductive methods for environmental measured data of aircraft flying:HB/Z 87-84[S].Beijing:China National Aero-Poly Technology Institute,1985(in Chinese).
[19]	中国航空工业集团公司. 振动、冲击环境测量数据归纳方法:GJB/Z 126—99[S].北京:中国标准出版社,1999. Aviation Industry Corporation of China.The inductive methods for environmental measured data of vibration and shock:GJB/Z 126—99[S].Beijing:Standards Press of China,1999(in Chinese).
[20]	NASA. Dynamic environmental criteria:NASA-hdbk-7005[S].[S.l:s.n.],2003.
[21]	王中宇,刘智敏, 夏新涛,等.测量误差与不确定度评定[M].北京:科学出版社,2008:137-139. WANG Z Y,LIU Z M,XIA X T,et al.Measurement error and uncertainty evaluation[M].Beijing:Science Press,2008:137-139(in Chinese).
[22]	王中宇,李强, 燕虎,等.基于GM(1,1)与灰区间估计的SPE通量水平长期预测[J].北京航空航天大学学报,2014,40(8):1134-1142. WANG Z Y,LI Q,YAN H,et al.Novel method for predicting SPE flux levels based on GM(1,1) model and grey interval predictions[J].Journal of Beijing University of Aeronautics and Astronautics,2014,40(8):1134-1142(in Chinese).
	Cited By in Cnki | Click to display the text