目前有不少国内外****较为深入地研究了空间折展机构的热、结构性能。Boley和Weiner[7]分析了热环境下结构的变形问题,并提出了“耦合系数”以衡量热与结构相互耦合作用的强弱。针对哈勃望远镜太阳能帆板的热环境,Thornton等基于一维梁理论,讨论了考虑热效应的帆板支撑杆的弯曲变形[8]和扭转失稳[9]。继Thornton等的研究后,丁勇等[10]针对同样的复合材料杆件结构,考虑杆件截面周向的温度分布,对其进行傅里叶展开,结合有限元方法,对结构的瞬态温度场进行了分析。Tamma等[11]基于热分析的Laplace变换解,构造了一种新的一维有限元单元,并应用到了相应的工程问题中。朱敏波[12]针对可展开天线的具体特点,从全轨道层面对不同工况下星载天线瞬态温度场进行了分析计算,并对天线的相关热参数进行了优化。刘锦贤[13]基于试验所测得的热参数,利用有限元数值模拟分析了薄壁杆件框架支撑结构的温度分布,并进一步讨论了相应的热应力与热变形。杨玉龙[14]采用热有限元法,分析了桁架式可展开反射天线的总体热特性,并考虑了热控涂层退化对极值温度指标的影响。目前国内对于索杆铰接式伸展臂这一特定结构形式的热分析相对不多;工程中现有的热分析通常都是基于有限元法等数值方法,对于时间历程较长的大型结构的热分析,往往会遇到文件过大以及迭代误差积累等困难。
本文以索杆铰接式伸展臂为研究对象,针对所关心的轴向热量传递与温度分布,提出了相应的简化模型。将边界条件进行傅里叶展开并分别求出各阶展开项作用下结构的瞬态温度响应,进而利用叠加原理得出了简化伸展臂总体的瞬态响应。通过与有限元结果的对比,验证了相关结论的合理性,对于概念设计阶段从总体上把握结构的热特性具有较好的实际参考意义。
1 基本模型本文研究的伸展臂结构的实际结构如图 1所示,其主体主要由横、纵杆组成,纵杆轴线与伸展臂长度方向平行,横杆轴线与伸展臂长度方向垂直,每相邻2层横杆及其之间的纵杆所构成的正方体结构称之为一个折展单元。折展单元外侧面的对角线上存在着拉索结构以提高结构刚度,拉索直径很细且由热控材料包裹,因此忽略其对热传导的影响。横、纵杆都是由环氧树脂基碳纤维复合材料编制成的空心圆管,每根杆件长度相等,均为700 mm,杆件横截面外径均为15 mm,壁厚1.2 mm,由于管壁较薄,认为横杆、纵杆的温度不随厚度变化。杆件沿长度轴线方向的热传导系数为8.16 W/(m·K),沿截面圆周切线方向的热传导系数为2.52 W/(m·K),杆件材料密度为1 800 kg/m3,定压比热容为1 081 J/(kg·K)。上述参数均为基于纤维/基体体积比以及结构铺层等效后的参数。
 |
| 图 1 空间伸展臂结构Fig. 1 Space cable-strut deployable articulated mast |
| 图选项 |
在轨状态下端部有效载荷结构所处热环境的变化,会引起伸展臂端部温度条件的改变,本文主要考虑这一因素对伸展臂结构的影响。用如图 2所示的90 min周期的动态温度循环模拟伸展臂端部边界的温度(仅显示了2个周期);伸展臂另一端(即根部)与载体航天器内部相连接,由于航天器热容较大且有热控措施,认为其温度恒定为0℃[15, 16]。初始时刻,结构所有位置处的温度均为Tinit=0℃为初始温度值。不考虑热辐射,即主要关心端部热环境因素对伸展臂结构本身的作用。
 |
| 图 2 端部边界处温度循环Fig. 2 Boundary temperature cycle at tip |
| 图选项 |
由于端部边界条件对伸展臂的影响主要表现为沿伸展臂长度轴线方向上总体的热量传递和温度分布,本文相应的分析中将伸展臂结构最终简化为了一维结构[2]。设伸展臂的长度为L,根据展开状态的不同,长度L可以取10、30、60 m等不同值,由于模型尺度较大时有限元模型也相应较复杂,为方便对比本文中取L=10 m。以伸展臂轴线方向为x轴,其承受循环温度边界的一端为原点,伸展臂的另一端(根部与载体航天器连接处)为x=L的位置,该处为恒定温度条件。
2 理论分析2.1 边界温度处理根据线性叠加原理(独立作用原理),对于一个线性系统,由各种主动因素(不依赖于过程的表征量)即强迫外源、边界条件和初始扰动引起的响应可以进行线性分解,即可以看作是这些主动因素各自独立作用引起的响应的叠加[17]。基于上述原理,同时考虑到伸展臂端部温度若直接表示,只能写成分段函数形式,不便于理论分析求解,本文采用傅里叶级数将边界温度分解为若干个三角函数的和的形式以便求解。为了简化计算,只取前几阶傅里叶级数而忽略高频变化的温度循环,因为由于固体材料的热惯性,低频率的温度循环对结构温度影响较显著,而较高频率的温度载荷对除边界附近的杆内温度的影响基本可以忽略。
设伸展臂端部温度循环为f(t),℃,其中t为时间,s。显然f(t)是满足Dilichret条件的周期函数,则f(t)的傅里叶级数展开一定收敛到原函数。即有
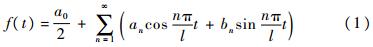
式中:an和bn为展开系数,且有
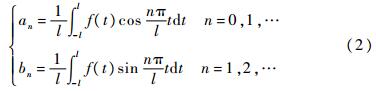
式中:l=Tp/2,Tp=5 400 s为温度循环的周期。图 2中的温度循环可表示为
将式(3)代入式(2)计算可得各傅里叶展开系数(如表 1所示),将相应项的系数代入式(1),即可获得原边界条件的三角函数表示,做出其对应的图像易知取16阶展开时已能较精确地反映边界上的温度循环。分别求解伸展臂结构在f(t)的各展开项作用下的温度响应,将所得的各个响应叠加即可得结构总体的温度响应。
表 1 边界温度的傅里叶展开系数Table 1 Fourier expansion coefficients of boundary temperature
| 编号n | an/℃ | bn/℃ |
| 1 | -62.675 | -42.275 |
| 2 | 1.598 7×10-14 | 7.105 4×10-15 |
| 3 | -0.437 98 | 2.060 6 |
| 4 | -7.105 4×10-15 | 5.329 1×10-15 |
| 5 | -3.537 6 | 0.623 77 |
| 6 | 8.881 8×10-16 | -8.881 8×10-16 |
| 7 | -0.522 60 | -0.836 33 |
| 8 | -1.110 2×10-16 | -8.881 8×10-15 |
| 9 | 0.535 35 | -0.388 95 |
| 10 | 4.440 9×10-16 | 2.220 4×10-16 |
| 11 | -0.709 52 | -0.176 90 |
| 12 | 3.552 7×10-15 | 8.881 8×10-16 |
| 13 | -1.045 1×10-2 | -7.436 4×10-2 |
| 14 | 4.440 9×10-16 | -8.881 8×10-16 |
| 15 | -0.303 96 | 0.175 49 |
| 16 | 3.330 7×10-16 | 1.804 1×10-16 |
表选项
2.2 热响应分析2.2.1 恒定分量下的响应对于恒定分量
,显然在这一分量的作用下,经过足够长的时间后,伸展臂结构温度分布会达到某一稳定状态。下面分析从初始时刻达到稳定状态的过程,即瞬态热响应。简化伸展臂的热响应定解问题:
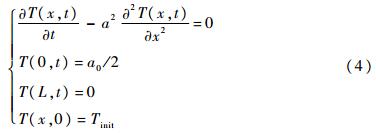
式中:T(x,t)为x位置处t时刻的温度;a2≡k/ρcp为热扩散系数,k为热传导系数,ρ为材料密度,cp为比热容;Tinit为初始时刻温度。先对边界条件进行齐次化处理,设方程式(4)的解为T0(x,t)=V(x,t)+W(x,t),其中
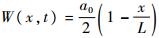,且V(0,t)=V(L,t)=0,代入式(4)可得到关于V(x,t)的齐次方程,易求得相应解为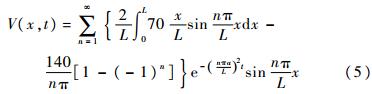
则式(4)的解为
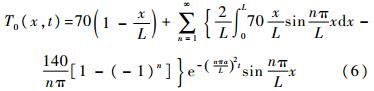
由此便得到了恒定温度分量作用下伸展臂结构的瞬态温度响应。
图 3中显示的是伸展臂一端边界为恒定分量时,结构的瞬态温度响应。不难看出,随着时间的推移,结构整体的温度逐渐上升,且越靠近端部边界的位置处温度上升越快。结构最终达到稳定状态,此时结构中温度梯度为恒定值,各点温度也保持不变。
 |
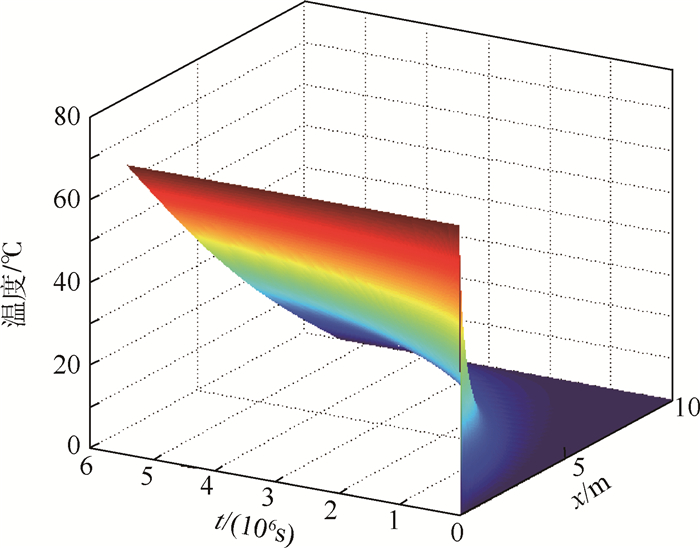| 图 3 稳态分量边界条件下结构瞬态温度响应Fig. 3 Transient temperature response under constant boundary temperature |
| 图选项 |
2.2.2 简谐分量下的响应前述温度响应计算中采用了分离变量解法,但缺憾是所求问题的边界条件和热源这2类非齐次项不能随时间变化[17]。为了求解更一般的问题,可以采用积分变换法或Duhamel卷积。本文将采用Laplace变换法求简谐温度边界下伸展臂的热响应。对于傅里叶展开所得的余弦温度边界,相应的定解问题可表达为
控制方程中对时间变量t取Laplace变换:
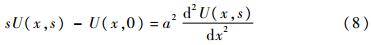
设
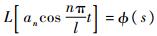,其中:L[*]代表对*求Laplace变换,U(x,s)为与T(x,t)对应的象函数。结合初始条件,易得式(8)的解为
式中:e为自然常数。
整理式(9)可得
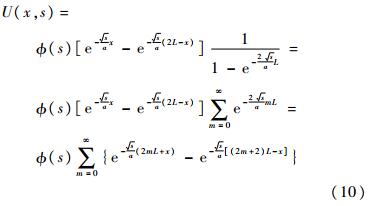
令
,则由Laplace逆变换的线性性质对其各项分别进行逆变换:
设Tan(x,t)为式(7)的解,由U(x,s)=φ(s)v,取Laplace逆变换并利用其卷积性质,有Tan(x,t)=L-1[U(x,s)]=L-1[φ(s)v],整理可得
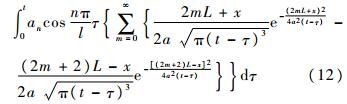
同理对于傅里叶展开所得的正弦温度边界,可利用同样方法求得对应解Tbn(x,t)为
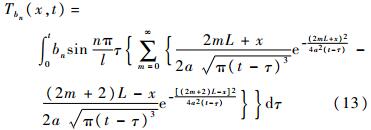
综合式(12)和式(13)可得简谐边界条件引起的温度响应T′(x,t)为
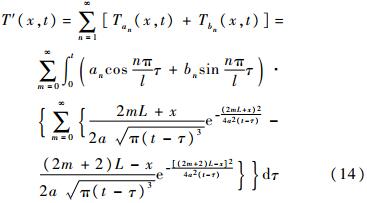
由式(14)得出的解满足所有边界条件与初始条件,是简化后伸展臂结构温度场的精确解,但式(14)涉及到多重无穷级数以及复杂积分,不易直观看出温度响应的特点。为简化表达式,考虑如下问题:伸展臂为半无限长,沿伸展臂轴线方向为x轴,其端部为原点,对应的边界条件为前述的简谐温度循环,另一端为无限长,热参数等其他条件与前述相同。利用Duhamel积分容易求得此时第n阶简谐分量边界条件下伸展臂结构的瞬态温度响应:
式中:φn和η为简化表达所引入的变量,其定义为
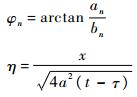
式(15)后2项均反映的是瞬态过程,经过较长时间后,即t很大时,后2项均趋向于0。另外由式(15)第1项可得,距离端部x处的结构点温度循环幅值随x的增大而迅速呈指数衰减。当x=L时,相应点处的温度循环的幅值几乎可以忽略,因此可以近似认为半无限伸展臂在x=L时总是满足T=0的边界条件,从而实际计算时可以利用上述半无限伸展臂在0~L段内的温度响应来近似伸展臂结构的温度响应。
图 4给出的是简谐边界条件下2个周期内的瞬态温度响应,显然在远离边界的位置处结构温度几乎恒为初始值,靠近边界的位置,结构温度为与边界温度周期相同的动态循环,但随着与边界距离的增大,其幅值逐渐衰减,与边界温度的相位差逐渐增大。
 |
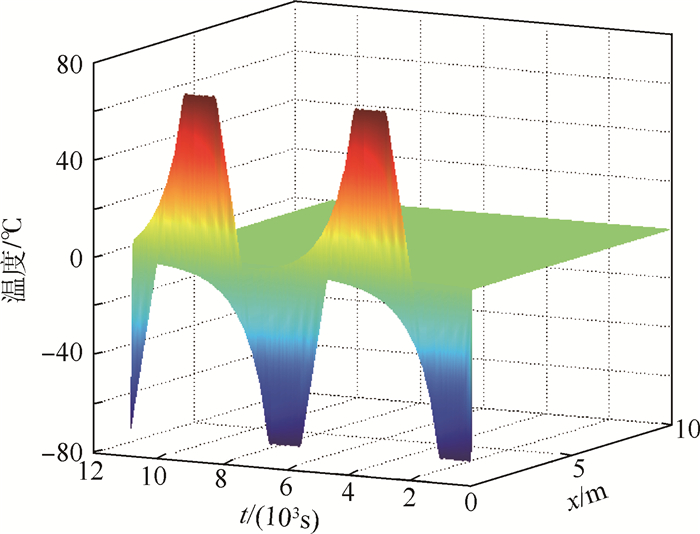| 图 4 简谐边界下的瞬态温度响应Fig. 4 Transient temperature response under harmonic boundary temperature |
| 图选项 |
综上可得,端部有效载荷处热环境作用下简化伸展臂结构的温度响应为
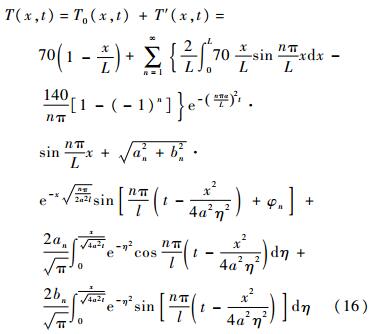
图 5表示简化伸展臂结构总体的瞬态温度响应,显然总体上结构温度逐渐上升,而越靠近动态温度边界的位置,温度的波动就越大,总体温度响应同时反映了恒定分量和简谐分量作用时的响应效果。
 |
| 图 5 简化伸展臂总体的瞬态温度响应Fig. 5 Overall transient temperature response of simplified deployable articulated mast |
| 图选项 |
3 数值分析对比为验证第2节结论的合理性,建立如图 6所示的有限元模型,利用二维壳单元模拟伸展臂。有限元模型中横、纵杆件,材料属性、边界条件等均与上述分析中一致,进行瞬态热分析得到了结构的瞬态温度响应。图 7分别给出了x=0.3 m处结点温度时间响应的有限元结果和本文方法计算的结果。
 |
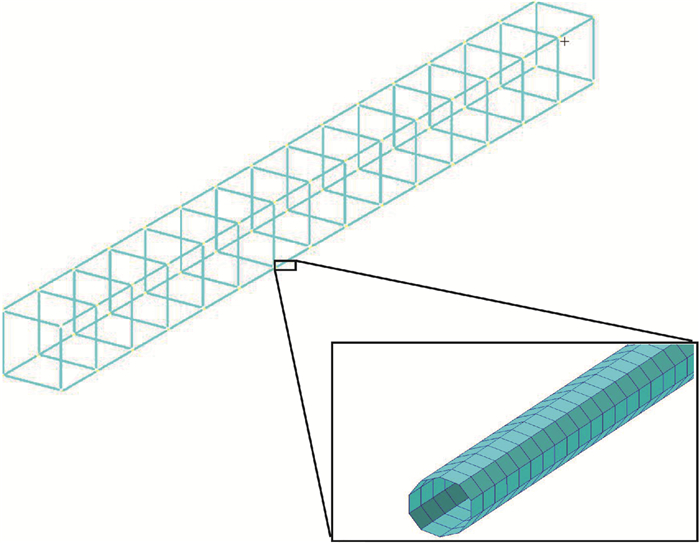| 图 6 有限元模型Fig. 6 Finite element model |
| 图选项 |
 |
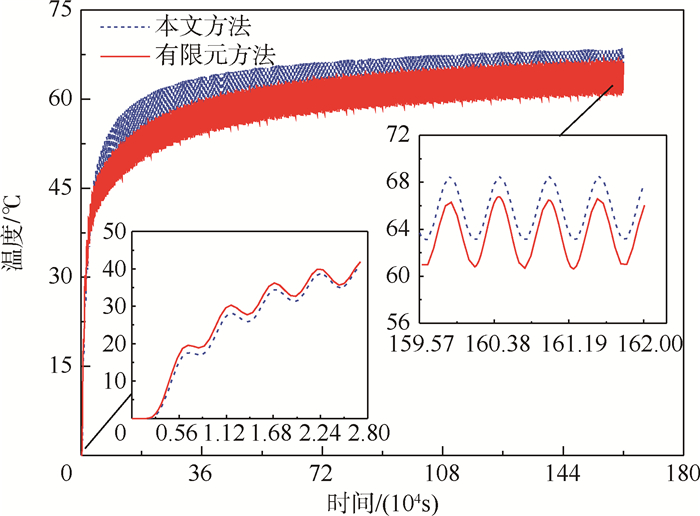| 图 7 本文方法与有限元方法结果的对比Fig. 7 Comparison of results obtained by proposed method and finite element method |
| 图选项 |
由图 7可以看出,本文方法所计算的结果与有限元分析结果总体趋势、最终状态是比较一致的,2种方法所得结果的温度波动的周期、幅值基本相同。在分析时间段内的中后期,本文方法计算的温度响应的整体升温速率要比有限元结果稍快,这是由于伸展臂结构的横杆的热传导会影响结构的温度响应,本文方法未考虑这一影响,这也是后续研究中需要考虑的问题。
4 结 论1) 基于傅里叶展开并利用叠加原理,能很好地模拟结构端部的热环境,且在本文所述情形下能较好地简化边界温度循环所致热响应的计算。
2) 本文方法所得响应的总体趋势、波动幅值和周期等均与有限元方法所得的结果较为一致,因此本文相关处理是较为合理的,且较好地解决了有限元计算时步长选取以及迭代误差等问题。
3) 本文研究的是L=10 m状态的伸展臂响应,随着其长度的增加,有限元模型的复杂程度也增加,此时本文方法相对更有优势。
本文方法对索杆铰接式伸展臂端部热环境作用下的热分析提供了一定的参考,为得出更精确的解,仍需对横杆热传导等因素做更加细致的处理。
参考文献
| [1] | 郭宏伟,刘荣强,邓宗全.空间索杆铰接式伸展臂性能参数分析与设计[J].北京航空航天大学学报,2008,34(10):1186-1190. GUO H W,LIU R Q,DENG Z Q.Performance parameters analysis and design of space cable-strut deployable articulated mast[J].Journal of Beijing University of Aeronautics and Astronautics,2008,34(10):1186-1190(in Chinese). |
| Cited By in Cnki (19) | |
| [2] | 邓宗全.空间折展机构设计[M].哈尔滨:哈尔滨工业大学出版社,2013:261-264. DENG Z Q.Design of space deployable structures[M].Harbin:Harbin Institute of Technology Press,2013:261-264(in Chinese). |
| [3] | BARCLAY D L,BROGREN E W,FOSTH D C,et al.Large space structures-Configuration,packaging,and response studies:NASA-CR-158928[R].Carpinteria:NASA,1978. |
| [4] | BROGREN E W,BARCLAY D L,STRAAYER J W.Simplified thermal estimation techniques for large space structures:NASA-CR-145253[R].Carpinteria:NASA,1977. |
| [5] | 杨玉龙,关富玲,张淑杰.可展桁架天线温度场和热变形分析[J].空间科学学报,2005,25(3):235-240. YANG Y L,GUAN F L,ZHANG S J.Thermal-structural analysis of deployable truss antenna[J].Chinese Journal of Space Science,2005,25(3):235-240(in Chinese). |
| Cited By in Cnki (33) | |
| [6] | MAHANEY J,STRODE K B.Fundamental studies of thermal-structural effects on orbiting trusses[J].AIAA Paper,1982,82(2):49-59. |
| Click to display the text | |
| [7] | BOLEY B A,WEINER J H.Theory of thermal stresses[M].Chicago:Courier Corporation,2012:243-251. |
| [8] | THORNTON E A,KIM Y A.Thermally induced bending vibrations of a flexible rolled-up solar array[J].Journal of Spacecraft and Rockets,1993,30(4):438-448. |
| Click to display the text | |
| [9] | CHUNG P W,THORNTON E A.Torsional buckling and vibrations of a flexible rolled-up solar array[J].AIAA Paper,1995,95(3):1654-1664. |
| Click to display the text | |
| [10] | 丁勇,薛明德,程乐锦,等.空间结构瞬态温度场的Fourier-有限元分析[J].清华大学学报(自然科学版),2002,42(2):198-202. DING Y,XUE M D,CHENG L J,et al.Fourier-finite element analysis of temperature fields in space structures[J].Journal of Tsinghua University(Science and Technology),2002,42(2):198-202(in Chinese). |
| Cited By in Cnki (27) | |
| [11] | TAMMA K,SPYRAKOS C,LAMBI M A.Thermal/structural dynamic analysis via a transform-method based on finite-element approach[J].Journal of Spacecraft and Rockets,1987,24(3):219-226. |
| Click to display the text | |
| [12] | 朱敏波.星载大型可展开天线热分析技术研究[D].西安:西安电子科技大学,2007:37-42. ZHU M B.Research on thermal analysis technology for the large deployable antenna[D].Xi'an:Xidian University,2007:37-42(in Chinese). |
| Cited By in Cnki (19) | |
| [13] | 刘锦贤.空间可展天线支撑结构热-结构分析[D].上海:上海交通大学,2013:40-44. LIU J X.Thermal-structural analysis for support structure of deployable space antenna[D].Shanghai:Shanghai Jiao Tong University,2013:40-44(in Chinese). |
| Cited By in Cnki (1) | |
| [14] | 杨玉龙.空间展开桁架结构设计理论与热控制研究[D].杭州:浙江大学,2007:49-55. YANG Y L.Structure design theory and thermal control study for space deployable truss structure[D].Hangzhou:Zhejiang University,2007:49-55(in Chinese). |
| Cited By in Cnki (23) | |
| [15] | 张晓宁.空间飞行器多层隔热系统传热特性的研究[D].哈尔滨:哈尔滨工业大学,2007:29-34. ZHANG X N.Research of heat transfer in multilayer insulation for space vehicles[D].Harbin:Harbin Institute of Technology,2007:29-34(in Chinese). |
| Cited By in Cnki (3) | |
| [16] | 安翔,张铎.太阳电池阵瞬态非线性温度场的精细算法[J].中国空间科学技术,2001,21(2):7-12. AN X,ZHANG D.Precise computation for nonlinear transient temperature distribution of solar array[J].Chinese Space Science & Technology,2001,21(2):7-12(in Chinese). |
| Cited By in Cnki (12) | |
| [17] | 胡汉平.热传导理论[M].合肥:中国科学技术大学出版社,2010:102-103. HU H P.Heat conduction theory[M].Hefei:University of Science and Technology of China Press,2010:102-103(in Chinese). |
