随着基础理论[8-9]和其他相关技术的发展,拓扑优化作为一种新兴的结构优化技术,已被广泛应用于各领域,例如汽车[10-12]、重型机械[13]和机器人[14]等。同时,拓扑优化为工程设计和分析人员提供了一条新的结构优化技术途径。这种方法自动化程度高,可以大大降低工程技术人员的工作量,同时也避免了因多次的重复设计所带来的不必要的开支,在工程中也已经得到了广泛的应用。因此,本文将利用拓扑优化技术对车体的隔热结构进行设计。
1 多目标拓扑优化方案 1.1 整体思路 以如图 1所示的结构为例,车体结构的型材部分主要用来承受载荷,而玻璃棉毡主要用来隔热。因此,假设铝型材仅参与传力,玻璃棉毡仅参与传热;由于沥水板不参与传热和传力,本文对其不予考虑。
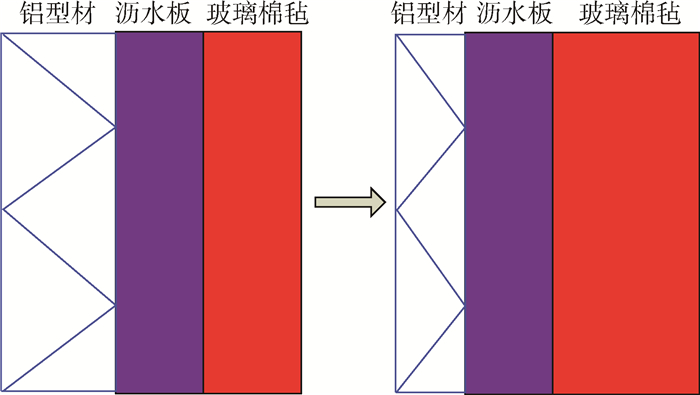 |
| 图 1 优化思路 Fig. 1 Scheme of optimization |
| 图选项 |
如图 1所示,在实际应用中,由于安装要求,型材、沥水板和玻璃棉毡的总厚度为定值。如果型材的整体厚度增加,刚度提高,但玻璃棉毡的厚度减小,隔热性能将变差;反之,刚度降低。另一方面,如果简单地增加型材内部的材料,刚度提高的同时质量增加,不满足车体结构轻量化的要求。
因此,车体隔热结构的优化是隔热、刚度和质量之间的折中。
本文的思路是在减小型材厚度、增加玻璃棉毡厚度的基础上,在型材质量降低的情况下,改变内部材料的分布,优化其传力特性,使得刚度增加。而由于玻璃棉毡厚度的增加,隔热性能也将得到提高。
由于玻璃棉毡厚度的增加较为简单,可用参数优化进行设计。而型材内部材料分布的改变较为复杂,必须采用拓扑优化技术。为此,本文将拓扑优化与参数优化相结合,参数优化主要目标是降低型材的厚度(增加玻璃棉毡的厚度),每一步降低厚度之后进行拓扑优化,使得在此型材厚度和质量限制下,得到最优的拓扑结构。
当然,多目标优化存在多个目标的折中问题。根据实际应用需要,本文主要以提高隔热性能为主,因此在拓扑优化中可设定优化后的刚度只要不小于优化前的结构即可,质量方面,要减小5%以上。
基于上述分析,项目的优化流程图如图 2所示,详细的技术方案将在1.2节介绍。
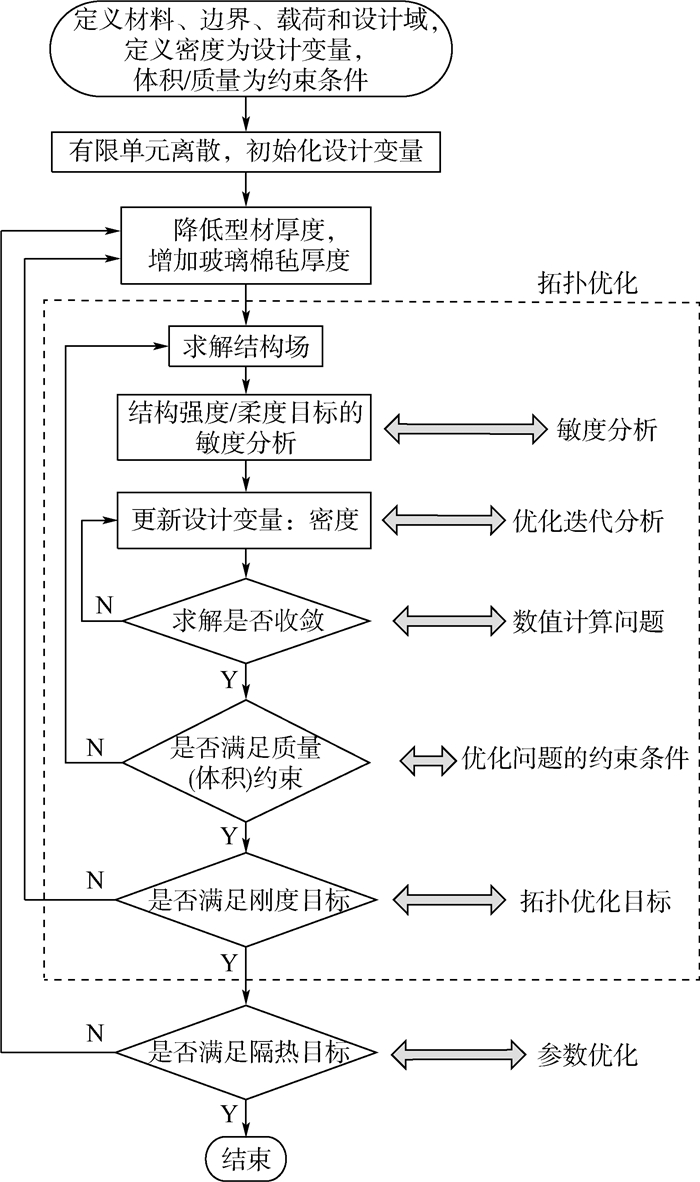 |
| 图 2 优化流程图 Fig. 2 Flowchart of optimization |
| 图选项 |
1.2 材料插值模型 拓扑优化中,有多种拓扑材料插值理论和拓扑结构描述方法,密度法材料插值模型在工程中得到了广泛研究。其中,固体各向同性材料惩罚(Solid Isotropic Material with Penalization,SIMP)模型对中间密度单元的惩罚效果好,能够尽可能地减少中间密度单元的数目,从而可避免多孔介质等现象[15]。本文选择SIMP材料插值模型。
设E0和Ee分别为单元初始弹性模量和优化后弹性模量,k0和ke分别为单元优化前和优化后的刚度矩阵,则存在以下关系式:
 |
式中:ρe为单元的材料相对密度,在(0,1]范围内取值;p为惩罚因子。
1.3 拓扑优化问题的描述 本文的拓扑优化以刚度最大,即柔度最小为优化目标;优化变量为各离散单元的密度;约束不仅要满足结构的平衡方程,而且需要限定结构的质量——即实体部分的体积。另外,单元相对密度也必须在(0,1]范围内。因此,离散优化问题就可变化为如下的连续型拓扑优化问题:
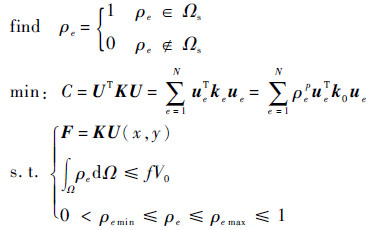 | (1) |
式中:目标函数C定义为结构的总体柔度;F为力向量;K为结构总刚度矩阵;U为位移列阵;ue为单元位移列矢量;N为结构离散单元总数目;V0为整个设计域的初始体积;f为优化体积比;ρemin和ρemax分别为单元相对密度的最小极限值和最大极限值,引入的目的是防止单元刚度矩阵的奇异;Ω为初始给定设计域;Ωs为优化后实体材料所占的区域。
由于在载荷F给定的条件下,K与U均为变量ρe的函数。因此对式(1)的第1个等式求导,可得到如下关系:
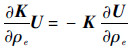 | (2) |
在优化算法进行求解时,需要求解目标函数敏度值,以得到最快的收敛算法。由式(1)和式(2)可得结构总体柔度的敏度方程为
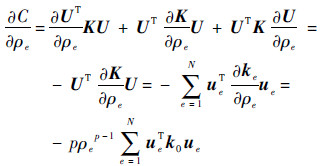 | (3) |
1.4 优化准则算法 建立了拓扑优化的模型之后,在求解时需要采用合适的优化求解数值算法,如优化准则算法、数学规划算法等。根据问题的特点,本文采用优化准则(Optimality Criteria,OC)算法进行优化。
对于1.3节中拓扑优化问题,由目标函数和约束条件构成的Lagrangian函数为[15-16]
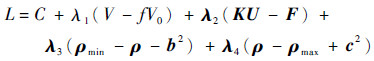 | (4) |
式中:V为优化后的结构体积;λ1、λ2、λ3和λ4为Lagrangian乘子,λ1为标量,λ2、λ3、λ4为标量λ2e、λ3e、λ4e组成的列向量;b和c为bi和ci组成的列向量,bi和ci为松弛因子;ρmin和ρmax为ρemin和ρemax组成的列向量;ρ为由ρe组成的列向量,当ρe取极值ρe*时,式(4)需满足如下的Kulm-Tucker条件:
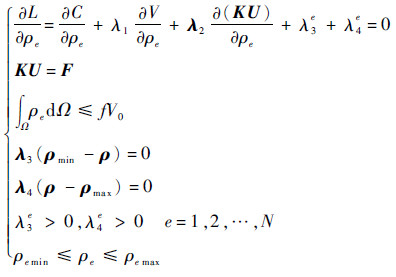 | (5) |
将表达式C=UTKU、ke=ρepk0和
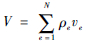
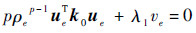 | (6) |
式中:ve为单元体积。令λ2=-2U,将式(3)代入式(6),可得
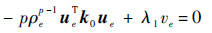 | (7) |
由式(7)可得优化设计准则:
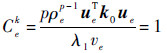 | (8) |
考虑式(8)及设计变量的上下限,可得到优化变量的迭代公式:
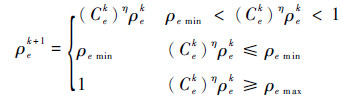 | (9) |
式中:η为阻尼系数,引入阻尼系数的目的是为了确保优化计算的稳定性和收敛性。用优化准则方法进行设计变量不断更新,采用式(10)进行收敛性判定,确定最终拓扑结构。
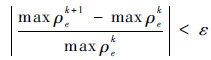 | (10) |
式中:ε为设定的收敛容差。
1.5 拓扑优化中的数值计算不稳定现象 由1.2节~1.4节可进行拓扑优化计算,但有可能出现多孔、棋盘格等计算结果以及数值不稳定等问题,不能应用于实际工程中。本项目将采用网格过滤方法来消除拓扑优化数值计算不稳定现象。
网格过滤方法由Diaz和Sigmund[17]提出,用于修改目标函数的敏度信息:
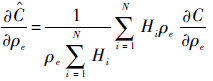 | (11) |
式中:
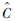
2 隔热结构拓扑优化模型的建立 2.1 工程化假设 高速列车的车体隔热结构具有自身的特点,针对铝型材、玻璃棉毡等结构的传热和传力特点,本文也提出了相应的解决方法:
1) 车体的很多部位,其受力与传热情况不同。本文将针对车体几个典型部位(如侧墙、地板和平顶等)进行拓扑优化,每个部位提出2种结构,以满足不同的使用环境和应用需要。
2) 考虑高速列车的实际应用,隔热结构必须满足外部的安装条件。因此,在拓扑优化的设计初始求解域中给予体现。同时,部分安装条件还需要在约束条件中给出,其中包括尺寸条件、边界环境条件等。例如,某结构需要留有线缆的通过孔,必须在约束条件中给予考虑。
3) 考虑高速列车的制造成本,隔热结构内部的加工必须满足可制造性优良、成本低廉的要求。为此,拓扑优化之后的结构要进行可制造化处理。首先,通过自动轮廓提取程序提取并建立模型。在此基础上,利用设计人员的工程经验,对模型进行修正。
2.2 传热与受力情况 如图 1所示,玻璃棉毡仅参与传热,传热方式仅考虑热传导。
如图 3所示,在高速运行过程中,车体受到的载荷可根据工程经验,做如下简化:
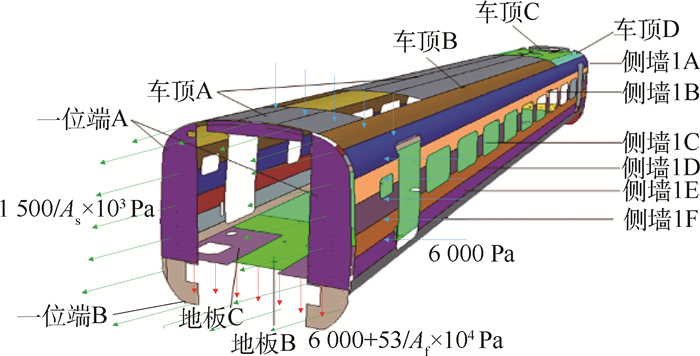 |
| 图 3 车体受力情况示意图 Fig. 3 Diagrammatic sketch of load case on a train |
| 图选项 |
1) 车体受到6 000 Pa的气密性载荷,方向垂直于车体各壁面。
2) 沿车身长度方向,受到1 500 kN的面内载荷。假设车体结构截面的面积为As,沿车身长度方向的面内应力为1 500/As×103 Pa。
3) 车体地板要承受旅客与货物的质量,此质量为53 t。假设地板的面积为Af,其将额外受到竖直向下的应力为53/Af×104 Pa。
2.3 拓扑优化的载荷、位移边界条件 本文以地板结构为例说明拓扑优化设计的载荷及位移边界。
首先,目前使用的地板型材结构为类似三角波的周期结构,本文根据此特点,选定拓扑优化的设计域为3个周期,结构总长度约为490 mm。同时参考现有结构,设定型材的初始厚度为70 mm;假设型材的宽度为1 m。其中结构两端的4个端点均为固支约束;如2.2节所述,地板所受的载荷有2种,如图 4所示:①车体受到6 000 Pa的气密性载荷,方向垂直于车体各壁面。②车体地板要承受旅客与货物的质量,受到竖直向下的载荷为53/Af×104 Pa。
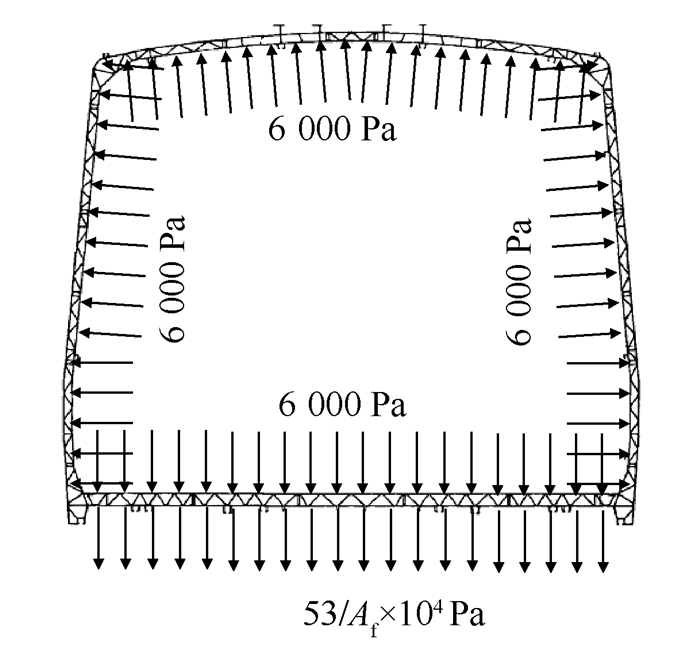 |
| 图 4 车体断面受力示意图 Fig. 4 Diagrammatic sketch of load case on cross-section of train |
| 图选项 |
地板的尺寸近似取为20 m×2.4 m(长×宽)。进一步将地板所受的均布载荷集中施加,得到的集中载荷为
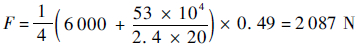 |
因此,拓扑优化的边界条件如图 5所示。
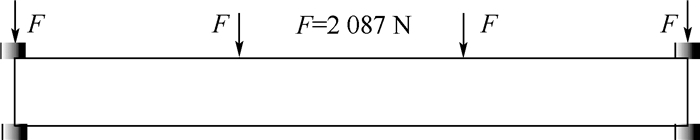 |
| 图 5 地板1的边界条件示意图 Fig. 5 Diagrammatic sketch of boundary condition of floor 1 |
| 图选项 |
同理,可以得到另一种地板及2种侧墙、2种平顶的边界条件,如图 6所示。
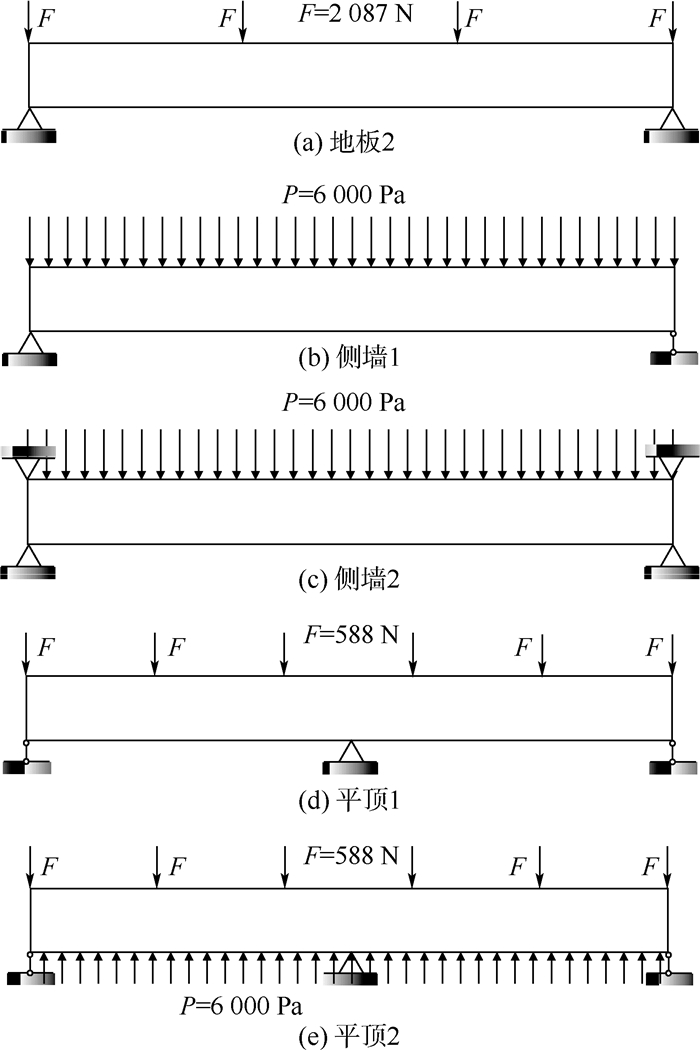 |
| 图 6 其他结构的边界条件示意图 Fig. 6 Diagrammatic sketch of boundary condition of other structures |
| 图选项 |
3 拓扑优化结果 根据第1节提出的拓扑优化模型与求解算法,得到了6种结构的拓扑优化结果,如图 7所示。
 |
| 图 7 拓扑优化结果 Fig. 7 Results of topological optimization |
| 图选项 |
从图 7可以看出,6个优化后的结构,都已不是优化前的类似三角波的周期循环结构,其传力路径得到了优化。如前所述,本文的优化目标为:优化后的刚度不小于优化前的结构,质量要减小5%以上;在此基础上,尽可能得降低型材厚度。各结构型材厚度的变化如表 1所示,可知,各优化后结构的型材厚度均得到了降低。
表 1 各结构型材厚度的变化 Table 1 Thickness change of profiles for all structures
| 结构 | 型材厚度/mm | |||||
| 地板1 | 地板2 | 侧墙1 | 侧墙2 | 平顶1 | 平顶2 | |
| 原结构 | 70 | 70 | 50 | 50 | 50 | 50 |
| 优化后结构 | 60 | 61 | 42 | 41 | 40 | 39 |
表选项
需要说明的是,如图 7所示的部分拓扑优化结果很难加工制造,需要进行可制造化处理。例如,尽量采用直线结构取代拓扑优化结果中曲线结构,尽可能组成三角形、封闭结构,尽可能减少连接点,填补棋盘格及多孔结构,删除部分短小且不封闭的结构等。这里以图 7(f)的平顶2为例,进行局部的处理,得到的结构如图 8所示。
 |
| 图 8 平顶2的可制造化处理结果 Fig. 8 Manufacturability processing result of ceiling 2 |
| 图选项 |
4 有限元仿真验证 以地板1为例,对拓扑优化后的结构进行有限元仿真,并与优化前的原结构进行刚度和应力性能对比。比较时,原结构和优化后的结构外部尺寸(除厚度外)、材料参数及边界条件设置均相同。因此,仅需要对比结构在受载情况下最大挠度和最大应力即可。为了提高计算速度,隔热结构的宽度取10 mm。
如图 9和图 10所示的仿真结果表明,优化后的结构,在刚度和强度性能方面都得到了提高。另外,由于玻璃棉毡的厚度增加,隔热性能得到增强。结构最终的总体性能对比如表 2所示,地板结构的整体性能得到了提高。
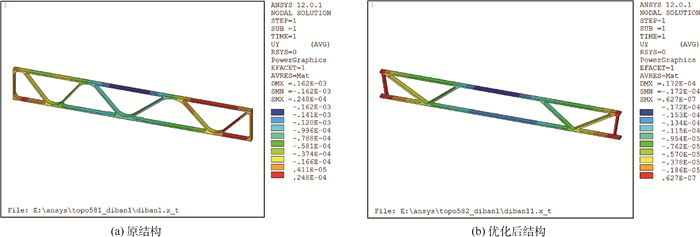 |
| 图 9 优化前后的刚度对比 Fig. 9 Stiffness comparison between pre and post optimization |
| 图选项 |
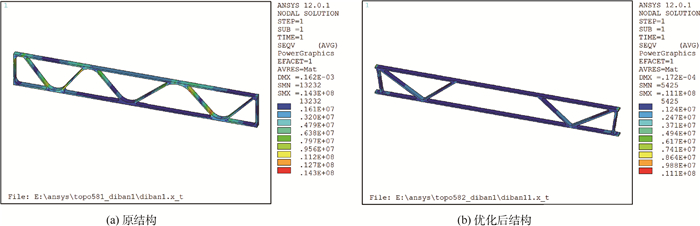 |
| 图 10 优化前后的应力对比 Fig. 10 Stress comparison between pre and post optimization |
| 图选项 |
表 2 总体性能对比 Table 2 Comparison of overall performance
| 结构 | 整体厚度/mm | 上边界厚度/mm | 下边界厚度/mm | 玻璃棉毡厚度/mm | 相对质量/% | 最大挠度/mm | 最大应力/MPa | 传热系数/(W·(m2·℃)-1) |
| 原结构 | 70 | 2.8 | 3 | 40 | 14.6 | 0.162 | 14.3 | 0.875 |
| 优化后结构 | 60 | 3.0 | 3 | 50 | 15.7 | 0.017 | 11.1 | 0.700 |
表选项
5 结 论 1) 车体的型材部分主要用来承受载荷,而玻璃棉毡主要用来隔热。因此,通过参数优化降低型材厚度(增加玻璃棉毡的厚度)来提高隔热性能,通过拓扑优化改善传力路径,提高刚度性能的设计方法是合理的。
2) 本文采用的SIMP材料插值模型、优化准则算法在车体隔热结构多目标拓扑优化的应用中可有效改善相关性能。
3) 根据设计人员的经验,可进行拓扑优化结果的可制造化处理,从而可应用于工程实际中。
在将来的工作中,将深入探索强度与隔热的耦合机理,建立更精确的模型,为高速列车提供性能更优的车体隔热结构。
参考文献
| [1] | 马晓婧.铝型材与多隔热层组合板传热特性的实验与数值研究[D].兰州:兰州交通大学,2014:7-20. MA X J.Experimental and numerical studies of heat transfer characteristics of the layer combined with aluminum extrusion and multi insulation material layers[D].Lanzhou:Lanzhou Jiaotong University,2014:7-20.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [2] | 尤芳, 陈建军, 曹鸿钧, 等. 随机变量下的热传导结构拓扑优化设计[J]. 西安电子科技大学学报,2014, 41(6): 127–134.YOU F, CHEN J J, CAO H J, et al. Topology optimization design of heat conduction structures with random variables[J]. Journal of Xidian University,2014, 41(6): 127–134.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [3] | 李红霞, 杨弘, 李德才. 高速列车车体断面优化数值分析[J]. 铁道车辆,2007, 45(2): 8–10.LI H X, YANG H, LI D C. Analysis of optimized values of the cross section of the carbodies of high speed trains[J]. Rolling Stock,2007, 45(2): 8–10.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [4] | 戚林, 张海柱, 黎荣, 等. 基于特征的高速列车铝合金车体断面参数化建模[J]. 兰州交通大学学报,2015, 34(1): 109–113.QI L, ZHANG H Z, LI R, et al. Parametric modeling of aluminum alloy body section of high-speed trains base on features[J]. Journal of Lanzhou Jiaotong University,2015, 34(1): 109–113.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [5] | 张军, 兆文忠, 李永华, 等. 基于APDL高速铝合金车体参数化建模[J]. 大连交通大学学报,2009, 30(4): 13–17.ZHANG J, ZHAO W Z, LI Y H, et al. Research on parameter modeling for aluminum alloy rail vehicle body[J]. Journal of Dalian Jiaotong University,2009, 30(4): 13–17.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [6] | 邹远.高速列车车体断面优化设计[D].成都:西南交通大学,2011:22-32. ZOU Y.Optimization design of carbody cross section for high speed trains[D].Chengdu:Southwest Jiaotong University,2011:22-32.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [7] | 李欣伟, 刘宇, 范乐天, 等. 基于拓扑优化的有轨电车车体设计技术研究[J]. 铁道机车车辆,2015, 35.LI X W, LIU Y, FAN L T, et al. Tram design technology study based on topology optimization[J]. Railway Locomotive & Car,2015, 35.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [8] | 何智成, 陈少伟, 李光耀, 等. 基于面光滑有限元的复杂三维结构拓扑优化[J]. 中国机械工程,2015, 26(7): 864–870.HE Z C, CHEN S W, LI G Y, et al. Topology optimization using FS-FEM for complex three-dimensional models[J]. China Mechanical Engineering,2015, 26(7): 864–870.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [9] | 杜家政, 卢立晗, 赵振洋. 基频约束的框架结构拓扑优化[J]. 北京工业大学学报,2015, 41(4): 534–541.DU J Z, LU L H, ZHAO Z Y. Topology optimization for frame structures with base frequency constraint[J]. Journal of Beijing University of Technology,2015, 41(4): 534–541.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [10] | 范文杰, 范子杰, 苏瑞意. 汽车车架结构多目标拓扑优化方法研究[J]. 中国机械工程,2008, 19(12): 1505–1508.FAN W J, FAN Z J, SU R Y. Research on multi-objective topology optimization on bus chassis frame[J]. China Mechanical Engineering,2008, 19(12): 1505–1508.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [11] | 刘宇, 张生芳, 宋雪萍, 等. 动力平板车车架结构的拓扑优化设计[J]. 中国机械工程,2014, 12(1): 34–37.LIU Y, ZHANG S F, SONG X P, et al. Topological optimization design on frame structure of power platform trailers[J]. China Mechanical Engineering,2014, 12(1): 34–37.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [12] | 臧晓蕾, 谷正气, 米承继, 等. 矿用车车架结构的静动态多目标拓扑优化[J]. 汽车工程,2015, 37(5): 566–570.ZANG X L, GU Z Q, MI C J, et al. Static/dynamic multi-objective topology optimization of the frame structure in a mining truck[J]. Automotive Engineering,2015, 37(5): 566–570.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [13] | 焦洪宇, 周奇才, 吴青龙, 等. 桥式起重机箱型主梁周期性拓扑优化设计[J]. 机械工程学报,2014, 50(23): 134–139.JIAO H Y, ZHOU Q C, WU Q L, et al. Periodic topology optimization of the box-type girder of bridge crane[J]. Journal of Mechanical Engineering,2014, 50(23): 134–139.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [14] | 李清伟. 焊接机器人大臂有限元分析及拓扑优化[J]. 组合机床与自动化加工技术,2014(11): 63–64.LI Q W. The finite element analysis and topological optimization design for welding robot's arm[J]. Modular Machine Tool & Automatic Manufacturing Technique,2014(11): 63–64.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [15] | ZUO K T. Research of theory and application about topology optimization of continuum structure[J]. Wuhan:Huazhong University of Science and Technology,2004: 31–35. |
| Click to display the text | |
| [16] | LI D M, ZHANG X M, GUAN Y S, et al. Multi-objective topology optimization of thermo-mechanical compliant mechanisms[J]. Chinese Journal of Mechanical Engineering,2011, 24(6): 1123–1129. |
| Click to display the text | |
| [17] | DIAZ A, SIGMUND O. Checkerboard patterns in layout optimization[J]. Structure Optimization,1995, 10(1): 40–45. |
| Click to display the text | |
