近年来,国内外许多****对诱导轮、叶轮的叶片型线或者从离心式机械的性能优化角度进行了大量研究,并取得了一定的成果。Cadirci等[5]利用插值模拟退火算法对离心风机叶片的进口安装角和出口安装角进行优化;Wang等[6]对叶片数目和叶片出口安装角进行了优化研究;彭茂林等[7]基于贝塞尔曲线和粒子群算法对涡轮叶片的型线进行了参数化建模;邓敬亮等[8]研究了离心式叶轮二元叶片型线的优化设计问题,在设计点调高了叶轮的性能;权辉等[9]通过数值模拟分析了螺旋离心泵不同叶轮型线部位的流体做功问题;马胜远等[10]对高压比跨声速离心式压气机的型线进行了优化研究,提高了其效率等。由此可见,近年来许多****从不同角度对离心式结构叶轮的型线进行了研究分析,并取得了一定的成果。然而,多级导流一体式诱导轮与叶轮和传统航空发动机燃油系统所使用的离心叶轮相比,由于结合了螺旋式叶轮与复合叶轮共有的特殊结构形式,提高了叶轮的进口压力,保证了较高的抗汽蚀特性,而且流体在叶轮中实现了多级增压且流道稳定,其大扭曲度的复杂型线将诱导轮与叶轮一体连接,避免了诱导轮与叶轮组合连接造成的能量损失,很大程度上提高了叶轮的效率,因此对多级导流一体式诱导轮与叶轮型线的研究至关重要,且实现型线的优化更是重中之重。
为此,本文对多级导流一体式诱导轮与叶轮的型线进行了优化研究。首先通过对比拟合模型仿真结果与原模型试验数据来验证拟合方法的准确性;然后分析了型线的不同参数化结果与叶轮结构参数之间的相关性联系;最后对不同的型线模型进行了性能仿真研究,给出了最优型线。
1 研究模型 航空发动机推重比不断增加,随之对主燃油前级增压泵提出了更高的性能要求。因此,需要研究满足需求的增压泵。
多级导流一体式诱导轮与叶轮新型结构的航空燃油离心泵能够为推重比为10的航空发动机提供前级增压,其多级导流一体式结构的型线复杂,加工难度大,但由于叶轮内多级导流增压的作用,使其效率较传统离心泵要高;且一体式型线结构有助于降低燃油的进口流速,提高进口压力,增强泵的抗汽蚀特性;其叶轮轮缘直径比传统组装叶轮更小,避免了不稳定力的发生,而且一体式结构不用考虑诱导轮与叶轮之间匹配连接的问题,减小了水力损失。因此,多级导流一体式诱导轮与叶轮结构较传统叶轮,其效率更高,具有更为优良的进口条件等[11]。
对多级导流一体式诱导轮与叶轮结构型线的研究成为突破航空燃油离心泵整体性能的关键,能够掌握该结构型线变化与叶轮结构参数的联系、实现型线的优化分析等更是重中之重。
多级导流一体式诱导轮与叶轮航空燃油离心泵的性能参数为:工作介质是密度为753 kg/m3的航空煤油,离心泵设计转速nd=8 000 r/min,设计流量Qd=77 000 L/h。
图 1为多级导流一体式叶轮的设计原理,可以看到诱导轮与叶轮的一体连接点设计结构。叶轮采用了长叶片2片,中长叶片2片,短叶片4片,基于圆柱坐标系构成叶型型线[12]。
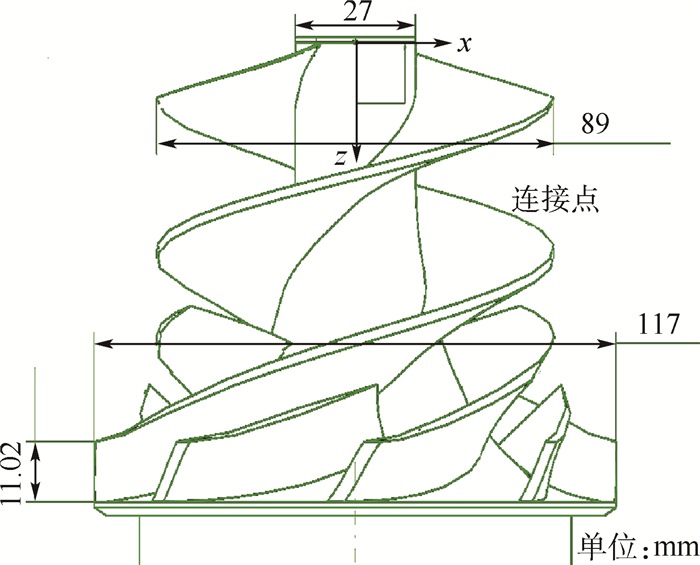 |
| 图 1 多级导流一体式叶轮设计原理 Fig. 1 Principle of multi-diversion combination inducer and impeller design |
| 图选项 |
通过合理选择经验系数,设计叶轮与蜗壳主要结构参数,从而对其进行样件加工。
2 型线参数化拟合数学模型 采用最小二乘法进行多级导流一体式诱导轮与叶轮型线的拟合参数化,基本思路[13]如下。令
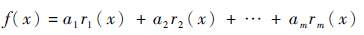 | (1) |
式中:rk(x)为实现选定的一组线性无关的函数;ak为待定系数(k=1,2,…,m,m<n)。
拟合准则为:使yi(i=1,2,…,n)与f(xi)的距离δi的平方和最小,即为最小二乘准则。
确定系数ak。记
 | (2) |
为求a1,a2,…,am使J达到最小,只需利用极值的必要条件J/ak=0(k=1,2,…,m),得到关于a1,a2,…,am的线性方程组:
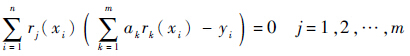 | (3) |
即
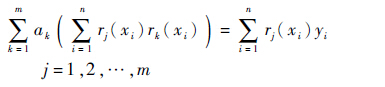 | (4) |
记
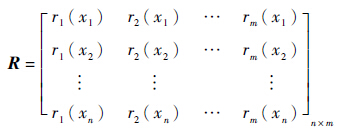 |
A=[a1,a2,…,am]T
Y=[y1,y2,…,yn]T
式(4)可表示为
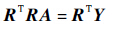 | (5) |
当{r1(x),r2(x),…,rm(x)}线性无关时,R列满秩,RTR可逆,于是式(5)有唯一解。
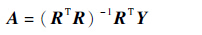 | (6) |
用线性最小二乘法进行曲线拟合时,首要的也是关键的一步是恰当地选取(r1(x),r2(x),…,rm(x))。即对叶片型线点集数据(xi,yi),i=1,2,…,n,通过机理分析,即可知道y与x之间的函数关系,则(r1(x),r2(x),…,rm(x))容易确定。若无法知道y与x之间的关系,通常可以将数据(xi,yi)(i=1,2,…,n)进行作图。对于多级导流一体式诱导轮与叶轮的型线拟合,采用多项式形式,即
y=a1xm+a2xm-1+…+amx+am+1
m=2,3,不宜太高
本节给出了型线拟合中最小二乘法的数学模型。基于商用软件MATLAB环境下,对多级导流一体式诱导轮与叶轮的型线拟合与优化进行研究,以实现提高该新型结构性能的目的。
3 型线拟合方法验证 3.1 拟合模型及网格模型 采用最小二乘法进行多级导流一体式诱导轮与叶轮型线的参数化拟合。研究对象为:主叶片(长叶片)轮毂轮缘型线、第一辅助叶片(中叶片)轮毂轮缘型线和第二辅助叶片(短叶片)轮毂轮缘型线,共12条曲线。由于轮毂型面长叶片扭曲度大,因此,为了提高拟合精度,对曲面型线进行分段,将其取6段进行拟合。
长叶片拟合需要多段分段,工作量较大,为了方便地研究参数化方程对叶轮性能的影响,因此取中叶片,即第一辅助叶片第一表面2条曲线(轮毂、轮缘曲线)作为参数化模型,并以2条拟合曲线为路径形成中长叶片受力曲面。图 2为拟合型线与原型线的对比。
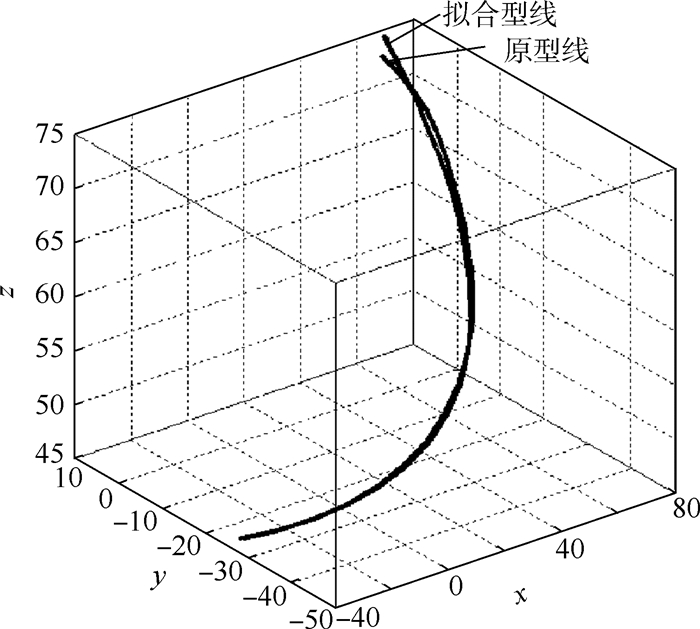 |
| 图 2 拟合型线与原型线对比 Fig. 2 Comparison between fitting profile and original profile |
| 图选项 |
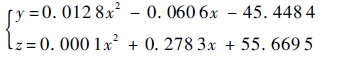 |
可以看出,拟合型线较原型线误差很小,且更为光滑。图 3为叶轮中叶片的轮毂、轮缘曲线拟合结果。
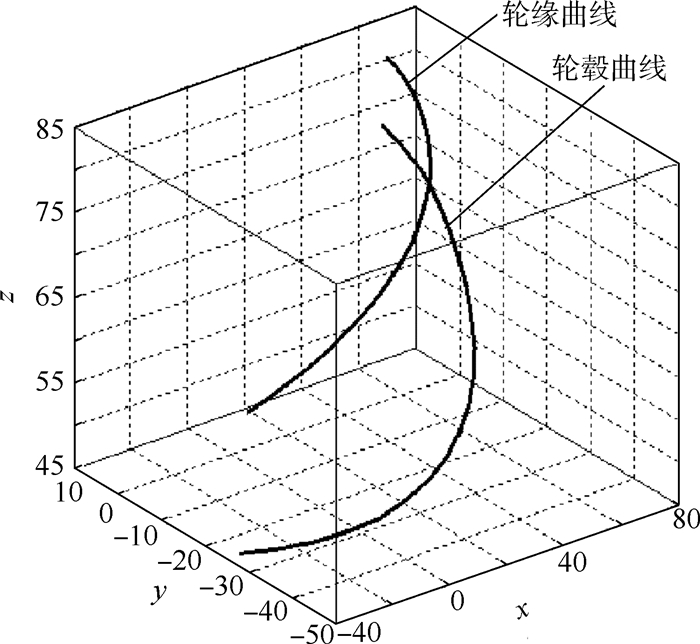 |
| 图 3 轮毂与轮缘的拟合型线结果 Fig. 3 Fitting profile results of hub and shroud |
| 图选项 |
建立多级导流一体式诱导轮与叶轮三维模型后,采用混合网格类型对该离心泵进行网格划分。组合式叶轮流道采用多块拓扑结构的方式划分结构网格,将叶轮计算域模型分为关于原点对称的2个周期模型使得复杂模型相对简单,更好地完成高质量结构网格。对单个模型进行网格划分时,将单独的计算域建立多区域划分即形成多块拓扑结构。图 4(a)为叶轮单独计算域划分的多块拓扑结构,图 4(b)为叶轮结构网格示意图。
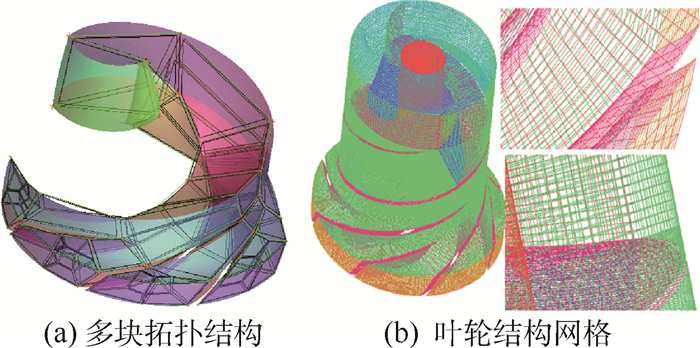 |
| 图 4 离心泵网格划分 Fig. 4 Mesh grid of centrifugal pump |
| 图选项 |
由图 4中可以看出,叶轮整体的结构化网格光滑,正交性好。在放大区域,叶片进口与叶片出口的网格排列整齐,网格光滑,叶片周围网格数目有所加密,数值模拟时叶片附近流动的精确度提高。蜗壳网格采用非结构网格的计算迭代方式,实现四面体网格划分。最终多级导流一体式诱导轮与叶轮航空燃油离心泵混合网格划分模型如图 5所示。
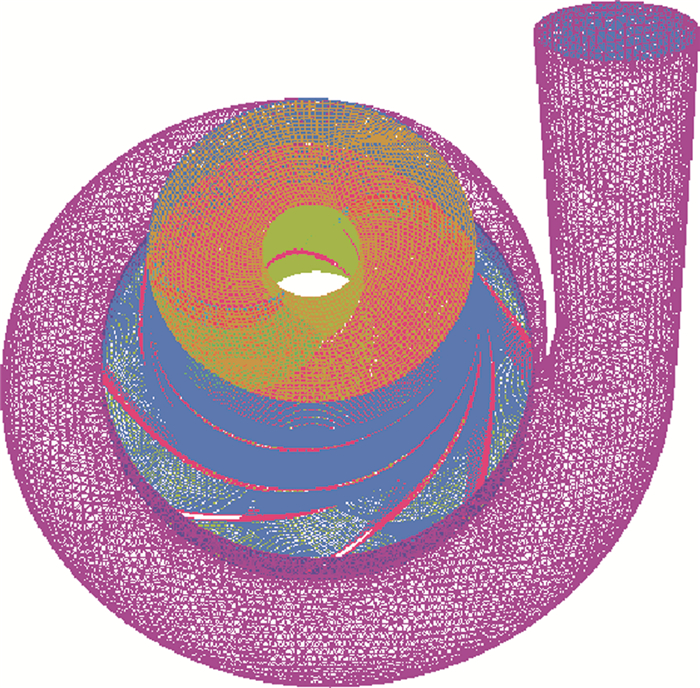 |
| 图 5 多级导流一体式诱导轮与叶轮航空燃油离心泵混合网格模型 Fig. 5 Aero fuel hybrid grid model of multi-diversion combination inducer and impeller centrifugal pump |
| 图选项 |
3.2 边界条件设置 取设计转速8 000 r/min的不同流量状态进行模拟,将计算结果与试验数据相对比,从而验证计算方法的适用性。计算借助计算流体力学(Computational Fluid Dynamics,CFD)软件Pumplinx[14],采用压力基隐式差分方法、2阶迎风差分格式以及COUPLED方法求解三维定常雷诺平均Navier-Stokes方程。选取k-ε模型为湍流模型[15-16],计算介质为航空煤油。为提高计算效率,计算中采用了多重网格法、局部时间步长和残差光顺等加速收敛措施。
将离心泵内部流动视为不可压缩流动,采用动静参考系解决旋转叶轮与静止泵体的耦合问题,叶轮设置为运动参考系,泵壳和其他流动域设置为静参考系。进口边界采用压力进口边界,给定来流总温总压;出口边界为体积流量出口边界;壁面边界,采用绝热无滑移条件。
3.3 仿真与试验结果对比 对拟合型线模型进行不同工况条件下的仿真研究。图 6为设计流量Qd工况下,拟合模型压力与速度分布云图。
 |
| 图 6 Qd=77 000 L/h时,中间轴向截面压力和速度云图 Fig. 6 Pressure and velocity contour of middle axial section at Qd=77 000 L/h |
| 图选项 |
由图 6中可以看到,设计流量工况下,从叶轮进口到出口顺着流动方向压力逐渐上升,叶轮内压力的最低点都在叶片吸力侧的进口前缘处,大量的工程实践和研究结果均表明,此处正是离心泵内部最易产生汽蚀的区域。叶轮通道内,相同半径处叶片压力侧的压力高于吸力侧的压力,符合离心叶轮内叶片对流体的做功原理。但离心叶轮各通道内的压力分布互不相同,呈现非常明显的非轴对称性特点。蜗壳中的压力分布也是在出口附近变化最为剧烈。
叶轮中远离蜗壳出口段和蜗舌附近区域的叶轮通道中的速度比较小,靠近蜗舌位置的通道内速度相对比较高,叶片压力侧固定位置处有低速团产生,但在离心力和科氏力压力梯度的作用下,该低速团迅速得到抑制,影响的范围很小,且都限于紧贴压力侧附近区域。蜗壳中速度的分布规律为:从蜗舌处开始一直到扩散管出口,速度的整体趋势是逐渐降低的,各个通道出口中间部位对应的区域有一小范围的高速区,这和压力分布图上该区域为低压区相对应,流体速度在扩散管中迅速下降。
从整体来看,拟合型线模型内流场压力分布与速度分布趋势稳定。
通过对比不同流量工况下拟合型线模型仿真结果与原型线模型试验结果(见表 1),验证拟合方法的正确性。
表 1 拟合型线与原型线性能结果对比 Table 1 Comparison of performance results between fitting profile and original profile
| 性能参数 | 流量/(L·h-1) | 拟合型线 | 原型线 | 误差/% |
| 扬程H/m | 77 000 | 121.8 | 121.0 | 0.6 |
| 55 000 | 146.3 | 145.2 | 0.7 | |
| 35 000 | 159.5 | 158.1 | 0.8 | |
| 15 000 | 175.4 | 173.8 | 0.9 | |
| 效率η/% | 77 000 | 63.63 | 63.27 | 0.6 |
| 55 000 | 61.18 | 60.73 | 0.7 | |
| 35 000 | 57.42 | 56.96 | 0.8 | |
| 15 000 | 53.95 | 53.49 | 0.9 |
表选项
通过不同工况下出口压力的仿真结果,按式(7)、式(8)分别计算扬程H和效率η。
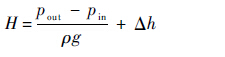 | (7) |
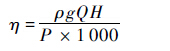 | (8) |
式中:pin为泵进口处的总压力;pout为泵出口处的总压力;Δh为泵进出口的高度差;P为轴功率;ρ为介质密度;g为重力加速度;Q为流量。
图 7、图 8给出了离心泵拟合型线与原型线流量-扬程、流量-效率曲线对比。
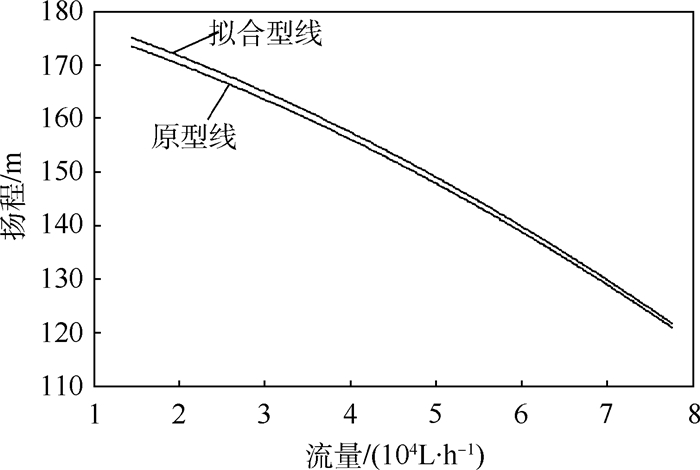 |
| 图 7 离心泵拟合型线与原型线流量-扬程曲线对比 Fig. 7 Comparison between fitting profile and original profile of centrifugal pump’s Q -H curves |
| 图选项 |
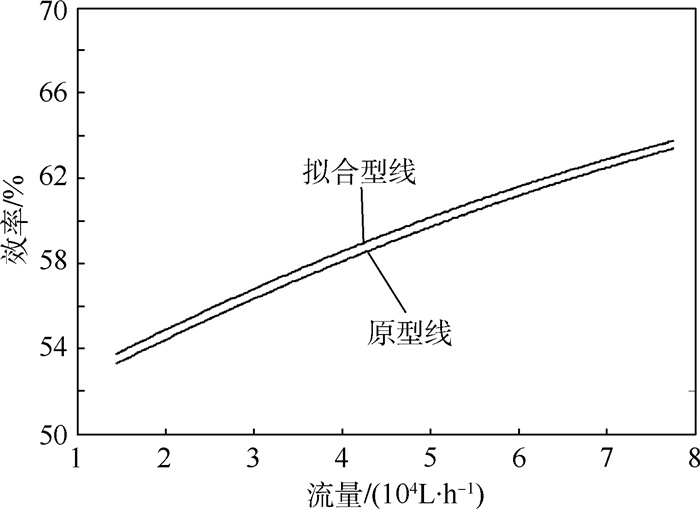 |
| 图 8 离心泵拟合型线与原型线流量-效率曲线对比 Fig. 8 Comparison between fitting profile and original profile of centrifugal pump’s Q-η curves |
| 图选项 |
由图 7、图 8可以看出,拟合型线模型的性能仿真结果与原型线模型性能试验结果变化趋势一致。随着流量增加,离心泵扬程逐渐下降,效率逐渐增加,且至设计点效率最高,由于设计流量为离心泵的最大流量,因此流量-效率曲线趋势逐步增加。通过对比可以看出,拟合模型的增压能力与效率值均高于原模型,且流量-扬程曲线与流量-效率曲线在设计流量(77 000 L/h)时,误差最小。误差随着流量的降低逐渐增大,但均低于2%。
根据以上分析,使用的拟合方法能够实现多级导流一体式诱导轮与叶轮型线的拟合研究,且拟合后的模型具有明显的性能优势。
4 型线优化设计 4.1 不同拟合型线与叶轮结构参数相关性分析 为了实现多级导流一体式诱导轮与叶轮型线优化研究,首先分析型线系数变化与叶轮的结构参数变化之间的相关性联系。通过一次项与常数项系数的大量拟合工作,给出了系数变化与叶轮的进出口叶片安装角的联系;并通过该结构参数的变化,实现叶轮的型线优化研究。图 9给出了叶轮轮毂型线参数和叶轮结构参数变化的联系。进而通过改变该结构参数实现多级导流一体式诱导轮与叶轮的性能优化。
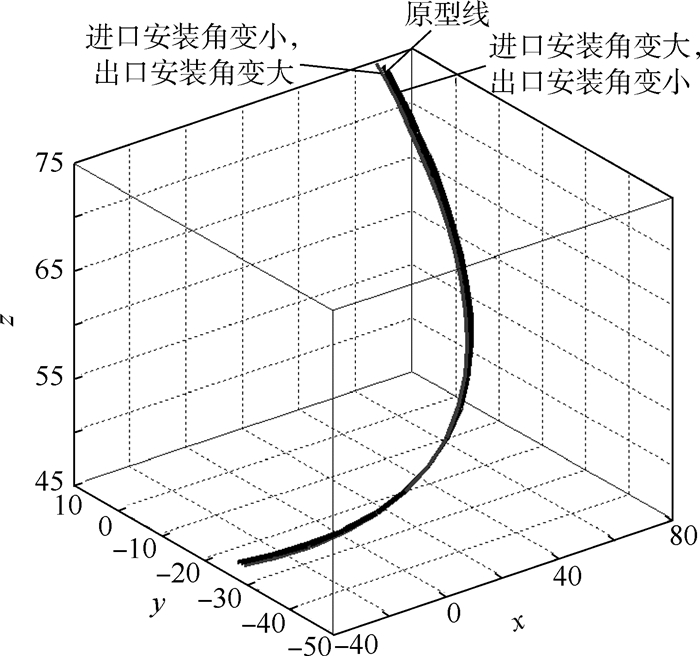 |
| 图 9 叶轮轮毂型线参数与叶轮结构参数变化的联系 Fig. 9 Contact of impeller hub profile parameters and impeller structural parameters |
| 图选项 |
4.2 优化拟合型线结果分析 通过第4.1节中针对不同拟合型线与叶轮结构参数相关性的分析,进而改变其进出口安装角等结构参数,实现3组叶轮型线的拟合表达式,最终通过性能对比达到叶轮的型线优化研究目标。
现给出3组参数化系数的型线表达式,如式(9)~式(11)所示。
型线1:
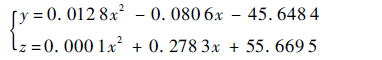 | (9) |
型线2:
 | (10) |
型线3:
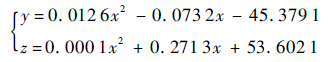 | (11) |
分别对3组离心泵的内流场性能进行仿真研究。在设计流量工况77 000 L/h时,3组型线模型的压力场与速度场仿真结果如图 10所示。
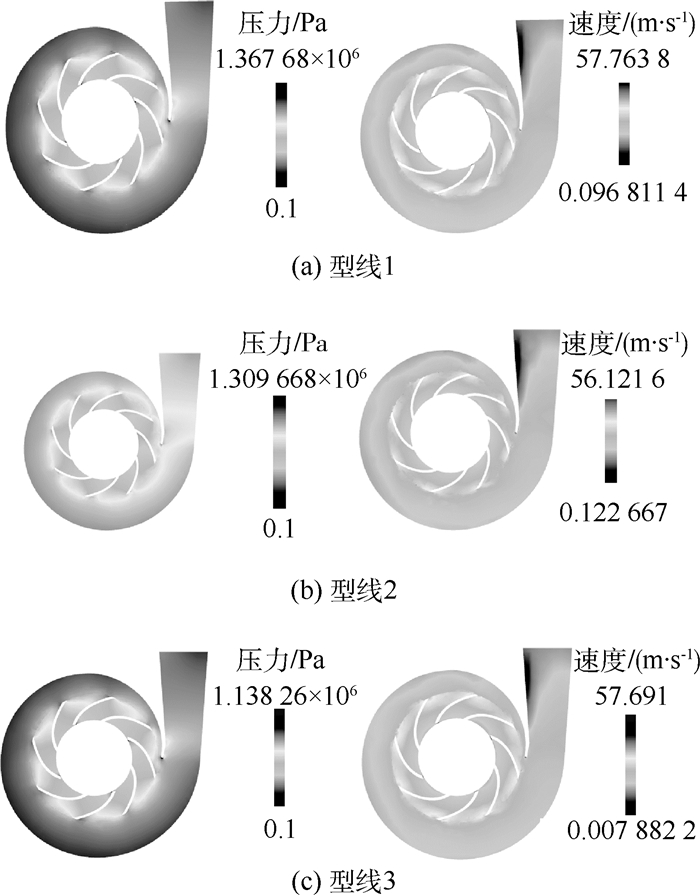 |
| 图 10 Qd=77 000 L/h时,3组型线模型中间轴向 Fig. 10 Pressure and velocity contour of three profiles model at Qd=77 000 L/h of middle axial section |
| 图选项 |
由图 10中可以看出,3组型线的内部流动整体变化趋势一致。压力场分布中,叶轮在各个流道出口处均存在一定区域的低压区;蜗壳隔舌处亦存在一定区域的低压区,该低压区一定程度上影响了扩散管的增压能力,型线2模型的分布中,该低压区范围最大。速度场分布中,叶轮出口处存在高速团流动,且与压力场趋势对应;扩散管出口左侧形成了一定范围的低速团,其是由蜗壳隔舌处的漩涡流动引起。整体上,3组型线模型的内部流动均属正常,但型线2模型的不利流动较大。
图 11给出了3组型线模型在设计流量工况下的出口压力仿真结果。根据3种型线在相同条件下的出口压力性能结果对比,结合式(7)、式(8),对扬程值与效率值的性能参数进行预测,如表 2所示。
 |
| 图 11 Qd=77 000 L/h时,3组型线模型出口压力仿真结果 Fig. 11 Simulation results of outlet pressures of three profiles model at Qd=77 000 L/h |
| 图选项 |
表 2 3种型线性能仿真结果对比 Table 2 Comparison of performance simulation results among three profiles
| 型线 | 流量/(L·h-1) | 扬程/m | 效率/% |
| 型线1 | 77 000 | 123 | 63.59 |
| 55 000 | 146 | 61.82 | |
| 35 000 | 160 | 56.65 | |
| 15 000 | 175 | 54.12 | |
| 型线2 | 77 000 | 119 | 62.35 |
| 55 000 | 143 | 60.32 | |
| 35 000 | 157 | 56.63 | |
| 15 000 | 172 | 52.70 | |
| 型线3 | 77 000 | 125 | 64.93 |
| 55 000 | 147 | 62.76 | |
| 35 000 | 161 | 58.09 | |
| 15 000 | 177 | 54.92 |
表选项
根据图 11及表 2给出的各组型线模型性能参数预测结果,分别绘制3组拟合型线模型的流量-扬程与流量-效率曲线,如图 12、图 13所示。
 |
| 图 12 离心泵3种型线模型流量-扬程曲线 Fig. 12 Centrifugal pump’s Q-H curves of three profiles model |
| 图选项 |
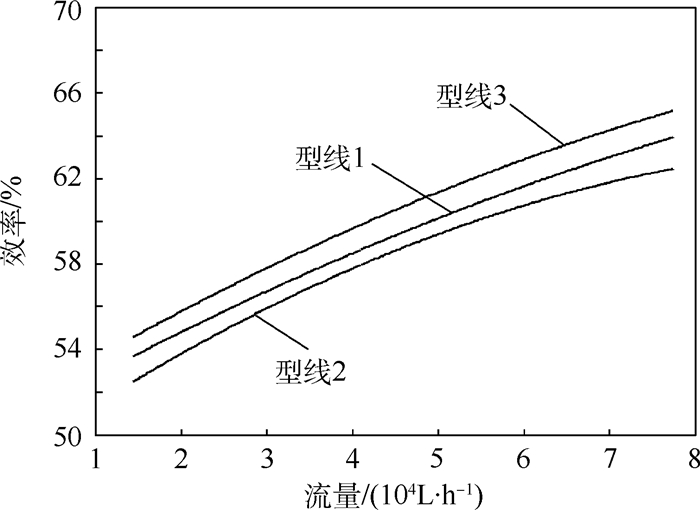 |
| 图 13 离心泵3种型线模型流量-效率曲线 Fig. 13 Centrifugal pump’s Q-η curves of three profiles model |
| 图选项 |
由图 12、图 13可以看出,型线1模型与型线3模型在各个流量工况下均比原模型的增压值和效率高,且型线3性能更优,在设计工况下,效率值和扬程值优化最大,随着流量降低,性能提高有所下降,但型线3在整个工况下均提高了原模型的性能。而型线2较原型线和其他型线的增压能力和效率值较低。因此,型线3能够满足多级导流一体式诱导轮与叶轮型线的优化目标,使原模型增压能力与效率的性能提高。
5 结 论 本文对多级导流一体式诱导轮与叶轮开展了型线优化研究工作,主要结论如下:
1) 采用最小二乘法实现了多级导流一体式诱导轮与叶轮型线的拟合,并基于CFD实现了拟合模型的性能仿真研究。仿真结果与原型线模型的试验数据对比表明,拟合曲线模型的流量-扬程、流量-效率曲线与原型线模型试验数据曲线吻合,误差均处于2%以内。因此,本文所用的型线拟合研究方法能够准确实现多级导流一体式诱导轮与叶轮的型线优化研究。
2) 多级导流一体式诱导轮与叶轮型线优化的内流场分布状态表明,3组型线模型叶轮的各个流道出口和蜗壳隔舌处存在一定范围的低压区,且由于隔舌处漩涡流动的影响使得扩散管出口存在一定区域的高速团,但3组型线内部流动整体上趋势稳定和正常。
3) 型线优化的仿真结果表明,型线3为最优的拟合型线模型,其扬程值与效率值均优于原型线模型和其他型线模型,且设计工况时,扬程值与效率值提高最为明显。
以上结论表明,本文准确给出了提高整体性能的最优型线,实现了多级导流一体式诱导轮与叶轮的优化研究,能够在一定程度上解决新型结构的航空燃油离心泵优化问题。
参考文献
| [1] | 刘尚勤. 离心泵用作航空发动机主燃油泵研究[J]. 航空发动机,2006, 32(2): 43–45.LIU S Q. Investigation of centrifugal pump used as aeroengine main fuel pump[J]. Aeroengine,2006, 32(2): 43–45.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [2] | 樊思齐. 航空发动机控制[M].西安: 西北工业大学大学出版社, 2008: 24-27.FAN S Q. Aeroengine control[M].Xi’an: Northwestern Polytechnical University Press, 2008: 24-27.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [3] | 刘尚勤, 王磊. 航空发动机的一种新型主燃油泵设计[J]. 航空发动机,2003, 29(2): 5–7.LIU S Q, WANG L. Design of a new main fuel pump for aeroengine[J]. Aeroengine,2003, 29(2): 5–7.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [4] | 牟介刚.离心泵现代设计方法研究和工程实现[D].杭州:浙江大学,2005:40-41. MU J G.Research on the modern design method of centrifugal pump project realization[D].Hangzhou:Zhejiang University,2005:40-41.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [5] | CADIRCI S,SELENBAS B,GUNES H.Optimization of a centrifugal fan impeller using kriging simulated annealing[C]//Proceedings of the ASME International Mechanical Congress and Exposition.New York:ASME,2011,6:991-997. |
| Click to display the text | |
| [6] | WANG S L,ZHANG L,WU Z R,et al.Optimization research of centrifugal fan with different blade number and outlet blade angle[C]//2009 ASIA-PACIFIC Power and Energy Engineering Conference(APPEEC).Piscataway,NJ:IEEE Press,2009:2985-2988. |
| Click to display the text | |
| [7] | 彭茂林, 杨自春, 曹跃云, 等. 基于贝赛尔曲线和粒子群算法的涡轮叶片型线参数化建模[J]. 中国电机工程学报,2012, 32(32): 101–108.PENG M L, YANG Z C, CAO Y Y, et al. Parameter modeling of turbine blade model line construction based on bezier curve and particle swarm optimization algorithm[J]. Proceeding of the CSEE,2012, 32(32): 101–108.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [8] | 邓敬亮, 楚武利, 张皓光. 离心叶轮二元叶片型线的优化设计与分析[J]. 推进技术,2014, 35(7): 926–931.DENG J L, CHU W L, ZHANG H G. Degign and analysis of 2D blade profile on a centrifugal impeller[J]. Journal of Propulsion Technology,2014, 35(7): 926–931.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [9] | 权辉, 李仁年, 苏清苗, 等. 基于型线的螺旋离心泵叶轮做功能力研究[J]. 机械工程学报,2013, 49(10): 156–162.QUAN H, LI R N, SU Q M, et al. Research on work capacity of screw centrifugal pump impeller based on profile lines[J]. Journal of Mechanical Engineering,2013, 49(10): 156–162.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [10] | 马胜远, 陈莹, 杨科, 等. 高压比跨音速离心叶轮的三维叶片型线优化[J]. 热能动力工程,2005, 20(6): 607–610.MA S Y, CHEN Y, YANG K, et al. Three-dimension blade profile optimization for a high pressure-ratio transonic and centrifugal impeller[J]. Journal of Engineering for Thermal Energy and Power,2005, 20(6): 607–610.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [11] | SINGHAL A K, ATHAVALE M M, LI H, et al. Mathematical basis validation of the full caviation model[J]. Journal of Fluids Engineering,2002, 124(3): 617–624. |
| Click to display the text | |
| [12] | 关醒凡. 现代泵技术手册[M].北京: 宇航出版社, 1995: 216-227. |
| Cited By in Cnki (0) | |
| [13] | 蒲志理. 航空油泵设计[M].北京: 国防工业出版社, 1983: 132-148.PU Z L. Aero fuel pump design[M].Beijing: National Defence Industry Press, 1983: 132-148.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [14] | 任璇,姜华川,王飞,等.基于Pumplinx的离心泵优化设计研究[C]//第15届中国科协年会第13分会场:航空发动机设计、制造与应用技术研讨会论文集.兰州:兰州理工大学出版社,2013:5-7. REN X,JIANG H C,WANG F,et al.Optimum design of centrifugal pump based on pumplinx[C]//15th Annual Meeting of the China Association 13th Venue:Aircraft Engine Design,Manufacture and Application of Technology Symposium.Lanzhou:Lanzhou University of Technology Press,2013:5-7.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [15] | CHEAH K W, LEE T S, WINOTO S H, et al. Numerical flow simulation in a centrifugal pump at design and off-design conditions[J]. International Journal of Rotating Machinery,2007, 115(10): 342–350. |
| Click to display the text | |
| [16] | MARX Y P. Unsteady simulations of impeller diffuser interactions centrifugal pump[J]. EPFL-SCR,1997, 11(9): 335–339. |
| Click to display the text | |
