本文以舰艇区域防空作战任务为例,将作战能力需求生成的输入问题转化为约束关系集,定义了舰艇防空作战效能的目标函数,提出了基于约束优化问题的能力需求生成模型,不同于约束满足机制,寻求既满足约束关系集又使舰艇作战效能最大的能力需求方案,定量生成舰艇完成区域防空作战任务所需的各项能力指标。
1 舰艇区域防空作战能力约束提取 舰艇区域防空作战能力需求生成可以看作是一个输入输出问题[4],作战能力需求生成问题描述,见图 1。输入的已知条件是研究对象、面临的军事威胁、要完成的使命任务等,而输出是能够有效完成这些使命任务目标或克服这些军事威胁的作战能力指标值。通过解析规则由作战任务向能力进行映射转化,首先需明确各种“输入”条件,而这些“输入”条件就如同对作战能力需求生成问题的约束,使之“输出”科学合理的需求方案,因此有效地提取约束条件是需求生成的重点。根据“输入”条件及多视图的思想,将约束类型分为如图 1所示的4种类型,在约束条件的制约下通过能力需求生成方法才能得到科学合理的能力需求生成方案。
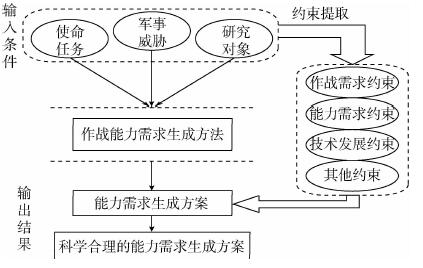 |
| 图 1 作战能力需求生成问题描述 Fig. 1 Combat capability requirement generation problem description |
| 图选项 |
1.1 作战需求约束 作战需求是指为实现所担负的使命任务所必须具备的能力,是战场态势对作战行动提出的要求,即水面舰艇对所担负使命中一系列具体任务的定量描述。以舰艇区域防空作战任务需求约束为背景,假定在距我舰艇400 km外有敌机以速度700 m/s向我舰艇袭来,要求能对敌机实施导弹拦截。为最大限度地对来袭敌机进行多次拦截,提高拦截成功的概率,则要求预警机最大预警距离Rdyj至少为400 km,拦截相当可靠,即命中概率Pn′达到90%~95%,下标n′为导弹的发数。根据作战需求提取约束集(Inequality Constraints)IC_1为
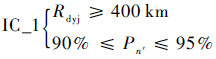 | (1) |
1.2 能力需求约束 能力需求约束是最重要的一类约束,是指对完成任务程度的定量描述,同时体现在能力需求指标之间相互影响关联的基础上。指标的生成并不是单一的指标求解,而是形成类似于网络状相互影响的结构体系关系,指标之间相互制约,相互影响,对彼此具有一定的约束关系。
图 2为舰艇作战能力指标关系图,其描述了舰艇杀伤区、发射区、预警机前出距离以及预警距离之间的关系。图中:X为目标的水平距离;P为目标的航路捷径;O为舰艇阵位;E为预警机阵位;敌目标以速度Vm、在高度hm沿航路捷径pm向舰艇袭来;αd为敌目标可能形成的威胁扇面角;Dqc和RE分别为预警机的最大前出距离及探测距离;Ssyj和Ssjj分别为杀伤区远近界[5];Sfyj和Sfjj分别为发射区远近界;ψmax为最大航路角;Rbyj为舰艇的必需预警距离。己方导弹的攻击速度为Vw,设k=Vw/Vm。
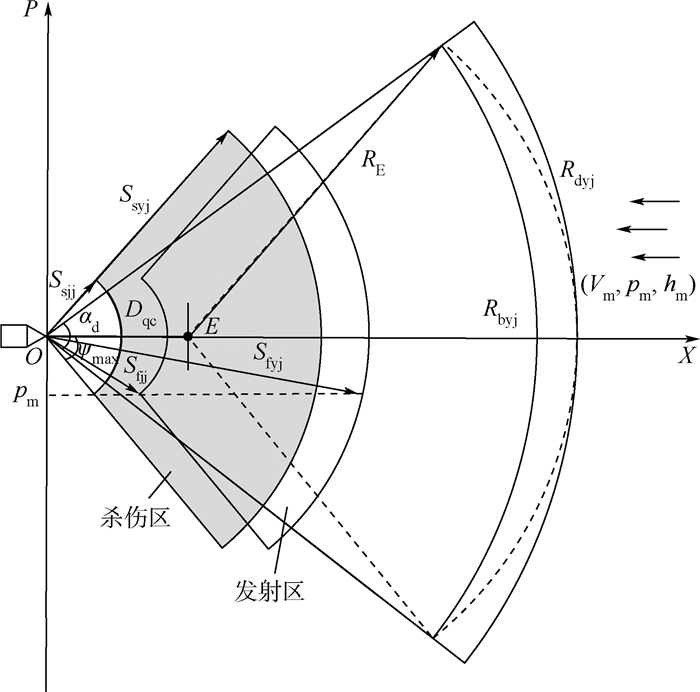 |
| 图 2 舰艇作战能力指标关系图 Fig. 2 Warship combat capability index relationship diagram |
| 图选项 |
通过以上模型已建立了能力指标之间的等式约束(Equality Constraints,EC)[6]关系为
 | (2) |
式中:Swgz为舰艇对目标的稳定跟踪距离;n为舰空导弹武器系统对敌目标的拦截次数[7];p为导弹的单发毁伤概率;s为一次齐射导弹的数量;P(t≤tjs)为t≤tjs时间内导弹的引入概率;twk为导弹无控段的飞行时间;σt为导弹引入结束时间的方差;tz为舰空导弹有动力飞行时间;txy为从接到预警和目标指示到导弹与目标相遇的时间;t为舰空导弹实施一次完整射击所需要的时间。ssyj和ssjj分别为Ssyj和Ssjj在水平面的投影;sfyj和ssjj分别为Sfyj和Ssjj在水平面的投影。
能力指标之间不仅具有EC关系,还存在一些不等式之间的关系。例如在预警机的配置上,考虑预警机的留空时间,前出距离必须在舰艇的有效通信范围之内,并且舰艇要为预警机提供有效的防空火力保护,确保预警机安全遂行作战任务[8];其次,舰艇对目标的发现距离、稳定跟踪距离与杀伤区远界都存在大小制约关系。提取约束集IC_2:
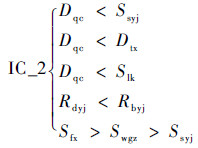 | (3) |
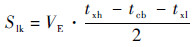 | (4) |
式中:Slk为预警机在保证巡逻时间的前提下,远离基准点的最大距离;txh为预警机的续航时间;tcb为预警机的储备时间;txl为上级对预警机在巡逻区巡逻时间的需求;Dtx为预警机与舰艇进行可靠通信的距离;Sfx为发现距离。
1.3 技术发展约束 技术发展需求描述了武器装备发展预测水平,装备标准随着技术发展不断进步,能力需求给出装备在未来一段时间内预期达到的水平。然而在装备体系发展建设中,往往采用保守的技术和标准来降低风险,根据武器装备建设发展水平,可以给定某一能力指标的技术发展约束,根据文献[9]中某中远型舰空导弹性能参数见表 1。
表 1 舰空导弹性能参数 Table 1 Performance parameters of ship-to-air missile
| 参数 | 数值 |
| 作战距离/km | 15~150 |
| 作战高度/m | 10~29000 |
| 速度/ Ma | 2.5 |
| 拦截概率/% | 80 |
| 系统反应时间/s | 1 |
表选项
提取约束集IC_3:
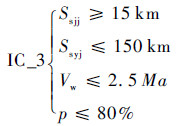 | (5) |
1.4 其他约束 除了以上几种约束之外,通过大量的作战模拟及仿真训练得到的历史数据,加上专家经验往往具有较高的可信度。从大量作战模拟训练数据分析获取指标约束,或者由专家依据自己的经验给定某一能力指标的约束关系也是指标约束获取的有效方法,但是对于经验约束需要进一步分析确定约束的可信度。
2 基于APSO算法能力需求约束优化 通过解析规则得到能力需求列表,可以成功执行每一个能力指标对应的作战任务,而科学合理的能力需求方案需要满足系统各方面的约束[10]。从本质上来讲,在使舰艇整体防空作战效能最大的前提下寻求满足各个约束条件下的能力需求方案是一个约束优化问题(constrained optimization problem),采用罚函数法约束处理技术把一个约束优化问题转化成一系列无约束优化问题,然后通过求解这些无约束优化问题使得整个约束优化问题得以解决[11]。由于建立模型是一个带约束的非线性方程最优值寻解,采用自适应粒子群寻优(Adaptive Particle Swarm Optimization,APSO)算法,实现对目标函数的寻优求解。
2.1 适应度函数的建立 能力指标的生成既要满足各个约束条件,又要使舰艇的综合作战效能最大,采用指数法建立舰艇防空作战的综合效能模型[12],将能力指标作为效能指标,为了使模型求解的最终结果统一为越小越优,将成本型指标作为分子,效益型指标作为分母,建立的适应度函数为
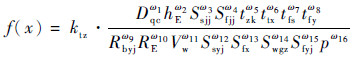 | (6) |
式中:ktz为调整系数;ωi为指标权重;tzk为指控时间;ttx为通信时间;tfs为导弹发射时间;tfy为反应时间。
利用层次分析(AHP)法,确定判断矩阵,求取特征向量μ即为能力指标的权重ωi,进行一致性检验判断矩阵是否具有满意的一致性。
2.2 约束处理的罚函数法 考虑如下约束优化问题:
最小化f(x)
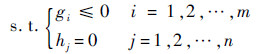 | (7) |
处理约束优化问题应用最广泛的就是罚函数法,根据约束条件构造如下辅助函数:
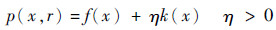 | (8) |
式中:p(x,r)为增广目标函数;η为罚因子;k(x)为罚项,其定义为
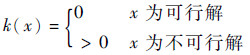 | (9) |
一般取
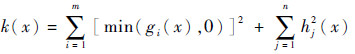 | (10) |
当x是不可行解时,p(x,r)>f(x);当x是可行解时,p(x,r)=f(x)。罚因子η越来越大时,不可行解的函数值也将越来越大,能够促使一系列无约束问题的极小值点靠近可行域,或者在可行域内移动,直到收敛到满足目标函数的最优值。因此,给原函数加了一个整数以示惩罚,当η足够大时,就可以保证原函数的最优解和增广目标函数的最优解一致[13]。
2.3 APSO算法流程 步骤 1 ????对粒子种群进行初始化(包括粒子数、迭代次数和衰减因子等),建立约束集(包括不等式约束集和等式约束集)。
步骤 2 ????对粒子进行约束求解,通过约束集建立罚函数,进行多维目标函数求解,返回粒子适应度值,更新个体最优值fbest,记录最优个体gbest。
步骤 3????更新随机性衰减因子,更新粒子位置,增加粒子在上下边界区间内的随机性。
步骤 4????判断是否满足迭代条件,如果满足,返回步骤2构成循环迭代,否则输出最优结果[14]。
2.4 实例求解 在预警机协同下的舰艇区域防空作战能力需求分析中,首先需要判断己方能够探测到敌目标距离,根据战场态势提出完成相应作战任务所需的作战能力。假定Vm=700 m/s,Vw=600 m/s,hm=3 500 m,αd=30°,ψmax=60°,pm=100 m,s=2,其余参数主要有tzk、ttx、tfs、σt、tfy、P(t≤tjs)、twk和tz假定服从正态分布,影响参数设定见表 2。
表 2 影响参数设定 Table 2 Influence parameters setting
| 参数 | μ′ | σ |
| tzk( s) | 10 | 2 |
| ttx( s) | 3 | 1 |
| tfs( s) | 20 | 3 |
| twk( s) | 3.5 | 0.05 |
| tfy( s) | 8 | 2 |
| σt | 3.1 | 0.1 |
| P( t≤ tjs) | 0.94 | 0.03 |
| tz( s) | 0.1 | 0.05 |
| μ′-参数期望;σ-参数方差。 | ||
表选项
根据作战需求约束描述,需对敌400 km以外的目标进行预警,设Sdyj=400 km,仅考虑等式约束条件下各能力指标的生成,当可设定的影响参数趋于2个极值时,得到作战能力指标生成,如表 3所示。
表 3 作战能力指标生成 Table 3 Combat capability index generation
| 能力指标 | 区间值 |
| Dqc/km | [88.69,95.10] |
| hE/m | [220.32,268.88] |
| Rbyj/km | [337.79,347.59] |
| RE/km | [304.89,311.30] |
| Ssyj/km | [149.12,149.12] |
| Ssjj/km | [4.72,6.17] |
| Sfyj/km | [323.02,323.02] |
| Sfjj/km | [10.23,13.37] |
| Sfx/km | [339.65,349.87] |
| Swgz/km | [323.38,323.45] |
| n | [1,4] |
| p/% | [31.23,90] |
表选项
由表 3可知Ssyj和Sfyj的区间上下限一致,因为影响Ssyj的因素主要是敌我速度和跟踪制导距离,Sfyj又主要受Ssyj的影响,影响参数的变化不会影响两者的取值,因此Ssyj和Sfyj的区间上下限一致。在能力指标区间值的基础上,综合考虑作战需求、能力需求、技术发展及其他约束,综合IC_1、IC_2、IC_3和EC,建立如下约束优化求解模型:
最小化f(x)
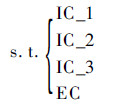 | (11) |
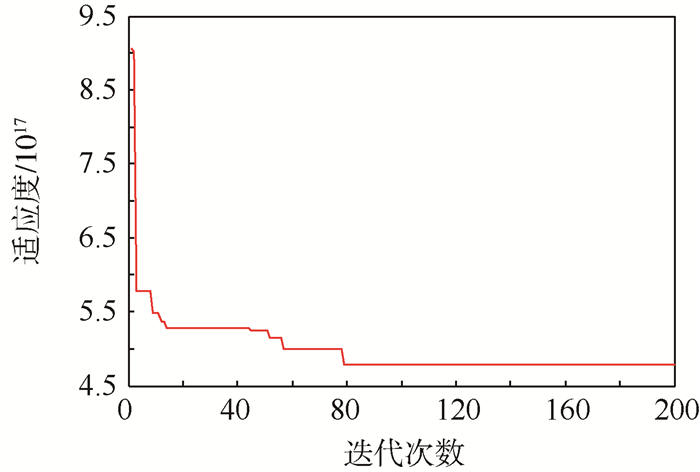
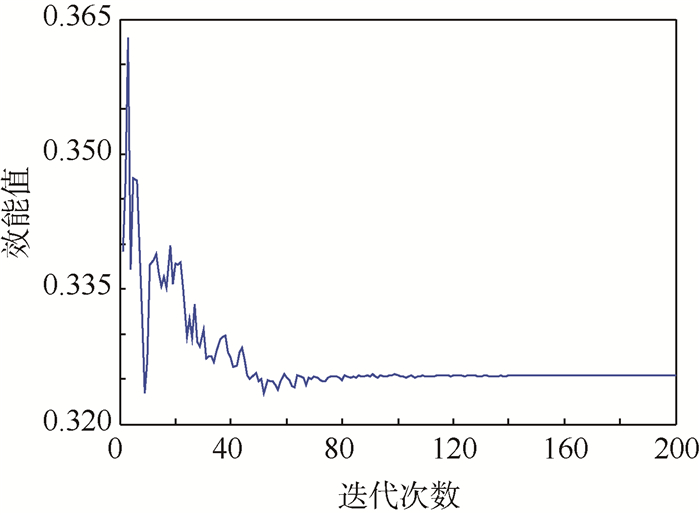
采用基于罚函数的粒子群寻优算法进行约束的求解[15],得到在约束条件下能力指标的最优值如表 4所示,图 3为APSO适应度曲线,图 4为最优个体效能值曲线。
表 4 约束优化后的能力指标最优值 Table 4 Optimum value capability index after constrained optimization
| 能力指标 | 指标值 |
| Dqc/km | 93.24 |
| hE/m | 256.14 |
| Rbyj/km | 384.82 |
| RE/km | 307.46 |
| Ssyj/km | 158.89 |
| Ssjj/km | 15.17 |
| Sfyj/km | 335.06 |
| Sfjj/km | 24.24 |
| Sfx/km | 372.82 |
| Swgz/km | 346.10 |
| n | 4 |
| p/% | 64.47 |
表选项
 |
| 图 3 APSO适应度曲线 Fig. 3 APSO fitness curve |
| 图选项 |
 |
| 图 4 最优个体效能值曲线 Fig. 4 Optimal individual effectiveness value curve |
| 图选项 |
从图 3和图 4中看出,对约束较为复杂的最优值寻优求解中,APSO算法表现出较好的健壮性,系统能够较快收敛,寻优解也与实际情况相符。
本文中定义舰艇防空作战效能为适应度函数,由于成本型指标作为分子,效益型指标作分母,因此值越小表示作战效能越大,对比图 3和图 4,两图的基本走势趋向一致,在算法迭代过程中最优个体gbest代表的效能值比较小,但是相对应的其适应度值fbest较大,即gbest违反了多个约束条件,罚函数作用使其适应度值比较大,随着迭代次数的增加gbest的适应度值越来越小,即gbest尽可能多地满足约束条件,其效能值忽高忽低直至最后稳定,说明在进化算法中,主要以满足约束条件为重要目标兼顾作战效能的大小。
算法在运行到90代左右时能够快速收敛,说明算法已经寻得满足约束条件的最优值,使其适应度值及效能值达到相对最优。然而对比可以发现,最后收敛后的适应度值与效能值并非完全一致,说明所得到的最优解并非完全满足所列的约束集,这与本文所采用的罚函数法有关系,罚因子的取值难以把握,太小起不到惩罚作用,太大则由于误差的影响会导致错误,分析算法最终得到的最优解,经粒子群算法约束优化后的最优解是可行的。
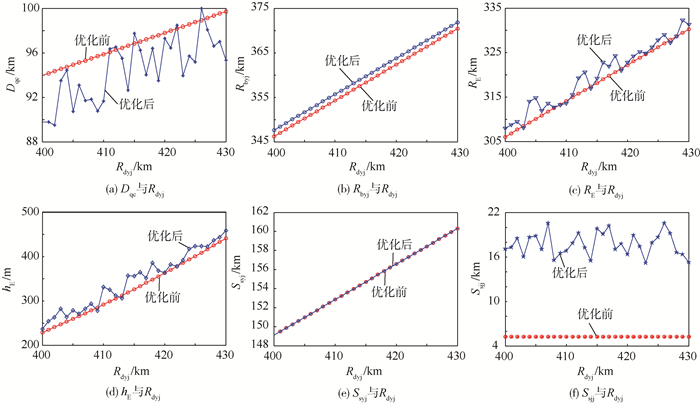
为了验证算法的可行性,考虑到对敌目标预警的全面覆盖,即对Rdyj=400~430 km进行预警探测,选取Dqc、Rbyj、RE、hE、Ssyj和Ssjj具有代表性的能力指标,做出其在Rdyj=[400,430] km区间中约束优化前后的曲线图,如图 5(a)~图 5(f)所示。
 |
| 图 5 Dqc、Rbyj、RE、hE、Ssyj、Ssjj与Rdyj之间优化前后关系 Fig. 5 Relationship between Dqc、Rbyj、RE、hE、Ssyj、Ssjj and Rdyj before and after optimization |
| 图选项 |
从图 5可以看出,各能力指标约束优化后的取值基本围绕在优化前取值的附近,对比约束关系集,可以肯定优化值符合约束关系;Ssyj的取值优化前后基本没变,原因是影响Ssyj因素已经给定,在能力指标之间的约束关系中,Ssyj又是作为影响其他能力指标的主要因素,因此Ssyj优化前后取值基本保持不变;Ssjj优化前后取值变化明显,因为Ssjj主要与己方舰空导弹的性能有关,在约束关系中,根据技术发展要求Ssjj≥15 km,因此优化后的Ssjj取值符合约束关系的要求。通过大量仿真得到优化前后能力指标数据曲线图,进一步验证了所建模型、算法的有效性。
3 结 论 本文以舰艇区域防空作战为例,以舰艇防空作战效能优化为原则建立了基于约束优化的能力需求生成模型,经仿真验证表明:
1) 较为全面地提取了能力需求生成所需满足的约束集,为约束优化模型提供了基础。
2) 采用指数法较好地表征了舰艇防空作战效能,使约束优化问题更具有目标性。
3) 建立的APSO算法模型可得到满足多维约束条件优化的能力需求生成方案,寻优速度快,优化效果较好。
本文最终得到的能力优化指标验证了仿真模型,为舰艇能力需求生成提供了一种定量化方法,对于舰艇装备的发展具有现实指导意义。
参考文献
| [1] | 陈英武, 豆亚杰, 程贲, 等. 基于作战活动分解的武器装备体系能力需求生成研究[J]. 系统工程理论与实践,2011, 31(1): 154–163.CHEN Y W, DOU Y J, CHENG B, et al. Research on capability requirement generation of weapon system-of-systems based on operational activity decomposition[J]. Systems Engineering-Theory & Practice,2011, 31(1): 154–163.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [2] | 王剑飞, 郭嘉诚, 周云富. 联合作战能力需求分析方法研究[J]. 军事运筹与系统工程,2009, 23(2): 30–34.WANG J F, GUO J C, ZHOU Y F. Study on analysis method of joint combat capability requirement[J]. Military Operations Research and Systems Engineering,2009, 23(2): 30–34.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [3] | 李涛, 熊光愣. 基于优化算法的冲突仲裁策略[J]. 计算机学报,2002, 25(1): 57–62.LI T, XIONG G L. Conflict resolving strategy based on optimization algorithm[J]. Chinese Journal of Computer,2002, 25(1): 57–62.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [4] | 张兵志, 郭齐胜. 陆军武器装备需求论证理论与方法[M].北京: 国防工业出版社, 2012: 83-91.ZHANG B Z, GUO Q S. Theory and method of requirement demonstration for army weapon equipment[M].Beijing: National Defense Industry Press, 2012: 83-91.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [5] | 董银文, 石章松, 李云. 舰空导弹协同制导杀伤区建立研究[J]. 指挥控制与仿真,2010, 32(6): 16–19.DONG Y W, SHI Z S, LI Y. Research on damage zone of surface-to-air missile in the mode of collaborative guidance[J]. Command Control and Simulation,2010, 32(6): 16–19.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [6] | 许俊飞, 邢昌风, 吴玲. 基于解析规则的舰艇区域防空作战能力需求生成[J]. 北京航空航天大学学报,2015, 41(1): 193–200.XU J F, XING C F, WU L. Capability requirement generation of warship area air defense based on analytic rules[J]. Journal of Beijing University of Aeronautics and Astronautics,2015, 41(1): 193–200.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [7] | 栗飞, 曲朋飞, 闫艳坤. 舰空导弹武器系统反导作战拦截次数建模与仿真[J]. 弹箭与制导学报,2012, 32(2): 32–34.SU F, QU P F, YAN Y K. Modeling and simulation of anti-missile interception frequency for ship-to-air missile weapon system[J]. Journal of Projectiles,Rockets,Missiles and Guidance,2012, 32(2): 32–34.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [8] | 沈治河, 朴成日. 航母编队在对空防御中歼击机空域配置方法[J]. 指挥信息系统与技术,2012, 3(3): 29–34.SHEN Z H, PIAO C R. Fighter airspace disposition method for carrier formation in air defense[J]. Command Information System and Technology,2012, 3(3): 29–34.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [9] | 张冬兴, 缪旭东. 美航母编队防空作战能力分析[J]. 飞航导弹,2010, 8(1): 60–65.ZHANG D X, MIU X D. The U.S.aircraft carrier fleet air defense combat capability analysis[J]. Cruise Missile,2010, 8(1): 60–65.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [10] | 王志亮, 张友良, 汪惠芬. 协同设计中定量化约束求解方法[J]. 计算机辅助设计与图形学报,2004, 16(8): 1114–1121.WANG Z L, ZHANG Y L, WANG H F. A quantified method for constraint resolution in collaborative design[J]. Journal of Computer-Aided Design & Computer Graphics,2004, 16(8): 1114–1121.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [11] | ANDREW K, WANG J. Dependency analysis in constraint negotiation[J]. IEEE Transactions on Systems,Man,and Cybernetics,1995, 25(9): 1301–1313. |
| Click to display the text | |
| [12] | 许俊飞, 邢昌风, 吴玲. 基于指数法的舰艇火控系统效能分析[J]. 指挥控制与仿真,2015, 37(1): 80–84.XU J F, XING C F, WU L. Ship fire control systems effectiveness analysis based on index method[J]. Command Control and Simulation,2015, 37(1): 80–84.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [13] | LI X D.Better spread and convergence:Particle swarm multi objective optimization using the maximum fitness function[C]//Proceedings of 2004,Genetic and Evolutionary Computation Part Ⅰ.[S.l.]:Springer,2004:128-177. |
| Click to display the text | |
| [14] | 高飞. MATLAB智能算法超级学习手册[M].北京: 人民邮电出版社, 2014: 241-248.GAO F. MATLAB super intelligent algorithm learning manual[M].Beijing: The Posts and Telecommunications Press, 2014: 241-248.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [15] | FAN S K S, ZAHARA E. A hybrid simplex search and particle swarm optimization for unconstrained optimization[J]. European Journal of Operational Research,2007, 181(2): 527–548. |
| Click to display the text | |
