航天器脉冲交会对接,是空间交会重要制导控制技术之一,为节省燃料,提高航天器载荷,其优化问题一直是人们研究的热点。众多****对双脉冲^[1-3]或多脉冲的圆轨道或椭圆轨道^[4]的交会对接问题,利用遗传算法^{[1, 5-6]}、差异演化(Differential Evolution,DE)算法^[2]、粒子群算法^{[3, 7]}、非线性规划算法^[8]和混合遗传算法^[9]等求解了“最优解”,但是由于算法特性,基于一定的随机概率或者过度依赖初始值选取,所求取的“优化解”在理论上无法证明全局性。
近几年来,一种在给定精度内可以求出问题的全部全局极小点,用区间运算代替点运算的基于区间分析的区间优化算法,发展势头良好,并初步应用于航天领域^[10-20]。但是区间优化算法也因为过多占用系统内存、计算量大及收敛速度慢等缺点,在实用中受到牵制。如文献[15]采用区间优化算法,运算超出系统内存。造成系统内存溢出的主要原因有,区间分割产生了过多的子区间、不能快速舍弃不包含最优解的子区间等。为此,****们针对区间优化算法的自身,设计了各类策略。例如区间Newton法、box一致性等区间紧缩策略^[13];3ⁿ、4ⁿ等的区间分割方式^[16];cut-off测试^[17]、单调性测试^[18]等区间舍弃策略等。但是其均有使用范围,受用性有限。另有一些****另辟蹊径,将区间优化算法与局部寻优算法结合。文献[15]采用先区间算法,后梯度算法的方式,得到一组“最优解”。该算法大幅减少了运算时间,降低了系统内存消耗,但是失去了区间优化算法的全局特性。文献[18]将区间优化算法和粒子群算法结合,同样无法保证解的全局性。
因此,为保证全局特性和一定的快速性,同时降低运算存储,防止内存运算溢出。本文将采用区间优化算法来保证求解的全局性,并为区间优化算法设计区间选择策略防止运算存储过大;引入梯度优化算法,结合非固定时间的双脉冲交会优化模型自身,设计区间分割方式、目标优化估计值更新方式等提高运算效率,以此研究解决非固定时间的航天器双脉冲交会优化问题。
1 优化模型 2个航天器之间的相对运动可采用Clohessy-Wiltshire(CW)方程近似描述:

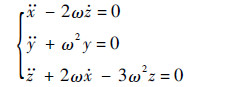(1)

式中:ω为目标航天器轨道角速度。
通过式(1),可得追踪航天器t时刻相对于目标航天器的相对位置和相对速度如下:

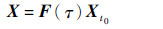(2)

式中:X=(x(t),y(t),z(t),(t),(t),?(t))^T；X_t0=(x(t₀),y(t₀),z(t₀),(t₀),(t₀),?(t₀))^T;

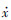
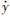
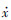
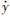
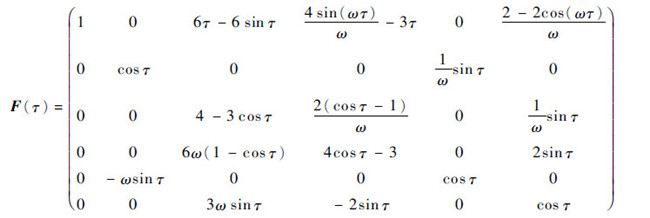其中:τ=ω(t-t₀);(x(t₀),y(t₀),z(t₀))^T和((t₀),(t₀),?(t₀))^T分别为追踪航天器t₀时刻初始相对位置和初始相对速度。
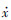
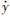
设航天器交会时刻为t_f。从t₀时刻开始,在t₁时刻,追踪航天器施加第1次脉冲,相对速度增量为Δv₁=(Δv_1x,Δv_1y,Δv_1z)^T。经过t_1→f=t_f-t₁时间,在t_f时刻,追踪航天器施加第2次脉冲,相对速度增量为Δv₂=(Δv_2x,Δv_2y,Δv_2z)^T,至此2个航天器交会。
通过式(2),交会时刻t_f的相对距离S=(S_x,S_y,S_z)^T和相对速度V=(V_x,V_y,V_z)^T为

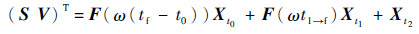(3)

式中:X_t1=(0,0,0,Δv_1x,Δv_1y,Δv_1z)^T;X_t2=(0,0,0,Δv_2x,Δv_2y,Δv_2z)^T。
由于航天器交会的终端状态为交会时刻t_f的相对距离S为(0,0,0)^Tm和相对速度V为(0,0,0)^Tm·s^-1,即

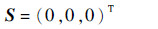(4)

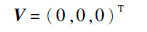(5)

则若给定了t_1→f,t_f,可以通过式(3)和式(4)求取Δv_1x,Δv_1y,Δv_1z,结合式(5)可以求取Δv_2x,Δv_2y,Δv_2z,即当给定了t_1→f,t_f时,整个交会轨道就确定了,故决策变量为t_1→f,t_f。
若只考虑对燃料消耗的要求,其优化指标为

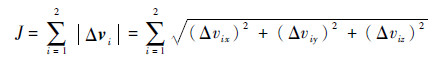(6)

J取最小值,则双脉冲交会燃料消耗最低。
2 基于梯度分割区间优化算法 结合航天器脉冲交会优化应用的需要,本文将区间数定义为大于实数a且小于实数b(b>a)的所有实数的集合,记为[a,b]。一个变量区间可记为[x]=[a,b],其中[x].inf=a,[x].sup=b,width([x])为[x]的区间宽度,即b-a。sgn([x])为区间符号判断函数,[x].inf≥0,返回1;[x].sup≤0,返回-1;[x].inf×[x].sup <0,返回0。
区间分析是关于区间数的运算。利用区间分析理论,通过不断分割变量区间,并使用区间优化策略方法舍弃不含全局最优解区间,直至找到指定精度下,全局最优解区间的过程,称为区间优化算法^[10]。
为了更好地解决航天器双脉冲交会轨迹优化问题,在区间优化算法的基础上,引入梯度优化算法和一些区间优化策略,构成基于梯度分割区间优化算法(GIOA),在保证全局性的同时,提高运算效率,算法主要分为以下6大模块。
2.1 算法预处理
2.1.1 决策变量区间的选取 根据式(3)、式(4),可以通过t_1→f,t_f求取Δv_1x,Δv_1y,Δv_1z,但是该区间运算中涉及区间除法运算,而当区间变量的区间宽度大于一定阈值或者在包含某一特定值的区间上,除数区间可能包含0,导致无法获得有限边界的[Δv_1x],[Δv_1y],[Δv_1z]。为此增加设计决策变量Δv_1x,Δv_1y,Δv_1z,并由此将第1节所述的无约束模型转化为以式(4)、式(5)为约束条件的优化模型。故决策变量区间取为[u]=[［Δv_1x];[Δv_1y];[Δv_1z];[t_1→f];[t_f]］。

2.1.2 约束条件的转化 式(5)相对速度约束V=(0,0,0)^T可以由第2次脉冲相对速度增量(Δv_2x,Δv_2y,Δv_2z)^T得以保证。
而式(4)相对距离约束S=(0,0,0)^T,将S_i(u)=0(i=x,y,z)在区间运算中数值上转化为[S_i]([u])<ε(相对距离精度ε为小正实数),在等式约束特征上转化为0∈[S_i]([u])。
2.2 区间选择 为了有效控制运算中子区间的生成数量和运算存储量,本文将对由若干决策变量区间[u]组成的区间群队列L中的决策变量区间进行选择操作。不同于文献[13]中对区间群队列L中决策变量区间以目标函数区间的下界排序,每次取目标函数区间下界最小对应的决策变量区间进行操作,下文称为“分而治之”区间选择策略。
设定当前区间群队列L有Q个决策变量区间,在每一次算法迭代前,在区间群队列L队尾提取出M个决策变量区间作为子区间队列L₁,当Q≤M时,令M=Q,同时从区间群队列L删除这M个决策变量区间。
在一次迭代运算中,区间队列L₁经过后续区间分割、区间紧缩等模块,生成子区间队列L_new。当一次迭代结束后,将子区间队列L_new置于区间群队列L队尾,以此新的区间群队列L进入下一次区间选择,并迭代运算。
2.3 区间分割 区间分割主要用于在无法继续紧缩区间宽度,又无法判断舍弃该区间时,将一个区间按给定策略分割成多个区间,以便继续利用区间分析方法寻找最优解。
在以往大多数文献中,均采用了如文献[20]所述的中点分割法。为了进一步提高运算速度,本文结合模型特性和梯度优化算法,分别设计了2种特定的分割方式。
1) 结合模型特性的符号分割法
由算法预处理可知,决策变量区间包含3个相对速度增量区间变量和2个时间区间变量。为了减少区间运算过程中由于区间包含“0”而引起的区间过度扩张,对决策变量区间中的相对速度增量区间变量以0值为界分割为2个区间,以使相对速度增量区间仅包含正值或负值;对时间区间变量,以优化模型中出现的三角函数的象限边值为界分割为多个区间,以使优化模型中的各三角函数区间仅包含正值或负值。该分割法仅限应用于算法第1次迭代。
2) 结合梯度优化算法的梯度分割法
在决策变量区间[u]指定的各区间变量范围内,采用梯度优化算法寻优,如若有解,则以该解对应的决策变量值为中心,以给定的数值为半径,将决策变量值扩展为包含有梯度优化算法解的扩展区间[I_Δ],以扩展区间[I_Δ]的各个区间变量的边界值分别去分割原决策变量区间[u]的各个区间变量。若梯度优化算法无解,则采用中点分割法。
梯度分割法将包含局部最优解或可行解的决策变量区间和非包含的决策变量区间分离开来,有利于不包含全局最优解的决策变量区间的舍弃和较快地得到包含全局最优解的小区间宽度的决策变量区间。
在区间分割时,为了降低算法的计算量和区间分割的维度,当决策变量区间[u]中相对速度增量区间的区间宽度大于2个时间区间变量区间宽度的最大值时,才对相应相对速度增量区间予以分割。相对速度增量区间变量区间宽度的减小主要依靠区间紧缩策略和约束条件测试间接判断法。
2.4 区间紧缩 区间紧缩策略主要应用于约束条件中决策变量区间,基于一定的策略,缩减决策变量区间的区间宽度。
本文给出了一种利用相对距离函数[S_i]([u])(i=x,y,z)单调性对[u]的区间宽度进行紧缩的区间紧缩策略。
若[S_i]([u])对决策变量区间[u]中的第k个区间变量[p_k]是单调的,且满足

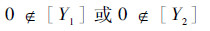(7)

式中:[Y₁]=[S_i]([p₁],…,[p_k].inf,…,[p₅]);[Y₂]=[S_i]([p₁],…,[p_k].sup,…,[p₅]),则在[p_k]内寻找满足如下条件的较大值q_k1：

(8)

式中:[Y₃]=[S_i]([p₁],…,q_k1,…,[p₅]),若没有,则令q_k1=[p_k].inf;在[p_k]内寻找满足如下条件的较小值q_k2：

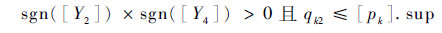(9)

式中:[Y₄]=[S_i]([p₁],…,q_k2,…,[p₅]),若没有,则令q_k2=[p_k].sup。用区间[q_k1,q_k2]更新决策变量区间[u]的第k个区间变量[p_k]。
由此将[u]中的第k个区间变量[p_k]紧缩为了[q_k1,q_k2],利于后续运算。
2.5 区间取舍和目标优化估计值更新 本文中将使用多种区间取舍和目标优化估计值更新方法。包括cut-off测试^[17]、单调性测试^[18]、结合模型的约束条件测试和基于梯度的目标优化估计值更新等。这里主要介绍后2种。
1) 约束条件测试
直接判断:若当前决策变量区间[u]不能满足约束条件,则去除相对应的决策变量区间[u],否则,需要进一步判断。
间接判断:由于相对距离约束S_i(u)=0(i=x,y,z)中速度增量是线性相关的,则利用决策变量区间[u]中的[［t_1→f],[t_f]］,通过[S_i]([u])=0解出[［v_{1x_t}],[v_{1y_t}],[v_{1z_t}]］,并计算其与[u]中[［v_1x],[v_1y],[v_1z]］的交集[［v_{1x_n}],[v_{1y_n}],[v_{1z_n}]］,若该交集为空集,则去除相对应的决策变量区间[u],否则,替换决策变量区间[u]中的[［v_1x],[v_1y],[v_1z]］为[［v_{1x_n}],[v_{1y_n}],[v_{1z_n}]］。
2) 基于梯度的目标优化估计值更新
不同于2.3节的梯度分割法,若在一个决策变量区间[u]指定的各区间变量范围内,梯度优化算法有解,则以该解对应的决策变量值为中心,以非常小的数值为半径,将决策变量值扩展为包含有梯度优化算法解的扩展区间[I_Δ1],以期得到接近或包含全局最优解的小区间宽度的决策变量区间。利用区间分析理论在扩展区间[I_Δ1]上计算,检查其是否满足航天器双脉冲交会优化模型的约束条件,若满足,则计算相应的目标函数区间[J]。假设当前目标优化估计值为J_min,若[J].sup < J_min,则更新目标优化估计值,即J_min=[J].sup,否则J_min保持不变。
这样能够快速地更新目标优化估计值,为后续运算快速地去掉区间群队列L中大量不包含全局最优解的决策变量区间打下了基础。
2.6 算法终止条件
2.6.1 决策变量区间运算终止条件 当决策变量区间[u]无法判别舍弃,且又满足下列条件时

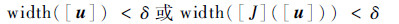其中:区间宽度精度δ为小正实数。将[u]从区间群队列L中删除,并将[u]置入设计结果区间队列R中,该队列包含了指定精度下,所有可能包含全局最优解的可行解区间。

2.6.2 运算终止条件 当区间群队列L中决策变量区间数目为0时,运算终止,算法结束。
上述算法的流程见图 1。图 1中,在指定精度下,包含全局最优解的可行解区间位于设计结果区间队列R中。

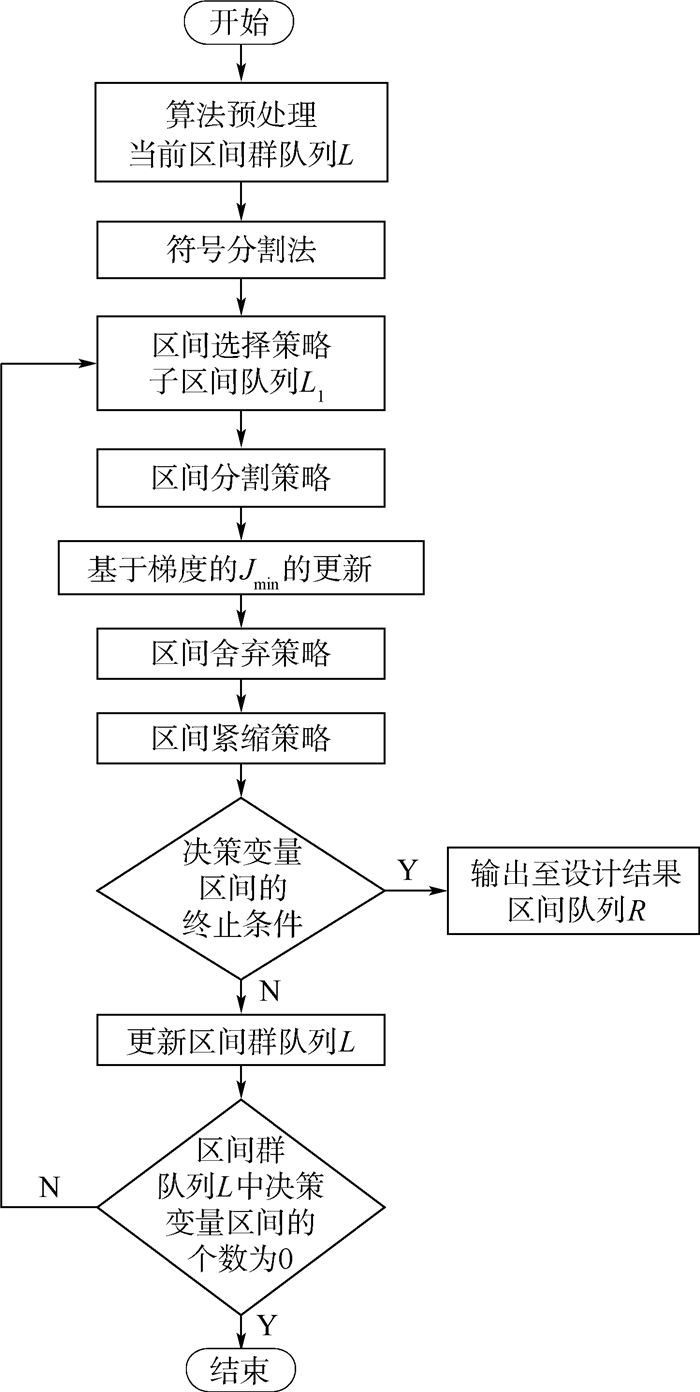图 1 基于梯度分割区间优化算法流程 Fig. 1 Flowchart of GIOA

图选项

3 算法的适用性、全局性和收敛性 3.1 适用性 GIOA是针对非固定时间的双脉冲交会优化问题而设计的,但是依然具有一定的普适性。在算法设计过程中由于采用了梯度优化算法、区间紧缩策略使用了单调性等,因此该算法针对在定义域某一局部范围内线性或非线性的目标函数和约束条件对决策变量连续可微的优化问题理论上均具有较好的应用效果。显然,本文要解决的非固定时间的双脉冲交会优化问题是符合的。
3.2 全局性和收敛性 GIOA是在区间优化算法的基础上,引入梯度优化算法,但不直接使用梯度优化算法结果,只是将其作为区间分割和目标优化估计值更新的一种手段,与其他模块设计一样,并没有破坏区间优化算法整体框架,因此整个算法实质上仍属于区间优化算法,其全局性和收敛性继承了区间优化算法的全局性和收敛性^[19]。
4 仿真算例 为说明所提出的GIOA在非固定时间双脉冲交会轨迹优化问题上的求解能力,并展示其正确性和有效性,进行了数学仿真分析。
4.1 仿真条件 设定目标航天器在400 km高的圆轨道上运行,参照文献[1-2]选取了3组追踪航天器处于以目标航天器为中心的相对坐标系的不同象限时的初始条件,如表 1所示。
表 1 基于梯度分割区间优化算法的双脉冲交会目标优化估计值对应的解区间 Table 1 Interval solution corresponding to optimal estimated value of double-impulse rendezvous using GIOA

组次	初始位置/km	初始速度/ (m·s－1)	[［Δv1x];[Δv1y]; [Δv1z]］/(m·s－1)	[［t1→f];[tf]］/s	[J]/(m·s－1)	设计结果区间 队列中区间个数	运算时间/ min
1	(-7,-1,5)	(2.820 3, 7.438 5, -7.93)	[7.416 511 185, 7.416 511 187] [-6.420 169 446, -6.420 169 444] [4.491 909 435, 4.491 909 437]	[2 371.772 220 606, 2 371.772 220 608] [2 568.085 214 200, 2 568.085 214 202]	[12.424 959 620 4, 12.424 959 620 7]	3 056	64
2	(2,-1,-5)	(-2.831 1, 7.433 0, 2.260 3)	[-7.197 484 639, -7.197 484 637] [-5.160 281 956, -5.160 281 954] [1.498 190 084, 1.498 190 086]	[2 887.638 905 907, 2 887.638 905 909] [2 986.254 943 073, 2 986.254 943 075]	[12.890 903 408 4, 12.890 903 408 8]	4 363	63
3	(-8,5,10)	(5.650 6, -7.441 2, -9.071 3)	[13.439 968 090, 13.439 968 092] [9.178 826 090, 9.178 826 092] [-3.568 758 729, -3.568 758 727]	[1 525.128 810 862, 1 525.128 810 864] [1 746.702 977 286, 1 746.702 977 288]	[22.017 747 598 8, 22.017 747 599 3]	4 164	85

表选项






设相对距离精度ε为0.01 m,区间宽度精度δ为0.01,目标优化估计值初值为100 m·s^-1,设决策变量区间初始值为[u]=[[-60,60];[-60, 60];[-60, 60];[0,8 000];[0,8 000]］。
仿真所使用计算机配置为Inter Core CPU i7-4710M 2.5 GHz,RAM DDR3 8 G。采用R2012a版MATLAB,使用并行工具spmd并行3 labs运算。
4.2 算法正确性验证 对3组初始条件,运用GIOA仿真运算得出的当前精度下,目标优化估计值对应的解区间如表 1所示。
表 1中[J].sup即为各初始条件下的目标优化估计值。在表 1中的第1组初始条件解区间内任意取值组合的相对轨迹如图 2所示。

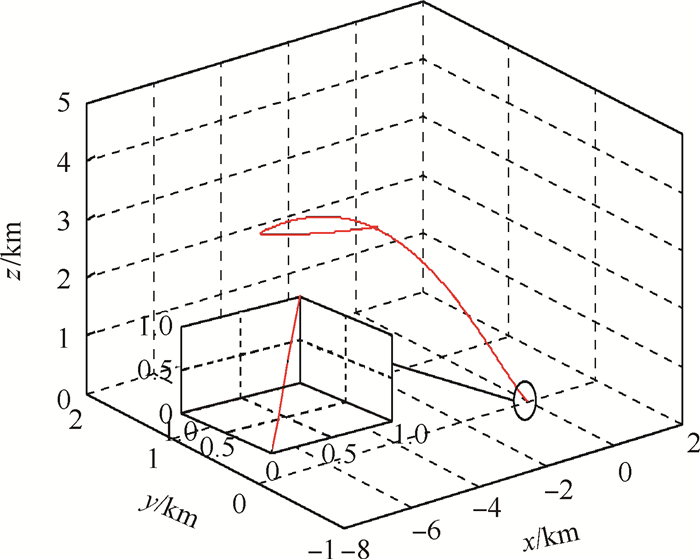图 2 表 1解区间任意取值的相对轨迹 Fig. 2 Relative path of value in interval solution of Table 1

图选项

由图 2可知,相对距离随着时间的推移,逐步缩减至0,误差在指定的0.01 m范围内。从路径上,直观地验证了优化解区间的正确性。
表 1中第1组初始条件,指定不同的求解区间宽度精度δ,对应的设计结果区间队列R如图 3所示。

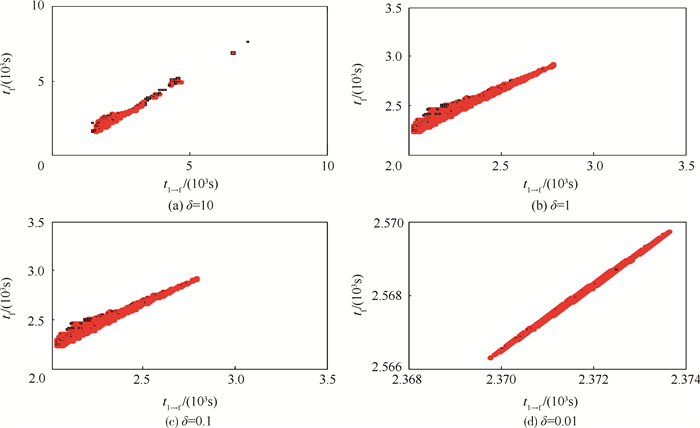图 3 不同区间宽度精度下的可行解[t1→f]-[tf] Fig. 3 Feasible solution [t1→f]-[tf] of various interval width precision

图选项

由图 3可知,在任意区间宽度精度下,GIOA能获取当前精度下所有可行解区间,体现了算法作为一种区间优化算法的全局性;随着区间宽度精度的提高,可行解区间逐步收敛至全局最优解附近,体现了算法的收敛性。
采用遗传算法求解该问题,以表 1中第2组数据为初始条件,令决策变量为t_1→f和t_f,搜索范围均为[0,8 000]s,设初始种群为500个,最大遗传代数为150代,求解10次,结果如表 2所示。
表 2 遗传算法结果 Table 2 Results of genetic algorithm

次数	Jmin/(m·s－1)	次数	Jmin/(m·s－1)
1	12.909 036 593 4	6	12.909 036 594 8
2	12.890 905 501 5	7	12.909 042 299 3
3	12.909 036 606 6	8	12.909 050 776 2
4	12.909 036 593 1	9	12.909 036 860 0
5	12.890 903 762 3	10	12.909 036 655 4

表选项






遗传算法求解时间虽然很短,但是因为其算法特性,表 2中10次运算,除了第2次和第5次,其余8次均陷入局部最优,经不起反复计算。
表 2中遗传算法最好的目标优化估计值为第5次的运算结果12.890 903 762 3,但是仍与表 1中GIOA求取的[J].sup(12.890 903 408 4)有略微差距,凸显了GIOA的寻优能力。
4.3 算法有效性验证 在文献[15]所述的改进前的区间优化算法的基础上,添加本文所设计的部分或全部算法模块,形成的算法A、B、C、D如表 3所示。
表 3 4种算法的特征 Table 3 Characteristics of four algorithms

算法模块	算法A	算法B	算法C	算法D
“分而治之”区间选择	×	√	√	√
符号分割法	√	√	√	√
梯度分割法	×	×	×	√
中点分割法	√	√	√	√
基于单调性的区间紧缩	√	√	√	√
约束条件测试	√	√	√	√
基于梯度目标优化估计值更新	×	×	√	√
注:“√”表示有;“×”表示没有。

表选项






以第1组初始条件为例,对算法A、B、C、D多方面比较。算法A、B仅能用满足约束条件的决策变量区间对应的目标函数区间的上界去更新目标优化估计值。由于区间扩张的影响,为了增强对算法A、B求解的可行性,将降低相对距离精度,令相对距离精度ε=1 m,同时区间宽度精度δ=0.01不变。
表 4中算法B、C、D的区间数目最大值较算法A,在有限次的迭代次数来看,低一个数量级,充分说明了“分而治之”区间选择策略能够有效控制区间群队列L中决策变量区间数目的增长,降低运算存储,由运算存储的降低同时,从运算时间上来看,运算效率也提高了近3倍。算法C较算法B,说明在相对距离精度ε=1 m时,基于梯度的目标优化估计值更新在实例中使得运算效率提高近13%。算法A较算法B,说明基于梯度的分割法,包含局部最优解或可行解的决策变量区间和非包含的决策变量区间分离开来,在实例中算法B的基础上,使得效率又提高了接近12%。算法A较算法C,说明引入梯度优化算法之后,在实例中,运算效率提高近25%。
表 4 迭代运算后子区间数目 Table 4 Number of subintervals after each iteration

迭代次数	区间群队列L中决策变量区间数目
	算法A	算法B	算法C	算法D
1	138	138	88	88
2	188	188	84	126
3	444	444	128	166
4	929	732	147	318
┇	┇	┇	┇	┇
14	14 261	1 223	389	1 838
15	21 437	1 485	501	1 668
16	15 723	1 262	685	1 509
17	3 435	1 001	885	1 646
18	0	932	940	1 583
┇		┇	┇	┇
71		561	585	244
72		494	421	133
73		606	366	6
74		661	317	0
┇		┇	┇
102		980	211
103		1 028	63
104		728	0
┇		┇
142		122
143		83
144		0
区间数目最大值	21 437	1 782	1 662	2 208
运算时间/min	316	83	72	64

表选项






表 5中算法B说明了使用“分而治之”策略的区间优化算法能够通过拉长迭代次数,在有限的内存资源内较快地更新目标优化估计值。而使用了基于梯度更新目标函数优化估计值的算法C、D则在第2次迭代中快速地更新了目标优化估计值,加快后续运算中不包含最优解区间变量的舍弃,提高了运算效率。
表 5 运算迭代过程中目标优化估计值的更新 Table 5 Updating table of optimal estimated value during each iteration

迭代次数	Jmin/(m·s－1)
	算法B	算法C	算法D
1	100	100	100
2	100	12.424 959 7	12.424 959 7
┇	┇	┇	┇
16	66.036 284 9	12.424 959 7	12.424 959 7
┇	┇	┇	┇

表选项






5 结论 为解决非固定时间的双脉冲交会优化问题,提出了GIOA。建立了燃料最省无约束优化模型,在使用GIOA的预处理中,为方便区间运算,将模型转化为了有约束的优化模型,决策变量为相对速度增量及脉冲施加时间相关变量,结果表明:
1) GIOA将梯度优化算法作为区间分割方式和目标优化估计值更新的重要手段,并对区间优化算法其他模块予以了改进,依然作为一种区间优化算法,继承了区间优化算法的全局性和收敛性。成功求解了非固定时间双脉冲交会问题不同精度下的全局优化解区间,并通过对比,全局性上明显优于遗传算法。
2) 梯度分割的区间优化算法中“分而治之”区间选择策略的使用,有效控制了决策变量区间数量的增长,降低算法运行的存储需求,由内存的降低而导致运算效率较算法A增长近3倍。
3) 由优化模型的约束条件和目标函数在局部连续可微而引入梯度优化算法,衍生的结合梯度优化算法区间分割方式和基于梯度的目标优化估计值更新,大幅提高了目标优化估计值的更新速率,在实例中分别提高了12%和13%的运算效率,整体提高了25%的运算效率。

参考文献

[1]	王华, 唐国金. 用遗传算法求解双冲量最优交会问题[J]. 中国空间科学技术,2003, 23(1): 26–30.WANG H, TANG G J. Solving optimal rendezvous using two impulses based on genetic algorithms[J]. Chinese Space Science and Technology,2003, 23(1): 26–30.(in Chinese).
	Cited By in Cnki (0) | Click to display the text
[2]	戴光明, 李晖. DE算法在空间交会中的应用[J]. 上海航天,2007, 24(3): 46–49.DAI G M, LI H. Study on application of differential evolution algorithm in space rendezvous[J]. Aerospace Shanghai,2007, 24(3): 46–49.(in Chinese).
	Cited By in Cnki (0) | Click to display the text
[3]	梁静静, 解永春. 基于粒子群算法优化双脉冲绕飞问题[J]. 空间控制技术与应用,2013, 39(5): 43–47.LIANG J J, XIE Y C. Double-impulsive fly-around problem based on particle swarm optimization algorithm[J]. Aerospace Control and Application,2013, 39(5): 43–47.(in Chinese).
	Cited By in Cnki (0) | Click to display the text
[4]	姬晓琴, 肖利红, 陈文辉. 基于T-H方程的多脉冲最优交会方法[J]. 北京航空航天大学学报,2014, 40(7): 905–909.JI X Q, XIAO L H, CHEN W H. Optimal multi-impulse rendezvous based on T-H equations[J]. Journal of Beijing University of Aeronautics and Astronautics,2014, 40(7): 905–909.(in Chinese).
	Cited By in Cnki (0) | Click to display the text
[5]	李晨光, 肖业伦. 多脉冲C-W交会的优化方法[J]. 宇航学报,2006, 27(2): 172–176.LI C G, XIAO Y L. Optimization methods of multi-pulse C-W rendezvous[J]. Journal of Astronautics,2006, 27(2): 172–176.(in Chinese).
	Cited By in Cnki (0) | Click to display the text
[6]	LUO Y Z, TANG G J, LEI Y J. Optimal multi-objective linearized impulsive rendezvous[J]. Journal of Guidance,Control,and Dynamics,2007, 30(2): 383–389.
	Click to display the text
[7]	GAO X,LIANG B,QIU Y.A PSO algorithm of multiple impulses guidance and control for GEO space robot[C]//Proceedings of the 13th ICARCV Conference.Piscataway,NJ:IEEE Press,2014:1560-1565.
	Click to display the text
[8]	XU L M,LIU H,ZHANG T.Optimal transfer orbit design based on multi-pulse thrust[C]//Proceedings of the 32nd Chinese Control Conference.Piscataway,NJ:IEEE Press,2013:5193-5197.
	Click to display the text
[9]	付磊, 安效民, 覃曌华, 等. 基于混合遗传算法的多冲量最优变轨[J]. 航天控制,2013, 31(3): 15–19.FU L, AN X M, QIN Z H, et al. The optimal multiple-impulse orbit transfer by using hybrid genetic algorithm[J]. Aerospace Control,2013, 31(3): 15–19.(in Chinese).
	Cited By in Cnki (0) | Click to display the text
[10]	MOORE R E, KEARFOTT R B, CLOUD M J. Introduction to interval analysis .2nd ed.[M].Philadelphia : Society for Industrial & Applied Mathematics , 2009: 7-35.
	Click to display the text
[11]	JULIANA S, CHU Q P, MULDER J A. Reentry flight clearance using interval analysis[J]. Journal of Guidance,Control,and Dynamics,2008, 31(5): 1295–1307.
	Click to display the text
[12]	DE WEERDT E,CHU Q P,MULDER J A.Global fuel optimization for constrained spacecraft formation rotations[C]//Proceedings of AIAA Guidance,Navigation,and Control Conference. Reston:AIAA,2009:1-21.
	Click to display the text
[13]	KAMPEN E V.Global optimization using interval analysis[D].Delft:Technische Universiteit Delft,2010:65-89.
	Click to display the text
[14]	高东迎, 岳晓奎. 基于区间算法的航天器再入轨迹优化[J]. 科学技术与工程,2012, 20(4): 852–856.GAO D Y, YUE X K. Trajectory optimization for reentry vehicle via interval algorithm[J]. Science Technology and Engineering,2012, 20(4): 852–856.(in Chinese).
	Cited By in Cnki (0) | Click to display the text
[15]	CHEN T, KAMPEN E V, YU H, et al. Optimization of time-open constrained Lambert rendezvous using interval analysis[J]. Journal of Guidance,Control,and Dynamics,2013, 36(1): 175–184.
	Click to display the text
[16]	CASADO L G, GARCIA I, CSENDES T. A new multisection technique in interval methods for global optimization[J]. Computing,2000, 65(3): 263–269.
	Click to display the text
[17]	NATARAY P S V, KOTECHA K. An algorithm for global optimization using the Taylor-Bernstein form as inclusion function[J]. Journal of Global Optimization,2002, 24(4): 417–436.
	Click to display the text
[18]	陈诚.基于区间数学的并行全局寻优算法的研究与系统实现[D].上海:上海大学,2014:25-36. CHEN C.Research and system implementation of parallel global optimal algorithm based on interval mathematics[D].Shanghai:Shanghai University,2014:25-36.(in Chinese).
	Cited By in Cnki (0) | Click to display the text
[19]	RATSCHEK H, ROKNE J. New computer methods for global optimization[M]. Chichester: Ellis Horwood Ltd, 1988: 85-89.
	Click to display the text
[20]	KAMPEN E V,CHU Q P,MULDER J A,et al.Nonlinear aircraft trim using interval analysis[C]//Proceedings of AIAA Guidance,Navigation,and Control Conference and Exhibit.Reston:AIAA,2007,4:4073-4087.
	Click to display the text