在阵风特性研究中,连续阵风模型是事先给定的风速功率谱密度(Power Spectral Density,PSD)函数,而响应的功率谱密度函数及统计特征通过概率论中的统计方法获得[3]。在目前使用的连续阵风模型中,许多参数通过试验结果的统计量获得,为确定性参数。实际上,阵风模型中存在很多不确定性因素,导致这些参数呈现很大的分散性,难以进行有效的统计特性分析。所以,连续阵风模型中统计特征量应视为不确定量。此外,由于阵风响应问题本身的复杂性以及飞行环境的多变性,在飞机阵风响应分析时,难以给出确定的有效阻尼值,并且飞机自身的重量等也会随着飞行时间产生变化,这些可变因素的存在会降低确定性阵风响应分析结果的可信度。因此,近年来很多****致力于不确定性阵风响应的研究[4, 5, 6, 7, 8]。宋述芳等[4]将机翼的结构参数处理为服从概率分布的随机变量,研究了机翼结构阵风响应的分布函数及灵敏度。苑凯华和邱志平[6]将结构参数和阵风模型参数视为区间不确定性参数,根据Taylor展开的区间方法研究了阵风响应问题,该方法只需知道不确定性参数较少的信息就能给出响应的区间界限,与文献[4]相比,更加简单适用,然而该方法也凸显了区间界值估计精度较低的缺点。
本文将机翼的结构参数和阵风模型参数处理为区间不确定量,基于第一类Chebyshev正交多项式和区间配点方案,结合有限元计算方法,提出了一种阵风响应问题的配点型区间分析方法(Collocation Interval Analysis Method,CIAM)。与传统区间方法相比,该方法的最大优点是放宽了对不确定性参数小范围变化的限制,能够在全局意义上给出高精度的响应界值,获得一个包含精确响应值的足够“紧”的阵风响应区间。
1 阵风响应的问题描述1.1 控制方程阵风按来流方向分为垂直阵风、侧向阵风和斜阵风。一般而言,垂直阵风对飞机的作用远强于其他方向的阵风作用。因此,本文只考虑飞机受到垂直阵风的作用。
考虑具有n个自由度的弹性机翼,结合机翼结构的惯性、刚度和结构阻尼,以及机翼在运动过程中引起的气动升力,根据变分原理,可以得到在阵风激励P作用下的机翼气动弹性运动方程为
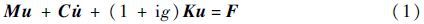
式中:u为机翼位移响应;F为机翼外部载荷;M、C和K分别为机翼质量矩阵、阻尼矩阵和刚度矩阵;g为机翼结构阻尼系数。
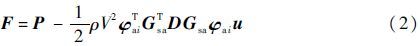
式中:ρ为飞行环境中的空气密度;V为飞行速度;φai为模态矩阵;Gsa为插值矩阵,其是由气动网格节点位移向结构网格节点位移转换的变换矩阵,可以通过线性样条插值和表面样条插值方法获得;D为气动力影响系数矩阵,其表达式形式取决于采用的气动力理论。
本文采用亚声速偶极子格网法[9]计算非定常气动力,该理论认为每个气动单元上的空气动力作用在单元中剖面与单元1/4弦线的交点,下洗控制点位于单元中剖面与单元3/4弦线的交点上,如图 1所示。升力面坐标系规定原点位于升力面翼根前缘,x轴顺气流方向,y轴沿翼展向外,z轴由右手定则确定。由线性非定常气动力理论可知
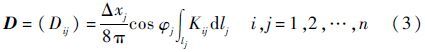
式中:Δxj为第j个网格的中剖面长度;φj为第j个网格的后掠角;lj为第j个网格的过1/4弦点的展长;Kij为核函数;n为升力面的气动网格单元数。
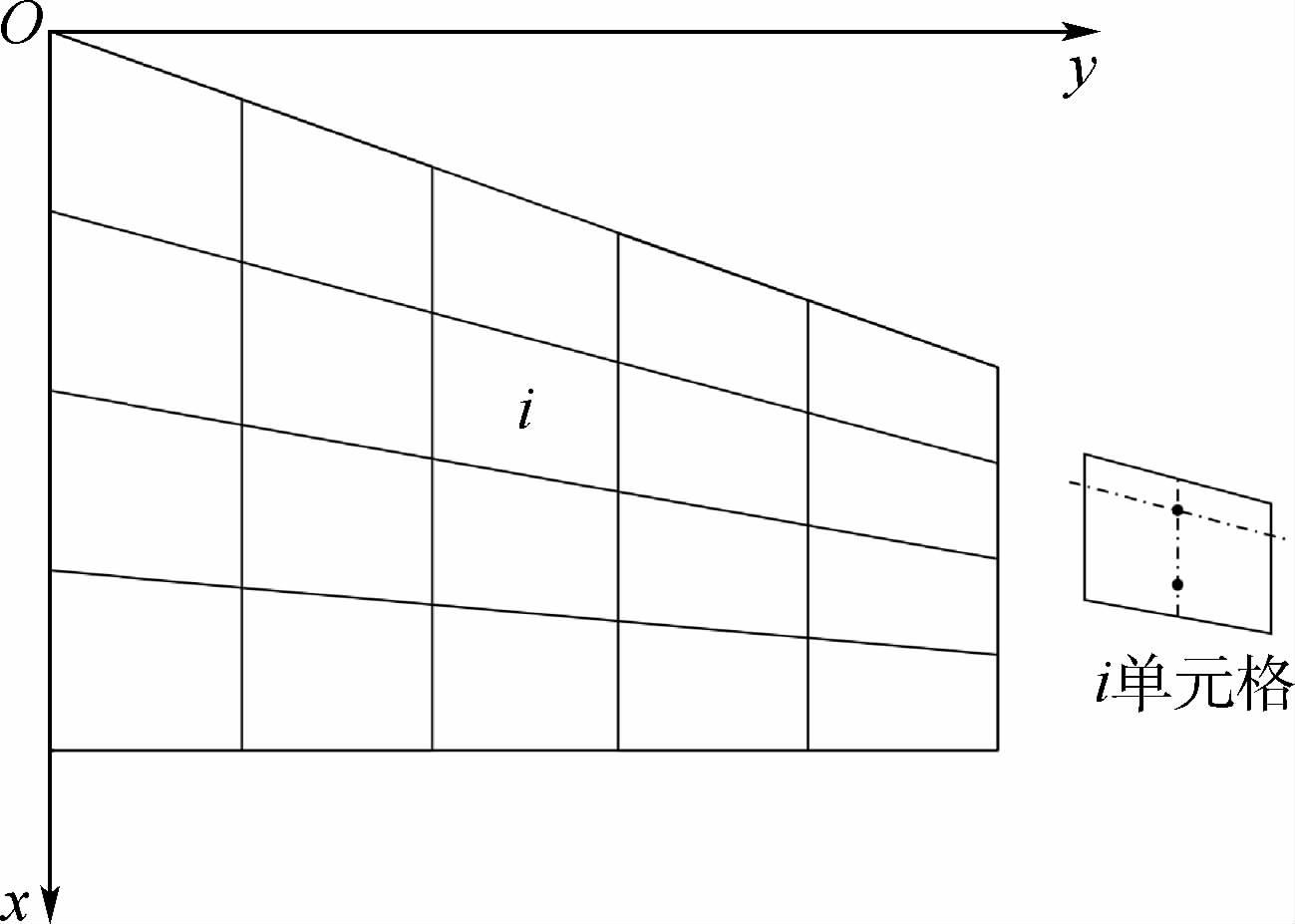 |
| 图 1 升力面网格上的压力点和控制点Fig. 1 Pressure point and control point of grid for lifting surface |
| 图选项 |
对式(1)和式(2)进行Fourier变换[10],可以得到频率域内的阵风响应控制方程[11]为
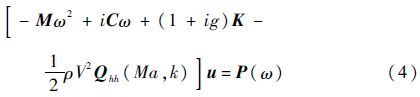
式中:ω为圆频率;Qhh(Ma,k)为广义气动力矩阵;Ma为飞行马赫数;k=ωc/(2V)为减缩频率,c为参考弦长;u为位移响应的模态幅值向量;P(ω)为频率域内的激励载荷向量,由阵风激励载荷和非气动力激励载荷组成,如式(5)所示。
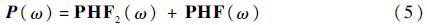
其中:PHF2(ω)为阵风激励载荷向量;PHF(ω)为非气动力激励载荷向量。
由于本文阵风激励载荷作用,所以式(5)简化为
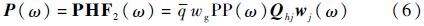
式中:q为飞行动压;wg为阵风尺度因子;PP(ω)为阵风频率变化的函数;Qhj为阵风下洗矢量引起的气动力矩阵;wj(ω)为单元节点下洗矢量,如式(7)所示。
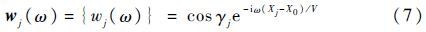
其中:γj为第j个气动单元的二面角;Xj-X0为气动力单元压力点与阵风作用点的距离。
1.2 连续阵风模型在连续阵风模型中,Von Karman谱模型是一种与试验观察数据相吻合的常用模型。它是用沿着或垂直于飞机飞行轨迹上空速的随机变化来表示连续阵风的,并且认为随机变量服从均值为零的Gauss分布。其描述方式为在频域中随频率变化而变化的阵风速度功率谱密度。垂直方向的Von Karman谱模型可表示为
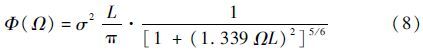
式中:Ω=ω/V为折算频率;σ为垂直方向阵风的均方根速度;L为阵风特征标尺波长。由垂直方向的Von Karman谱模型可以得到阵风速度功率谱密度随折算频率的变化关系(见图 2),其中均方根速度σ=1m/s,特征标尺波长L=762m。
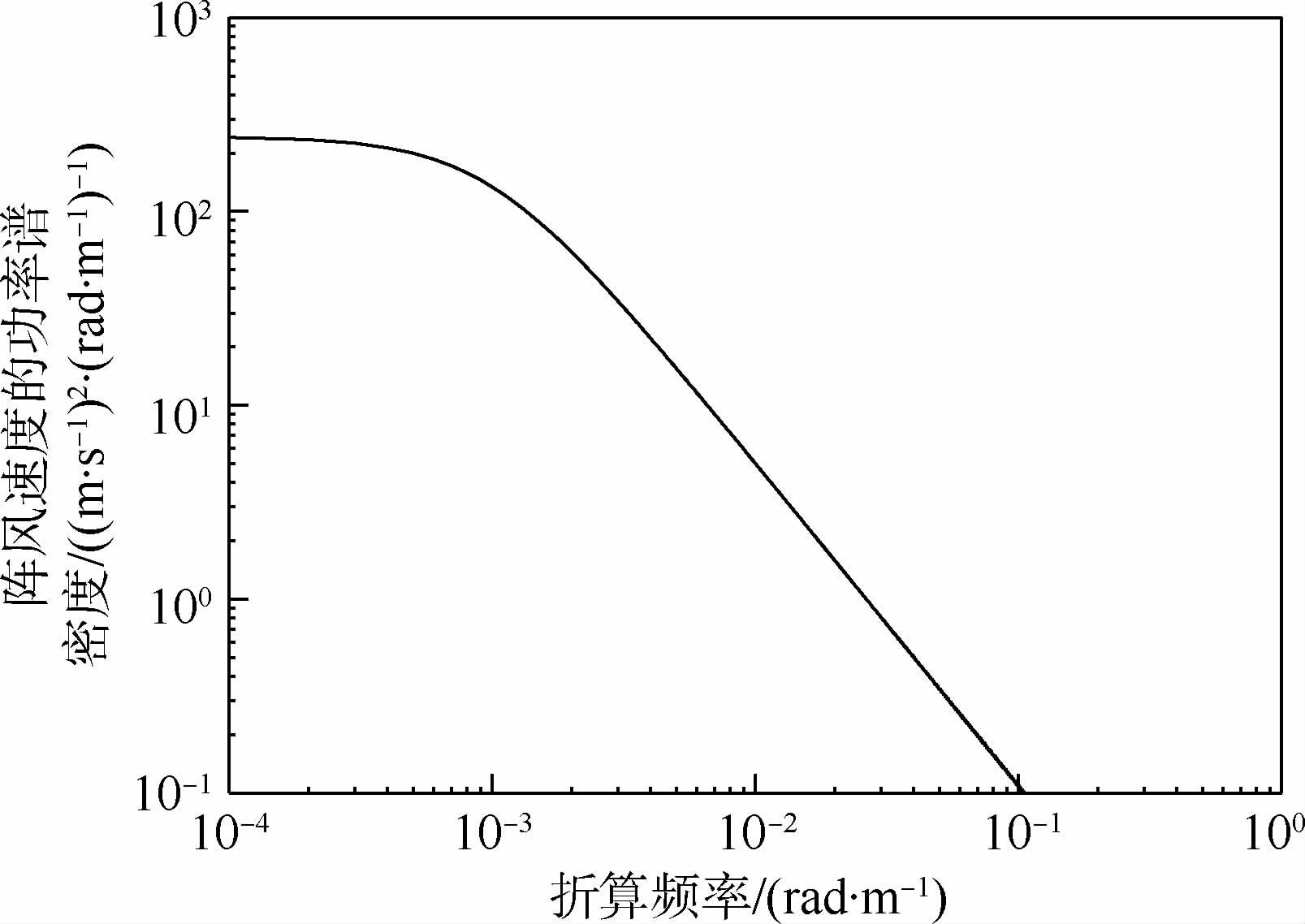 |
| 图 2 Von Karman阵风速度功率谱密度随折算频率的变化(σ=1m/s,L=762m)Fig. 2 Von Karman power spectral density of gust velocity for different reduced frequencies (σ=1m/s,L=762m) |
| 图选项 |
为了得到阵风速度的时间历程以便获取阵风响应的位移时间历程,本文采用谐波叠加法[12]数值模拟阵风速度的随机过程。通过有限项的三角级数展开,得到垂直方向阵风速度的平稳随机过程为
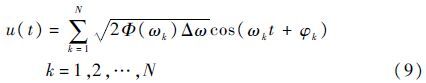
式中:ωk=(k-1/2)Δω,Δω为频率的增量;φk为服从[0,2π)上均匀分布的随机相位。尽管选择不同的相位将获得不同的阵风速度时间历程,但是由于它们均由同一个特定谱确定,因此在长时间范围内将具有相同的统计特性。本文主要研究谱模型参数不确定性对阵风响应的影响,因此,为了得到明显的结果,在每次分析过程中,随机相位都取一组特定的数值。根据图 2确定的Von Karman谱模型,图 3给出了阵风风速随机过程的一个样本函数,即本文所采用的阵风速度随时间变化的历程。
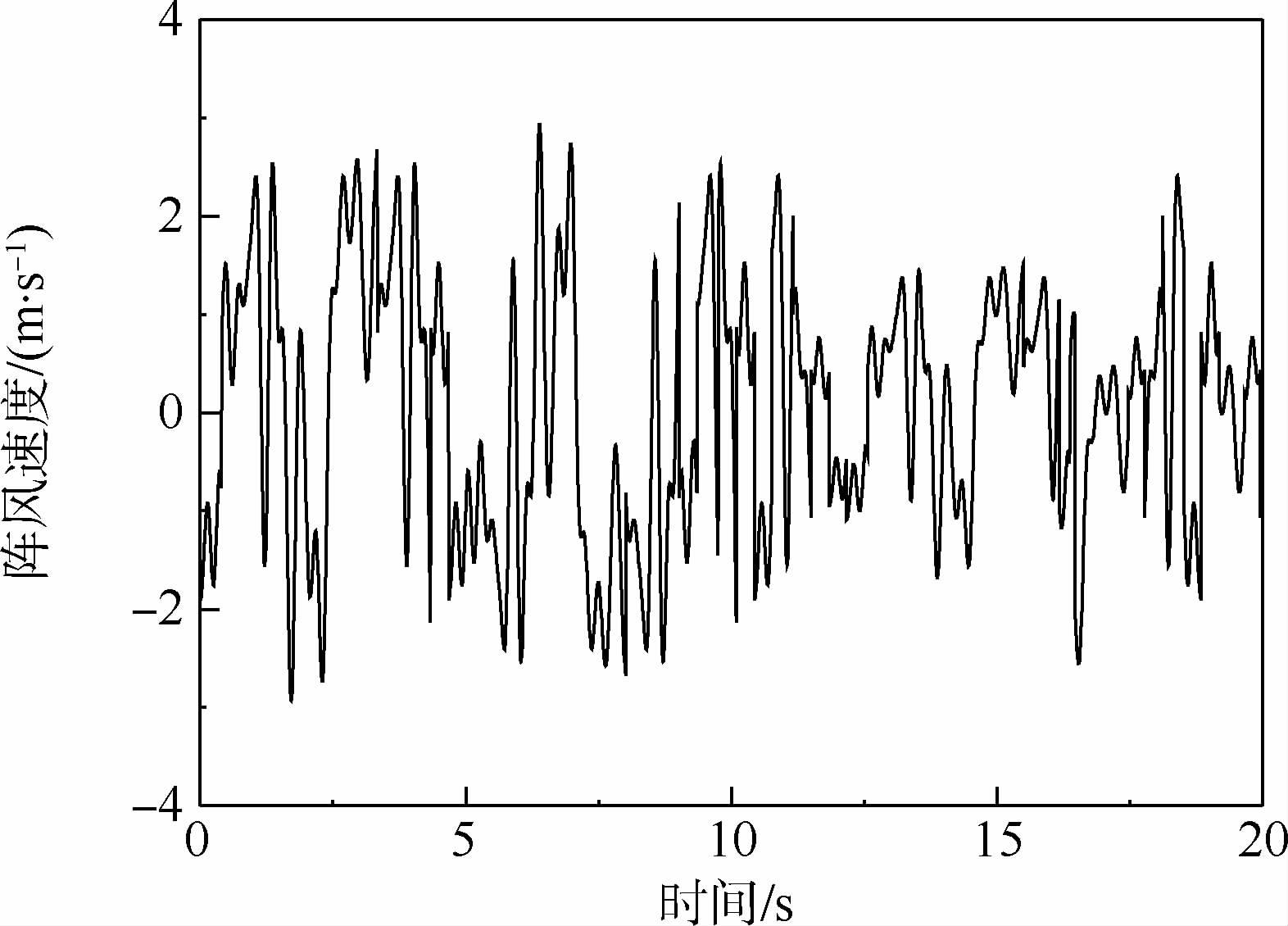 |
| 图 3 假定条件下阵风速度的时间历程Fig. 3 Time history of gust velocity under assumption |
| 图选项 |
1.3 阵风分析模型中的不确定量在式(8)描述的Von Karman谱模型中,模型参数σ、L由试验结果确定,由于测量统计结果数据分散性很大,采用概率方法很难求解统计特征量,但是这些结果数据可呈现出确定的变化区间。由于参数σ、L为区间参数,因此频域中的Von Karman谱具有不确定性。按照第1.2节中选定的一组特定相位,根据式(9)可以得到具有不确定性的阵风速度时间历程,其不确定性表现为任意时刻的阵风速度在区间内变化,即存在速度上界和下界。此外,受到阵风激励的结构模型中也存在不确定性,如结构刚度、结构阻尼系数以及机翼质量等,这些参数的不确定性均可以用区间数表示。值得指出的是,结构模型中的不确定性在时域和频域间的转换是很自然的。
2 配点型区间分析方法2.1 一元化区间不确定量假设阵风响应控制方程中的不确定性参数可用向量b表示,b∈bI=[$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b}$,b]。结构的位移响应矢量u是不确定性参数向量b的函数。根据区间数学理论,不确定性参数向量b的中值及其相应的分量形式表示为
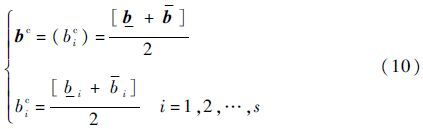
式中:bc=(bic)为不确定性参数向量b的中值,也称标称值;s为不确定性参数的数量。
不确定性参数向量的变化范围表示为
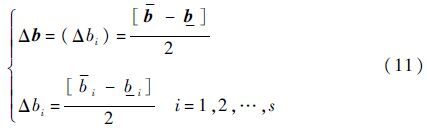
式中:Δb=(Δbi)为不确定性参数向量b的区间半径。
将区间向量bI=[$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b}$,b]表达成另外一种有用的形式:
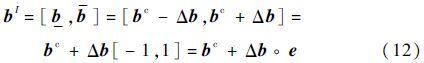
式中:e∈IIs,IIs定义为全部分量属于[-1,1]内的s维向量集合;符号“。”定义为2个向量的Hadamard积,即向量间对应分量相乘的算子,乘积仍然为维数相同的向量。
定义e中的第i(1≤i≤s)个分量为x,剩余分量为0,表示为

式中:x∈[-1,1]。由式(12)和式(13)得到一元化的区间不确定性参数向量为

式中:bi为一元化的区间不确定性参数向量,上标i表示bi中第i个分量为不确定区间变量。由此可见,1个s维的不确定区间向量可以通过一元化处理变为s个一元化的区间不确定性参数向量。
2.2 配点方案及结构响应基于Taylor展开的区间方法仅利用了不确定性参数中心值处的信息(包括响应值和灵敏度)线性近似响应在整个区间上的变化情况。由于线性近似在很多情况下难以有效逼近真实的结构响应,因此很自然的想法是利用区间内更多点处的信息实现非线性函数近似。为此,本文采用最佳平方逼近多项式逼近结构响应函数。
引入r阶第一类Chebyshev正交多项式[13],其正交多项式系{Tj(x)}为
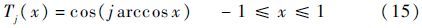
式中:j(0≤j≤r)为非负整数;{Tj(x)}为区间[-1,1]上带权$1/\sqrt{1-{{x}^{2}}}$的正交多项式系,可由如下递推关系获得:
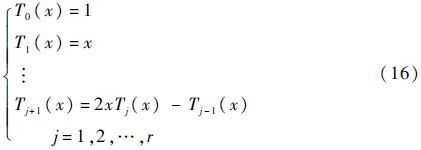
在r阶多项式系{Tj(x)}张成的子空间Hr=span{T0,T1,…,Tr}中,结构响应的最佳平方逼近多项式函数为
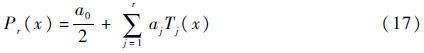
式中:aj为逼近函数展开式系数,可表示为
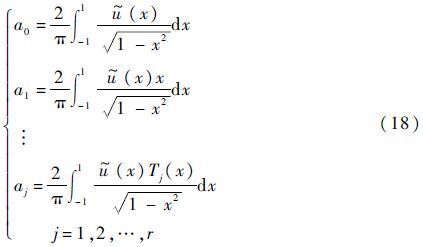
其中:$\tilde{u}$(x)为真实的结构响应函数。
根据Gauss-Chebyshev求积公式,在计算多项式系数aj时,需要在[-1,1]上配置q个Gauss积分点,记为xk。Gauss积分点xk(k=1,2,…,q)为Tq(x)的零点,如式(19)所示。
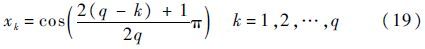
利用[-1,1]上的Gauss积分点,式(18)中的积分可通过Gauss-Chebyshev求积公式方便地计算,如式(20)所示。
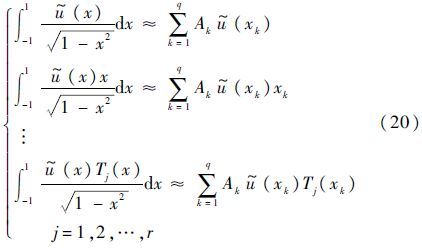
式中:$\tilde{u}$(xk)为配点xk处的结构响应;Tj(xk)为多项式系在配点xk处的值;Ak为求积系数,可表示为
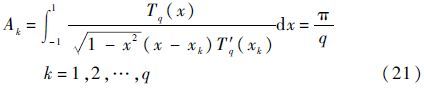
将式(20)、式(21)代入式(18),可以得到

将式(22)代入式(17),可得到结构响应的最佳平方逼近多项式函数,如式(23)所示。
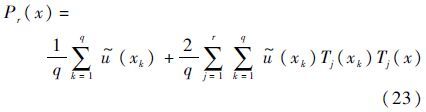
2.3 响应的界值估计不失一般性,首先针对第i个不确定性参数,考虑结构响应的一元逼近函数,即
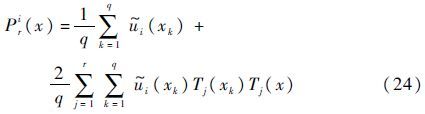
式中:Pri(x)为结构响应对第i个不确定性参数的一元逼近函数;$\tilde{u}$i(xk)为第i个不确定性参数区间内配点xk处的结构响应。式(24)可简记为

式中:
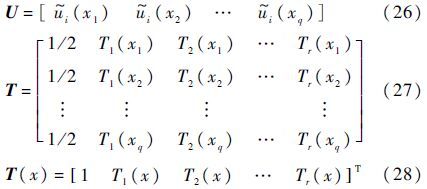
先考虑如何求解Pri(x)的最值,对式(25)关于x求导并令导数为零,得
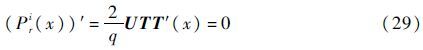
求解式(29)的根,并联合Pri(-1)和Pri(1),根据连续函数在闭区间上的最值定理,可得一元逼近函数的最小值点和最大值点,分别记为xmini和xmaxi。
重复以上过程,直到i遍历完1~s时,就能得到具有s个元素的最值点向量,记为
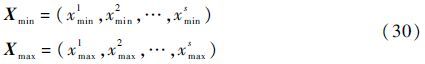
由式(14)可知,Xmin和Xmax是s维向量集合IIs中的向量。进而通过式(12)和式(14)可以得到结构响应关于所有不确定性参数的最值点向量,此时可用最值点向量对结构响应直接进行界值评估,得到结构响应的近似区间估计uI=[$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u}$,u],按式(31)计算:
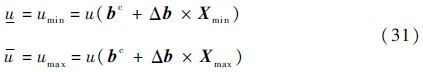
3 配点型区间分析方法与Taylor区间分析方法的比较实际结构系统的响应一般是非线性函数,区间分析方法的目的是在参数区间内有效地近似响应函数,进而得到响应的边界估计。为方便比较,直接给出Taylor区间分析方法(Taylor Interval Analysis Method,TIAM)获得的响应近似区间估计为
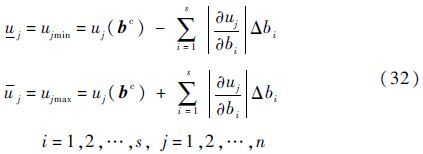
计算式(32)时需要计算响应对区间参数在中值处的灵敏度。为此,对式(1)两边求偏导:
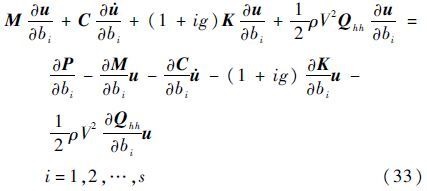
式(33)中的系统矩阵M、C、K、Qhh和P关于区间参数的灵敏度未知,通常利用差分替代微分的方法近似计算灵敏度,即
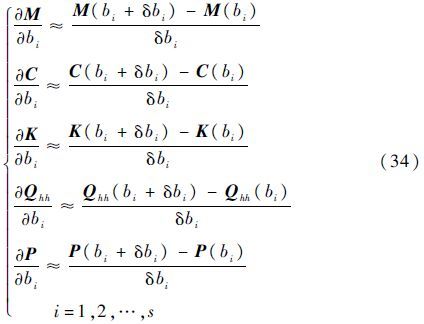
由式(32)可知,Taylor区间分析方法是利用Taylor级数在展开点处近似响应函数,在展开点附近级数收敛很快,但随着区间的增大,收敛速度变慢。这将导致Taylor区间分析方法获得的响应近似区间估计与真实的响应区间差别很大。此外,利用Taylor区间分析方法估计响应的界值时,常会发生一个边界估计不足,而另一个边界估计过盈的现象[14],如图 4所示,特别对非单调函数的区间估计精度更低。相比之下,配点型区间分析方法利用了区间内多个点(Gauss点)的信息而非单一标称值(中值),可见式(19),并且基于结构系统参数均为正值和参数之间具有相互独立性的事实,使得由式(31)得到的边界可以视为全局意义上结构响应的界值估计。
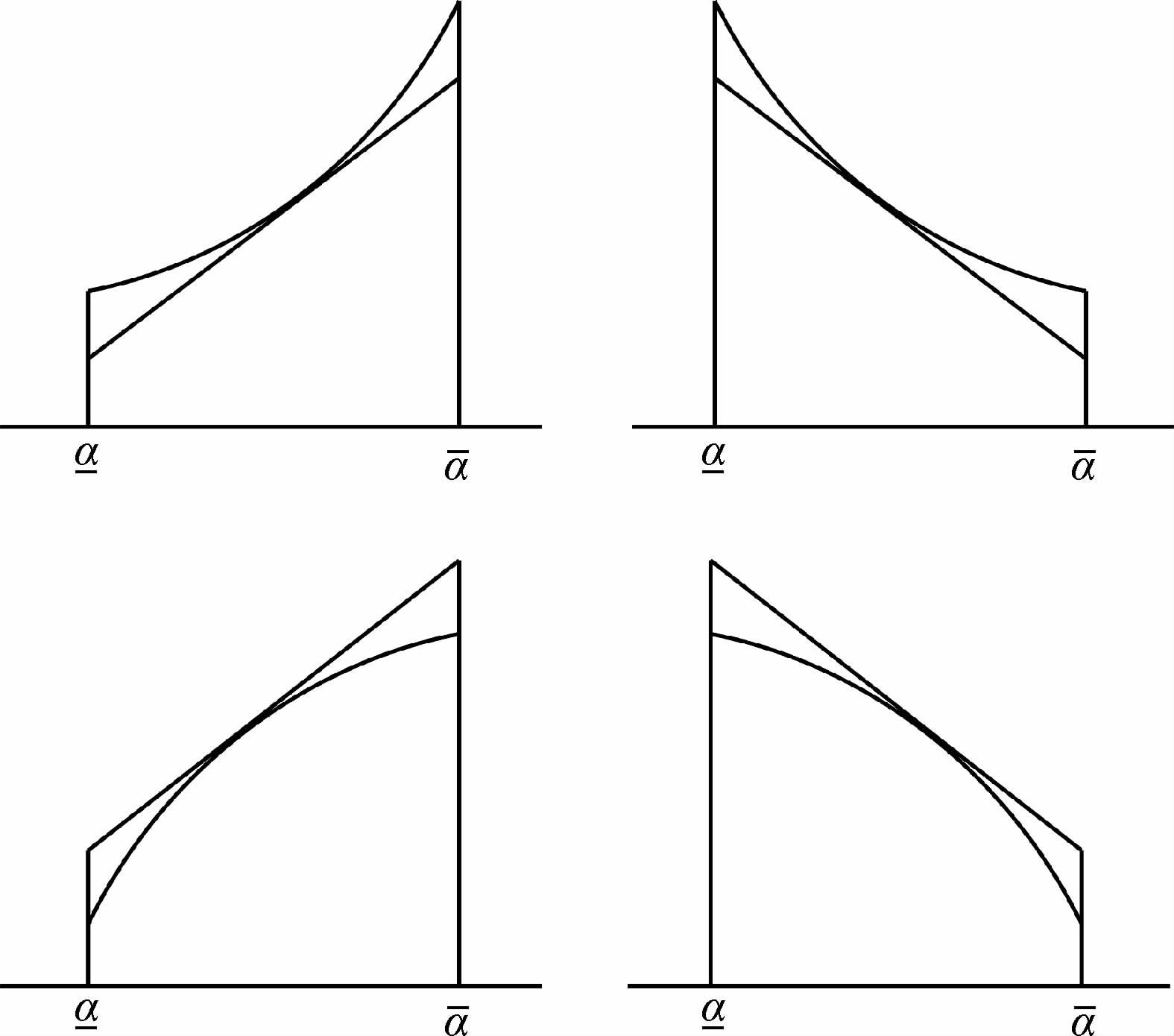 |
| 图 4 Taylor区间分析方法逼近单调函数的情形Fig. 4Approximation formula of TIAM with respect to monotonic function |
| 图选项 |
在计算量方面,配点型区间分析方法主要集中于计算式(29)中的U矩阵和T矩阵。由式(26)可见,对于每一个不确定性参数,需要进行q次分析得到U矩阵,若系统含有s个不确定性参数时,需要进行s×q次分析。而T矩阵的维数为q×(r+1),对于大型工程结构,T矩阵的计算量可忽略。而Taylor区间分析方法需要计算标称值处的响应值和响应函数对不确定性参数的灵敏度。1阶Taylor区间分析方法仅需进行s+1次分析。显然,从计算代价来看,Taylor区间分析方法优于配点型区间分析方法。
值得注意的是,在提高计算效率的同时,Taylor区间分析方法的估计精度明显不足,加之工程中以差分替代微分(见式(34))存在难以预估的计算误差[15]。因此,Taylor区间分析方法目前只能用于低精度的1阶估计。而对于配点型区间分析方法,q的大小直接影响计算量的多少。庆幸的是,对于Gauss求积公式,不多的配点便能获得高精度的结果,通常当q=10时便能获得非常好的近似效果。工程中,一般取q=3~5即能获得满意的精度。
4 数值算例本文以某型飞机的翼面为例,如图 5所示,分析机翼受到连续阵风作用时的响应特征。飞机参数为:Ma=0.62,q=0.0276MPa。机翼的结构参数列于表 1,其中机翼质量和结构阻尼系数均为不确定性参数。阵风模型选用常见的Von Karman连续阵风模型,L/V=0.718,阵风速度的均方根值是不确定量,用区间数表示为σI=[0.9,1.1]m/s。
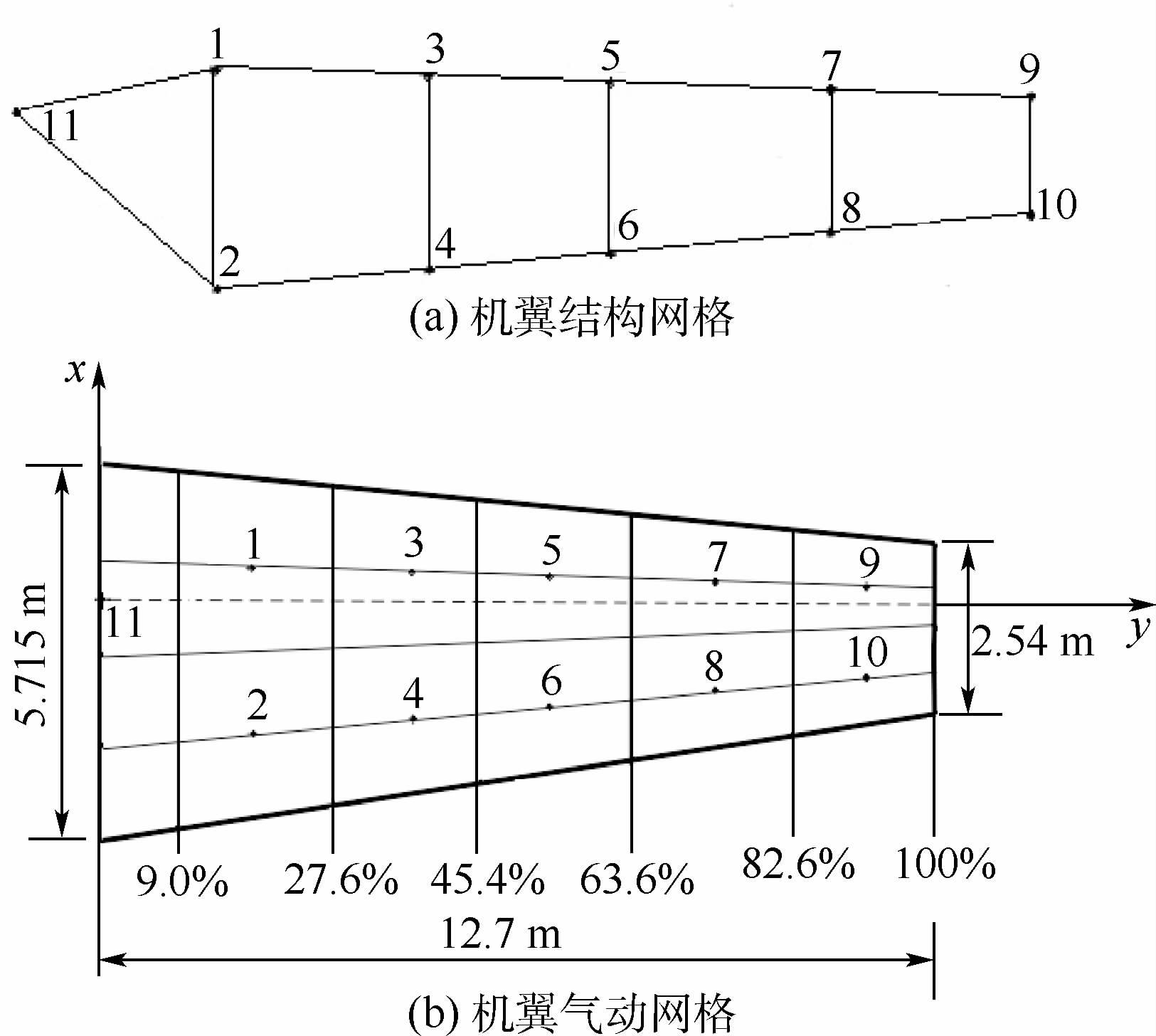 |
| 图 5 机翼翼面Fig. 5 Airfoil surface |
| 图选项 |
表 1 机翼结构属性参数Table 1 Property parameters of wing structure
| 参数 | 数值 |
| 参考半弦长/m | 2.06 |
| 机翼展长/m | 25.4 |
| 俯仰惯性矩/(N·m2) | 1.27×106 |
| 滚转惯性矩/(N·m2) | 1.28×104 |
| 机翼质量/kg | [7530, 8730] |
| 结构阻尼系数 | [0.017,0.023] |
表选项
图 5(a)和图 5(b)分别为机翼结构网格和气动网格。在结构方面,节点1~11是结构节点,仅考虑机翼垂直方向的自由度;在气动力方面,机翼沿弦向划分4个单元,沿展向划分6个单元。其中展向空气动力单元采用非等矩划分,如图 5所示。
图 6为机翼翼根垂直弯矩频响函数曲线,该曲线反映了单位简谐阵风激励下翼根垂直弯矩的响应(注意:此处区间参数取中值参与计算)。
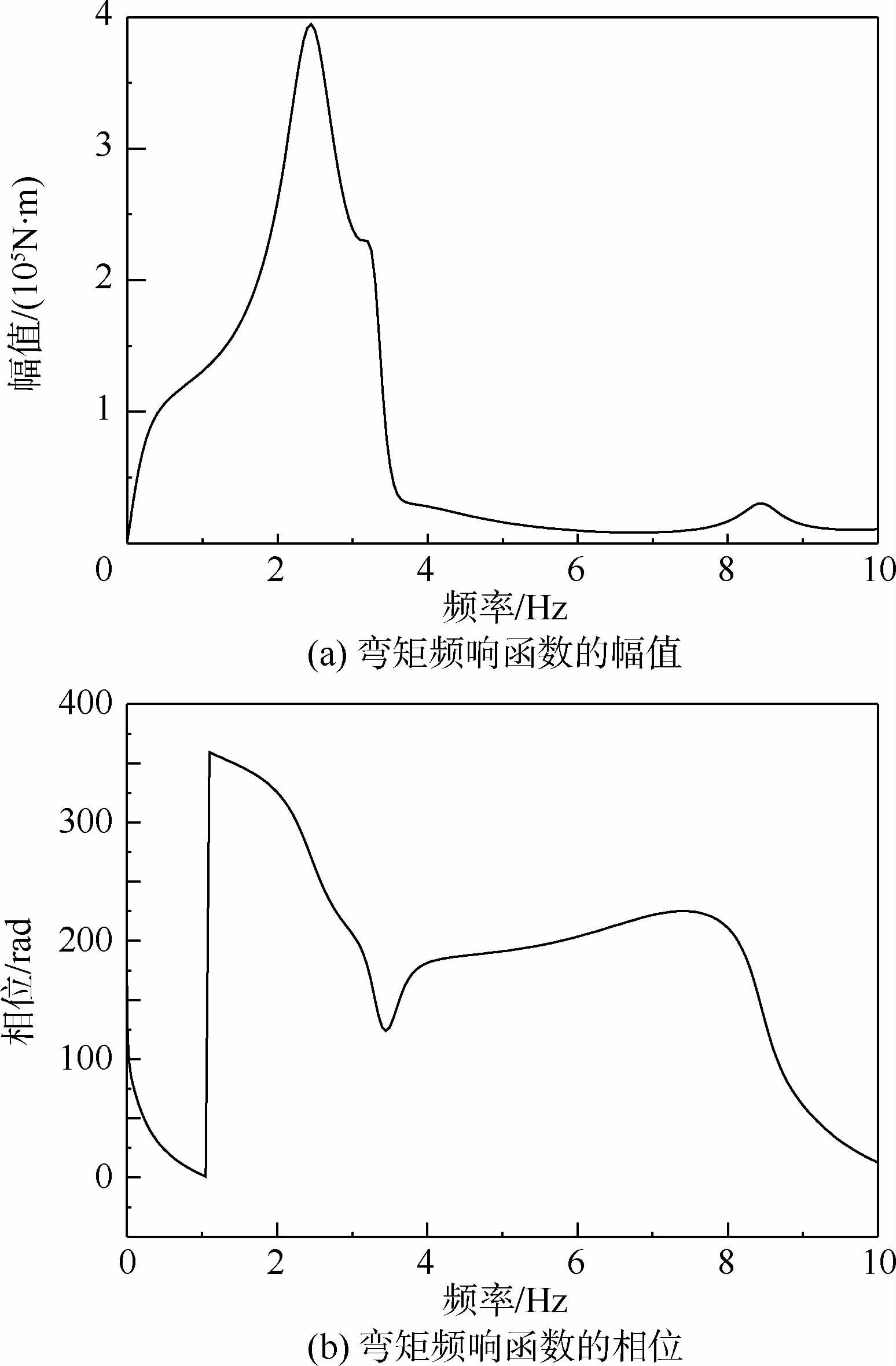 |
| 图 6 翼根弯矩频响函数的幅值和相位Fig. 6 Amplitude and phase of frequency response function of root bending moment |
| 图选项 |
按本文提出的基于配点型区间分析方法能够求得机翼阵风响应的上下界,如翼根(节点11)垂直弯矩的功率谱密度、加速度功率谱密度及翼尖(节点10)的加速度功率谱密度上下界等。计算时,每个不确定性参数区间内配置3个Gauss积分点,即q=3。同时采用基于Taylor区间分析方法求得机翼阵风响应的上下界。图 7为翼根垂直弯矩的功率谱密度。
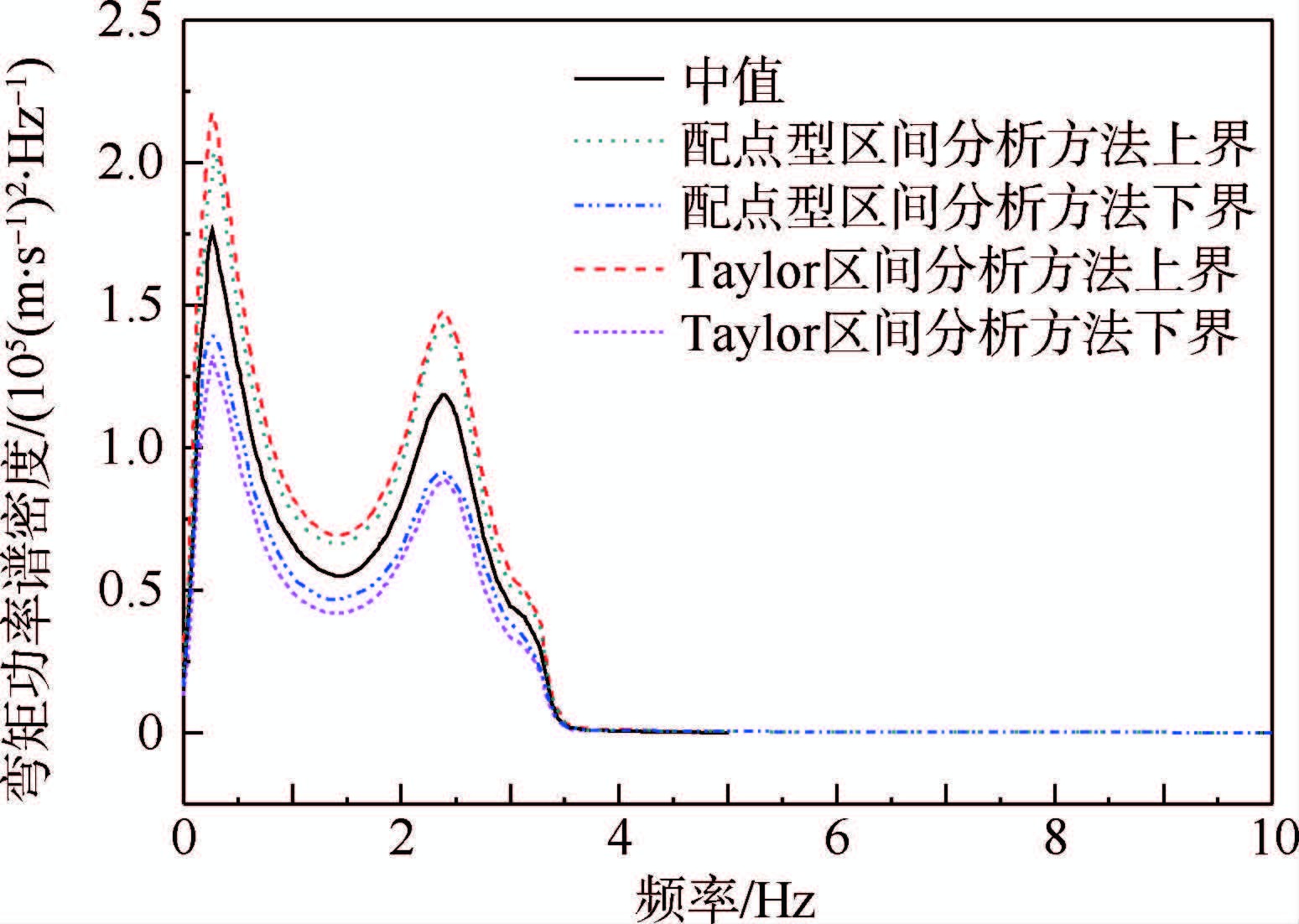 |
| 图 7 翼根弯矩功率谱密度函数Fig. 7Power spectral density function of root bending moment |
| 图选项 |
根据Von Karman阵风模型,利用图 3的阵风时间历程,计算得到翼尖位移随时间的变化历程,选取时间段15~18s的结果如图 8和图 9所示。从图 8、图 9可以看出,2种方法得到的翼尖位移上下界随时间变化的趋势相同。为了清晰显示Taylor区间分析方法与配点型区间分析方法的结果比较,选取6个典型时刻的翼尖位移进行比较,如表 2所示。
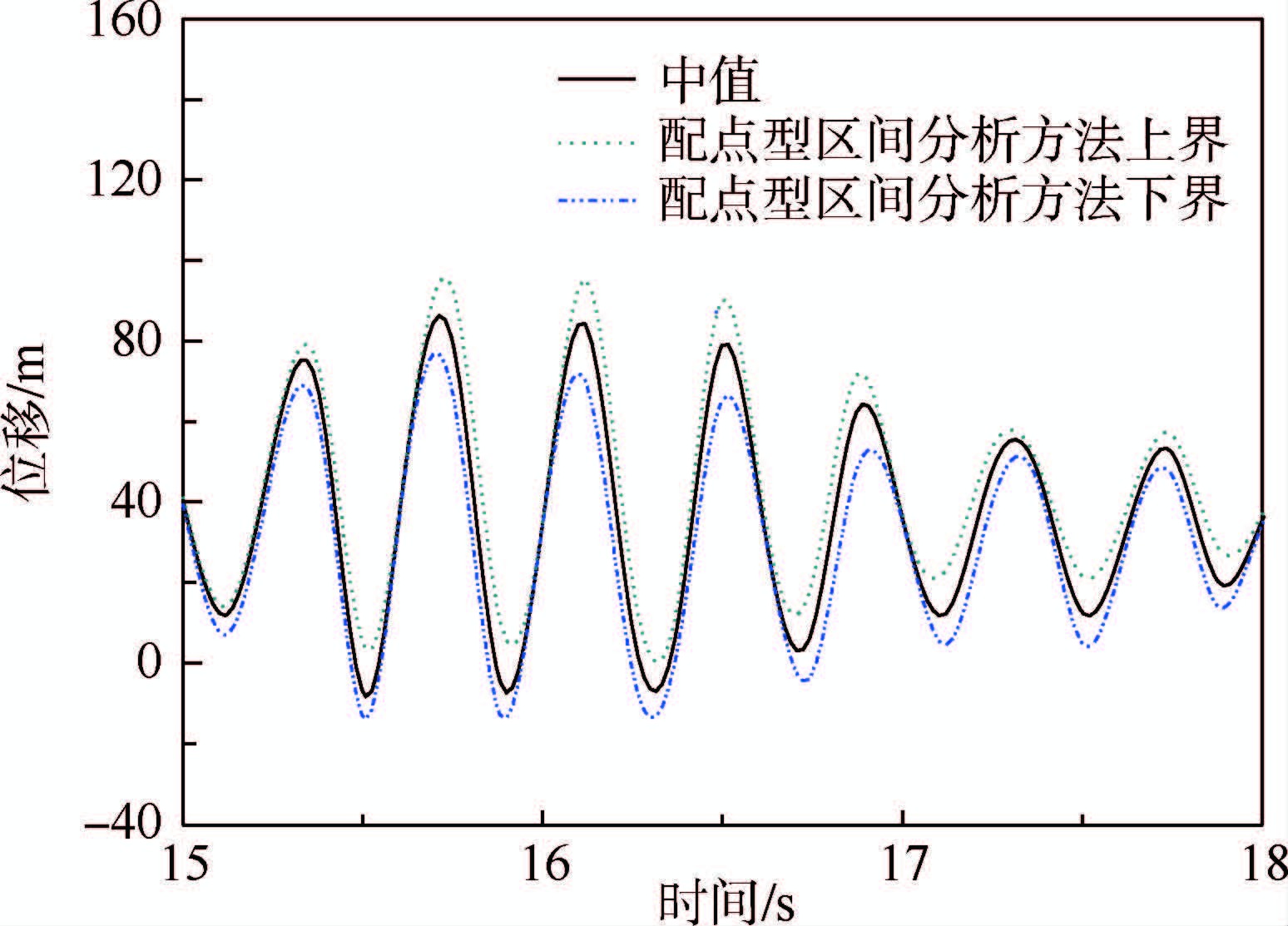 |
| 图 8 翼尖位移随时间变化历程(CIAM)Fig. 8 Time history of displacement for wing tip via CIAM |
| 图选项 |
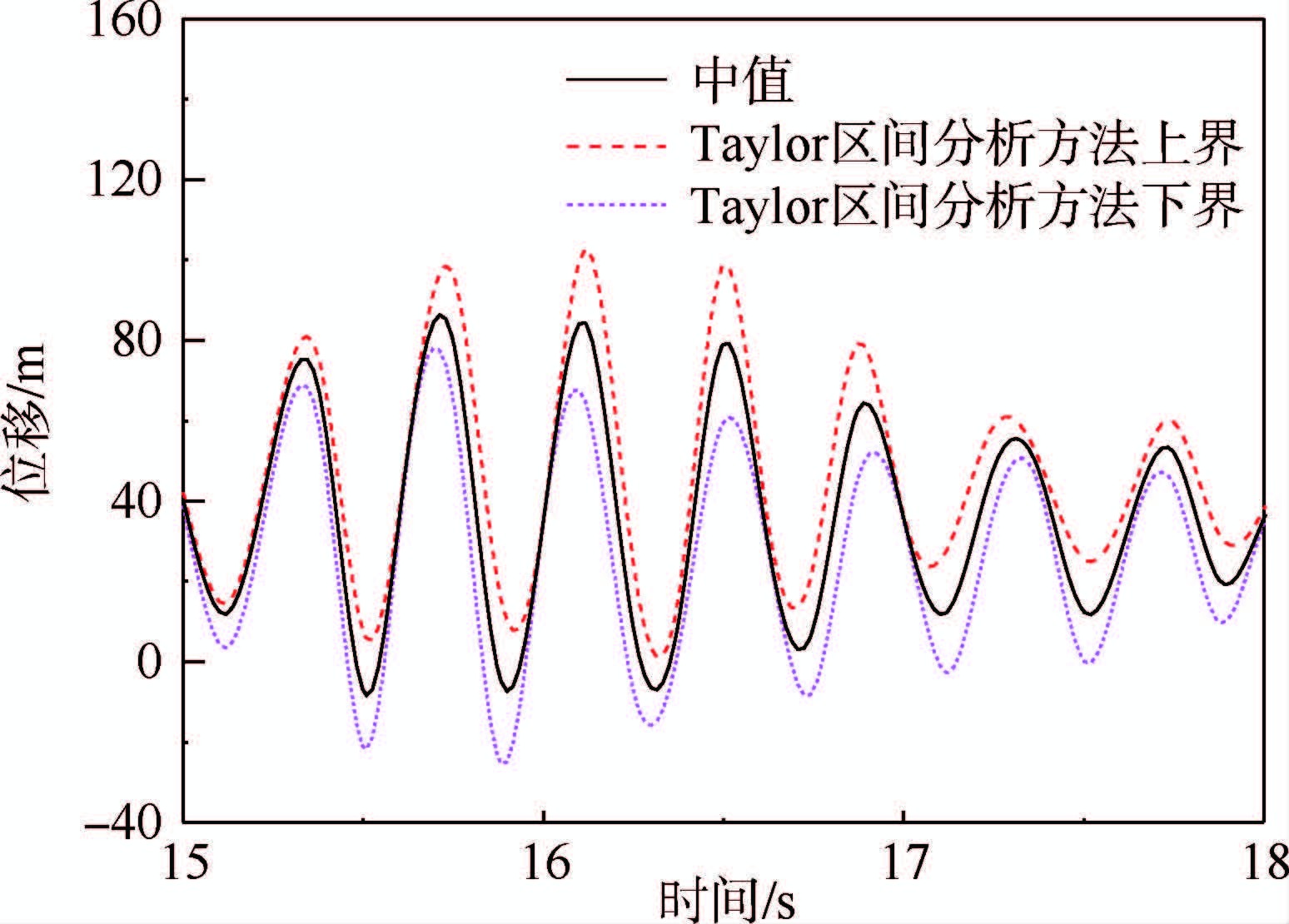 |
| 图 9 翼尖位移随时间变化历程(TIAM)Fig. 9 Time history of displacement for wing tip via TIAM |
| 图选项 |
表 2 配点型区间分析方法与Taylor区间分析方法翼尖位移比较Table 2 Comparison of displacement for wing tip via CIAM and TIAM
| 时间/s | 标称值 | 配点型区间分析方法 | Taylor区间分析方法 | ||
| 上界 | 下界 | 上界 | 下界 | ||
| 15.5 | -7.1053 | 5.1754 | -19.3860 | 7.3684 | -21.5790 |
| 16.0 | 36.0526 | 36.8421 | 35.2631 | 37.8070 | 34.2982 |
| 16.5 | 78.8596 | 90.0877 | 67.6315 | 98.5965 | 59.1227 |
| 17.0 | 35.4386 | 36.5789 | 34.2983 | 36.8421 | 34.0351 |
| 17.5 | 12.5439 | 21.6667 | 3.4211 | 25.5263 | -0.4385 |
| 18.0 | 35.4386 | 36.9298 | 33.9474 | 38.0702 | 32.8070 |
表选项
通常,Taylor区间分析方法获得的结果偏于保守,可见文献[6]。由数值算例可以看出,与Taylor区间分析方法得到的结果比较,配点型区间分析方法求得的阵风响应结果更接近标称值,表明该方法能够得到一个包含精确响应值的足够“紧”的阵风响应区间。在某种程度上,本文方法提高了响应界值估计精度。当难以获得不确定性参数可靠的统计信息时,配点型区间分析方法不仅为解决阵风响应这类复杂不确定性问题提供了一种方便可行的方法,同时也为工程设计人员提供了可信的响应结果。
5 结 论本文以弹性机翼构件在飞行过程中遭遇连续阵风为例,考虑了阵风模型和机翼结构参数中存在的不确定性,提出了一种新的计算阵风响应的配点型区间分析方法,主要结论有:
1) 将阵风响应问题中的不确定性参数用区间定量化,结合配点方案和第一类Chebyshev正交多项式,推导了基于配点型区间分析方法的阵风响应表达式。避免了计算响应函数对不确定性参数的灵敏度,与此同时,配点方案充分利用了区间内更多点处的信息,放宽了不确定性参数变化范围为小区间的要求。
2) 在不确定性参数统计信息未知的情况下,与Taylor区间分析方法相比,配点型区间分析方法得到的阵风响应结果更接近标称值,表明本文方法很好地提高了阵风响应结果精度。克服了Taylor区间分析方法低精度的缺点,对于后续的可靠性分析非常有利。
3) 配点型区间分析方法的计算量依赖于配点方案和不确定性参数的个数。客观上讲,其计算代价大于Taylor区间分析方法。然而,对于Gauss求积公式,不多的配点便能获得高精度的结果。因此,相比于阵风响应结果精度,少量增加的计算代价是可以接受的。
参考文献
| [1] | AZOULAY D,KARPEL M.Characterization of methods for computation of aeroservoelastic response to gust excitation:AIAA-2006-1938[R].Reston:AIAA,2006. |
| Click to display the text | |
| [2] | BISPLINGHOFF R L,ASHLEY H,HALFMAN R L.Aeroelasticity[M].Upper Saddle River,NJ:Addison-Wesley,1955:10-11. |
| [3] | SIMON F,GUILLEN P,SAGAUT P,et al.A gPC-based approach to uncertain transonic aerodynamics[J].Computer Methods in Applied Mechanics and Engineering,2010,199(17-20):1091-1099. |
| Click to display the text | |
| [4] | 宋述芳,吕震宙,张伟伟,等.随机机翼结构阵风响应的分布函数及灵敏度分析[J].航空学报,2011,32(10):1770-1777. SONG S F,LYU Z Z,ZHANG W W,et al.Analysis of CDF and sensitivity of gust response of stochastic BAH wing structure[J].Acta Aeronautica et Astronautica Sinica,2011,32(10):1770-1777(in Chinese). |
| Cited By in Cnki (2) | |
| [5] | PRADLWARTER H L,PELLISSETTI M F,SCHENK C A,et al.Realistic and efficient reliability estimation for aerospace structures[J].Computer Methods in Applied Mechanics and Engineering,2005,194(12-16):1597-1617. |
| Click to display the text | |
| [6] | 苑凯华,邱志平.阵风响应问题的区间分析方法[J].工程力学,2009,26(1):7-12. YUAN K H,QIU Z P.Interval analysis method of gust response[J].Engineering Mechanics,2009,26(1):7-12(in Chinese). |
| Cited By in Cnki (5) | |
| [7] | QIU Z P,ELISHAKOFF I,STARNES JR J H.The bound set of possible eigenvalues of structures with uncertain but non-random parameters[J].Chaos,Solitions & Fractals,1996,7(11):1845-1857. |
| Click to display the text | |
| [8] | QIU Z P,NI Z.An inequality model for solving interval dynamic response of structures with uncertain-but-bounded parameters[J].Applied Mathematical Modelling,2010,34(8):2166-2177. |
| Click to display the text | |
| [9] | 管德. 非定常空气动力计算[M].北京:北京航空航天大学出版社,1991:103-129. GUAN D.Calculation of non-steady aerodynamics[M].Beijing:Beihang University Press,1991:103-129(in Chinese). |
| [10] | 道尔E H,小柯蒂斯H C,斯坎伦R H,等.气动弹性力学现代教程[M].陈文俊,尹传家,译.北京:中国宇航出版社,1991:62-64. DOWELL E H,CURTISS H C,SCANLAN R H,et al.Modern tutorial of aeroelasticity[M].CHEN W J,YIN C J,translated.Beijing:China Astronautic Publishing House Press,1991:62-64(in Chinese). |
| [11] | RODDEN W P,JOHNSON E H.MSC/NASTRAN aeroelastic analysis user's guide[M].Los Angeles:MacNeal-Schwendler Corporation Publication,1994:76-77. |
| [12] | DI PAOLA M. Digital simulation of wind field velocity[J].Journal of Wind Engineering and Industrial Aerodynamics,1998,74-76:91-109. |
| Click to display the text | |
| [13] | 颜庆津. 数值分析[M].北京:北京航空航天大学出版社,2006:124-125. YAN Q J.Numerical analysis[M].Beijing:Beihang University Press,2006:124-125(in Chinese). |
| [14] | QI W C,QIU Z P.A collocation interval analysis method for interval structural parameters and stochastic excitation[J].Science China-Physics Mechanics & Astronomy,2012,55(1):66-77. |
| Click to display the text | |
| [15] | MOENS D,VANDEPITTE D.A survey of non-probabilistic uncertainty treatment in finite element analysis[J].Computer Methods in Applied Mechanics and Engineering,2005,194(12-16):1527-1555. |
| Click to display the text |
