现代机械系统构件的工作环境恶劣,本身结构又比较复杂,原始的可靠性分析方法不能较好地解决构件的工程实际问题。机械零部件的结构尺寸、材料属性和外载荷都存在随机特性,导致实际分析研究时无法准确完整地获得所有的概率统计信息[6, 7, 8],而且各随机因素对结构可靠性的影响程度不同,进行优化设计时仅凭经验太具盲目性。这就需要知道各个因素分别对整个机械系统可靠度的影响规律,即这些因素对可靠度的敏感程度,如果某因素对可靠性影响较大,则在设计制造过程中就需要对其严格控制以降低其对整个结构可靠性影响的灵敏度,即使其稳健以提高机械产品的可靠性[9, 10, 11, 12]。
可靠性灵敏度分析是得到机械构件各个结构参数对其可靠性的不同影响规律,进而对机械系统可靠性的稳健优化设计进行指导,具有十分重要的意义,很多专家****提出了十分有效的可靠性灵敏度设计分析方法,得到了大量的研究成果[12, 13, 14, 15]。
本文提出了针对多种失效模式下的机械零部件可靠性和可靠性灵敏度分析方法,并依据灵敏度分析的结果进一步提出机械零部件多目标优化的可靠性稳健设计模型,结合履带车辆行走系统的扭力轴进行了计算验证。通过四阶矩技术,获得各种失效模式下机械系统构件的可靠度,针对机械构件发生一种失效模式即整个失效的特点,将含相关性的不同失效模式当作串联失效模型进行计算,获得了零部件对各个结构参数的均值和方差的灵敏度矩阵,并且提出质量最轻和可靠度对结构参数变化的灵敏度最小这2个优化目标,对扭力轴的结构参数进行稳健性优化设计。计算结果表明了本文方法的适用性,且可以推广到其他机械系统的可靠性稳健优化设计中。
1 可靠性分析机械零部件存在多种失效模式时,其可靠度和状态函数可以表示为
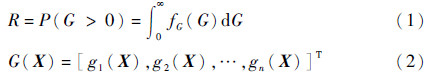
式中:X=[X1,X2,…,Xn]T为随机变量的矩阵;gi(X)为第i种失效模式的状态函数;G(X)为零部件整体的状态函数;fG(G)为多个失效模式对应的概率密度函数。
由可靠性理论可知,不同失效模式的可靠性指标为
式中:μgi、σgi和β2Mi分别为各状态函数的均值、标准差和可靠性指标;Φ(·)为正态分布函数。
当结构随机参数服从正态分布时,通过式(4)可以计算得到准确的结果。然而实际中各个结构参数的分布概型是未知的,无法获得相关分布函数,只能通过统计方法得到各结构参数的前几阶矩。查阅文献[6]得到根据状态函数前四阶矩近似计算不同失效模式的可靠性指标如下:
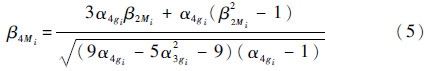
式中:α3gi=θgi/σgi3;α4gi=ηgi/σgi4,θgi和ηgi分别为第i种失效模式的三阶和四阶中心矩,由可靠性的随机摄动理论可知
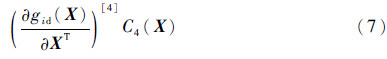
其中:ε为参数,且0<|ε|<1;id为随机变量确定部分;(·)[3]和(·)[4]分别为(·)的三阶和四阶Kronecker积，且(·)[3]=(·)⊗(·)⊗(·);C3和C4分别为随机变量的三阶矩和四阶矩。
不同失效模式的可靠度为
考虑多失效模式机械零部件失效模式间相关性,应用概率摄动法确定的各阶失效模式间协方差和相关系数为
机械结构系统往往存在多种失效模式,而且发生一种失效模式以后机械零部件整体基本就失效了,因此可将机械零部件的多种失效模式当作串联失效模型来计算。考虑各失效模式之间的相关性,则系统整体可靠度为
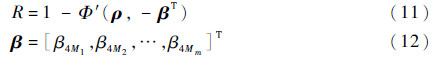
式中:Φ′为多维标准正态联合概率分布函数;β为各阶失效模式四阶矩可靠性指标;ρ为失效模式相关系数矩阵,其每个元素由式(10)求得。
2 可靠性灵敏度分析可靠性灵敏度是结构参数对系统可靠度的影响敏感程度,数学上可以表示为系统的可靠度对结构参数的偏导。通过灵敏度分析,可以将设计变量对可靠度影响的大小进行排序,以此指导可靠性稳健优化设计。存在多种失效模式时,机械零部件的可靠度为
可确定系统可靠度R对随机参数向量X中任意元素x的参数灵敏度为
式中:
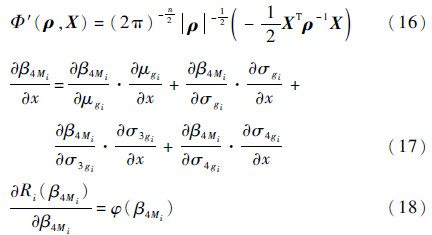
式中：φ(·)为正态分布的概率密度函数。
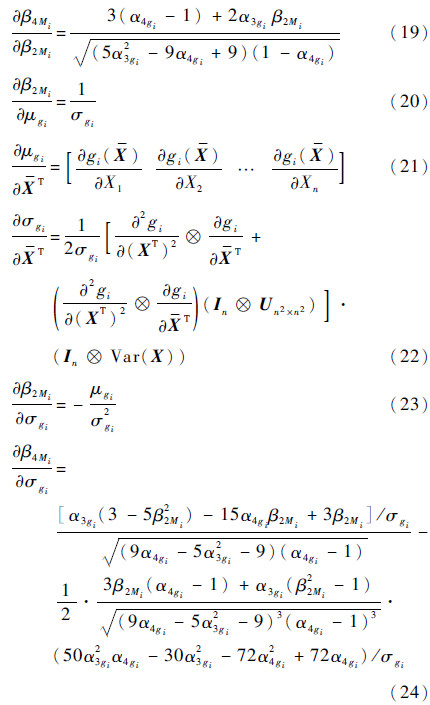
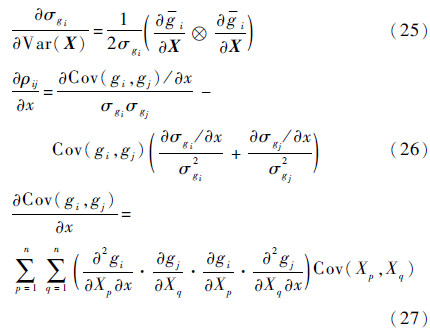
其中:U为单位上三角矩阵。
将式(16)~式(27)代入式(14)、式(15),便可求得多种失效模式下机械零部件可靠度对于随机变量均值和方差的灵敏度。
3 可靠性稳健设计多种失效模式、多优化目标机械构件稳健设计问题的数学模型如下:
式中:x为基本随机变量;ωk为单个目标函数fk(
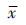)的加权因子,ωk≥0,其值由不同目标的重要程度决定,本文中确定机械零部件整体的质量最轻和零部件可靠度对结构设计参数变化的灵敏度最小这2个目标函数;R1,R2,…,Rn为机械系统单一失效模式下的可靠度;R0为稳健设计要满足的可靠度;qi(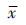)和hj( 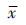)分别为不等式约束和等式约束方程。4 数值算例运用本文提出的多种失效模式下可靠性灵敏度分析计算公式,以履带车辆行走系统的扭力轴为例,对其进行可靠性灵敏度分析及可靠性稳健设计。
扭力轴是行走系统重要的传动构件,主要承受扭矩和弯矩载荷以平衡履带车辆底盘系统,并且推动整车运动,结构简图见图 1。图中：D为扭力轴外径；d为扭力轴轴径；l为扭力轴半轴长。其危险截面上的最大正应力和剪切应力分别为σ=M/Wx和τ=T/Wρ,M和T分别为履带车辆扭力轴所承受的弯矩和转矩,Wx和Wρ分别为结构的抗弯和抗扭截面系数,且有
 |
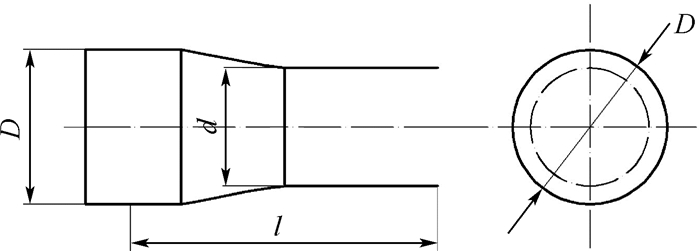| 图 1 扭力轴结构简图Fig. 1 Structure sketch of torque axis |
| 图选项 |
扭力轴各种失效模式的状态函数如下。
静强度失效:
式中:σs为材料静强度极限。
疲劳强度失效:
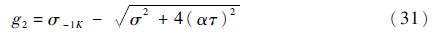
式中:σ-1K为材料疲劳强度极限;α为剪切应力折算系数,一般取0.6。
扭转刚度失效:
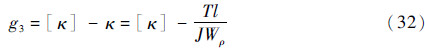
式中:[κ]为轴的许用偏转角;κ为偏转角;J为材料的切变模量。
经查阅相关资料,扭力轴材料的相关属性参数数值如下:σs=450MPa,σ-1K=360MPa,J=220MPa。将传动轴结构的尺寸参数及其承受的外载荷作为随机变量进行可靠性灵敏度计算,即Xs=[d,l,M,T]T,其概率统计特性如表 1所示。
表 1 随机变量的统计特性Table 1 Statistical properties of random variables
| 随机变量 | μ | σ | C3 | C4 |
| d/mm | 200 | 0.6 | 6.793×10-5 | 4.662×10-5 |
| l/mm | 2500 | 5.0 | 5.063 | 1.368×102 |
| M/(N·mm) | 3.5×106 | 1.75×105 | 1.736×1015 | 3.296×1021 |
| T/(N·mm) | 3.1×106 | 1.55×105 | 1.207×1015 | 2.028×1021 |
表选项
应用式(11)和式(12),求得各阶失效模式间相关系数矩阵为
可见,由于扭力轴结构各阶失效模式的随机参数的同一性和载荷的同源性,失效模式是相关的。由四阶矩方法计算得到各阶可靠性指标、各阶可靠度以及结构整体可靠度,如表 2所示。
表 2 扭力轴结构可靠度Table 2 Structure reliability of torque axis
| 可靠度参数 | 静强度失效 | 疲劳强度失效 | 扭转刚度失效 |
| βi | 1.9276 | 2.4062 | 2.5439 |
| Ri | 0.9569 | 0.9907 | 0.9915 |
| R | 0.9421 |
表选项
假设各失效模式之间是相互独立的,即不考虑失效模式的相关性可得扭力轴整体的可靠度为Rind=R1R2R3=0.9399
运用Monte Carlo数学模拟方法得到传动轴构件多种失效模式下的可靠度为RMCS=0.9461
可见,运用本文方法考虑多失效模式的相关性可以更加准确地计算扭力轴的可靠度,相对误差为
εrel=|R-RMCS|/RMCS=0.423%
进而,由式(14),代入相关已知数值计算可得随机变量均值的灵敏度矩阵为
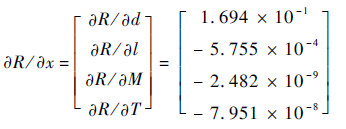
从计算结果可以看出,扭力轴直径参数均值的增加将使构件可靠度增加,而扭力轴承受的扭矩作用长度l、弯矩M和转矩T的增加,都将使构件可靠度降低,趋于失效。另外,从具体的影响数值来看,结构尺寸均值的灵敏度大于外载荷的灵敏度,也即扭力轴结构参数对可靠度影响的灵敏度从大到小依次是结构尺寸、扭矩作用长度和外载荷。因此,在机械构件产品的设计阶段,可以通过优化设计结构参数的均值来提高产品的可靠度。
由式(15),同样代入已知参数值计算后可以得到可靠度对结构随机变量方差的灵敏度为
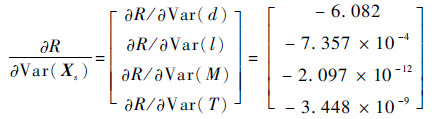
从计算结果可以看出,各个随机变量方差的增加都会导致扭力轴结构可靠度降低,即趋于失效。从具体的影响数值上来看,结构尺寸方差的灵敏度大于外载荷方差的灵敏度,也即扭力轴随机变量方差的灵敏度从大到小依次是结构尺寸、扭矩作用长度和外载荷。因此,在机械构件产品的制造阶段,应该严格控制加工精度等对随机参数方差有影响的因素,提高机械产品的可靠度。
依据随机参数灵敏度分析结果对扭力轴进行稳健优化设计,设扭力轴的优化设计目标可靠度R0=0.999。
首先,建立优化目标函数:①要求扭力轴的质量最轻,其长度不变,即令其截面面积最小,为f1(x);②要求扭力轴结构的可靠度对随机变量参数均值变化的灵敏度最小,为f2(x)。分别如下:
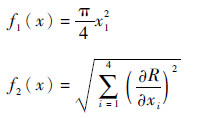
式中:x1=d;x2=l;x3=M;x4=T。
然后,建立约束条件:结构整体可靠度不低于R0,则R-R0≥0,x1>0。
最后,进行优化求解:选取初值d=200mm,运用MATLAB工具箱里面的fmincon函数进行求解,求得扭力轴优化设计的直径d=182.85mm。
依据此优化设计结果,计算得到扭力轴结构的可靠性指标、可靠度以及可靠度对各随机变量参数的灵敏度矩阵分别为
从计算结果可以看出,经过优化设计的扭力轴结构整体可靠度提高了,可靠度对各个结构参数的灵敏度也降低了;且扭力轴结构的可靠度R越大,对结构参数变化的灵敏度越小,也即设计参数对扭力轴结构的可靠度影响越不灵敏,稳健性越好。
5 结 论本文针对多种失效模式下机械零部件的稳健性优化设计问题进行了研究,以履带车辆底盘的扭力轴构件为例进行计算,得出如下结论:
1) 机械系统零部件的失效模式较少,且出现一种失效模式零部件就失效了,故将零部件的失效看作各种失效模式的串联作用,考虑各失效模式的相关性,建立机械系统零部件多失效模式相关性可靠性分析模型,较独立假设模型更接近工程实际需要。
2) 运用可靠性摄动理论和四阶矩技术获得了机械零部件对结构随机变量参数均值和方差的灵敏度计算公式,应用到履带车辆行走系统的扭力轴上进行灵敏度分析计算,其结果是准确的,表明该公式对机械构件是适用的。
3) 基于可靠性灵敏度分析理论提出多目标优化的稳健性设计方法,应用到履带车辆行走系统扭力轴上进行多目标优化的稳健设计,其结果表明本文方法对机械系统构件的稳健性优化设计是可行的,此方法可以推广到其他机械可靠性优化设计领域,具有一定的指导意义。
参考文献
| [1] | LI J P, THOMPSON G.A method to take account of in-homogeneity in mechanical component reliability calculations[J].IEEE Transactions on Reliability,2005,54(1):159-168. |
| Click to display the text | |
| [2] | 喻天翔,宋笔锋, 万方义,等.机械零件多失效模式相关可靠度算法研究[J].机械强度,2006,28(4):508-511. YU T X,SONG B F,WAN F Y,et al.Research on calculating the reliability of mechanical component with correlated failure modes[J].Journal of Mechanical Strength,2006,28(4):508-511(in Chinese). |
| Cited By in Cnki (31) | |
| [3] | 崔海涛,马海全, 温卫东.基于随机有限元的接触问题可靠性形状优化设计[J].中国机械工程,2004,15(11):983-986. CUI H T,MA H Q,WEN W D.Reliability based structural shape optimtzation with contact using stochastic FEM[J].China Mechanical Engineering,2004,15(11):983-986(in Chinese). |
| Cited By in Cnki (8) | Click to display the text | |
| [4] | JENSEN H A, VALDEBENITO M A,SCHUELLER G I,et al.Reliability-based optimization of stochastic systems using line search[J].Computer Methods in Applied Mechanics Engineering,2009,198(49-52):3915-3924. |
| Click to display the text | |
| [5] | 吕震宙,冯元生. 元件强度可靠性的模糊概率计算模型[J].航空学报,1996,17(6):752-754. LU Z Z,FENG Y S.The reliability analysis of component and structure system based on the fuzzy distribution parameters[J].Acta Aeronautica et Astronautica Sinica,1996,17(6):752-754(in Chinese). |
| Cited By in Cnki (25) | Click to display the text | |
| [6] | 金雅娟,张义民, 张艳林.基于鞍点逼近的机械零部件可靠性及其灵敏度分析[J].机械工程学报,2009,45(12):102-107. JIN Y J,ZHANG Y M,ZHANG Y L.Analysis of reliability and reliability sensitivity for machine components by mean-value first order saddlepoint approximation[J].Journal of Mechanical Engineering,2009,45(12):102-107(in Chinese). |
| Cited By in Cnki (28) | Click to display the text | |
| [7] | 张义民,朱丽莎, 唐乐,等.刚柔混合非线性转子系统的动态应力可靠性及可靠性灵敏度研究[J].机械工程学报,2011,47(2):159-165. ZHANG Y M,ZHU L S,TANG L,et al.Dynamical stress reliability and sensitivity analysis of nonlinear rotor system with rigid-flexible structure[J].Journal of Mechanical Engineering,2011,47(2):159-165(in Chinese). |
| Cited By in Cnki (8) | Click to display the text | |
| [8] | 李云贵,赵国藩. 结构体系可靠度的近似计算方法[J].土木工程学报,1993,26(5):70-76. LI Y G,ZHAO G F.An approximate method for structural system reliability analysis[J].China Civil Engineering Journal,1993,26(5):70-76(in Chinese). |
| Cited By in Cnki (92) | Click to display the text | |
| [9] | 贺向东. 机械结构可靠性稳健设计若干问题的研究[D].长春:吉林大学,2005:57-66. HE X D.Research on several key issues of mechanical and structural reliability-based robust design[D].Changchun:Jilin University,2005:57-66(in Chinese). |
| Cited By in Cnki (59) | |
| [10] | 王新刚,张义民, 王宝艳.机械零部件的动态可靠性分析[J].兵工学报,2009,30(11):1510-1514. WANG X G,ZHANG Y M,WANG B Y.Dynamic reliability analysis of mechanical components[J].Acta Armamentarii,2009,30(11):1510-1514(in Chinese). |
| Cited By in Cnki (25) | Click to display the text | |
| [11] | 王正,谢里阳, 李兵.考虑失效相关的系统动态可靠性模型[J].兵工学报,2008,29(8):986-989. WANG Z,XIE L Y,LI B.Dynamic reliability model of the system with dependent failure[J].Acta Armamentarii,2008,29(8): 986-989(in Chinese). |
| Cited By in Cnki (14) | Click to display the text | |
| [12] | ZHAO Y G, ONO T S.Moment methods for structural reliability[J].Structural Safety,2001,23(1):47-75. |
| Click to display the text | |
| [13] | AU S. Reliability-based design sensitivity by efficient simulation[J].Computers & Structures,2005,83(14):1048-1061. |
| Click to display the text | |
| [14] | 张义民,张旭方, 杨周,等.多失效模式机械零部件可靠性灵敏度设计[J].机械强度,2009,31(6):926-931. ZHANG Y M,ZHANG X F,YANG Z,et al.Reliability sensitivity design for mechanical components with multi-failure modes[J].Journal of Mechanical Strength,2009,31(6):926-931(in Chinese). |
| Cited By in Cnki (19) | Click to display the text | |
| [15] | 卢昊,张义民, 黄贤振,等.多失效模式典型结构系统可靠性稳健设计方法研究[J].工程力学,2011,28(8):226-231. LU H,ZHANG Y M,HUANG X Z,et al.Practical method for reliability-based robust design of typical structural system with multiple failure modes[J].Engineering Mechanics,2011,28(8): 226-231(in Chinese). |
| Cited By in Cnki (8) | Click to display the text |
