非合作目标逼近轨迹规划问题的求解方法主要分为间接法和直接法[9-10]。间接法对共轭变量的初值高度敏感且难以估计,很难收敛,如果存在路径约束,推导过程过于复杂[11]。相对于间接法,直接法在收敛的鲁棒性和解决实际问题的适应性上具有优势[11]。高斯伪谱法是直接法的一种,它将状态量和控制量在一系列Legendre-Gauss(LG)点上进行离散,将最优控制问题转化为非线性规划问题,然后采用常规的非线性规划算法求得近似解。该方法具有较高的求解精度和收敛速度,在处理含初始和终端约束的问题上具有优势[8, 12-13]。邵龙飞等[12]采用高斯伪谱法研究了电磁航天器运动规划方法。Boyarko等[8]采用高斯伪谱法研究了非合作目标的轨迹规划,考虑了避免追踪航天器与非合作目标碰撞及有限推力限制。本文作者课题组的段传辉和董云峰[13]采用高斯伪谱法求解了有限推力小伴星的最优释放轨迹。
然而,轨迹规划实际上是对逼近过程中推力器开关状态的规划。高斯伪谱法的规划结果是随时间连续变化的推力,必须通过脉冲调制技术[13]才能转化为推力器的开关状态。为了使推力器输出的推力与规划结果中连续变化的推力冲量等价,并且保证较高的精度,要求推力器有很高的开关频率。最终逼近段距离短、控制频繁,对开关频率的要求更高,但实际工程中推力器开关频率存在限制。另外,高斯伪谱法等直接法寻优结果的最优性得不到保证[11]。
如果直接优化推力器开关状态,则可以降低对推力器开关频率的要求。推力器的开关状态是时间轴上离散的点,遗传编程善于求解离散变量的优化问题[14]。遗传编程利用遗传算法的进化原理自动进化出表达式,不仅可以优化参数,还可以优化表达式的结构,实现表达式进化,是对遗传算法的一次突破性发展[15],其已经在机器学习[16]、模式识别[17]和控制律设计[18]等多个领域取得成功。同时,遗传编程是一种全局最优智能搜索技术[19-20],可以解决高斯伪谱法等直接法不能保证寻优结果最优性的问题。
本文提出了一种使用遗传编程直接优化推力器开关状态的有限推力航天器逼近非合作目标最终逼近段的轨迹规划方法。通过引入基函数,把推力器开关状态转化为待优化表达式,以燃料最省为目标,并把约束条件以罚函数形式增加到目标函数转化成的适应度函数中,建立了直接优化开关状态表达式的轨迹规划模型,再采用遗传编程算法进行轨迹规划设计。
1 逼近轨迹规划的数学模型 有限推力航天器逼近非合作目标时,在最终逼近段,追踪航天器和目标航天器相对运动方程的矢量表示为[6]
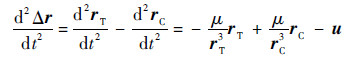 | (1) |
式中: Δr为相对位置矢量;rC为追踪航天器到地球中心的矢量;rT 为目标航天器到地球中心的矢量;μ为地球引力常数;u为追踪航天器通过有限推力产生的加速度。
将式(1)在追踪航天器的轨道坐标系中展开,得到完整的相对运动动力学方程:
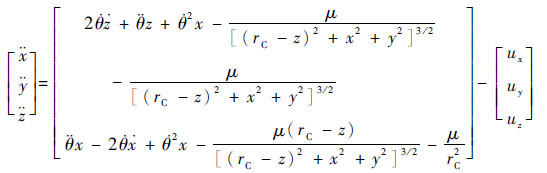 | (2) |
式中:
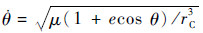
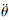
式(2)中非零的加速度[ux uy uz]T表示存在轨道机动。航天器轨道机动的推力通常由推力器提供,3个轴的加速度与三轴推力器的开关状态的关系为
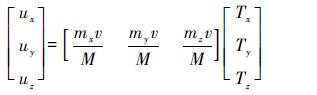 | (3) |
式中: M为追踪航天器质量;mx、my和mz为三轴推力器燃气质量流速;v 为推力器燃气排气速度;Tx、Ty和Tz 为三轴推力器的开关状态,有正向开、关和负向开3种,对应的取值为{1,0,-1}。
综合式(2)和式(3),可得到由三轴推力器开关状态作为控制量的追踪航天器在有限推力下逼近非合作目标的轨道动力学模型。
逼近过程中,要求追踪航天器质心(xC,yC,zC)与障碍物质心(xB,yB,zB)的距离大于追踪航天器和障碍物的包络半径之和,定义距离与包络半径之和的差值ξ1如下:
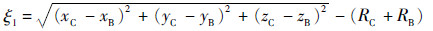 | (4) |
式中: RC 为追踪航天器的包络半径;RB为障碍物的包络半径。
若追踪航天器的尺寸为[a,b,c],则追踪航天器的包络半径RC 为
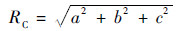 | (5) |
RB有类似的定义。
同时,在逼近非合作目标过程中,追踪航天器质心(xC,yC,zC)与目标航天器质心(xT,yT,zT)的距离大于追踪航天器包络半径RC 和目标航天器包络半径RT之和,定义距离与包络半径之和的差值为ξ2。
假设追踪航天器逼近非合作目标后悬停时两者间的相对距离为L,则终端位置约束为
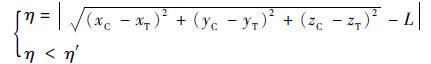 | (6) |
式中: η′为位置约束容差; η为位置误差。
考虑到逼近后会进行一定时间的悬停,终端速度约束为
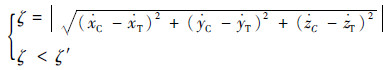 | (7) |
式中: ζ′为速度约束容差;ζ 为速度误差。
2 基于遗传编程的逼近轨迹规划 针对第1节中逼近轨迹规划的数学模型,采用基函数概念将式(3)中的开关状态表示为基函数,并建立基函数组成的树型表达式,然后根据优化目标和约束条件建立适应度函数,最终可以根据每个树型表达式对应的适应度函数值采用遗传操作优化树型表达式,对轨迹规划问题进行求解。
2.1 推力器开关状态的基函数 假设推力器分别安装在本体坐标系坐标轴的正负向,2个推力器一对,则可以实现正向推力、零和负向推力。为了实现3个方向的轨道机动,至少需要6个推力器。所有开关状态有x轴(±1,0)、y轴(±1,0)和z轴(±1,0)共9种,经排列组合,所有存在推力器开启的状态共26种,以开启状态作为基函数,用Xk(k=1,2,…,26)表示,这26种都是机动状态。除此之外,还有一种“匀速”状态为所有推力器均不开启,定义为基函数X27,如表 1所示。
表 1 三轴推力器开关状态基函数 Table 1 Basis functions of switch state of thrusters in three axises
| 基函数 | 开关状态 | 基函数 | 开关状态 | ||||
| Tx | Ty | Tz | Tx | Ty | Tz | ||
| X1 | 0 | 1 | 0 | X15 | 1 | 0 | 1 |
| X2 | 0 | -1 | 0 | X16 | 1 | 0 | -1 |
| X3 | 0 | 0 | 1 | X17 | -1 | 0 | 1 |
| X4 | 0 | 0 | -1 | X18 | -1 | 0 | -1 |
| X5 | 1 | 0 | 0 | X19 | 1 | 1 | -1 |
| X6 | -1 | 0 | 0 | X20 | 1 | -1 | 1 |
| X7 | 0 | 1 | -1 | X21 | 1 | 1 | 1 |
| X8 | 0 | -1 | 1 | X22 | 1 | -1 | -1 |
| X9 | 0 | 1 | 1 | X23 | -1 | 1 | -1 |
| X10 | 0 | -1 | -1 | X24 | -1 | -1 | 1 |
| X11 | 1 | 1 | 0 | X25 | -1 | 1 | 1 |
| X12 | 1 | -1 | 0 | X26 | -1 | -1 | -1 |
| X13 | -1 | 1 | 0 | X27 | 0 | 0 | 0 |
| X14 | -1 | -1 | 0 | ||||
表选项
2.2 树型表达式 表 1中1个基函数代表 1次开关状态。在追踪航天器逐渐向目标航天器机动过程中,每种开关状态出现的次序和持续时间会不同,比如可能出现n个持续时间分别为ti(i=1,2,…,n)的机动段和l个持续时间分别为tj(j=1,2,…,l)的匀速段。机动段和匀速段出现的次序及持续时间组成了推力器开关状态的历程。一种典型的开关状态历程下逼近轨迹如图 1所示,其中,机动段的轨迹为曲线,匀速段的轨迹为直线。
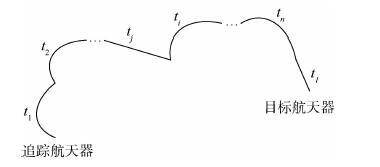 |
| 图 1 逼近轨迹示意图 Fig. 1 Schematic diagram of approaching trajectory |
| 图选项 |
图 1中逼近轨迹的开关状态历程函数表达式如式(8)所示,其也是遗传编程的个体。
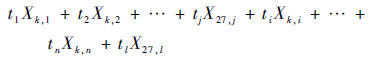 | (8) |
基函数在式(8)中的出现顺序代表机动段或匀速段执行的先后顺序。
对任一个开关状态历程函数,遗传编程算法生成的树型结构如图 2所示,其主要特点如下:
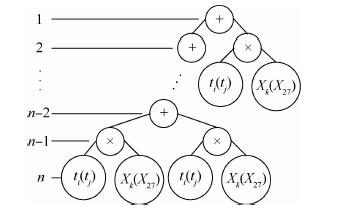 |
| 图 2 树型结构 Fig. 2 Tree structure |
| 图选项 |
1) 运算符集合为{+,×},末端集合为{持续时间ti和tj,基函数Xk和X27 }。
2) 最后一层+节点的左子树为×,其余各层+节点的左子树均为+。
3) 所有层+节点的右子树均为×。
4) ×节点的左子树为持续时间ti或者tj,右子树为基函数Xk或者X27。
2.3 适应度函数 建立树型结构之后,对开关状态的优化转化为对树型结构的优化。为了保证优化结果,使得燃料最省,可以规避障碍物和满足终端逼近精度,轨迹规划的适应度函数由1个质量项和2个距离项组成。质量项为 n个机动段推力器消耗燃料的总和(l个匀速段不消耗燃料),即
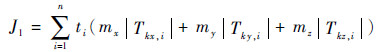 | (9) |
式中:丨Tkx,i丨、丨Tky,i丨和丨Tkz,i丨分别为Xk 对应的三轴推力器开关状态(见表 1)。
障碍物规避采用罚函数法处理,定义为距离项J2。考虑到当ξ1 <0时,追踪航天器与障碍物会发生碰撞,即使ξ1非常接近0也会发生碰撞;同时,当ξ1≥0时,不会发生碰撞,即使ξ1非常接近0也不会发生碰撞。所以,规避障碍物的罚函数采用阶跃函数,当ξ1 <0会发生碰撞时,罚函数取值为q,当 ξ1≥0不会发生碰撞时,罚函数取值为0。对追踪航天器规避目标航天器时采用相同的函数形式,当ξ2 <0会发生碰撞时,罚函数取值为q,当ξ2≥0不会发生碰撞时,罚函数取值为0。距离项J2表达式为
 | (10) |
式中:q为罚函数系数。
为了保证终端逼近精度,希望位置误差η和速度误差ζ尽量小,因此,采用罚函数法处理终端位置约束和终端速度约束,定义距离项J3为
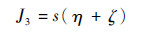 | (11) |
式中: s为罚函数系数。
当优化结果中J3 <smin(η′,ζ′)时,式(6)和式(7)成立,终端约束满足。
轨迹规划的适应度函数J取为J1 、 J2及J3的和,把J1 、 J2及J3采用式(9)~式(11)代替,适应度函数J 表示为
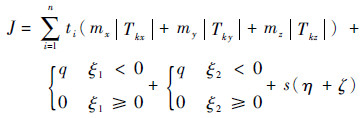 | (12) |
2.4 遗传操作 遗传编程算法根据每一次优化生成的树的适应度函数,采用遗传操作对树进行修改优化。为了保证遗传操作过程中树的形状不变,复制和交叉操作只能在相同运算的2个节点(+或者×)之间进行,复制和交叉操作对基函数出现的顺序和次数进行优化。突变操作对所有节点的持续时间ti或tj 进行突变,突变操作对基函数持续时间进行优化。
2.5 轨迹规划整体流程 基于遗传编程的航天器轨迹规划的整体流程如图 3所示。遗传编程模块随机产生个体(表达式),并将表达式传给航天器动态模拟器的轨道控制子系统;轨道控制子系统解析表达式,得到每时刻三轴推力器的开关状态;推力器模块根据开关状态计算推力历程和适应度函数的质量项;动力学模块对非合作目标的逼近进行数值仿真,根据仿真结果计算适应度函数的距离项,将距离项与质量项相加得到适应度函数,并反馈给遗传编程模块;遗传编程模块根据适应度进行遗传操作,产生新的个体,依次循环。
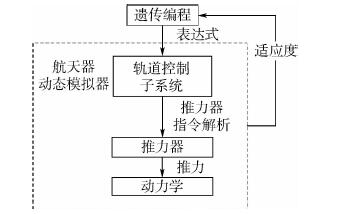 |
| 图 3 轨迹规划整体流程 Fig. 3 Flowchart of trajectory planning |
| 图选项 |
3 数值仿真结果与分析 3.1 非合作目标最终逼近段轨迹规划算例 假设追踪航天器和目标航天器的轨道六要素如表 2所示。在t=0时刻两者相距10 m,并有相对速度。建立轨道坐标系So,原点在追踪航天器质心,z轴指向地球,x轴沿速度方向,y轴符合右手定则,即沿轨道面负法向。在该坐标系下,目标航天器相对于追踪航天器的相对位置和相对速度分别为
表 2 追踪航天器与目标航天器轨道六要素 Table 2 Six general orbital elements of chaser and target spacecraft
| 轨道六要素 | 追踪航天器 | 目标航天器 |
| 半长轴/m | 42 164 003 | 42 164 000 |
| 偏心率 | 1.479×10-6 | 0 |
| 轨道倾角/(°) | 1.305×10-4 | 0 |
| 升交点赤经/(°) | 8.952×10-1 | 0 |
| 近地点辐角/(°) | 87.581 | 0 |
| 真近点角/(°) | -88.476 | 0 |
表选项
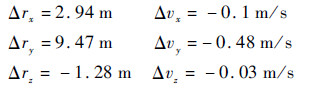 |
障碍物的位置为(2,5,-1)。
假设要求逼近结束时两者的相对距离降为L=3 m,相对速度为0,位置约束容差η′=0.01 m,速度约束容差ζ′=0.01 m/s。
3.2 轨迹规划过程 针对第3.1节中提出的问题,设置遗传编程的种群每代中共有200个个体,每个个体语法树的深度为5~10层,从每代个体中选出进行变异操作的个体数占总数的40%,进行交叉操作的个体数占总数的60%,进行复制操作的个体数占总数的30%。取三轴6个推力器推力均为10 N,罚函数系数q=100,s=200;持续时间为4~5 s。图 4给出每一代内适应度函数最小值的进化过程。
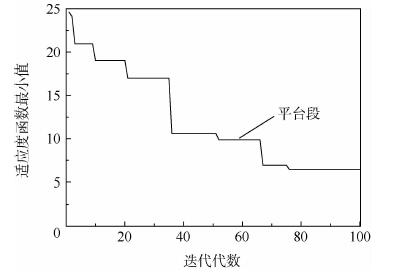 |
| 图 4 适应度函数最小值的进化过程 Fig. 4 Evolution process of minimum of fitness function |
| 图选项 |
由图 4可见适应度函数值随规划迭代代数的增加逐渐趋于最小值的过程。图中出现了很多平台段,这些平台段表明在相邻的几代内前一代的最优解在后续的进化过程中保持不变。在76代后出现了较长的平台段,到100代时都没有变化,因此,选择第76代的平台作为轨迹规划结果。
3.3 轨迹规划结果 轨迹规划结果的推力器开关状态表达式如式(13)所示,树型结构如图 5所示。
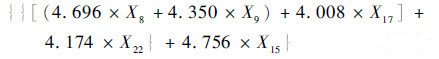 | (13) |
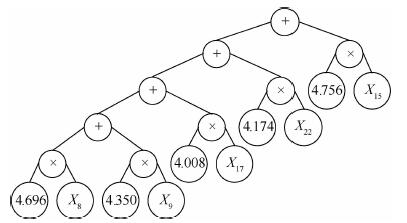 |
| 图 5 规划结果树型结构 Fig. 5 Tree structure of planning result |
| 图选项 |
由图 5可见,轨迹规划结果共需进行5次机动,总机动时间为21.98 s。执行顺序为
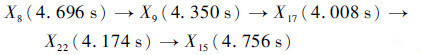 | (14) |
轨迹规划结果中,适应度函数值为6.42,适应度函数的距离项J3为1.61,消耗燃料为4.81 kg。
轨道坐标系So下2个航天器的相对位置和相对速度及推力器推力随时间变化曲线如图 6所示。
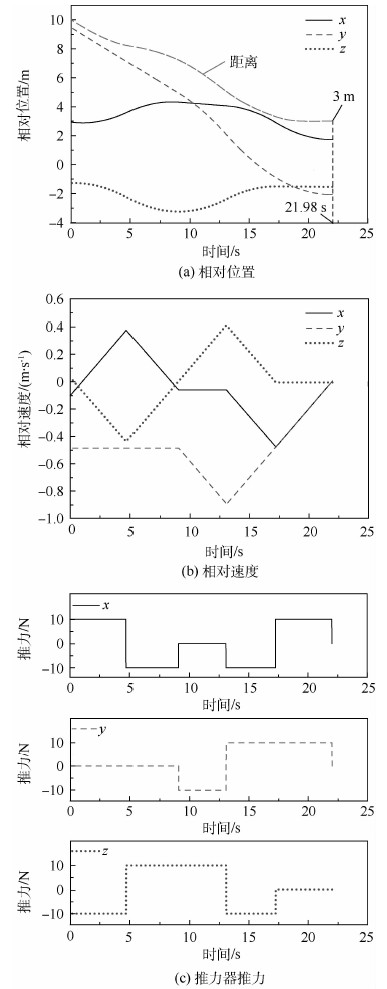 |
| 图 6 推力器推力和2个航天器相对位置及相对速度变化曲线 Fig. 6 Variation curves of thrust of thruster and relative velocity and position between two spacecrafts |
| 图选项 |
由图 6(a)可见,0时刻时,2个航天器的相对位置为10 m,当时间为21.98 s时,相对位置下降到期望值3 m;由图 6(b)可见,3个方向的相对速度在21.98 s全部达到期望的零点;所有曲线倾斜段斜率的绝对值相同,表明所有方向推力的大小相同,这是以开关状态作为控制量时轨迹规划结果的特点。上述结果表明,在有限推力下实现了非合作目标航天器逼近。由图 6(c)可见,整个逼近过程推力器开关5次,远小于通过脉冲调制技术[21]得到的开关状态的频率。
分析图 6可知,第1、2次机动在x和z方向实现了远离障碍物,主要目的是避障;第3次机动y和z方向的加速均为了接近目标;第4次机动y和z方向开始减速以满足终端速度为零的约束,x方向加速是为了接近目标;第5次机动,x和y方向减速是为了以满足终端速度为零的约束。可见,整个逼近过程在x和z方向经历了避障、接近目标和减速3个过程,在y向经历匀速接近、加速接近和减速3个过程。这符合逼近轨迹规划的运动特点。
3.4 与原有的轨迹规划方案比较 图 7给出原有的轨迹规划方案。原有方案中作者课题组采用高斯伪谱法对连续的非合作目标逼近数学模型进行离散,建立了代数约束的参数优化模型,用序列二次规划法求解[13]。
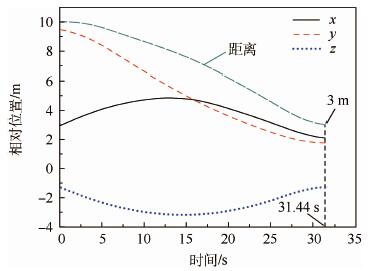 |
| 图 7 采用高斯伪谱法轨迹规划结果的相对位置变化曲线 Fig. 7 Relative position curves of trajectory planning based on Gauss pseudospectral method |
| 图选项 |
由图 7可见,逼近时间约为31.44 s。另外,结果中适应度函数值为6.22,适应度函数的距离项为1.20,消耗燃料为5.02 kg。比较2种结果可见,本文方案比原方案逼近时间降低了30.09%,燃料消耗降低了4.18%。本文方案比原方案适应度函数有所增加,主要是逼近精度低于原方案,但是本文方案逼近位置精度的绝对误差为0.001 2 m,速度精度的绝对误差为0.006 8 m/s,满足终端约束要求。采用脉冲调制技术[21]计算图 7中规划结果的推力器开关状态,当最小脉冲宽度为20 ms、脉冲推力产生的飞行轨迹与图 7中的飞行轨迹在3个方向上位置的相对误差小于1%时,三轴开关状态共48次,所以本文方法可以大大降低开关次数。然而,类似遗传算法[14],本文的方法也存在计算效率低的问题,考虑到航天器中运算器的计算能力相对较低,本文方法计算时间会较长,当任务时间不充裕时,可以采用离线规划。因此,对于本文中算例,采用遗传编程算法的规划结果比原方案采用高斯伪谱法的规划结果具有较小的逼近时间、较低的燃料消耗和较少的开关次数,但是计算效率较低。
4 结论 1) 通过引入基函数,提出了一种使用遗传编程算法直接优化推力器开关状态的有限推力非合作目标逼近的轨迹规划方法。
2) 基函数使得遗传编程个体表达式简单、简洁,树型结构的引入使得对开关次序和持续时间的优化实现解耦。
3) 以某非合作目标最终逼近段轨迹规划为例,遗传编程经过100次迭代得到了满意的结果。整个逼近过程推力器开关5次,对开关频率的要求很低,并且逼近时间和燃料消耗都比原方案明显减少。
本文方法存在计算效率低的问题,当任务时间不充裕时,需采用离线规划。通过构造合适的基函数,本文的轨迹规划方法可以适用于其他有限推力下的轨迹规划问题,本文提供了一种直接优化推力器开关状态的有限推力航天器轨迹规划方法。
参考文献
| [1] | STAMM S,MOTAQHEDI P.Orbital express capture system:Concept to reality[C]//Proceedings of the Society of Photo-optical Instrumentation Engineers. Bellingham:SPIE,2004,5419:78-91. |
| Click to display the text | |
| [2] | ODA M. Space robot technology experiments on NASDA's ETS-VII satellite[J]. Advanced Robotics the International Journal of the Robotics Society of Japan,1998, 13(1): 335–336. |
| Click to display the text | |
| [3] | LANDZETTEL K,PREUSCHE C,ALBU-SCHAFFER A,et al.Robotic on-orbit servicing-DLR's experience and perspective[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems.Piscataway,NJ:IEEE Press,2006:4587-4594 |
| Click to display the text | |
| [4] | 郭继峰, 张立佳, 崔乃刚. 空间非合作目标燃料最优终端接近策略研究[J]. 宇航学报,2010, 31(2): 386–390.J F, ZHANG L J, CUI N G. Optimal control for space capture of noncooperative target[J]. Journal of Astronautics,2010, 31(2): 386–390.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [5] | 朱仁璋, 林彦. 航天器交会最终逼近段相对姿态估计与控制[J]. 北京航空航天大学学报,2007, 33(5): 544–548.R Z, LIN Y. Relative attitude estimation and control schemes for the final approach phase of spacecraft rendezvous[J]. Journal of Beijing University of Aeronautics and Astronautics,2007, 33(5): 544–548.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [6] | 卢山, 徐世杰. 非合作目标的自主接近控制律研究[J]. 中国空间科学技术,2008(5): 7–12.S, XU S J. Control laws for autonomous proximity with non-cooperative target[J]. Chinese Space Science and Technology,2008(5): 7–12.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [7] | PHILLIP J M,KAVRAKI L E,BEDROSSIAN N.Spacecraft rendezvous and docking with real-time randomized optimization:AIAA-2003-5511[R].Reston:AIAA,2003. |
| Click to display the text | |
| [8] | BOYARKO G, YAKIMENKO O, ROMANO M. Optimal rendezvous trajectories of a controlled spacecraft and a tumbling object[J]. Journal of Guidance,Control,and Dynamics,2011, 34(4): 1239–1252. |
| Click to display the text | |
| [9] | 雍恩米, 陈磊, 唐国金. 飞行器轨迹优化数值方法综述[J]. 宇航学报,2008, 29(2): 397–406.E M, CHEN L, TANG G J. A survey of numerical methods for trajectory optimization of spacecraft[J]. Journal of Astronautics,2008, 29(2): 397–406.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [10] | HUANG G Q, LU Y P, NAN Y. A survey of numerical algorithms for trajectory optimization of flight vehicles[J]. Science China Technological Sciences,2012, 55(9): 2538–2560. |
| Click to display the text | |
| [11] | 彭坤, 果琳丽, 向开恒, 等. 基于混合法的月球软着陆轨迹优化[J]. 北京航空航天大学学报,2014, 40(7): 910–915.K, GUO L L, XIANG K H, et al. Optimization of lunar soft landing trajectory based on hybrid method[J]. Journal of Beijing University of Aeronautics and Astronautics,2014, 40(7): 910–915.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [12] | 邵龙飞, 师鹏, 赵育善. 电磁航天器编队动力学建模与运动规划方法[J]. 北京航空航天大学学报,2015, 41(4): 737–743.L F, SHI P, ZHAO Y S. Dynamics modeling and motion programming for electromagnetic formation flight[J]. Journal of Beijing University of Aeronautics and Astronautics,2015, 41(4): 737–743.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [13] | 段传辉, 董云峰. 利用高斯伪谱法求解小推力伴星最优释放轨迹[J]. 中国空间科学技术,2011(5): 18–24.DUAN C H, DONG Y F. Optimal control spacecraft fly-around releasing using continuous thruss based on Gauss pseudospectral method[J]. Chinese Space Science and Technology,2011(5): 18–24.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [14] | 冯消冰, 黄海, 王伟. 基于遗传算法的大型风机复合材料叶片根部强度优化设计[J]. 复合材料学报,2012, 29(5): 196–202.X B, HUANG H, WANG W. Strength optimization of large wind turbine blade root on the genetic algorithm[J]. Acta Materiae Compositae Sinica,2012, 29(5): 196–202.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [15] | GANDOMI A H, YUN G J. Coupled SelfSim and genetic programming for non-linear material constitutive modeling[J]. Inverse Problems in Science and Engineering,2015, 23(7): 1101–1119. |
| Click to display the text | |
| [16] | WEMER J C,KALGANOVA T.Disease modeling using evolved discriminate function[C]//Proceedings 6th European Conference on Genetic Progrmming.Berlin:Springer,2003,2610:465-474. |
| Click to display the text | |
| [17] | KISHORE J K, PATNAIK L M, MANI V, et al. Application of genetic programming for multi-category pattern classification[J]. IEEE Transactions on Evolutionary Computation,2000, 4(3): 242–258. |
| Click to display the text | |
| [18] | 钟山, 董云峰. 基于机器学习的卫星姿态控制律设计[J]. 航天控制,2011, 29(4): 61–65.ZHONG S, DONG Y F. The design of satellite attitude control law based on machine learning[J]. Aerospace Control,2011, 29(4): 61–65.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [19] | 白焰, 蒋毅恒, 朱耀春, 等. 基于遗传编程的火电厂主汽温系统建模研究[J]. 系统仿真学报,2008, 20(4): 1076–1079.Y, JIANG Y H, ZHU Y C, et al. Modeling main steam temperature system of power plant using genetic programming[J]. Journal of System Simulation,2008, 20(4): 1076–1079.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [20] | 李良敏, 屈梁生. 遗传编程在无量纲指标构建中的应用[J]. 西安交通大学学报,2002, 36(7): 736–739.L M, QU L S. Genetic programming for dimensionless parameters construction[J]. Journal of Xi'an Jiaotong University,2002, 36(7): 736–739.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [21] | 郭清晨.常值推力姿态控制方法研究[D].哈尔滨:哈尔滨工业大学, 2006:8-19 GUO Q C.Research of constant thrust attitude control method[D].Harbin:Harbin Institute of Technology,2006:8-19.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
