针对状态不可测的多输入多输出(Multi-Input Multi-Output,MIMO)仿射型非线性极值搜索系统,为了在不增加控制系统设计难度的情况下实现对被控对象的极值控制,提出了一种输出反馈滑模控制方法。该方法不要求被控对象的状态量可测,将MIMO仿射型非线性极值搜索系统分解为若干个单输入单输出(Single-Input Single-Output,SISO)极值搜索子系统,并以新建子系统的输出量作为反馈控制量,利用斜坡函数作为输出量的参考跟踪信号,以输出跟踪误差以及该误差符号函数的积分值构建切换函数,从而设计得到系统的滑模极值搜索控制律。该输出反馈滑模控制方法不仅可以实现对被控对象的极值控制,更可以提高控制方法的鲁棒性。稳定性分析证明:无论在任何初始条件下,该方法都可使系统的输出量全局收敛至其期望极值的任意小邻域内,且所有状态量均一致范数有界。
1 问题阐述 针对如下MIMO仿射型非线性极值搜索系统:
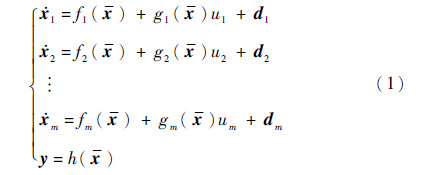
式中:
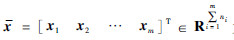为不可测量的状态量,xi=[xi1xi2…xini]T,1≤i≤m;u=[u1u2…um]T∈Rm为输入量;y=[y1y2…yp]T∈Rp为可测的输出量,且存在极值y*=[y1*y2*…yp*]T,不失一般性,假设输出量y具有极大值y*;fi(·)和gi(·)(1≤i≤m)为非线性光滑函数;h(x)=[h1(x11,x12,…,x1h1)h2(x21,x22,…,x2h2)…hp(xp1,xp2,…,xphp)]T为关于状态量x的光滑极值函数,且函数hi(·)中的状态量互不重复,
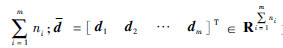为系统参数扰动或外界干扰引起的不确定项。假设1针对MIMO仿射型非线性极值搜索系统(见式(1)),存在输入量u使得状态量x和输出量y均稳定且有界。
假设2在MIMO仿射型非线性极值搜索系统(见式(1))中,光滑函数gi(x)存在非零下界,即0<Gi≤‖gi(x)‖,其中,Gi为下界值,1≤i≤m。
假设3对于MIMO仿射型非线性极值搜索系统(见式(1)),存在极值点x*,使得输出量y取得极大值y*,因此,
,
(i∈[1,2,…,m],j∈[1,2,…,p]),且对于给定的常数Δ>0,总是存在一个常数
1(Δ)>0,使得1(Δ)≤‖H′(x)‖,∀x∉DΔ:={x:‖x-x*‖<Δ/2},其中,
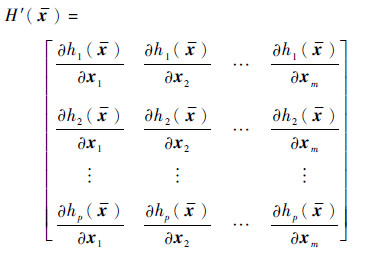
DΔ为关于极值点x*的Δ邻域。显然,常数
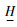1(Δ)将随着Δ的变化而变化。为方便描述,1(Δ)简写为1。假设4在MIMO仿射型非线性极值搜索系统(见式(1))中,信号d存在上确界,即满足‖d‖≤dmax,dmax为已知值。
既定控制目标:针对MIMO仿射型非线性极值搜索系统(见式(1)),设计一种输出反馈滑模控制方法,使得闭环控制系统稳定,且系统的状态量和输出量均一致范数有界,输出量y全局收敛至极大值y*的有界邻域内。
为了实现既定的控制目标,对MIMO仿射型非线性极值搜索系统(见式(1))进行一定转换,重新构建m个子系统,其中,第i(1≤i≤m)个极值搜索子系统的模型为
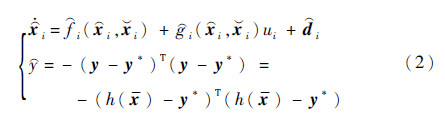
式中
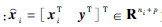为第i个极值搜索子系统的状态量;
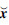i为在状态量x中除去xi以外的其余状态量;
为输出量,∈R。
当分析第i个极值搜索子系统(见式(2))时,可假设其他子系统的状态量均有界,这也符合一般系统的设计要求,而且本文设计的输入量必须确保所有极值搜索子系统的状态量有界。
通过分解得到的极值搜索子系统(见式(2))属于MIMO仿射型非线性极值搜索系统(见式(1))的子系统,同样具有输出极大值,因此也满足假设3的条件:对于给定的常数Δi>0(Δi<Δ),总是存在一个常数
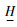2i(Δi)>0,使得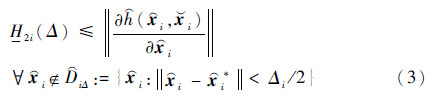
式中:
为关于极值点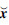i*的Δi邻域,且DΔ。假设5存在已知的K∞函数α1i和α2i,即α1i,α2i∈K∞,使得Lipschitz连续函数fi(xi,
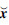i)和h(x)满足如下条件: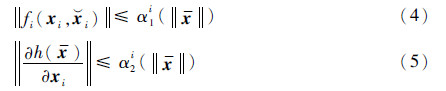
由于极值搜索子系统(见式(2))属于MIMO仿射型非线性极值搜索系统(见式(1))的子系统,根据既定的控制目标,可转换得到新的控制子任务:设计一种输出反馈滑模控制方法,使得闭环控制系统(见式(2))全局渐近稳定,且该系统的状态量和输出量均一致范数有界,输出量
全局收敛至极大值*的有界邻域内。2 方法设计 针对第i个极值搜索子系统(见式(2))的模型,定义e为输出量
的跟踪误差,其具体形式为
式中:yr为输出量的参考信号,其初值为yr0，其形式为斜坡函数,即
其中:kr>0为设计参数。
对跟踪误差e求取1阶微分,并将式(2)、式(7)代入,可得
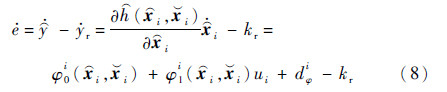
式中:
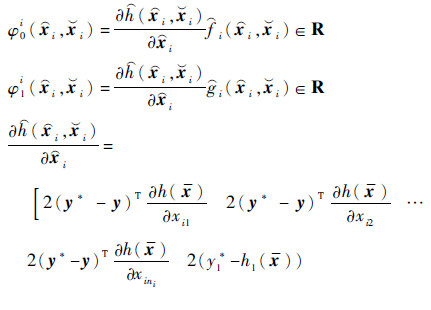
根据
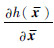的定义可知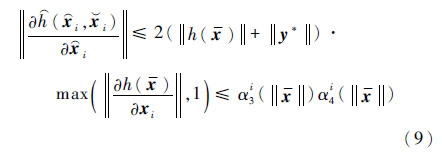
式中:α3i(‖x‖)=2‖h(x)‖+2‖y*‖;α4i(‖x‖)=max(α2i(‖x‖),1),α3i和α4i为K∞函数。
根据式(4)和式(9),可得
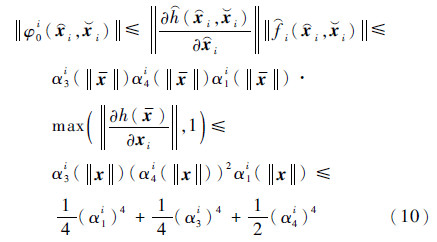
根据假设4和式(9),可知
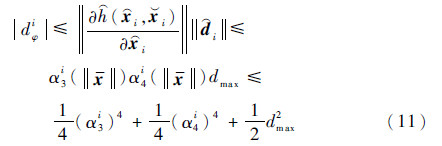
根据假设2、假设3和式(3),对于
i∉,可知
式中:kφi为满足kφi≤
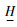2imin(Gi,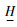1Gi)的已知下界值。针对非线性极值搜索子系统(见式(2)),设计基于输出反馈滑模控制的输入量ui为
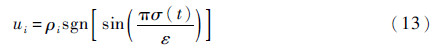
式中:ρi为调节函数;σ(t)为切换函数;sgn(·)为符号函数;ε>0为设计常数。
调节函数ρi设计为
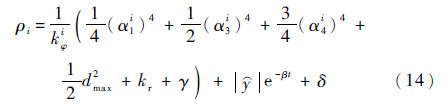
式中:γ>0为设计常数;β>0为衰减指数;δ>0为设计的任意小常数。
切换函数σ(t)设计为
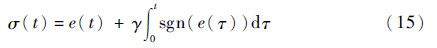
对切换函数σ(t)求取1阶微分,并将式(8)代入,可得
评注虽然K∞函数α1i、α2i、α3i和α4i涉及到状态量x,但是根据极值搜索子系统(见式(2)),应用所设计的输入量ui(见式(13))和范数观测器,可以在无需状态量x可测的情况下,实现函数α1i、α2i、α3i和α4i。
3 控制系统的稳定性分析针对非线性极值搜索子系统(见式(2)),当采取式(13)~式(15)所示的基于输出反馈滑模控制的输入量ui时,构成的闭环控制系统如图 1所示。
 |
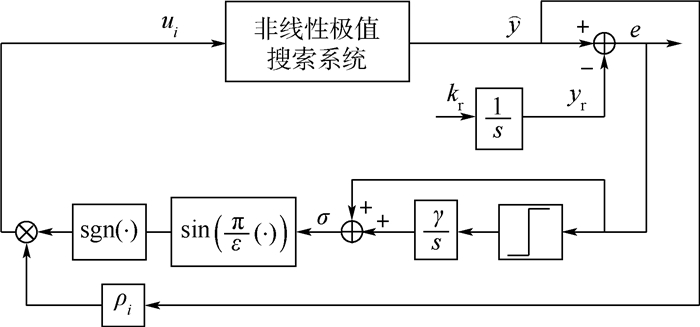| 图 1 非线性极值搜索闭环控制系统框图Fig. 1 Frame of nonlinear extremum seeking closed-loop control system |
| 图选项 |
定理1针对非线性极值搜索子系统(见式(2)),采用输入量ui如式(13)~式(15)所示,则在有限的时间内,系统的状态量
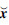i、输出量和切换函数信号σ(t)都不会出现发散现象,且切换函数σ(t)会运动到滑模面kε,即σ(t)=kε,其中k为正整数。证明积分型函数S1(σ(t))和S2(σ(t))设计如下:
当σ(t)≥0时,
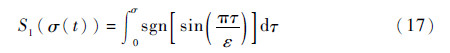
当σ(t)<0时,
此外,
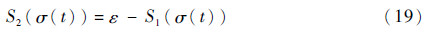
函数S1(σ(t))和S2(σ(t))的曲线如图 2所示。可知,函数S1(σ(t))和S2(σ(t))始终满足S1(σ(t))≥0，S2(σ(t))≥0,且关于零点都具有对称性,在此主要对式(17)和式(19)进行分析。
 |
| 图 2 函数S1(σ(t))和S2(σ(t))的曲线Fig. 2 Curves of functions S1(σ(t)) and S2(σ(t)) |
| 图选项 |
对S1(σ(t))和S2(σ(t))分别求取1阶微分,并代入式(8)和式(13),可得
当sgn(φ1i(
i,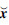i))<0时,考虑到调节函数ρi≥0和-‖φ1i(i,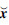i)‖<-kφi,并代入式(10)、式(11)和式(14),可得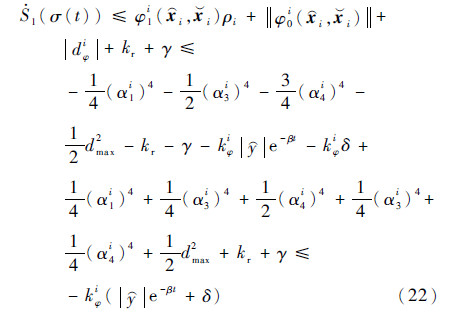
当sgn(φ1i(
i,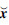i))>0时,存在
针对切换函数σ(t)是否发散的命题,采用反证法进行分析。首先假设在时刻t1∈[0,∞)时,切换函数σ(t)会出现发散现象,则根据σ(t)的定义式(15)可知,跟踪误差e(t)和输出量
(t)都会出现发散现象。因此,假设存在时刻t2∈[0,t1),使得在[t2,t1)区间内,(t)≥eβt(δ1-δkφi)/kφi成立,其中δ1为任意小的正数。将(t)≥eβt(δ1-δkφi)/kφi代入式(22)和式(23),可得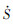
1(σ(t))≤-δ1,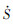2(σ(t))≤-δ1。由于假设当t≥t1时,切换函数σ(t)已发生了发散现象,并且考虑到切换函数σ(t)的连续性,则存在时刻t3∈[t2,t1)和整数kσ,使得Σ(t3)=kσε。由图 2可知,当kσ为偶数时,S1(σ(t3))=0;当kσ为奇数时,S2(σ(t3))=0。考虑到S1(σ(t))≥0,S2(σ(t))≥0,
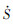1(σ(t))≤-δ1,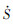2(σ(t))≤-δ1和δ1>0,则存在S1(σ(t))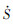1(σ(t))≤-δ1S1(σ(t))≤0和S2(σ(t))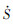2(σ(t))≤-δ1S2(σ(t))≤0。由此可知,对于任意时刻t∈[t3,t1),S1(σ(t))=0或者S2(σ(t))=0,此时切换函数σ(t)=kσε。由于切换函数σ(t)是连续函数,而结论“当t∈[t3,t1)时,σ(t)=kσε”与前提假设“在时刻t1∈[0,∞)时,切换函数σ(t)会出现发散现象”是相互矛盾的。因此该假设不成立,σ(t)、
i(t)和(t)在有限时间内都不会出现发散现象。由于|
|e-βt是随时间变化的指数递减函数,根据上述分析可知,存在ta≥0,使得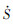i(σ(t))≤-δa(i=1,2)和||e-βt→0,其中0<δa<kφiδ。根据文献[15]的相关引理可知,对于t≥ta,存在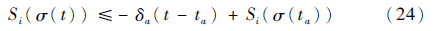
针对式(24),当t≥ta时,存在Si(σ(t))=0。当Si(σ(t))=0时,存在σ(t)=kε。由于在σ(t)=kε的邻域内,当k为偶数时,
;当k为奇数时,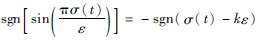
。定义Lyapunov函数如下:
对式(25)求取1阶微分,并将式(13)和式(16)代入,可得
根据切换函数σ(t)的定义式(15)可知,当sgn(φ1i(
i,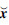i))<0时,切换函数σ(t)会运动至σ(t)=kε,其中k为偶数,此时,将其与式(10)、式(11)和式(14)代入式(26),当t≥ta时,可得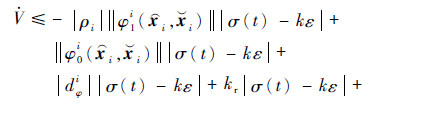
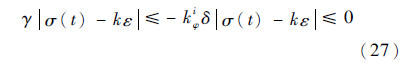
当sgn(φ1i(
i,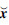i))>0时,切换函数σ(t)也会运动至σ(t)=kε,其中k为奇数,此时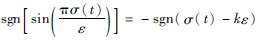,同理可得
由于V≥0,且
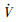≤0,根据Lyapunov稳定性理论可知,存在σ(t)=kε。由此说明,在有限时间内,切换函数σ(t)总会趋于一个滑模面σ(t)=kε,其中k为整数。证毕
定理2针对非线性极值搜索子系统(见式(2)),满足假设1~假设5,如果采用输入量ui如式(13)~式(15)所示,则状态量
i将在有限时间内全局收敛至邻域内,并且对于足够小的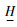2i,输出量在极大值*附近的振荡幅值是关于参数ε的无穷小量,即|-*|=O(ε),同时状态量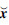i以及输出量都一致范数有界。证明1) 采用反证法,证明状态量
i将在有限时间内全局收敛至邻域内。首先假设状态量
i在所有时间内都不能进入邻域内,则根据定理1可知,存在时刻ts>0,使得切换函数的变化率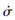
(t)=0。根据切换函数σ(t)的定义式(15)可知,∀t≥ts,
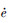(t)=-γsgn(e(t))。由此可知,跟踪误差e=-yr将趋近于零,由于kr>0,则随着参考轨迹yr的严格递增,输出量也会逐渐增加。由于已知输出量具有极大值*,因此当时间t足够大时,总会使得输出量趋近于极大值*,此时状态量i进入邻域内。显然,结论“当时间t足够大时,状态量
i进入邻域内”与前提条件“状态量i在所有时间内都不能进入邻域内”是相互矛盾的。因此,状态量i必将在有限时间内全局收敛至邻域内,输出量也将趋于极大值*的很小邻域内。随着
趋于极大值*,依据=-(y-y*)T·(y-y*),可知y会收敛于y*,根据假设3可知,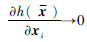
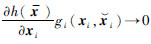针对式(2),当控制矩阵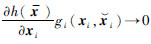时,系统对y的控制作用将越来越弱,直至失去控制作用,则将围绕极大值*进行振荡。在此振荡过程中,切换函数σ(t)将从一个滑模面kε转换到另一个滑模面(k+1)ε。为此,进一步证明输出量在极大值*附近的振荡幅值是关于参数ε的无穷小量。2) 证明输出量
在极大值*附近的振荡幅值是关于参数ε的无穷小量。针对输出量
在极大值*附近的振荡问题,分2种情况进行讨论:①情况1:状态量i一直在邻域内进行振荡运动;②情况2:状态量i的振荡运动会逃出邻域,然后再返回进入邻域内。① 情况1:如果状态量
i一直在邻域内进行振荡运动,则通过选取合适的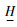2i,可以使得Δ任意小,从而满足|-*|=O(ε)。② 情况2:如果状态量
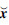i的振荡运动会逃出邻域,然后再返回进入邻域,则就需要证明输出量在此以外的振荡范围也是关于参数ε的无穷小量。由于参考轨迹yr是严格递增的,且输出量
存在极大值*,则一定存在时间t*>0,使得sgn(e(t))=-1。由切换函数σ(t)的定义式(15),可得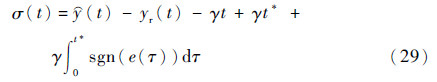
假设当时刻t=t1(t1>t*)时,状态量
i从邻域内运动到其边缘处。对于∀t>t1,存在
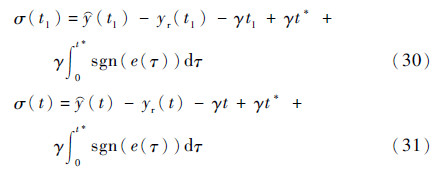
将式(30)与式(31)相减,可得
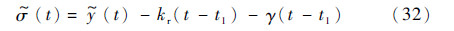
式中:
由式(32)可得
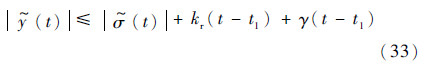
设定t2(t2>t1)为切换函数σ(t)达到下一个滑模面的时刻,t3(t3>t1)为切换函数σ(t)从邻域DΔ外部再次返回到邻域DΔ边缘的时刻。
① 如果t3>t2,则可将时间分为2个阶段:t∈[t1,t2)和t∈[t2,t3]。
当t∈[t1,t2)时,切换函数σ(t)并不处于滑模面上,即kε<σ(t)<(k+1)ε,则|
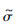(t)|=|σ(t)-σ(t1)|=O(ε)。根据式(8)、式(13)和式(16),同时考虑到t*可以适当大,使得|
|e-βt→0,可得
切换函数σ(t)是递增的,对于∀t∈[t1,t2),存在
由式(33)、式(35)以及|
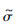(t)|=|σ(t)-σ(t1)|=O(ε)可知,|
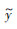(t)|=O(ε)。当t∈[t2,t3]时,切换函数σ(t)处于滑模面上,
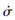(t)=0。根据时刻t2和t3的定义可知,在t∈[t2,t3]时,
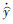=kr+γ>0,则输出量(t)是单调递增运动,它将从滑模面上朝着极大值*方向运动,因此说明与(t1)距离最远的位置是(t2),而由于已证明得知|(t2)-(t1)|=O(ε),所以∀t∈[t2,t3],存在|(t)-(t1)|=O(ε)。综合t∈[t1,t2)和t∈[t2,t3]的分析情况,可以得到对于∀t∈[t1,t3],
(t)-(t1)=O(ε)。② 如果t2≥t3>t*,分析输出量
从t1运动到t3的情况,由于此时切换函数σ(t)不处于滑模面上,则对于∀t∈[t1,t3],输出量的运动情况可以类比于①中t∈[t1,t2)的情况,因而,可知此时|(t)-(t1)|=O(ε)。对于∀t∈[t3,t2),由于状态量
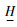i已处于邻域内,此时通过选取合适的2i,可以使得Δ任意小,从而满足|(t)-(t1)|=O(ε)。由于状态量
i会收敛至邻域内,因此i也是一致范数有界的。此外,由于输出函数=
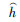(i,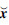i)是连续函数,当状态量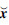i一致范数有界性时,输出量也是一致范数有界的。证毕
由于非线性极值搜索子系统(见式(2))属于MIMO仿射型非线性极值搜索系统(见式(1))的任意子系统,因此根据定理2,可得到如下推论。
推论1针对MIMO仿射型非线性极值搜索系统(见式(1)),满足假设1~假设5,如果输入量ui(1≤i≤m)采取如式(13)~式(15)所示,则状态量x将在有限时间内全局收敛至邻域DΔ内,并且对于足够小的
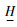1,输出量y在极大值y*附近的振荡幅值是关于参数ε的无穷小量,即‖#8214;y-y*‖=O
,同时状态量x和输出量y都一致范数有界。证明根据定理2可知,对于MIMO仿射型非线性极值搜索系统(见式(1))中的第i(1≤i≤m)个极值搜索子系统(见式(2)),当采取如式(13)~式(15)所示的输入量ui时,状态量
i可在有限时间内全局收敛至邻域内时,即存在‖xi-xi*‖<Δi/2与‖-*‖<Δi/2。因此,当采取与定理2相类似的控制条件时,MIMO仿射型非线性极值搜索系统(见式(1))的状态量x都能在有限时间内全局收敛至‖x-x*‖<Δ/2,根据假设3可知,此时状态量x处于邻域DΔ内。此外,由于函数y=h(x)是连续函数,当状态量x一致范数有界性时,输出量y也是一致范数有界的。根据定理2可知,‖
-*‖=O(ε),由于已知极大值*=0,则根据=-(y-y*)T(y-y*),可得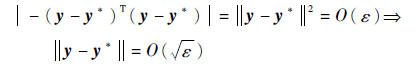
采用式(13)~式(15)所示的输入量ui,可使得第i个极值搜索子系统(见式(2))中的状态量
i是一致范数有界的,这也是分析其他极值搜索子系统的前提条件,从而说明了采用本文提出的方法是确保状态量x和输出量y一致范数有界的充分条件。证毕
4 仿真分析 考虑一类纳什均衡解的搜索控制问题,该问题具有如下系统模型:
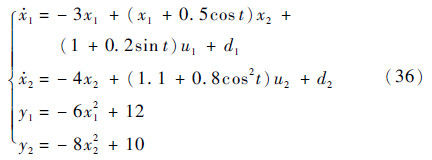
式中:x=[x1x2]T为系统的状态量;u=[u1u2]T和y=[y1y2]T分别为系统的输入量和输出量,分别表示代价输入量和惩罚函数输出量;d=[d1d2]T为系统建模不完善所引起的干扰。通过分析该模型可知,当x1=0和x2=0时,输出量y1和y2才具有极大值y1*=12和y2*=10。此例的控制目标是利用所设计的基于输出反馈滑模控制的输入量u,使得输出量y1和y2全局收敛至各自的极大值y1*和y2*,且状态量x1和x2均有界。
应用本文方法,设计控制参数分别为:kr=1,γ=0.3,β=3,δ=0.1,ε=0.02。考虑干扰项d1=0,d2=0,当系统状态量的初始条件分别为x1(0)=3和x2(0)=2时,得到的仿真结果分别如图 3~图 8所示。
 |
| 图 3 不存在干扰时状态量x1的仿真结果Fig. 3 Simulation result of state x1 without interference |
| 图选项 |
 |
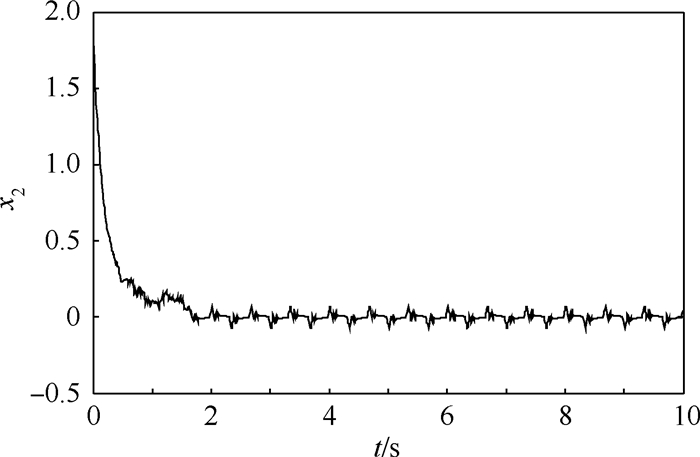| 图 4 不存在干扰时状态量x2的仿真结果 Fig. 4 Simulation result of state x2 without interference |
| 图选项 |
 |
| 图 5 不存在干扰时输出量y1的仿真结果 Fig. 5 Simulation result of output y1 without interference |
| 图选项 |
 |
| 图 6 不存在干扰时输出量y2的仿真结果 Fig. 6 Simulation result of output y2 without interference |
| 图选项 |
 |
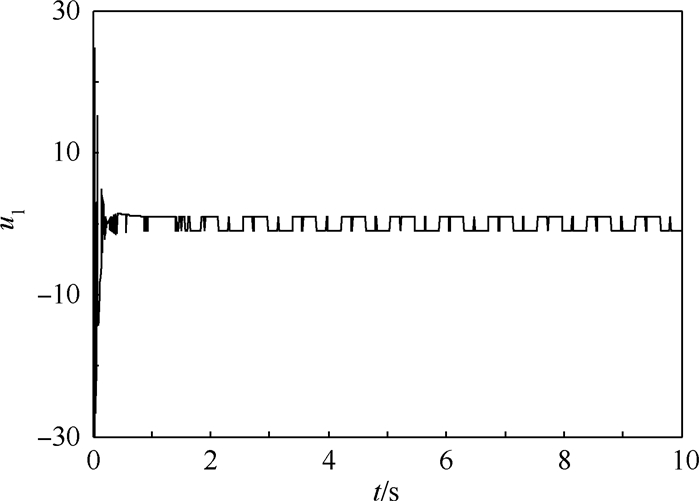| 图 7 不存在干扰时控制输入量u1的仿真结果 Fig. 7 Simulation result of control input u1 without interference |
| 图选项 |
 |
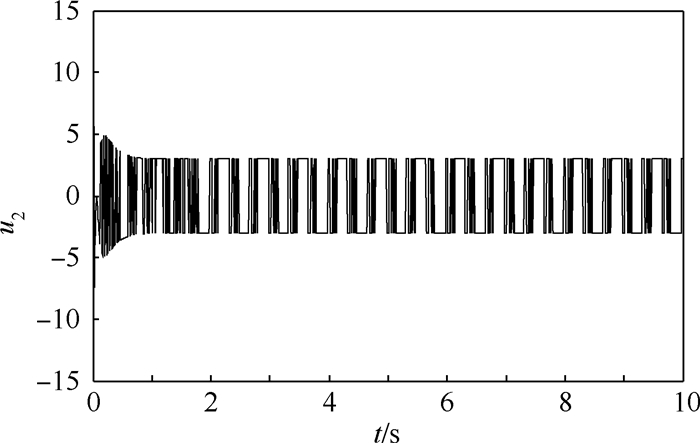| 图 8 不存在干扰时控制输入量u2的仿真结果 Fig. 8 Simulation result of control input u2 without interference |
| 图选项 |
通过上述仿真结果可知,在控制输入量u的作用下,输出量y1和y2能很快地收敛至极大值y1*=12和y2*=10(见图 5和图 6),此时状态量x1和x2也分别收敛至x1*和x2*的有界邻域内(见图 3和图 4)。由于滑模控制自身的性质,控制输入量u存在来回切换的问题,为了弱化其影响,可以采取双曲正切函数代替符号函数的方法。
为了进一步验证本文方法的鲁棒性,分别假设干扰项d1为单位幅值的正弦周期信号,干扰项d2为在工作时间6~7s内的2倍幅值脉冲信号,同时状态量的初始值和设计参数均保持不变,得到的仿真结果分别如图 9~图 14所示。
 |
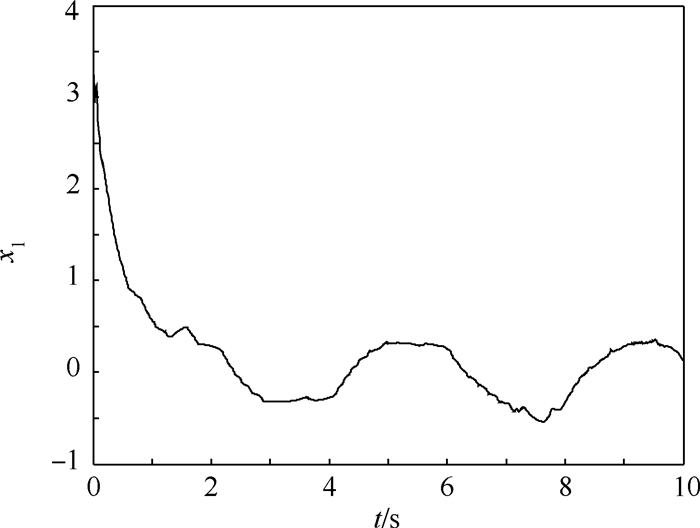| 图 9 存在干扰时状态量x1的仿真结果Fig. 9 Simulation result of state x1 with interference |
| 图选项 |
 |
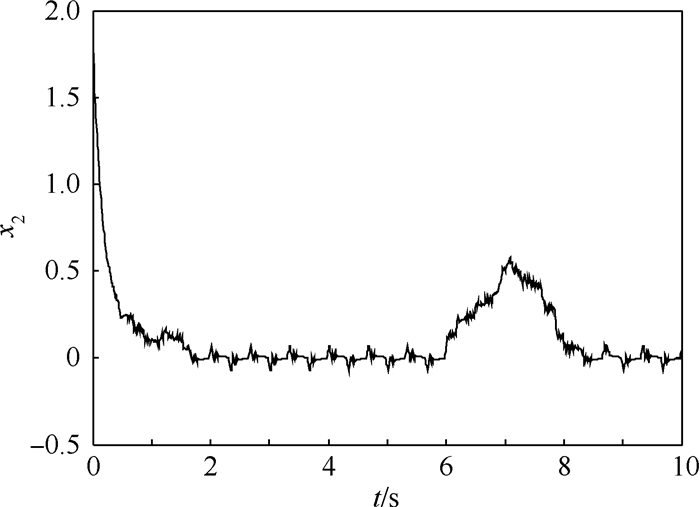| 图 10 存在干扰时状态量x2的仿真结果 Fig. 10 Simulation result of state x2 with interference |
| 图选项 |
 |
| 图 11 存在干扰时输出量y1的仿真结果 Fig. 11 Simulation result of output y1 with interference |
| 图选项 |
 |
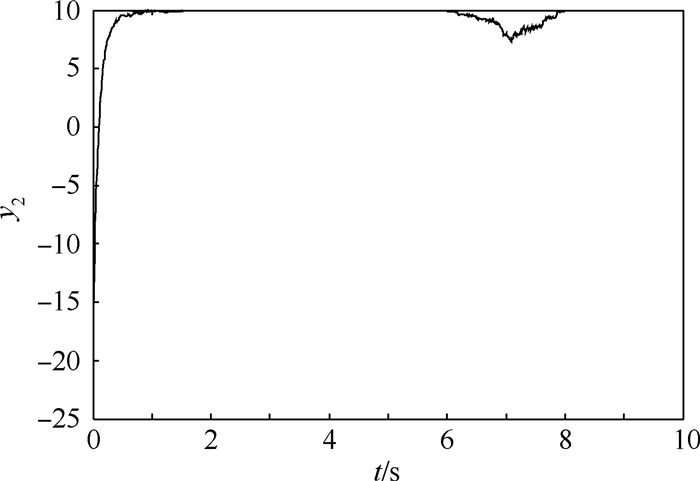| 图 12 存在干扰时输出量y2的仿真结果 Fig. 12 Simulation result of output y2 with interference |
| 图选项 |
 |
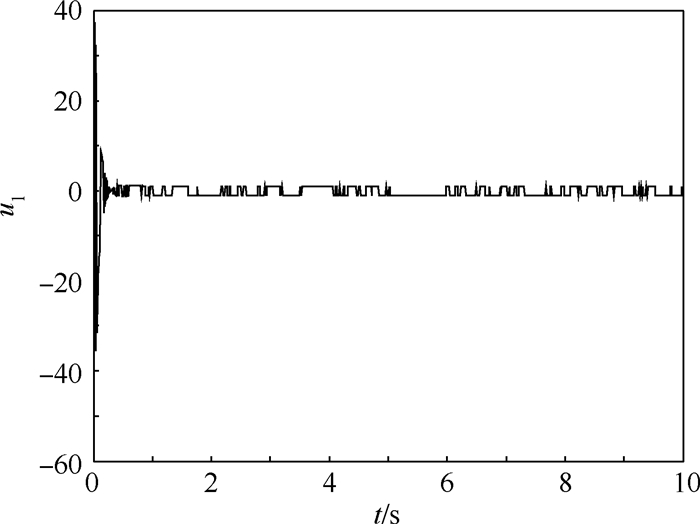| 图 13 存在干扰时控制输入量u1的仿真结果 Fig. 13 Simulation result of control input u1 with interference |
| 图选项 |
 |
| 图 14 存在干扰时控制输入量u2的仿真结果 Fig. 14 Simulation result of control input u2 with interference |
| 图选项 |
通过上述仿真结果可知,当系统(见式(36))在遭受不同形式的干扰时,利用原有控制器的作用,输出量y1和y2仍然能较快地收敛至各自极大值y1*和y2*的有界邻域内,由此说明本文方法确实具有很好的鲁棒性。
5 结 论本文综合分析了当状态量不可测时的MIMO仿射型非线性极值搜索系统,提出了一种输出反馈滑模控制方法,稳定性分析及仿真验证表明:
1) 该控制方法可在任何初始条件下使系统的输出量全局收敛至其期望极值的任意小邻域内,且所有状态量均一致范数有界。
2) 该控制方法确保了切换函数在任何时刻都可以全局收敛至滑模面上,提升了控制方法的鲁棒性。
3) 该方法属于一种在线反馈控制方法,在许多状态量不易测量或者不可测量的MIMO极值搜索系统中有着广泛的应用前景。
参考文献
| [1] | DEHAAN D, GUAY M.Extremum-seeking control of state-constrained nonlinear systems[J].Automatica,2005,41(9):1567-1574. |
| Click to display the text | |
| [2] | CENTIOLI C, IANNONE F,MAZZA G,et al.Extremum seeking applied to the plasma control system of the frascati tokamak upgrade[C]//Proceedings of the 44th IEEE Conference on Decision Control/European Control Conference 2005.Piscataway,NJ:IEEE Press,2005:8227-8232. |
| Click to display the text | |
| [3] | KRSTIC M, BANASZUK A.Multivariable adaptive control of instabilities arising in jet engines[J].Control Engineering Practice,2006,14(7):833-842. |
| Click to display the text | |
| [4] | PETERSON K S, STEFANOPOULOU G.Extremum seeking control for soft landing of an electromechanical valve actuator[J].Automatica,2004,40(6):1063-1069. |
| Click to display the text | |
| [5] | BASTIN G, NESIC D,TAN Y,et al.On automatic seeking of optimal steady-states in biochemical processes[C]//7th IFAC Symposium on Nonlinear Control Systems.Pretoria:Curran Associates,Inc.,2007:814-819. |
| Click to display the text | |
| [6] | DEWASME L, VANDE W A.Adaptive extremum-seeking control applied to productivity optimization in yeast fed-batch cultures[C]//Proceedings of the 17th World Congress and the International Federation of Automatic Control.Seoul:Curran Associates,Inc.,2008:9713-9718. |
| Click to display the text | |
| [7] | ZHONG Z D, HUO H B,ZHU X J,et al.Adaptive maximum power point tracking control of fuel cell power plants[J].Journal of Power Sources,2008,176(1):259-269. |
| Click to display the text | |
| [8] | GWAK K W. Application of extremum seeking control to turbodynamic blood pumps[J].ASAIO Journal,2007,53(4):403-409. |
| Click to display the text | |
| [9] | KRSTIC M. Toward faster adaptation in extremum seeking control[C]//Proceeding of the 38th IEEE Conference on Decision and Control.Piscataway,NJ:IEEE Press,1999:4766-4771. |
| Click to display the text | |
| [10] | TAN Y, NESIC D,MAREELS I.On stability properties of a simple extremum seeking scheme[C]//Proceedings of the 45th IEEE Conference on Decision & Control.Piscataway,NJ:IEEE Press,2006:2807-2812. |
| Click to display the text | |
| [11] | 左斌,李静,胡云安. 极值搜索算法研究及其应用[M].北京:国防工业出版社,2014:1-10. ZUO B,LI J,HU Y A.Research on extremum seeking algorithm and its application[M].Beijing:National Defence Industry Press,2014:1-10(in Chinese). |
| [12] | ARIYUR K B, KRSTIC M.Slope seeking:A generalization of extremum seeking[J].International Journal of Adaptive Control and Signal Processing,2004,18(1):1-22. |
| Click to display the text | |
| [13] | 左斌,胡云安, 李静.基于混沌退火的参数扰动递归神经网络极值搜索算法及其应用研究[J].电子学报,2009,37(12): 2651-2656. ZUO B,HU Y A,LI J.Research on extremum seeking algorithm based on chaotic annealing recurrent neural network with parameter disturbances and its application[J].Acta Electronica Sinica,2009,37(12):2651-2656(in Chinese). |
| Cited By in Cnki (4) | Click to display the text | |
| [14] | OLIVEIRA T R, LIU H,PEIXOTO A J.Output feedback global tracking for unknown control direction plants with application to extremum-seeking control[J].Automatica,2011,47(6):2029-2038. |
| Click to display the text | |
| [15] | FILIPPOV A F. Differential equations with discontinuous right-hand side[J].American Mathematical Society Translations,1964,42(2):199-231. |
