由于导弹大攻角下的动力学系统的不确定性,自身具有较强的鲁棒性的变结构控制很早就被用于敏捷转弯的自动驾驶仪设计。文献[1]提出的方法基于滑模控制,使用气动力/直接力复合控制实现了铅垂平面内的180°快速调头机动。神经网络可以用于提高不确定非线性系统的近似动态逆控制能力,在文献[2]中该方法被用于基于直接力系统的敏捷导弹自驾仪,仿真给出了典型的导弹对尾后目标拦截的弹道仿真结果。除此之外,其他方法也被用于敏捷导弹的自驾仪设计,如H∞方法[3]、极点配置方法[4]和反步法[5]等。最近,一种仅使用气动力控制来完成敏捷转弯的新方法[6]被提出,文献[7]深入研究了该方法并给出了仿真结果。上述研究在设计自驾仪时往往假设气动力系数是已知信息,通过插值、工程估算或风洞试验得到,但实际上大攻角下的气动系数是高度不可测的,应当在控制器设计时充分考虑气动不确定性的影响[8]。
滑模变结构控制因其理想的鲁棒性而得到广泛关注与应用,而非奇异Terminal滑模(Nonsingular Terminal Sliding Mode,NTSM)控制方法的提出解决了传统滑模控制的收敛时间趋于无穷的问题。本文采用NTSM方法设计能够实现空空导弹大角度敏捷转弯的姿态控制律。对于NTSM方法,当系统在远离平衡点的位置进入滑动模态时会存在收敛缓慢的问题,针对该问题文献[9]对滑模面进行了改进,文献[10]不仅改进了滑模面形式,还利用终端吸引子思想构造了新的趋近律,文献[11]在此基础上设计了一种指数形式的快速Terminal滑模面。但文献[9, 10, 11]提出的方法都存在收敛停滞的问题,而且对控制参数的选取要求严苛。
另一方面,大攻角飞行空空导弹的动力学具有较大的气动不确定性,而NTSM方法依靠自身的鲁棒性来对抗被控对象的不确定性,这会导致抖振现象的产生且会消耗更多的能量。解决该问题的关键在于对系统不确定量的处理。文献[8]设计的敏捷导弹控制律不需要气动数据,将系统动力学方程中与气动力相关的部分作为未知量来处理。文献[12]采用时间滞后自适应律对包含气动不确定性的未建模动力学进行在线预测,但为系统带来了滞后特性,另外该文献处理的是小攻角(α<35°)的仿真情形。对于空空导弹的大角度机动问题,实时估计不确定量是一种有效提高控制系统性能的方法。
由上述分析可知,将NTSM方法直接应用于空空导弹的大角度机动控制系统设计有其弊端,对此本文在NTSM方法的基础上设计新的控制律以满足实际需要。首先建立了包含气动不确定性的空空导弹数学模型,基于此设计并分析了导弹的NTSM控制律。为提高系统收敛速度,提出了复合滑模面方法,然后在控制系统设计中引入了抗扰机制,有效削弱了大攻角下气动不确定性造成的严重的抖振现象。详细分析了所提方法的稳定性,最后给出的数值仿真结果证明了所提方法的有效性。
1 空空导弹数学模型本文研究的空空导弹采用配有×型尾翼的无翼式布局(见图 1),这种干净弹身外形更利于导弹的大攻角飞行。鉴于空空导弹需具备在无滚转条件下实施控制的能力,本文采用推力大小可连续调节的侧向控制发动机[2, 13],以实现导弹的大攻角机动能力。直接力控制装置安装于导弹质心之前,并假设该装置可以分别沿弹体系的+Oy1、-Oy1、+Oz1和-Oz1这4个方向提供直接控制力。空空导弹在发射后进行大角度姿态变化,此阶段导弹攻角会经历迅速增大(可增大至约180°),再由大变小,直至完成整个敏捷转弯的过程。由于在大攻角下气动舵效率降低,甚至失效,故本文单独使用直接力控制完成导弹的敏捷转弯。在敏捷转弯后导弹进入中制导以及末制导阶段,可以使用气动舵进行控制,该阶段的控制问题不是本文的研究内容。
 |
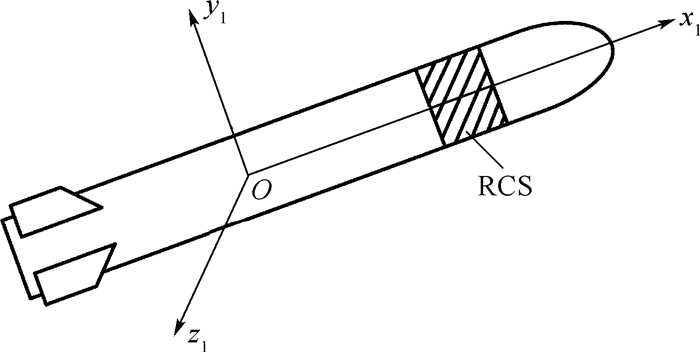| 图 1 空空导弹外形示意图 Fig. 1 Sketch of air-to-air missile configuration |
| 图选项 |
本文仅针对导弹的俯仰通道进行研究,故只考虑Oy1轴方向上的直接力,其大小记为uR,沿+Oy1轴方向为正。直接力大小可调节且变化连续,定义直接力喷流装置的喷管阀门开度为
式中:uRmax为直接力喷流装置的最大稳态推力;δR取值范围为[-1,1]。
描述导弹在纵向平面内运动的非线性数学模型为
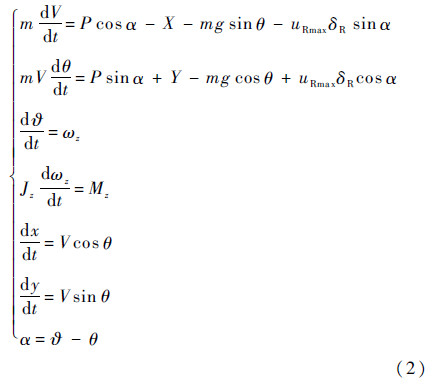
式中:m为导弹质量;V为导弹飞行速度;P为主发动机推力;X为阻力;Y为升力;g为重力加速度;θ为弹道倾角;?为俯仰角;ωz为俯仰角速度;Jz为导弹对弹体系Oz1轴的转动惯量;Mz为俯仰力矩;x和y为导弹质心相对于地面系的坐标。
在大攻角飞行条件下,导弹的气动力具有很大的不确定性。研究表明,当攻角增大至一定程度时(约30°～60°),导弹背风区将产生非对称涡流动现象,此时气动力具有明显的随机不确定性[13],致使导弹的大攻角气动力数据难以预估与建模。为了在导弹数学模型中体现大攻角下的气动不确定性,本文在适当简化条件下建立的导弹俯仰力矩Mz的模型为
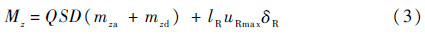
式中:Q为动压;S为特征面积;D为特征长度;mza为俯仰力矩系数近似值;mzd为俯仰力矩系数扰动值;lR为直接力作用点到导弹质心距离。将俯仰力矩系数分为近似值mza和扰动值mzd。近似值采用Missile Datcom软件计算得到,该软件可以给出导弹大攻角下气动数据的大致估计[14, 15]。扰动值代表气动数据的不确定性,通过人工设定的方式给出。
2 敏捷转弯的Terminal滑模控制导弹实现敏捷转弯的控制策略与方法有很多种,但无论采用何种方式,导弹在完成敏捷转弯时,其弹体指向与速度方向都应该大致指向拦截目标。本文按照文献[7]采用的方式,对导弹姿态进行控制,但不同于文献[7]采用的气动舵控制方式,本文采用直接力控制使弹体指向在短时间内迅速改变方向。与此同时恰当选择主发动机的开机工作时刻,在主发动机推力的作用下完成速度方向的反转。与控制攻角完成敏捷转弯的方式[2, 12, 13]相比,该转弯方式不需要导弹在大攻角机动时实时获取攻角信息,同时更利于导引头快速捕获目标。
对于本文采用的敏捷转弯方式,在主发动机工作之前,弹体姿态已经迅速改变(以?增大为例),此时导弹速度方向变化缓慢(
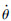≈0),故有α≈?,可知攻角会迅速增大。在主发动机开始工作后,当?已趋近于期望值?c,即ωz趋近于0,此时近似有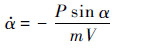
攻角α在推力P的作用下会迅速减小,而此时在直接力控制的作用下可保持?=?c。当α较小时,可单独采用气动舵进行控制,近似满足
式中:Cyα为升力系数对攻角的导数。可知α最终趋近于0。这样,?与θ均趋近于?c,导弹完成敏捷转弯。
基于此想法,在设计控制系统时仅考虑导弹的姿态动力学模型:
式中:f=QSDmza/Jz;Δ=QSDmzd/Jz;u=lRuRmaxδR/Jz。f与Δ分别代表系统中的已知量与未知量,且满足条件丨Δ丨≤lΔ且lΔ>0,lΔ表示系统未知量大小的上界,u代表系统的控制输入。
对于二阶SISO非线性不确定系统式(4),本节采用传统NTSM控制方法设计滑模控制律。采用的滑模面函数s与控制输入u0分别为
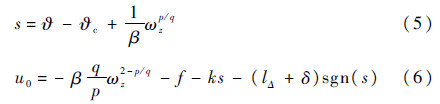
式中:期望俯仰角?c为一常值;β、p、q、k和δ均为待定的正参数,其中p和q为正奇数,且1<p/q<2。
在控制输入u的作用下,系统将快速到达滑模面s=0,之后进入滑动模态,此时有
对于导弹的大角度机动而言,?的初始值(例如0°)与期望值?c(例如180°)差距较大,当系统到达滑模面时仍远离平衡点(?c,0)。而式(7)中?-?c的指数小于1,导致系统的收敛速度较慢。另外,大攻角下的气动不确定性较严重,因此lΔ需要较大的取值,以保证系统的鲁棒性。在控制律式(6)中切换增益的大小直接影响抖振的幅值,故较大的lΔ取值会使控制输入u出现明显的抖振现象。
3 改进Terminal滑模控制律设计3.1 复合滑模面设计由第2节的分析可知,当系统处于滑动模态时收敛较慢的原因在于?-?c的指数小于1。如果当丨?-?c丨较大时令指数取值增大,则丨
丨增大,系统将更快地收敛。基于该想法,本节采用复合滑模面的方法来加快控制初期的收敛速度,对于不同的?值采用不同的滑模面函数,进而设计出分阶段的控制律。称此种控制方法为基于复合滑模面的NTSM(NTSM based on Compound sliding surface,NTSMC)控制方法。对于系统式(4),定义2个滑模面函数:
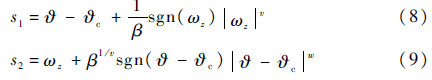
式中:β、v和w均为待定参数,且满足β>0,1<v<2,w>1。当丨?-?c丨<1时,控制系统取滑模面为s1=0;当丨?-?c丨≥1时,控制系统取滑模面为s2=0。如图 2所示,系统的滑模面具有复合形式。基于复合滑模面,相应的控制律为
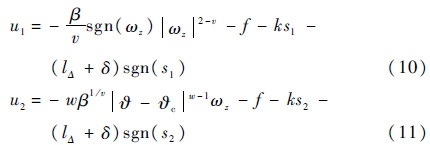
当丨?-?c丨<1时,控制系统取控制律式(10);当丨?-?c丨≥1时,取控制律式(11)。易验证控制律式(10)与控制律式(11)非奇异。
 |
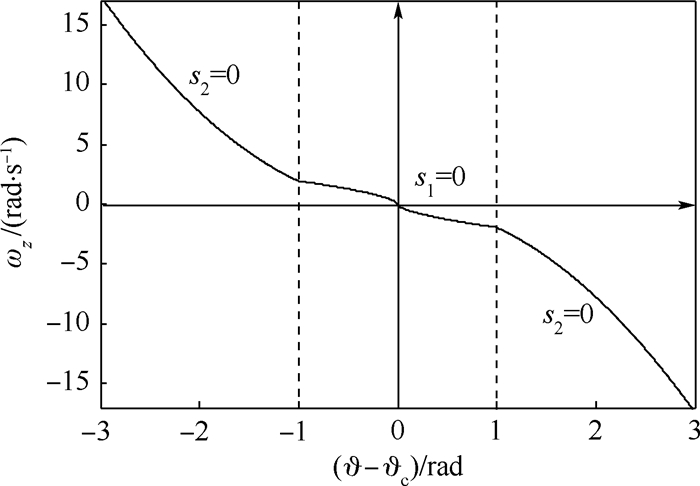| 图 2 复合滑模面 Fig. 2 Compound sliding surface |
| 图选项 |
3.2 基于扩张状态观测器的气动不确定量估计与补偿抖振现象是滑模控制方法的一大缺陷。对于在大攻角下飞行的导弹,严重的气动扰动是主要的动力学不确定因素,未建模动力学对控制系统的影响十分严重。对于传统NTSM控制方法,为消除系统不确定量Δ的影响,控制律式(6)采用切换增益lΔ来被动地抑制不确定性以实现控制系统的稳定性。但本文研究的被控系统不确定性较大,需要选取较大的lΔ值,导致控制量的抖振现象十分严重。
为了既能保证控制系统的稳定性与鲁棒性,又能尽可能减小抖振,本节采用扩张状态观测器(Extended State Observer,ESO)来实时估计系统不确定量,并在控制律中予以补偿。ESO理论是中国科学院韩京清[16]提出的自抗扰控制方法的核心部分。ESO能在线估计出系统不确定量的大小,它的出现为处理控制系统中的不确定量提供了新的方式,相关研究[17, 18]已表明ESO突出的扰动观测能力使其在飞行器控制领域具有巨大的应用价值。对于具有强不确定性的动力学系统,采用这种具有主动抗扰机制的控制器更能满足控制系统的实际需要。
下面采用文献[19]提出的一种非线性ESO形式,构造用于在线估计动力学系统式(4)中不确定量Δ的ESO:
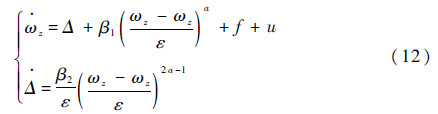
式中:ωz和Δ分别为ωz和Δ的估计值;β1、β2、a和ε为待定正参数;定义函数[·]a=sgn(·)丨·丨a。ESO将系统中所有未知量的总和作为扩张状态(这里为Δ)进行状态观测,由于系统式(4)中状态?与ωz均是可观测量,故在状态变量中仅选取ωz作为ESO输入,观测量Δ作为ESO输出,构造出二阶ESO。
对于控制系统的设计,在获得ESO在线估计的扰动观测值Δ后就可以对不确定量进行补偿,原控制律改为
式中:δESO为ESO的不确定量观测误差上界。分别用控制律式(13)与式(14)替换控制律式(10)与式(11),称此控制方法为基于ESO的NTSMC(NTSMC with ESO,NTSMCE)控制。
3.3 稳定性分析至此,完成了适用于空空导弹大角度机动的改进Terminal滑模控制律的设计。对于不确定非线性系统式(4),当丨?-?c丨<1时,取控制律为u3,对应的滑模面为s1=0;当丨?-?c丨≥1时,取控制律为u4,对应的滑模面为s2=0。下面对上述控制方法进行稳定性分析。
定义ESO的观测误差为e1=ωz-ωz,e2=Δ-Δ。用式(4)减去式(12),可得ESO的观测误差动态方程:
在满足一定条件下,ESO的观测量将以有限时间收敛于被观测量的邻域内,关于ESO的收敛性证明参见文献[19]中的定理2.2。当ESO稳定时,有
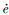1=0,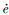2=0,则观测误差可以表示为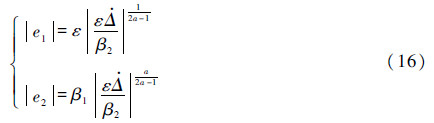
可见观测误差由参数β1、β2、a和ε确定。其中最重要的参数是ε,尽管
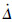是未知的,当ε趋近于零时,丨e1丨与丨e2丨分别趋近于零。若丨e1丨和丨e2丨被限制到足够小,那么ωz与Δ就可以分别收敛于实际状态ωz与Δ的很小的邻域内。这里假设e2≤δESO。对于丨?-?c丨<1的情况,取滑模面s1=0与控制律u3。将滑模面方程式(8)对时间求导,结合动力学方程式(4)与控制律式(13),可得
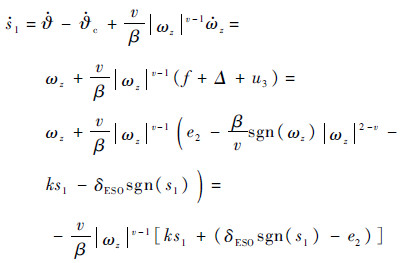
当ωz≠0时,有s1
<0,满足滑模面到达条件;当ωz=0时,有=0,将控制律u3代入系统方程式(4)中,可得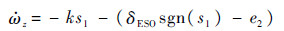
当s1>0时,有
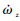<0;当s1<0时,有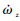>0。系统轨迹将穿过直线ωz=0而趋向滑模面s1=0[20]。综上,系统将以类似于指数趋近律的趋近速度趋向滑模面s1=0,文献[21]称之为伪指数趋近律。系统到达滑模面s1=0后将处于滑动模态,最终以有限时间收敛于平衡点(?c,0),滑动模态上的收敛性证明可参见文献[21]中的定理2。
对于丨?-?c丨≥1的情况,取滑模面s2=0与控制律u4。将滑模面方程式(9)对时间求导,结合动力学方程式(4)与控制律式(14),可得
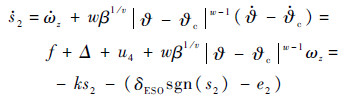
可知s2
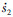<0,满足滑模面到达条件,系统趋向于滑模面s2=0。假设在丨?-?c丨>1的区域,系统到达滑模面s2=0,记此时?=?(tr),到达时刻记为tr,即t=tr时,s2(tr)=0。此后系统将处于滑动模态,假设在t=tr+ts时刻满足丨?(tr+ts)-?c丨=1。处于滑动模态时有s2=0,即
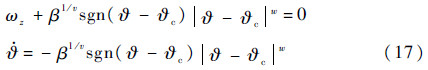
对式(17)进行积分,得
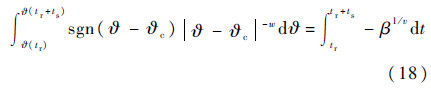
式中：
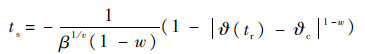
由式(18)可知系统于有限时间到达丨?-?c丨=1处,之后系统将沿滑模面s1=0趋近于平衡点(?c,0)。进一步分析式(18),若将其看作是以w为自变量的函数,取?(tr)为一任意常数,且满足丨?(tr)-?c丨>1,则容易验证ts为不连续的单调减函数,w=1为间断点。故当系统处于滑模面上时,本文提出的复合滑模面方法(?-?c的指数大于1)比传统NTSM方法(?-?c的指数小于1)具有更大的收敛速度。
假设系统起始点位于丨?-?c丨>1的区域,当丨?-?c丨=1时系统尚未到达滑模面s2=0,此后系统进入丨?-?c丨<1的区域,按照滑模面s1=0与控制律u3进行控制。如前文所述,系统于有限时间到达滑模面s1=0,最终收敛于平衡点(?c,0)。
综上所述,在所提新控制律的作用下,系统式(4)具有有限时间收敛特性。
值得注意的是,由于采用了复合滑模面,系统会出现滑模面s2=0向s1=0以及控制律u4向u3的切换。令s1=0,s2=0且丨?-?c丨=1,易验证复合滑模面是连续的,切换点为(?c+1,-β1/v)和(?c-1,β1/v)。在切换点(?c+1,-β1/v)处,2种控制律分别为
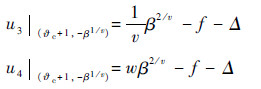
在切换点(?c-1,β1/v)处,2种控制律分别为
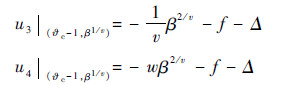
可知切换时控制量不连续,控制量的变化量为
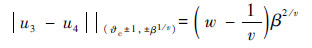
理想情况下,在切换点处控制律由u4直接切换至u3,则系统可以由滑动模态s2=0直接过渡至滑动模态s1=0。但实际的控制系统无法瞬时切换,控制律切换的滞后会导致系统偏离滑模面s1=0而进入其微小邻域内。但由上文分析可知,在控制律u3作用下系统会迅速回到滑模面s1=0从而进入滑动模态,最终收敛于平衡点(?c,0)。
4 数值仿真与分析在本节,采用第3节提出的控制方法,对直接力控制空空导弹进行敏捷转弯的数值仿真研究,模拟典型的攻击尾后目标的掉头机动飞行。假设导弹在铅垂平面内飞行,仿真全程采用直接力控制方式。设导弹初始飞行高度为5 km,初始马赫数为0.8,初始俯仰角与攻角均为0°,初始俯仰角速度为0(°)/s,主发动机推力为18 kN,直接力喷流装置的最大稳态推力uRmax为3 kN,仿真时间取为4 s。为完成导弹的180°转弯,俯仰角指令?c取为180°,对于主发动机点火时刻的选择,依据不同选择的仿真结果最终确定,当俯仰角大于140°时主发动机开始工作。
如第1节所述,导弹在大攻角下飞行存在严重的气动不确定性,故需要在动力学模型中加入气动扰动,并采用人工设定的方式确定其大小。图 3为导弹俯仰力矩系数扰动值mzd随时间的变化情况。在0~3 s阶段mzd按正弦规律变化,结合之后给出的仿真结果可知在3 s之后导弹姿态已经稳定地以小攻角飞行,取mzd=0。图 4为导弹俯仰角、攻角以及弹道倾角的仿真结果。结果表明，无论是传统NTSM方法,还是本文提出的改进NTSM方法——NTSMCE方法,都可以满足俯仰角指令的跟踪要求,且控制性能良好,响应无超调。但采用了复合滑模面与ESO的控制方法具有更快的响应速度,上升时间由NTSM方法的1.11 s缩短为0.77 s。飞行过程中,2种方法的最大攻角分别达到165°(NTSMCE方法)与161°(NTSM方法),在主发动机推力的作用下(?>140°时),攻角与弹道倾角剧烈变化,最终攻角趋于0°,弹道倾角趋于180°,导弹完成敏捷转弯。导弹的俯仰角速度变化曲线如图 5所示。由图可知NTSMCE方法下的俯仰角速度变化更剧烈。由图 6所示的导弹速度的时间历程可知,在攻角急剧变化的过程中2种方法下的速度先减小至15 m/s左右,后迅速增大。
 |
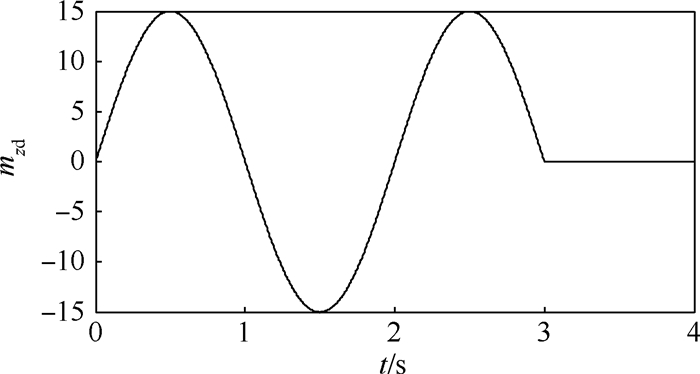| 图 3 俯仰力矩系数扰动值变化曲线 Fig. 3 Variation curve of disturbed value for pitching moment coefficient |
| 图选项 |
 |
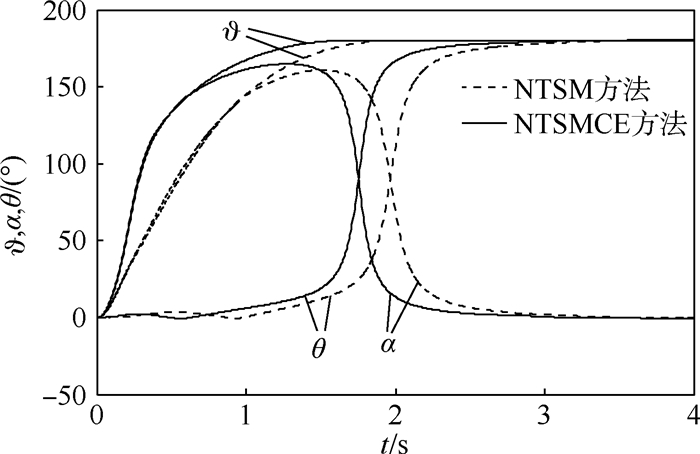| 图 4 ?、α与θ的变化曲线 Fig. 4 ?, α and θ |
| 图选项 |
 |
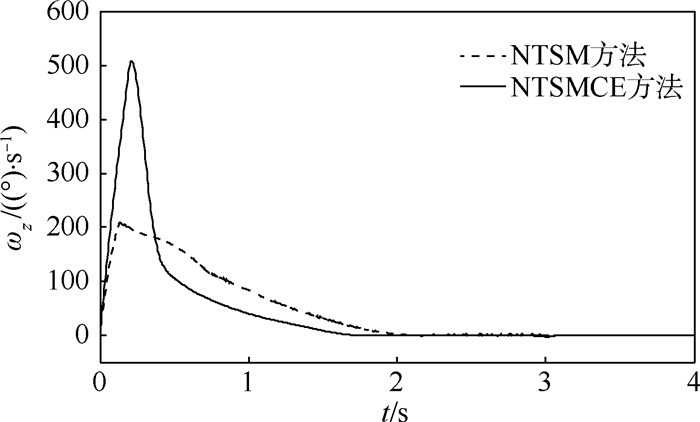| 图 5 俯仰角速度变化曲线 Fig. 5 Variation curves of pitch angular velocity |
| 图选项 |
 |
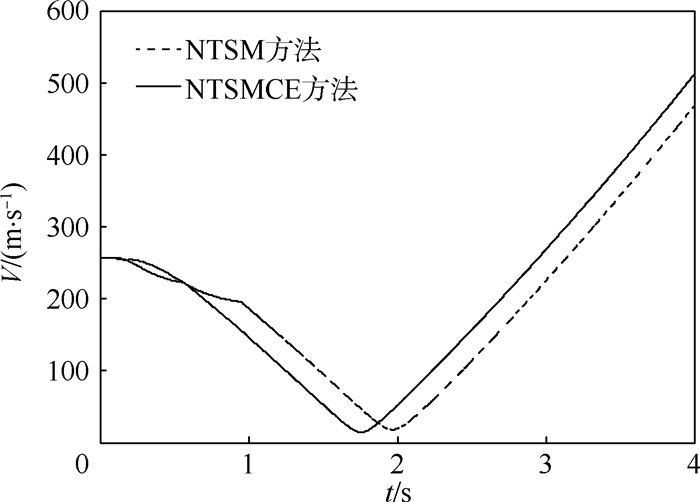| 图 6 速度变化曲线 Fig. 6 Variation curves of velocity |
| 图选项 |
图 7给出了导弹在2种方法下的法向过载的大小,NTSM方法下的过载出现了明显的抖振现象,这是由于该方法下的控制量的抖振造成的,如图 8所示。在小攻角飞行条件下,NTSM方法出现了类似于Bang-Bang控制的抖振现象(约3 s后),而NTSMCE方法下的控制量基本无抖振,即使在小攻角下亦是如此,这得益于ESO提供的抗扰动机制。ESO对系统不确定量的在线估计情况如图 9所示,初期的观测误差较大且变化剧烈,一方面是由于控制饱和导致ESO的观测出现偏差,另一方面在于ESO中的大增益导致观测误差大时观测量的导数较大,故观测值变化快。
 |
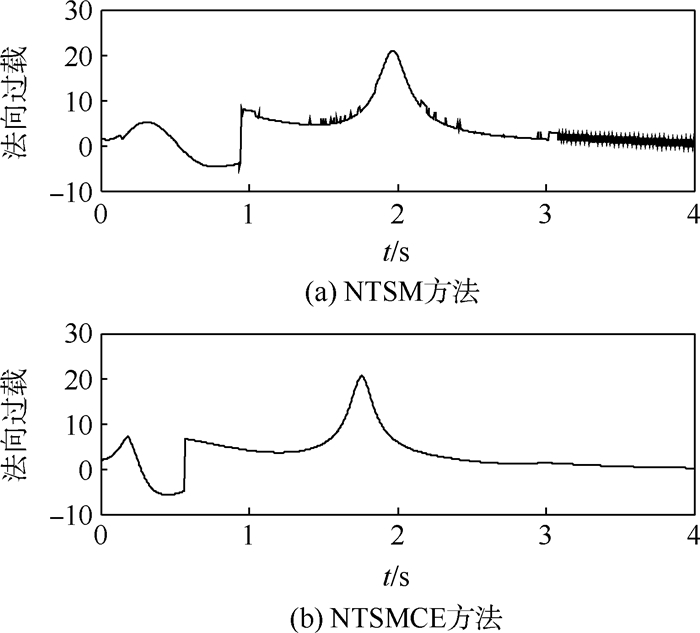| 图 7 法向过载变化曲线 Fig. 7 Variation curves of normal overload |
| 图选项 |
 |
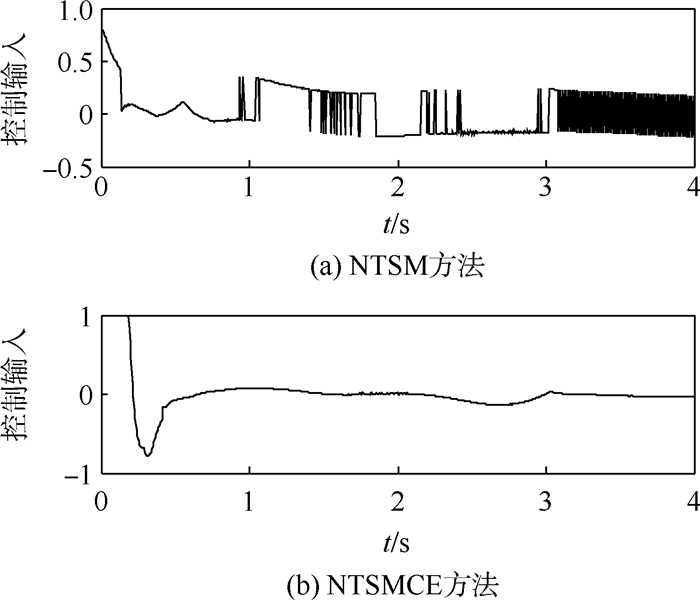| 图 8 控制输入变化曲线 Fig. 8 Variation curves of control input |
| 图选项 |
 |
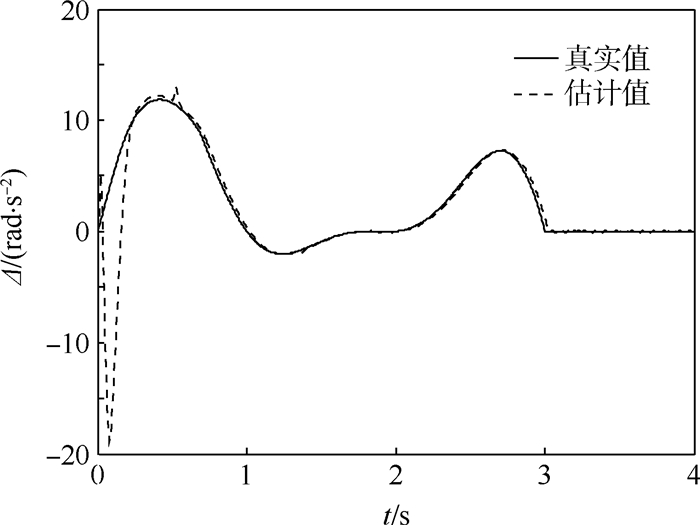| 图 9 不确定量的估计 Fig. 9 Estimation of uncertainty |
| 图选项 |
鉴于现阶段推力连续可调RCS较难实现,一种技术手段是采用脉宽脉频(Pulse Width Pulse Frequency,PWPF)调制技术[22]将连续控制量等效为离散控制量,得到常推力RCS工作状态的开关逻辑。图 10给出了采用经过PWPF调制的RCS仿真后的控制量输出结果,可近似复现控制律所需的变推力效果。
 |
| 图 10 经PWPF调制的控制输入变化曲线 Fig. 10 Variation curves of control input through PWPF modulation |
| 图选项 |
5 结 论本文在传统NTSM方法的基础上设计了一种改进控制方法,依靠姿态控制实现了空空导弹的大角度敏捷转弯。与原方法相比,复合滑模面的使用提高了系统的收敛速度,特别适用于空空导弹大角度机动这种初始状态远离平衡点的情况。而使用ESO对大攻角下气动不确定量进行在线估计与补偿,使导弹控制系统具备了干扰抑制能力,有效削弱了采用原方法时出现的严重的抖振现象。这样形成了一种基于复合滑模面与ESO的非奇异Terminal滑模(NTSMCE)控制方法,对该方法的稳定性分析证明了控制系统的有效时间收敛特性,最终通过与传统NTSM控制器的对比数值仿真验证了改进方法的有效性。本文所提方法对含有较严重未建模动力学的导弹控制系统的设计具有较好的工程应用价值。
参考文献
| [1] | THUKRAL A, INNOCENTI M.A sliding mode missile pitch autopilot synthesis for high angle of attack maneuvering[J].IEEE Transactions on Control Systems Technology,1998,6(3):359-371. |
| Click to display the text | |
| [2] | MCFARLAND M B, CALISE A J.Neural networks and adaptive nonlinear control of agile antiair missiles[J].Journal of Guidance,Control,and Dynamics,2000,23(3):547-553. |
| Click to display the text | |
| [3] | KANG S, KIM H J,LEE J I,et al.Roll-pitch-yaw integrated robust autopilot design for a high angle-of-attack missile[J].Journal of Guidance,Control,and Dynamics,2009,32(5):1622-1628. |
| Click to display the text | |
| [4] | RYU S M, WON D Y,LEE C H,et al.High angle of attack missile autopilot design by pole placement approach[C]//The 3rd International Symposium on Systems and Control in Aeronautics and Astronautics.Piscataway,NJ:IEEE Press,2010:535-539. |
| Click to display the text | |
| [5] | KIM K U, KANG S,KIM H J,et al.Realtime agile-turn guidance and control for an air-to-air missile[C]//AIAA Guidance,Navigation,and Control Conference.Reston:AIAA,2010. |
| Click to display the text | |
| [6] | RATLIFF R T, RAMSEY J A,WISE K A,et al.Advances in agile maneuvering for high performance munitions[C]//AIAA Guidance,Navigation,and Control Conference.Reston:AIAA,2009. |
| Click to display the text | |
| [7] | KIM Y, KIM B S,PARK J H.Aerodynamic pitch control design for reversal of missile's flight direction[J].Proceedings of the Institution of Mechanical Engineers,Part G:Journal of Aerospace Engineering,2014,228(9):1519-1527. |
| Click to display the text | |
| [8] | KIM Y,KIM B S. Pitch autopilot design for agile missiles with uncertain aerodynamic coefficients[J].IEEE Transactions on Aerospace and Electronic Systems,2013,49(2):907-914. |
| Click to display the text | |
| [9] | YANG L, YANG J Y.Nonsingular fast terminal sliding-mode control for nonlinear dynamical systems[J].International Journal of Robust and Nonlinear Control,2011,21(16):1865-1879. |
| Click to display the text | |
| [10] | 李升波,李克强, 王建强,等.非奇异快速的终端滑模控制方法[J].信息与控制,2009,38(1):1-8. LI S B,LI K Q,WANG J Q,et al.Nonsingular and fast terminal sliding mode control method[J].Information and Control,2009,38(1):1-8(in Chinese). |
| Cited By in Cnki (37) | Click to display the text | |
| [11] | 胡庆雷,姜博严, 石忠.基于新型终端滑模的航天器执行器故障容错控制[J].航空学报,2013,34(1):1-9. HU Q L,JIANG B Y,SHI Z.Novel terminal sliding mode based fault tolerant attitude control for spacecraft under actuator faults[J].Acta Aeronautica et Astronautica Sinica,2013,34(1):1-9(in Chinese). |
| Cited By in Cnki (8) | Click to display the text | |
| [12] | LEE C H, KIM T H,TAHK M J.Agile missile autopilot design using nonlinear backstepping control with time-delay adaptation[J].Transactions of the Japan Society for Aeronautical and Space Sciences,2014,57(1):9-20. |
| Click to display the text | |
| [13] | WISE K A, BROY D J.Agile missile dynamics and control[J].Journal of Guidance,Control,and Dynamics,1998,21(3):441-449. |
| Click to display the text | |
| [14] | SIMON J M, BLAKE W B.Missile Datcom:High angle of attack capability[C]//The 24th Atmospheric Flight Mechanics Conference.Reston:AIAA,1999. |
| Click to display the text | |
| [15] | ABNEY E J, MCDANIEL M A.High angle of attack aerodynamic predictions using Missile Datcom[C]//The 23rd AIAA Applied Aerodynamics Conference.Reston:AIAA,2005,2:1111-1129. |
| Click to display the text | |
| [16] | HAN J Q. From PID to active disturbance rejection control[J].IEEE Transactions on Industrial Electronics,2009,31(3):900-906. |
| Click to display the text | |
| [17] | 马悦悦,唐胜景, 郭杰,等.基于自抗扰与模糊逻辑的大攻角控制系统设计[J].系统工程与电子技术,2013,35(8):1711-1716. MA Y Y,TANG S J,GUO J,et al.High angle of attack control system design based on ADRC and fuzzy logic[J].Systems Engineering and Electronics,2013,35(8):1711-1716(in Chinese). |
| Cited By in Cnki (10) | |
| [18] | KORI D K, KOLHE J P,TALOLE S E.Extended state observer based robust control of wing rock motion[J].Aerospace Science and Technology,2014,33(1):107-117. |
| Click to display the text | |
| [19] | GUO B Z, ZHAO Z L.On the convergence of an extended state observer for nonlinear systems with uncertainty[J].Systems & Control Letters,2011,60(6):420-430. |
| Click to display the text | |
| [20] | FENG Y, YU X H,MAN Z H.Non-singular terminal sliding mode control of rigid manipulators[J].Automatica,2002,38(12):2159-2167. |
| Click to display the text | |
| [21] | 张巍巍,王京. 基于指数趋近律的非奇异Terminal滑模控制[J].控制与决策,2012,27(6):909-913. ZHANG W W,WANG J.Nonsingular terminal sliding model control based on exponential reaching law[J].Control and Decision, 2012,27(6):909-913(in Chinese). |
| Cited By in Cnki (17) | Click to display the text | |
| [22] | ANTHONY T C, WIE B,CARROLL S.Pulse-modulated control synthesis for a flexible spacecraft[J].Journal of Guidance,Control,and Dynamics,1990,13(6):1014-1022. |
| Click to display the text |
