弹射座椅的程序控制技术先后经历了单态程序控制、双态程序控制和多模态程序控制3个主要发展阶段[1]。现役第三代弹射座椅主要采用双态程序控制,根据弹射启动时飞机的速度和高度划分大约3~5种弹射模式,以控制开伞时间[2]。双态程序控制可以有效减小中低速弹射情况下的射伞延迟时间,从而改善低空救生性能。而当弹射高度较高时,通过高度临界值增加额外的射伞延迟时间,以使飞行员尽快离开高空低温缺氧等不利环境,避免受到高空不利因素造成的生理损伤。美国空军ACES-Ⅱ型座椅[3, 4]、美国海军NACES型座椅[5, 6]、俄罗斯K36系列座椅[7]均采用双态程序控制技术,分别划分了3种、5种和7种工作模式,救生成功率基本达到100%,是最具代表性的现役第三代弹射座椅。
为了尽可能缩短中低空弹射开伞时间,马丁-贝克公司在MK16A型座椅的程序控制器中将低空减速模式的开伞时间进一步细分为254种[8],以满足开伞动载不超过人体生理耐限要求的前提下,尽快展开救生伞。该方法虽然暂时解决了问题,但也暴露出以模式划分为基本原理的程序控制规律设计的致命缺陷。即为了保证控制参数的全局最优性,模式划分需足够精细,当状态参数较多时,该方法很难实现。
随着第四代战斗机的逐渐服役,低空不利姿态条件下的安全救生能力成为第四代弹射座椅的首要任务和基本目标[9]。其关键技术之一在于姿态控制,即弹射座椅出舱后能够根据自身感受的状态参数,纠正运动姿态使弹射轨迹能够向着有利于救生成功率增加的方向发展。美国CREST计划[10]、第四代弹射座椅验证计划[11]以及Aerojet公司的多轴针栓姿态控制(MAXPAC)[12]均开展了完全推力矢量控制在弹射座椅姿态调整方面的应用研究。但由于关键技术不成熟,尚处于工程验证阶段。美国和俄罗斯联合研制的K36Л-3.5型座椅[13],通过安装在头靠伞箱后部的2个侧向姿态调整火箭,实现对横滚方向的纠正,有效改善了弹射座椅低空横滚姿态下的救生性能,且技术成熟,是目前切实可行的一种弹射座椅改进方案。
针对不利姿态调整装置的程序控制方案,仍然采用开环控制规律算法。即根据弹射启动瞬时的飞行状态参数,确定姿态调整装置的工作参数。目前对于控制规律算法的设计思路,仍然是利用模式划分的基本方法,将弹射状态划分成对应的模式,不同模式采用不同的控制参数。如K36Л-3.5型座椅根据弹射启动时的不利姿态参数,划分了50种工作模式[14]。国内封文春等[15, 16],也展开了不利姿态下多模态控制规律的初步研究。
但是,基于模式划分的控制规律设计存在很大的局限性。随着状态参数的增加,在多维空间内进行模式划分变得异常复杂,各参数的临界值也难以确定。此外,每种工作模式采用单一的控制参数,很难保证控制规律的最优性。本文提出了一种基于最优化理论模型和神经网络模型的弹射座椅控制规律设计方法,并以单滚转不利姿态控制为例,进行了方法的设计验证。
1 设计方案弹射座椅的弹射过程是一个非常复杂的过程,弹射启动时存在大量的状态参数,各参数均会对弹射姿态轨迹产生各种程度的影响。通过某些姿态调整装置和相应控制规律算法,可以纠正人椅系统的空间运动向着有利的方向发展。而控制规律算法需要满足不同弹射状态下,控制参数的最优性。本文提出的控制规律设计方案流程如图 1所示。
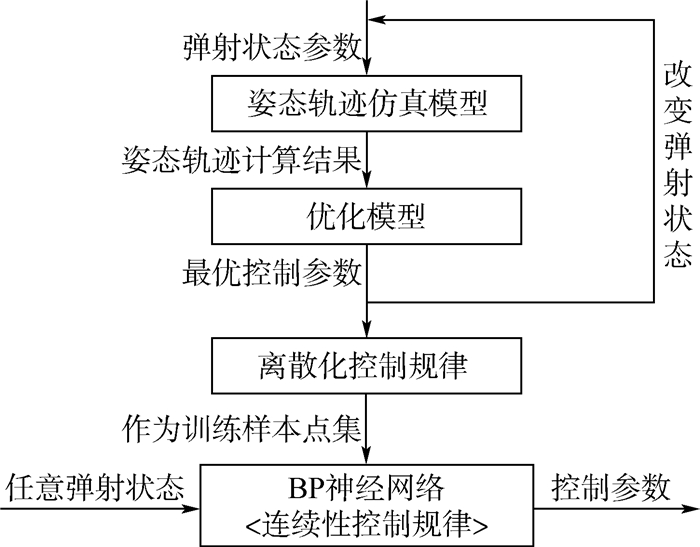 |
| 图 1 控制规律设计方案 Fig. 1 Design program for control law |
| 图选项 |
通过弹射座椅姿态轨迹仿真计算程序和最优化模型,必然可以寻求到某固定弹射状态下所对应的最优控制参数值,使弹射座椅满足最佳救生性能指标。在弹射状态参数的全局范围内重复如上寻优过程,即可得到包含足够样本点数据的离散化控制规律点集。利用该点集作为样本数据,设计神经网络模型并进行训练,即可完成控制规律算法的连续非线性映射过程。训练收敛后的神经网络数值模型,即为最终的控制规律算法。对于任意的弹射启动状态参数,可由此算法计算得到相应的控制参数值。
2 弹射姿态轨迹计算2.1 数学模型在弹射救生仿真研究中,通常将弹射过程划分为弹射出舱、空中自由飞、救生伞拉直、救生伞充气张满和稳定降落5个阶段。由于每个阶段约束和受力不同,需分别建立相应的动力学模型。具体坐标系定义和数学模型可参见文献[17, 18, 19, 20]。由于不利姿态下弹射姿态轨迹的调整控制主要作用于人空中自由飞阶段,故仅列出该阶段人椅系统在体轴坐标系下的六自由度动力学方程,如式(1)和式(2)所示:
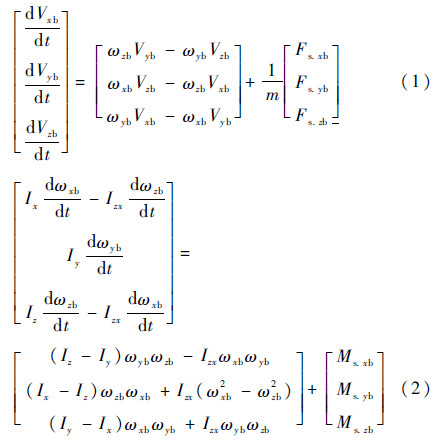
式中:[Vxb Vyb Vzb]为人椅系统航迹速度在体坐标系上的分量,航迹速度即对地绝对速度,当忽略风速时,航迹速度等于对空速度;[ωxb ωyb ωzb]为人椅系统旋转角速度在体坐标系上的分量;m为人椅系统质量;[Fs.xb Fs.yb Fs.zb]和[Ms.xb Ms.yb Ms.zb]分别为人椅系统所受合力和合力矩在体坐标系的分量;Ix、Iy和Iz为惯性矩;Izx为惯性积,由于假设人椅系统具有纵向对称面,故Ixy=Iyz=0。当安装了不利姿态调整装置,如横滚姿态火箭时,只需根据推力情况及火箭包安装位置,附加相应的力及力矩项,即可计算采用姿态调整后人椅系统的运动轨迹。此外,在高速弹射过程中,气动力是人椅系统所受到的主要外力,由于人椅系统外形不规则,气动力系数也极为复杂。本文在计算过程中采用风洞试验所得相关数据,可以确保计算的准确性。
2.2 数值仿真模型以MSC.EASY5系统仿真软件为基础平台,根据弹射座椅的功能及结构特点,建立通用的弹射座椅模型库。以各阶段运动特点及数学模型为基础,搭建具体阶段的数值仿真模型。设计规范的外部数据接口,方便数据的输入和输出。由于固定弹射状态下的寻优过程需要计算不同的控制参数,而完整的控制规律又需要在弹射状态的全局范围内进行重复计算,本文通过批处理命令的方式,完成计算过程的自动化。仿真模型示意图如图 2所示。
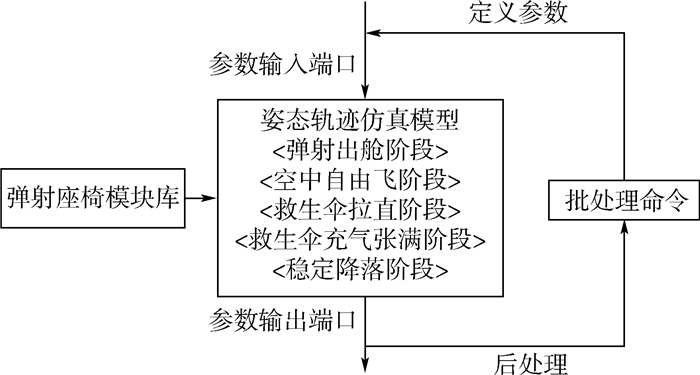 |
| 图 2 仿真模型示意图 Fig. 2 Simulation model chart |
| 图选项 |
2.3 模型验证为了验证模型的准确性,将数值仿真计算结果与地面火箭滑车弹射试验结果进行对比。地面弹射试验的弹射速度为 0 km·h-1,由于试验缺乏风速数据,故仿真计算作无风处理。仿真计算所有数据参数与试验情况保持一致。人椅系统沿铅垂方向速度(Vz)和轨迹高度(h)的仿真与试验对比曲线如图 3所示。
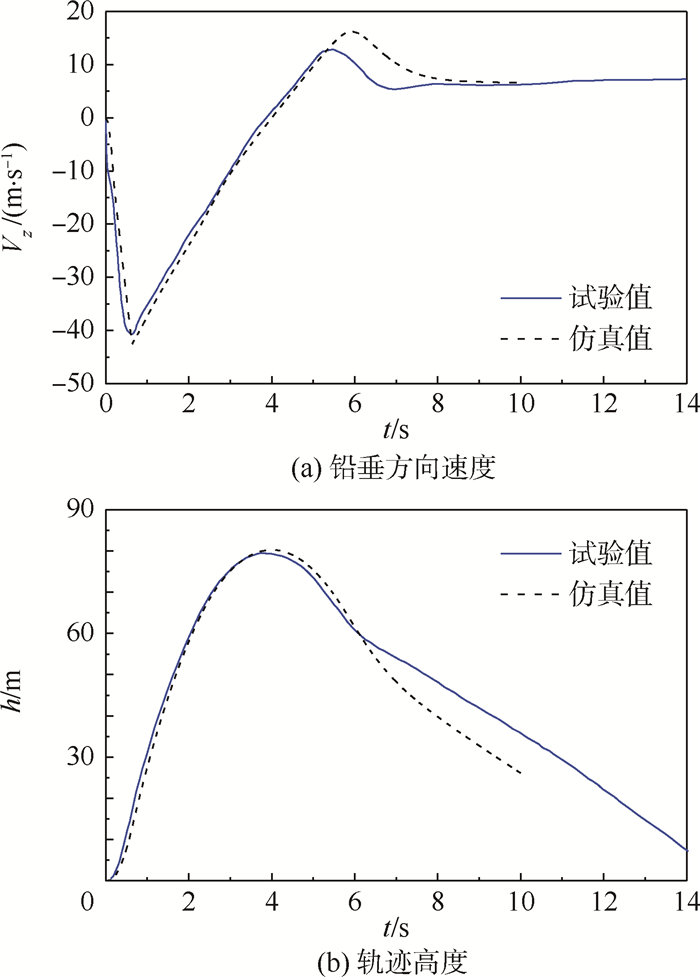 |
| 图 3 0 km·h-1弹射仿真与试验结果对比 Fig. 3 Comparison of simulation and experimental results at 0 km·h-1 ejection |
| 图选项 |
由图 3可知,仿真与试验结果曲线变化趋势一致,纵向速度极值与轨迹最高点吻合较好,主要误差出现在弹射启动后6 s左右,而最终的稳定降落速度又趋于重合。分析误差产生的原因主要有两点:①误差产生时刻处于救生伞充气张满阶段,该阶段过程非常复杂,数学模型简化较多,必然导致一定程度的偏差;②通过分析其他试验数据可知,6 s左右的时间出现了瞬时阵风的影响,而仿真计算按无风情况处理,由此也会产生偏差。综合而言,仿真结果与试验结果吻合较好,所建立数学模型精度较高,满足仿真分析的要求。
3 控制规律设计3.1 控制方案当飞机处于低空滚转姿态下进行弹射救生时,弹射座椅的救生性能会严重下降。因此,对于弹射座椅横滚姿态的纠正尤其重要。本文即以单滚转不利姿态控制为例,进行控制规律设计方法的设计验证。
所采用控制方案包括两方面:①在头靠伞箱后部增设一对横滚姿态调整火箭,如图 4所示,通过滚转力矩对滚转姿态进行纠正;②增加主火箭包通断开关,当横滚姿态调整火箭无法产生有效纠正时,切断主火箭包,避免由主火箭推力引起的救生高度损失。
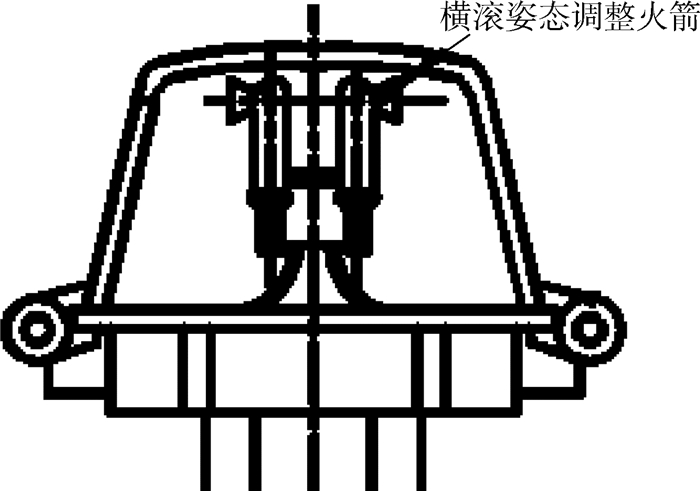 |
| 图 4 横滚姿态调整火箭安装 Fig. 4 Installation of roll adjusting rockets |
| 图选项 |
为了与K36Л-3.5型座椅性能参数以及封文春等[15, 16]提出的多模态控制规律结果进行有效对比,横滚姿态调整火箭总冲以及救生伞开伞时间维持不变。最终确定的控制参数为左右横滚火箭点火时间间隔与主火箭包点火通断开关。通过分析可知,前者主要在于不同弹射状态下的最优取值问题,而后者则在于临界参数值的确定,这恰恰是模式划分控制规律设计方法的主要局限。
3.2 优化计算模型由图 1控制规律设计方案可知,针对每一个固定的弹射状态,需要通过优化计算模型确定最优的控制参数值。对于该优化问题,决策变量即为控制参数,分别是两侧滚转姿态火箭点火时间间隔和主火箭包通断开关。约束条件仅考虑决策变量的取值范围。考虑到工程实际应用的控制精度,滚转姿态火箭延迟点火时间间隔精度定义为0.1 s,且必然小于救生伞开伞时间,大于等于救生伞开伞时间意味着单侧火箭并没有实际作用。主火箭包通断开关取值定义为0或1,0表示切断,1表示正常工作。对于目标函数的设定,由于并没有改变开伞时间,故认为开伞动载仍然满足人体生理耐限基本要求。以最低安全救生高度为基础,将目标函数和优化目标定义为救生伞张满时的轨迹高度最高,即认为弹射座椅具有最佳的救生性能。综上,最终优化问题的数学描述如式(3)所示。

式中:fh为救生伞张满时的轨迹高度;td为滚转火箭延迟点火时间间隔;sr为主火箭包切断开关;tp为救生伞开伞时间。针对优化问题的具体特点,自定义优化算法计算流程如图 5所示。按照图 5所示的计算流程,即可确定某固定弹射状态下的最优控制参数值。利用批处理命令的方法,共批量计算了164组弹射状态参数所对应的最优控制参数,即离散化的控制规律点集。
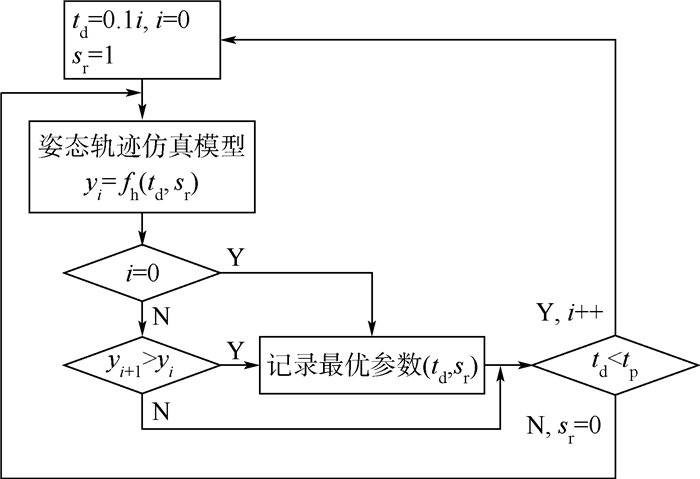 |
| 图 5 优化算法计算流程 Fig. 5 Flowchart of optimization algorithm |
| 图选项 |
3.3 神经网络模型通过轨迹姿态计算模型和优化计算模型得到的最优控制参数为离散化的空间样本点集,为了获得状态参数到控制参数的连续非线性映射关系,并且保证一定的容错性、自适应性,本文采用神经网络模型的方法。
由第3.1节分析可知,对滚转姿态火箭延迟点火时间的控制类似函数逼近或高维空间插值问题,而对主火箭包切断开关的控制更接近模式识别问题。为了使神经网络具有更强的适应性及容错性,有效减小网络规模,并且在最终的算法实现时减少计算量,故将上述问题分解为2个神经网络分别实现。网络1负责完成主火箭包通断开关的模式识别,网络2则负责完成滚转火箭延迟点火时间的非线性映射。当网络1判断得到的数值为0,即主火箭包切断,则不再需要对网络2进行处理计算。
在人工神经网络的实际应用中,基于误差反向传播算法的人工神经网络,即BP网络被广泛应用于函数逼近、模式识别与分类、数据压缩等,具有很好的适应性等特性[21]。本文作者也在前期的研究中,利用BP神经网络建立了弹射过载与弹射速度的映射关系[22, 23],验证了神经网络模型在弹射救生领域应用的可行性。故本文仍采用BP网络进行仿真设计计算。
网络1及网络2采用相同的神经网络结构,网络层数为2层。第1层为输入层神经元,神经元数量为50。第2层为输出层神经元,神经元数量为1。输入向量为二维向量,分别对应弹射速度及滚转姿态角。输出向量为一维,网络1输出主火箭包通断开关状态,网络2输出滚转姿态火箭延迟点火时间。所对应的算法函数如式(4)所示,具体神经网络结构如图 6所示。
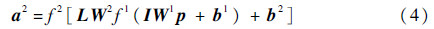
式中:上标1和2表示网络层数;p为输入向量;IW为输入层权值矩阵;LW为网络层权值矩阵;b为阈值向量;n为加权和向量;a为输出向量;f为传递函数,本文选用S型传递函数,其表达式为

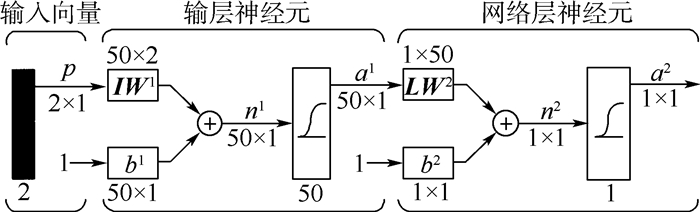 |
| 图 6 神经元网络结构 Fig. 6 Structure of neural network |
| 图选项 |
利用第3.2节计算得到的离散控制规律样本点集对神经网络进行训练。由于功能不同,根据相关经验,神经网络1采用RPROP训练算法,神经网络2采用LM算法。训练完成之后,即得到神经网络的所有权值和阈值矩阵。将其代入式(4)中,即可得到最终的控制规律算法函数。利用该算法,可根据任意的弹射状态参数构成输入向量,从而得到相应的输出向量,即控制参数值。神经元网络处理流程如图 7所示。
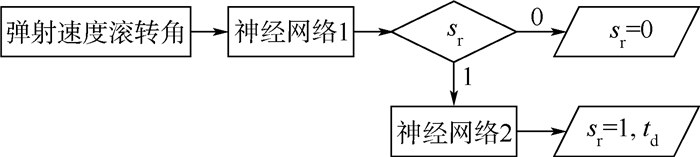 |
| 图 7 神经元网络处理流程 Fig. 7 Processing flowchart of neural networks |
| 图选项 |
对完成训练的神经网络进行相应测试,以验证其精度,共进行了3方面的测试内容。
测试1 神经网络对样本点集的吻合度为100%。
测试2 任意选取低、中、高弹射速度,不同滚转角时的非样本点弹射状态进行测试,对比神经网络的输出结果与另外通过仿真计算得到的最优控制参数值。网络1的准确度为100%,即对主火箭包通断开关的判断无误差。网络2的处理结果在90%左右的状态时无误差,10%左右的弹射状态下会出现0.1 s的误差。该精度完全满足工程需要,若想进一步提高精度,可适当改进神经元网络结构,增加网络层数和神经元个数。
测试3 当传感器出现故障从而得到异常的弹射状态参数值时,神经元网络仍然可以得到比较准确的控制参数值。
综上可知,通过神经元网络处理得到的控制规律算法,在全局范围内逼近理论最优解,并且具有很强的自适应性和容错能力。
4 结果分析4.1 与多模态控制规律对比使用完全相同的轨迹姿态仿真模型与计算参数,分别对比不加姿态控制、采用本文设计的控制规律与采用多模态控制规律时,不同弹射状态下的轨迹曲线如图 8与图 9所示。受篇幅所限,只列出0 km·h-1弹射和400 km·h-1弹射时,滚转角分别为45°、90°、120°和180°对应的结果。
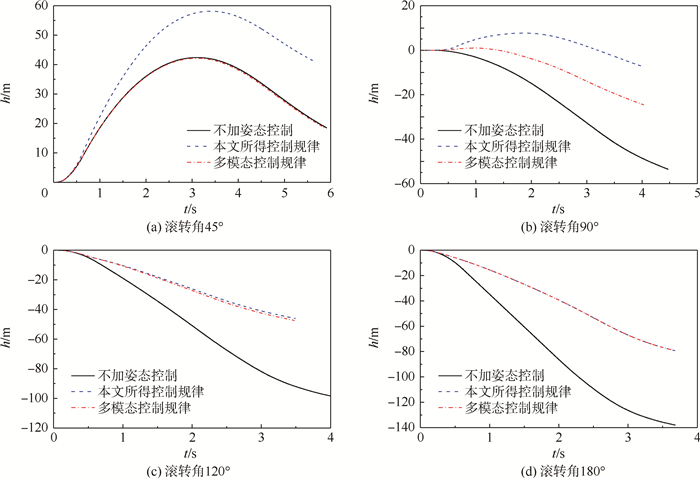 |
| 图 8 0 km·h-1弹射不同控制规律下轨迹高度对比 Fig. 8 Comparison of ejection height under different control law at 0 km·h-1 |
| 图选项 |
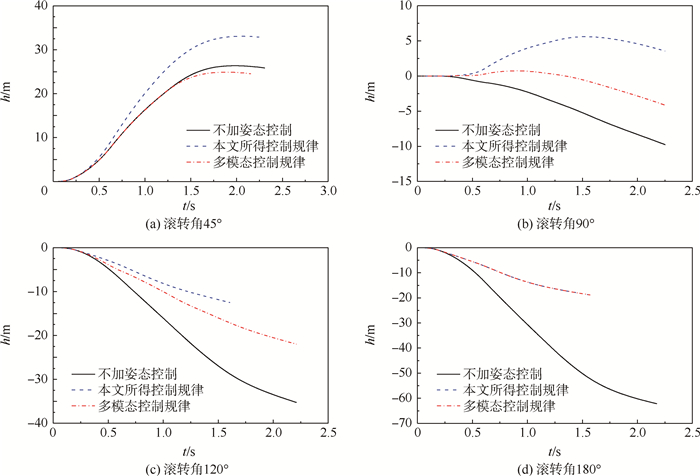 |
| 图 9 400 km·h-1弹射不同控制规律下轨迹高度对比 Fig. 9 Comparison of ejection height under different control law at 400 km·h-1 |
| 图选项 |
当滚转角较小,例如45°滚转时,如图 8(a)和图 9(a)所示。此时由于多模态控制规律中滚转姿态火箭延迟点火时间参数不合理,导致弹射座椅滚转姿态纠正不足或纠正过头,从而使得弹射座椅轨迹高度并没有增加甚至反而降低。但采用本文控制规律后,弹射轨迹高度有了明显的提高,说明对横滚姿态纠正效果显著。
当滚转角为90°时,如图 8(b)和图 9(b)所示,此时多模态控制对轨迹姿态调整也起到了一定的作用。但与本文控制规律相比,控制效果仍然不足。说明本文控制规律所得控制参数对于姿态轨迹的调整,具有更优性。
当滚转角为120°,即滚转角较大时,此时控制规律的关键在于判断主火箭包是否切断。当滚转姿态调整火箭已经无法及时有效地将滚转角调整为正时,必需切断主火箭包开包,从而避免由主火箭引起的安全高度损失。由图 8(c)可知,在0 km·h-1弹射时,2种控制规律给出的主火箭包控制参数相同,即主火箭包正常工作,但姿态调整火箭参数略有不同,故本文控制规律结果稍优于多模态控制。但是在400 km·h-1弹射,如图 9(c)所示,此时多模态控制规律给出的控制参数为主火箭包正常工作,而本文控制规律得出的结果则为切断主火箭包。由轨迹曲线可知,本文控制规律给出的判断结果显然更为准确。
当滚转角为180°,如图 8(d)和图 9(d)所示,2种控制规律给出的控制参数完全一致,故曲线重合。
综上可知,采用滚转姿态控制方案,配合相应的控制规律算法,可以起到轨迹高度的纠正,从而提高弹射座椅的救生性能。而本文得出的控制规律算法对轨迹高度的纠正效果,显然更优于多模态控制规律。不论是在滚转姿态火箭延迟点火时间参数的最优性方面,还是在主火箭包是否切断的临界值判断方面,本文控制规律算法都具有更佳的性能。
4.2 与K36Л-3.5性能对比根据文献[14]提供的资料,将本文控制规律的计算结果与K36Л-3.5型座椅的性能进行对比,如表 1所示。
表 1 本文控制规律计算结果与K36Л-3.5型座椅[14]最低安全救生高度的对比 Table 1 Comparison of minimum lifesaving height result calculated by proposed control law and with K36Л-3.5 ejection seat[14]
| 弹射速度/(km·h-1) | 滚转角0° | 滚转角60° | 滚转角120° | 滚转角180° | ||||
| MLHK/m | MLHa/m | MLHK/m | MLHa/m | MLHK/m | MLHa/m | MLHK/m | MLHa/m | |
| 150 | 0 | 0 | 0 | 0 | 37 | 38.14 | 46 | 53.14 |
| 250 | 0 | 0 | 0 | 0 | 29 | 25.76 | 36 | 35.08 |
| 400 | 0 | 0 | 9 | 0 | 38 | 14.55 | 62 | 21.62 |
| 600 | 0 | 0 | 35 | 0 | 62 | 16.39 | 66 | 20.82 |
| 注:MLH—最低安全救生高度,即救生伞能够达到张满状态飞机应具有的最低飞行高度;带上标K的为K36Л-3.5型座椅数据;带上标a的为采用本文控制规律得到的数据。 | ||||||||
表选项
从表 1中数据可知,在弹射速度为150 km·h-1,且滚转角为120°和180°时,本文结果略高于K36Л-3.5的最低安全救生高度,但相差不大。其余弹射状态时,本文结果均优于K36Л-3.5。特别是在400 km·h-1和600 km·h-1的中高速弹射状态下,采用本文控制规律对最低安全救生高度的改善要远远优于K36Л-3.5,最大相差50 m左右。
4.3 与国军标要求对比国军际GJB-1800A-2007“弹射座椅型乘员应急离机救生系统通用规范”[24]规定了120种弹射条件所要求的最低安全救生高度。由于本文暂时只考虑了单滚转的情况,且平飞状态均能够满足救生性能要求,文中也不作比较,故只列出12种弹射条件,结果如表 2所示。
表 2 本文控制规律计算结果与GJB-1800A-2007[24]最低安全救生高度的对比 Table 2 Comparison of minimum lifesaving height result calculated by proposed control law and with GJB-1800A-2007[24]
| 弹射速度/(km·h-1) | 滚转角45° | 滚转角90° | 滚转角180° | ||||||
| MLHG/m | MLHa/m | MLHb/m | MLHG/m | MLHa/m | MLHb/m | MLHG/m | MLHa/m | MLHb/m | |
| 0 | 0 | 0 | 0 | 6 | 7.22 | 53.67 | 52 | 83.4 | 123.77 |
| 250 | 0 | 0 | 0 | 3 | 0 | 20.13 | 37 | 35.08 | 85.11 |
| 450 | 0 | 0 | 0 | 3 | 0 | 9.79 | 27 | 18.87 | 62.01 |
| 1 100 | 0 | 0 | 0 | 12 | 0 | 32.22 | 43 | 42.87 | 92.7 |
| 注:带上标G的为国军标对应参数;带上标b的为多模态控制规律计算结果。 | |||||||||
表选项
从表 2中数据可以看出,本文控制规律只有在弹射速度为0 km·h-1、滚转角为90°和180°弹射时不满足国军标最低安全救生高度的要求,其余情况均能满足。由于控制参数基本接近理论最优值,故只能通过改进控制方案或进一步缩短开伞时间,才有可能达到国军标的要求。而多模态控制规律只有在滚转角为45°时满足要求,在90°和180°所有弹射速度下均不满足国军标要求。
5 结 论1) 本文提出的弹射座椅控制规律设计方法切实可行,设计流程简单明确,结果算法便于实现。
2) 利用BP神经网络模型可以很好地处理控制规律算法中的连续非线性映射问题和模式识别问题,最终结果非常逼近理论最优值,且具有一定的容错性。
3) 以单滚转不利姿态弹射为例,进行了控制规律的设计验证。通过与多模态控制结果、K36Л-3.5型座椅性能参数以及国军标对最低安全救生高度的要求对比可知,本文得到的控制规律算法可以达到非常优异的控制效果。
4) 需要进一步研究存在俯冲、下沉等其他不利姿态时的控制方案及控制规律,同时对救生伞开伞时间展开优化计算。
参考文献
| [1] | 徐世坤. 弹射救生程序控制的发展[J].航空科学技术,1994(4):14-17. XU S K.The development of control law for escape system[J].Aeronautical Science and Technology,1994(4):14-17(in Chinese). |
| Cited By in Cnki (3) | |
| [2] | 周方. 提高低空不利姿态下救生成功率的措施[J].航空科学技术,1998(6):18-20. ZHOU F.Measures to improve the successfulness of ejection-escaping in the low altitude positions[J].Aeronautical Science and Technology,1998(6):18-20(in Chinese). |
| Cited By in Cnki (4) | |
| [3] | ROSS D A, CULHANE D,FERRELL S.Digital recovery sequencer-ACES ejection seats[C]//Proceedings of the 42nd Annual SAFE Symposium.Creswell,OR:SAFE,2004:305-312. |
| Click to display the text | |
| [4] | CALKINS R B. ACES Ⅱ ejection seat improvements[C]//Proceedings of the 34th Annual SAFE Symposium.Creswell,OR:SAFE,1996:86-91. |
| [5] | MILLER B A. NACES-The program and the seat[C]//Proceedings of the 24th Annual SAFE Symposium.Creswell,OR:SAFE,1987:134-139. |
| Click to display the text | |
| [6] | D'AULERIO L O U, YOST P.Navy aircrew common ejection seat(NACES)program summary[J].SAFE Journal,1991,21:25-29. |
| Click to display the text | |
| [7] | 李锐. K36Л-3.5弹射座椅工作模式的探索[J].中航救生,2004,26(3):1-6. LI R.Exploration of K36Л-3.5 ejection seat operation mode[J].China Aeronautical and Astronautical Life-Support,2004,26(3):1-6(in Chinese). |
| [8] | MCCAULEY D, SUMMER M H,WOOD D,et al.Future advanced sequencer technology(FAST)[C]//Proceedings of the 39th Annual SAFE Symposium.Creswell,OR:SAFE,2001:95-110. |
| Click to display the text | |
| [9] | 李锐. 第四代弹射座椅的关键技术[J].航空科学技术,1995(4):14-17. LI R.The crucial technology of the 4th generation ejection seat[J].Aeronautical Science and Technology,1995(4):14-17(in Chinese). |
| Cited By in Cnki (2) | Click to display the text | |
| [10] | SWANSON D E, HERNDON G F.CREST system design[C]//Proceedings of the 24th Annual SAFE Symposium.Creswell,OR:SAFE,1987:27-31. |
| [11] | WHEELER C M, NIEDZIELSKI P,BARNETTE B,et al.Fourth generation escape system technology demonstration pintle nozzle controllable propulsion system[C]//Proceedings of the 36th Annual SAFE Symposium.Creswell,OR:SAFE,1998:133-141. |
| [12] | CARLSON R, LUCAS C,TAM B.Multi-axis pintle attitude control(MAXPAC)device for ACES Ⅱ seat stabilization[C]//Proceedings of the 33rd Annual SAFE Symposium.Creswell,OR:SAFE,1995:225-232. |
| [13] | EVERS S. Russian ejection seat may fly in U.S.JAST[J].Aviation Week and Space Technology,1995,143(8):64-65. |
| [14] | 李锐. K36Л-3.5弹射座椅性能分析[J].中航救生,2005,28(1):1-6. LI R.Performance analysis of K36Л-3.5 ejection seats[J].China Aeronautical and Astronautical Life-Support,2005,28(1):1-6(in Chinese). |
| [15] | 封文春,林贵平. 弹射座椅多参数多模态控制仿真分析[J].系统仿真学报,2007,19(10):2283-2292. FENG W C,LIN G P.Multi-parameter and multi-mode control simulation analyses of ejection seat[J].Journal of System Simulation,2007,19(10):2283-2292(in Chinese). |
| Cited By in Cnki (5) | Click to display the text | |
| [16] | 封文春. 弹射座椅多参数多模态控制规律设计与仿真[D].北京:北京航空航天大学,2006:90-113. FENG W C.The multi-parameter and multi-mode control law design and simulation of ejection seat[D].Beijing:Beihang University, 2006:90-113(in Chinese). |
| [17] | 张汉镔. 飞行器安全救生[M].北京:北京航空航天大学出版社,1990:104-120. ZHANG H B.Aircraft escape system[M].Beijing:Beihang University Press,1990:104-120(in Chinese). |
| [18] | 郁嘉,毛晓东, 林贵平,等.风对弹射座椅救生性能的影响[J].航空学报,2013,34(4):727-740. YU J,MAO X D,LIN G P,et al.Impact of wind on ejection seat escape performance[J].Acta Aeronautica et Astronautica Sinica,2013,34(4):727-740(in Chinese). |
| Cited By in Cnki (1) | Click to display the text | |
| [19] | 郁嘉,林贵平, 毛晓东.弹射救生数值仿真及不利姿态下救生性能分析[J].航空学报,2010,31(10):1927-1932. YU J,LIN G P,MAO X D.Numerical simulation of ejection seat and analysis of performance under adverse attitudes[J].Acta Aeronautica et Astronautica Sinica,2010,31(10):1927-1932(in Chinese). |
| Cited By in Cnki (3) | Click to display the text | |
| [20] | 郁嘉,林贵平, 吴铭.弹射座椅减速性能的数值仿真计算[J].航空学报,2006,27(6):1033-1038. YU J,LIN G P,WU M.Numerical simulation of deceleration performance for ejection seat[J].Acta Aeronautica et Astronautica Sinica,2006,27(6):1033-1038(in Chinese). |
| Cited By in Cnki (7) | Click to display the text | |
| [21] | 周开利,康耀红. 神经网络模型及其MATLAB仿真程序设计[M].北京:清华大学出版社,2005:121-148. ZHOU K L,KANG Y H.Neural network model and MATLAB simulating program design[M].Beijing:Tsinghua University Press,2005:121-148(in Chinese). |
| [22] | 毛晓东,郁嘉, 林贵平.过载与弹射速度关系研究及神经网络实现[J].航空学报,2010,31(10):1907-1913. MAO X D,YU J,LIN G P.Study of relationship between load factor and ejection velocity and its neural network implementation[J].Acta Aeronautica et Astronautica Sinica,2010,31(10):1907-1913(in Chinese). |
| Cited By in Cnki (2) | Click to display the text | |
| [23] | MAO X D, YU J,LIN G P.Predicting ejection velocity of ejection seat via back propagation neural network[J].Journal of Aircraft,2011,48(2):668-672. |
| Click to display the text | |
| [24] | 中华人民共和国国防科学技术工业委员会. 弹射座椅型乘员应急离机救生系统通用规范:GJB-1800A-2007[S].北京:中国航空工业集团公司, 2007. The Commission of Science,Technology and Industry for National Defense of the PRC.General specification for ejection seat type of aircrew emergency escape system:GJB-1800A-2007[S].Beijing:Aviation Industry Corporation of China,2007(in Chinese). |
| Cited By in Cnki |
