框架伺服系统是DGMSCMG的重要组成部分,其角速率的稳定性及精度直接决定着陀螺的输出力矩的稳定性和精度[4]。在DGMSCMG输出力矩时,陀螺效应引起的内、外框架之间非线性强耦合力矩将直接影响整个陀螺系统的稳定性和精度。为了减小框架伺服系统的体积和质量,DGMSCMG一般要加入减速机构对力矩进行放大。由于谐波传动具有精度高、承载力大、效率高、体积小和质量轻等优点,特别是其可以在真空和介质辐射的条件下进行工作,因此谐波传动是DGMSCMG框架传动机构的最佳选择。但由于其结构的特点,谐波减速器也存在非线性传动特性,这严重影响了框架伺服系统的角速率精度[5]。
DGMSCMG框架伺服系统的扰动可分为内扰和外扰,其中内扰主要包括伺服电机的力矩脉动、轴系的摩擦力矩、传动部件的误差及反馈部件的误差,外扰主要是内、外框架之间的耦合力矩。针对内、外框架由于陀螺效应引起的耦合力矩,文献[6]提出一种针对耦合力矩进行补偿的电流前馈方法,但模型过于简单,解耦效果不明显。文献[7]采用自适应逆方法对DGMSCMG的内、外框架伺服系统进行解耦,并进行了仿真验证,但该方法由于系统未引入谐波减速器仍然需要比较精确的数学模型,具体实现难度较大。针对框架伺服系统的伺服电机的力矩脉动、轴系的摩擦力矩、传动部件的误差及反馈部件的误差,文献[1]提出一种三相直流无刷力矩电机的自适应电流控制方法,抑制了电机的转矩脉动。文献[4]提出一种角速度估计方法对由角位置获取角速率带来的噪声进行抑制。针对谐波减速器这种非线性传动部件,文献[8]分别针对谐波减速器的非线性摩擦、传动误差及非线性扭转刚度进行了建模,但模型复杂,实际应用较难。文献[9, 10]分别采用重复控制和复合闭环控制的方法对谐波减速器引起的误差进行补偿,提高了系统的角位置精度,能够较好地适用于转速较高的系统,但很难适用于CMG框架伺服系统这种低速率系统。文献[11]对谐波减速器的非线性摩擦进行建模,并在双框架控制力矩陀螺的框架伺服系统中采用前馈方式对摩擦进行补偿。
从1991年Kokotovic提出反步控制理论以来,这种方法已经成为解决参数不确定的非线性系统鲁棒控制的有效途径之一,并且在工业、航天和机器人等领域得到了广泛的应用[12, 13, 14, 15]。文献[16]采用自适应反步控制方法对感应电机的摩擦进行补偿。文献[17]针对交流伺服系统负载惯量和负载力矩的变化设计了自适应反步控制器,并在DSP硬件系统上进行验证。本文基于反步控制理论对框架伺服系统进行动力学分析,推导耦合力矩、谐波减速器的非线性扭转刚度及非线性阻尼这些未知参数的自适应律,并在每步的设计过程中选用合适的Lyapunov函数保证了系统的稳定性。
1 系统建模与问题描述 DGMSCMG包括磁悬浮高速转子系统和内、外框架伺服系统。框架转动强制改变高速转子角动量方向而输出陀螺力矩,高速转子的角动量Hr=Jrωr,Jr为转子的转动惯量,ωr为高速转子的角速度。若内框架和外框架的合成角速度为ω,则DGMSCMG对外输出力矩为M=Hr×ω。图 1为DGMSCMG的工作原理示意图,定义坐标系如下:惯性坐标系为Oxiyizi;与CMG外框相连的坐标系为Oxjyjzj;与CMG内框相连的坐标系为Oxgygzg;θd为内框相对外框的转动角度;φd为外框相对惯性系的转动角度;ωg为内框架的角速度。
 |
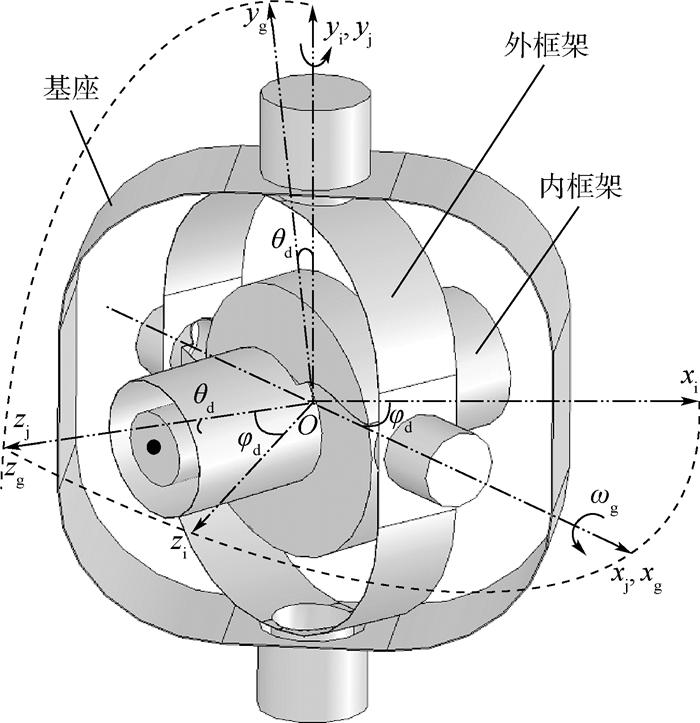| 图 1 DGMSCMC工作原理示意图Fig. 1 Schematic diagram of coordinates definition of DGMSCMG |
| 图选项 |
陀螺正常工作后转子高速自转,高速转子绕z轴旋转的角动量Hrz达到较大值时,根据坐标变换与欧拉方程化简可以得到DGMSCMG内、外框架伺服系统的动力学方程[18]:
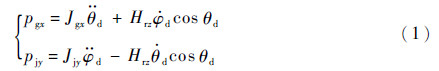
式中:pgx为作用在内框架负载轴上沿xg方向的力矩;pjy为外框架负载轴上沿yj方向的力矩;Jgx为内框架沿x轴的转动惯量;Jjy为外框架沿y轴的转动惯量。
由式(1)可知，由于陀螺效应的存在导致内、外框架伺服系统之间存在耦合力矩项,且耦合力矩项中不仅包含内、外框架的角速度项还包含内框架转角的余弦项,因此该耦合力矩是非线性时变的。从上述分析可以看出,陀螺效应引起的内、外框架伺服系统之间耦合力矩项将影响框架角速率的精度。
此外,本系统通过引入谐波减速器对电机输出到负载的力矩进行放大。由于内、外框架伺服系统的结构相似,这里仅给出内框架的结构原理，如图 2 所示。
 |
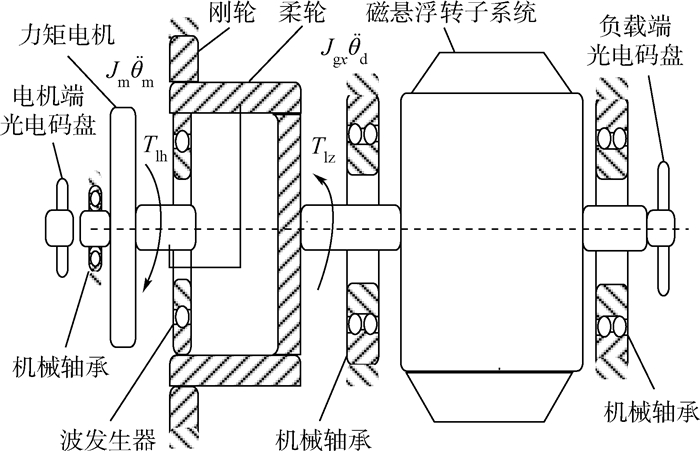| 图 2 内框架伺服系统结构Fig. 2 Structure of inner gimbal servo system |
| 图选项 |
综合考虑谐波减速器的非线性扭转刚度及非线性阻尼对传动力矩的影响,对内框架电机端建立力矩平衡方程:
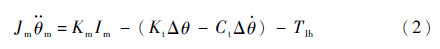
式中:Jm为内框架电机端转动惯量;θm为内框架电机端角位置;Km为电机力矩系数;Im为电机绕组电流;Kt为谐波减速器的扭转刚度;Δθ=θm-iθd，i为谐波减速器减速比;Ct为谐波减速器的阻尼系数;T1h为内框架电机端负载力矩,T1h=Tlz/i，Tlz为谐波减速器端负载力矩。
由式(2)可知,作用到内框架负载轴上的耦合力矩:
综合式(1)~式(3),考虑内框架伺服系统负载端传动机构的非线性影响,可以得到内框架伺服系统负载轴上沿xg方向的力矩:
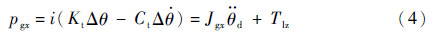
令x1=θd,x2=
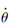d,x3=Δθ,x4=Δ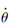,式(2)和式(4)的状态方程可表述为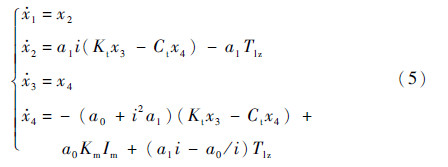
式中:a0=1/Jm和a1=1/Jgx都为常数。
2 自适应反步控制方法设计控制器设计的目标是在谐波减速器的扭转刚度Kt、阻尼系数Ct及负载轴上的扰动力矩Tlz未知的情况下使框架负载端角位置θd能够快速准确地跟踪参考指令角位置θd*。因此本节采用反步控制方法逐步递推各层控制变量及未知变量的自适应律,并设计适当的Lyapunov函数保证系统的稳定性。
由于谐波减速器的输入及输出端角位置可测,角速率可间接计算,且假定期望角位置输出θd*有界、可微,Kt、Ct及Tlz有界。
第1步位置跟踪控制
令e1=θd-θd*,则对位置误差e1求导可得
选取Lyapunov函数:
求其微分可得
设x2的期望值为η1,选择控制律η1=-k1e1+
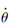d*,k1为正常数,令e2=x2-η1,考虑式(6)和式(8)可以得到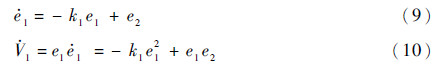
因此,若e2→0,则
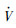1<0。第2步速度跟踪控制
对e2求导可得
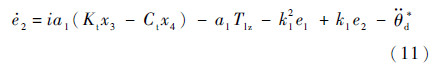
对于谐波减速器来说,其扭转刚度Kt可以分解为平均扭转刚度与时变扭转刚度之和,即:Kt=Ktc+ΔKt,Ktc为平均扭转刚度,是一个恒定的常量,ΔKt为与负载有关的非线性时变量。阻尼系数Ct为时变阻尼系数。因此式(11)可以写为
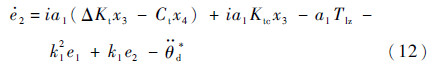
选取Lyapunov函数:
则由式(10)和式(12)可得V2的微分为
式中:λ1=1-k12;λ2=k1+k2,k2>0;Ktc、λ1及λ2都是常量,由于ΔKt和Ct为未知变量,Tlz为未知扰动力矩,因此选取其估计值来代替。设x3的期望值为η2,选择控制律:
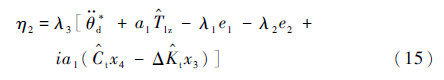
式中:
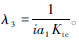
将式(15)代入式(12)可得
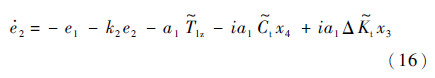
式中:
lz=T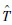lz-
lz,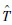lz为Tlz的估计值;Δ
t=ΔK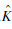t-Δ
t,Δ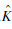t为ΔKt的估计值;
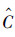t=Ct-
t,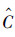t为Ct的估计值。在V2的基础上,选取增广Lyapunov函数:
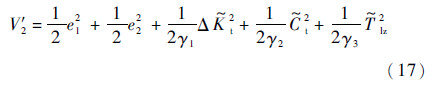
式中:γ1>0;γ2>0;γ3>0。
将式(9)和式(16)代入V′2的微分:
因此,若存在自适应控制律使得
lz→0、Δt→0及t→0,则可保证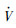′2=-k1e12-k2e22<0负定,使得e1、e2都趋近于零。第3步电流控制及参数自适应律
令x3与其期望值η2之间的误差为
则由式(5)、式(9)、式(15)和式(16)可以得到e3的微分:
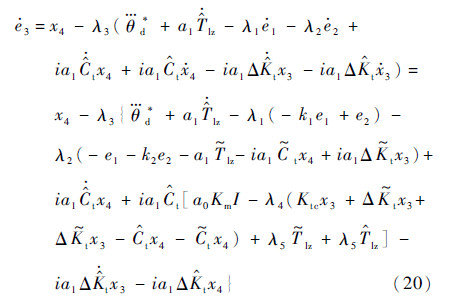
式中:
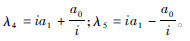
为得到使系统稳定的控制输入I及不确定参数的自适应律,在V′2的基础上选取Lyapunov函数如下:
则由式(18)和式(20)可以得到V3的微分如下:
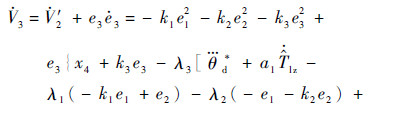
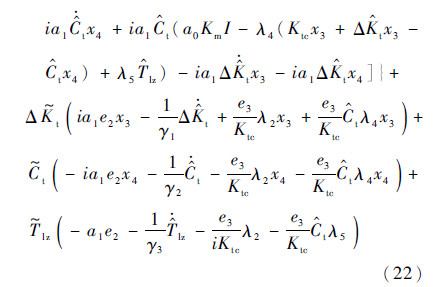
式中:k3为正的设计参数。由式(22)得到控制律为
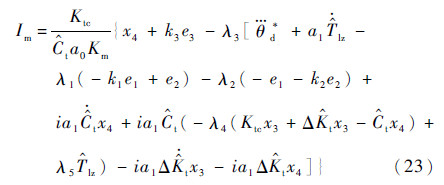
参数的自适应律为
由式(23)~式(26)可以得到
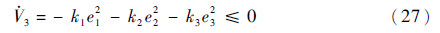
由此可知V3是有界的且ei(i=1,2,3)为平方可积的,即ei、Δ
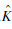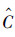t、t和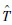lz都是有界的。因ΔKt、Ct和Tlz皆为常数,从而Δt、t和lz也都是有界的,易知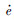
i为有界的。应用Barbalat引理[19]可得误差的渐近收敛性。所以内框架伺服系统能够渐近稳定地跟踪期望的位置轨迹。3 系统仿真研究文献[5]提出采用电流前馈的方式可以有效抑制内、外框架耦合力矩引起的框架角速率波动,因此分别以电流前馈控制方法和自适应反步控制方法对DGMSCMG的框架伺服系统进行仿真,系统参数如表 1所示。
表 1 系统参数Table 1 System parameters
| 参数 | 数值 |
| Jm/(kg·m2) | 0.000 46 |
| Jg x/(kg·m2) | 0.045 |
| Jj y/(kg·m2) | 0.081 |
| Km | 0.72 |
| Ce | 0.074 |
| Ktc/(N·m·rad-1) | 3 800 |
| i | 100 |
| 注: Ce—力矩电机反电势系数。 | |
表选项
假定内、外框架初始位于正交位置,内框架给定角位置信号为斜坡信号,角速率为0.087 rad/s(5(°)/s),外框架给定角速率信号为0 rad/s(0(°)/s),采样频率为10 kHz。利用电流前馈控制方法和自适应反步控制方法对系统进行仿真,仿真结果如图 3和图 4所示。
 |
| 图 3 电流前馈控制下内框架启动外框架角速率波形Fig. 3 Waveform of outer gimbal angular speed based on current feed-forward control and inner gimbal starting |
| 图选项 |
 |
| 图 4 自适应反步控制下内框架启动外框架角速率波形 Fig. 4 Waveform of outer gimbal angular speed based on adaptive backstepping control and inner gimbal starting |
| 图选项 |
由图 3可知,利用电流前馈控制方法能够消除耦合力矩的影响,但由于谐波减速器运动误差的影响会出现0.3(°)/s的速率波动。由图 4可知,利用自适应反步设计的控制器进行控制,最大的速率波动量为0.007 2(°)/s,实验表明所设计的自适应反步控制器具有较强的抗干扰能力。
角速率带宽是DGMSCMG很重要的一个指标。给定角速率参考为3 Hz的正弦信号,以外框架伺服系统为被控对象,分别采用电流前馈控制方法和自适应反步控制方法得到了外框架角速率跟踪正弦波形如图 5和图 6所示。
 |
| 图 5 电流前馈控制下外框架角速率跟踪正弦波形Fig. 5 Outer gimbal angular speed tracking sine waveform under current feed-forward control |
| 图选项 |
 |
| 图 6 自适应反步控制下外框架角速率跟踪正弦波形Fig. 6 Outer gimbal angular speed tracking sine waveform under adaptive backstepping control |
| 图选项 |
由图 5和图 6可以得出,采用自适应反步控制方法,系统在1/4个正弦周期后能够完全跟踪3 Hz的角速率指令。而采用电流前馈控制方法时,系统的调节速度比较慢,实际速率在幅值上有19.8%的衰减,相位上有32.4°的相位滞后。
4 系统实验研究为了验证所设计的自适应反步控制器的有效性,以北京航空航天大学新型惯性仪表与导航系统技术国防重点学科实验室2008年研制的小型DGMSCMG系统为对象进行实验研究,小型DGMSCMG系统如图 7所示。
 |
| 图 7 DGMSCMG实验系统Fig. 7 DGMSCMG experimental system |
| 图选项 |
采用基于DSP(TMS320VC33)与FPGA的数字控制系统,利用DSP(TMS320VC33)的高速浮点运算能力实现内外框架的控制算法,利用FPGA实现控制系统中的逻辑运算,设计方案如图 8所示。
 |
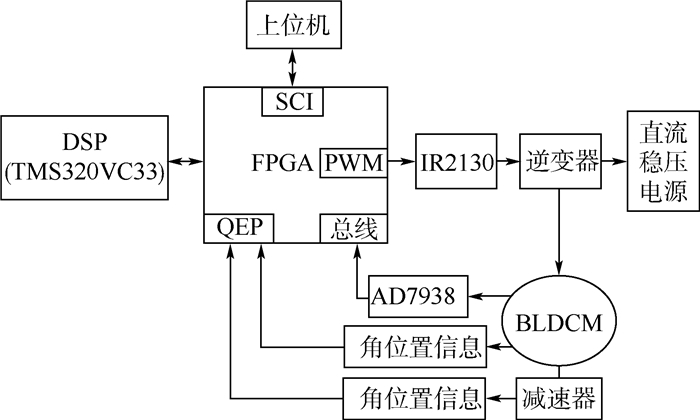| 图 8 控制器结构框图Fig. 8 Structure block diagram of controller |
| 图选项 |
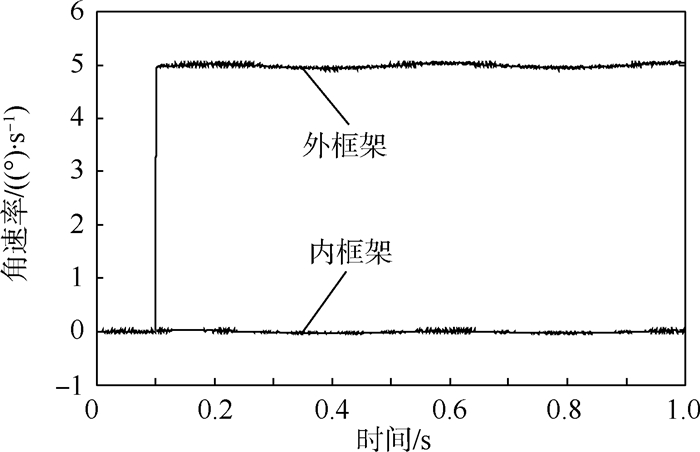
为了验证自适应反步算法在扰动抑制及提高框架的转速精度方面的优越性,在转子30 000 r/min,内外框架初始位于正交位置时,给定内框架速率指令5(°)/s,外框架保持静止状态。则在电流前馈控制方法和自适应反步控制方法下得到2组角速率波形如图 9和图 10所示。
 |
| 图 9 电流前馈控制下双框架角速率波形Fig. 9 Waveform of double gimbal angular speed under current feed-forward control |
| 图选项 |
 |
| 图 10 自适应反步控制下双框架角速率波形Fig. 10 Waveform of double gimbal angular speed under adaptive backstepping control |
| 图选项 |
如图 9所示,当内框架以5(°)/s的速率阶跃时,由于耦合力矩的存在,用电流前馈控制方法时内框架出现了峰值为1.4(°)/s的速率波动。如图 10所示,当采用自适应反步控制方法时,外框架没有产生速率波动。而且当内框架以5(°)/s稳速时,用电流前馈控制方法下的速率波动范围为4.3~5.7(°)/s,而采用自适应反步控制时外框架速率波动为4.9~5.05(°)/s。
比较自适应反步控制器与电流前馈控制的动态响应,在转子30 000 r/min的情况下,给定外框架幅值10(°)/s、频率3 Hz的正弦指令,则在电流前馈控制方法和自适应反涉控制方法下的外框架角速率跟踪正弦波形如图 11和图 12所示。
 |
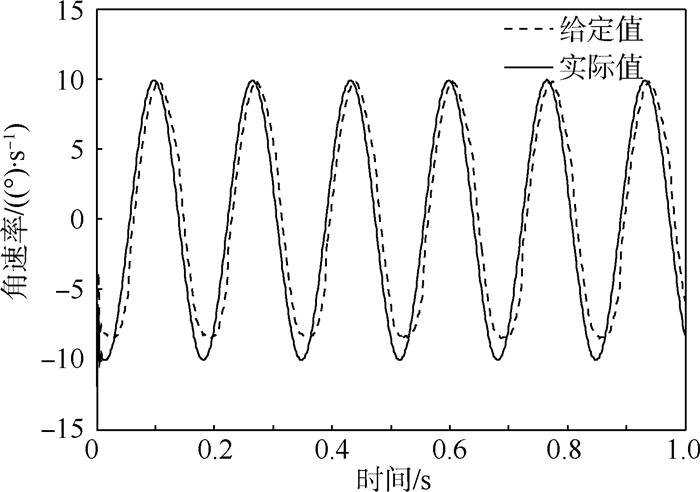| 图 11 电流前馈控制下外框架角速率跟踪正弦波形Fig. 11 Outer gimbal angular speed tracking sine waveform under current feed-forward control |
| 图选项 |
 |
| 图 12 自适应反步控制下外框架角速率跟踪正弦波形Fig. 12 Outer gimbal angular speed tracking sine waveform under adaptive backstepping control |
| 图选项 |
从图 11中可知,在电流前馈控制下,外框架角速率在相位和幅值上都不能跟踪上给定角速率指令,由图 12可知,在自适应反步控制方法下,外框架角速率能够较好地跟踪速率指令。
5 结 论 DGMSCMG内、外框架耦合力矩、谐波传动是影响框架角速率的稳定性与精度的主要因素,本文提出了一种基于反步的系统自适应控制器设计方法,并通过构造适当的Lyapunov函数并逐级反推得到控制律。通过仿真及实验与电流前馈控制进行比较,得出如下主要结论:
1) 在框架角速率稳定性方面,自适应反步控制方法具有更强的抗干扰能力。
2) 在框架角速率跟踪精度方面，自适应反步控制方法显著提高了框架角速率的跟踪精度。
参考文献
| [1] | FANG J C, LI H T,HAN B C.Torque ripple reduction in BLDC torque motor with nonideal back EMF[J].IEEE Transactions on Power Electronics,2012,27(11):4630-4637. |
| Click to display the text | |
| [2] | FANG J C, ZHENG S Q,HAN B C.AMB vibration control for structural resonance of double-gimbal control moment gyro with high-speed magnetically suspended rotor[J].IEEE/ASME Transactions on Mechatronics,2013,18(1):32-43. |
| Click to display the text | |
| [3] | 魏彤,郭蕊. 自适应卡尔曼滤波在无刷直流电机系统辨识中的应用[J].光学精密工程,2012,20(10):2308-2313. WEI T,GUO R.Application of adaptive Kalman filtering in system identification of brushless DC motor[J].Optics and Precision Engineering,2012,20(10):2308-2313(in Chinese). |
| Cited By in Cnki (27) | Click to display the text | |
| [4] | 李海涛,房建成. 自适应角速度估计器在磁悬浮控制力矩陀螺框架伺服系统中的应用[J].光学精密工程,2008,16(1): 97-102. LI H T,FANG J C.Application of adaptive angle-rate estimator to gimbal of MGCMG[J].Optics and Precision Engineering,2008,16(1):97-102(in Chinese). |
| Cited By in Cnki (12) | Click to display the text | |
| [5] | 房建成,陈萌, 李海涛.磁悬浮控制力矩陀螺框架系统谐波减速器的迟滞建模[J].光学精密工程,2014,22(11):2950-2958. FANG J C,CHEN M,LI H T.Hysteresis modeling for harmonic drive in DGMSCMG gimbal system[J].Optics and Precision Engineering,2014,22(11):2950-2958(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [6] | 魏彤,房建成, 刘珠荣.双框架磁悬浮控制力矩陀螺动框架效应补偿方法[J].机械工程学报,2010,46(2):159-165. WEI T,FANG J C,LIU Z R.Moving-gimbal effects compensation of double gimbal magnetically suspended control moment gyroscope based on compound control[J].Journal of Mechanical Engineering,2010,46(2):159-165(in Chinese). |
| Cited By in Cnki (15) | Click to display the text | |
| [7] | 陈晓岑,周东华, 陈茂银.基于逆系统方法的DGMSCMG框架伺服系统解耦控制研究[J].自动化学报,2013,39(5):502-509. CHEN X C,ZHOU D H,CHEN M Y.Decoupling control of gimbal servo system of DGMSCMG based on dynamic inverse system method[J].Acta Automatic Sinica,2013,39(5):502-509(in Chinese). |
| Cited By in Cnki (40) | Click to display the text | |
| [8] | TUTTLE T D, SEERING W P.A nonlinear mode l of a harmonic drive gear transmission[J].IEEE Transactions on Robotics and Automation,1996,12(3):368-374. |
| Click to display the text | |
| [9] | GODLER I, OHNISHI K,YAMASHITA T.Repetitive control to reduce speed ripple caused by strain wave gearing[C]//Proceedings of the 20th International Conference on Industrial Electronics, Control and Instrumentation.Piscataway,NJ:IEEE Press,1994,2:1034-1038. |
| Click to display the text | |
| [10] | GANDHI P, GHORBEL F.Closed loop compensation of kinematic error in harmonic drives for precision control applications[J].IEEE Transactions on Control Systems Technology,2002,10(6):759-768. |
| Click to display the text | |
| [11] | 韩邦成,马纪军, 李海涛.谐波减速器的非线性摩擦建模及补偿[J].光学精密工程,2011,19(5):1095-1103. HAN B C,MA J J,LI H T.Modeling and compensation of nonlinear friction in harmonic driver[J].Optics and Precision Engineering, 2011,19(5):1095-1103(in Chinese). |
| Cited By in Cnki (16) | Click to display the text | |
| [12] | CHEN M, JIANG C S,WU Q X.Backstepping control for a class of uncertain nonlinear systems with neural network[J].International Journal of Nonlinear Science,2007,3(2):137- 143. |
| Click to display the text | |
| [13] | LIN F J, TENG L T,SHIEH P H.Intelligent adaptive backstepping control system for magnetic levitation apparatus[J].IEEE Transactions on Magnetics,2007,43(5):2009-2018. |
| Click to display the text | |
| [14] | LIN F J, WAI R J,CHOU W D,et al.Adaptive backstepping control using recurrent neural network for linear induction motor drive[J].IEEE Transactions on Industrial Electronics,2002,49(1): 134-146. |
| Click to display the text | |
| [15] | JIA Q Z, LIU Y S,LIU Z Z.Backstepping design for nonlinear control system with uncertainties[J].Journal of System Simulation,2007,19(21):5002-5007. |
| [16] | TAN Y L, CHANG J,TAN H.Adaptive friction compensation for induction motors with inertia and load uncertainties[C]//Proceedings of the American Control Conference.Piscataway,NJ:IEEE Press,2000:615-620. |
| Click to display the text | |
| [17] | CHANG J, TAN Y L,YU J T.Backstepping approach of adaptive control,gain selection and DSP implementation for AC servo system[C]//IEEE 38th Annual Power Electronics Specialists Conference.Piscataway,NJ:IEEE Press,2007:535-541. |
| Click to display the text | |
| [18] | 李红,杭影, 韩邦成,等.DGCMG框架伺服系统摩擦力矩建模与辨识.[J].振动、测试与诊断.2014,12(5):1001-1007. LI H,HANG Y,HAN B C,et al.Analysis of friction torque model of DGCMG gimbal servo system with its identification[J].Journal of Vibration Measurement and Diagnosis,2014,12(5): 1001-1007(in Chinese). |
| Cited By in Cnki (1) | Click to display the text | |
| [19] | 闵颖颖, 刘允刚.Barbalat引理及其在系统稳定性分析中的应用.[J].山东大学学报(工学版),2007,37(1):51-55. MIN Y Y,LIU Y G.Barbalat lemma and its application in analysis of system stability[J].Journal of Shandong University (Engineering Science),2007,37(1):51-55(in Chinese). |
| Cited By in Cnki (118) | Click to display the text |
