空间绳系拖拽离轨是利用系绳与任务星相连的空间绳网/抓爪等捕获废弃卫星后,由任务星机动,实现对废弃卫星拖拽转移的新概念在轨操作技术[2, 3],可将地球静止轨道(GEO)废弃卫星拖拽转移至坟墓轨道,从而释放轨道资源。与动辄几千米到几十千米距离的传统绳系系统[4]和电动力绳系系统[5]相比,空间绳系拖拽离轨系统具有系绳短(约10~200 m)、需在主动的集中推力下进行轨道机动的特点。由于采用柔绳连接,如何在轨道转移时避免系绳松弛造成缠绕、系绳张力过大造成断裂或两星接近发生碰撞,实现平稳的控制十分重要。作为近年一项新兴的在轨操作概念,目前对此问题的理论研究还不广泛。其中,文献[6]对张力作用下,绳系机器人捕获目标后构成的复合体的姿态控制问题进行了研究。而针对自身完全不具备控制能力的废星的拖拽转移问题,具有代表性的研究有:文献[7]针对绳系相对运动的3种风险的避免问题,提出了由加速、平衡、旋转和返回构成的4阶段绳系拖拽离轨方案;文献[8]提出了一种优化轨道转移方案,利用最优控制设计连续推力,从而实现绳系系统圆轨间的转移;文献[9, 10]推导了沿多种方向常值推力作用下离轨绳系系统的一阶摆动解析解,并分析了系统的摆动特性以及摆振耦合特性;文献[11]推导了系绳处于张紧状态时离轨绳系系统姿态的平衡位置解析解,并设计了基于分层滑模的张力控制方法以解决绳系系统机动过程中的姿态跟踪问题。前述研究揭示了拖拽离轨中的绳系系统动力学特性,并为控制策略提出了新的思路,研究中主要沿袭了传统绳系的建模方法,采用将星体视为质点的哑铃模型进行绳系组合体姿态研究。但当在模型中考虑星体姿态运动后,结果表明星体姿态摆动将激发出系统的高阶摆动[12, 13],直接影响到绳系系统尤其是短距离绳系系统姿态稳定;文献[14]通过仿真分析得出废星的面内姿态摆动会对任务星面内姿态产生扰动力矩,增加姿态稳定控制消耗,并提出了一种用于废星面内姿态摆动抑制与绳长保持的张力控制方法。而在考虑更具一般性的星体三维姿态运动时,离轨系统运动状况更为复杂,需进一步研究其运动规律与控制方法。在离轨过程中,绳系系统需满足安全与平稳两方面的要求,其中,安全是指拖拽过程中,任务星与废星需保持足够大的相对距离,以避免碰撞;而平稳一方面要求两星保持稳定的星间距,另一方面要求任务星姿态、废星姿态以及组合体系统面内外摆角处于稳定状态,以降低拖拽转移风险,并为组合体轨道转移精度和效率的提高提供条件。
本文针对切向连续常值推力作用下的废星绳系拖拽离轨问题,考虑了两星的姿态运动,建立了绳系拖拽离轨系统动力学与控制模型,分析了废星的姿态摆动、组合体面内外摆动和任务星姿态运动变化规律及其相互影响关系;将文献[14]中提出的张力控制方法由轨道面内推广至三维空间,并通过仿真验证了利用该方法结合任务星姿态控制进行绳系拖拽转移安全、稳定控制的有效性。
1 系统描述 离轨操作中绳系拖拽系统由任务星、废星和连接两星体的系绳三部分组成,连接关系如图 1所示。任务星上系绳牵挂点在其本体坐标系负x轴,废星上系绳牵挂点偏离其本体坐标系x轴。任务星利用喷气与动量轮控制实现三轴姿态稳定,废星姿态不能自控。任务星上施加切向连续常值推力,实现轨道转移。
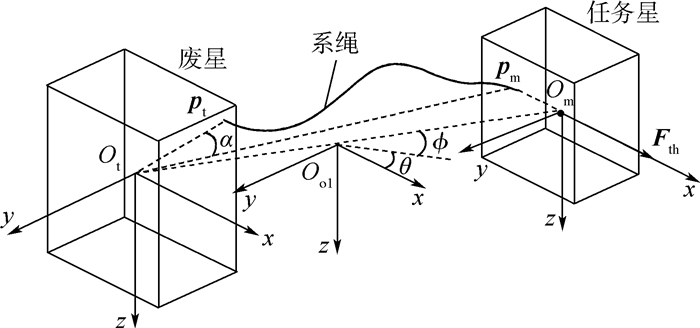 |
| Oo1-xyz—第二轨道坐标系;Ot-xyz—废星本体坐标系;Om-xyz—任务星本体坐标系;pm—本体坐标系下任务星系绳牵挂点矢量; pt-本体坐标系下废星系绳牵挂点矢量;α—Otpt到Otpm的夹角;θ—系统面内摆角;Φ—系统面外摆角;Fth—任务星上施加的轨控推力。图 1 绳系拖拽系统组成与连接关系Fig. 1 Composition and connection of tether tugging system |
| 图选项 |
2 系统建模2.1 相关坐标系1) 地心惯性坐标系O-XYZ:原点位于地球质心,X轴指向春分点,Z轴沿地球自转轴指向北极,Y轴由右手规则定义,三轴向用矢量i、j和k表示。
2) 第二轨道坐标系Oo1-xyz:原点位于系统绳系组合体质心,z轴指向地心,x轴在轨道平面内指向飞行方向,y轴按照右手规则定义,三轴向用矢量io1、 jo1和ko1表示。
3) 任务星/废星本体坐标系Om-xyz/Ot-xyz:原点位于星体质心,三坐标轴与星体惯量主轴重合。
2.2 系绳张力模型拖拽离轨操作中系绳长度较短,其质量(百克量级)远小于星体质量(百千克以上量级),建模中采用无抗压能力的弹性杆模型[15],不计系绳的质量、阻尼,系绳有纵向弹性变形,不能抗压,系绳只存在拉应力。系绳张力只与形变量ΔL相关。定义星体上两系绳牵挂点连线矢量Ltm,方向由废星牵挂点指向任务星牵挂点,则有
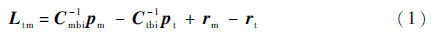
式中:Cmbi和Ctbi分别为地心惯性坐标系到任务星和废星本体坐标系的姿态转移矩阵;rm和rt分别为任务星、废星质心在地心惯性坐标系中的位置矢量。则
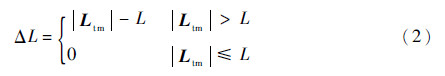
式中:L为系绳松弛时的原长,即零应变长度。
系绳张紧方向为系绳张力方向,则系绳张力为
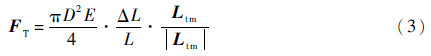
式中:D为系绳直径;E为系绳弹性模量。
2.3 质心动力学模型 绳系拖拽系统动力学建模中,主要考虑影响系统摆动的主要因素。系统所受外力中除任务星轨控推力和地球中心引力外,可忽略其他外部摄动;由于短期内任务星燃耗质量远小于任务星质量,任务星质量变化对绳系系统摆动特性的影响可以忽略。由此,地心惯性坐标系下任务星和废星质心动力学方程为
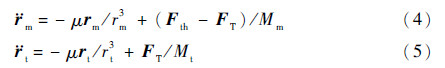
式中:μ为地球引力常数;Mm和Mt分别为任务星、废星质量;rm为rm的模;rt为rt的模。
则系统质心位置与速度为
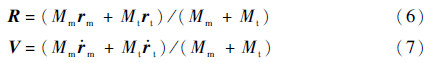
第二轨道坐标系三轴向量可表示为
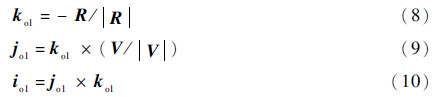
地心惯性坐标系到第二轨道坐标系的姿态转移矩阵可以表示为

第二轨道坐标系下废星质心到任务星质心连线矢量为

定义系统面内摆角θ、面外摆角Φ为
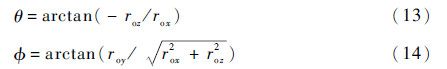
2.4 星体姿态动力学模型 忽略任务星与废星的柔性,将其视为刚体,则可采用动量矩定律建立任务星与废星姿态动力学方程:
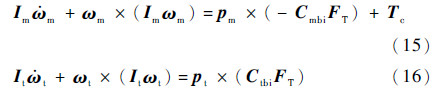
式中:Im和It分别为任务星、废星的转动惯量矩阵;ωm和ωt分别为两星体角速度在各自本体坐标系下的投影;Tc为任务星的姿态控制力矩。
2.5 姿态四元数与欧拉角绳系拖拽过程中,不排除星体姿态剧烈变化的情况,为了防止模型中出现奇点,采用四元数描述星体姿态运动方程。设四元数Q=q0+q,q0为四元数标量项,q为矢量项,q=[q1 q2 q3]T,则姿态运动学方程为
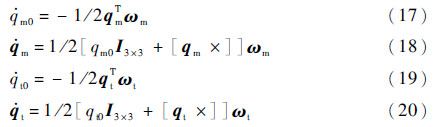
式中:Qm为任务星姿态四元数;Qt为废星姿态四元数;I3×3为单位矩阵;[qm×]和[qt×]为叉乘矩阵。
根据姿态四元数可得到姿态转移矩阵:
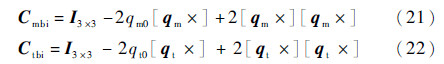
则第二轨道坐标系到两星体本体坐标系的姿态转移矩阵为

记第二轨道坐标系到任务星和废星本体坐标系的四元数分别为Q1m和Q1t,则有

式中:函数

由第二轨道坐标系以3-2-1的顺序转动到任务星和废星本体坐标系,所对应的欧拉旋转角γ、β和ψ分别为
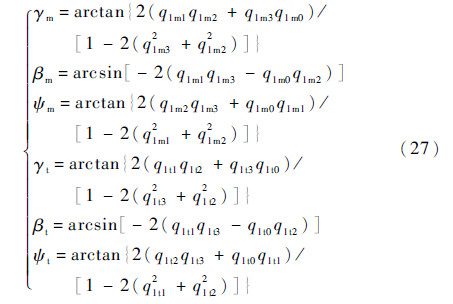
2.6 任务星姿态控制模型在任务星控制律的设计中,用姿态误差四元数和误差角速度来描述姿态运动[16],则有
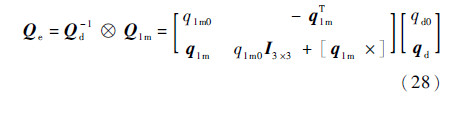

式中:Qd为任务星期望姿态四元数;Qe为姿态误差四元数,Qe=qe0+qe;ωd为任务星相对系统质心第二轨道坐标系的期望角速度;ωe为误差角速度。
1) 喷气控制系统模型
采用限制姿态反馈PD控制,控制律为
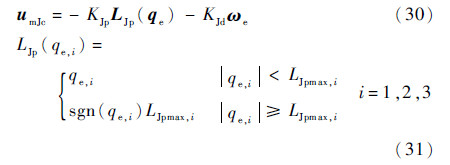
式中:LJpmax为姿态反馈限制系数;KJp和KJd为反馈增益;umJc为控制信号。
喷气系统为开关控制,连续的控制信号需转换为开关信号来决定喷气推进的开关。各喷气推进的开关信号与控制信息的关系为
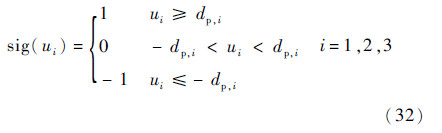
喷气控制力矩为
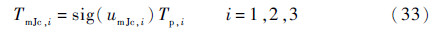
式中:Tp为三轴喷气控制力矩配置向量;dp为喷气机构开关阀值。
2) 零动量轮控制系统模型
在任务星本体坐标系的3个轴上各安装一个反作用轮。采用PD控制律
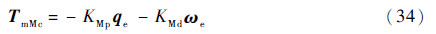
式中:KMp和KMd为反馈增益;TmMc为任务星本体坐标系下的动量轮控制力矩。
则任务星上姿态控制力矩为

3 绳系拖拽离轨系统摆动特性分析地球同步轨道废弃卫星的离轨操作是绳系拖拽技术的典型应用目标,通常拖拽转移的要求是在轨道面内将其轨道提高300 km左右至坟墓轨道。
由此,拟定GEO轨道上一个绳系拖拽离轨系统,其中任务星质量Mm=1 000 kg,惯量Im=diag{1 000,1 000,1 000}kg·m2,废星质量Mt=2 000 kg,惯量It=diag{2 000,2 000,2 000}kg·m2;两星体质心初始距离为52.8 m,两星体初始角速度为零,初始系统摆角为零;初始时刻系绳为松弛状态,张力为零,系绳直径D=0.001 m,弹性模量E=7×109 N/m2,初始绳长49.8 m;系绳在两星体上牵挂点在各自本体坐标系下的矢量为pm=[-1 0 0]T m,pt=[2 0.816 5 -0.816 5]T m。
零时刻开始在任务星上施加沿轨道正切向的连续常值离轨推力Fth=60 N。为保证离轨推力准确施加及系统安全飞行,需进行任务星姿态稳定控制,使任务星本体坐标系x轴与系统质心第二轨道坐标系x轴重合,故给出任务星相对于系统质心第二轨道坐标系的期望姿态四元数Qd=[1 0 0 0]T;喷气开关信号dp=[4 4 4]T,三轴喷气控制力矩为Tp=[15 20 25]T N·m,限制姿态反馈控制参数LJpmax=[0.8 0.8 0.8]T,KJp=6 000,KJd= 1 200;动量轮控制参数KMp=120,KMd=24。
利用所建立的动力学与控制模型进行拖拽仿真,结果如图 2~图 7所示。
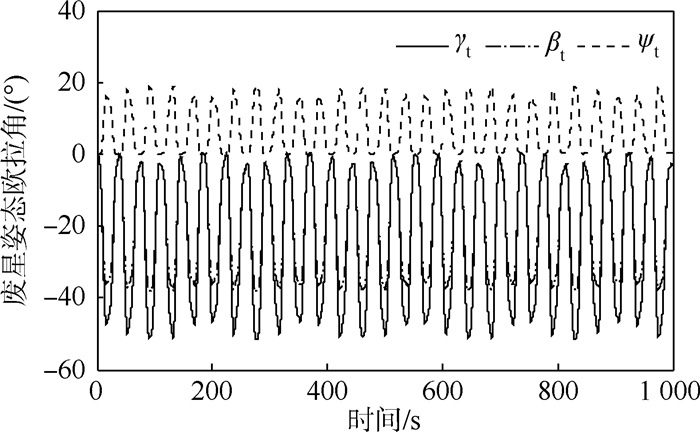 |
| 图 2 废星姿态Fig. 2 Attitude of abandoned satellite |
| 图选项 |
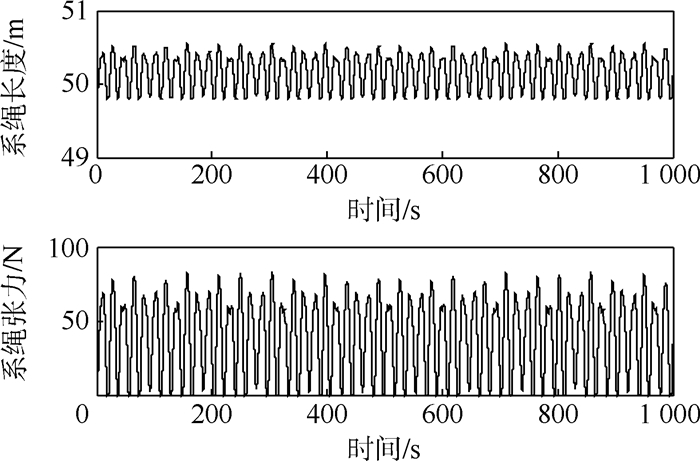 |
| 图 3 系绳长度和系绳张力 Fig. 3 Tether length and tether tension |
| 图选项 |
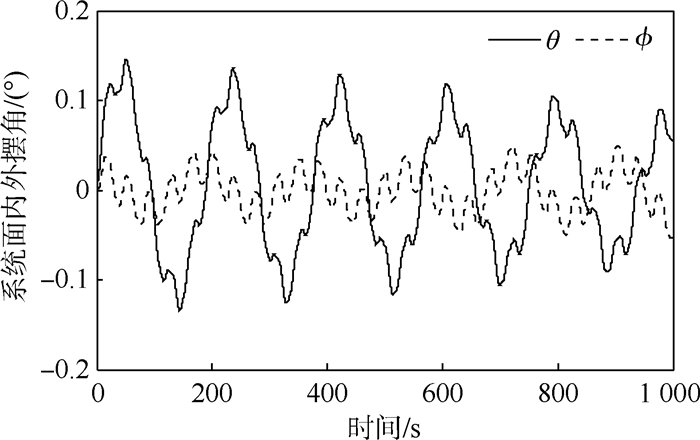 |
| 图 4 绳系拖拽系统面内外摆角 Fig. 4 In-plane angle and out-plane angle of tether tugging system |
| 图选项 |
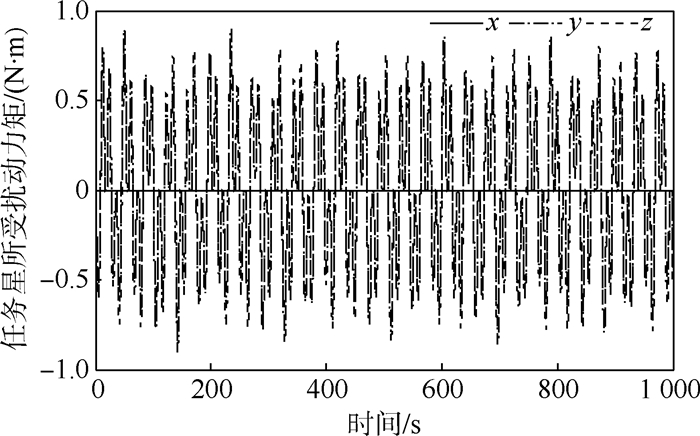 |
| 图 5 任务星所受扰动力矩 Fig. 5 Disturbance torque to mission satellite |
| 图选项 |
 |
| 图 6 动量轮控制力矩和任务星姿态 Fig. 6 Momentum wheel control torque and attitude of mission satellite |
| 图选项 |
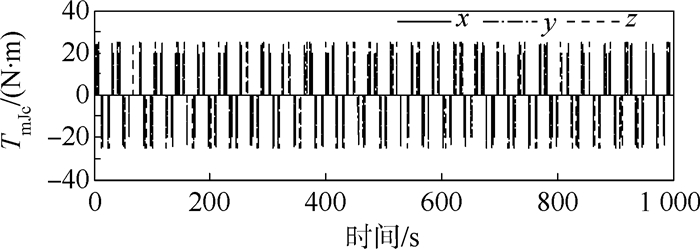 |
| 图 7 喷气控制力矩 Fig. 7 Jet control torque |
| 图选项 |
可以看出离轨过程中废星姿态、组合体系统面内外摆角及任务星姿态周期性变化,为便于分析,将废星姿态、系统面内外摆角、任务星所受扰动力矩和任务星姿态进行快速傅里叶变换(FFT)到频域,如图 8~图 11所示。
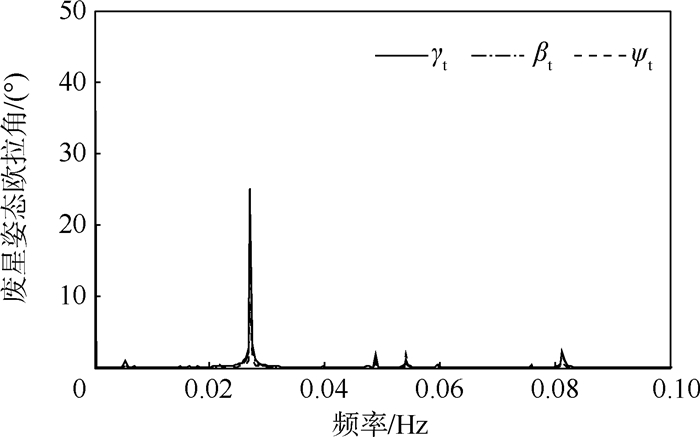 |
| 图 8 废星姿态欧拉角FFTFig. 8 FFT of Euler attitude angles of abandoned satellite |
| 图选项 |
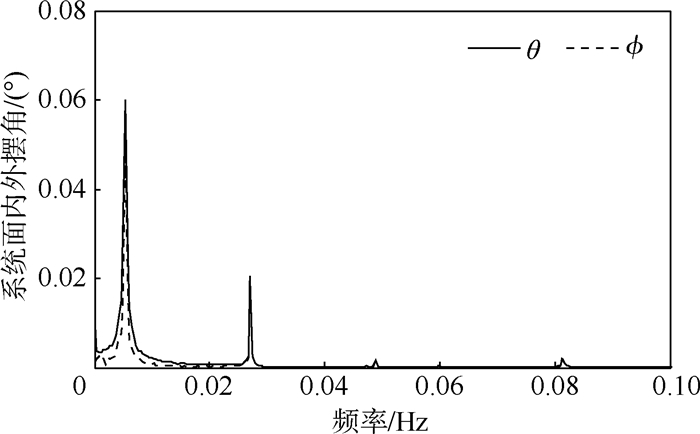 |
| 图 9 绳系拖拽系统面内外摆角FFT Fig. 9 FFT of in-plane angle and out-plane angle of tether tugging system |
| 图选项 |
 |
| 图 10 任务星所受扰动力矩FFT Fig. 10 FFT of disturbance torque to mission satellite |
| 图选项 |
 |
| 图 11 任务星姿态欧拉角FFT Fig. 11 FFT of Euler attitude angles of mission satellite |
| 图选项 |
从图 2和图 8可以看出,由于牵挂点偏置,废星姿态作大幅度往复摆动,其摆动频率为 0.027 1 Hz。
从图 4和图 9可以看出系统面内外摆动既包含低阶摆动也包含着高阶摆动,其低阶摆动频率为0.005 4 Hz,与文献[10]所述系统面内外一阶摆动频率一致,另一频率点为0.027 1 Hz,与废星姿态摆动频率一致,表明废星姿态摆动激发出了组合体系统面内外高阶摆动。
从图 3~图 7可以看出摆动的系绳和变化的系绳张力对任务星产生扰动力矩,任务星需要频繁开启喷气控制和动量轮控制协同将姿态稳定在±0.08°范围内,喷气时间占空比为0.014。
从图 10和图 11看出,任务星所受扰动力矩及姿态运动有2个峰值频率,分别为0.027 1 Hz和0.081 2 Hz,较高峰值频率对应废星摆动。
综上可知星体姿态摆动是影响拖拽过程稳定性的主要因素,废星姿态处于无控状态,其摆动会同时引起组合体系统面内外高阶摆动,扰动任务星姿态,增加姿态控制喷气能耗,不利于进行长时间的安全稳定离轨操作。
如果转移过程不采用喷气控制,则任务星摆角变化曲线如图 12所示。
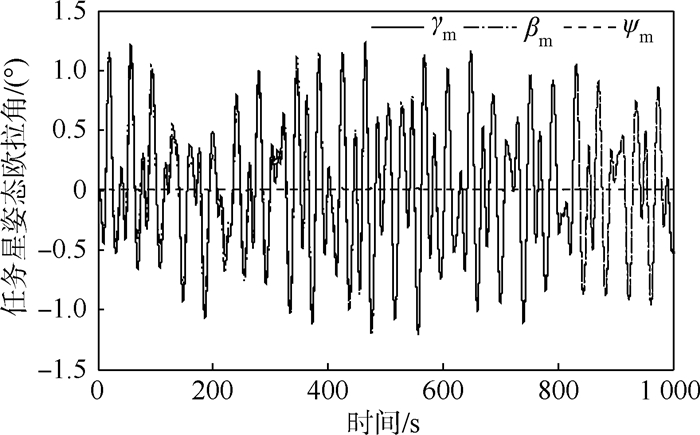 |
| 图 12 不加喷气控制下的任务星姿态Fig. 12 Attitude of mission satellite without jet control |
| 图选项 |
可以看出,在不施加喷气控制的情况下,拖拽机动中仅采用动量轮难以实现任务星姿态的稳定控制,不仅不利于系统的飞行安全,而且无法保证轨道转移推力矢量的方向稳定。因此要实现轨道转移推力的精确施加,安全平稳地完成轨道转移过程,需要消除废星姿态摆动,保持任务星姿态稳定。
4 废星姿态摆动抑制方法由于废星无自主调节控制能力,要对其进行姿态稳定控制,只能通过对系绳张力的调节来实现。与传统绳系系统一样,可在任务星上配置响应灵敏的系绳收放装置,用于调节系绳张力[17]。将文献[14]中结合留位控制和阻尼控制的张力控制方法推广应用于废星三维姿态摆动抑制与绳长保持,实现系绳张力的复合控制。
考虑到短时间内废星做近似平面摆动,故动力学方程可以简化为

式中:I为废星垂直于摆动面且过质心的摆动轴上的转动惯量;ω为废星摆动角速度;TFT为系绳张力作用力矩在摆动轴上的分量。此外,夹角α应近似满足

则式(36)又可简化为

式中:pt为废星牵挂矢量长度;Ft为系绳张力大小。
则有

基于二阶阻尼系统,姿态抑制控制律可设计为
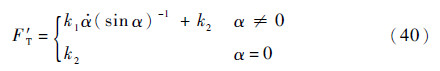
式中:k1为摆角增益参数;k2为常值反馈参数。
为了避免星体间的碰撞,系绳长度应被控制在期望值上,故设计距离保持补偿控制律为

式中:l0为系绳期望长度;l为系绳当前长度;k3为系绳长度速率反馈增益;k4为系绳长度反馈增益。则复合控制器可以表述为

5 绳系拖拽离轨平稳控制方法验证 在第3节典型案例的仿真模型中增加张力复合控制。取摆角反馈增益k1=39,常值反馈k2=40,系绳期望长度l0=50.16 m,系绳长度速率反馈增益k3=15,系绳长度反馈增益k4=10。在初始时刻系绳松弛状态下,拖拽转移过程仿真结果如图 13~图 18 所示。
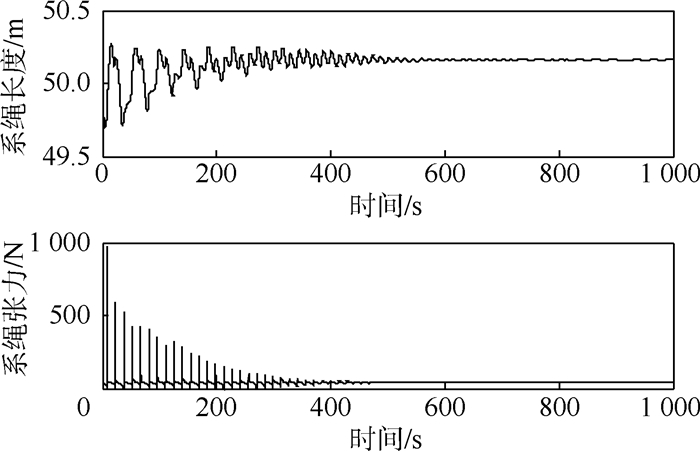 |
| 图 13 张力控制下的系绳长度和系绳张力Fig. 13 Tether length and tether tension under tension control |
| 图选项 |
 |
| 图 14 张力控制下的废星姿态和夹角α Fig. 14 Attitude of abandoned satellite and α angle under tension control |
| 图选项 |
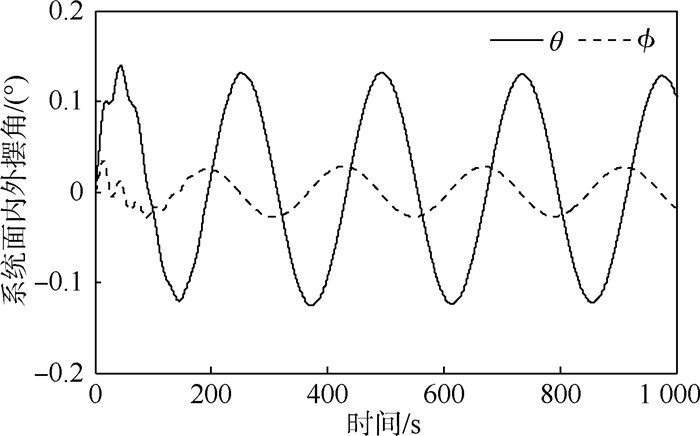 |
| 图 15 张力控制下的绳系拖拽系统面内外摆角 Fig. 15 In-plane angle and out-plane angle of tether tugging system under tension control |
| 图选项 |
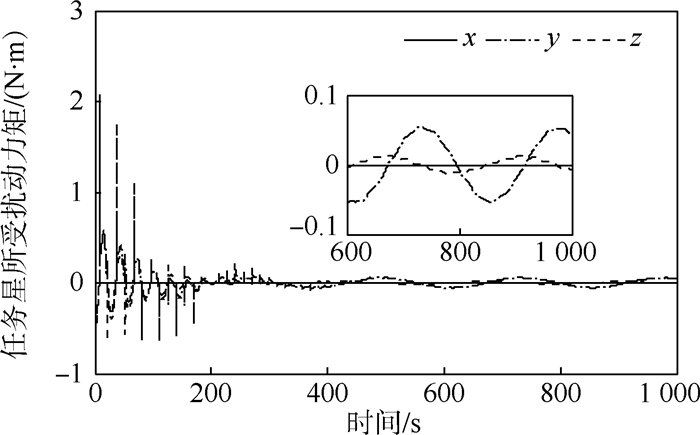 |
| 图 16 张力控制下的任务星所受扰动力矩 Fig. 16 Disturbance torque to mission satellite under tension control |
| 图选项 |
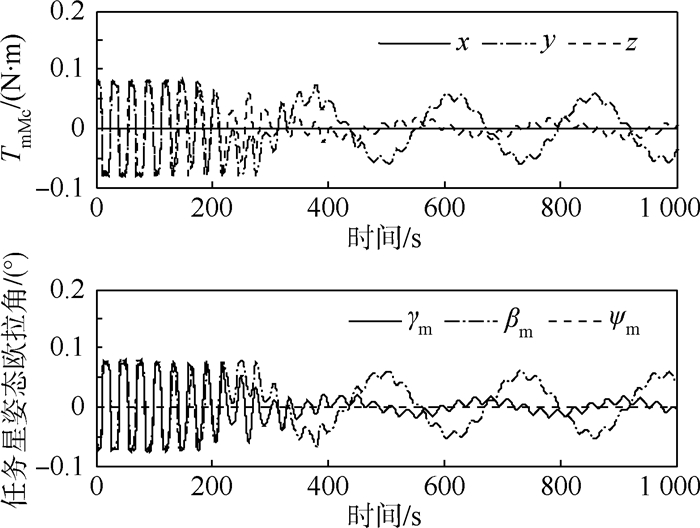 |
| 图 17 张力控制下的动量轮控制力矩和任务星姿态 Fig. 17 Momentum wheel control torque and attitude of mission satellite under tension control |
| 图选项 |
 |
| 图 18 张力控制下的喷气控制力矩 Fig. 18 Jet control torque under tension control |
| 图选项 |
从仿真结果可以看出,系绳张力快速稳定在40 N,系绳长度保持在期望长度50.16 m左右,废星的偏航角、俯仰角和滚转角被控制在-22.2°、-20.6°和4.2°左右;夹角α被抑制在0.18°左右,对系统的影响属于小量;系统面内外摆角在±0.15°和±0.04°范围内,由废星姿态摆动引起的高阶摆动得到了抑制,但组合体系统面内外摆动仍然存在,并未消除。
系绳对任务星的扰动力矩被控制在±0.06 N·m 范围内;喷气控制次数明显减小,截止到275 s喷气时间占空比为0.004 5,相比复合控制之前减少了67.8%,并且在275 s之后任务星姿态只需要动量轮控制,相比文献[14],适当增大动量轮控制参数后,控制效果更好,燃耗更低。
6 结 论 1) 在绳系拖拽转移过程中,若废星姿态处于无控状态,废星姿态、组合体系统面内外摆角和任务星姿态呈周期性运动,其中废星上系绳牵挂点的偏置诱发的废星姿态周期性摆动是影响拖拽离轨安全平稳进行的主要因素,不仅会激发组合体系统面内外高阶摆动,且会导致系绳张力对任务星产生较大幅度的姿态扰动力矩,任务星须增加额外的控制力矩以保证其姿态的平稳。
2) 采用留位和阻尼控制相结合的系绳张力复合控制方法,可有效抑制废星姿态摆动,极大地减弱废星姿态摆动对任务星姿态以及组合体系统面内外摆动的影响,尽管对组合体系统面内外摆动抑制不明显,但仍然可以使离轨过程更加平稳可靠,并减少任务星姿控能耗,延长任务星的工作寿命。
参考文献
| [1] | 邴启军,冯书兴. 基于卫星相撞事件的空间安全新思考[J].装备指挥技术学院学报,2009,20(5):63-67. BING Q J,FENG S X.Reflection on space security concerning the satellites collision[J].Journal of the Academy of Equipment Command & Technology,2009,20(5):63-67(in Chinese). |
| Cited By in Cnki (7) | Click to display the text | |
| [2] | XU W F, LIANG B,GAO D,et al.A space robotic system used for on-orbit servicing in the geostationary orbit[C]//2010 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS).Piscataway,NJ:IEEE Press,2010:4089- 4094. |
| Click to display the text | |
| [3] | MANKALA K K, AGRAWAL S K.Dynamic modeling and simulation of impact in tether net/gripper systems[J].Multibody System Dynamics,2004,11(3):235-250. |
| Click to display the text | |
| [4] | 朱仁璋,林华宝. 论绳系卫星系统的运动中心[J].中国空间科学技术,1998,18(5):7-12. ZHU R Z,LIN H B.The motion center of tethered satellite systems[J].Chinese Space Science and Technology,1998,18(5): 7-12(in Chinese). |
| Cited By in Cnki (11) | Click to display the text | |
| [5] | PELAEZ J, LORENZINI E C,LOPEZ-REBOLLAL O,et al.A new kind of dynamic instability in electrodynamic tethers[C]//Advances in the Astronautical Sciences.San Diego:AAS,2000,105:1367-1386. |
| [6] | 王东科,黄攀峰, 孟中杰,等.空间绳系机器人抓捕后复合体姿态协调控制[J].航空学报,2013,34(8):1998-2006. WANG D K,HUANG P F,MENG Z J,et al.Coordinate attitude of the combination system after target capture by a tethered space robot[J].Acta Aeronautica et Astronautica Sinica,2013,34(8):1998-2006(in Chinese). |
| Cited By in Cnki (5) | Click to display the text | |
| [7] | 刘海涛,杨乐平, 张青斌,等.地球静止轨道废弃卫星绳系拖曳离轨研究[J].中国科学:技术科学,2012,42(7):780-787. LIU H T,YANG L P,ZHANG Q B,et al.An investigation on tether-tugging de-orbit of defunct geostationary satellites[J].Science China Technological Sciences,2012,42(7):780-787(in Chinese). |
| Cited By in Cnki (1) | Click to display the text | |
| [8] | CHO S, MCCLAMROCH N H.Optimal orbit transfer of a spacecraft with fixed length tether[J].The Journal of the Astronautical Sciences,2003,51(2):195-204. |
| Click to display the text | |
| [9] | ZHAO G W, SUN L,TAN S P,et al.Librational characteristics of a dumbbell modeled tethered satellite under small,continuous,constant thrust[J].Proceedings of the Institution of Mechanical Engineers,Part G:Journal of Aerospace Engineering,2013,227(5):857-872. |
| Click to display the text | |
| [10] | 孙亮,赵国伟,黄海,等. 面内轨道转移过程中的绳系系统摆振特性研究[J].航空学报,2012,33(7):1245-1254. SUN L,ZHAO G W,HUANG H,et al.Analysis of librational and vibrational characteristics for tethered systems during orbital transfer in plane[J].Acta Aeronautica et Astronautica Sinica,2012,33(7):1245-1254(in Chinese). |
| Cited By in Cnki (2) | Click to display the text | |
| [11] | SUN L,ZHAO G W, HUANG H.Stability and control of tethered satellite with chemical propulsion in orbital plane[J].Nonlinear Dynamics,2013,74(4):1113-1131. |
| Click to display the text | |
| [12] | SANTANGELO A. Optimal attitude control of a tethered end mass in the earth's upper atmosphere:AIAA-1997-0533[R].Reston:AIAA,1997. |
| [13] | 王晓宇,金栋平. 计入姿态的绳系卫星概周期振动[J].振动工程学报,2010,23(4):361-365. WANG X Y,JIN D P.Quasi-periodic oscillation of a tethered subsatellite with attitude[J].Journal of Vibration Engineering,2010,23(4):361-365(in Chinese). |
| Cited By in Cnki (8) | Click to display the text | |
| [14] | ZHAO G W, TANG B,SUN L,et al.Effect and control of pendular motion of abandoned satellite on tether drag system[J].Applied Mechanics and Materials,2014,513:3900-3906. |
| Click to display the text | |
| [15] | 钟睿,徐世杰. 基于直接配点法的绳系卫星系统变轨控制[J].航空学报,2010,31(3):572-578. ZHONG R,XU S J.Orbit-transfer control for TSS using direct collocation method[J].Acta Aeronautica et Astronautica Sinica,2010,31(3):572-578(in Chinese). |
| Cited By in Cnki (7) | Click to display the text | |
| [16] | 刘海颖. 微小卫星姿态控制系统关键技术研究[D].南京:南京航空航天大学,2008:23-30. LIU H Y.Research on attitude control system key technologies for micro-satellite[D].Najing:Nanjing University of Aeronautics and Astronautics,2008:23-30(in Chinese). |
| Cited By in Cnki (17) | |
| [17] | MENON C, KRUIJFF M,VAVOULIOTIS A.Design and testing of a space mechanism for tether deployment[J].Journal of Spacecraft & Rockets,2007,44(4):927-939. |
| Click to display the text |
