在METRIC模型理论的基础上,许多****对基本METRIC模型的假设进行了扩展,并对METRIC模型的求解方面进行了改进。Graves[3]采用负二项分布替代泊松分布来描述基层期望缺货值,推出了VARI-METRIC模型。Muckstadt[4]把装备的系统结构体现到模型中,建立了MOD-METRIC模型。Diaz和Fu[5]以及Lau和Song[6]放宽了维修资源无限的假设,拓展了METRIC模型。Sleptchenko等[7]扩展了VARI-METRIC模型,研究了备件网络中维修优先级的影响。
基本METRIC模型的假设是需求服从稳态泊松分布,适合于解决需求固定状态下多类备件配置优化问题。建立在稳态的泊松分布的故障率上的这种方法在初期较好地解决了对需求率的计算,然而随着研究的深入,人们发现这种方法所计算的需求率总是会高于实际值,从而对备件的保障产生影响。在许多情况下,发现当一个部件故障时,它会影响在同一系统中的其他部件的使用。而故障部件被送到维修站后,这个系统剩余部件就不再继续工作,这意味着这些部件在系统被修复这段时间将不会产生新的备件需求。这一现象被称为passivation[8]。
Hillestad[9]提出了DYNA-METRIC模型,使用非稳态的复合泊松分布过程,得到实际的初始备件供应环境的动态特征。Slay等[10]建立了飞机持续性模型(ASM),研究了两级、单层次、多备件在维修资源有限、需求不固定情况下的备件配置优化问题。张衡等[11]利用离散事件仿真,提出了一种考虑时变需求的可修备件库存模型。但是,这些模型只能处理任务强度随时间变化的情形,而不是passivation。
为了提高优化模型的计算效率,部分****引入了动态算法[12]来进行复杂计算。但是动态规划方法只能适用于单级模型或者有限的备件数,更为主流的算法是凸优化算法[13-14]。但是当引入时间参数后,目标函数在整个时域内不一定都满足凸性条件,只有在不满足凸性的时间段上进行凸构造,然后才能继续使用凸优化方法进行求解。
本文以费用约束下的时变可用度为目标函数,根据扩展帕姆定理[15]将当前时刻之前时段的累积需求率糅合入泊松分布的形状参数,建立考虑备件累积需求率的凸优化算法,得到每一时段的最优配置方案。然后利用众数法,选择适当的全局库存策略。
1 优化模型 在考虑passivation的情况下,备件的实际需求率依赖于可用系统的数量,而系统的可用数量又受前一时刻瞬时可用度的影响。备件i的时变需求率λi(t)为
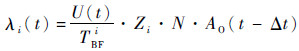 | (1) |
式中:U(t)为根据时间t变化的使用率;Zi为备件LRUi的安装数;N为系统数量;Δt为2次计算的时间间隔;TBFi为备件i的平均故障间隔时间;AO(t)为时变可用度。
把时间段分为n段(n+1个时间点,t0,t1,…,tj,…,tn)。假设时间间隔足够小,认为λip(tj)在(tj-1,tj)时间段内是固定值。
根据扩展帕姆定理且假设修理时间服从指数分布,备件i在tn时刻的期望在修件数E[Ri(tn)]为
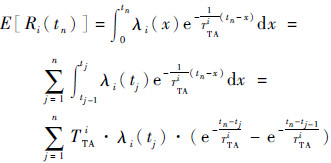 | (2) |
式中:TTAi为备件i的平均周转时间。
如果备件i的库存为si,其时变期望短缺量EBO(si,t)为
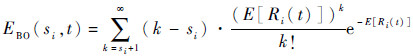 | (3) |
所以备件i的保障可用度AMi(t)为
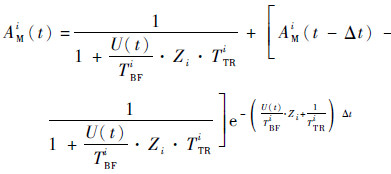 | (4) |
式中:TTRi为备件i的平均修复时间。
最后,时变可用度AO(t)可以通过式(5)求得。如此可以通过迭代求出各时刻的可用度,从而求出每个时刻的瞬时需求率。
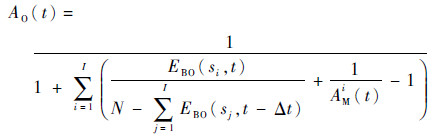 | (5) |
式中:I为备件种类数。
如引言所述,费用约束下的最优库存是随时间变化的。为了得到每一时段的最优库存,建立时变优化模型:
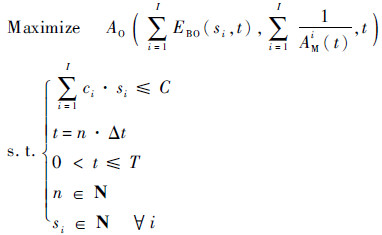 |
式中:ci为备件i的单价;C为最大可接受费用;EBO(si,t)为期望短缺量。
本模型有3点假设:
1) 备件的故障时间服从指数分布。
2) 库存策略为可修产品的及时送修策略——(s-1,s)策略。
3) 除备件外,其他维修资源均供应充足且维修都是成功的。
2 优化算法 2.1 EBO(si,t)凸函数分析 在将时间变量引入期望备件短缺数后,时变EBO(si,t)是一个含有2个变量的函数。因为可用度在整个任务周期内是不断变化的,为了满足费效下的最优配置,需要不停得对库存进行优化再分配,显然相邻两时刻的优化方案没有直接连贯性,从而时变EBO(si,t)在时间维上很可能不是凸的。判断EBO(si,t)的凸性,可从它的偏导矩阵
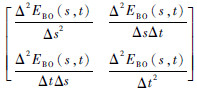
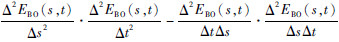
不总是大于或者小于0,所以时变EBO(si,t)不是一个凸函数。
为了应用凸优化方法解决该模型,需要移除时间参数并保证EBO(si,t)在固定时刻是凸函数。
虽然EBO(si,t)不是凸函数,但只要EBO(si)是凸函数,就可以通过在算法中做出相应的改进,令优化模型按凸规划的解法求出全局最优解。下面移除时间参数并证明EBO(si,t)在固定时刻是凸函数。
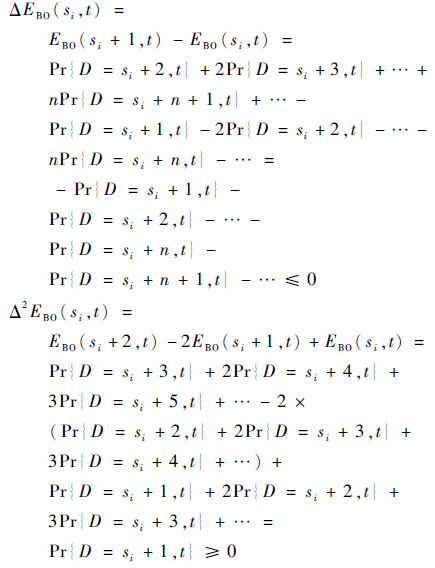 |
式中:D为在修件数量。
由以上证明可知EBO(si,t)虽然不是凸函数,但EBO(si,t)在固定时刻是凸函数。又因为EBO越小,AO就越大。所以AO在固定时刻也是凸函数。
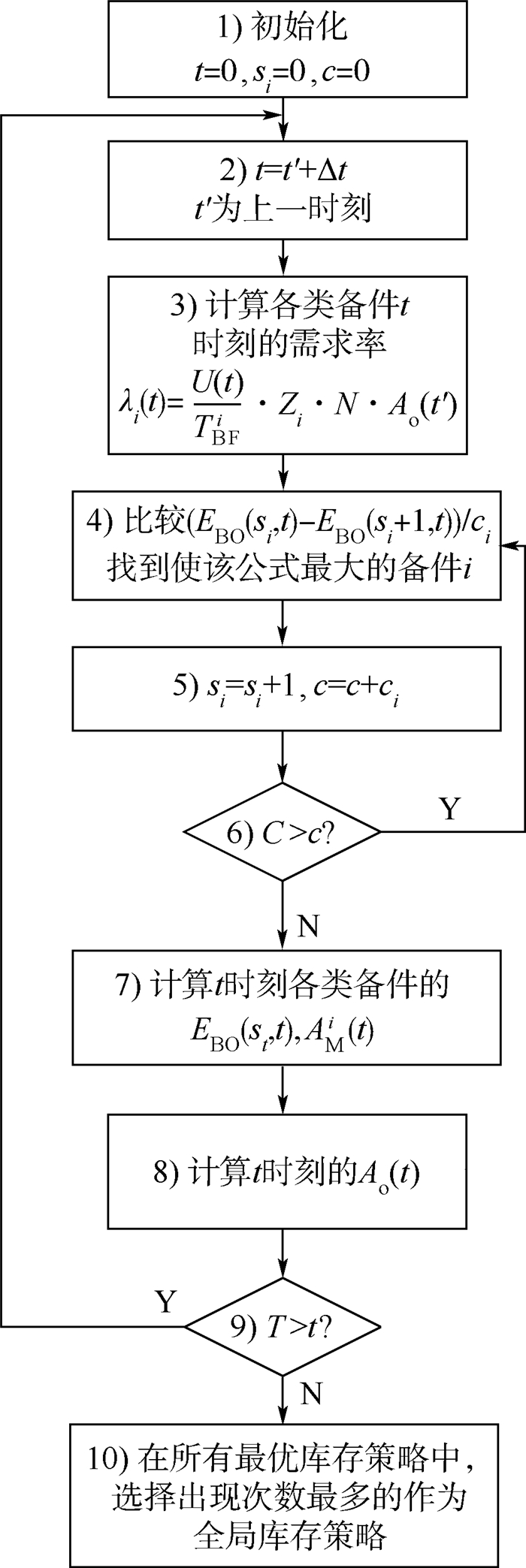
2.2 算法设计 在第2.1节已说明时变备件短缺数在时间维不具备凸性,当时间发生改变时备件的最优方案是会变动的,从而在每个时刻对备件进行优化,得到最优的方案,然后计算得出当前所能达到的最大可用度作为下一时刻需求率的输入。假设时间t是从0时刻到T时刻的连续变量,为了能对时间维进行优化,首先需要对连续变量t离散化,将整个任务周期分为N段,标为n=1,2,…,N。如果每个时刻的需求率可以看作是一个常量,并且每个时间间隔足够小从而误差尽量小。在每个时间间隔内,就可以用边际分析法对备件库存进行优化。这样,就得到了每个时刻的最优库存配置。优化算法流程如图 1所示。
 |
| 图 1 优化算法流程 Fig. 1 Optimization algorithm flowchart |
| 图选项 |
虽然最优库存配置是随时间变化的,但在实际中不可能在短时间内随便改变备件的库存数。所以需要选择一种库存配置,保证该配置通常是最优的,并使可用度在费用的约束下,始终保持在一个较高的水平。具体流程如下所示:
1) 初始化备件库存、时间和备件总费用(c)。
2) 时间推到下一时刻。
3) 根据式(1),计算此时刻各类备件的需求率。
4) 比较(EBO(si,t)-EBO(si+1,t))/ci,找到使该公式值最大的备件种类。
5) 第i类备件的库存加1,总费用加ci。
6) 当备件总费用小于最大可接受费用(C)时,跳至步骤4),否则进行步骤7)。
7) 根据式(2)~式(4),计算此时刻的EBO(si,t)和AiM(t)。
8) 根据式(5),计算此时刻的AO(t)。
9) 当前时刻小于规定计算时长(T)时,回到步骤2),否则进行步骤10)。
10) 在得到的每时刻最优库存配置中,选择出现次数最多的配置,作为时长T内的全局库存策略。
3 应用案例 首先,证明本文提出的时变模型适用于不考虑passivation的情况。在零库存下,利用时变模型计算稳态EBO和AO,并将计算结果与通过METRIC模型得到的结果进行比较。接下来,将passivation引入到EBO的计算过程,并分析其对库存的影响。最后,比较3种库存策略,证明全局库存策略选择方法的优越性。
3.1 不考虑passivation的凸优化方法 因为EBO和可用度AO之间可以互相转化,所以将EBO作为目标函数,并且它能反映每种备件的变化。使用表 1的示例,将本文使用的时变EBO和经典METRIC模型的稳态EBO进行比较,分析两者之间的差异。表 1为外场可更换单元(Line-Replaceable Unit,LRU)的可靠性参数。
表 1 LRU的可靠性参数 Table 1 Reliability parameters of LRU
| 备件种类 | 维修时间/h | 故障间隔时间/h | 周转时间/h | 安装数 |
| LRU1 | 1 | 400 | 220 | 2 |
| LRU2 | 1 | 500 | 200 | 3 |
| LRU3 | 1 | 400 | 220 | 2 |
| LRU4 | 1 | 500 | 200 | 3 |
| LRU5 | 1 | 440 | 180 | 2 |
| LRU6 | 1 | 400 | 200 | 1 |
| LRU7 | 1 | 500 | 220 | 2 |
| LRU8 | 1 | 440 | 190 | 1 |
| LRU9 | 1 | 400 | 200 | 1 |
| LRU10 | 1 | 440 | 180 | 2 |
表选项
假设有10架飞机去执行任务且任务的利用率U(t)≡U=0.3。图 2为零库存下时变EBO和稳态EBO的变化情况,由图可知时变EBO随着时间上升并且当时间趋于1 000 h时其值和稳态EBO相近。EBO1~EBO10为备件1~备件10的时变EBO。
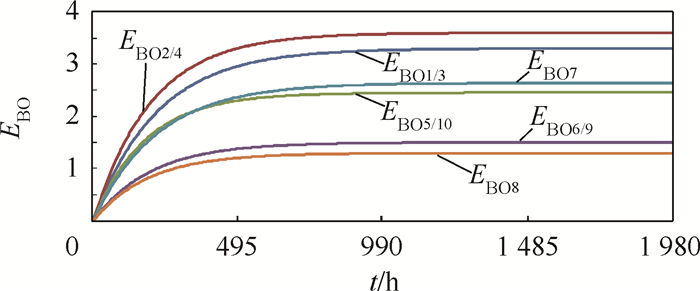 |
| 图 2 零库存下的时变EBO Fig. 2 EBO as a function of time under situation of zero inventory |
| 图选项 |
然后为每类备件增加库存数并通过凸优化算法去比较时变模型和经典METRIC模型的差别,如表 2所示。
表 2 时变模型和METRIC模型的优化库存 Table 2 Optimal inventory under time-varying model and METRIC
| 备件种类 | 时变库存 | METRIC | ||||
| 5 h | 120 h | 150 h | 225 h | 405 h | ||
| LRU1 | 3 | 4 | 4 | 4 | 4 | 4 |
| LRU2 | 4 | 4 | 5 | 5 | 5 | 5 |
| LRU3 | 3 | 3 | 3 | 3 | 4 | 4 |
| LRU4 | 4 | 4 | 4 | 4 | 4 | 4 |
| LRU5 | 3 | 3 | 3 | 2 | 2 | 2 |
| LRU6 | 3 | 2 | 2 | 3 | 2 | 2 |
| LRU7 | 3 | 4 | 3 | 4 | 4 | 4 |
| LRU8 | 2 | 2 | 2 | 2 | 2 | 2 |
| LRU9 | 3 | 2 | 2 | 2 | 2 | 2 |
| LRU10 | 3 | 4 | 4 | 4 | 4 | 4 |
表选项
时变库存下每类备件的最初优化库存集合都是平均分配的,随着时间转移,需求率增加,可用度降低,每类备件的库存发生巨大变化,备件的购置趋向于那些对当前可用度提升最大的备件,并且从405 h开始,最优的备件库存和稳态的一致。
3.2 考虑passivation的凸优化算法 因为passivation的影响,没有工作的备件被认为在处于工作状态,从而导致备件的需求被高估,所以通过METRIC模型计算的备件可用度会被低估。图 3为passivation对可用度的影响。
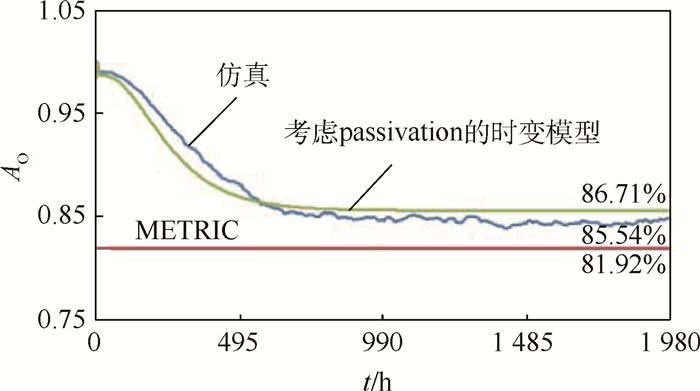 |
| 图 3 Passivation对可用度的影响 Fig. 3 Effect of passivationon on availability |
| 图选项 |
图 3中时变模型和仿真计算的结果非常相似,只有非常小的误差。而METRIC模型计算得出的可用度值低于考虑passivation的时变模型或仿真值。
因为passivation指的是因其他备件故障而导致停止工作的完好件,如果可用装备数比较多,passivation的影响是非常小的,并且最优库存也会比较相近。然而,当可用度比较低时,passivation将会非常明显地影响最优库存。
基于表 1所示的各备件的可靠性参数,并设利用率为0.3,考虑/不考虑passivation的时变最优库存如表 3所示。
表 3 U=0.3时考虑/不考虑passivation的时变最优库存 Table 3 Optimal time-varying model inventory with/without passivation for U=0.3
| 备件种类 | 考虑/不考虑passivation的时变最优库存 | |||||
| 5 h | 80 h | 150 h | 225 h | 405 h | 465 h | |
| LRU1 | 3/3 | 4/4 | 4/4 | 4/4 | 4/4 | 4/4 |
| LRU2 | 4/4 | 4/4 | 4/5 | 5/5 | 5/5 | 5/5 |
| LRU3 | 3/3 | 3/3 | 3/3 | 3/3 | 3/4 | 4/4 |
| LRU4 | 3/3 | 4/4 | 4/4 | 4/4 | 4/4 | 4/4 |
| LRU5 | 3/3 | 3/3 | 3/3 | 3/3 | 2/2 | 2/2 |
| LRU6 | 3/3 | 2/2 | 2/2 | 2/2 | 2/2 | 2/2 |
| LRU7 | 3/3 | 3/3 | 4/3 | 3/3 | 4/4 | 4/4 |
| LRU8 | 3/3 | 2/2 | 2/2 | 2/2 | 2/2 | 2/2 |
| LRU9 | 3/3 | 2/2 | 2/2 | 2/2 | 2/2 | 2/2 |
| LRU10 | 3/3 | 4/4 | 4/4 | 4/4 | 4/4 | 4/4 |
表选项
当时间趋向无穷大时,此刻库存下的可用度为85.54%,并且这两组库存的差别很小。接下来将利用率增加到0.45和0.6并观察可用度的变化情况。利用率U为0.45和0.6时passivation对备件库存的影响分别如表 4和表 5所示。
表 4 U=0.45时考虑/不考虑passivation的时变最优库存 Table 4 Optimal time-varying model inventory with/without passivation for U=0.45
| 备件种类 | 考虑/不考虑passivation的时变最优库存 | |||||
| 5 h | 80 h | 150 h | 225 h | 405 h | 465 h | |
| LRU1 | 3/3 | 4/4 | 4/4 | 4/4 | 4/4 | 4/4 |
| LRU2 | 4/4 | 5/5 | 5/5 | 5/5 | 5/6 | 5/6 |
| LRU3 | 3/3 | 3/3 | 3/3 | 3/4 | 4/4 | 4/4 |
| LRU4 | 3/3 | 4/4 | 4/4 | 4/4 | 4/4 | 4/4 |
| LRU5 | 3/3 | 3/3 | 3/3 | 2/2 | 2/2 | 2/2 |
| LRU6 | 3/3 | 2/2 | 2/2 | 2/2 | 2/2 | 2/2 |
| LRU7 | 3/3 | 3/3 | 3/3 | 4/4 | 4/4 | 4/4 |
| LRU8 | 3/3 | 2/2 | 2/2 | 2/1 | 2/1 | 2/1 |
| LRU9 | 3/3 | 2/2 | 2/2 | 2/2 | 2/2 | 2/2 |
| LRU10 | 3/3 | 4/4 | 4/4 | 4/4 | 4/4 | 4/4 |
表选项
表 5 U=0.6时考虑/不考虑passivation的时变最优库存 Table 5 Optimal time-varying model inventory with/without passivation for U=0.6
| 备件种类 | 考虑/不考虑passivation的时变最优库存 | |||||
| 5 h | 115 h | 130 h | 175 h | 355 h | 385 h | |
| LRU1 | 3/3 | 4/4 | 4/4 | 4/4 | 4/5 | 4/5 |
| LRU2 | 4/4 | 5/5 | 5/5 | 5/6 | 6/7 | 6/7 |
| LRU3 | 3/3 | 3/3 | 3/3 | 3/4 | 4/3 | 4/4 |
| LRU4 | 3/3 | 4/4 | 4/4 | 4/4 | 4/4 | 4/4 |
| LRU5 | 3/3 | 3/2 | 2/3 | 3/2 | 2/1 | 2/0 |
| LRU6 | 3/3 | 2/2 | 2/2 | 2/2 | 2/2 | 2/2 |
| LRU7 | 3/3 | 3/4 | 4/4 | 4/4 | 4/5 | 4/5 |
| LRU8 | 3/3 | 2/2 | 2/1 | 1/1 | 1/1 | 1/1 |
| LRU9 | 3/3 | 2/2 | 2/2 | 2/2 | 2/2 | 2/2 |
| LRU10 | 3/3 | 4/4 | 4/4 | 4/4 | 4/5 | 4/5 |
表选项
当利用率上升时,稳态下的最终库存差别很大。下面比较这2组库存下的可用度。U=0.45和U=0.6时考虑/不考虑passivation的AO变化如图 4所示。
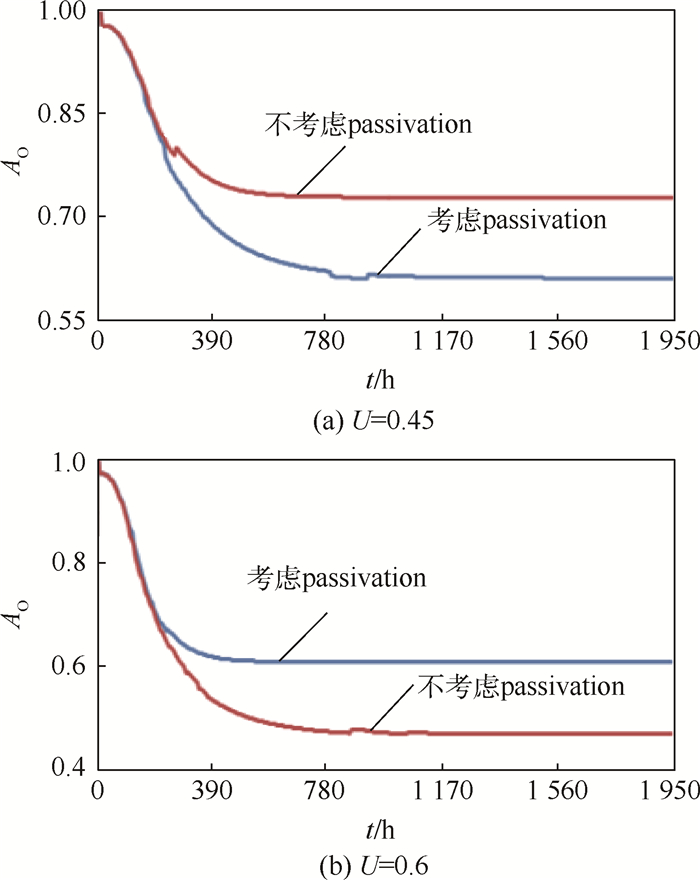 |
| 图 4 U=0.45和U=0.6时考虑/不考虑passivation的AO Fig. 4 AO with/without passivation when U=0.45 and U=0.6 |
| 图选项 |
基于图 4可以看出passivation对可用度的影响非常大,特别是在高强度的任务条件下(任务利用率高且可用度低)。
3.3 全局库存策略的选择 在相同的费用约束下,备件的最优库存配置是随时间变化的。但当时间间隔很小时,不可能频繁地改变备件的库存数量,所以需要选择一种全局最优库存配置,保证该配置通常是最优的。
在这里,以利用率0.6为例,运用众数法,选择出现次数最多的配置作为全局最优库存策略。全局最优库存策略如表 6所示。同时也引入了初始库存(0时刻)和稳态库存来做比较。
表 6 库存配置 Table 6 Stock allocation
| 备件种类 | 库存水平 | ||
| 全局最优 | 初始库存 | 稳态库存 | |
| LRU1 | 4 | 3 | 4 |
| LRU2 | 5 | 3 | 5 |
| LRU3 | 3 | 3 | 4 |
| LRU4 | 4 | 3 | 4 |
| LRU5 | 3 | 3 | 2 |
| LRU6 | 2 | 3 | 2 |
| LRU7 | 3 | 3 | 4 |
| LRU8 | 2 | 3 | 2 |
| LRU9 | 2 | 4 | 2 |
| LRU10 | 4 | 3 | 4 |
表选项
下面,比较这3种库存策略下的AO(t),如图 5所示。
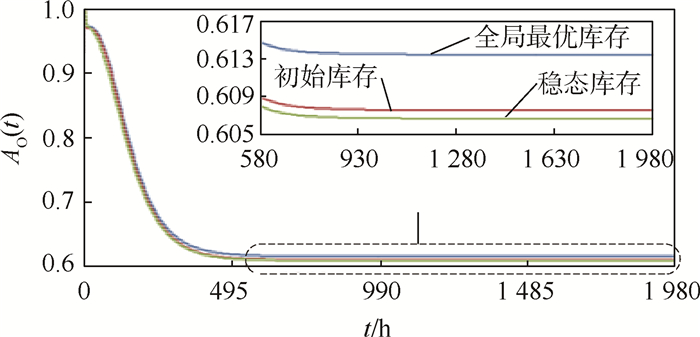 |
| 图 5 3种库存策略下的AO(t) Fig. 5 AO(t) for 3 inventory policies |
| 图选项 |
从图 5中可以看出:在全局最优库存配置下,可用度始终保持在一个较高的水平。在前240 h,初始库存要优于全局最优库存;但在240 h以后,全局最优库存策略要明显优于其他2种策略。
4 结 论 1) 考虑passivation对可用系统数量的影响,在稳态库存的基础上,引入时间变量,建立了时变库存优化模型。
2) 研究基于非稳态备件需求下的备件库存优化方法,并构建了考虑passivation的时变优化应用案例,为时变优化分析工作的开展提供了一套可行的优化方法。
下一步的工作将着眼于考虑更多的维修资源以及资源相关性,建立维修能力有限的时变优化模型。
参考文献
| [1] | SHERBROOKE C C. METRIC:A multi-echelon technique for recoverable item control[J]. Operations Research,1968, 16(2): 122–141. |
| Click to display the text | |
| [2] | 郭峰, 刘臣宇, 李元垒. 基于边际分析法的可修复备件最优库存研究[J]. 价值工程,2010, 29(14): 95–96.GUO F, LIU C Y, LI Y L. Optimal inventory research of repairable spares based on marginal analysis method[J]. Value Engineering,2010, 29(14): 95–96.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [3] | GRAVES S. A multi-echelon inventory model for a repairable item with one-for-one replenishment[J]. Management Science,1985, 31(10): 1247–1256. |
| Click to display the text | |
| [4] | MUCKSTADT J. A model for multi-item,multi-echelon,multi-indenture inventory system[J]. Management Science,1973, 20(4): 472–481. |
| Click to display the text | |
| [5] | DIAZ A, FU M C. Models for multi-echelon repairable item inventory systems with limited repair capacity[J]. European Journal of Operational Research,1997, 97(1): 480–492. |
| Click to display the text | |
| [6] | LAU H C,SONG H.Two-echelon repairable item inventory system with limited repair capacity under non-stationary demands[C]//Proceedings of 35th Meeting of the Decision Sciences Institute (DSI).Boston:Research Collection School of Information Systems,2004,11:1901-1908. |
| Click to display the text | |
| [7] | SLEPTCHENKO A, VAN DER HEIJDEN M C, VAN HARTEN A. Using repair priorities to reduce stock investment in spare part networks[J]. European Journal of Operational Research,2005, 163(3): 733–750. |
| Click to display the text | |
| [8] | LAU H C, SONG H, SEE C T, et al. Evaluation of time-varying availability in multi-echelon spare parts systems with passivation[J]. European Journal of Operational Research,2006, 170(1): 91–105. |
| Click to display the text | |
| [9] | HILLESTAD R J. Dyna-METRIC:Dynamic multi-echelon technique for recoverable item control.3rd ed[M].Santa Monica,CA: Rand Corporation, 1982: 61-71. |
| Click to display the text | |
| [10] | SLAY F M,BACHMAN T C,KLINE R C,et al.Optimizing spares support,the aircraft sustainability model:ADA320502[R].Mclean,VA:Logistics Management Institute,1996:1-19. |
| Click to display the text | |
| [11] | 张衡, 花兴来, 许绍杰. 可修复备件系统库存决策仿真优化模型[J]. 系统工程与电子技术,2009, 31(6): 1510–1514.ZHANG H, HUA X L, XU S J. Simulation optimization model of inventory decision for repairable spares systems[J]. Systems Engineering and Electronics,2009, 31(6): 1510–1514.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [12] | SARANGA H, KUMAR U D. Optimization of aircraft maintenance/support infrastructure using genetic algorithms-level of repair analysis[J]. Annals of Operations Research,2006, 143(1): 91–106. |
| Click to display the text | |
| [13] | NENES G, PANAGIOTIDOU S, TAGARAS G. Inventory management of multiple items with irregular demand:A case study[J]. European Journal of Operational Research,2010, 205(2): 313–324. |
| Click to display the text | |
| [14] | CAGGIANO K E, JACKSON P L, MUCKSTADT J A, et al. Efficient computation of time-based customer service levels in a multi-item,multi-echelon supply chain:A practical approach for inventory optimization[J]. European Journal of Operational Research,2009, 199(3): 744–749. |
| Click to display the text | |
| [15] | CARRILLO M J. Note-Extensions of Palm's theorem:A review[J]. Management Science,1991, 37(6): 739–744. |
| Click to display the text | |
