系统内的非定常流动,在瞬变条件发生初始会出现极短时间的大幅高频振荡特性,称之为瞬变流,视其幅值大小、频率高低和时间长短,分为强瞬变和弱瞬变2类[1, 2]。对于发动机来说,弱瞬变一般指发动机的常规加减速过程,气路参数的瞬变周期持续数s以上,远大于气流扰动在空气系统网络中的传播时间。而对于强瞬变过程,如发动机的突发失效,气路参数往往发生剧烈振荡,瞬变周期只有数ms到几百ms,与气流扰动在空气系统网络的传播时间同等量级。此时,强瞬变容易发生,在此瞬变过程中,空气系统高压力梯度的气流扰动将在空气系统管路系统中传播和反射。空气系统强瞬变特性主要受容腔和管路的耦合振荡所主导,并且与容腔和管路几何参数密切相关,所以通过合适的几何参数的选择可以避免或削弱此强瞬变过程。而容腔和管道基本模型的准确建立是此强瞬变研究的基础。Dutton和Coverdill[3]针对非定常、可压缩气体的单腔充放气进行了实验，在阻塞和未阻塞的工作条件下对比了绝热模型和等熵模型的区别。2007年，Thorncroft等[4]建立了1个可以预测在充放气过程中箱内压力和温度变化的模型。模拟空气是个多变过程。通过模型和实验过程相比较经验确定多变指数n约为1.17。直到2009年,Calcagni和Gallar[5, 6, 7]建立了瞬态空气系统模型。将系统看成是一系列腔和管道组成的。分别对于管道、单腔、双腔和De Halle模型用流体网络法建立了模型并进行了瞬态下压力变化的计算,结果与实验数据吻合的很好。并分析了轴失效条件下的轴向力变化。但是,并没有考虑容腔管道耦合下的管道压力波动。
国内吕亚国等[8]发展了一种全新的航空发动机空气系统通用分析软件,网络具有自动识别技术,并考虑了网络的换热情况。然而关于空气系统的瞬态研究比较少,侯升平和陶智[9, 10, 11]做了关于压力修正方法和积分方法的非稳态空气系统求解,但是关于瞬态容腔和管道内压力波动的分析很少。刘传凯等[12]针对强瞬变空气系统,提出了一种模块化的建模方法,并且通过双腔和De Halle模型验证了算法的准确性。另外压力瞬变的强度与时间和元件的几何尺寸有很大的影响。基于这方面的考虑,为了分析发动机容腔和管道内的压力变化强度和时间,就需要对瞬变过程下的压力变化规律有很好的预测。所以,本文将建立由容腔、管道组成的空气系统基本瞬变单元,针对突发失效下的强瞬变过程进行研究,在模型校验的基础上,给出管道不同位置的压力变化。然后,分析几何偏差对空气系统强瞬变特性的影响规律。为发动机在突发情况下的瞬变强度提供参考。
1 建模方法本文在之前国内传统的稳态流体网络法[13, 14]基础上增加了描述容积效应和流体惯性力的控制方程,同时,基于模块化的建模思想将空气系统分为节点元件、容腔元件、管道元件和节流元件4类。各元件的控制方程如下。
1)管道元件管道元件具有一定的体积,所以在瞬变过程时,管道内气体的惯性和压缩性可能导致沿程气体参数出现剧烈突变。假设管道各截面处的面积相等。则质量方程为
式中:wi为进口质量流量;wo为出口质量流量;m为气体质量;t为时间。
能量方程一般为
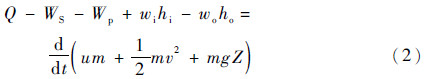
式中:Q为与外界的能量交换;WS为剪切功;Wp为管道体积变化下压力所做的功;um为内能,u为单位气体内能;
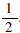mv2为系统的动能,v为管道内气体平均速度;mgZ为系统的势能,g为重力加速度,Z为相对位置;hi和ho分别为元件进、出口单位气体总焓。在此管道开口系统中,不考虑与外界的热量交换和功交换,并且在计算时不考虑系统中的势能和体积的变化。所以能量方程简化为
动量方程为
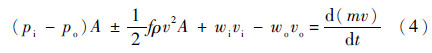
式中:左端第1项为压力项,po为出口静压力,pi为进口静压力;左端第2项为阻力项,A为管道的横截面积,阻力系数
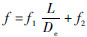,L为管道长度，f1为摩擦阻力系数,De为管道的当量直径,f2为局部阻力系数[15, 16],主要考虑管道进出口截面突然扩张或收敛造成的总压损失,另外,“+”表示逆流,即与预定的方向相反,“-”表示顺流,即与预定的方向相同;左端第3项为进出口的单位时间动量之差,2)节流元件空气系统中的蓖齿封严、小孔和缝,轴向间隙等阻力单元的内部空间微小,容积和气体惯性均可以忽略。节流元件在顺流和逆流状态下的进、出口质量流量与气体参数的定性关系可分别表示为式(5)的通用形式:
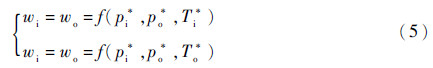
式中:pi*和po*分别为节流元件上游和下游节点总压,分别取值相邻容腔元件或节点元件的试给总压;Ti*和To*分别为节流元件上游和下游的来流总温。
3)节点元件一般为虚拟连接点,包括内部节点和边界节点。节点元件一般不考虑体积,因此方程是不带时间项的质量和能量平衡方程。假设内部节点与M个支路连接,其方程为
式中:wj和hj分别为节点元件第j个支路的质量流量和单位气体总焓。而边界节点则需考虑边界流量和能量,只需在上述方程中添加1项即可。
式中:wb为边界质量流量;hb为边界单位气体总焓。
4)容腔元件一般为空气系统内体积较大的容腔。容腔内部气体参数只与时间有关,与空间无关。由于有容腔效应的影响,会造成容腔的质量和能量的存储,所以连续方程、能量方程与节点元件不同。假设容腔元件与M个支路连接,其方程为
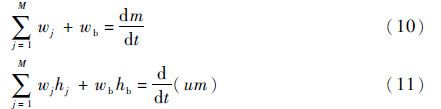
此节简要说明了各个元件的建模思路及控制方程。详细的建模思路可参考文献[12]。
2 双腔模型研究流体网络法是计算发动机空气系统的基本方法,本文在传统网络法的基础上增加容腔与管道元件,在Visual Studio 2010上编写的面向对象的空气系统可压缩流的网络法程序。鉴于容腔元件的容腔效应和管道元件内可压缩流体的惯性是压力波动的主要原因,所以这里简单的将压气机盘腔和涡轮盘腔通过管道连接组成双腔耦合模型进行研究。采用文献[6]中的双腔模型进行建模,并通过瞬变过程的对比来验证算法的准确性。管道动力系统中非定常流动工况是不可避免的,并且在一定条件下,具有压力波动的特性。所以,本文在此基础上考虑了管道不同位置的压力变化,并且对影响此压力波动的关键几何参数进行了分析。为了方便建模,模型基于绝热条件建立,并且没有考虑内部换热影响。主要原因是因为换热所需时间较长,而压力波动的动态变化过程也就在几ms到几百ms之间,鉴于换热在这段时间内的效果不明显,所以在分析时不考虑换热影响。
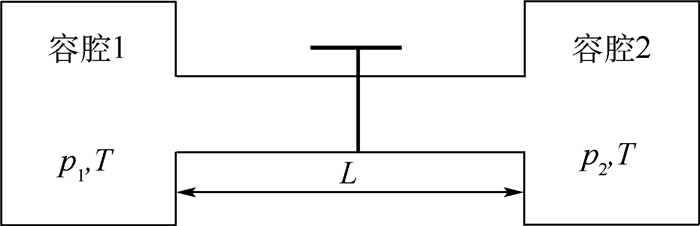
2.1 双腔模型验证及分析空气系统是由很多容腔和其他元件组成的。盘腔、卸荷腔等都可以用容腔元件模拟;空气系统中的管道、长轴间隙等都可以用管道元件来模拟。当发动机快速加速或发生突发失效时,由于容腔元件的容腔效应与管道元件中可压缩流体的惯性在一定条件下会产生压力波动。此压力波动可能影响某些部件的强度或使轴向力突然逆向、产生波动,可能会造成某些部件的损坏。因此,这里针对容腔和管道组成的双腔模型进行研究,了解其压力波动变化的规律。双腔模型如图 1所示。
 |
| 图选项 |
在文献[12]中,已经对此双腔模型进行了验证,容腔压力pc的对比结果见图 2。其中关键的几何参数如下:容腔1的初始压力为600 kPa,容腔2的初始压力为520 kPa,温度为600 K,容腔的体积为0.1 m3,管道流通面积为0.005 m2,长度为0.6 m,模型为绝热模型。此结果基本吻合,并且将作为之后几何参数影响对比的基本结果。另外,容腔的压力发生波动,且需要经过一段时间的振荡才会慢慢稳定下来,最终达到初始压力的中间值。此压力的波动可能造成某些继发性安全问题,而压力波的最大幅值将是本文关注的一个重要参数。基于此考虑,这里定义压力波动幅值的无量纲量来表征压力波动的强弱:
 |
| 图 2 容腔压力的变化对比[12] Fig. 2 Comparison of pressure changes of cavities[12] |
| 图选项 |
式中:pwm为压力波的最大幅值;ps为压力最终稳定的值。a越大表示压力波峰值越大,越容易发生不安全问题。由图 2中的压力变化结果求得a=0.028。
另外对于瞬态模型的计算,时间步长的选取很重要。步长太长,不易描述其完整的动态响应过程,步长太短又影响计算效率,所以合理的时间步长的选取很重要。文献[5]中,在管道模型的计算时,给出了管道的时间步长选取范围:
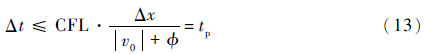
式中:φ为声速;v0为初始速度;0.5≤CFL<1;tp为管道的特征时间常数;Δx为管道单元之间的长度。对于容腔来说,由状态方程pV=mRT,p为静压力,R为气体常数,V为容腔的体积,对时间微分后,可得
式中:质量流量w=ρAv,ρ为密度。
对于绝热过程,温度和压力的关系为
式中:k为绝热指数。
将式(15)微分后,代入式(14),则
w=ρAv代入式(16),可得
式中:C为常数。
可见容腔的特征时间常数
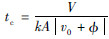。因此,对于此双腔模型的时间步长为
管道动力系统中非定常流动工况是不可避免的,并且在一定条件下,具有压力波动的特性。管道内可压缩流体的惯性力在某条件下将导致压力产生脉动,形成压力波。压力波动的形状与可压缩流体的惯性力有关。惯性力直接取决于质量的大小,质量越大,惯性越大,反之,惯性越小。在某些工程问题中,管道中压力的变化也是很重要的观察对象。但是,文献中并没有管道中压力的变化规律。本文采用将管道元件离散化的方法,分成20段管道元件,管道元件之间用节点元件连接。这样就可以观察管道不同位置的压力变化。模型如图 3所示。
 |
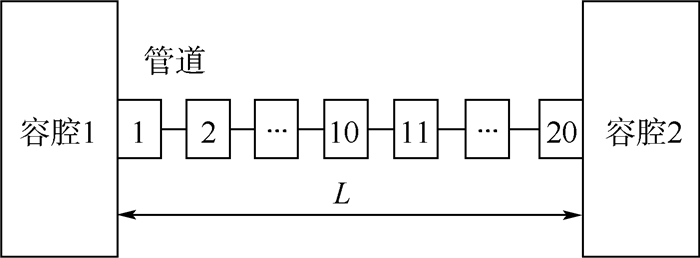| 图 3 管道离散化双腔模型 Fig. 3 Double-cavity model with pipe discretization |
| 图选项 |
假设规定流体的运动方向为从左向右。设x为沿流动方向的位移，则管道内初始压力为
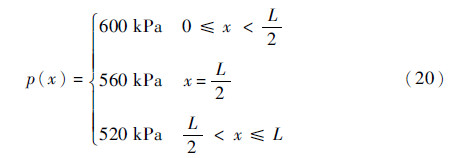
在t=0时刻打开阀门,观察管道内管道1、管道10、管道11和管道20 4个不同位置的静压变化,结果如图 4所示。
 |
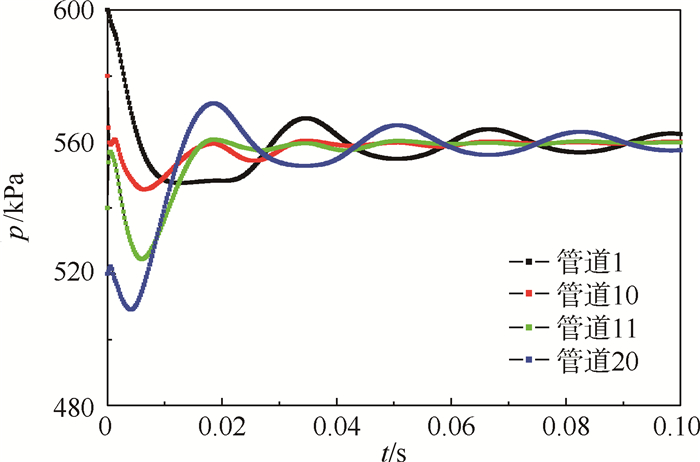| 图 4 管道不同位置的静压变化 Fig. 4 Static pressure changes in different positions of pipe |
| 图选项 |
从图 4结果可以看出,此系统在短时间内,管道静压力同样发生了波动,且不同位置的波动幅度不同,两端的波动幅度明显比中间位置的大,此时,a=0.021。中间位置的压力经过很短的时间就会稳定。另外刚开始管道中压力的下降主要是由于管道平均速度的快速增加造成的(见图 5)。刚开始,速度很快到最大值,导致管道11和管道20的总压的增加比速度增加的慢,所以其静压力一开始是下降的。管道1与管道10的总压一开始就是下降的,速度的快速增加,导致其压力下降更快。
 |
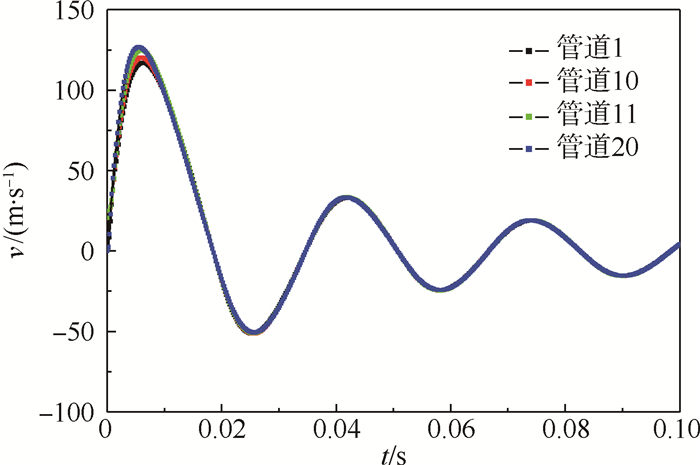| 图 5 管道不同位置的平均速度变化 Fig. 5 Mean velocity changes in different positions of pipe |
| 图选项 |
2.2 影响因素分析上述分析的压力波动主要与容腔元件的容积效应和管道元件内的流体惯性有关。容积效应主要与容腔的体积有关。流体惯性主要与管道内气体的质量有关,即与管道的几何流通面积和几何长度有关。因此,这里重点分析此3个几何参数对压力变化的影响。
2.2.1 管道长度影响分析将每段管道长度减小为原来的1/10,总管道长度为0.06 m,其他参数不变。按同样的方法计算,观察管道长度对容腔压力和管道静压的变化,结果如图 6和图 7所示。
 |
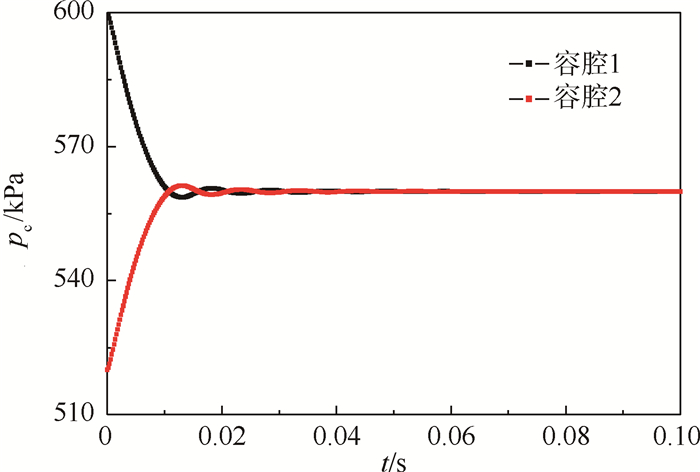| 图 6 管道长度变化后容腔压力的变化 Fig. 6 Pressure changes of cavities after change of pipe length |
| 图选项 |
 |
| 图 7 管道长度变化后管道不同位置的静压变化 Fig. 7 Static pressure changes in different positions of pipe after change of pipe length |
| 图选项 |
图 6中a=0.002 5，图 7中a=0.002 1,相比于图 2和图 4中的a值小了一个数量级。可见,管道长度减小时,管道内的流体惯性大幅减小,所以容腔和管道的压力波动幅度很小,并且很快达到平衡。如果管道长度继续减小,则压力波就不会产生了。管道内的静压只是在刚开始时有很大的不同,此主要受管道平均速度的影响。所以,管道长度的减小会减小压力波动的幅度,波动时间也大幅减小,进而可以削弱此强瞬变。
2.2.2 管道流通面积影响分析将每段管道元件的流通面积减为5×10-4 m2,其他参数全都不变,按同样的方法计算,观察其流通面积对容腔压力及管道静压的变化，结果如图 8和图 9所示。
 |
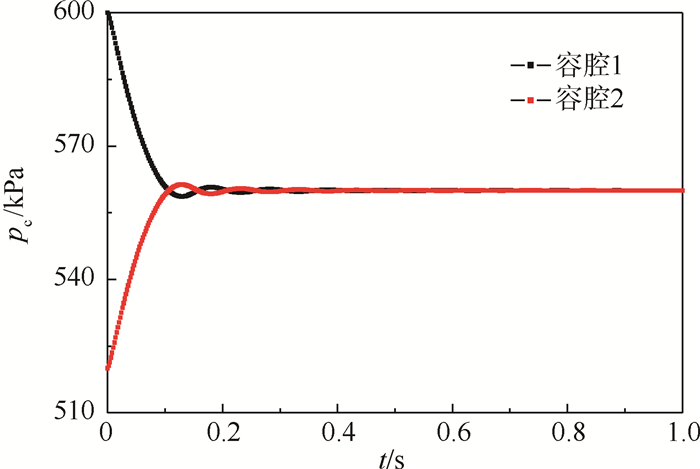| 图 8 管道流通面积变化后容腔压力的变化 Fig. 8 Pressure changes of cavities after change of pipe flow area |
| 图选项 |
 |
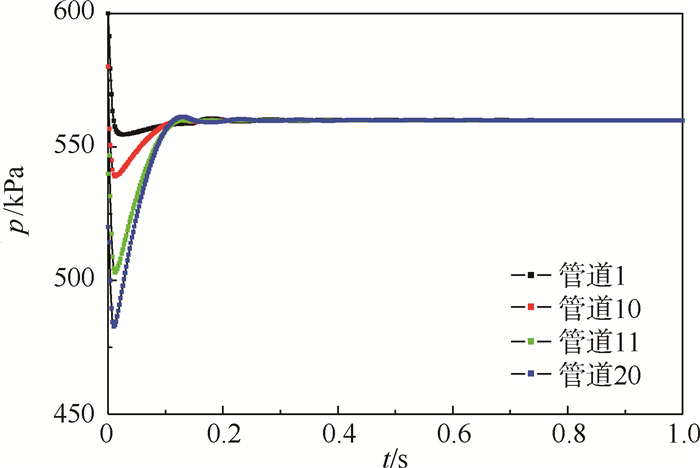| 图 9 管道流通面积变化后管道不同位置的静压变化 Fig. 9 Static pressure changes in different positions of pipe after change of pipe flow area |
| 图选项 |
图 8中a=0.002 4,图 9中a=0.002 2,相比于图 2和图 4中的a值减小。仿真结果反映出管道流通面积的缩小,可以减小振荡幅度,但是会增加达到平衡的时间。这主要是由于管道流通面积缩小时,管道中流体的质量减小,惯性较小,所以压力振荡幅度减小。同样如果管道流通面积减小到一定程度,则压力波不再产生。此外,管道流通面积的减小影响到管道的进口速度变小,从而需要较长的时间达到稳定。所以,管道流通面积越小,惯性越小,压力波振荡幅度越小,达到稳定的时间越长。
2.2.3 容腔体积影响分析将容腔元件的体积都减小为0.001 m3,其他参数不变,按同样的方法计算,观察其体积对容腔压力及管道静压的变化，结果如图 10和图 11所示。
 |
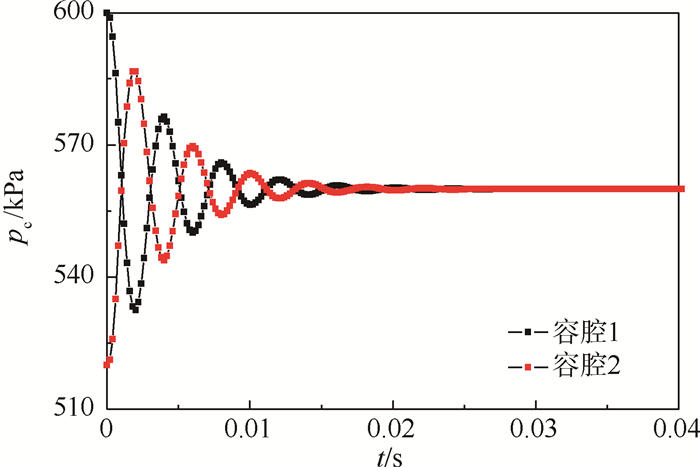| 图 10 两容腔体积都变化后容腔压力的变化 Fig. 10 Pressure changes of cavities after change of both cavity volume |
| 图选项 |
 |
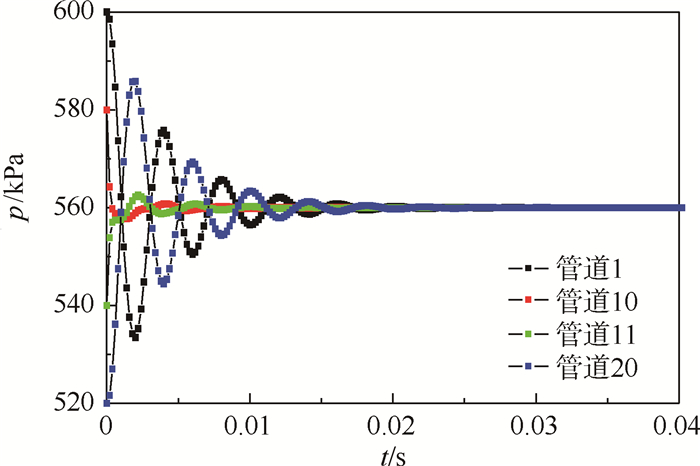| 图 11 两容腔体积都变化后管道不同位置的静压变化 Fig. 11 Static pressure changes in different positions of pipe after change of both cavity volume |
| 图选项 |
图 10中a=0.049,图 11中a=0.047,相比于图 2和图 4中的a值,明显增大。所以容腔体积的减小增加了容腔和管道压力的波动幅度,并且从图中10可以看出压力的波动频率明显增加,达到稳定的时间明显缩短。另外,图 11的管道11和管道20初始段压力已经不再下降,反而增加。主要是速度的增加已经落后于总压的增加速率。
空气系统中的容腔肯定不尽相同,只将容腔2的体积减小为0.001 m3,其他参数不变。如图 12所示。
 |
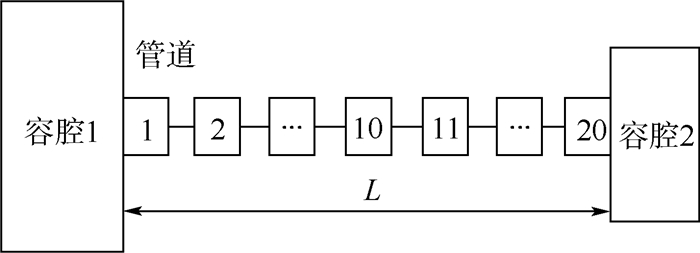| 图 12 容腔体积不相等的双腔模型 Fig. 12 Double-cavity model with different cavity volume |
| 图选项 |
按同样的方法计算,观察容腔体积对容腔压力及管道静压的变化，结果如图 13、图 14所示。
 |
| 图 13 容腔2体积变化后容腔压力的变化 Fig. 13 Pressure changes of cavities after volume change of cavity 2 |
| 图选项 |
 |
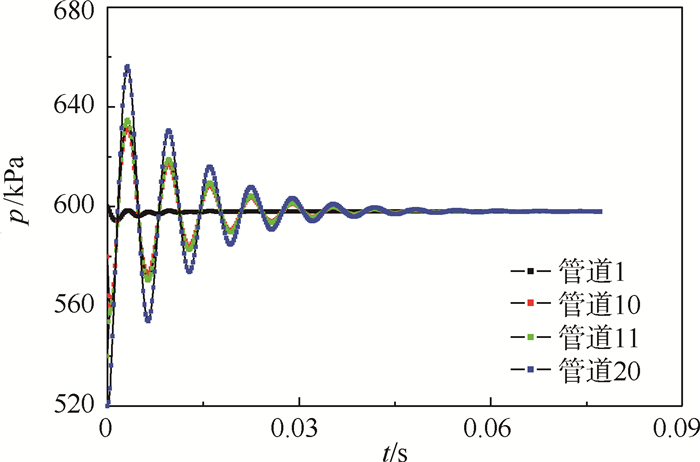| 图 14 容腔2体积变化后管道不同位置的静压变化 Fig. 14 Static pressure changes in different positions of pipe after volume change of cavity 2 |
| 图选项 |
图 13中a=0.173,图 14中a=0.171,相比与图 2和图 4的a值,明显增大。可见容腔2体积的减小,使系统波动幅度增大。两容腔的体积不再相等,导致两容腔的压力波动有很大的不同,容腔1的波动幅度变的很小,很快达到稳定,容腔2的波动幅度反而变的很大。管道不同位置的波动幅度不一样,管道1靠近容腔1,其波动与容腔1类似,沿着流动正方向,其波动幅度越来越大。说明容腔体积的减小,对容腔和管道的压力波动有很大的影响。体积小的一端,压力波动大,越靠近此容腔的管道压力波动幅度大。反之,体积大的一端,波动幅度小。另外,振荡频率有所不同,达到稳定的时间略有减小。
以上模型的计算可以看出所建立的流体网络法可以模拟空气系统瞬变的特性,为以后整机空气系统瞬变特性的研究奠定了基础。另外,为避免发动机失效时空气系统内压力波动的产生,或者是减小压力波动的振荡幅度,空气系统在设计时应注意这3个参数。合理的设计可以避免压力的波动,从而可以提高空气系统的可靠性和安全性。
3 结论本文针对瞬变空气系统,在Visual Studio平台上发展了具有面向对象的瞬变空气系统网络法程序,对管道元件与容腔元件组成的双腔模型进行了强瞬变过程分析。在与文献中数据基本吻合的情况下,将管道离散化处理,分析了管道不同位置的压力变化,并分析了关键元件的几何偏差对压力变化的影响。
1)管道中可压缩流体的流动惯性和容腔效应是瞬变压力波动的主要原因,管道长度越小,惯性越小,振荡幅度越小,可见波动强度越弱。
2)管道流通面积越小,惯性越小,振荡幅度越小,可见波动强度越弱。
3)若两容腔体积相等,则体积越小,则管道和容腔的压力波动振荡幅度越大,频率越快,达到稳定的时间越短。若两容腔体积不相等,则体积小的一端压力波动频率快,幅度大;体积大的一端,压力变化幅度小,频率小。通过模型分析的结论,采取合理的尺寸设计控制波动强度,为空气系统的安全防护提供一种新方法。
所建立的模型可以很好地模拟基本空气系统的瞬态压力变化规律，为以后整机空气系统的建模以及准确预测各截面的参数提供了很好的方法。
参考文献
| [1] | 徐晓菊. 动力系统中瞬变流动的特性研究[J].机械管理开发,2010,25(5):50-52. XU X J.On characteristic research of transient flow in dynamic system[J].Mechanical Management and Development,2010,25(5):50-52(in Chinese). |
| Cited By in Cnki | Click to display the text | |
| [2] | 郭建明. 管道动力系统中非定常流动特性[J].科技情报开发与经济,2006,16(9):179-181. GU J M.The characters of the unsteady flow in the dynamical system of the pipeline[J].SCI-TECH Information Development & Economy,2006,16(9):179-181(in Chinese). |
| Cited By in Cnki | Click to display the text | |
| [3] | DUTTON J C, COVERDILL R E.Experiments to study the gaseous discharge and filling of vessels[J].International Journal of Engineering Education,1997,13(2):123-134. |
| Click to display the text | |
| [4] | THORNCROFT G P, GORDON J S,GORDON R.Modeling compressible air flow in a charging or discharging vessel and assessment of polytropic exponent[C]//Proceedings of ASEE Annual Conference and Exposition,2007.Chantilly,VA:American Society for Engineering Education,2007:AC 2007-2695. |
| [5] | CALCAGNI C, GALLAR L.Development of a one dimensional dynamic gas turbine secondary air system model-Part I:Tool components development and validation[C]//Proceeding of ASME Turbo Expo 2009:Power for Land Sea and Air.New York:ASME Press,2009,4:457-465. |
| Click to display the text | |
| [6] | CALCAGNI C, GALLAR L.Development of a one dimensional dynamic gas turbine secondary air system model-Part II:Assembly and validation of a complete network[C]//Proceedings of ASME Turbo Expo 2009:Power for Land,Sea and Air.New York:ASME Press,2009,4:435-443. |
| Click to display the text | |
| [7] | GALLAR L, CALCAGNI C.Time accurate modelling of the secondary air system response to rapid transients[J].Journal of Aerospace Engineering,2011,225(8):946-958. |
| Click to display the text | |
| [8] | 吕亚国,刘振侠, 黄生勤.航空发动机内流空气系统通用分析软件开发[C]//全国博士生学术论坛.北京:计算机仿真出版社,2009:99-103. LV Y G,LIU Z X,HUANG S Q.General analysis software design of aero-engine internal air system[C]//National Doctoral Academic Forum.Beijing:Computer Simulation Press,2009:99-103(in Chinese). |
| [9] | 候升平,陶智. 非稳态流体网络方法在发动机空气冷却系统中的应用[J].航空动力学报,2009,24(3):494-498. HOU S P,TAO Z.Study on application of unsteady fluid network to the air system in engine[J].Journal of Aerospace Power,2009,24(3):494-498(in Chinese). |
| Cited By in Cnki (17) | |
| [10] | 陶智,候升平. 流体网络法在发动机空气冷却系统设计中的应用[J].航空动力学报,2009,24(1):1-6. TAO Z,HOU S P.Study on application of fluid network to the design of air system in engine[J].Journal of Aerospace Power,2009,24(1):1-6(in Chinese). |
| Cited By in Cnki (18) | |
| [11] | 候升平,陶智. 非稳态流体网络模拟新方法及其应用[J].航空动力学报,2009,24(6):1253-1257. HOU S P,TAO Z.New simulation approach to the unsteady fluid network and the application[J].Journal of Aerospace Power,2009,24(6):1253-1257(in Chinese). |
| Cited By in Cnki (10) | Click to display the text | |
| [12] | 刘传凯,刘海明, 李艳茹,等.强瞬变空气系统的模块化仿真建模[J].航空动力学报,2015,30(8):1826-1833. LIU C K,LIU H M,LI Y R,et al.Modularized simulation of air.Modularized simulation of air system with fast transient[J].Journal of Aerospace Power,2015,30(8):1826-1833(in Chinese). |
| Cited By in Cnki (1) | |
| [13] | 吴丁毅. 内流系统的网络计算法[J].航空学报,1996,17(6): 653-657. WU D Y.Network technique of internal system[J].Acta Aeronautica et Astronautica Sinica,1996,17(6):653-657(in Chinese). |
| Cited By in Cnki (35) | Click to display the text | |
| [14] | 倪维斗,苟建兵,孙怠. 热动力系统流体网络及算法处理[J].系统仿真学报,1997,9(3):78-83. NI W D,GOU J B,SUN X.Research on fluid network in thermal power system[J].Journal System Simulation,1997,9(3):78-83(in Chinese). |
| Cited By in Cnki (40) | |
| [15] | 陈卓,周萍. 传递过程原理[M].长沙:中南大学出版社,2011:75-78. CHEN Z,ZHOU P.Principle of transport processes[M].Changsha:Central South University Press,2011:75-78(in Chinese). |
| [16] | 王华阁. 航空发动机设计手册-空气系统及传热[M].北京:航空工业出版社,2001:76-77. WANG H G.Aero engine design manual-air system and heat transfer[M].Beijing:Aviation Industry Press,2001:76-77(in Chinese). |
