Rodriguez[9]研究了BWB飞行器上BLI效应下进气道的多学科优化问题,结果表明,采用分布式动力布局的BWB飞行器的推进效率提高了2%。Lundbladh和Gr?nstedt[10]研究了发动机数目对采用分布式动力布局的BWB飞行器的巡航效率和油耗的影响,发现采用埋入式动力系统能减小起飞重量并降低油耗。Felder等[11]也认为在BWB飞行器上采用分布式推进系统可以进一步发挥BLI效应的优势,因为连续分布的风扇可以在整个翼展范围内吸入边界层气流并填充尾迹。闫万方等[12]对采用分布式动力并带BLI效应的BWB客机布局的气动特性进行了分析,给出了流量系数(Mass Flow Rate,MFR)、进气道高度和整流罩长度等关键参数对全机气动特性的影响。
为了进一步探索BLI效应对飞行器气动特性的影响及原因,也有一些****将研究对象简化为二维模型。Ko等[7]研究了二维模型中推进系统进排气速度、尾迹形状及气流宽度对推进效率的影响,并对这种布局推进系统的潜在优势进行了评估,认为在诱导阻力占总阻力50%的情况下,这种推进系统的最高效率可达80%~90%。Wick等[13]对二维和三维情形下分布式动力推进系统的位置和尺寸等参数进行了研究,认为在上翼面后缘布置的进排气装置是几种布局中最好的,可以提高约8%的气动效率。Manti-Lugo等[14]给出了亚声速飞行条件下考虑BLI效应的翼型设计,研究了流量系数、来流攻角、整流罩长度、进气道高度和进气道位置等参数对翼型升力特性和发动机进气品质的影响。在这些研究中,所涉及的设计参数主要是推进系统的位置和尺寸等,对整流罩外形参数的研究较少。另外,由于这种耦合布局形式中涉及的设计变量较多,单纯地研究单个变量对飞行器气动特性的影响不仅工作量大,且不易发现设计参数之间是否存在耦合关系。基于此,本文采用数值模拟方法,首先分析包括整流罩外形参数在内的主要设计参数对气动特性影响的敏感性,然后选择典型的敏感设计变量和非敏感设计变量进行详细的单变量分析,最后解释这些设计变量对气动特性影响的物理原因。
1 模型和方法 1.1 模型定义 本文采用的模型及其参数定义参照文献[14]。研究对象采用RAE2822翼型,其上所布置的进排气模型如图 1所示。图中:Hmax、Hh、Hth和H分别为进排气模型最大高度、唇口高度、进气边界高度和排气边界高度。整流罩上表面分为2段:前段外形由NACA-1系翼型[15]给出,其长度为Lfront,高度为Hmax-Hh;后段为圆弧,在进排气模型轴线方向的投影长度为Laft,半径为
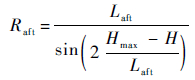 | (1) |
唇口部分是一个1/4椭圆,其长短轴为
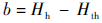 | (2) |
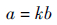 | (3) |
式中:k为唇口的椭圆比,这里取k=2。由式(1)~式(3)可以看出,整流罩外形由Hmax、Hh、Hth、H、Lfront和Laft确定。
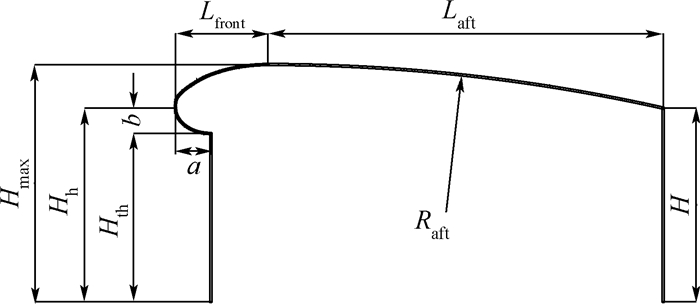 |
| 图 1 进排气模型几何参数定义 Fig. 1 Geometric parameter definition of nacelle |
| 图选项 |
进排气模型在翼型上的布置及计算网格模型如图 2所示。其中,进气边界与翼型上翼面垂直,进气边界与翼型前缘的水平距离(即进气边界弦向位置)为Lf,整流罩长度为Lnacelle=Lfront+Laft。
 |
| 图 2 进排气模型在翼型上的布置及计算网格模型 Fig. 2 Nacelle configuration on airfoil and computational mesh model |
| 图选项 |
为了便于研究,选取一个基本构型。采用翼型弦长c作为无量纲参考长度后,基本构型的几何参数取值为:Hh=0.018,Hmax=0.022,Hth=0.017,H=0.020,Lfront=0.029,Laft=0.071,Lf=0.8。此外,研究中还涉及到的一些参数定义如下。
整流罩最大厚度t:
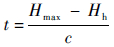 |
整流罩最大厚度位置xt:
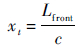 |
流量系数MFR:
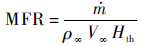 |
式中:?为进排气质量流量;ρ∞和V∞分别为远场来流的密度和速度。
为了满足计算流体力学(Computational Fluid Dynamics,CFD)求解对流场分辨率、求解收敛性的要求,通过求解Poisson方程来生成C型计算网格(见图 2),远场边界为120倍弦长。
1.2 数值方法及验证 本文采用有限体积法求解二维定常可压缩雷诺平均Navier-Stokes方程组。空间离散采用基于压力方法,2阶精度。湍流模型为两方程SST k-ω模型。进气边界设置为压力出口条件,给定目标质量流量。排气边界设置为质量流量入口条件,远场设置为压力远场条件。
本文用到的升力系数CL、阻力系数CD和俯仰力矩系数CM分别定义为:CL=L/(0.5ρ∞V∞2c),CD=D/(0.5ρ∞V∞2c),CM=M/(0.5ρ∞V∞2c2),其中,L、D和M分别为翼型和整流罩表面共同受到的升力、阻力和俯仰力矩,M的取矩点距前缘1/4弦长。
为了验证本文所用的网格和数值方法,使用上述网格生成程序和求解器计算了RAE2822翼型的气动特性,并与文献[16]的试验数据进行对比。计算条件为:马赫数Ma=0.73,雷诺数Re=6.5×106,攻角α=3.19°。采用3种不同密度的网格进行计算,以确定合适的网格节点数,对比结果见表 1。可见,网格2与网格3的计算结果已较接近,且耗时远少于网格3,综合考虑计算精度与效率,选取网格2进行本文研究是合适的。
表 1 网格无关性验证 Table 1 Mesh independency validation
| 网格编号 | 单元数 | CL | CD | 耗时/s |
| 1 | 21 600 | 0.776 6 | 0.017 36 | 3 547 |
| 2 | 86 400 | 0.801 5 | 0.018 28 | 9 928 |
| 3 | 345 600 | 0.807 3 | 0.018 29 | 37 809 |
表选项
将网格2的计算结果与文献[14]的计算结果以及文献[16]的试验结果进行比较(见表 2)。可以看出,本文计算结果与文献数据吻合较好。
表 2 本文结果与文献[14, 16]结果的比较 Table 2 Result comparison of present work with Ref.[14] and Ref.[16]
| 计算结果来源 | CL | CD |
| 网格2 | 0.801 5 | 0.018 28 |
| 文献[14] | 0.800 0 | 0.018 60 |
| 文献[16] | 0.800 0 | 0.016 80 |
表选项
由于进排气所引起的BLI效应使得翼型周围的流场更为复杂,因此需要对进气边界处的速度型进行分析验证,进一步确保所采用的计算模型是合适的。图 3为不同计算网格模型下进气边界速度型分布。图中:V/V∞为进气边界处速度与远场来流速度之比;y*为进气边界高度与翼型弦长之比。可以看出,网格2的速度型与网格3差别很小,进一步表明选取网格2作为本文的计算模型是合适的。
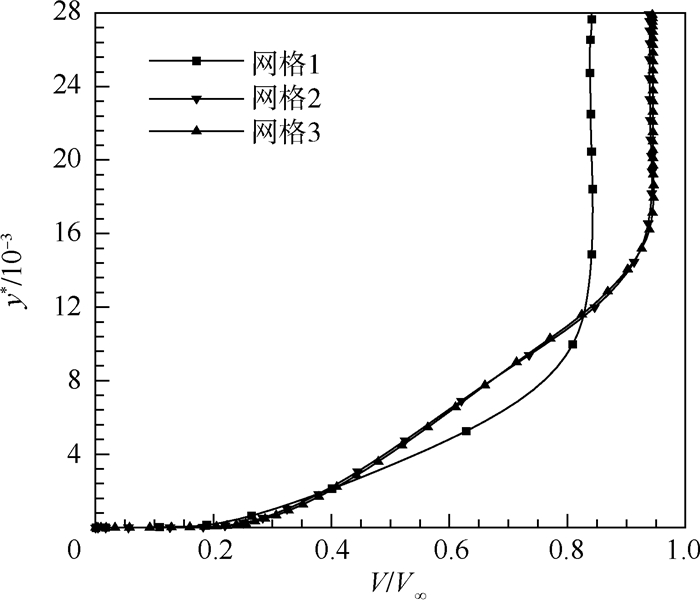 |
| 图 3 不同计算网格模型下进气边界速度型分布 Fig. 3 Velocity profile of inlet boundary distribution with different computational mesh models |
| 图选项 |
另外,本文研究的问题可能使流场扰动的传播范围比常规翼型流场分析中的更大,因此需要对网格的远场边界大小进行验证(见图 4)。可见,选取120倍弦长作为远场边界是比较合适的。
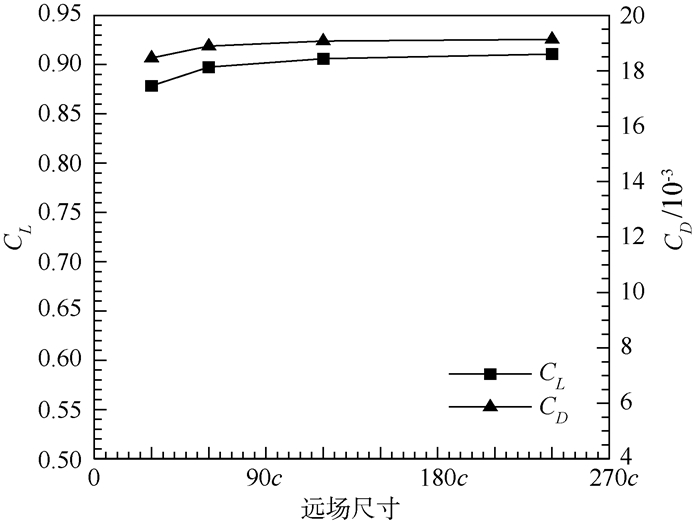 |
| 图 4 远场尺寸验证 Fig. 4 Validation of far-field size |
| 图选项 |
按照文献[14]的计算条件,对比带BLI效应下翼型的CL-MFR曲线(见图 5)。可以看出,本文结果与文献[14]符合较好,证明了本文所用数值方法的可靠性以及网格的适用性。
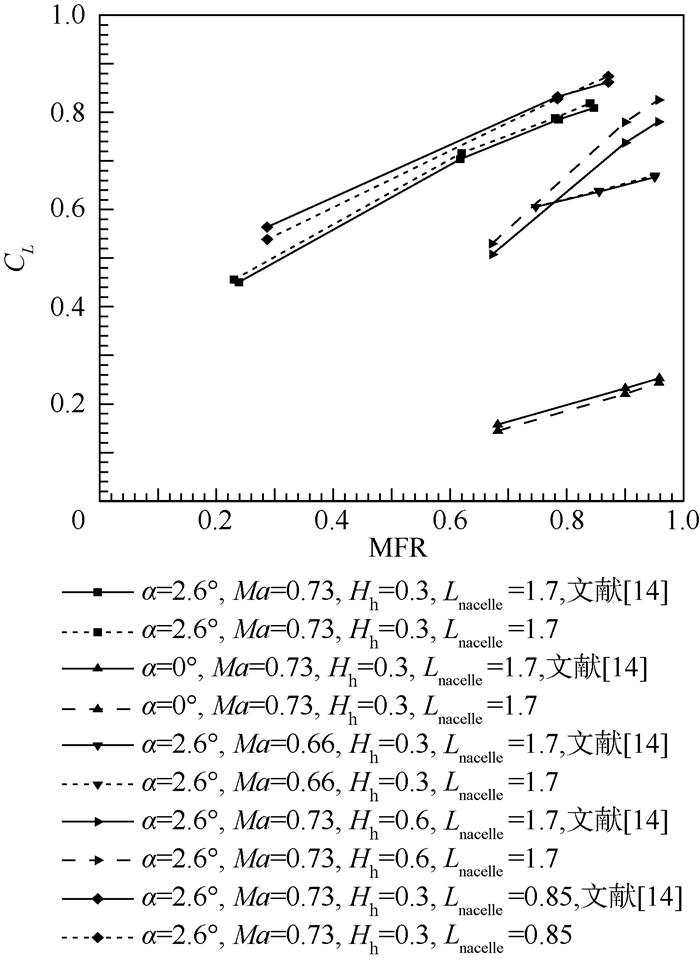 |
| 图 5 本文与文献[14]中CL-MFR曲线的对比 Fig. 5 Comparison of CL-MFR curves between present work and Ref. [14] |
| 图选项 |
2 结果和讨论 2.1 参数敏感性分析 为了评价整流罩外形参数与进排气装置位置参数对翼型CL、CD和CM影响的重要程度,使用Morris敏感度分析法[17]进行参数敏感度分析。
1) 需选取典型参数作为研究对象。整流罩的外形近似翼型,因此可以由t、xt来描述。进排气模型的整体尺寸由Hth、Lnacelle决定,位置由Lf决定。基于文献[12]的工作可知,在这些参数中,进排气模型长度Lnacelle并非敏感参数。因此,选取t、xt、Hth和Lf作为典型研究参数。
2) 需给定t、xt、Hth和Lf这4个参数在各自的基准值Pi附近的变化区间。由于各参数对应的几何尺度不同,为了使各个参数的变化区间合理,本文定义第i个参数的参考变化区间[l*,u*]i为
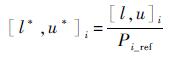 |
式中:Pi_ref为各个参数对应的参考特征量;u和l分别为该参数变化的上界和下界。本文描述整流罩外形的t、xt所对应的Pi_ref为整流罩长度;描述进排气模型位置的Hth、Lf所对应的Pi_ref为翼型弦长。考虑到xt和Lf的变化范围受到几何约束,t作为整流罩翼型厚度也不能过大,所以将4个参数的参考变化区间[l*,u*]统一取为[-4%,6%],由此可得参数的实际变化区间(见表 3)。
表 3 参数的实际变化区间 Table 3 Actural range of parameters
| 序号 | 参数 | Pi_ref | Pi | [Pi-l,Pi+u] |
| 1 | t | 0.1 | 0.004 7 | [0.000 7,0.010 7] |
| 2 | xt | 0.1 | 0.029 | [0.025,0.035] |
| 3 | Hth | 1 | 0.02 | [0.016,0.026] |
| 4 | Lf | 1 | 0.8 | [0.76,0.86] |
表选项
在选定参数及其变化范围后,综合考虑取样的随机性和CFD计算量的规模,选取重复抽样次数r=50来计算这4个参数在巡航和起飞状态下对CL、CD和CM的影响。计算条件为:巡航条件下,高度11 000 m,Ma=0.73,MFR=1.0,α=2.6°;起飞条件下,高度为海平面,Ma=0.21,MFR=1.2,α=10°。各参数对气动系数影响的均值与标准差见图 6。图中:d和S分别为Morris敏感度分析法中基本效应(elementary effect)的均值和标准差,表示参数对目标函数的影响大小和参数影响目标函数时与其他参数的相互作用大小[17]。
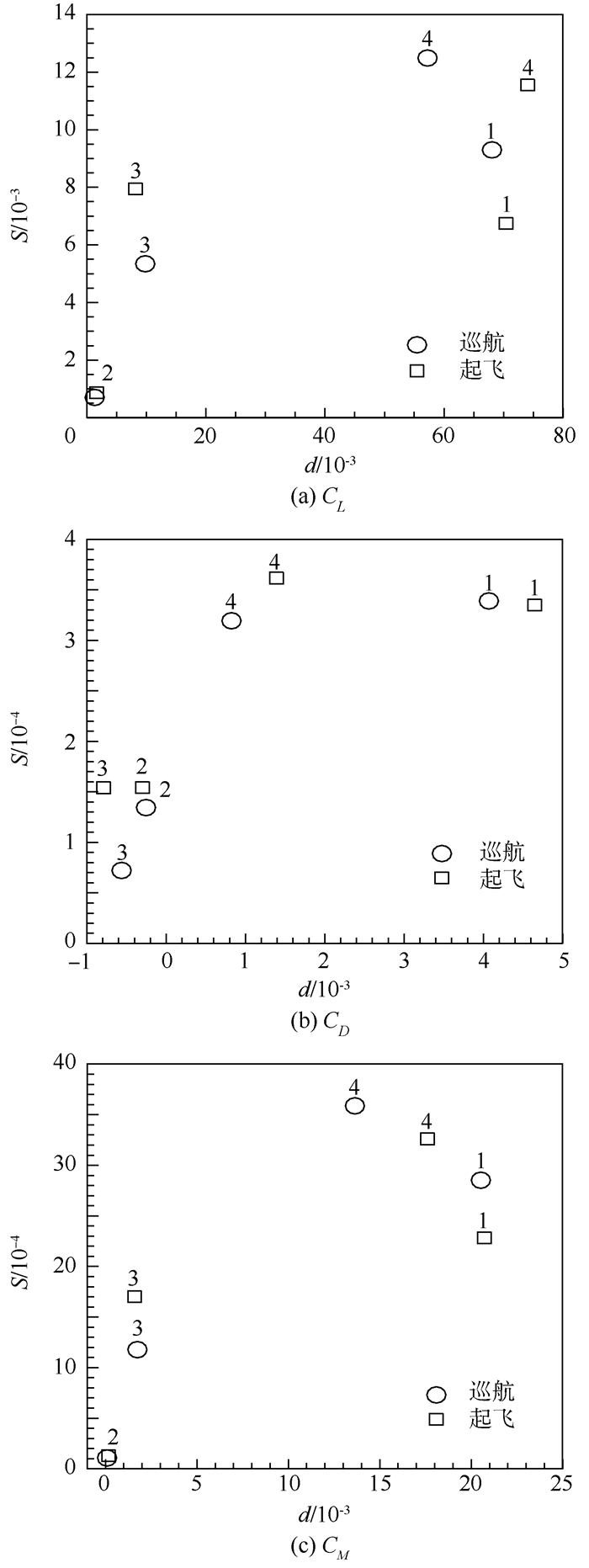 |
| 1-t;2-xt;3-Hth;4-Lf。 图 6 各参数对气动系数影响的均值与标准差 Fig. 6 Mean values and standard deviations of effects of parameters on aerodynamic coefficients |
| 图选项 |
从图 6可知,巡航状态下,这4个参数对CL和CM的影响大小排序是一致的,均为t、Lf、Hth、xt;对CD影响大小排序为t、Lf、xt、Hth。从量级上看,按对气动系数的影响大小可将这4个参数分为2类,其中t、Lf属于对气动特性影响相对较大的,xt、Hth属于对气动特性影响相对较小的。另外,t、Lf属于与其他变量之间的相互耦合作用相对较强的参数。从图 6中还可以看出,在起飞状态下,这4个参数对气动特性的影响关系与巡航状态的定性一致。
2.2 典型参数影响 基于上述分析,选择对气动特性影响较敏感的参数(t)和不敏感的参数(xt)进行详细讨论,以确定产生这种结果的原因。
2.2.1 整流罩最大厚度t 基准外形下,气动系数随t变化规律见表 4。巡航状态下,随t增大,CL和CM先增大后减小,CD单调增大。起飞状态下,随t增大,CL、CD和CM均单调增大。
表 4 t对气动特性的影响 Table 4 Effect of t on aerodynamic performance
| 飞行状态 | t | CL | CD | CM |
| 巡航 | 0.000 7 | 0.848 | 0.015 01 | 0.103 9 |
| 0.004 7 | 0.906 | 0.019 07 | 0.120 8 | |
| 0.008 7 | 0.803 | 0.019 17 | 0.105 2 | |
| 起飞 | 0.000 7 | 1.589 | 0.013 02 | 0.112 4 |
| 0.004 7 | 1.610 | 0.016 07 | 0.119 0 | |
| 0.008 7 | 1.629 | 0.018 79 | 0.125 3 |
表选项
整流罩的外形接近低速翼型,进排气流动使得整流罩附近流场与翼型流场的性质接近,因此在分析整流罩几何参数对气动特性的影响时,可以把整流罩视为一个等效翼型。当t增大时,等效翼型的厚度和弯度都增加,因此在失速之前,CL和压差阻力系数都增大;失速之后,CL下降,压差阻力系数继续增大。巡航状态整流罩上部流速较高,当等效翼型厚度增加时,容易产生后缘分离,而起飞状态流速较低,等效翼型在厚度较大时也能保持附着流动,因此CL、CD有上述变化趋势。CM主要受升力影响,因此变化趋势与CL一致。
图 7为巡航状态不同t下的流线。可以看出,t=0.008 7时整流罩后部已经出现分离,造成CL降低。
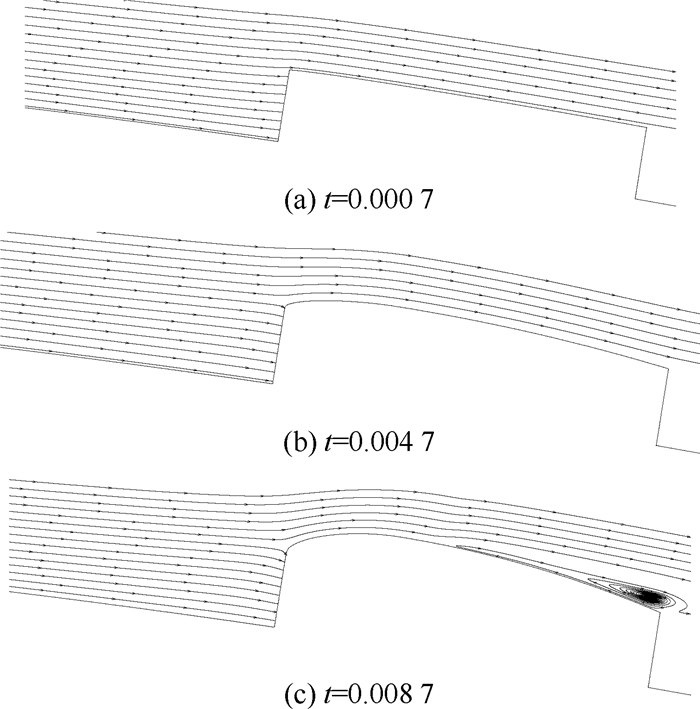 |
| 图 7 巡航状态不同t下的流线 Fig. 7 Streamline in cruise condition at different t |
| 图选项 |
为了进一步分析气动特性的变化机理,图 8给出不同t下的表面压力系数Cp分布。可见,t的变化还影响到进气边界上游流场。随着t增大,整流罩前缘的驻点逐渐上移,整流罩前缘吸力峰也逐渐增大。在整流罩后缘失速后,后缘部分的气流不再与排气边界的高速气流接触,造成整个上翼面气流速度降低,从而显著降低了升力。
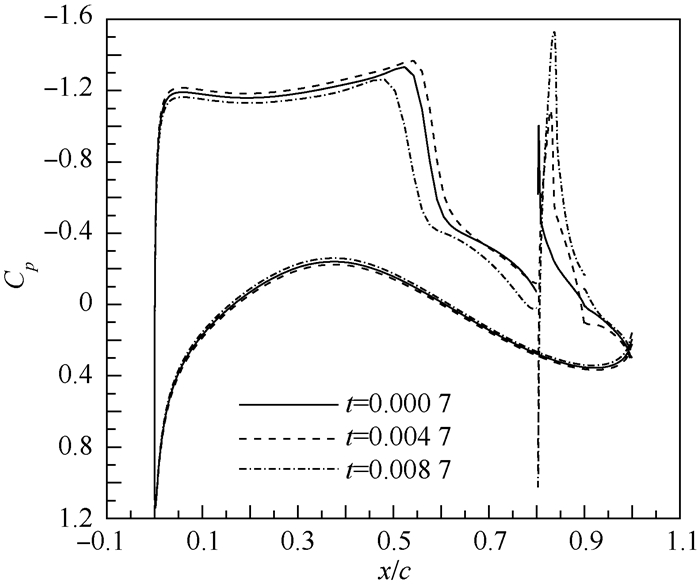 |
| 图 8 不同t下的表面压力系数分布 Fig. 8 Surface pressure coefficient distribution at different t |
| 图选项 |
图 9给出了巡航状态下t对进气边界处速度型的影响。可以看出,随着t增大,在进气边界上部产生了一个低速区,从而降低了速度型的均匀性。在整流罩失速之后,上翼面气流的减速也使得进气边界的速度降低。
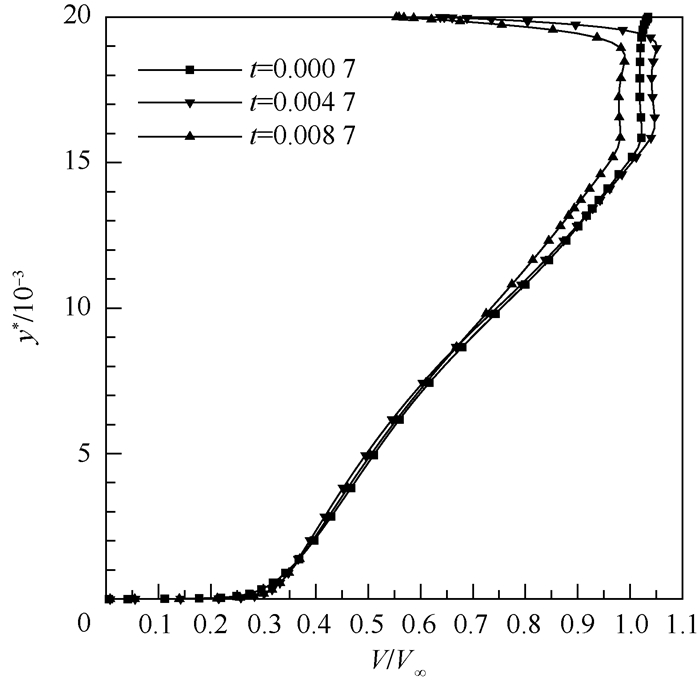 |
| 图 9 不同t下的进气边界速度型 Fig. 9 Velocity profile of inlet boundary at different t |
| 图选项 |
另外,本文还研究了t对CD-MFR曲线的影响,结果如图 10所示。图中:CD,vis、CD,pre,nacelle和CD,pre,airfoil分别为CD的黏性阻力分量、整流罩压差阻力分量和翼型压差阻力分量。可见,当t取基准值(t=0.004 7)时,随MFR增大,CD单调递增,而t=0.000 7时,随MFR增大,CD先减小后增大,极小值点在MFR=1.0附近。从阻力的组成可知,产生这些趋势上的差异的主要原因是t不同造成的压差阻力不同。
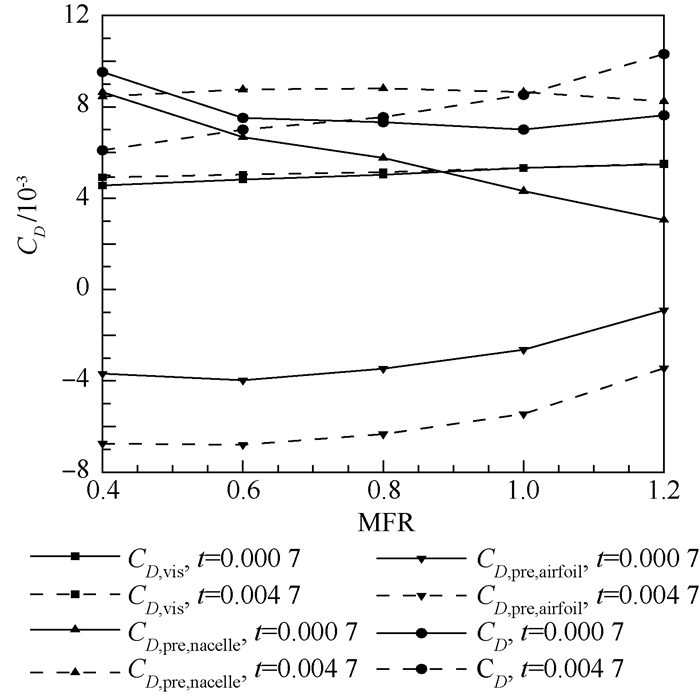 |
| 图 10 不同t下的CD-MFR曲线 Fig. 10 CD-MFR curves at different t |
| 图选项 |
2.2.2 整流罩最大厚度位置xt 气动特性随xt的变化规律见表 5。巡航状态下,随xt增大,CL和CM单调增大,CD单调减小。起飞状态下,随t增大,CL、CM基本不变,CD单调减小。从气动系数的变化量看,xt的影响较t弱,这与敏感度分析的结论一致。
表 5 xt对气动特性的影响 Table 5 Effect of xt on aerodynamic performance
| 飞行状态 | xt | CL | CD | CM |
| 巡航 | 0.025 | 0.902 | 0.019 09 | 0.120 0 |
| 0.029 | 0.906 | 0.019 07 | 0.120 8 | |
| 0.033 | 0.908 | 0.019 04 | 0.121 2 | |
| 起飞 | 0.025 | 1.610 | 0.016 24 | 0.119 0 |
| 0.029 | 1.610 | 0.016 07 | 0.119 0 | |
| 0.033 | 1.610 | 0.015 93 | 0.119 0 |
表选项
为了分析xt对升力系数的影响原因,给出了巡航状态下不同xt的表面压力系数Cp分布(见图 11)。可以看出,整流罩部分的压力分布变化与翼型是一致的,随着xt的增加,吸力峰值下降,整流罩部分的升力下降。而整流罩的压力变化影响到上翼面压力分布,xt的增加使得上翼面吸力增加。这两者作用的总效果是总升力略微增加。
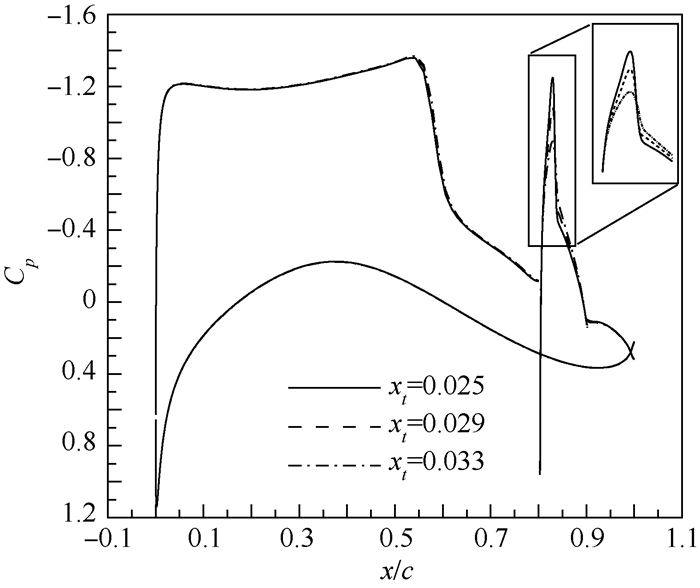 |
| 图 11 不同xt下的表面压力系数分布 Fig. 11 Surface pressure coefficient distribution at different xt |
| 图选项 |
巡航状态下xt对进气边界处速度型的影响见图 12。可见,xt的变化基本不影响进气边界处速度型分布,因此对进气边界上游的压力分布也没有影响。
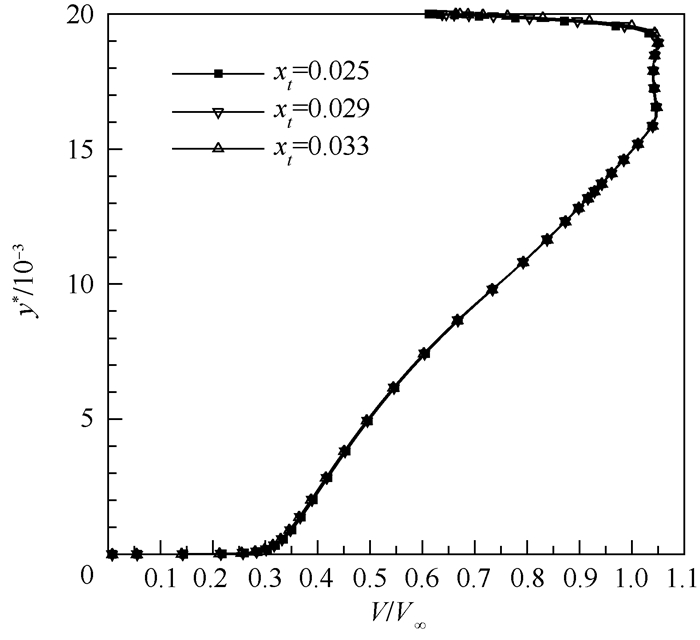 |
| 图 12 不同xt下的进气边界速度型 Fig. 12 Velocity profile of inlet boundary at different xt |
| 图选项 |
2.3 参数耦合影响分析 敏感度分析结果表明,t和Lf是对气动系数影响较大的2个参数,并且耦合作用较强。下面分析这2个参数耦合变化对气动特性影响的原因。考察2个参数在基准值附近的变化,定义这2个参数同时产生相同增量(即在各自的参考变化区间内增加或减少4%)时函数值的增量为d1,这2个参数单独产生相同增量时函数值增量之和为d2。易知d2即为d1的线性主部,因此两者的相对差别(d2-d1)/d1越大,则代表这2个变量的耦合影响越强。基于以上分析,将巡航和起飞状态下气动特性随这2个参数耦合变化的规律列于表 6。可见,t和Lf同时增加时,两者对气动系数的耦合影响作用比两者同时减少时更强,这是因为t和Lf都较大时,整流罩表面难以维持附着流动,从而发生后缘失速,增强了气动系数的非线性。另外,从表 6中可以看出,巡航状态下的耦合影响作用比起飞状态下更强,这是因为起飞状态上表面流速较低,不易产生分离,从而气动系数在t和Lf较大时仍然保持线性。
表 6 t和Lf耦合对气动特性的影响 Table 6 Coupled effect of t and Lf on aerodynamic performance
| 飞行状态 | 气动特性 | 算例 | d1 | d2 | |
| 巡航 | CL | 1 | -0.100 0 | -0.103 0 | -3.00 |
| 2 | 0.078 0 | -0.069 0 | -188.46 | ||
| CD | 1 | -0.005 8 | -0.006 2 | -6.92 | |
| 2 | 0.007 8 | 0.002 2 | -71.61 | ||
| CM | 1 | -0.025 6 | -0.027 3 | -6.64 | |
| 2 | 0.024 9 | -0.006 4 | -125.70 | ||
| 起飞 | CL | 1 | -0.038 0 | -0.038 0 | 0 |
| 2 | 0.046 0 | 0.042 0 | -8.70 | ||
| CD | 1 | -0.004 0 | -0.004 0 | -0.75 | |
| 2 | 0.003 8 | 0.003 8 | 0.79 | ||
| CM | 1 | -0.011 6 | -0.012 1 | -4.31 | |
| 2 | 0.014 7 | 0.013 6 | -7.48 | ||
| 注:算例1、算例2分别代表t和Lf同时减少和同时增加。 | |||||
表选项
3 结 论 本文使用CFD方法和Morris敏感度分析法研究了BLI效应下整流罩设计对翼型气动特性的影响,得到了以下结论:
1) 对整流罩最大厚度、最大厚度位置、进气边界弦向位置和进气边界高度4个整流罩设计的主要参数进行翼型气动特性敏感度分析,结果表明:在巡航状态下,它们对气动特性影响的大小可分为2类,整流罩最大厚度和进气边界弦向位置对气动特性影响相对较大;最大厚度位置和进气边界高度影响相对较小。对在起飞状态下的分析结果与巡航状态下的定性一致。
2) 整流罩最大厚度对翼型气动特性影响的主要原因为:在整流罩局部失速前,升力系数、阻力系数和俯仰力矩系数都随整流罩最大厚度增加而增加;失速后,升力系数和力矩系数随整流罩最大厚度增加而减小。整流罩最大厚度的变化还影响进气边界速度型的分布和上翼面压力分布。此外,整流罩最大厚度的变化还会改变阻力-流量系数曲线的趋势,使其由先减小后增大变为单调递增。整流罩最大厚度位置的变化虽影响整流罩和翼型表面的压力分布,但作用较小,且基本不影响进气边界速度型分布。这与敏感度分析结果是一致的。
3) 进气边界弦向位置和整流罩最大厚度对气动特性影响的耦合作用较强,这是因为当进气边界弦向位置较靠后时,整流罩上部的流速较高,此时若整流罩最大厚度也较大,其上会产生失速而使气动特性变成非线性。另外,分析表明,巡航状态下这2个参数的耦合作用比起飞状态下更强,这是因为起飞状态下整流罩表面流速较低,更易保持附着流动。
参考文献
| [1] | LIEBECK R H. Design of the blended wing body subsonic transport[J]. Journal of Aircraft,2004, 41(1): 10–25. |
| Click to display the text | |
| [2] | QIN N, VAVALLE A, LE MOIGNE A, et al. Aerodynamic considerations of blended wing body aircraft[J]. Progress in Aerospace Sciences,2004, 40(6): 321–343. |
| Click to display the text | |
| [3] | LABAN M,ARENDSEN P,ROUWHORST W,et al.A computational design engine for multi-disciplinary optimisation with application to a blended wing body configuration:AIAA-2002-5446[R].Reston:AIAA,2002. |
| Click to display the text | |
| [4] | GOHARDANI A S, DOULGERIS G, SINGH R. Challenges of future aircraft propulsion:A review of distributed propulsion technology and its potential application for the all electric commercial aircraft[J]. Progress in Aerospace Sciences,2011, 47(5): 369–391. |
| Click to display the text | |
| [5] | KIM H D,BROWN G V,FELDER J L.Distributed turboelectric propulsion for hybrid wing body aircraft[C]//9th International Powered Lift Conference.London:Royal Aeronautical Society,2008:1-11. |
| Click to display the text | |
| [6] | HILEMAN J I, SPAKOVSZKY Z S, DRELA M, et al. Airframe design for silent fuel-efficient aircraft[J]. Journal of Aircraft,2010, 47(3): 956–969. |
| Click to display the text | |
| [7] | KO A,LEIFSSON L T,SCHETZ J A,et al.MDO of a blended-wing-body transport aircraft with distributed propulsion:AIAA-2003-6732[R].Reston:AIAA,2003. |
| Click to display the text | |
| [8] | KO A,SCHETZ J A,MASON W H.Assessment of the potential advantages of distributed-propulsion for aircraft[C]//XVIth International Symposium on Air Breathing Engines (ISABE).Reston:AIAA,2003:71-79. |
| Click to display the text | |
| [9] | RODRIGUEZ D L. Multidisciplinary optimization method for designing boundary-layer-ingesting inlets[J]. Journal of Aircraft,2009, 46(3): 883–894. |
| Click to display the text | |
| [10] | LUNDBLADH A,GR?NSTEDT T.Distributed propulsion and turbofan scale effects[C]//ISABE 2005,17th Symposium on Airbreathing Engine.Reston:AIAA,2005. |
| Click to display the text | |
| [11] | FELDER J L,KIM H D,BROWN G V.Turboelectric distributed propulsion engine cycle analysis for hybrid-wing-body aircraft:AIAA-2009-1132[R].Reston:AIAA,2009. |
| Click to display the text | |
| [12] | 闫万方, 吴江浩, 张艳来. 分布式推进关键参数对BWB飞机气动特性影响[J]. 北京航空航天大学学报,2015, 41(6): 1055–1065.YAN W F, WU J H, ZHANG Y L. Effects of distributed propulsion crucial variables on aerodynamic performance of blended wing body aircraft[J]. Journal of Beijing University of Aeronautics and Astronautics,2015, 41(6): 1055–1065.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [13] | WICK A T,HOOKER J R,HARDIN C J.Integrated aerodynamic benefits of distributed propulsion:AIAA-2015-1500[R].Reston:AIAA,2015. |
| Click to display the text | |
| [14] | MANTIC-LUGO V, DOULGERIS G, SINGH R. Computational analysis of the effects of a boundary layer ingesting propulsion system in transonic flow[J]. Proceedings of the Institution of Mechanical Engineers,Part G:Journal of Aerospace Engineering,2013, 227(8): 1215–1232. |
| Click to display the text | |
| [15] | NICHOLS M R,KEITH A L.Investigation of a systematic group of NACA 1-series cowlings with and without spinners:NACA-Report-950[R].Washington,D.C.:U.S.Government Printing Office,1950. |
| Click to display the text | |
| [16] | BARCHE J.Experimental data base for computer program assessment:AGARD-AR-138[R].[S.l.]:AGARD-Report,1979:2002-0843. |
| Click to display the text | |
| [17] | MORRIS M D. Factorial sampling plans for preliminary computational experiments[J]. Technometrics,1991, 33(2): 161–174. |
| Click to display the text | |
