为解决上述问题,本文采用过程神经网络(Process Neural Network,PNN)建立预测模型,作为一种近年来快速发展的数据驱动算法,过程神经网络可以同时处理时空二维信息,具有容错性好、预测精度高和自适应性强等优点,对复杂时变系统的输入/输出问题具有较强的建模能力。近年来,已经有不少****将过程神经网络用于解决复杂系统状态预测问题,并取得了一系列的研究成果[6-10]。这些研究成果为过程神经网络在复杂系统状态预测问题上的应用奠定了坚实的基础,但是要将其用于液体火箭发动机的状态预测还存在以下两个问题需要解决:①液体火箭发动机的测量数据多为离散数据,而采用过程神经网络建模时,需要将离散数据拟合成连续函数作为网络输入,由于测量数据很少存在解析函数形式,拟合时会造成一定的信息丢失和精度损失;②一般的过程神经网络模型多采用离线数据进行训练,网络结构固定不变,不能对新获取的测量样本进行有效利用。
针对上述问题本文提出一种基于极限学习算法的离散过程神经网络(Discrete Process Neural Network,DPNN)预测模型,首先利用离线数据训练网络,然后基于极限学习算法对过程神经网络隐层到输出层的权值进行更新,进而提高过程神经网络预测精度和适应能力。通过对液体火箭发动机涡轮泵扬程进行预测试验证明了算法的可行性,并采用无权值更新的过程神经网络模型进行了对比分析。结果表明,通过自动更新权值可以使过程神经网络具有更高的预测精度和较强的适应能力。
1 离散过程神经网络预测模型 当液体火箭发动机处于稳定工作状态时,各个组件性能的变化或者故障均会引起状态监测参数的改变[11-13],因此可以通过预测状态监测参数的变化来预测发动机的工作状态。状态监测参数的变化一般由传感器采样获取,可将其视为一种时间序列。因此,液体火箭发动机状态预测问题可以归结为状态监测参数时间序列的预测问题。
设某一监测参数时间序列为{xl},其预测问题等价于应用历史测量数据{xl, xl-1, …, x1}对未来数据xl+h(h>0)进行估计。假设存在如下映射关系:
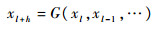 | (1) |
此时监测参数的预测问题可以转化为应用过程神经网络对函数G(·)进行逼近的问题。由于液体火箭发动机工作时间相对较短一般h取1,此时称为单步预测或短期预测。
双并联前馈离散过程神经网络具有良好的泛化能力和较快的收敛速度,因此本文采用双并联前馈过程神经网络对G(·)进行逼近,其结构如图 1所示。网络主要由输入层、隐层和输出层组成,其中输入层直接并联到输出层。
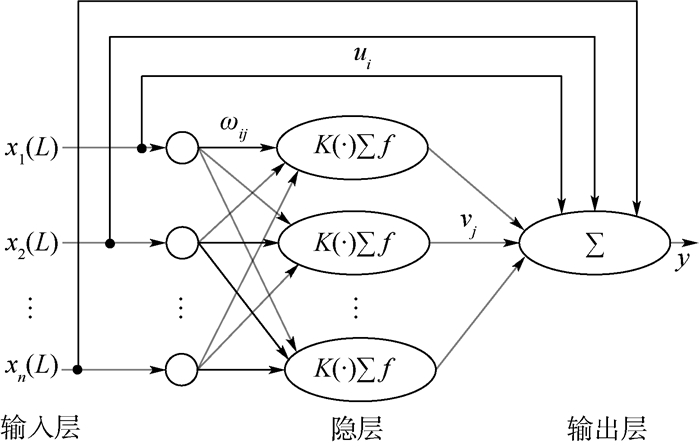 |
| 图 1 双并联前馈离散过程神经网络结构 Fig. 1 Structure of double parallel feedforward discrete process neural network |
| 图选项 |
一般过程神经网络的输入为连续函数,需要将离散数据拟合成时变函数作为过程神经网络的输入。为了直接利用传感器的采样数据作为过程神经网络输入,根据文献[14]采用卷积和作为时间聚合算子,建立双并联前馈离散过程神经网络(Double Parallel Feedforward Discrete Process Neural Network,DPFDPNN)模型。设过程神经网络输入向量为
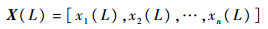 | (2) |
式中:xn(L)为某一状态监测参数构成的时间序列,其长度为L。设K(·)为时间聚合算子,记xi(l)(i=1, 2, …, n,l=1, 2, …, L)为序列xi(L)中第l个元素,其对应的权值为ωiL-l+1,ωi为随机初始值,则时间聚合运算可以表示为[14]
 | (3) |
增加时间聚合算子的过程神经网络输入和输出映射关系为
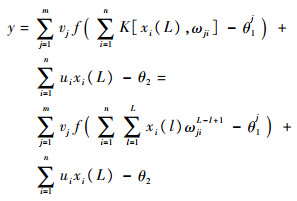 | (4) |
式中:m为隐层神经元个数;ωji为输入层第i个输入单元与隐层第j个神经元之间的连接权值;ui为输入层第i个输入单元与输出层过程神经元之间的连接权值;vj为隐层第j个神经元与输出层的权值;θ1j为隐层第j个神经元的激励阈值;θ2为输出层激励阈值。
根据历史测量数据给定的S组离线学习样本为{x1s(L), x2s(L), …, xns(L); ds}s=1S,其中xns(L)为第s组样本的第n个时间序列,其长度为L;ds为第s组样本的期望输出,ys为相应的真实输出,则离散过程神经网络的期望输出与真实输出之间的平方和误差函数(SSE)可以定义为
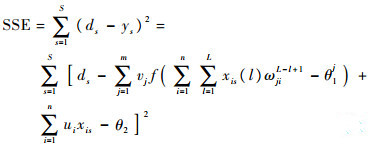 | (5) |
令ET=[e1, e2, …, es]es=ds-ys
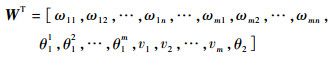 |
根据Levenberg-Marquardt(LM)算法[15],W的迭代调整规则为
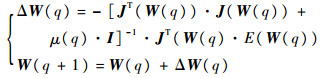 | (6) |
式中:J(W)为关于W的雅可比矩阵; q为迭代次数; I为单位矩阵; μ为学习速率。网络的离线学习步骤如下:
Step 1确定过程神经网络结构并设置过程神经网络学习误差精度ε,最大迭代次数M,初始化过程神经网络参数ωji、vj、θ1j、θ2和迭代次数q。
Step 2将所有样本输入到过程神经网络,计算误差平方和SSE和矩阵J(W)。
Step 3根据式(6)调整参数向量W,将调整后的参数向量代入式(5)重新计算SSE,如果新SSE的值大于Step 2中的SSE,则重复Step 3;如果新SSE的值小于Step 2中的SSE,则转到Step 4。
Step 4如果SSE小于ε或者q大于M,则转到Step 5;否则转到Step 3。
Step 5输出学习结果,停机。
至此,可采用训练好的过程神经网络代替函数G(·),根据式(1)对发动机状态进行预测。
2 网络权值更新算法 虽然离线过程神经网络预测模型可以方便地对液体火箭发动机工作状态进行预测,但是其结构和阈值是预先设定好的,不能根据新获取的数据样本进行调整,对新的数据样本不能有效利用。另一方面,液体火箭发动机工作环境恶劣工况复杂,当出现故障或者干扰后,离线预测模型精度将受到较大影响。为有效利用更新数据的信息,提高过程神经网络容错能力和适应性,本文在文献[16]基础上提出一种基于极限学习算法(Extreme Learning Algorithm,ELA)的过程神经网络权值更新算法,根据新获取的数据样本对过程神经网络隐层到输出层权值进行自动更新,以提高预测精度。
设在线更新N0个样本为
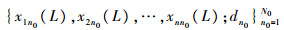 |
对于每一个更新的样本,若网络输出误差为0,则有
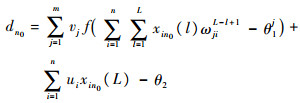 | (7) |
对于N0个样本,则有
 | (8) |
式中:
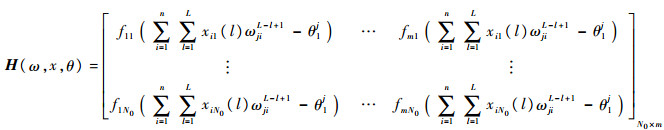 | (9) |
称为隐层输出矩阵,其中:fmN0(·)表示输入为第N0个样本在第m个神经元作用下的输出;β为权值矩阵,由隐层到输出层的权值组成,即
 | (10) |
其中:v′m为第m个待求权值。由式(7)将N0个样本的期望输出表示为
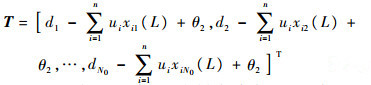 | (11) |
对于式(8),当N0个样本确定后,矩阵T和H也为确定的数值矩阵,权值矩阵β为待求矩阵。β可以通过Moore-Penrose广义逆和线性系统最小范数最小二乘解得到[16],即
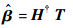 | (12) |
式中:
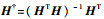
 |
此时新的权值矩阵为[17]
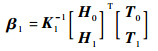 | (13) |
式中:
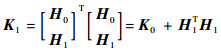 | (14) |
对式(13)进行整理有
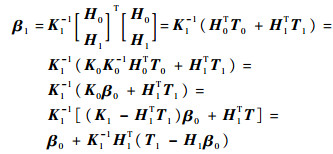 | (15) |
以此类推,当第k+1次更新Nk+1个样本之后有如下递推公式成立:
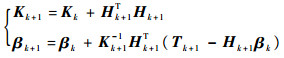 | (16) |
根据Woodbury规则[18]有
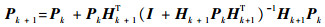 | (18) |
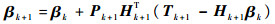 | (19) |
根据式(18)和式(19)就可对权值进行迭代更新。综上,采用权值更新算法的过程神经网络进行预测时,其过程可分为如下两个阶段:
1) 离线训练阶段
根据预测参数的历史数据设置离线过程神经网络结构,并根据第2节的内容对过程神经网络进行训练获得离线预测模型。
2) 更新权值预测阶段
① 利用离线模型进行预测,并同步记录实时更新的样本,当样本更新个数为N0时(取N0≥m),根据式(9)计算初始隐层输出矩阵H0与初始权值矩阵β0=P0H0TT0,其中P0=(H0TH0)-1。
② 利用①中更新权值的过程神经网络模型进行在线预测,并同步记录更新样本,当样本更新个数为N1时(可取N1≥N0),根据式(18)和式(19)在线更新输出权值矩阵。
③ 重复②的过程,每当样本更新Nk(可取Nk≥N0)后,利用递推公式求出新的权值矩阵进行预测,直至停机。完整流程如图 2所示。
 |
| 图 2 液体火箭发动机状态预测流程 Fig. 2 Condition prediction process of liquid propellant rocket engine |
| 图选项 |
3 验证算例 涡轮泵是泵压式液体火箭发动机的重要部件,也是故障多发部位[19-20]。当发动机稳定工作时,涡轮泵的性能衰退或故障均会引起涡轮泵扬程的改变,所以涡轮泵扬程是涡轮泵状态预测的重要对象,也是判断液体火箭发动机健康状态的重要依据。本文以某型号火箭发动机氢涡轮扬程预测为例,分别采用有权值更新和无权值更新的过程神经网络模型对扬程进行预测,并对仿真结果进行了比较和讨论。
取某型号液体火箭发动机2次地面试车氢涡轮扬程数据,试车编号分别为C0716和C0725,每组数据200个采样点,采样间隔为0.1 s,采样数据构成的时间序列分别为
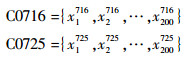 |
扬程采样数据经归一化处理后如表 1所示。将上述时间序列中连续的9个数据作为历史数据,即{xra, xr+1a, …, xr+8a},a取716或者725。
表 1 归一化扬程数据 Table 1 Normalization lift data
| 编号 | 扬程 |
| 1 | 0 |
| 2 | 0.250 0 |
| 3 | 0.166 7 |
| 4 | 0.166 7 |
| 5 | 0.166 7 |
| 6 | 0.250 0 |
| 7 | 0.333 3 |
| 8 | 0.333 3 |
| 9 | 0.250 0 |
| 10 | 0.333 3 |
| 11 | 0.666 7 |
| 12 | 0.750 0 |
| 13 | 0.583 3 |
| 14 | 0.333 3 |
| 15 | 0.250 0 |
| | |
| 186 | 0.500 0 |
| 187 | 0.583 3 |
| 188 | 0.533 3 |
| 189 | 0.650 0 |
| 190 | 0.500 0 |
| 191 | 0.416 7 |
| 192 | 0.500 0 |
| 193 | 0.650 0 |
| 194 | 0.600 0 |
| 195 | 0.616 7 |
| 196 | 0.500 0 |
| 197 | 0.333 3 |
| 198 | 0.500 0 |
| 199 | 0.583 3 |
| 200 | 0.583 3 |
| | |
| 386 | 0.166 7 |
| 387 | 0.166 7 |
| 388 | 0.250 0 |
| 389 | 0.250 0 |
| 390 | 0.250 0 |
| 391 | 0.083 3 |
| 392 | 0.166 7 |
| 393 | 0.166 7 |
| 394 | 0.250 0 |
| 395 | 0.166 7 |
| 396 | 0.083 3 |
| 397 | 0.083 3 |
| 398 | 0.166 7 |
| 399 | 0.166 7 |
| 400 | 0.166 7 |
表选项
以相邻第10个数据xr+9a作为过程神经网络预测模型的理想输出,即假设:
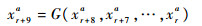 |
这样每次试车数据都可以得到191组试验样本,各取前91组样本,共182组样本对离散过程神经网络进行训练样,其余样本用于预测试验。过程神经网络隐层神经元个数取10,输入和输出节点均为1,过程神经网络拓扑结构为1-10-1。离线训练采用LM算法,过程神经网络误差精度为0.001,分别采用有权值更新和无权值更新2种预测模型进行预测试验。更新权值时,每新增10组测试样本进行一次权值更新,C0716次试车预测结果如图 3和图 4所示,C0725次试车预测结果如图 5和图 6所示。
 |
| 图 3 C0716次试车扬程预测结果 Fig. 3 Lift predicted value of No. C0716 ground-test |
| 图选项 |
 |
| 图 4 C0716次试车预测误差 Fig. 4 Predicted error of No. C0716 ground-test |
| 图选项 |
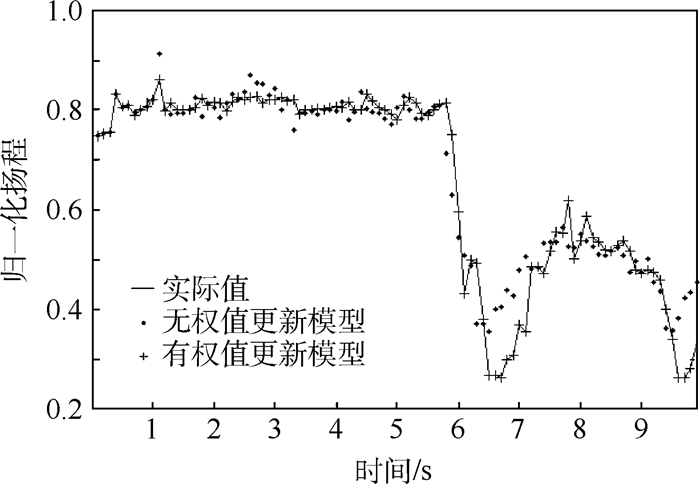 |
| 图 5 C0725次试车扬程预测结果 Fig. 5 Lift predicted value of No. C0725 ground-test |
| 图选项 |
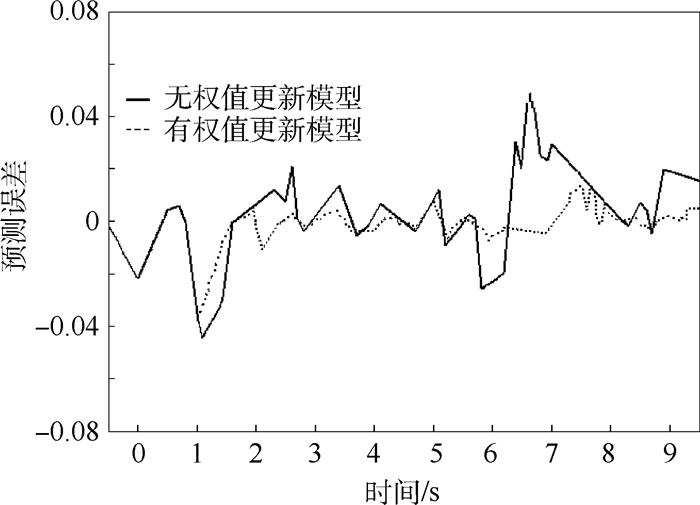 |
| 图 6 C0725次试车预测误差 Fig. 6 Predicted error of No. C0725 ground-test |
| 图选项 |
由图 3可以看出,对C0716次试车,前10组测试样本没有进行权值更新,所以2种预测方式结果相同。从1 s以后开始进行权值更新,更新权值后的预测精度有明显提高。图 4为C0716次试车数据预测误差的变化,没有更新权值的离散过程神经网络预测最大相对误差为7.82%,平均相对误差3.61%。经过权值更新后最大相对误差为1.43%,平均相对误差为0.68%,所以通过在线更新权值可以使双并联离散过程神经网络的预测精度得到较大提高。实际上,离散过程神经过程短期预测是比较精确的,但是随着测量数据的不断更新,系统信息的不断变化,预测误差会不断累积,离线模型的预测精度也会有所下降。通过极限学习算法对网络权值进行调整,可以有效地利用更新数据信息,进一步提高网络的预测精度。
图 5和图 6分别为C0725次试车的预测结果和预测误差示意图。由于发动机在5.6 s进行了工况微调,氢涡轮泵扬程有所下降,由图 5可知有权值跟新和无权值跟新的预测模型都能够较为准确地预测到发动机的状态变化,但是无权值更新的预测模型在工况微调后预测精度有明显下降。结合图 6可知,进行权值更新后预测的平均相对误差为0.86%,最大相对误差为1.55%,无权值更新模型预测的平均相对误差为5.23%,最大相对误差为8.79%。可见经过权值更新后的过程神经网络能够保持较高的预测精度,并能够有效地提高过程神经网络的抗干扰能力,增强过程神经网络的适应性。液体火箭发动机在实际工作中受各种因素影响,其工作状态复杂多变,当预测时间较长时,固定权值的过程神经网络很难保持良好的预测效果。为此,对网络隐层到输出层的权值进行更新,进一步增强网络的外推能力,使网络在长期预测时仍具有较高的精度。
4 结论 液体火箭发动机结构复杂,其工作状态受多种因素影响且随时间变化,难以建立准确的数学模型来预测其状态变化。为此,本文提出一种基于极限学习算法的离散过程神经网络模型来解决发动机状态预测问题。该模型具有如下特点:
1) 预测模型是基于卷积和时间聚合算子与双并联前馈网络结构建立的过程神经网络,可以直接处理离散采集数据并具有较快的收敛速度和泛化能力。
2) 采用极限学习算法,在更新数据样本的基础上对网络隐层到输出层的权值进行更新,进一步提高了模型的预测精度和适应能力。
实验研究表明,该方法较无权值更新的过程神经网络模型具有更高的预测精度和适应能力,可以有效地解决液体火箭发动机状态预测问题。但是,对于不同性质的监测参数时间序列,本方法在更新样本的选择策略以及权值更新机制等问题上还需进一步通过实验进行分析研究。
参考文献
| [1] | 彭宇, 刘大同, 彭喜元. 故障预测与健康管理技术综述[J].电子测量与仪器学报, 2010, 24(1): 1–9.PENG Y, LIU D T, PENG X Y. A review:Prognostics and health management[J].Journal of Electronic Measurement and Instrument, 2010, 24(1): 1–9.DOI:10.3724/SP.J.1187.2010.00001(in Chinese) |
| [2] | 田路, 张炜, 杨正伟. Elman型神经网络在液体火箭发动机故障预测中的应用[J].弹箭与制导学报, 2009, 29(1): 191–194.TIAN L, ZHANG W, YANG Z W. Application of Elman neural network on liquid rocket engine fault prediction[J].Journal of Projectiles, Rockets, Missiles and Guidance, 2009, 29(1): 191–194.(in Chinese) |
| [3] | 陈世立, 陈新民. 改进BP神经网络在冲压发动机性能预测中的应用[J].导弹与航天运载技术, 2007(3): 45–49.CHEN S L, CHEN X M. Improved BP neural network and its application in performance predicting of ramjet[J].Missile and Space Vehcile, 2007(3): 45–49.(in Chinese) |
| [4] | 王晔, 段志信. 基于Matlab和BP神经网络的固体火箭发动机比冲性能的预测[J].内蒙古科技与经济, 2007(8): 73–74.WANG Y, DUAN Z X. Solid propellant rocket engine specific impulse performance predicting based on Matlab and BP neural network[J].Inner Mongolia Science Technology & Economy, 2007(8): 73–74.(in Chinese) |
| [5] | 田干, 张炜, 杨正伟, 等. SVM方法在火箭发动机故障预测中的应用研究[J].机械科学与技术, 2010, 29(1): 63–67.TIAN G, ZHANG W, YANG Z W, et al. Study on SVM methods of liquid rocket engine fault prediction[J].Mechanical Science and Technology for Aerospace Engineering, 2010, 29(1): 63–67.(in Chinese) |
| [6] | 钟诗胜, 李洋. 基于小波过程神经网络的飞机发动机状态监视[J].航空学报, 2007, 28(1): 68–71.ZHONG S S, LI Y. Condition monitoring of aeroengine based on wavelet process neural networks[J].Acta Aeronautica et Astronautica Sinica, 2007, 28(1): 68–71.(in Chinese) |
| [7] | 钟仪华, 李榕, 张志银, 等. 基于主成分分析的离散过程神经网络水淹层动态预测方法[J].测井技术, 2010, 34(5): 432–437.ZHONG Y H, LI R, ZHANG Z Y, et al. Dynamic recognition method for water-flooded layer with discrete process neural network based on the principal component analysis[J].Well Logging Technology, 2010, 34(5): 432–437.(in Chinese) |
| [8] | 金向阳, 林琳, 钟诗胜, 等. 航空发动机振动趋势预测的过程神经网络法[J].振动、测试与诊断, 2011, 31(3): 331–336.JIN X Y, LIN L, ZHONG S S, et al. Aeroengine vibration tendency prediction based on process neural network[J].Journal of Vibration, Measurement & Diagnosis, 2011, 31(3): 331–336.(in Chinese) |
| [9] | 宫唤春. 基于双隐层径向基过程神经网络的汽轮机排汽焓在线预测[J].热力发电, 2014, 43(7): 32–36.GONG H C. Double hidden layer RBF process neural network based online prediction of steam turbine exhaust enthalpy[J].Thermal Power Generation, 2014, 43(7): 32–36.(in Chinese) |
| [10] | 刘菲菲, 彭荻, 贺彦林, 等. 基于极限学习的过程神经网络研究及化工应用[J].上海交通大学学报, 2014, 48(7): 977–981.LIU F F, PENG D, HE Y L, et al. Research and chemical application of extreme learning based process neural network[J].Joural of Shanghai Jiao Tong University, 2014, 48(7): 977–981.(in Chinese) |
| [11] | 魏鹏飞, 吴建军, 刘洪刚. 液体火箭发动机一种通用模块化仿真方法[J].推进技术, 2005, 26(2): 147–150.WEI P F, WU J J, LIU H G. Investigation of a general model simulation method for liquid propellant rocket engine[J].Journal of Propulsion Technology, 2005, 26(2): 147–150.(in Chinese) |
| [12] | 王建波, 于达仁, 王广雄. 液体火箭发动机泄漏故障实时仿真[J].推进技术, 1999, 20(5): 1–5.WANG J B, YU D R, WANG X. Real-time simulation of leak fault of liquid rocket engine[J].Journal of Propulsion Technology, 1999, 20(5): 1–5.(in Chinese) |
| [13] | 吴建军, 张育林, 陈启智. 液体火箭发动机实时故障仿真系统实现[J].推进技术, 1997, 18(1): 26–30.WU J J, ZHANG Y L, CHNE Q Z. The real-time fault simulation system for liquid propellant rocket engines[J].Journal of Propulsion Technology, 1997, 18(1): 26–30.(in Chinese) |
| [14] | 钟诗胜, 丁刚, 付旭云. 过程神经网络模型及其工程应用[M].北京: 国防工业出版社, 2014: 119-121.ZHONG S S, DING G, FU X Y. Process neural network models and its engineering applications[M].Beijing: National Defense Industry Press, 2014: 119-121.(in Chinese) |
| [15] | HAGAN M T, MENHAJ M B. Training feedforward networks with the Marquardt algorithm[J].IEEE Transactions on Neutral Networks, 1994, 5(6): 989–993.DOI:10.1109/72.329697 |
| [16] | HUANG G B, DING X J. Optimization method based on extreme learning machine for classification[J].Neurocomputing, 2010, 74(1): 155–163. |
| [17] | LIANG N Y, HUANG G B, SARATCHANDRAN P, et al. A fast and accurate online sequential learning algorithm for feedforward networks[J].IEEE Transactions on Neural Networks, 2006, 17(6): 1411–1423.DOI:10.1109/TNN.2006.880583 |
| [18] | ZHANG R, LAN Y, HUANG G B. Universal approximation of extreme learning machine with adaptive growth of hidden nodes[J].IEEE Transactions on Neural Networks, 2012, 23(2): 365–371.DOI:10.1109/TNNLS.2011.2178124 |
| [19] | 谢光军.液体火箭发动机涡轮泵实时故障检测技术及系统研究[D].长沙:国防科学技术大学, 2006:1-3.XIE G J.Research on real-time fault detection technology and system for liquid rocket engine turbopump[D].Changsha:National University of Defense Technology, 2006:1-3(in Chinese). |
| [20] | 夏鲁瑞.液体火箭发动机涡轮泵健康监控关键技术及系统研究[D].长沙:国防科学技术大学, 2010:1-3.XIA L R.Research on key technology and system for turbopump health monitoring of liquid rocket engine[D].Changsha:National University of Defense Technology, 2010:1-3(in Chinese). |
