无线传感器网络(Wireless Sensor Networks,WSNs)由多个具有无线通信能力的传感器节点组成,部署在特定的监测环境中,对物理环境信息的收集是其主要应用之一^[1]。典型的WSNs数据收集过程是:传感器节点周期性地感知物理环境信息,并将采集到的传感器数据通过多跳转发的方式汇聚到基站节点。传感器节点不仅要传输自己采集到的数据,还要转发其他节点的数据。越靠近基站的节点参与转发的次数越多,越容易因能量耗尽而失效,成了影响WSNs网络生命周期的一个瓶颈问题。
压缩感知(Compressive Sensing,CS)^[2-4]作为一种新兴的信息处理理论,为解决WSNs数据收集中的能量瓶颈问题提供了一个新的思路。文献^[5]在CS理论的基础上提出了一种压缩数据收集模型。基于压缩数据收集模型的WSNs数据收集方法^[5-9]能够减少传感数据的传输量,并让通信代价平均分配到每个节点上,从而有效地缓解了WSNs数据收集中的能量瓶颈问题。这些方法^[5-9]使用的都是固定的稀疏字典,然而WSNs的应用场景是多样化的,不同的应用场景下传感数据的稀疏特性是不同的。固定的稀疏字典缺乏对多样化场景的适应能力,局限了压缩数据收集的应用范围。此外,WSNs通常部署在复杂的环境中,其中大量存在的环境噪声会不可避免地影响到数据收集的精度。如何优化压缩数据收集系统的设计来减小环境噪声所造成的影响是一个值得考虑的问题。
为此,本文提出了一种优化字典学习算法来自适应地构造压缩数据收集中的稀疏字典。从训练数据中学习得到稀疏字典,提升对不同应用场景下的传感数据的稀疏表示能力。考虑到环境噪声的存在,对字典学习的算法进行优化设计,减小了环境噪声对数据收集精度的干扰。
1 问题描述 1.1 压缩数据收集模型 典型的压缩数据收集过程如图 1所示。假设在一条多跳传输路径上有N个节点。每个节点分别感知客观环境以获得传感数据,用x_j表示节点S_j采集的传感数据。在压缩数据收集模型中,每个节点不再直接传输自己采集的传感数据,也不直接转发其他节点的传感数据,而是传输多个传感数据的加权和^[5]。例如,节点S₁向其父节点S₂发送M个加权数据{₁₁x₁,₂₁x₁,…,_M1x₁},其中:{₁₁,₂₁,…,_M1}为节点S₁的随机测量系数。节点S₂接收到这些数据后,再在其中加上自己采集的传感数据,得到新的加权数据{₁₁x₁+₁₂x₂,₂₁x₁+₂₂x₂,…,_M1x₁+_M2x₂},并将其发送给父节点S₃。如此反复进行,则基站将接收到M个加权数据,用M维列向量y来表示,有

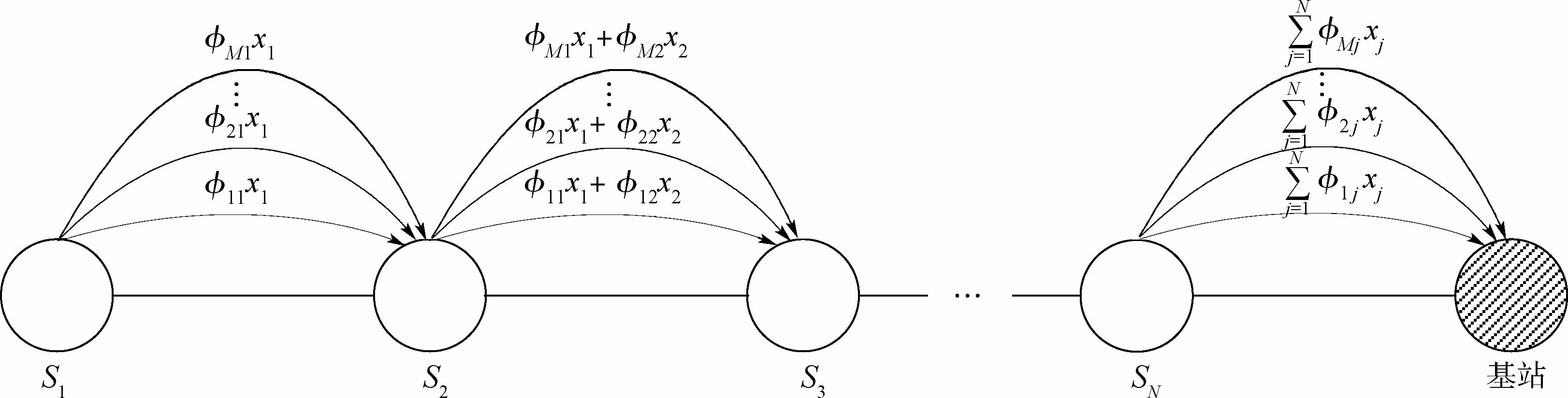图 1 多跳路径上的压缩数据收集过程 Fig. 1 Compressive data gathering process in a multi-hop route

图选项

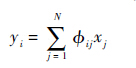(1)

用矩阵形式表示,有

(2)

式中:Φ∈R^M×N为测量矩阵;x∈R^N为传感数据向量。
如果x在某个稀疏字典D∈R^N×K上是稀疏的(其中:K为字典原子数,K≥N)

(3)

式中:系数向量θ=[θ₁ θ₂ … θ_K]^T的非零元素的个数远小于K;而且测量矩阵Φ是高斯随机矩阵,那么求解

(4)

得到唯一解θ,式中L为训练数据的数量。再通过计算x=Dθ便可恢复出原始的传感数据。
1.2 字典学习 现有的基于压缩数据收集模型的WSNs数据收集方法所使用的稀疏字典都是固定的正交矩阵,如离散余弦变化矩阵(Discrete Cosine Transform,DCT)等。然而WSNs的部署环境是复杂多变的,不同应用场景下的传感数据具有不同的稀疏特性,很难用固定的字典来描述。为此,有必要采用字典学习的方法,从不同类型的传感数据中学习得到相应的稀疏字典,以提升压缩感知数据收集对多样化应用场景的适应能力。
用一组传感数据{xⁱ}^L_i=1作为字典学习的训练数据,其中xⁱ∈R^N表示一个N维传感数据向量。用矩阵X∈R^N×L来表示这些训练数据：

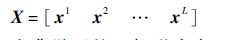(5)

字典学习的一般形式为

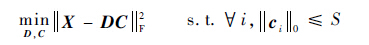(6)

式中:为矩阵Frobenius范数;C∈R^K×L为稀疏表示矩阵;S为稀疏度,矩阵C中的每一列都是S-稀疏向量。
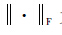
通过求解优化问题式(6)就可以得到稀疏字典D。对问题式(6)的求解有K-SVD^[10]等经典的字典学习方法。
2 环境噪声对压缩数据收集的影响 在实际情况中,环境背景噪声会对压缩数据收集产生干扰,使得测量数据中包含了噪声分量,

(7)

式中:e∈R^N为独立同分布的随机向量,服从正态分布Ν(0,σ²)。由于x能由字典D稀疏表示,将式(3)代入式(7)中,得到

(8)

用均方误差(Mean Squared Error,MSE)来衡量压缩数据收集的误差:

(9)

式中:θ为θ的估计值;E_θ,e[·]为随机向量θ和e联合分布下的数学期望。
为了便于理论分析,在这里使用oracle假设^[11],即假设系数向量θ中非零元素的位置是已知的,并用一个集合Γ?{1,2,…,K}来表示。那么式(8)变形为如下形式:

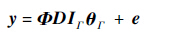(10)

式中:I_Γ∈R^K×S为删除了单位矩阵I∈R^K×K中不在集合Γ中的一些列后得到的矩阵;θ_Γ∈R^S为删除了θ中的零元素后的向量,S为θ中非零元素的个数。对式(10)求得θ_Γ的最小二乘估计量:

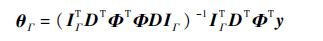(11)

因此有

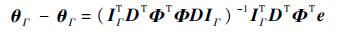(12)

把式(12)代入式(9)中,得到

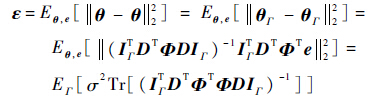(13)

式中:Tr[·]表示矩阵的迹;E_Γ[·]为随机集合Γ的数学期望。
文献^[12]指出E_Γ[σ²Tr[(I^T_ΓD^TΦ^TΦDI_Γ)^－1]]与是正相关的。因此为了减小环境噪声对数据收集精度的影响,在字典学习的过程中要让的取值尽量地小。但是,为了避免字典学习与非确定性的测量矩阵Φ耦合,不能直接把作为字典学习的惩罚项。由文献^[13]可知,在Φ是高斯随机矩阵的情况下,如果的取值较小则的取值也较小。为此,本文选择将作为自相干惩罚项加入到式(6)中,得到一个优化的字典学习模型：

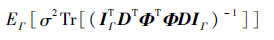
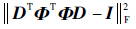
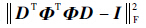
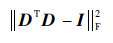
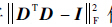
(14)

式中:λ>0为权衡因子;c_i为矩阵C中的第i个列向量。
3 优化字典学习算法 将问题式(14)称为优化字典学习(Optimized Dictionary Learning,ODL)。本文提出一种ODL算法来求解式(14)。ODL算法采用交替迭代的求解方法,在每次迭代过程中包含了2个步骤:①稀疏逼进;②字典更新。
3.1 稀疏逼进 在稀疏逼进阶段,固定字典D,求解训练数据X在字典D上的稀疏表示矩阵C,即

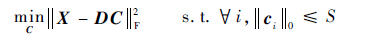(15)

问题式(15)可以用正交匹配追踪算法^[14]求解。
3.2 字典更新 在字典更新阶段,固定矩阵C,根据下面的优化问题求解出新的字典D:

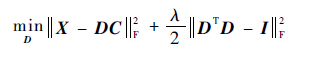(16)

显然,式(16)是一个凸问题,其必有全局最优解。令F ,则有

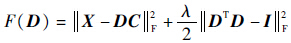
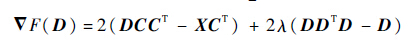(17)

由于F(D)是凸函数,所以当F(D)取到最小值时,必有ΔF(D)=0,即

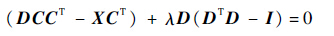(18)

由式(18)可得到

(19)

用式(19)作为优化问题式(16)的最优解的近似估计,即在迭代过程中使用以下公式对字典进行更新：

(20)

式中:D_k+1为第k+1轮迭代中更新的字典;D_k为第k轮迭代中更新的字典。得到新的字典D_k+1后,还要将D_k+1的各列依次进行归一化。综上所述,ODL算法的具体执行步骤如下:
1) 初始化D₀为随机矩阵,令k=0。
2) 主循环:重复运行步骤3)~5),直到迭代达到收敛。
3) 稀疏逼进:

4) 字典更新:

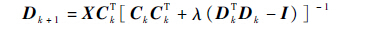5) 将D_k+1的各列归一化,令k=k+1。
4 实验分析 4.1 实验方案 为了验证本文提出的ODL算法的有效性,在北京航空航天大学传感网络与仪器实验室自主研发的无线传感器网络实验平台^[15]上进行模拟实验。实验平台由50个无线传感器节点组成,具体部署情况如图 2所示。

图 2 无线传感器网络实验平台 Fig. 2 Wireless sensor networks testbed

图选项

本次模拟实验使用的实验数据为50个传感器节点在2014-11-05—2014-12-03期间所记录的温度与湿度数据。记录间隔为10 min,每个节点分别记录了4 000个温度数据和4 000个湿度数据。
按照时间顺序,将前400个数据划分为训练数据集,将后3 600个数据划分为测试数据集。实验过程分为3个步骤:
1) 在训练数据集上用ODL算法进行字典学习得到稀疏字典D。
2) 评估字典D在测试数据集上的稀疏表示能力。
3) 在测试数据集上运行压缩数据收集算法,并评估在不同环境噪声强度下的数据收集精度。
为了充分验证通过ODL算法学习得到的字典(记作ODL字典)在压缩数据收集中的效用,选择固定的离散余弦变换矩阵(记作DCT字典)和通过K-SVD^[10]算法学习得到的字典(记作K-SVD字典)作为比较对象。实验过程中使用的具体参数如表 1所示。在压缩数据收集中使用的测量矩阵是高斯随机矩阵,环境噪声是人为模拟的高斯随机噪声。为了减少实验的随机性带来的影响,每组实验重复50次,取平均值作为最终的实验结果。
表 1 实验参数 Table 1 Experimental parameters

参数名称	N	M	L	K
取值	50	20	400	100

表选项






4.2 实验结果
4.2.1 对不同字典的稀疏表示能力的比较 从训练数据集上学习得到字典D后,评估其在测试数据集上的稀疏表示能力。通过式(21)求解某个测试数据x在字典D上的稀疏表示：

(21)

用均方根误差(Root Mean Square Error,RMSE)来衡量字典的稀疏表示误差。通过式(22)计算某个测试数据的RMSE:

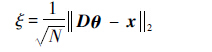(22)

由于测试数据集有多个测试数据,所以对各个测试数据分别求得稀疏表示误差后再统一求均值,作为测试数据集的稀疏表示误差。
图 3显示了ODL字典、DCT字典以及K-SVD字典在温度数据集和湿度数据集上的稀疏表示能力。

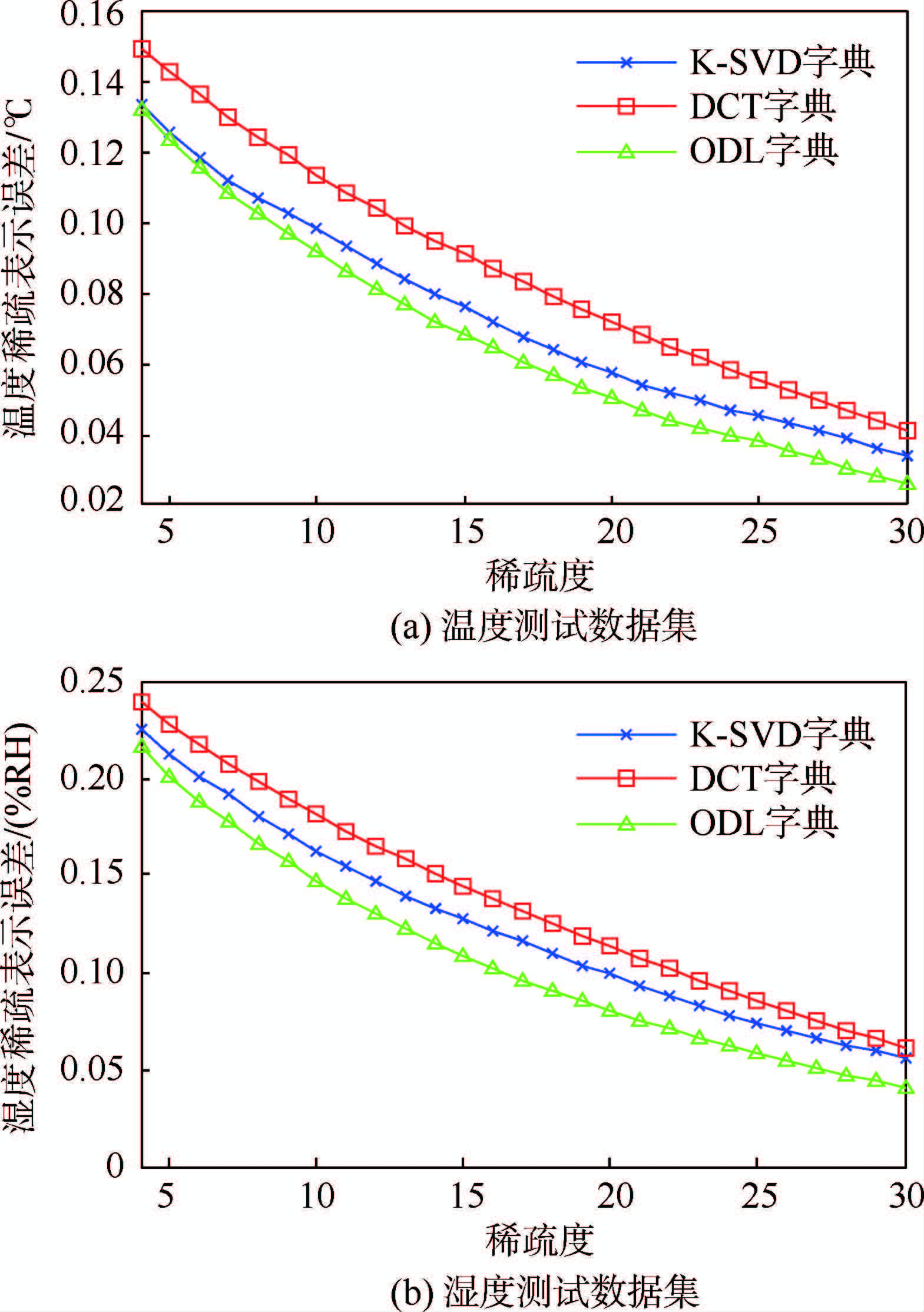图 3 不同字典的稀疏表示能力 Fig. 3 Sparse representation performance of different dictionaries

图选项

由图 3可知,在同样的稀疏度下,ODL字典的稀疏表示误差最小,其次是K-SVD字典,DCT字典的稀疏表示误差最大;在同样的稀疏表示误差下,ODL字典需要的稀疏度最小,其次是K-SVD字典,DCT字典需要的稀疏度最大。由此可知,ODL字典对测试数据的稀疏表示能力最强,而固定的DCT字典对测试数据的稀疏表示能力最差。
和预期的一致,通过字典学习算法得到的字典的稀疏表示能力要好于固定的DCT字典。而在字典学习得到的字典中,ODL字典的稀疏表示能力比K-SVD字典要好,这是因为ODL算法中加入的自相干惩罚项减少了字典学习过程中对训练数据的过拟合。

4.2.2 环境噪声对收集精度的影响 在测试数据中添加高斯随机噪声以模拟环境噪声对压缩数据收集的影响。环境噪声的信噪比(Signal Noise Ratio,SNR)定义如下:

(23)

在压缩数据收集中分别使用ODL字典、DCT字典以及K-SVD字典作为稀疏字典,然后测试其在不同环境噪声信噪比下的数据收集精度。
实验结果如图 4所示。当环境噪声的信噪比很大时,使用ODL字典的数据收集误差最小,其次是K-SVD字典,固定字典的误差最大。这和4.2.1节中的实验结果是一致的,因为ODL字典的稀疏表示能力最好,固定字典的稀疏表示能力最差。随着信噪比的减小,使用K-SVD字典的数据收集误差将超过使用固定字典的误差,而使用ODL字典的数据收集误差始终是最小的。这是因为ODL算法在设计时就考虑到了如何抑制环境噪声的影响。通过引入了一个自相干惩罚项,ODL算法使得在字典学习中得到的稀疏字典具有低自相干结构,从而能够抑制环境噪声对数据收集精度的影响。

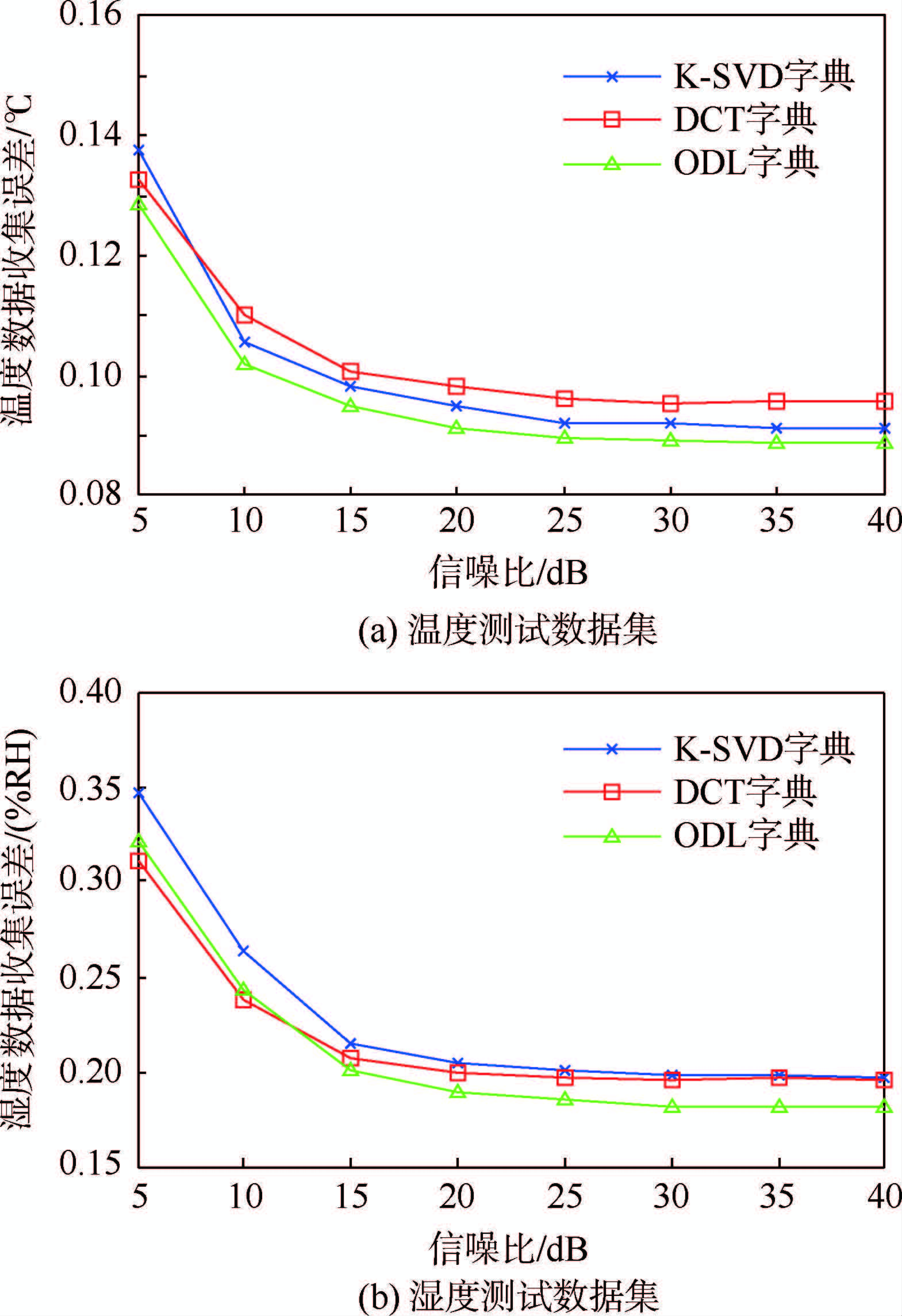图 4 环境噪声对收集精度的影响 Fig. 4 Impact of environmental noise on accuracy of compressive data gathering

图选项

4.2.3 权衡因子λ对ODL算法性能的影响 注意到ODL算法中包含了一个可变的参数，即权衡因子λ,该参数的取值势必会影响到ODL算法的性能。为此,通过仿真实验来分析λ的取值对ODL算法性能的影响。4.2.1节与4.2.2节中的实验结果表明,ODL算法在温度数据集上的性能和在湿度数据集上的性能十分类似。所以只在温度数据集上测试λ对ODL算法性能的影响。
首先通过仿真实验来分析λ对ODL算法稀疏表示能力的影响。在仿真中,将稀疏度S固定为10,从0~0.4逐渐改变λ的取值,然后测试由ODL算法训练得到的字典在温度数据集上的稀疏表示误差。仿真结果如图 5所示。

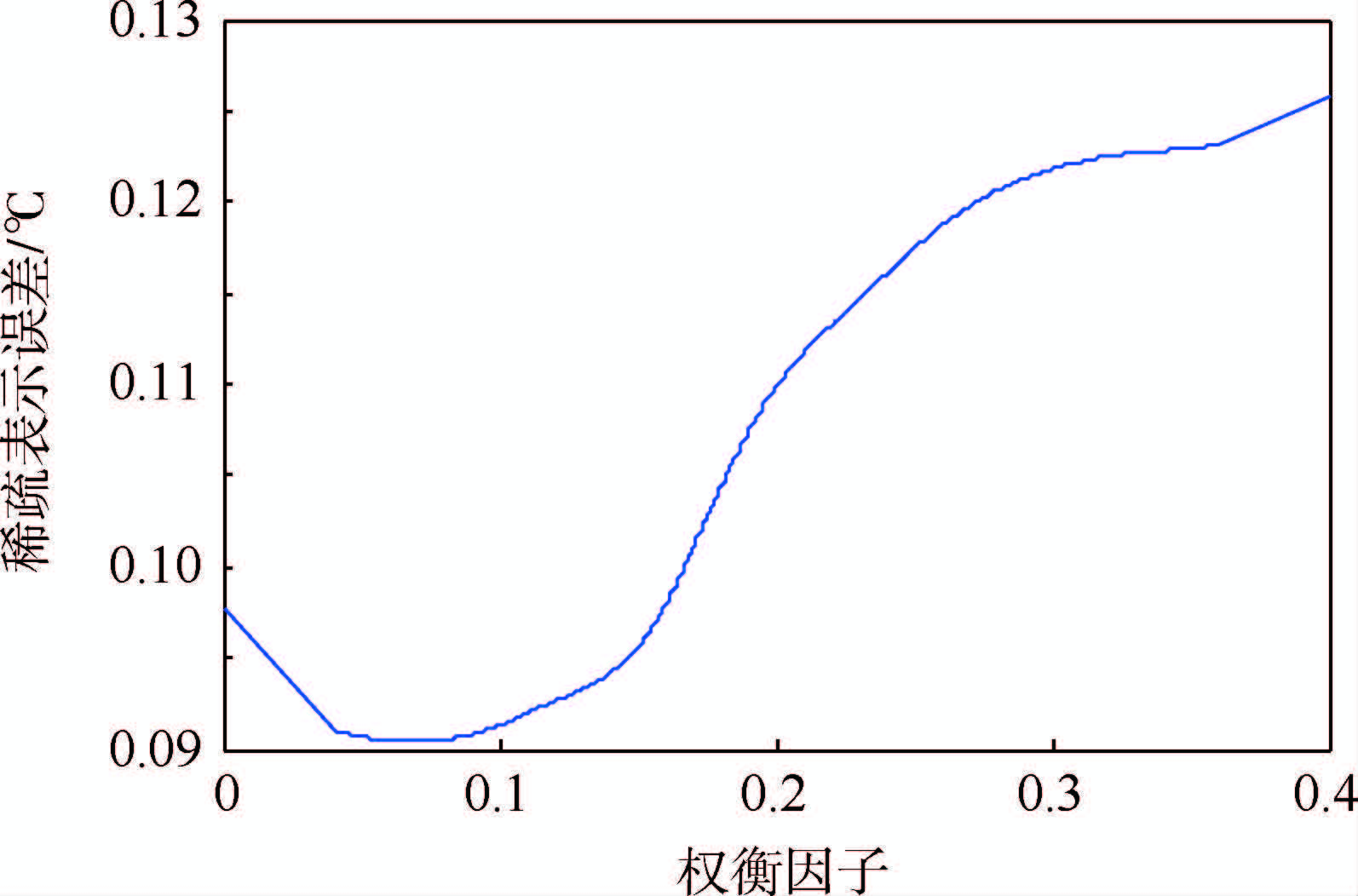图 5 权衡因子对温度稀疏表示误差的影响 Fig. 5 Impact of tradeoff factor on temperature sparse representation error

图选项

首先,随着λ从0开始逐渐增长,稀疏表示误差也逐渐降低。这是因为自相干惩罚项随着λ从0增长而开始发挥作用,减少了对训练数据的过拟合。然而,当λ于一定值时(例如λ>0.1),稀疏表示误差将随着 λ的增加而增加。这是因为当λ取值过大时,自相干惩罚项的惩罚作用过于强烈,反而抑制了字典对传感数据的稀疏表示能力。
通过仿真实验来分析λ对ODL算法数据收集误差的影响。在仿真中,信噪比η固定为10,从0~0.4逐渐改变λ的取值,然后测试基于ODL算法的压缩数据收集在温度数据集上的数据收集误差。仿真结果如图 6所示。

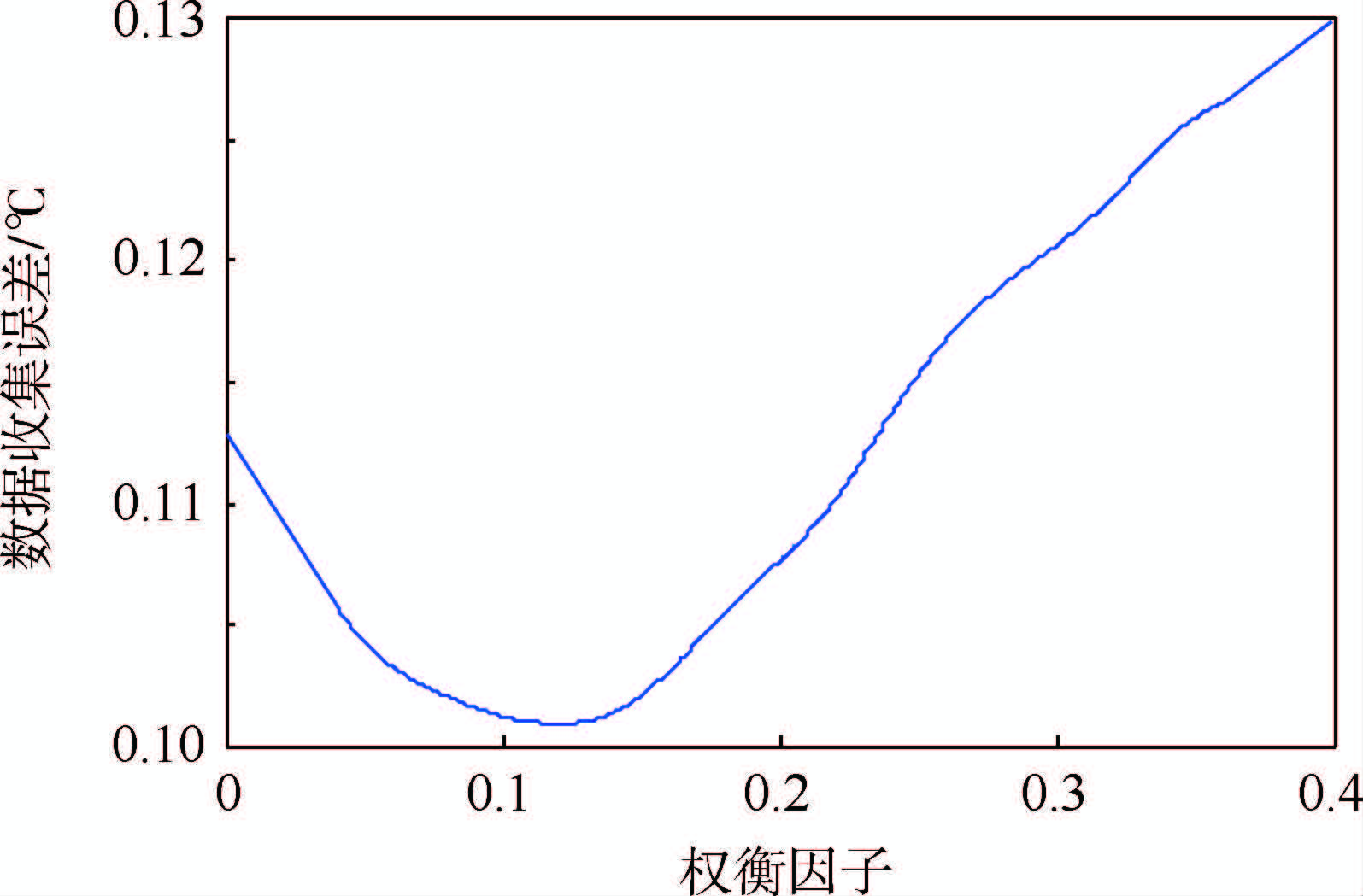图 6 权衡因子对温度数据收集误差的影响 Fig. 6 Impact of tradeoff factor on temperature data gathering error

图选项

和图 5中的结果十分类似,随着λ从0开始增长,数据收集误差也逐渐降低。但和图 5相比,图 6中的曲线下降幅度更大。这是因为随着λ从0开始增长,ODL算法训练得到的字典的稀疏表示能力将逐渐提高;更重要的是,ODL算法中的自相干惩罚项开始发挥作用,字典对环境噪声的抑制能力将逐渐提升。因此,在这2种因素的叠加作用下,数据收集误差的下降幅度大于稀疏表示误差的下降幅度。当λ大于一定值时,数据收集误差将随着λ的增加而增长。这是因为当λ取值过大时,ODL算法的稀疏表示能力变差。
综上所述,在具体应用中需要权衡考虑λ的取值:既不能因取值过小而牺牲了字典对环境噪声的抑制能力,也不能因取值过大而损害了字典的稀疏表示性能。
5 结 论 本文在压缩数据收集中引入了一种优化字典学习(ODL)算法,实验结果表明:
1) ODL算法引入的自相干惩罚项能减少在字典学习过程中对训练数据的过拟合,提高了稀疏表示能力。
2) ODL算法通过引入自相干惩罚项,使学习得到的稀疏字典具有低自相干结构,能有效地抑制环境噪声对数据收集精度的影响。

参考文献

[1]	RAJAGOPALAN R, VARSHNEY P K. Data-aggregation techniques in sensor networks:A survey[J]. IEEE Communications Surveys and Tutorials,2006, 8(4): 48–63.
	Click to display the text
[2]	CANDES E J, WAKIN M B. An introduction to compressive sampling[J]. IEEE Signal Processing Magazine,2008, 25(2): 21–30.
	Click to display the text
[3]	DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory,2006, 52(4): 1289–1306.
	Click to display the text
[4]	BARANIUK R G. Compressive sensing[J]. IEEE Signal Processing Magazine,2007, 24(4): 118–121.
	Click to display the text
[5]	LUO C,WU F,SUN J,et al.Compressive data gathering for large-scale wireless sensor networks[C]//Proceedings of the 15th Annual International Conference on Mobile Computing and Networking.Washington,D.C.:ACM,2009:145-156.
	Click to display the text
[6]	LUO C, WU F, SUN J, et al. Efficient measurement generation and pervasive sparsity for compressive data gathering[J]. IEEE Transactions on Wireless Communications,2010, 9(12): 3728–3738.
	Click to display the text
[7]	陈正宇, 杨庚, 陈蕾, 等. 基于压缩感知的WSNs长生命周期数据收集方法[J]. 电子与信息学报,2014, 36(10): 2343–2349.CHEN Z Y, YANG G, CHEN L, et al. Data gathering for long network lifetime in WSNs based on compressed sensing[J]. Journal of Electronics & Information Technology,2014, 36(10): 2343–2349.(in Chinese).
	Cited By in Cnki (0) | Click to display the text
[8]	WU X P, WANG Q S, LIU M Y. In-situ soil moisture sensing:Measurement scheduling and estimation using sparse sampling[J]. ACM Transactions on Sensor Networks,2015, 11(2): 1-26–29.
	Click to display the text
[9]	TANG Y, ZHANG B, JING T, et al. Robust compressive data gathering in wireless sensor networks[J]. IEEE Transactions on Wireless Communications,2013, 12(6): 2754–2761.
	Click to display the text
[10]	AHARON M, ELAD M, BRUCKSTEIN A. K-SVD:An algorithm for designing overcomplete dictionaries for sparse representation[J]. IEEE Transactions on Signal Processing,2006, 54(11): 4311–4322.
	Click to display the text
[11]	CANDES E, TAO T. The Dantzig selector: Statistical estimation when p is much larger than n[J]. The Annals of Statistics,2007, 35(6): 2313–2351.
	Click to display the text
[12]	LI G, ZHU Z, YANG D, et al. On projection matrix optimization for compressive sensing systems[J]. IEEE Transactions on Signal Processing,2013, 61(11): 2887–2898.
	Click to display the text
[13]	RAUHUT H, SCHNASS K, VANDERGHEYNST P. Compressed sensing and redundant dictionaries[J]. IEEE Transactions on Information Theory,2008, 54(5): 2210–2219.
	Click to display the text
[14]	TROPP J A, GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory,2007, 53(12): 4655–4666.
	Click to display the text
[15]	YI K,FENG R,YU N,et al.PARED:A testbed with parallel reprogramming and multi-channel debugging for WSNs[C]//IEEE Wireless Communications and Networking Conference,WCNC.Piscataway,NJ:IEEE Press,2013:4630-4635.
	Click to display the text