在现实工程应用中,解决传感器数据缺失问题一般有3种途径:①去掉含缺失值的样本;②用期望来替代缺失值;③通过建立合适的模型进行预测并用预测值取代缺失值。去掉含缺失值的样本或用期望值代替缺失值的做法容易丢失样本信息,很可能丢弃的样本就是对发动机监视至关重要的一个样本或者平均值掩盖了发动机的当前状态真实情况。用合适的模型如回归模型、神经网络等,都是利用传感器之间的相关性,利用数据融合思想,用其他传感器信息提供缺失的传感器数据。这些模型的合理性和可用性是解决数据重构的关键所在[5]。针对航空发动机在线数据处理的实时性需求,需要一种高效、实时的方法对数据进行特征表示,完成数据重构。
子空间思想长久以来作为一个有力的工具用于数据建模和分析,被用于通信[6]、雷达和声呐目标定位和追踪[7]以及医学图像[8]中的子空间建模以恢复感兴趣的信号并且去除噪声,其基本思想是采用低秩子空间代替高维的原始空间,从而数据处理时减少复杂度,并且能够最大程度上表示原始空间的特征,属于压缩感知领域。栗茂林等[9]用非负稀疏表示的敏感特征提取方法(Non-negation SPCA,NSPCA)对滚动轴承试验数据进故障特征提取;耿宏等[10]考虑的快速存储记录器(Quick Access Recorder,QAR)数据在某种正交基下具有稀疏性性质,利用Cosamp算法对QAR数据进行随机测量,重构出原始QAR数据。文献[9]中的NSPCA方法只是对数据特征进行压缩提取,并不能处理数据缺失情况;文献[10]中使用的Cosamp算法[11]是对某时刻某一信号进行重构,没有考虑不同时刻同一信号的自相关性,并且对有缺失的多数据重构鲁棒性差。
本文首先对民航飞机的仿真数据进行分析,发现航空发动机各参数之间有着很强的相关性,且数据拥有很大的条件数,此时观测矩阵就是一个病态矩阵。如果利用传统的主成分分析、压缩感知方法如Cosamp,或鲁棒性子空间跟踪算法(如GRASTA[12])来处理就会对噪声非常敏感,会导致在数据重构过程中,主成分的一点点扰动都会对其他成分造成很大偏差。所以,本文利用极化增量矩阵填充(Polar Incremental Matrix Completion,PIMC)算法[13],针对条件数特别大的航空发动机数据进行重构,用子空间表述系统特征,实现数据重构和一定程度的降噪。将本文模型和文献[1]提出的变异AANN模型应用于仿真数据和真实数据,实验结果证明本文模型适用于航空发动机气路数据在线重构,有较好的降噪效果,且稳定、快速。
1 问题模型及数据说明 1.1 问题模型 稳态工作条件下,健康或缓慢退化的发动机性能数据可由一个子空间表示数据特征,子空间记为U∈Rm×d,m为实际观测参数个数,d为数据特征值的个数,d<m。t时刻的航空发动机传感器观测数据vt∈Rm×1,每次观测值vt可由子空间U和子空间系数wt∈R1×d以及误差et∈Rm×1表示:
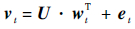 | (1) |
假设已有一组观测矩阵A=[v1,v2,…,vn]∈Rm×n,A可表示为
 | (2) |
式中:系数矩阵W=[w1;w2;…;wn]∈Rn×d;误差矩阵e=[e1,e2,…,en]∈Rm×n。
则t时刻的观测量可估计为
 | (3) |
式中:
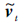
因此,可以通过截止到t时刻的一组可能存在缺失信息的观测数据计算出发动机的特征子空间Ut和系数矩阵Wt,通过特征子空间和对观测值(包括缺失信息)进行重构(见式(4)),可得到去除一定噪声的完整估计值。
 | (4) |
式中:

当新来一批观测值,可将新观测值输入模型再次更新特征子空间及系数,实现在线重构数据及降噪。
1.2 数据说明及分析 本文采用雅典国家技术大学的仿真软件Laboratory of Thermal Turbo machine(LTT)生成2组缓慢性能退化数据,分别是:风扇叶片污垢(fan fouling)数据和风扇叶尖间隙(fan tip clearance)数据。
LTT仿真软件生成的气路参数不含噪声,但实际工程应用中传感器数据会含有测量噪声,所以为使仿真数据更符合实际应用,本文在2组退化数据上都添加高斯噪声来模拟实际测量噪声,即各测量参数的高斯噪声的3倍标准差(3σ)。典型涡扇发动机气路参数测量噪声见表 1[14]。
表 1 典型涡扇发动机气路参数测量噪声[14] Table 1 Measurement noise of typical turbofan engine gas path parameters[14]
| 测量噪声 | 参数 | ||||||
| NL/(r·min-1) | NH/(r·min-1) | P13/Pa | T13/K | P3/kPa | T3/K | T6/K | |
| 3σ | 6 | 12 | 300 | 2 | 5 | 2 | 2 |
| 注:NL—低压转子转速;NH—高压转子转速;P13—风扇出口压力;T13—风扇出口温度;P3—高压压气机出口压力;T3—高压压气机出口温度;T6—尾气排气温度。 | |||||||
表选项
利用MATLAB的SVD命令对含噪数据进行奇异值分解后,得到LTT仿真数据SVD结果,如表 2所示(表中: δi为第i个主成分的奇异值,i=1,2,…,7)。观察奇异值情况:如果取前3个主成分的话,观测矩阵的条件数达到102级,意味着对子空间及系数的求解会使观测数据的噪声扰动非常敏感,同时可能也会导致有些算法收敛慢,这些在工程应用中是不可接受的。所以,采用PIMC算法来解决病态矩阵的子空间和系数求解问题。
表 2 LTT仿真数据SVD结果 Table 2 Results of LTT simulation data by SVD
| ????数据集 | δ1 | δ2 | δ3 | δ4 | δ5 | δ6 | δ7 |
| fan fouling | 9.555 6×103 | 82.555 2 | 0.297 0 | 0.215 8 | 0.117 6 | 0.009 1 | 0.001 91 |
| fan tip clearance | 9.460 7×103 | 97.053 8 | 0.428 3 | 0.273 1 | 0.193 5 | 0.012 1 | 0.002 1 |
表选项
2 PIMC算法 PIMC算法是Balzano等[15]为了解决病态矩阵的重构问题而提出的一种算法,它基于格拉斯曼秩-1子空间估计(Grassmanian Rank-One Update Subspace Estimation,GROUSE)算法和极化分解。GROUSE算法在某一特定步长情况下等价于增量奇异值分解(Incremental Singular Value Decomposition,ISVD)[16-17],通过GROUSE算法的增量分解形式,可以得到子空间和系数的迭代更新公式。但是GROUSE算法、ISVD方法对病态矩阵进行恢复时可能不收敛[13],在有数据缺失情况下进行增量奇异值分解得到的奇异值可能不是最优的,且增量奇异值分解要求系数矩阵也是正交的,而在GROUSE算法中没有对系数矩阵加以正交的约束。因此,Balzano等[15]将子空间缩放权重和极化分解引入GROUSE算法以解决上述问题,对观测矩阵的重构不再使用式(4),而是在迭代过程中将系数矩阵进行极化分解以求解子空间。式(5)就是利用极化分解形式表示的数据估计:
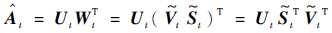 | (5) |
对照矩阵的奇异值分解式,可知
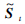
在t时刻,通过前t-1组观测数据可得到更新的子空间记为Ut,rt为实际观测值和重构值的残差,st为子空间缩放权重,γ是一个常数。t+1时刻的观测矩阵可表示为
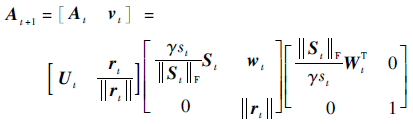 | (6) |
具体算法步骤参看文献[13]。
3 基于PIMC算法的数据重构 3.1 数据重构模型 PIMC算法是一个在线算法,因此可以利用此算法在线快速重构航空发动机的数据。航空发动机传感器数据重构模型如图 1所示。
 |
| 图 1 航空发动机传感器数据重构模型 Fig. 1 Aeroengine sensor data reconstruction model |
| 图选项 |
设初始有n个观测序列组成了观测矩阵A,设置常数γ,降维后的秩d,最大迭代次数lmax,迭代变量i=1,观测序号t=1:n;初始化一个正交矩阵为系数矩阵W,一个d×d的单位阵作为S0,一个随机正交阵作为初始子空间U0,子空间缩放权重s0=0,顺序按列从观测矩阵取观测向量vt,即vt=A(:,t),Ωt∈{1,2,…,m}为观测到的传感器序号,vΩt表示实际观测到的数据,子空间系数wt为
 | (7) |
若是离线数据重构,直接按照文献[13]所述算法步骤即可对数据重构。若是在线数据,首先初始化一个正交的系数矩阵W∈Rp×d,其中设置

3.2 实验结果分析
3.2.1 重构性能分析 将加噪后的仿真数据作为实际观测数据,将AANN模型和本文模型重构后的数据和原始的干净数据比较以分析2种算法对数据的重构和降噪性能。
实验中2种算法的参数设置见表 3。
表 3 算法参数设置 Table 3 Algorithm parameters setting
| 算法 | ??????参数 | 参数数值 |
| PIMC | d | 3 |
| γ | 0.001 | |
| lmax | 20 | |
| AANN | 映射层神经元个数 | 26 |
| 瓶颈层神经元个数 | 6 | |
| 解映射层神经元个数 | 26 |
表选项
用Case 1~Case 7分别表示NL、NH、P13、T13、P3、T3和T6传感器失效情况,即相应的传感器数据缺失或异常情况;不同的传感器故障,对仿真数据分别按照总数据的50%、60%、70%、80%、90%和100%划分出历史数据,将剩余的数据作为在线数据进行在线数据重构。
为了比较本文模型和AANN方法性能,本文分别选取不同数据比例设置、不同气路参数数据缺失情况下,AANN模型和本文模型对含噪数据进行重构,由于篇幅所限,此处仅列出若干情况下的重构结果图,如图 2~图 4所示。
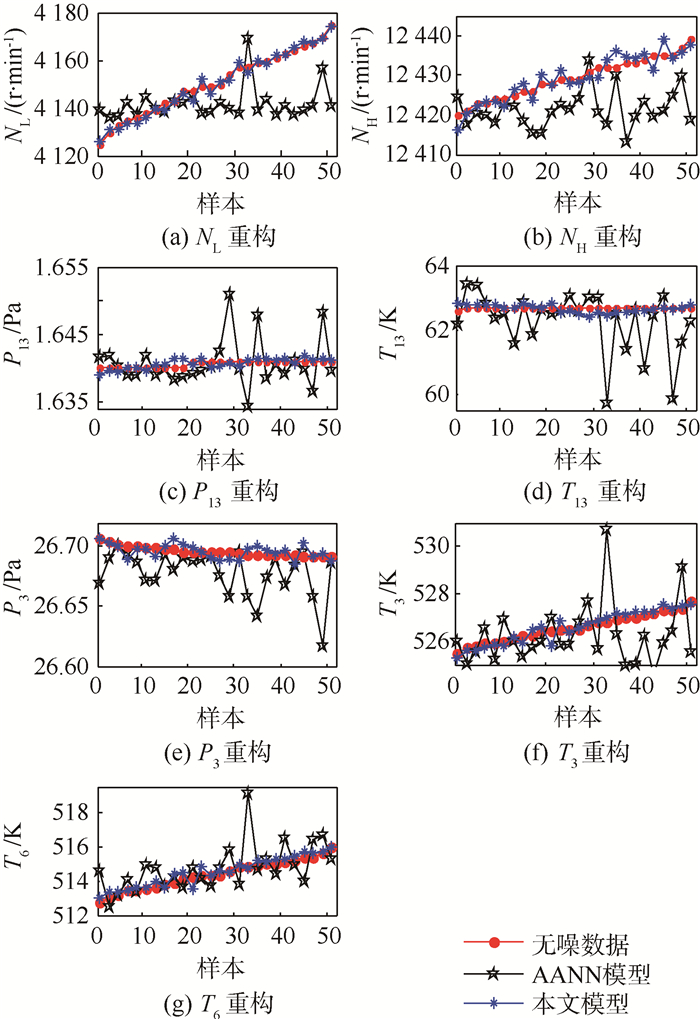 |
| 图 2 Case 1,50%风扇叶片污垢数据重构结果 Fig. 2 Reconstruction results of 50% fan fouling data under Case 1 |
| 图选项 |
 |
| 图 3 Case 3,60%风扇叶尖间隙退化数据重构结果 Fig. 3 Reconstruction results of 60% fan tip clearance degradation data under Case 3 |
| 图选项 |
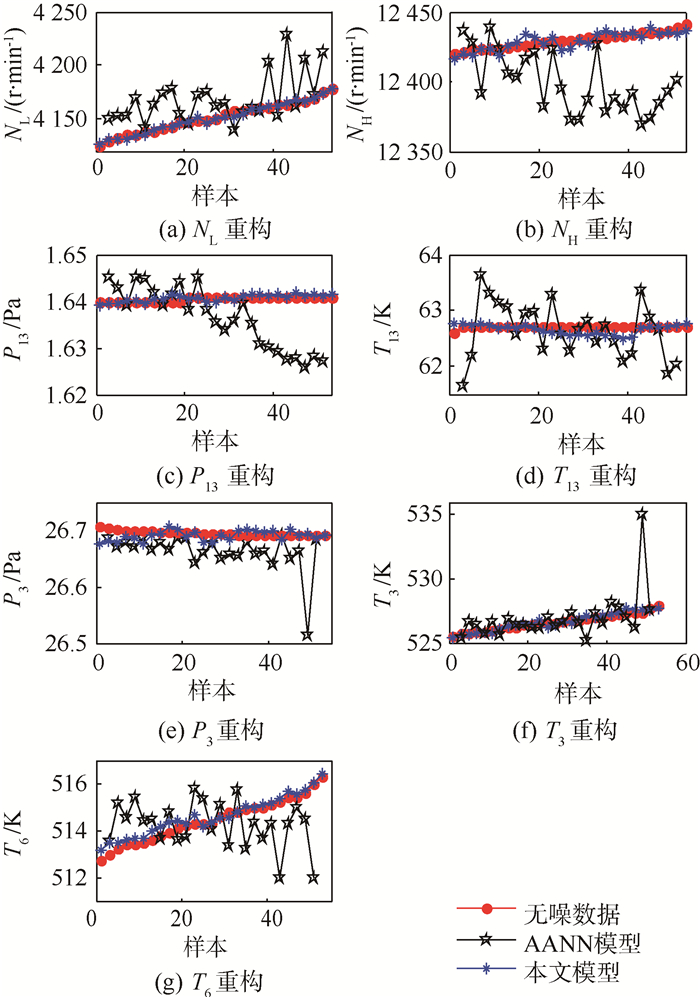 |
| 图 4 Case 4,80%风扇叶片污垢数据重构结果 Fig. 4 Reconstruction results of 80%fan fouling data under Case 4 |
| 图选项 |
图 2描述了2种算法对风扇叶片污垢数据的重构结果,采用50%的数据作为历史数据。明显的,本文模型重构的结果比AANN模型的结果更接近于无噪数据,这说明对于风扇叶片污垢数据,本文模型的降噪效果要优于AANN模型且能真实地反映发动机退化趋势。因为本文模型能够利用所有的数据估计出模型的子空间,并且它是一种在线算法,所以它还能够利用新来的观测数据跟踪发动机的退化趋势;虽然NL数据有缺失,但是AANN模型只是将没有数据缺失的其他6个参数(NH、P13、T13、P3、T3和T6)作为模型输入,而完全抛弃了观测到的部分NL数据,这样没有充分利用已有信息。AANN模型只是根据前50%的历史数据挖掘7个传感器之间的相关性,它反映的只是前50%数据的趋势,而无法反映发动机整体性能退化特征,所以对后面新来的观测数据重构效果差。
当P13数据有缺失时,2种模型利用60%的历史数据对高压压气机风扇叶尖间隙退化数据进行重构的结果如图 3所示。图 3(d)、图 3(f)显示本文模型对T13和T3重构后能很好地逼近无噪数据,其他5个气路参数的重构均能反映退化状态趋势。
再选取80%的数据作为历史数据,看到2种模型对T13有缺失的风扇叶片污垢数据进行重构的结果,如图 4所示。本文模型对NL、T13、T3和T6的重构体现了该退化状态下的数据特征,尤其是T13、T3和T6这3个参数,随着在线数据的增加对子空间的不断修正,第35个样本后的估计值越来越接近无噪数据。
对于全部数据,本文按照数据量的2%随机设置了参数缺值,因为AANN模型无法对随机缺值情况进行处理,所以此处只给出本文模型对所有数据进行重构的结果,如图 5和图 6所示。
 |
| 图 5 风扇叶片污垢数据(随机数据缺失)重构结果 Fig. 5 Reconstruction results of fan fouling data (with randomized missing data) |
| 图选项 |
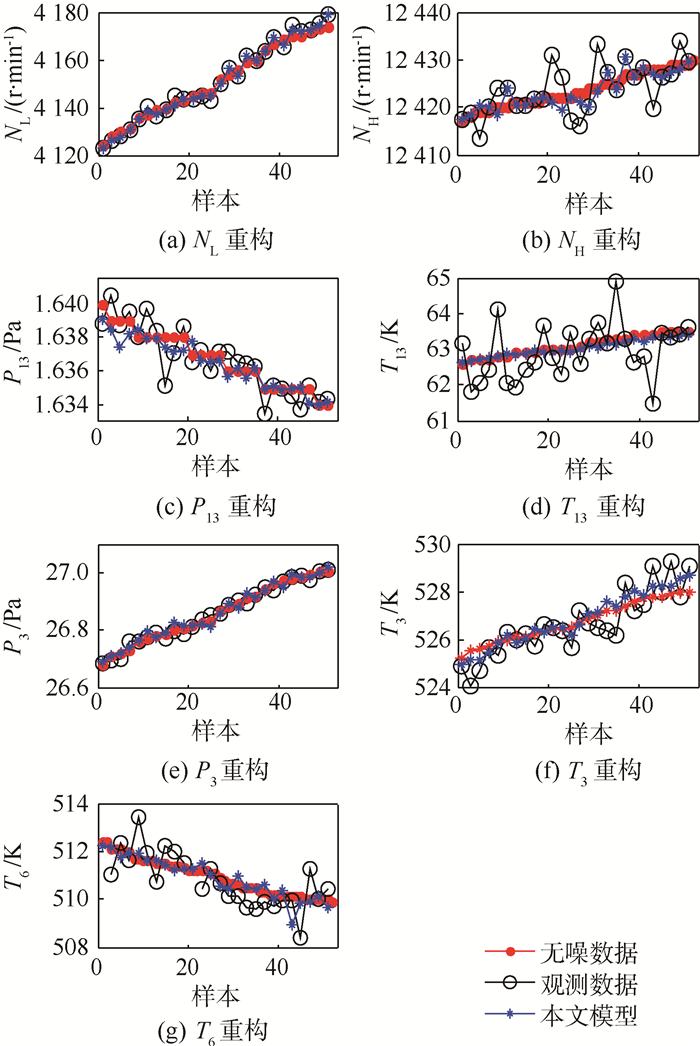 |
| 图 6 风扇叶尖间隙退化数据(随机数据缺失)重构结果 Fig. 6 Reconstruction results of fan tip clearance degradation data (with randomized missing data) |
| 图选项 |
所有退化数据在随机缺值情况下,对NL、NH、P13和P3的重构较观测数据都要平滑些,对T13、T3和T6 3个数据降噪效果很好,重构值接近无噪数据。
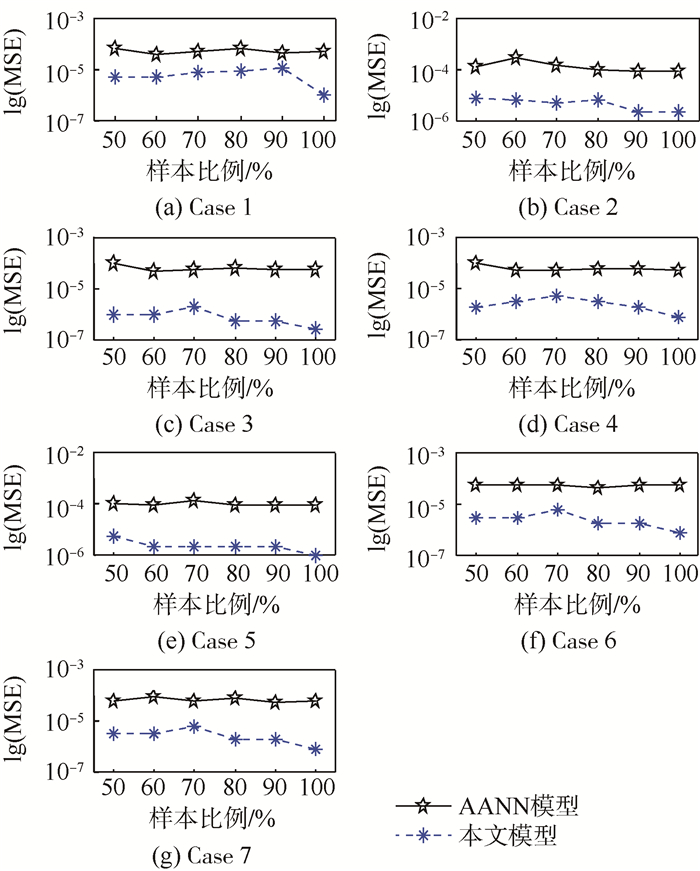
因为7个传感器数据的数量级不一样,所以对数据进行归一化后,利用重构数据和无噪数据的均方误差来评价算法的准确率,又因为均方误差数量级非常小,所以本文对归一化均方误差(MSE)取对数给出2个模型的均方误差图,关于风扇叶尖间隙和风扇叶片污垢数据的性能比较如图 7和图 8所示。
 |
| 图 7 风扇叶尖间隙数据的性能比较 Fig. 7 Performance comparison of fan tip clearance data |
| 图选项 |
 |
| 图 8 风扇叶片污垢数据的性能比较 Fig. 8 Performance comparison of fan fouling data |
| 图选项 |
对于这2组退化数据,AANN模型的均方误差是10-4级而本文模型的均方误差是10-6级。在各种数据缺失情况下,随着历史数据的增加(比例提高),AANN模型的数据重构性能有所提高,因为AANN模型是通过历史数据确定的,所以该模型性能受制于历史数据的多少,又因无法利用新观测到的信息来更新网络参数,所以在线重构数据性能较差;但是PIMC算法在各种情况下,数据重构性能稳定,这和它的在线学习特性有关:它首先利用历史数据得到合适的子空间,当有新的观测数据到来时,会对新的观测数据进行在线计算以更新子空间,通过不断更新子空间和系数实现在线恢复数据。
3.2.2 实时性分析 在不同的传感器数据失效、不同比例的历史数据情形下,训练AANN模型和本文模型平均耗时t1、对历史和实时数据重构所用平均耗时t2如表 4所示。
表 4 模型训练及数据重构平均耗时 Table 4 Average time-consumption of model training and data reconstruction
| ?????模型 | 风扇叶尖间隙 | 风扇叶片污垢 | ||
| t1/s | t2/s | t1/s | t2/s | |
| AANN模型 | 1.626 2 | 0.053 4 | 1.336 2 | 0.052 3 |
| 本文模型 | 0.119 7 | 0.040 4 | 0.123 5 | 0.041 8 |
表选项
无论是风扇叶尖间隙数据还是风扇叶片污垢数据,就模型训练平均耗时t1而言,本文模型比AANN模型减少了90%多;对历史数据和在线数据重构平均耗时t2来说,虽然2个模型相差不大,但是本文模型仍然耗时比AANN模型缩短0.01 s。在随机缺值情况下,风扇叶尖间隙数据和风扇叶片污垢数据,训练本文模型耗时分别是0.153 5 s和0.165 4 s,对数据重构耗时分别是0.002 2 s和0.002 s。这些表明本文模型无论是在模型训练上还是对实时数据进行在线重构或对历史数据进行重构,所花时间均比AANN模型少,尤其是对不断更新的实时数据进行在线重构平均只需0.04 s,这个性质能够很好地满足工程应用需求。
4 结 论 本文研究了传感器数据证实中的数据重构问题,提出了利用子空间对发动机数据进行在线重构模型。经过实验,将本文模型重构结果对比无噪数据,发现:
1) 利用PIMC算法可解决信息缺失情况下的航空发动机传感器数据进行重构问题,该方法性对数据重构降噪效果好、重构结果接近干净数据;并且,该算法收敛快耗时少,对仿真数据在线重构平均耗时0.04 s。
2) 提出的航空发动机传感器数据重构模型能够利用航空发动机各参数间的相关性,用子空间表示系统演化特征,并利用历史数据和新获得的数据进行子空间更新,从而可实时跟踪并表示系统特征,快速在线重构数据,对工程应用有很大的实用价值。下一步继续研究快速、准确地确定模型最优参数以及尝试通过子空间表示的数据特征来对不同退化数据进行分类。
参考文献
| [1] | 唐雅娟.发动机试验传感器数据证实的软计算方法与系统实现研究[D].长沙:国防科学技术大学,2007:1. TANG Y J.Study on methods and system realization of sensor data validation by soft computing technique for engine test[D].Changsha:National University of Defense Technology,2007:1.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [2] | 黄向华, 孙建国. 基于自联想网络的发动机传感器解析余度技术[J]. 航空动力学报,1999, 14(4): 433–436.HUANG X H, SUN J G. Analytical redundancy based on autoassociative neural network for aeroengine sensors[J]. Journal of Aerospace Power,1999, 14(4): 433–436.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [3] | 单晓明, 宋云峰, 黄金泉, 等. 基于神经网络和模糊逻辑的航空发动机状态监视[J]. 航空动力学报,2009, 24(10): 2356–2361.SHAN X M, SONG Y F, HUANG J Q, et al. Condition monitoring of aero-engine based on neural network and fuzzy logic[J]. Journal of Aerospace Power,2009, 24(10): 2356–2361.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [4] | [4]QIU X J, HUANGJ Q, LUF, 等. Fault diagnosis system design for the sensors and components of aircraft engine based on cloud relational analysis[J]. Journal of Aerospace Power,2012, 26(11): 2584–2592. |
| Cited By in Cnki (0) | |
| [5] | 任淑红.民航发动机性能可靠性评估与在翼寿命预测方法研究[D].南京:南京航空航天大学,2010:19-20. RENG S H.Research on methods of performance reliability assessments and life on wing prediction for civil aeroengine[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2010:19-20.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [6] | MOULINES E, DUHAMEL P, CARDOSO J F, et al. Subspace methods for the blind identification of multichannel FIR filters[J]. IEEE Transactions on Signal Processing,1995, 43(2): 516–525. |
| Click to display the text | |
| [7] | KRIM H, VIBERG M. Two decades of array signal processing research:The parametric approach[J]. IEEE Signal Processing Magazine,1996, 13(4): 67–94. |
| Click to display the text | |
| [8] | AUDETTE M A, FERRIE F P, PETERS T M. An algorithmic overview of surface registration techniques for medical imaging[J]. Medical Image Analysis,2000, 4(3): 201–217. |
| Click to display the text | |
| [9] | 栗茂林, 梁霖, 王孙安. 基于稀疏表示的故障敏感特征提取方法[J]. 机械工程学报,2013, 49(1): 73–80.LI M L, LIANG L, WANG S A. Sensitive feature extraction of machine faults bsed on sparse representation[J]. Journal of Mechanical Engineering,2013, 49(1): 73–80.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [10] | GENGH, LIP P, LIUJ X, 等. QAR data sapling and reconstructruction based on compressive sensing[J]. Computer Measurement and Control,2013, 21(5): 1351–1353. |
| Cited By in Cnki (0) | |
| [11] | NEEDELL D, TROPP J A. CoSaMP:Iterative signal recovery from incomplete and inaccurate samples[J]. Applied and Computational Harmonic Analysis,2009, 26(3): 301–321. |
| Click to display the text | |
| [12] | HE J, BALZANO L, LUI J. Online robust subspace tracking from partial information[J]. Mathmatics,2011. |
| Click to display the text | |
| [13] | KENNEDY R,TAYLOR C J,BALZANO L.Online Completion of Ⅲ-conditioned low-rank matrices[C]//IEEE Global Conference on Signal and Information Processing (GlobalSIP).Piscataway,NJ:IEEE Press,2014:507-511. |
| Click to display the text | |
| [14] | MATHIOUDAKIS K, KAMBOUKOS P, STAMATIS A. Gas turbine component fault detection from a limited number of measurements[J]. Proceedings of the Institution of Mechanical Engineers,Part A:Journal of Power and Energy,2004, 218(8): 609–618. |
| Click to display the text | |
| [15] | BALZANO L,NOWAK R,RECHT B.Online identification and tracking of subspaces from highly incomplete information[C]//201048th Annual Allerton Conference on Communication,Control,and Computing (Allerton).Piscataway,NJ:IEEE Press,2010:704-711. |
| Click to display the text | |
| [16] | BRAND M.Incremental singular value decomposition of uncertain data with missing values[M]//Computer Vision-ECCV 2002.Berlin:Springer,2002:707-720. |
| Click to display the text | |
| [17] | BUNCH J R, NIELSEN C P. Updating the singular value decomposition[J]. Numerische Mathematik,1978, 31(2): 111–129. |
| Click to display the text | |
