为表征损伤对结构参数的改变,许多静、动力指标被提了出来。固有频率是结构振动特性中的重要参数,通常能以很高的精度测得,早期出现了许多基于频率的损伤识别研究。Chondros和Dimarogonas[7]提出以扭簧模拟梁结构的损伤裂纹,由理论和试验证明了通过检测固有频率的改变量能得知损伤的存在。Cawley和Adams[8-9]基于一阶Taylor展开,在结构小损伤的前提下证明了损伤前后任意两阶固有频率变化量的比值只是结构损伤位置的函数。此后该结论得到了进一步的研究与改进[10-11]。然而基于频率的损伤识别方法有着较多不足,如小损伤的情况下,频率变化主要体现在高阶,而获得高阶固有频率较困难,此外,由于固有频率反映的系统信息较少,通常只能够发现破损的存在,但难于对其进行定位,且不同位置处的损伤可能产生相同的频率改变[3]。不同于固有频率,结构位移模态反映了系统更多的信息,因此位移模态也可作为损伤识别的指标,常用的方法有模态置信度判据(MAC)和坐标模态置信度判据(COMAC)[12-13]等,这些判据的实质是损伤前后任意两个模态向量夹角余弦值的平方,当结构无损伤时,由模态正交性知MAC矩阵是单位阵,而当结构存在损伤时,损伤后模态与损伤前模态不满足正交性,便可由MAC矩阵判断结构损伤。由于损伤位置附近自由度上的振型变化量相对较大,利用损伤前后振型相对变化量便可对损伤进行定位。相比于位移模态,模态曲率对结构损伤更加敏感,因此模态曲率也被当作损伤识别的参数。实际中直接利用位移模态参数往往存在着对局部小损伤不够敏感的问题,而模态曲率法大都是基于位移模态的差分,引入了误差。考虑到应变类参数对结构损伤一般比位移类参数更加敏感,而且通常能由应变计直接测出[14],应变模态指标逐渐在结构损伤识别中得到广泛应用。目前,随着实际工程结构越来越复杂以及学科间的相互交叉,许多新方法不断被提出与应用,如基于小波分析、控制理论和人工智能等的损伤识别方法[3, 5]。
实际工程中由于环境温差、测量误差和材料分散性等因素,结构的参数会存在着不同程度的不确定性[15-18],这会对结构损伤识别有着不同的影响,甚至影响结果导向[4, 16],因此研究含不确定参数结构的损伤识别有着重要的意义。通常分析不确定性主要是基于概率思想,而该方法中需要解决的一个基础性问题就是结构参数的概率分布,为此人们提出了多种解决方法,Bayesian模型修正法的基本思想是用参数的概率分布描述结构的不确定性,根据观测数据修正模型参数的不确定性,进而确定模型的后验概率分布[16],然而由于后验概率密度函数计算的复杂性,Bayesian方法较难应用于未知参数较多的大规模计算问题。区别于Bayesian方法,随机有限元修正法认为模型不确定性、测量误差对修正参数的影响可以通过观测数据的统计平均有效降低,因此利用实测数据和模型参数摄动的随机模拟来获得相应参数的统计特征[17-18]。但测试数据往往是非常有限的,因此很多情况下仍然必须采用Monte Carlo随机模拟的方法,这会降低计算分析效率[16]。
鉴于此,本文直接将结构不确定参数建模为区间数,实际应用中不需要确定参数的统计信息,而只要知道相应的上下界。以应变模态为损伤识别判据,结合一阶Taylor展开与区间分析,提出了一种考虑含区间参数的结构损伤识别方法。通过数值算例对不同损伤程度以及不同不确定量下的损伤识别进行了分析,证明了本文方法的可行性与合理性。本文方法对于含不确定参数结构的损伤识别提供了一种新的思路与方向。
1 基于应变模态的结构损伤识别 对于给定的位移模态,必然有特定的应变分布状况与之对应,这种固有应变分布状态被称为结构的应变模态。国内外****[19-20]对应变模态的表达式、正交性等进行了相关研究,下面从有限元角度对应变模态进行推导。
将实际结构离散为有限元模型,设ue为单元节点位移列向量,则单元内部任意一点的位移为
 | (1) |
式中:N为形函数矩阵。
利用应变与位移的关系,可得单元内部任意一点的应变:
 | (2) |
式中:A为微分算子矩阵; B为应变矩阵。根据有限元理论,节点位移满足如下微分方程:
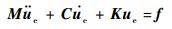 | (3) |
式中:M、C、K和f分别为结构总体的质量矩阵、阻尼矩阵、刚度矩阵和载荷列向量,对于简谐激励,可令f=Fejωt,其中F为激励力幅值向量,ω为激励力频率,j为虚数单位。则频域内稳态位移响应可表示为ue=Uejωt,代入式(3)可得
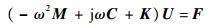 | (4) |
基于模态叠加原理,将式(4)的解表示为
 | (5) |
式中:Φ=[φ1 φ2…φk…φm],φk为结构第k阶位移模态向量; Y=diag[Y1 Y2…Yk…Ym],Yk=(kk-ω2mk+jωck)-1,kk、mk和ck分别为模态刚度矩阵、质量矩阵和阻尼矩阵的第k个对角元(本文所考虑的是无阻尼结构或比例黏性阻尼结构)。则系统位移响应可表示为
 | (6) |
将式(6)代入式(2),可得
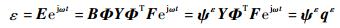 | (7) |
式中:E为应变幅值向量;ψε=BΦ即为系统正应变模态振型矩阵;qε为应变模态的模态坐标。将式(7)写为分量形式:
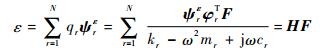 | (8) |
式中:N为系统自由度数;ψrε为第r阶应变模态向量;qr为位移模态坐标的第r个分量;H称为应变频响函数矩阵,且有
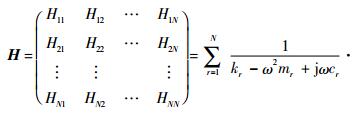 |
 | (9) |
其中:Hst代表在第t个自由处施加载荷时对s自由度处的频响函数值;ψirε为第r阶应变模态的第i个分量;φir为第r阶位移模态的第i个分量。
由式(9)可以看出,与位移频响矩阵不同,应变频响函数矩阵并不对称,但矩阵的任一列仍包含了应变模态的全部信息。因此在实际测量中,只需要在某一点处施加激励,测得各点处的应变频率响应,对于第r阶固有频率处的测量值,可以认为该阶振动模态占主导地位而忽略其他阶次的影响。由于结构模态特性只反映了各自由度上相应量的比值关系,因此只需采取一定的归一化方法即可获得相应的第r阶应变模态。对于损伤后的结构,测试的方法与此相同,但由于在损伤区域附近结构应变会有明显的重分布,因此对比完好结构的相应模态就能对损伤进行识别。
2 不确定结构的应变模态区间分析 2.1 区间分析理论 受到腐蚀性环境、制造与测量误差、材料的分散性等因素的影响,结构的几何、物理参数通常存在一定的不确定性。实际工程中,这些不确定参数往往缺乏足够的数据来准确定义结构参数的概率分布,因此采用只需要确定上下界的区间数来描述系统不确定参数是较为可行的一种思路。设结构参数向量可以表示为
 | (10) |
基于区间数学思想,认为结构参数向量b属于某一区间参数向量bI,即b∈bI,写成分量形式
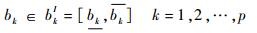 | (11) |
式中:区间数bkI为区间向量bI的第k阶分量;bk、bk分别为其上、下界。区间参数向量bI的名义值bc和不确定半径Δb分别定义如下:
 | (12) |
式中:bkc=(bk+bk)/2;Δbk=(bk-bk)/2, k=1, 2, …, p。上述参数向量b可以分解为bI的名义值bc=[b1c, b2c, …, bpc]与偏差δ=[δ1, δ2, …, δp]的和的形式:
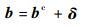 | (13) |
其分量满足
 | (14) |
式中:δk∈δkI=[-Δbk, Δbk]为bk的不确定部分。基于有限元分析理论,式(3)中的系统矩阵可以表示为不确定参数的函数,即
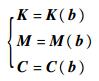 | (15) |
则由上述矩阵所求得的系统位移模态矩阵φ与应变模态矩阵ψε也是上述参数的函数, 即
 | (16) |
由于b在某一有界区间内变动,因此应变模态ψε也在某一有界区间内,但由于其关于不确定量的函数通常是隐式的,因此很难直接求得ψε的区间,一个可行的办法是将ψε在不确定变量中值处进行Taylor展开,进一步基于区间扩张理论确定ψε的上下界。
2.2 应变模态的区间分析方法 基于Taylor展开,结合式(16),将结构第r阶应变模态向量在结构参数中值bc=[b1c, b2c, …, bpc]处进行一阶Taylor展开:
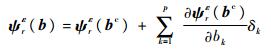 | (17) |
基于区间运算与区间扩张原理,利用方程式(17),可以得到基于Taylor展开的含不确定参数结构的应变模态的上下界:
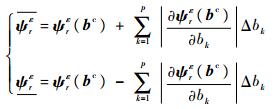 | (18) |
式中:ψrε(bc)可通过令b=bc并结合式(7)得到。一阶偏导eψrε(bc)/ebk计算的推导如下,为表达方便,下文中将K(b)、M(b)和ψrε(b)等量简记为K、M和ψrε。由式(7)易知:
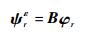 | (19) |
式(19)两边同时关于参数bk求导,可得
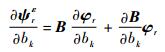 | (20) |
由式(2)知,应变矩阵B只与形函数矩阵和微分算子矩阵有关,当bk为结构的几何或物理参数时,eB/ebk=0。对于有限自由度系统孤立特征值的情况,结构的特征向量可以张成一个完备的正交空间,eφr/ebk可由特征向量的线性组合表示:
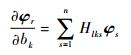 | (21) |
式中:相关系数Hlks可由方程式(22)求出:
 | (22) |
模态向量对应的特征值。事实上,通常只需取前几阶特征向量就能取得较好的精度。将式(21)、式(22)代入式(20)即可得eψrε/ebk,利用式(18)即可得到结构系统各阶应变模态的上下界。至此便得到了含区间参数结构各阶应变模态向量的区间,即
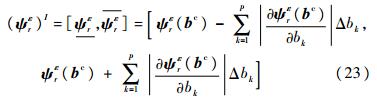 | (23) |
利用本文方法分析不确定条件下结构应变模态的方法流程如图 1所示。
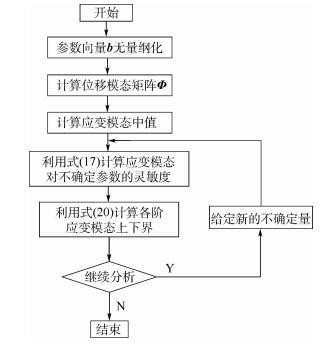 |
| 图 1 考虑不确定性的应变模态分析流程 Fig. 1 Flowchart of uncertain analysis of strain modal |
| 图选项 |
2.3 与概率方法的比较 下面基于概率方法对不确定结构应变模态进行分析,假定结构变量的总体统计参数已知,即
 | (24) |
式中:E(b)、var(b)和σ(b)分别为不确定参量的期望、方差与标准差。对式(17)两侧同时求期望,并注意到E(δbj)=E(bj-bjc)=0,可得
 | (25) |
同样,对式(17)两边同时取方差,由于本文中考虑的各随机变量相互独立,协方差为零,则
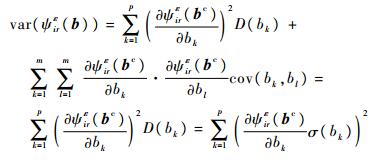 | (26) |
式中:cov(bk, bl)为bk与bl的协方差,bk和bl为不确定变量的第k、l个分量。
由此得到了应变模态响应的期望与方差,取距离应变模态响应均值m倍标准差处所确定的区域为应变模态概率解的区间,即有
 | (27) |
由Chebyshev不等式可知,具有有限方差的随机应变模态落在式(27)所确定范围内的概率不小于1-1/m2。此时,对应的不确定量范围下由区间方法求得的应变模态的相应区间上下界为
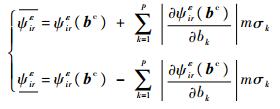 | (28) |
考虑到对于非负xi,有
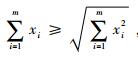
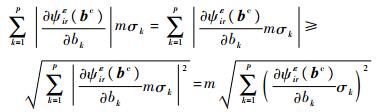 | (29) |
综合式(27)~式(29)可知,在通过概率信息确定的不确定参数区间向量的条件下,由区间方法所得的应变模态区间比概率方法得到的要宽,这通常会使结果趋于保守,因此当不确定参数的统计信息能够准确获得时,还是采用概率方法,而当不确定量统计信息难于获得时,采用区间估计方法是较为合理的。
3 数值算例 考虑损伤梁结构的应变模态,梁两端简支,结构几何尺寸及梁截面形状如图 2所示,以梁轴线方向为x轴,梁横截面所在平面为yOz平面。梁的材料为45Cr合金钢,材料的弹性模量E、密度ρ、泊松比μ等为不确定参数,且认为其统计信息未知,基于区间思想,上述参数可表示为E∈EI=[1-β1, 1+β1]Ec, ρ∈ρI=[1-β2, 1+β2]ρc, μ∈μI=[1-β3, 1+β3]μc,其中Ec=2.06×1011Pa、ρc=7.90×103 kg/m3和μc=0.29分别为上述各参数的名义值,β1、β2和β3分别为各参数的不确定量,相互独立。为验证方法,算例中将不确定参数均视为区间数,且变异系数β分别取了2%、4%和6%等不同值。在实际应用中,材料参数取值区间可通过手册、规范等给出的物理性能范围来确定,几何、尺寸的区间可通过加工制造的公差来具体选取。分别在梁的1/4跨以及跨中处给定宽度为1 mm的不同深度的缺陷来模拟结构损伤,定义裂纹深度与截面原始高度的比值为损伤程度。实际中能够较方便准确测出的通常是正应变,因此以x方向的应变分量为识别参量。
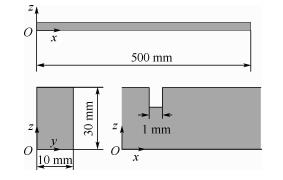 |
| 图 2 梁结构示意图 Fig. 2 Diagrammatic sketch of beam structure |
| 图选项 |
图 3为结构跨中存在不同程度损伤时,结构各阶应变模态的情况。图中横坐标表示沿梁轴线方向的位置,纵坐标为对应的应变,本文中应变模态向量的具体值按质量矩阵进行归一化。
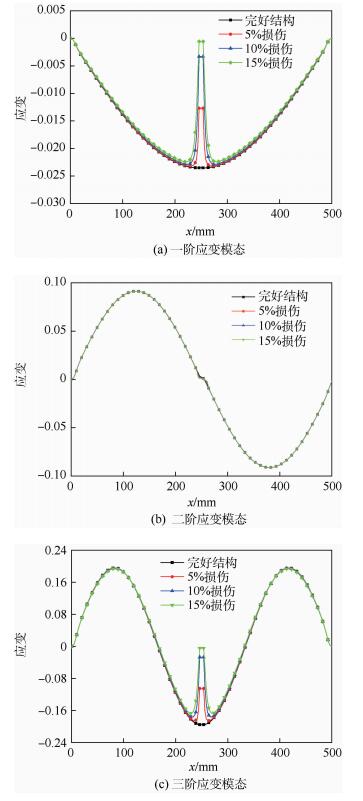 |
| 图 3 结构跨中不同损伤程度下各阶应变模态 Fig. 3 Various order strain modal under different damage levels at midspan |
| 图选项 |
不难看出,由于结构的损伤,应变模态在损伤附近区域会发生突变,且损伤量增加时,应变模态突变量也随之增大。计算发现,结构在完好时和5%损伤时一阶固有频率分别为288.523 Hz与288.064 Hz,二者相差约0.15%,这表明结构小损伤主要影响结构在损伤处局部的参量,对总体特性影响不大,这也是基于固有频率等指标的方法存在缺陷的重要原因。在离损伤位置稍远处,损伤结构的应变与完好结构的相差很小,这说明在实际测试时若应变传感器距损伤位置较远,识别会相对困难,这可以通过合理设置传感器来克服,实际应用中,传感器间距为跨长的6%左右时即能较好识别梁的损伤区域[20],且随着光纤光栅传感器等新型传感器的发展与应用,这一问题将能得到更好的解决。此外,当损伤位于结构某阶应变模态中应变值较大处(高应变区)时,该阶应变模态对损伤很敏感,能够识别结构较小的损伤;但当损伤位于应变值较小处尤其是模态节点附近时(见图 3(b)),应变模态对损伤很不敏感,难于识别损伤,好在实际应用中可以采用多阶模态向量的组合,因此基本都能较好地识别结构损伤。图 4反映的是梁跨中存在5%损伤的情况下,结构参数具有不同程度的不确定量时,结构的各阶应变模态的上下界(为方便作图显示,取β=β1=β2=β3)。
图 4为结构跨中5%损伤时不同不确定量下结构各阶应变模态的上下界。由图 4可以发现,结构参数存在不同程度的不确定性时,应变模态也会有不同程度的变化。与损伤程度不同所引起的应变模态的变化不同,结构参数不确定对系统应变模态的影响主要表现为总体的影响,而对损伤处局部的应变模态影响相对较小。这是由于结构在损伤附近的应变分布主要受损伤本身控制,而对结构密度、弹性模量和泊松比等总体性参数不够敏感,因此这些参数的不确定性主要会引起结构应变模态整体性的变化。另外,由图 4还可以发现模态振型中应变较大的位置,由参数不确定性所引起的应变模态的变化量也越大,对于应变较小的低应变区尤其是振型节点附近,应变值受不确定参数的影响较小。图 5反映的是梁结构在1/4跨处存在5%损伤的情况下,结构参数具有不同程度的不确定量时,结构的各阶应变模态的上下界。
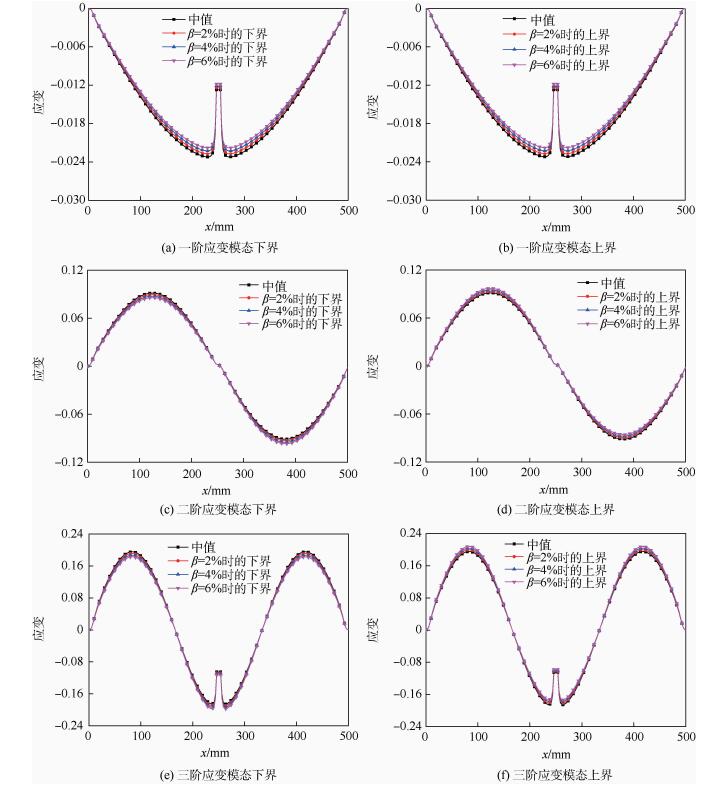 |
| 图 4 结构跨中5%损伤时不同不确定量下结构各阶应变模态的上下界 Fig. 4 Upper and lower bounds of various order strain modal under different uncertainties with 5% damage at midspan |
| 图选项 |
 |
| 图 5 1/4跨5%损伤时不同不确定量下结构各阶应变模态的上下界 Fig. 5 Upper and lower bounds of various order strain modal under different uncertainties with 5% damage at quarter span |
| 图选项 |
在1/4跨损伤工况下,结构应变模态同样在损伤处发生了突变,同时结构参数不确定量对应变模态的影响与跨中损伤时类似。
在工程应用中,损伤指标不可避免地会受到噪声的影响,本文采用如下的方法计算含噪声应变模态振型[17], 即
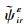
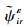
 |
| 图 6 不同噪声水平下的损伤识别正确率 Fig. 6 Correct damage identification rate under different noise levels |
| 图选项 |
4 结论 1)应变模态对结构局部损伤较敏感,对于梁结构来说,只要传感器布置合理,该指标能很好地识别结构较小的损伤。
2)若损伤位于某阶模态的低应变区,该阶模态对损伤不太敏感,实际应用时可采用综合多阶应变模态的方法对损伤进行识别以克服这一问题。
3)不确定参数主要影响结构特性的总体数值,就本文算例来看,当参数的不确定量小于损伤程度或与损伤程度相当时,不确定性对结构损伤识别结果影响不大;当噪声水平低于2%~3%时,本文方法有着较好的识别率,但噪声对识别指标有着较明显的影响,这也是后续研究中需重点考虑的问题。
参考文献
| [1] | DOEBLING S W, FARRAR C R, PRIME M B. A summary review of vibration-based damage identification methods[J].Shock and Vibration Digest, 1998, 30(2): 91–105.DOI:10.1177/058310249803000201 |
| [2] | LIU Y, NAYAK S. Structural health monitoring:State of the art and perspectives[J].Journal of the Minerals, Metals and Materials Society, 2012, 64(7): 789–792.DOI:10.1007/s11837-012-0370-9 |
| [3] | 郑栋梁, 李中付, 华宏星. 结构早期损伤识别技术的现状和发展趋势[J].振动与冲击, 2002, 21(2): 1–6.ZHENG D L, LI Z F, HUA H X. A summary review of structural initial damage identification methods[J].Journal of Vibration and Shock, 2002, 21(2): 1–6.(in Chinese) |
| [4] | SALAWU O S. Detection of structural damage through changes in frequency:A review[J].Engineering Structures, 1997, 19(9): 718–723.DOI:10.1016/S0141-0296(96)00149-6 |
| [5] | OU J, LI H. Structural health monitoring in mainland China:Review and future trends[J].Structural Health Monitoring, 2010, 9(3): 219–231.DOI:10.1177/1475921710365269 |
| [6] | 李德葆, 陆秋海. 实验模态分析及其应用[M].北京: 科学出版社, 2001: 29-36.LI D B, LU Q H. Experimental modal analysis and its application[M].Beijing: Science Press, 2001: 29-36.(in Chinese) |
| [7] | CHONDROS T G, DIMAROGONAS A D. Identification of cracks in welded joints of complex structures[J].Journal of Sound and Vibration, 1980, 69(4): 531–538.DOI:10.1016/0022-460X(80)90623-9 |
| [8] | CAWLEY P, ADAMS R D. The location of defects in structures from measurements of natural frequencies[J].The Journal of Strain Analysis for Engineering Design, 1979, 14(2): 49–57.DOI:10.1243/03093247V142049 |
| [9] | ADAMS R D, CAWLEY P, PYE C J, et al. A vibration technique for non-destructively assessing the integrity of structures[J].Journal of Mechanical Engineering Science, 1978, 20(2): 93–100.DOI:10.1243/JMES_JOUR_1978_020_016_02 |
| [10] | ZHU H P, HE B, CHEN X Q. Detection of structural damage through changes in frequency[J].Wuhan University Journal of Natural Sciences, 2005, 10(6): 1069–1073.DOI:10.1007/BF02832469 |
| [11] | 杜思义, 殷学纲, 陈淮. 基于频率二阶摄动的结构损伤识别方法[J].应用力学学报, 2007, 23(4): 613–617.DU S Y, YIN X G, CHEN H. Structural damage identification based on second-order perturbation of frequency[J].Chinese Journal of Applied Mechanics, 2007, 23(4): 613–617.(in Chinese) |
| [12] | YI T H, LI H N, GU M. Optimal sensor placement for structural health monitoring based on multiple optimization strategies[J].Structural Design of Tall and Special Buildings, 2011, 20(7): 881–900.DOI:10.1002/tal.712 |
| [13] | ALLEMANG R J. The modal assurance criterion-twenty years of use and abuse[J].Sound and Vibration, 2003, 37(8): 14–23. |
| [14] | 董聪, 丁辉. 结构损伤识别和定位的基本原理与方法[J].中国铁道科学, 1999, 20(3): 89–94.DONG C, DING H. The basic principle and method for recognition and location of structural damage[J].China Railway Science, 1999, 20(3): 89–94.(in Chinese) |
| [15] | QIU Z P, CHEN S H, ELISHAKOFF I. Natural frequencies of structures with uncertain but nonrandom parameters[J].Journal of Optimization Theory and Applications, 1995, 86(3): 669–683.DOI:10.1007/BF02192164 |
| [16] | 宗周红, 牛杰, 王浩. 基于模型确认的结构概率损伤识别方法研究进展[J].土木工程学报, 2012, 45(8): 121–130.ZONG Z H, NIU J, WANG H. A review of structural damage identification methods based on finite element model validation[J].China Civil Engineering Journal, 2012, 45(8): 121–130.(in Chinese) |
| [17] | 林秀萍.基于概率统计方法的结构损伤识别研究[D].重庆:重庆大学, 2009:15-20.LIN X P.The studies on structural damage detection based on probability statistics method[D].Chongqing:Chongqing University, 2009:15-20(in Chinese).http://cdmd.cnki.com.cn/article/cdmd-10611-2009149189.htm |
| [18] | PALMA R, RUS G, GALLEGO R. Probabilistic inverse problem and system uncertainties for damage detection in piezoelectrics[J].Mechanics of Materials, 2009, 41(9): 1000–1016.DOI:10.1016/j.mechmat.2009.05.001 |
| [19] | 村井秀児, 伊藤博幸, 内海栄一. ダイナミックデザインアナリシスの研究(パート2)[J].コマツ技報, 1979, 25(2): 73–82.MURAI S, ITO H, UTSUMI E. Study of dynamic design analysis (Part 2)[J].Komatsu Technical Report, 1979, 25(2): 73–82.(in Chinese) |
| [20] | 顾培英.基于应变模态技术的结构损伤诊断直接指标法研究[D].南京:河海大学, 2006:28-33.GU P Y.Study on structural damage diagnosis method based on direct indicators of strain mode technology[D].Nanjing:Hohai University, 2006:28-33(in Chinese).http://cdmd.cnki.com.cn/article/cdmd-10294-2007017229.htm |
