在实际工程中,某些系统除“正常工作”和“完全失效”2种状态外,可以在多个性能水平下运行,这样的系统称为多态系统(Multi-State System,MSS)^[1],与二态系统模型相比,多态系统模型能够准确地描述部件的多态性,更加灵活地表征部件性能变化对系统性能和可靠性的影响^[2]。
20世纪70年代多态系统的概念被提出后^[3-4],关于其可靠性的研究就得到了****的广泛关注。在理论方法方面,文献^{[1-2, 5-6]}对基本概念、评估方法和优化设计等进行了详细阐述。文献^[7]对基于不完全维修的多态系统更换维修决策问题进行了深入的研究。在工程应用方面,相关理论已经应用到电力^[8-9]、机械^[10-11]等领域。
对于高可靠性部件构成的系统,通常情况下,很难得到准确有效的部件或系统的失效数据。因此,通过获得精确的失效数据去评估系统的精确概率和状态性能显得十分困难。针对上述问题,一些****对传统的多态系统理论进行了推广。Ding等^[12-13]针对离散多态系统认知不确定性问题,在给定模糊状态性能和模糊状态概率的前提下,对模糊多态系统的可靠性进行分析。针对文献^[12-13]模糊数计算过程复杂的问题,Li^[14]等将对应的模糊数转换为区间数,采用区间分析理论和通用生成函数方法分析了多态系统的区间可靠性。Destercke和Sallak^[15]在Ding和Li^[12-14]等研究基础上,根据随机集理论中质量函数处理不确定问题的优势,将传统的通用生成函数方法进行扩展,对认知不确定性的多态系统可靠性进行研究。针对实际工程中多态系统的性能及其概率分布无法准确获得和不完全覆盖的问题,鄢民强等^[16]提出了一种考虑不完全覆盖的模糊多态系统的可靠性计算方法,有效解决了未覆盖失效条件下的模糊多态系统可靠性分析问题。Liu和Huang^[17]对上述研究成果做了进一步拓展,采用模糊马尔可夫过程模型求解部件的动态模糊状态概率,采用Ding等^[12-13]的模糊通用生成函数方法对模糊多态系统可靠性进行了分析。文献^[18-20]将模糊数学理论和贝叶斯网络处理系统多态性和事件不确定性的优势相结合,从不同角度对多态系统的模糊可靠性进行分析,解决了多状态不确定性系统可靠性分析问题。但是该类方法在处理事件的逻辑关系时,专家所提的先验信息对结果有一定影响,使得客观的求解问题具有一定主观误差。
由上述研究结果不难发现,对于认知不确定性多态系统的可靠性研究,主要集中于3个方面：一是运用模糊数学理论、区间分析理论和随机集理论,在给定状态性能和状态概率的前提下,对系统的可靠性进行分析,状态性能和状态概率的给定值对结果的影响较大,而且未给出多态系统可靠性随时间的动态变化关系；二是运用模糊数学理论和贝叶斯网络对认知不确定性系统的可靠性进行分析,过于依赖专家知识,所得结果具有一定主观性；三是大部分研究主要集中于对离散多态系统的研究。对高可靠性部件构成的连续状态性能多态系统的可靠性研究相对较少,对其进行可靠性分析研究时,通常会采用加速试验对其部件状态特性进行分析,由于对部件性能分布信息的认知存在一定的不确定性,无法准确地对其性能分布进行描述。
因此,本文提出了考虑认知不确定性的多态系统可靠性评估方法,对某型雷达功率放大分系统的可靠性进行分析。
1 多态系统状态分析 1.1 多态部件状态分析
1.1.1 部件性能分布模型 对于一些高可靠性退化部件,短时间内很难得到精确的退化数据,以此为基础,建立的性能退化分布模型往往是不精确的,分析结果可能会出现很大的偏颇。鉴于此,可以认为部件的性能参数的分布参数为区间变量,分析之前可做如下假设：
1) 部件只有一个性能参数x,对应一个性能退化过程,且退化过程不可逆。
2) 在任意时刻t,假设部件的性能参数为x(t),服从均值为μ_x(t)、方差为σ²_x(t)的正态分布,μ_x(t)、σ²_x(t)分别为在[μ—(t),μ—(t)]和[σ—²(t),σ—²(t)]上服从均匀分布的区间变量,x(t)为独立同分布。
3) 部件在任意给定时刻t,性能参数x(t)的分布参数为服从均匀分布的区间变量,则此时部件的性能分布函数为

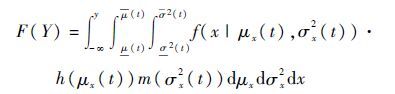(1)

式中：


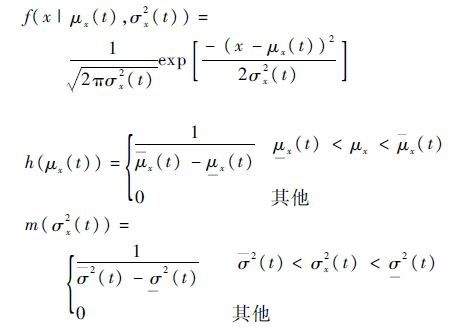1.1.2 部件性能区间划分准则 定义^[21]设R为实数域,对于给定的2个实数,x，x∈R,且x≤x,则[x]=[x,x]={x:x∈R,x≤x≤x}称为有界闭区间,也称区间数,简称区间。其中,x为区间的下界,x为区间的上界。令(x+x)/2=x^c为区间的中值。
对部件性能参数区间进行划分时,采用系统最低任务需求与部件性能参数分布特性相结合的方法。具体如下：
1) 将部件i的性能参数区间划分为M_i=3个连续的子区间,以此为例进行说明。

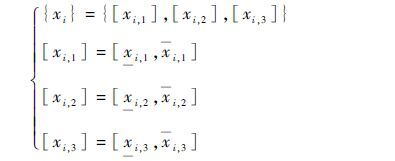(1) 在给定t时刻,部件i的性能参数服从均值为μ_i(t)、方差为σ²_i(t)的正态分布,μ_i(t)=μ^c_i(t),σ²_i(t)=σ^2,c_i(t)分别为区间[μ_i(t)]和[σ²_i(t)]的中值。以标准差σ_i(t)为间隔将部件的整个性能参数分布区间划分为8部分,具体如图 1所示。

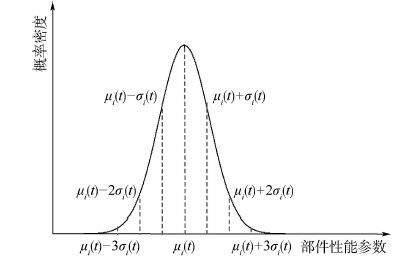图 1 部件性能参数分布 Fig. 1 Performance parameter distribution of components

图选项

(2) 根据系统的最小任务性能区间需求和系统结构函数确定分配到部件的近似最小任务性能参数区间为[w_x],且其中值为w^c_x,并在该区域附近尽量将其细化,增大系统状态性能与系统的最小任务性能需求区分度,提高系统可靠度的计算精度。
(3) 假定部件i的最大性能参数为x_i,max,为便于表示,假定x_i,ε1=μ_i－3σ_i,x_i,ε2=μ_i－2σ_i,x_i,ε3=μ_i－σ_i,x_i,ε4=μ_i,x_i,ε5=μ_i+σ_i,x_i,ε6=μ_i+2σ_i,x_i,ε7=μ_i+3σ_i。假定部件的性能参数x的区间族由3个连续的性能区间构成,对部件的性能参数区间进行划分时,结合(1)和(2),根据w_x^c与{x_i,ε1,x_i,ε2，…,x_i,ε7}中各元素的大小关系进行划分。
① 当w_x^cx_i,ε1时,

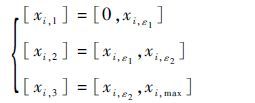② 当x_i,εj≤w_x^c＜x_i,εj+1时,

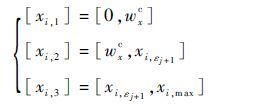式中：j=1,2，…,6。
③ 当x_i,ε7≤w_x^c＜x_i,max时,

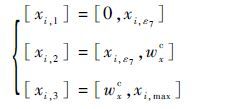④ 当w_x^c＞x_i,max时,表明部件i的性能参数大小已不满足系统的需求,对其进行性能参数区间的划分已经没有实际的工程意义,故此时可认为部件i失效。
2) 部件i的性能参数区间个数为M_i=2时,

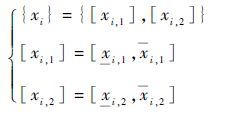令部件i第1个性能参数区间上边界的值为其3个性能参数区间划分时和的均值,即

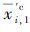
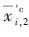
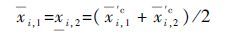可得部件i的状态性能区间[x_i,1]=[0,x_i,1],[x_i,2]=[x_i,2,x_max]。
3) 部件i的性能区间个数为M_i时,M_i＞3,
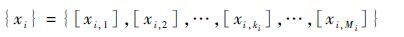
对其性能参数区间进行划分时,同样以部件的性能参数区间个数为3时的划分依据为基础。在近似最小任务性能参数w_x^c附近,结合{x_i,ε1,x_i,ε2,…,x_i,ε7},按照距离w_x^c由近到远的原则,将其不断细化,进一步增加系统状态在最小任务性能参数需求附近的区分度。
1.2 部件状态概率分析
1.2.1 部件状态性能区间定义 定义部件i的状态性能区间形式为

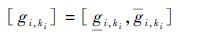其表示部件处于不同性能参数水平时对整个系统正常工作性能的贡献比率,在此用百分比表示。通常结合系统结构函数与部件的性能参数区间进行定义,可分为以下2种情况：
1) 当部件i单独构成分系统l,且分系统l可以与其他分系统近似地认为是串联结构,可得

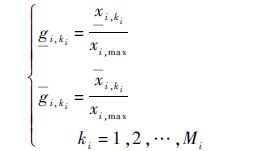2) 当n_i个部件i构成分系统l时,且分系统l的性能输出为n_i个部件i输出和时,分系统l可以与其他分系统近似地认为是串联结构,可得


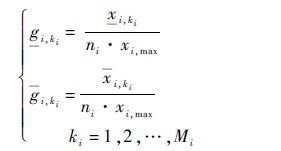1.2.2 部件状态概率求解 假设t时刻部件性能参数区间为[x_i,ki(t)]=[x_i,ki(t),x_i,ki(t)]时,且满足x_i,ki≤x_i,ki,根据第1.1.1 节假设3)分析,可得在给定t时刻部件i在第k_i个状态的状态性能概率p_i,ki(t)为

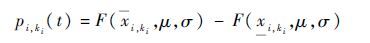(2)

式中：[x_i,ki(t)]为在t时刻部件i的第k_i个性能参数区间。
2 运算法则 对连续性能区间部件分析时,通常将状态性能区间分为区间上边界、区间中值和区间下边界3种情况进行讨论分析^[2]。但上述3种情况仅表征性能区间的特殊点,并不能充分地描述该区间内的性能特性,为解决该问题,提高计算的准确性,定义了部件性能区间边界补偿方法,以边界“伪置信区间”的形式代替部件性能区间的上边界、区间中值和下边界,而后对区间通用生成函数及其运算法则进行定义。
2.1 状态性能区间边界补偿 根据部件状态性能水平区间的区间上边界、区间中值和区间下边界3种情况和概率论中参数置信区间求解的相关理论,对上述3种情况的状态进行边界补偿,具体如下：
1) 状态性能水平区间上边界补偿。假定t时刻部件i的第k_i个状态性能水平区间为[g_i,ki]=[g_i,ki,g_i,ki],则性能区间上边界为g_i,ki,根据概率论中参数区间估计方法,在方差σ²已知的情况下,将补偿半径定义为

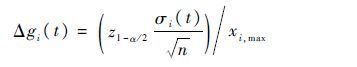在给定α=0.05时,可得z_1－α/2=z_0.975=1.96,对于高可靠性部件,通常采用加速试验的方法得到部件的性能分布,实际工程中,最小样本量为5,因此,可得最大补偿半径为

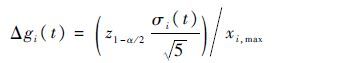此外,若σ_i(t)随着时间的变化逐渐增大,那么补偿半径Δg_i(t)可能会超过性能区间的宽度,出现过度补偿的情况,此时Δg_i(t)=g_i(t)-g_i(t),结合上述2种情况,可得最大补偿半径为

以状态性能区间上边界g_i,ki为状态性能时,损失了上边界以下的部分状态性能,为解决此问题,将状态性能水平区间上边界向下边界方向补偿,可得补偿后的状态性能水平区间为

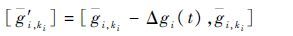2) 状态性能水平区间下边界补偿。同理,根据状态性能水平区间上边界补偿分析,可得状态性能水平区间下边界g_i,ki的最大补偿半径为

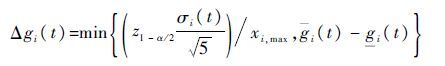以状态性能水平区间下边界g_i,ki为状态性能水平时,损失了下边界以上的部分状态性能,为解决此问题,将状态性能水平区间下边界向上边界方向补偿,可得补偿后的状态性能水平区间为

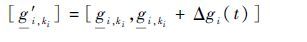3) 状态性能水平区间中值补偿。同理,根据状态性能水平区间上边界补偿分析,可得状态性能水平区间中值g_i,ki^c的最大补偿半径为

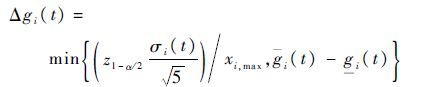以状态性能区间中值g_i,ki^c为状态性能水平时,与前两者相比,在一定程度上降低了状态性能水平,为尽量包含一些状态水平信息,将状态性能水平区间中值向上边界和下边界双侧方向进行补偿,可得补偿后的状态性能水平区间为

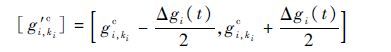后续将以状态性能水平区间中值补偿方法为例进行分析。
2.2 区间通用生成函数定义 定义部件i的状态性能区间族形式为

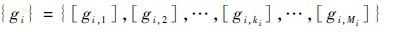式中：[g_i,ki]=[g_i,ki,g_i,ki]为部件i的第k_i个状态性能水平。
部件i的状态概率族形式为

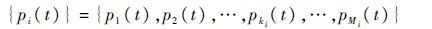式中：p_ki(t)为部件i在t时刻第k_i个状态概率。
定义部件i的区间通用生成函数为

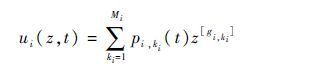(3)

2.3 区间通用生成函数运算法则 在对区间通用生成函数的运算法则进行定义之前,先对区间扩张理论进行简单描述,具体如下：
假设部件i和j的状态性能区间分别为[g_i,ki]和[g_j,kj],状态概率分别为p_i,ki和p_j,kj,其中,[g_i,ki]=[g_i,ki,g_i,ki],[g_j,kj]=[g_j,kj,g_j,kj],i=1,2，…,n,j=1,2，…,n。对于2个部件,现有[g_i,ki]=[g_i,ki,g_i,ki],[g_j,kj]=[g_j,kj,g_j,kj],假设具有函数f满足g_ks=f(g_i,ki,g_j,kj),根据给出的函数区间扩展定义^[21]可知,g_ks=f(g_i,ki,g_j,kj)的区间扩张为[g_ks]=f([g_i,ki],[g_j,kj])。因此,[g_ks]的区间通用生成函数可通过如下运算获得：

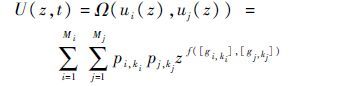(4)

根据系统结构特点,定义如下运算符：
1) 当[g_ks]为[g_i,ki]与[g_j,kj]的和时,定义δ₁运算符如下：

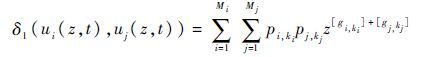2) 当[g_ks]为[g_i,ki]与[g_j,kj]的乘积时,定义δ₂运算符如下：

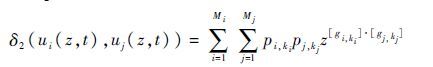3) 当[g_ks]为[g_i,ki]与[g_j,kj]的最小值时,定义δ₃运算符如下：

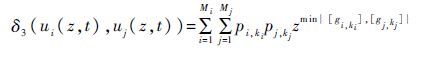3 多态系统可靠性分析 根据第2.3节运算法则的分析,假定得到的多态系统区间通用生成函数为

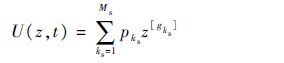(5)

定义多态系统的最小性能区间需求为[w]=[w,w],则系统的可靠度为

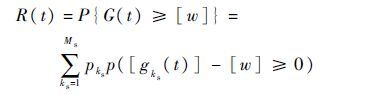式中：P{G(t)≥[w]}为G(t)≥[w]的概率；G(t)={[g₁(t)],[g₂(t)],…,[g_ks(t)],…,[g_Ms(t)]}。
如果[g_ks]和[w]均为区间变量,则上述问题的关键就在于区间[g_ks]－[w]和0之间的关系^[22]。
1) 若，则
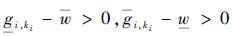
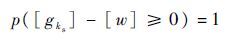
2) 若,则
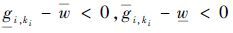
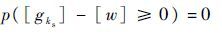
3) 若,可定义[g_ks]－[w]的可能度为

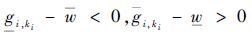
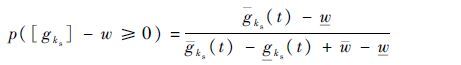综合上述3点,可以将[g_ks(t)]－[w]的可能度定义为

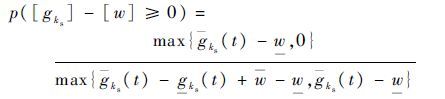因此,系统的可靠度为

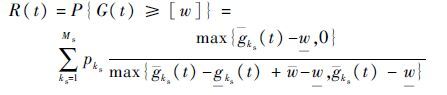(6)

4 多态系统平均瞬态区间性能分析 多态系统可靠性评估的核心思想是对系统的状态性能、状态概率和最小任务性能区间三者之间的关系进行分析。因此,对系统的状态性能进行分析具有重要意义。在此,采用状态性能的期望来描述多态系统的平均输出性能,具体如下所述。
定义多态系统在t时刻的平均瞬态性能区间大小为

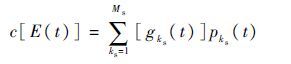(7)

式中：[g_ks(t)]为系统在t时刻的状态性能水平区间；p_ks(t)为系统在t时刻的状态概率。
5 算例分析 某型雷达功率放大分系统主要由4个分系统构成,包含5个性能退化部件、2个二态部件,具体如图 2所示。分系统1为性能退化部件预放大器组件；分系统2为二态部件1∶4功率分配器；分系统3为性能退化部件功率放大器组件1～4,且均为同型部件,分系统4为二态部件4∶1功率合成器。根据部件处于不同性能参数大小时对整个雷达功率放大分系统正常工作性能的贡献比率划分部件的状态性能水平区间,系统的最小需求状态性能区间为w=[75%,80%]。求t=1000d时系统的可靠度。

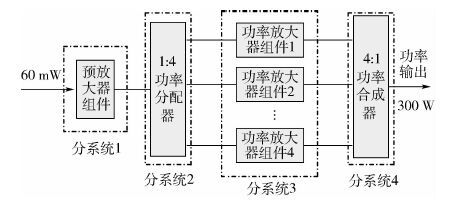图 2 某型雷达功率放大分系统 Fig. 2 Radar power amplification subsystem

图选项

假定各部件性能参数的分布参数如表 1、表 2所示。
表 1 二态部件性能参数分布 Table 1 Binary state component performance parameters distribution

部件	分布类型	性能参数分布/d	部件状态水平/%	分系统结构函数
1∶4功率分配器	指数分布	λ=[6.25,8.25]×10-5	0,100	分系统2G2(t)=X2(t)
4∶1功率合成器	指数分布	λ=[6.25,8.25]×10-5	0,100	分系统4G4(t)=X4(t)

表选项






表 2 多态部件退化性能参数、分系统结构函数和系统结构函数 Table 2 Multi-state component degraded performance parameters,subsystems’ structure functions and system’s structure functions

部件	部件退化性能参数分布	分系统结构函数	系统结构函数(状态水平)
预放大器组件	x1服从[0,6]范围内的正态分布,其中,μ1(t)=([5.445,5.565]-[1.05,1.25])10-4t,σ1(t)=([0.105,0.135]-[1.65,1.85])10-5t	分系统1G1(t)=X1(t)分系统3G3(t)=X3(t)+X4(t)+…+ X6(t)	Gsys(t)=min{G2(t),Gsub13(t),G4(t)}
功率放大器组件	x3服从[0,75]范围内的正态分布,其中,μ3(t)=([68.55,69.55]-[0.85,1.05])10-3t,σ3(t)=([1.25,1.45]-[1.85,2.05])10-4t	分系统13Gsub13(t)=G1(t)·G3(t)

表选项






5.1 基于状态性能区间边界补偿的系统可靠性评估
5.1.1 部件区间通用生成函数 t=1000d时,根据第2.2节性能水平划分规则,假定预放大器组件的性能参数区间族为{x₁}={[x_1,1],[x_1,2],[x_1,3],[x_1,4],[x_1,5]},其中,性能参数区间分别为[x_1,1]=[0,4.9775],[x_1,2]=[4.9775,5.1150],[x_1,3]=[5.1150,5.2525],[x_1,4]=[5.2525,5.3900],[x_1,5]=[5.3900,6.0000]。
根据第2.1节状态性能水平区间中值补偿方法可得,{g₁}={[g_1,1],[g_1,2],[g_1,3],[g_1,4],[g_1,5]},其中,[g_1,1]=[40.47%,42.48%],[g_1,2]=[83.10%,85.11%],[g_1,3]=[85.39%,87.40%],[g_1,4]=[87.68%,89.69%],[g_1,5]=[93.91%,98.92%]。
功率放大器组件的性能参数区间族为{x₃}={[x_3,1],[x_3,2],[x_3,3],[x_3,4],[x_3,5]},其中,功率放大器组件的性能参数区间分别为[x_3,1]=[0,63.4650],[x_3,2]=[63.4650,65.0100],[x_3,3]=[65.0100,66.5550],[x_3,4]=[65.5550,68.1000],[x_3,5]=[68.1000,75.0000]。
同理可得,{g₃}={[g_3,1],[g_3,2],[g_3,3],[g_3,4],[g_3,5]},其中,[g_3,1]=[10.35%,10.80%],[g_3,2]=[21.19%,21.64%],[g_3,3]=[21.70%,22.15%],[g_3,4]=[22.22%,22.67%],[g_3,5]=[23.62%,24.08%]。
根据第2.2节部件状态概率计算方法,可得预放大器组件对应的状态概率族为{p₁}={0.0023,0.0261,0.1410,0.3306,0.5000},1∶4功率分配器对应的状态概率族为{p₂}={0.0722,0.9278},功率放大器组件对应的状态概率族为{p₃}={0.0018,0.0240,0.1390,0.3352,0.5000］},4∶1功率合成器的状态概率族为{p₁₁}={0.0722,0.9278}。
根据区间通用生成函数的定义,可得系统中各部件的区间通用生成函数为


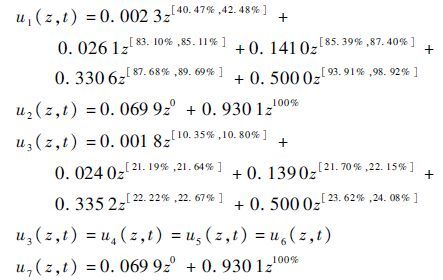5.1.2 基于状态性能区间中值补偿的多态系统可靠性评估 由图 2可知,分系统1由部件1组成,可得分系统1的区间通用生成函数为

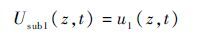分系统2的区间通用生成函数为

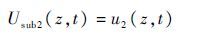分系统3的性能由部件3～部件6构成,且为其状态性能的和,根据第2.3节运算法则定义的δ₁运算符,可得分系统3的区间通用生成函数为

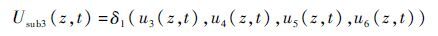分系统4的区间通用生成函数为

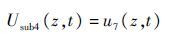将分系统1、分系统3采用第2.3节运算法则定义的δ₃运算符,可得分系统的通用生成函数为

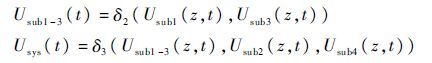根据式(6)可得t=1000d时,系统的可靠度为

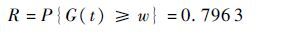5.2 对比分析
5.2.1 基于二态模型的系统可靠性评估 如果采用传统的方法进行系统可靠性分析,一般假设部件仅有“正常工作”和“完全失效”2个状态,根据系统总的状态性能输出要求w,假定分系统1部件的性能水平的失效阈值为w_componet1=w₁x_1,max,x_1,max为部件1处于完好状态时对应的性能参数，w₁为部件1的最小性能需求。因此分系统1的状态性能水平大于w_subsys1=w_componet1时,预放大器组件功能完好,则在t时刻分系统1正常和失效的概率分别为R_subsys1(t)和1－R_subsys1(t)。分系统1和分系统3的性能水平具有一定的相关性,且分系统1性能输出的大小将直接影响分系统3的输出,假定分系统3的失效阈值为w_subsys3=(w/w₁)x_subsys3，x_subsys3为分系统3处于完好状态时对应的性能参数。分系统3中4个功率放大器组件并不是简单的并联关系,采用传统思路进行分析,将分系统失效阈值均分给4个功率放大器组件,则其失效阈值w_componet3=w_subsys3/4。假定在t时刻其正常和失效的概率分别为p_trad3(t)和1－p_trad3(t),则分系统3正常的概率为R_subsys3=(p_trad3(t))⁴,采用传统方法可得系统的可靠度为

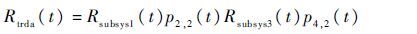t=1000d时,系统的可靠度为R_trda(t)=0.5221

5.2.2 基于性能区间方法的系统可靠性评估 为了充分分析本文所提方法的优缺点,在t=1000d时,将部件状态按传统的点区间进行划分,部件的区间通用生成函数为

按照第5.1.2 节基于区间通用生成函数的多态系统可靠性评估方法可得系统的可靠度为R=P{G(t)≥w}=0.7651

5.2.3 基于Monte Carlo仿真的系统可靠性评估 t=1000d时,采用Monte Carlo仿真方法进行分析。在分析过程中,因分系统3所含部件较多,部件的状态数N_componet3≥20,分系统的状态数N_subsys3≥20⁴,仿真规模巨大,使得后续对系统可靠性的分析面临严重的挑战,为了降低计算的复杂度和仿真规模,假设N_componet3=20,为了充分表述Monte Carlo仿真方法在每次仿真计算过程中所得计算结果的可能性,取L=500次仿真结果的平均值作为Monte Carlo仿真方法的结果,可得可靠度为0.8070,其中,实现L=500次仿真时间大概为7980s,而本文方法耗时大约为40s。
采用本文所提方法、传统可靠性方法、性能区间方法和Monte Carlo仿真方法所得系统可靠度如图 3所示。

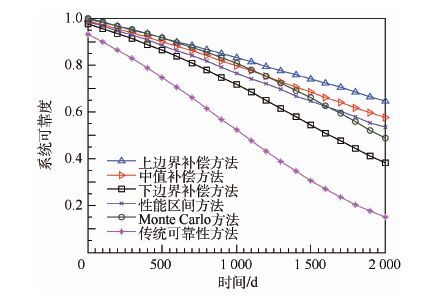图 3 不同方法所得可靠度结果对比 Fig. 3 Comparison of reliability results respectively obtained by different methods

图选项

由图 3可以得出以下结论：
1) 采用本文所提状态性能区间边界补偿方法,分别对状态性能区间下边界、中值和上边界
进行补偿,所得计算结果总体上呈增大趋势,状态性能区间的上边界和下边界均未完全包含状态性能区间中的状态信息,而状态性能区间的中值为上边界和下边界的折中,故所得结果一定程度上更加接近客观值。
2) 将传统可靠性方法、状态性能区间中值补偿方法和Monte Carlo仿真方法三者所得结果进行对比,传统可靠性方法与后两者相比误差较大。在传统可靠性方法中,部件失效阈值的选取对系统可靠性的影响较为敏感,因此其成为影响系统可靠度评估精度的薄弱环节,进一步体现了多态系统理论在描述系统可靠性时的准确性优势。
3) 状态性能区间中值补偿方法、性能区间方法和Monte Carlo仿真方法三者相比,状态性能区间中值补偿方法的结果与Monte Carlo仿真方法的结果更加接近,虽然随着时间的推移,误差具有增大的趋势,但实际工程中,雷达装备每隔2～3a(700～1200d)进行一次大修,状态性能区间中值补偿方法的分析精度已经满足预防性维修的需求,因此其克服了Monte Carlo仿真方法仿真规模大、耗时长的不足。
5.3 雷达功率放大分系统平均瞬态性能分析 根据第4节多态系统平均瞬态性能分析,可得状态性能区间补偿方法和性能区间方法的平均瞬态性能区间的大小,具体如表 3所示。
表 3 不同方法所得平均瞬态性能区间大小对比分析 Table 3 Contrastive analysis of mean instantaneous performance of interval respectively obtained by different methods

方法	t/d
	400	600	800	1000	1200
上边界补偿方法	[81.66%,84.77%]	[78.43%,81.51%]	[75.26%,78.83%]	[68.53%,71.44%]	[65.20%,68.05%]
中值补偿方法	[72.68%,79.42%]	[73.66%,76.61%]	[69.89%,72.77%]	[66.01%,68.80%]	[62.02%,64.72%]
下边界补偿方法	[71.91%,74.75%]	[67.23%,67.97%]	[62.13%,64.74%]	[56.78%,59.24%]	[51.20%,53.48%]
性能区间方法	[73.25%,83.14%]	[69.06%,78.57%]	[65.00%,74.62%]	[60.50%,69.64%]	[56.54%,65.70%]

表选项






对上述4种方法所得平均瞬态性能区间取均值,可得图 4所示分析结果。

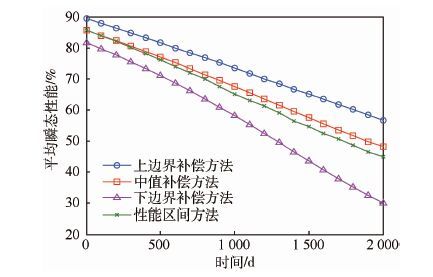图 4 不同方法所得平均瞬态性能结果对比 Fig. 4 Comparison of mean instantaneous performance respectively obtained by different methods

图选项

由表 3和图 4可得以下结论：
1) 采用本文所提状态性能区间边界补偿方法,分别对状态性能区间下边界、中值和上边界进行补偿,所得平均瞬态性能结果整体上呈增大的趋势。
2) 状态性能区间方法所得平均瞬态性能结果介于状态性能区间下边界补偿方法和状态性能区间上边界补偿方法之间,与状态性能区间中值相近。
3) 采用上述方法所得的平均瞬态性能结果与可靠性评估结果是相对应的,即其所求平均瞬态性能的值较大时,其对应的可靠度的值较大,因此平均瞬态性能可作为可靠度分析结果的有效补充,也可作为评价系统可靠性的指标。
6 结论 针对某型雷达功率放大分系统,提出了一种考虑认知不确定性的多态系统可靠性评估方法。
1) 利用本文定义的连续状态部件的状态划分规则和给出的部件状态及其对应概率随时间变化关系的求解方法,解决了给定状态和对应状态概率对可靠性分析的影响,得到了多态系统可靠性随时间的动态变化关系。
2) 通过解析法获得部件状态及其对应概率随时间变化关系,采用区间通用生成函数对系统可靠性进行分析,克服了贝叶斯等方法对专家知识的依赖性。
3) 本文方法适用于连续状态系统的可靠性分析,是对多态系统可靠性分析方法的有效补充。
4) 通过算例分析验证了本文方法的正确性和有效性,且结果表明所提方法相比于传统可靠性方法、性能区间方法和Monte Carlo仿真方法具有一定优势。

参考文献

[1]	LISNIANSKI A, LEVITIN G. Multi-state system reliability:Assessment,optimization and applications[M].Singapore: World Scientific, 2003: 1-2.
	Click to display the text
[2]	李春洋.基于多态系统理论的可靠性分析与优化设计方法研究[D].长沙:国防科学技术大学,2010: 1-5.LI C Y. Research on reliability analysis and optimization based on the multi-state system theory[D].Changsha:National University of Defense Technology,2010:1-5(in Chinese).(in Chinese).
	Cited By in Cnki (0) | Click to display the text
[3]	李春洋, 陈循, 易晓山, 等. 基于向量通用生成函数的多性能参数多态系统可靠性分析[J]. 兵工学报,2010, 31(12): 1604–1610.C Y, CHEN X, YI X S, et al. Reliability analysis of multi-state system with multiple performance parameters based on vector universal generating function[J]. Acta Armamentarii,2010, 31(12): 1604–1610.(in Chinese).
	Cited By in Cnki (0) | Click to display the text
[4]	BARLOW R E, WU A S. Coherent systems with multi-state components[J]. Mathematics of Operations Research,1978, 3(4): 275–281.
	Click to display the text
[5]	NATVIG B. Multi-state systems reliability theory with applications[M].New York: Wiley, 2011: 11-30.
	Click to display the text
[6]	LEVITIN G. The universal generating function in reliability analysis and optimization[M].London: Springer, 2005: 99-262.
	Click to display the text
[7]	刘宇.多状态复杂系统可靠性建模及维修决策[D].成都:电子科技大学,2011:48-100.LIU Y.Multi-state complex system reliability modeling and maintenance decision[D].Chengdu:University of Electronic Science and Technology of China,2011:48-100(in Chinese).(in Chinese).
	Cited By in Cnki (0) | Click to display the text
[8]	LI Y, ZIO E. A multi-state model for the reliability assessment of a distributed generation system via universal generating function[J]. Reliability Engineering and System Safety,2012, 106: 28–36.
	Click to display the text
[9]	TABOADA H A, ESPIRITU J F, COIT D W. Design allocation of multi-state series-parallel systems for power systems planning:A multiple objective evolutionary approach[J]. Journal of Reliability and Safety,2008, 222(3): 381–391.
	Click to display the text
[10]	史新红, 齐先军, 王治国. 基于UGF的发电系统区间可靠性评估及其仿射算法改进[J]. 合肥工业大学学报(自然科学版),2014, 37(3): 286–291.X H, QI X J, WANG Z G. Interval reliability estimation of power generating system based on UGF method and its modification by using affine arithmetic[J]. Journal of Hefei University of Technology(Natural Science),2014, 37(3): 286–291.(in Chinese).
	Cited By in Cnki (0) | Click to display the text
[11]	尚彦龙, 蔡琦, 赵新文, 等. 基于UGF和Semi-Markov方法的反应堆泵机组多状态可靠性分析[J]. 核动力工程,2012, 33(1): 117–123.Y L, CAI Q, ZHAO X W, et al. Multi-state reliability for pump group in nuclear power system based on UGF and Semi-Markov process[J]. Nuclear Power Engineering,2012, 33(1): 117–123.(in Chinese).
	Cited By in Cnki (0) | Click to display the text
[12]	DING Y, ZUO M J, LISNIANSKI A, et al. Fuzzy multi-state systems:General definitions,and performance assessment[J]. IEEE Transactions on Reliability,2008, 57(4): 589–594.
	Click to display the text
[13]	DING Y, LISNIANSKI A. Fuzzy universal generating functions for multi-state system reliability assessment[J]. Fuzzy Sets and Systems,2008, 159(3): 307–324.
	Click to display the text
[14]	LI C Y, CHEN X, YI X S. Interval-valued reliability analysis of multi-state systems[J]. IEEE Transactions on Reliability,2011, 60(1): 323–330.
	Click to display the text
[15]	DESTERCKE S, SALLAK M. An extension of universal generating function in multi-state systems considering epistemic uncertainties[J]. IEEE Transactions on Reliability,2013, 62(2): 504–514.
	Click to display the text
[16]	鄢民强, 杨波, 王展. 不完全覆盖的模糊多状态系统可靠性计算方法[J]. 西安交通大学学报,2011, 45(10): 109–114.M Q, YANG B, WANG Z. Reliability assessment for multi-state system subject to imperfect fault coverage[J]. Journal of Xi'an Jiaotong University,2011, 45(10): 109–114.(in Chinese).
	Cited By in Cnki (0) | Click to display the text
[17]	LIU Y, HUANG H. Reliability assessment for fuzzy multi-state system[J]. International Journal of Systems Science,2010, 41(4): 365–379.
	Click to display the text
[18]	陈东宁, 姚成玉. 基于模糊贝叶斯网络的多态系统可靠性分析及在液压系统中的应用[J]. 机械工程学报,2012, 48(16): 175–183.D N, YAO C Y. Reliability analysis of multi-state system based on fuzzy Bayesian networks and application in hydraulic system[J]. Chinese Journal of Mechanical Engineering,2012, 48(16): 175–183.(in Chinese).
	Cited By in Cnki (0) | Click to display the text
[19]	马德仲, 周真, 于晓洋, 等. 基于模糊概率的多状态贝叶斯网络可靠性分析[J]. 系统工程与电子技术,2012, 34(12): 2607–2611.D Z, ZHOU Z, YU X Y, et al. Reliability analysis of multi-state Bayesian networks based on fuzzy probability[J]. Systems Engineering and Electronics,2012, 34(12): 2607–2611.(in Chinese).
	Cited By in Cnki (0) | Click to display the text
[20]	陈东宁, 姚成玉, 党振. 基于T-S模糊故障树和贝叶斯网络的多态液压系统可靠性分析[J]. 中国机械工程,2013, 24(7): 899–905.D N, YAO C Y, DANG Z. Reliability analysis of multi-state hydraulic system based on T-S fuzzy fault tree and Bayesian network[J]. China Mechanical Engineering,2013, 24(7): 899–905.(in Chinese).
	Cited By in Cnki (0) | Click to display the text
[21]	邱志平. 非概率集合理论凸方法及其应用[M].北京: 国防工业出版社, 2005: 30-43.Z P. Convex method of non-probabilistic set-theory and its application[M].Beijing: National Defense Industry Press, 2005: 30-43.(in Chinese).
	Cited By in Cnki (0) | Click to display the text
[22]	高峰记. 可能度及区间数综合排序[J]. 系统工程理论与实践,2013, 33(8): 2033–2040.F J. Possibility degree and comprehensive priority of interval numbers[J]. Systems Engineering-Theory and Practice,2013, 33(8): 2033–2040.(in Chinese).
	Cited By in Cnki (0) | Click to display the text