国外自1965年起,就有关于直升机吊挂飞行的研究。Sampath[1]对此有较为系统的综述。Lucassen和Sterk[2]共同建立了一个简单的三自由度直升机纵向悬停方程,忽略了吊挂受到的气动力和气动力矩。1986年,Ronen[3]建立了一个新的单点悬挂携带载荷的CH-53A/D直升机模型,用以改善当前的动力学模型,并开始研究系统的开环特性。Stucky[4]和Cicolani等[5]分别用数值仿真和飞行试验的方法对带吊挂的直升机本体运动模态进行了研究。稍后,Cliff和Bailey[6]使用了一个只考虑阻力的单吊挂直升机简化模型来研究吊挂飞行。在他们提供的公式中,非线性方程在稳定的水平飞行状态下被线性化,扰动方程就被分成纵向和横向。
国内吊挂飞行的研究起步较晚,起始于20世纪80年代,而且基本停留在理论分析上。崔瑛[7]在文献[8]的基础上,研究了直升机气动导数在吊挂引入后的变化。齐万涛和陈仁良[9]又继续开展了弹性绳索、吊挂构型和操稳特性等方面的研究和分析。对于带外吊挂直升机品质问题,由于吊挂物与直升机之间的运动耦合,使整个系统的运动更为复杂,崔利等[10]建立了带吊挂载荷的直升机飞行动力学模型, 分析了当施加纵向周期变距阶跃输入、横向周期变距阶跃输入以及尾桨距阶跃输入时带吊挂直升机的动力学响应历程。
本文在直升机本体模型的基础上,建立了六自由度刚体吊挂物气动模型,得到了完整的直升机-吊挂耦合系统动力学方程,并基于文献[11-12]给出了相应的控制系统模型,建立了完整的闭环直升机-吊挂耦合系统动力学模型。在此基础上,根据军用旋翼飞行器驾驶品质要求(ADS-33E)[13]对带吊挂物直升机闭环状态下的飞行品质进行计算,分析了吊挂飞行操纵响应的时域特性和频域特性,以及吊挂物质量、吊挂绳长和直升机前飞速度对耦合系统飞行品质的影响。
1 直升机-吊挂耦合系统闭环模型 1.1 直升机-吊挂耦合系统模型及小扰动线化
1.1.1 线性全量方程 本文所采用的直升机吊挂动力学模型来自于文献[14]。假设吊挂物为质点模型,没有转动自由度,忽略绳索气动力和吊挂物上作用的力矩,其所受的气动力仅为当地来流方向的准静态阻力。忽略绳索质量,绳索为刚性模型,且时刻处于绷紧状态。故在此假设下绳索为连结着直升机挂点和吊挂质心的一条直线,提供一个双侧的完整约束。
直升机本体的状态变量包括前飞速度vcg=[u?v?w]T(u、v和w分别为x、y和z方向速度)、姿态角θ=[φ?θ?ψ]T(φ、θ和ψ分别为滚转角、俯仰角和偏航角)和姿态角速度ω=[p q r]T(p、q和r分别为滚转角速度、俯仰角速度和偏航角速度),控制变量为u=[θom B′1 A′1θot](θom为飞行员的总距,B′1为纵向周期变距,A′1为横向周期变距,θot为脚蹬输入)。在直升机的体轴系内衡量吊挂位移的广义坐标即吊挂姿态角,如图 1所示。图中,θl和φl分别为吊挂物的后摆角和侧摆角。记吊挂姿态角θl=[θl φl]T,吊挂姿态角速度ωl=
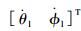
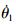
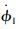
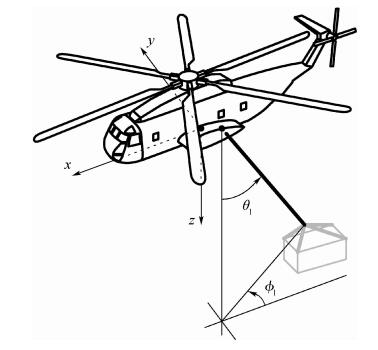 |
| 图 1 直升机体轴系与吊挂姿态角定义 Fig. 1 Definition of helicopter body reference frame and attitude angles of slung-load |
| 图选项 |
直升机-吊挂耦合系统动力学方程组[15]的矩阵形式为
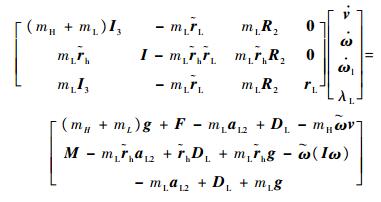 | (1) |
方程式(1)中,只有等号左边的向量
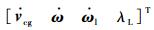
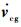
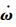
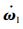
1.1.2 小扰动线化 直升机-吊挂耦合系统全量动力学方程的微分代数形式为
 | (2) |
式中:xL为耦合系统的状态变量,xL=[vcgω θ θl ωl]T为13阶向量; M(xL)为惯性矩阵,详细参见文献[16]。
此时,耦合系统的非线性状态空间方程为
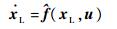 | (3) |
式中:
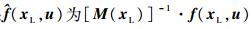
所以,线化系统的状态矩阵和控制矩阵是
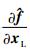
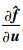
1.2 带控制系统的直升机-吊挂耦合系统模型 本文所采用的控制系统来自于NASA CR-3144、CR-3145报告[11-12]。δ=[δC δB δA δP]T分别为飞行员的总距、纵/横向周期变距、脚蹬输入的操纵行程百分比,即操纵输入。θMR、B1s、A1s和θTR分别为执行机构上的主旋翼总距角、纵/横向变距角(自动倾斜器倾角)和尾旋翼总距角,它们就是旋翼气动模型中的控制变量θom、B′1、A′1和θot。控制系统按不同操纵对象分为4个通道:总距通道、纵向通道、横向通道、脚蹬通道。总距操纵δC会交叉进给至横向和脚蹬通道,以在一定程度上抵消由于总距操纵而引起的滚转和偏航力矩。纵向通道与其他3个通道没有关联。直接接收飞行员操纵输入的有7个环节,分别是各操纵通道的机构联动、纵向通道前馈以及总距输入的交叉进给[16]。
由文献[11-12]给出的控制系统模型,可以写出控制系统执行机构的主旋翼总距角、纵/横向变距角(自动倾斜器倾角)、尾旋翼总距角与系统各变量之间动态关系的频域表达式为
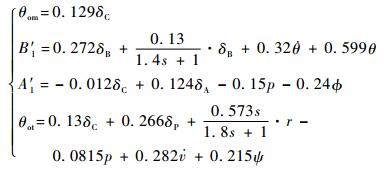 | (4) |
令
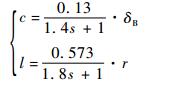 | (5) |
进一步转化成时域形式可得
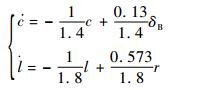 | (6) |
从方程式(6)可以看到,控制系统的引入使整个系统增加了两阶动态,对应的状态变量可以取为c和l,记ξ=[c l]。将其代入直升机本体小扰动线化模型的表达式,变形后可得到加了控制系统后的小扰动线化模型方程为
 | (7) |
式中:AL和BL为直升机-吊挂耦合系统线化方程的状态矩阵和控制矩阵,即
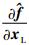
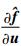
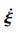
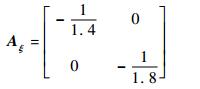 | (8) |
 | (9) |
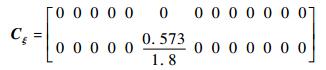 | (10) |
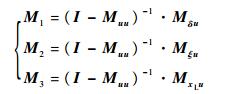 | (11) |
而Mδu、Mξu、MxLu和Muu分别为控制变量[θom B′1 A′1 θot]T与δ、ξ、xL和u相对应的系数矩阵。具体的矩阵形式为
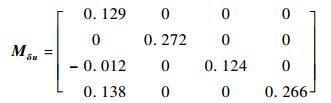 | (12) |
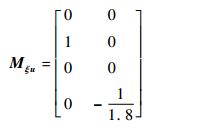 | (13) |
 | (14) |
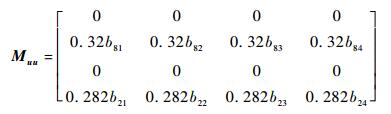 | (15) |
式中:aij(i=1, 2, …, 13;j=1, 2, …, 13)为直升机-吊挂耦合系统小扰动线化模型中状态矩阵的各项;bij(i=1, 2, …, 13;j=1, 2, 3, 4)为直升机-吊挂耦合系统小扰动线化模型中控制矩阵的各项。
则引入控制系统后的新直升机-吊挂耦合线化模型的状态矩阵AL-aug和控制矩阵BL-aug分别为
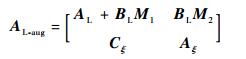 | (16) |
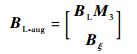 | (17) |
2 基于ADS-33E的飞行品质 2.1 带宽分析 本部分选取了直升机在吊挂物质量为4t、吊挂绳长分别为40m和60m时的算例。根据带宽定义分别画出了俯仰通道和滚转通道的幅相曲线,算例伯德图如图 2和图 3所示。根据规范要求进一步计算了带宽与相位滞后,数据如表 1所示。
表 1 俯仰和滚转通道带宽和相位延迟对比 Table 1 Comparison of bandwidth and phase delay in pitch and roll channel
| 吊挂 绳长/m | 吊挂物 质量/t | 俯仰通道 | 滚转通道 | |||
| ωBW, θ/ (rad·s-1) | τp, θ/s | ωBW, φ/ (rad·s-1) | τp, φ/s | |||
| 60 | 4 | 0.402 | 3.8296 | 0.420 | 1.0749 | |
| 40 | 4 | 0.574 | 5.4538 | 0.611 | 0.8943 | |
| 无吊挂 | 0.442 | 0.1844 | 0.663 | 0.5389 | ||
| 注:ωBW, θ—俯仰通道带宽;τp, θ—俯仰通道相位延迟;ωBW,φ—滚转通道带宽;τp, φ—滚转通道相位延迟。 | ||||||
表选项
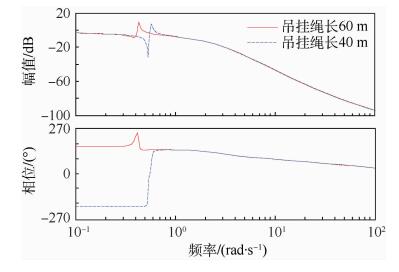 |
| 图 2 俯仰通道伯德图 Fig. 2 Bode diagram of pitch channel |
| 图选项 |
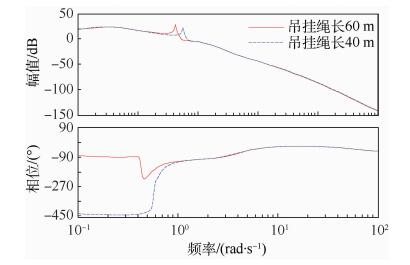 |
| 图 3 滚转通道伯德图 Fig. 3 Bode diagram of roll channel |
| 图选项 |
闭环系统的带宽在频域分析中是很重要的参数,它度量了系统具有一定信号复现能力的频率变化范围。当输入信号频率低于带宽时,系统可以产生足够强度的响应。一般情况下,系统的阶跃响应速度与带宽成正比,调节时间与带宽成反比。因此,在保证系统的合理时域指标的前提下,总是希望系统有较大的带宽。在本算例中,带吊挂闭环状态下,由伯德图可以看出:
1)幅频特性的峰值Mr随绳长增加而增大,这意味着系统的平稳性随绳长增加而变差,阶跃响应的超调量也变大。而幅频响应峰值频率ωr随绳长增加而变小,这是由于绳长增加后,吊挂摆动的固有频率减小而造成的。2个算例中CH-53A/D的带宽均较小,意味着驾驶员可用的、距不稳定边界尚有适当余量的最大操纵频率较小。并且随着吊挂绳长的增加,俯仰通道和滚转通道的带宽均是减小的。这说明,吊挂的绳长越长,系统对阶跃输入的响应越慢,所需的调节时间越长。
2)对于相位滞后指标,表示驾驶员操纵频率接近相角穿越频率ωg时,直升机走向不稳定的快慢程度。2个算例的俯仰通道和滚转通道的指标数值均不小,说明相频曲线下降较快,直升机走向不稳定的趋势也较快,但与绳长的关系表现的并不明显。但滚转通道的相位滞后指标明显优于俯仰通道,说明直升机在滚转通道的飞行品质优于俯仰通道。无吊挂时,滚转通道带宽品质劣于俯仰通道,说明吊挂对俯仰通道的影响更严重。
3)等级方面,对比ADS-33规范要求,2个算例中,直升机在实现目标捕捉及跟踪任务时,俯仰通道和滚转通道的指标均在等级3范围。其他任务,当可用感示环境UCE>1时,在等级3范围;在UCE=1时,均在等级2范围。评价结果表明,CH-53A/D直升机俯仰(滚转)通道带宽偏小,这使得驾驶员应特别注意直升机的操纵频率,否则操纵频率过大极有可能引发驾驶员诱发振荡。
2.2 轴间耦合特性分析
2.2.1 总距-偏航特性 ADS-33品质规范规定[13],为实现某一轴上的响应,飞行员施加的操纵输入不得在另一个或另几个轴上引起不适宜的响应。而对于总距-偏航耦合来说,即在俯仰和滚转姿态基本保持不变的情况下,偏航角速度的响应不宜过大。该品质要求已显示在图 4中,其中,|r1/w(3)|和r3/|w(3)|为总距-偏航耦合品质的评价指标。
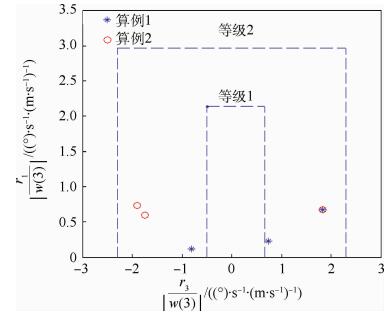 |
| 图 4 总距-偏航耦合品质指标算例 Fig. 4 Example of yaw due to collective coupling |
| 图选项 |
本节选取的2组算例为吊挂质量8t,固定绳长下前飞速度变化和固定前飞速度下吊挂绳长变化的情况。算例1为绳长40m,前飞速度分别为20、30、50m/s;算例2为前飞速度为30m/s,绳长分别为20、40、80m。
由图 4可见,所有算例的总距-偏航特性指标均在等级2范围内。说明总距的操纵输入对偏航的角速度有一定影响。
2.2.2 滚转-俯仰耦合特性 迅猛机动中的滚转-俯仰耦合是在时域响应中进行研究。在一个突然的横向操纵机构的阶跃输入后,4s内轴外响应的峰值与4s末目标响应之比,即θφ/φ4,可以作为品质指标来确定该项耦合品质。ADS-33品质规定等级1为θφ/φ4不超过±0.25,等级2为θφ/φ4不超过±0.6。航向基本保持不变。
本部分选取的算例为前飞速度50m/s、吊挂绳长分别为40m和60m、吊挂质量由1t变化至8t的情况。结果如图 5所示,数据点全部在等级1和等级2的范围内,并且由数据可以看出相同的前飞速度和吊挂质量下,滚转-俯仰耦合品质受吊挂绳长的影响不大。综合而言,带吊挂闭环状态下的CH-53A/D的滚转通道对俯仰通道影响较小,能够达到比较满意的滚转-俯仰耦合飞行品质要求。
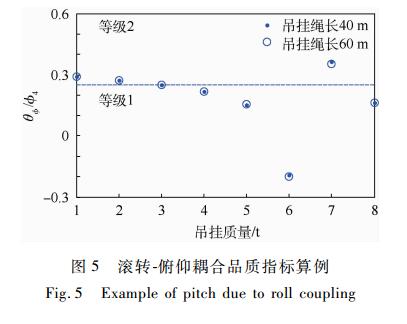 |
| 图 5 滚转-俯仰耦合品质指标算例 Fig. 5 Example of pitch due to roll coupling |
| 图选项 |
2.3 垂直轴操纵功效 垂直轴操纵功效是直升机十分重要的飞行品质评价内容之一。品质规范[13]规定,自总距快速偏离直升机平衡位置起1.5s后,直升机产生的垂向速度w1.5将作为垂直轴操纵功效的评价指标。具体的品质要求已显示在图中。在计算本品质指标时,对总距施加1%的阶跃输入,求解由总距操纵引起的垂向速度响应曲线。
2.3.1 垂直轴操纵功效随吊挂质量变化 本节取了2组算例,第1组前飞速度为50m/s,吊挂绳长为60m,吊挂质量由2t变化至6t;第2组前飞速度为50m/s,吊挂绳长为40m,吊挂质量也由2t变化至6t。所得到的w1.5均标注在图 6中。由图可见,随着吊挂质量增加,2组算例的垂直轴操纵功效品质等级均变差,吊挂质量为2t和3t的算例在等级1范围;吊挂质量为4、5和6t的算例在等级2范围。且同样的前飞速度和吊挂质量下,w1.5随绳长的变化关系并不明显。
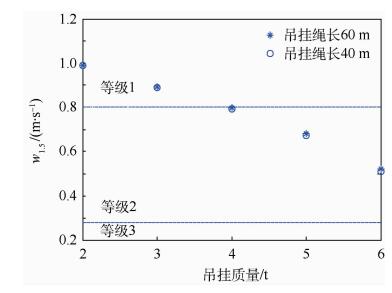 |
| 图 6 垂直轴操纵功效随吊挂质量变化算例 Fig. 6 Example of vertical control power changing with slung-load mass |
| 图选项 |
2.3.2 垂直轴操纵功效随前飞速度变化 本节取的两组算例为吊挂质量8t,吊挂绳长分别为40m和60m,前飞速度单调递增的情况。所得到的w1.5均标注在图 7中。由图可见,随着前飞速度的增加,2组算例的垂直轴操纵功效品质呈现先变差后变好的趋势,在速度提高到60m/s后,垂直轴操纵功效品质均在等级1范围内。且同样的前飞速度和吊挂质量下,w1.5受绳长的影响并不明显。
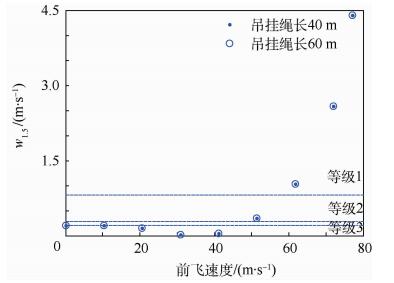 |
| 图 7 垂直轴操纵功效随前飞速度变化算例 Fig. 7 Example of vertical control power changing with velocity |
| 图选项 |
3 结论 本文以CH-53A/D型直升机为算例,在所建立的飞行动力学模型的基础上,基于直升机单质点吊挂假设和控制系统模型,建立了直升机-吊挂耦合闭环系统的非线性动力学模型,并对系统方程进行了小扰动线性化处理。
在此基础上对直升机-吊挂耦合闭环系统的线化模型进行了时域特性和频域特性分析,进一步参照ADS-33E品质规范分析了吊挂物质量、吊挂绳长和直升机前飞速度对耦合系统飞行品质的影响。结果表明:
1)耦合系统的带宽随绳长增加而减小,平稳性随绳长增加而变差;阶跃响应的超调量也变大;幅频响应峰值频率ωr随绳长增加而变小;相位滞后指标随绳长变化不明显。综合来看绳长越短,耦合系统的时域特性越好,同时吊挂的引入对俯仰通道的相位滞后指标影响更严重。
2)对于轴间耦合特性来说,总距的操纵输入对偏航的角速度有一定影响;而相同的前飞速度和吊挂质量下,绳长对滚转-俯仰耦合品质的影响不大。
3)对于垂直轴操纵功效,随着吊挂质量增加,系统的垂直轴操纵功效品质等级变差;随着前飞速度增加,该项指标呈现先变差后变好的趋势;但同样的前飞速度和吊挂质量下,该项指标受绳长的影响并不明显。
参考文献
| [1] | SAMPATH P.Dynamics of a helicopter-slung load system [D].Maryland:University of Maryland, 1980:16-21.http://www.oalib.com/paper/4250559 |
| [2] | LUCASSEN L R, STERK F J. Dynamic stability analysis of a hovering helicopter with a sling load[J].Journal of the American Helicopter Society, 1965, 10(2): 6–12.DOI:10.4050/JAHS.10.6 |
| [3] | RONEN T.Dynamics of a helicopter with a slung load [D].Stanford: Stanford University, 1986:11-26.http://www.oalib.com/paper/4250559 |
| [4] | STUCKY R A.Mathematical modeling of helicopter slung-load system: DSTO-TR-1257 [R].[S.l.:s.n.], 2002:6-37.http://www.oalib.com/paper/4250559 |
| [5] | CICOLANI L S, CONE A, THERON J N. Flight test and simulation of a cargo container slung load in forward flight[J].Journal of the American Helicopter Society, 2009, 54(3): 032006–1.DOI:10.4050/JAHS.54.032006 |
| [6] | CLIFF E M, BAILEY D B. Dynamic stability of a translating vehicle with a simple sling load[J].Journal of Aircraft, 1975, 12(10): 773–777.DOI:10.2514/3.44492 |
| [7] | 崔瑛.直升机吊挂飞行稳定性分析[D].南京:南京航空航天大学, 2005:18-50.CUI Y.Stability analysis of a helicopter with an external slung load [D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2005:18-50(in Chinese).http://cdmd.cnki.com.cn/article/cdmd-10287-2006118875.htm |
| [8] | FUSATO D, GUGLIERI G, CELI R. Flight dynamics of an articulated rotor helicopter with an external slung load[J].Journal of the American Helicopter Society, 2001, 46(1): 3–13.DOI:10.4050/JAHS.46.3 |
| [9] | 齐万涛, 陈仁良. 直升机吊挂飞行稳定性和操纵性分析[J].南京航空航天大学学报, 2011, 43(3): 406–412.QI W T, CHEN R L. Stability and control characteristic analysis for flight of helicopter with slung-load[J].Journal of Nanjing University of Aeronautics and Astronautics, 2011, 43(3): 406–412.(in Chinese) |
| [10] | 崔利, 曹义华, 李国知. 直升机吊挂飞行平衡、稳定性与操纵性研究[J].航空动力学报, 2010, 25(10): 2307–2311.CUI L, CAO Y H, LI G Z. Studies on trims, stability, and control ability of helicopter with slung-load[J].Journal of Aerospace Power, 2010, 25(10): 2307–2311.(in Chinese) |
| [11] | HEFFLEY R K, JEWELL W F, LEHMAN J M, et al.A compilation and analysis of helicopter handling qualities data, volume one:Data compilation:NASA-CR-3144[R].Washington, D.C.:NASA, 1980:303-357. |
| [12] | HEFFLEY R K.A compilation and analysis of helicopter handling qualities data, Volume two:Data analysis:NASA-CR-3145[R].Washington, D.C.:NASA, 1979:120-142. |
| [13] | Aeronautical design standard performance specification, handling qualities requirements for military rotorcraft:ADS-33E-PRF [S].[S.l.]:United States Army Aviation and Missile Command, 2000.http://www.dtic.mil/cgi-bin/GetTRDoc?Location=U2&doc=GetTRDoc.pdf&AD=ADA515904 |
| [14] | STURGEON W R.A mathematical model of the CH-53 helicopter:NASA TM-81238 [R].Washington, D.C.:NASA, 1980:1-50. |
| [15] | 曹龙, 曹义华, 李春华. 直升机-吊挂耦合系统平衡特性和稳定性分析[J].北京航空航天大学学报, 2014, 40(9): 1219–1224.CAO L, CAO Y H, LI C H. Equilibrium characteristics and stability analysis of helicopter-slung-load coupling system[J].Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(9): 1219–1224.(in Chinese) |
| [16] | 曹龙.直升机外吊挂动力学建模与飞行性能分析[D].北京:北京航空航天大学, 2014:81-98.CAO L.Dynamics modeling and flying performance analysis of helicopter with slung-load [D].Beijing: Beihang University, 2014:81-98 (in Chinese).http://www.cnki.com.cn/Article/CJFDTotal-YYLX201503019.htm |
