针对非线性控制分配问题,文献[1]给出了近年的研究现状;文献[2-3]提出了有关基于分段线性化函数的非线性控制分配方法,该方法虽然能够解决非线性过驱动系统计算复杂、难度大的问题,但是控制分配的精度和线性函数段个数相矛盾;文献[4]提出用遗传算法解决非线性控制分配问题,该方法虽然能够得到不错的结果,但是计算比较慢,且容易陷入局部最优解;文献[5]给出了一种基于补偿的线性规划方法来解决飞翼布局飞机的交叉耦合效应,但其通用性不强;文献[6]提出了一种直接处理非线性控制分配问题的方法,充分利用冗余操纵面,实现不同飞行条件和任务下对多种目标的综合权衡分配;文献[7]采用序列线性规划 (Sequence Linear Programming,SLP) 方法解决了非线性控制分配问题,但其精度不高;文献[8]将卫星运载火箭的非线性过驱动问题转化为独立的线性矩阵不等式 (Linear Matrix Inequality,LMI)问题进行处理,但其通用性不强;文献[9]针对分布式电动车直接航向控制(Direct Yaw-moment Control,DYC)中的非线性控制分配问题,提出了单次迭代序列二次规划 (Single-iteration Sequential Quadratic Programming,S-SQP)方法,取得了不错的控制效果;文献[10]将滚转阻尼器作为控制分配问题的约束条件,保证了航向控制的稳定性,但其实时性不能保证;文献[11-12]给出了一种全局优化的非线性控制分配方法,通过KKT条件寻找局部最优解,而后在所有的局部最优解中进行比较来获得全局最优解,但其计算量很大;文献[13]针对高性能飞机,结合动态逆控制器,基于多元样条函数解决了非线性控制分配问题,但其结构比较复杂不易实现;文献[14]利用补偿思想解决了多目标非线性控制分配问题,其通用性不强;文献[15]通过阻尼最小二乘方法解决了船舶过驱动系统中的非线性控制分配问题,结合PID控制律取得了不错的控制效果,但其实时性未得到验证;文献[16]中利用SLP方法和微分进化算法解决了非线性控制分配问题,但其分配精度不高。
为了解决上述方法计算量大、实时性差和通用性不强的问题,本文提出了一种实用新型的基于舵面位置反馈的非线性控制分配方法,该方法对过驱动系统典型的3种非线性控制分配问题都适用,并且精度较高,实时性较强,具有科学研究和工程应用价值。
1 问题描述 以某小型无尾飞翼飞机(Tailless Flying Wing Aircraft,TFWA)为对象,说明力矩系数与舵面偏角之间的非线性问题。图 1为TFWA的气动布局。图中:δ1L~δ5L分别为第1~5号左侧舵面偏角;δ1R~δ5R分别为第1~5号右侧舵面偏角。该TFWA共有10个可操纵的气动舵面,在飞行过程中可利用不同舵面的组合实现对飞机相同的操纵效果。
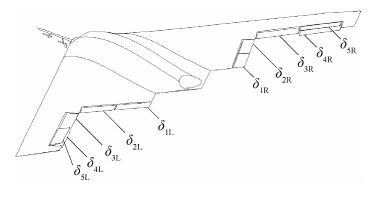 |
| 图 1 TFWA气动布局 Fig. 1 Aerodynamic configuration of TFWA |
| 图选项 |
该TFWA利用外侧2组阻力开裂式方向舵(Split Drag Rudder,SDR)[16-18]进行航向控制。其中,当SDR采用单侧上下舵面对称偏转的方式进行控制,即当SDR偏角小于0°时,右侧4、5号舵面组合偏转(左侧4、5号舵面保持不动);反之,当SDR偏角大于0°时,左侧4、5号舵面组合偏转(右侧4、5号舵面保持不动)。当SDR上舵面与下舵面采取非对称偏转时,5号舵面向上偏转为负,4号舵面向下偏转为正。
当TFWA处于某个低速大迎角飞行状态时,对TFWA的模型进行计算流体力学(Computational Fluid Dynamics,CFD)解算,三轴力矩系数与操纵面之间的偏转关系由文献[19]给出,可简写为
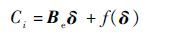 | (1) |
式中:Ci为三轴力矩系数;δ为10个可操纵气动舵面偏角;Be为操纵效能矩阵;f(δ)为舵面偏角与三轴力矩系数的非线性关系。
从式(1)中可知,三轴力矩系数与气动舵面偏角之间不再是简单操纵效能矩阵形式的线性关系。此飞行状态下,三轴力矩系数与舵面偏角的2次方或3次方以及4、5号舵面的耦合作用相关。考虑到舵面偏角的3次方项与其他项相比非常小,可忽略其影响。具有非线性和耦合性的实际三轴力矩系数v表示为[16]
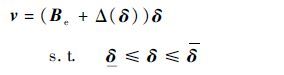 | (2) |
式中:

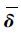
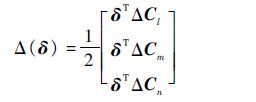 |
其中:δ=[δ1δ2…δn]T,δi为第i个操纵面;ΔCl、ΔCm和ΔCn为2个控制面组合对滚转、俯仰和偏航力矩的效能,分别描述为
 |
图 2给出了三轴力矩系数随SDR(上下舵面对称偏转)偏角δSDR的变化曲线。图中:SDR偏角80°对应左侧SDR上下舵面偏转夹角为80°,右侧SDR不偏转;SDR偏角-80°对应的左右SDR偏转则相反。
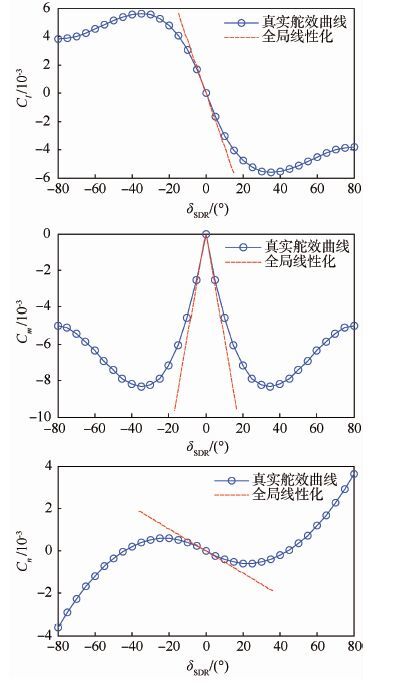 |
| 图 2 三轴力矩系数随SDR偏角变化曲线 Fig. 2 Curves of moment coefficients of three-axis change with deflection of SDR |
| 图选项 |
由图 2可以看出,三轴力矩系数与SDR偏角呈现非线性非单调关系,尤其当SDR偏角大于30°或小于-30°时,舵面偏角增大,其三轴力矩系数反而减小,即出现了操纵反效的问题。
采用SDR非对称偏转,可改善其非线性,但同时需要考虑SDR上下舵面的耦合性问题。已有的二次规划、非线性规划以及智能迭代算法等非线性控制分配方法,求解这类问题时只是对这种情形简化或者不考虑解算的实时性。上述方法无法真实地描述三轴力矩系数与舵面偏角的关系,且计算量较大,造成飞机舵效损失。
为了解决这些方法的不足,本文针对TFWA低速大迎角下三轴力矩系数与舵面偏角非线性相关的问题,提出了一种实用新型的基于舵面位置反馈的非线性控制分配方法,该方法能对单调非线性、非单调非线性和耦合非线性3种问题统一处理,其精度高,通用性强,实时性强。
2 非线性控制分配方法的具体实现 2.1 设计思想 针对已有非线性控制分配方法计算量大、实时性差等问题,本文提出了一种实用新型的基于舵面位置反馈的非线性控制分配方法,其控制结构如图 3所示。图中:vd∈Rq×1为期望三轴力矩系数;δ(n)∈Rp×1为第n拍的舵面偏角。
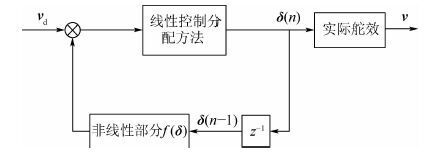 |
| 图 3 基于舵面位置反馈的非线性控制分配方法的结构 Fig. 3 Structure of nonlinear control allocation method based on feedback of position of surface |
| 图选项 |
如图 3所示,本文提出的基于舵面位置反馈的非线性控制分配方法的基本思想是:利用线性控制分配方法来解决非线性控制分配方法。考虑到相邻的2次解算周期内,舵面偏角的变化不大,因此在期望三轴力矩系数中除去由前一拍舵面位置产生的非线性三轴力矩系数,进而对剩余的期望三轴力矩系数用线性控制分配方法来求解本拍中的舵面偏角。其中,线性控制分配方法部分包含了所有的线性控制分配方法,如伪逆法、加权伪逆法、串接链法、不动点迭代方法和相邻面搜索方法等。根据式(2),以基于伪逆法的线性控制分配方法为例,给出本文提出的非线性控制分配方法的数学描述形式如下:
 | (3) |
式中:v∈Rp×1;Be∈Rq×p;δ(n)∈Rp×1;对于本文中的TWFA,q=3,p=10。
对于本文所提出的非线性控制分配方法,下面给出其稳定性证明和稳态误差的计算。
2.2 稳定性证明 定义1 式(3)所示的离散非线性系统可以使用如下差分方程描述:
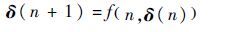 | (4) |
式中:δ∈Rp;f∈C[N+×Rp,Rq],N+为非负整数集合。
设V(n,δ)∈C[N+×Rp,R+],则V(n,δ)沿系统的差分定义为
 | (5) |
函数K(·): Rp×1→R称为K函数,如果其是严格单调增加的连续函数,且K(0)=0。
定理1 当期望三轴力矩系数vd=0时,式(3)的平衡点δ=0的一致稳定充分必要条件是:存在K函数和与n0无关的常数σ>0,使得
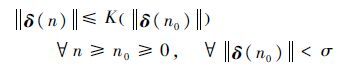 | (6) |
证明:(1)充分性。
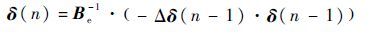 |
由此可知,上述系统的平衡点为δ(n)=0。
构造K函数Kδ(n)=δ(n),考虑到δ(n)为舵面偏角,而舵面偏角受舵面偏转位置限制,具有偏转极限,从而δ(n)有界,所以存在K函数和与n0无关的常数σ>0,使得
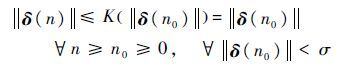 |
则?ε>0,令
 |
由于‖δ(n0)‖有界,从而存在M(ε),使得‖δ(n0)‖<M(ε),都有
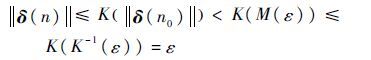 |
因此,系统的平衡点δ=0一致稳定。
(2)必要性。若系统的平衡点δ=0一致稳定,即
 |
使得
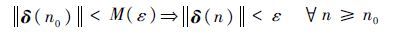 |
固定ε,记
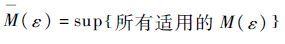
 |
这样取定的
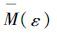
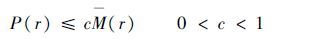 |
设K(r)=P-1(r),则K(r)为K函数,记$\sigma =\underset{r\to \infty }{\mathop{\lim }}\,P(r)$,则σ与n0无关。
于是,对于任意满足:‖δ(n0)‖<σ的δ(n0),取ε=K(‖δ(n0)‖)>0,则
 |
且满足
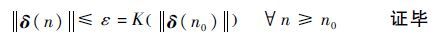 |
故本文提出的非线性控制分配方法在平衡点δ(n)=0处一致稳定。
2.3 稳态误差计算 根据基于舵面位置反馈的非线性控制分配方案的结构可知:
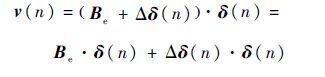 | (7) |
式中:
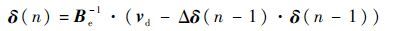 |
将式(7)展开,得
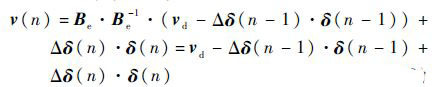 | (8) |
整理式(8),得
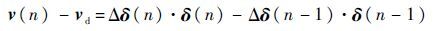 |
当n→∞时,由稳定性证明可知舵面不再偏转,从而δ(n)=δ(n-1),由于
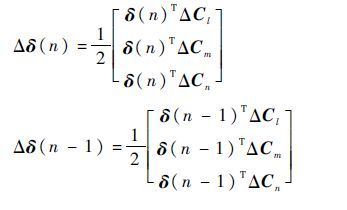 |
当n→∞时,Δδ(n)=Δδ(n-1),则
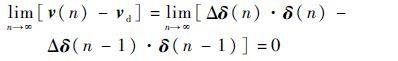 |
故本文提出的非线性控制分配方法的稳态误差为0。对于该方法中基于其他线性方法的处理,其证明过程与伪逆法相同,不再给出。
2.4 可行性分析 本文所提出的实用新型非线性控制分配方法,其核心在于对舵面位置反馈信号的获取。
1) 在实际中,舵面位置信息是可获得的。以德国VOLZ舵机为例,其众多型号舵机都带有位置信息的模拟反馈或数字反馈。
2) VOLZ舵机有效脉冲宽度一般在0.9~2.1ms之间,而一般飞控计算机的解算周期在12ms左右。
3) 本文方法通过舵面位置反馈将非线性控制分配问题转化为线性控制分配问题进行求解,其实时性取决于线性控制分配方法的实时性,而已有的部分线性控制分配方法(伪逆法、串接链法和相邻面搜索方法等)实时性满足要求。
因此,本文所提出的基于舵面位置反馈的非线性控制分配方法在工程中很容易实现。
3 仿真验证 根据图 4中TFWA的转矩可达集(Attainable Moment Subset,AMS),首先选择期望三轴力矩系数点为
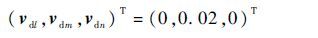 |
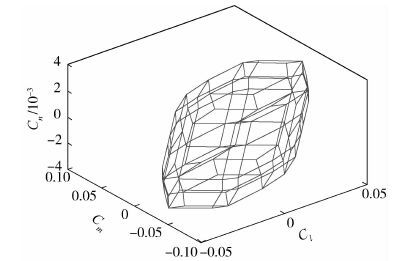 |
| 图 4 TFWA的转矩可达集 Fig. 4 AMS of TFWA |
| 图选项 |
在上述单点下进行100次仿真取其平均值,对比SLP方法、SQP方法、遗传算法和本文方法,其结果如表 1所示。
表 1 不同方法单点解算对比 Table 1 Comparison of different methods of solving single point problem
| 方法 | 实际三轴力矩系数 | 解算时间/ms |
| SLP方法 | (0,0.0114,0) | 6.917 |
| SQP方法 | (0,0.0200,0) | 37.670 |
| 遗传算法 | (0.0001,0.0200,-0.0005) | 88.576 |
| 本文方法 | (0,0.0202,0) | 0.258 |
表选项
从表 1中可以看出,在解算精度方面,SQP方法误差为0,但是其解算时间超出了一般飞控解算时间12ms的限制;对于SLP方法,其解算时间虽然在12ms以内,但是其精度较差;遗传算法解算时间最长;本文方法解算时间在ms级别内,同时其精度也高。综合上述比较可知,本文方法精度高、解算快。
比较完单点的情形,再比较三轴力矩系数连续变化的情形。根据图 4选取期望三轴力矩系数曲线如图 5所示,在这种情况下,三轴力矩系数变化剧烈,因此可以验证方法的有效性。
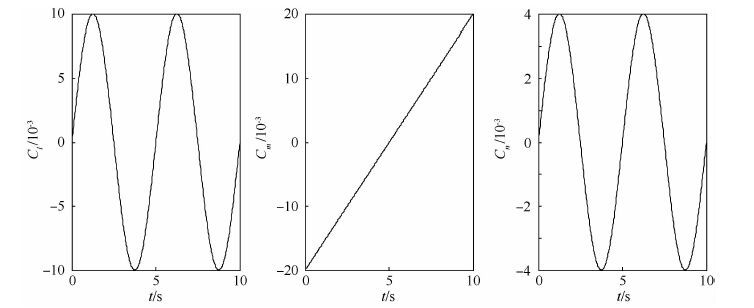 |
| 图 5 期望三轴力矩系数 Fig. 5 Desired three-axis moment coefficients |
| 图选项 |
根据图 5中的期望三轴力矩系数,对比SLP方法、SQP方法、遗传算法和本文方法,其跟踪结果如图 6所示。图 7给出了不同方法对期望三轴力矩曲线跟踪误差。从图 6和图 7的对比结果中可知,与单点情形相似,SLP方法对期望三轴力矩系数曲线的跟踪效果最差,其误差可达到跟踪值的60%左右;遗传算法对于期望滚转力矩曲线和俯仰力矩曲线跟踪效果好,对于偏航力矩曲线跟踪效果差,且在期望力矩曲线附近振荡;SQP方法和本文方法跟踪效果最好,其跟踪误差都非常小,但考虑到SQP方法解算时间长,所以对于三轴力矩系数曲线的跟踪,本文方法效果最好。
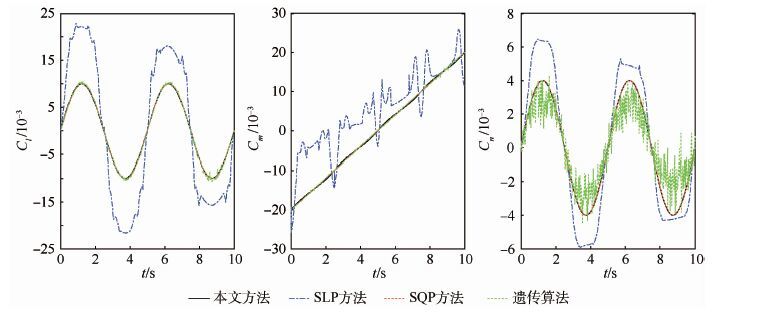 |
| 图 6 不同方法对期望三轴力矩系数曲线跟踪结果 Fig. 6 Results of tracking desired three-axis moment coefficients by different methods |
| 图选项 |
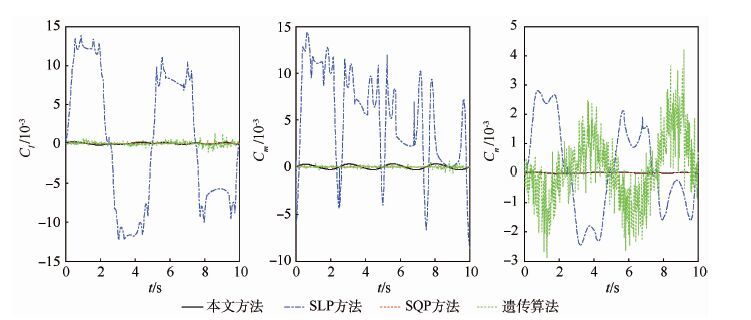 |
| 图 7 不同方法对期望三轴力矩系数曲线跟踪误差 Fig. 7 Errors of tracking desired three-axis moment coefficients by different methods |
| 图选项 |
通过比较不同方法对期望三轴力矩系数单点和曲线的跟踪,可发现本文方法精度高,解算用时少。根据图 2中本文所提出的基于舵面位置反馈的非线性控制分配方法结构,针对线性控制分配方法部分,选择伪逆法、不动点迭代方法和相邻面搜索方法[20]进行了仿真比较分析,结果如图 8和图 9所示。
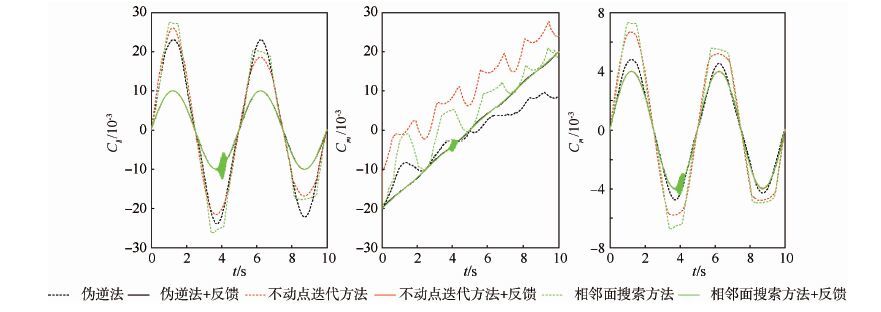 |
| 图 8 基于伪逆法、不动点迭代方法和相邻面搜索方法的跟踪结果 Fig. 8 Results of tracking based on pseudo inverse method,fixed-point iteration methed and neighbor search method |
| 图选项 |
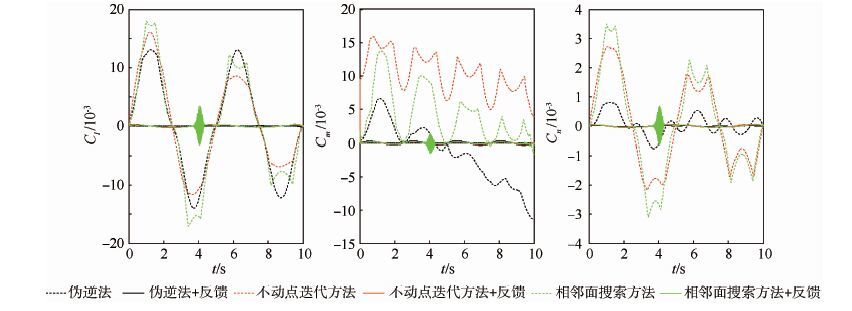 |
| 图 9 基于伪逆法、不动点迭代方法和相邻面搜索方法的跟踪误差 Fig. 9 Errors of tracking based on pseudo inverse method,fixed-point iteration methed and neighbor search method |
| 图选项 |
根据图 8和图 9的仿真结果可知,如果仅采用伪逆法、不动点迭代方法和相邻面搜索方法处理非线性控制分配问题,其跟踪误差可达到100%以上。而通过除去舵面位置上拍产生的非线性力矩系数,利用3种线性控制分配方法获得的跟踪误差几乎为0。因此,基于舵面位置反馈的非线性控制分配方法可将非线性问题转化为线性问题进行处理,同时利用已有的线性控制分配方法可取得不错的控制效果。
以TFWA、F18(其舵效拟合结果见文献[17])等为对象在xPC-DSP半物理仿真平台上验证了本文方法的通用性和实时性。其中,xPC实时内核模拟真实飞机,而DSP模拟控制律指令解算和控制指令分配的飞控计算机,两者借助RS232串口进行通信,其解算周期都设置为12ms。
以F18为例,对于SDR非线性和耦合性的三轴力矩系数问题的处理,半物理仿真结果如图 10所示。图中:红线为利用线性控制分配方法得到的分配结果,蓝线为本文方法得到的分配结果。由于现有的非线性控制分配方法很难进行实时仿真,所以只给出了本文提出的非线性控制分配方法和线性控制分配方法的比较。从图 10中可以看出,对于期望三轴力矩系数,本文方法与线性控制分配方法相比精度高,其跟踪误差几乎为0。对于俯仰力矩系数,如果仅采用线性控制分配方法来处理,得到的结果与期望结果偏差很大。同时,在半物理仿真平台上实现了本文方法,说明了其在实际中满足实时性要求。
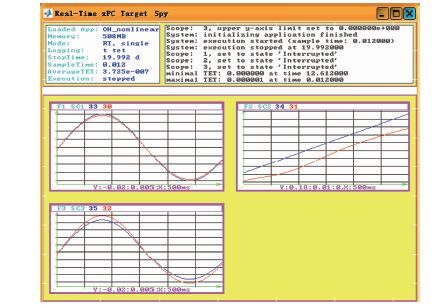 |
| 图 10 基于xPC-DSP半物理仿真平台仿真验证 Fig. 10 Simulink and test based on xPC-DSP semi-physical simulation platform |
| 图选项 |
4 结论 本文针对飞机力矩系数与舵面偏角之间的非线性问题,提出了一种实用新型的基于舵面位置反馈的非线性控制分配方法:
1) 在理论上证明了该方法具有一致渐近稳定性,且稳态误差为0。
2) 通过对比仿真不同方法在期望三轴力矩系数单点和曲线情形下的结果,可知本文提出的方法跟踪误差在1%以内,而解算时间在1ms以内,具有精度高、解算快的优点。
3) 在将非线性控制分配问题转化为线性控制分配问题后,可利用已有的线性方法进行求解,其方法选择灵活性强。
4) 以TWFA、F18为对象,结合数字仿真和xPC-DSP半物理仿真平台,说明本文所提出方法在处理力矩系数和舵面偏角之间的非线性问题时具有通用性强、实时性好和精度高等优点。
参考文献
| [1] | JOHANSEN T A, FOSSEN T I. Control allocation-A survey[J]. Automatica,2013, 49(5): 1087–1103. |
| Click to display the text | |
| [2] | 王鹏, 周洲, 王睿. 基于分段线性的飞翼布局飞机控制分配方法[J]. 西北工业大学学报,2009, 27(3): 321–325.WANG P, ZHOU Z, WANG R. A piecewise linear control allocation approach for a flying wing aircraft[J]. Journal of Northwestern Polytechnical University,2009, 27(3): 321–325.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [3] | BOLENDER M A, DOMAN D B. Nonlinear control allocation using piecewise linear functions[J]. Journal of Guidance Control and Dynamics,2004, 27(6): 1017–1027. |
| Click to display the text | |
| [4] | 何光宇, 周军, 呼卫军. 基于遗传算法的多执行机构控制分配策略[J]. 西北工业大学学报,2010, 28(1): 23–26.HE G Y, ZHOU J, HU W J. A novel control allocation algorithm based on genetic algorithm and quadratic programming[J]. Journal of Northwestern Polytechnical University,2010, 28(1): 23–26.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [5] | 徐明兴, 祝小平, 周洲, 等. 一种考虑交叉耦合效应的飞翼布局飞机控制分配方法[J]. 西北工业大学学报,2014, 32(1): 69–74.XU M X, ZHU X P, ZHOU Z, et al. A control allocation method for flying wing aircraft with control effector interactions considered[J]. Journal of Northwestern Polytechnical University,2014, 32(1): 69–74.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [6] | 杨恩泉, 高金源, 李卫琪. 多目标非线性控制分配方法研究[J]. 航空学报,2008, 29(4): 995–1001.YANG E Q, GAO J Y, LI W Q. Research on multi-object nonlinear control allocation method[J]. Acta Aeronautica et Astronautica Sinica,2008, 29(4): 995–1001.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [7] | OPPENHEIMER M W,DOMAN D B.A method for including control effector interactions in the control allocation problem[C]//AIAA Guidance,Navigation and Control Conference.Reston:AIAA,2007:1074-1083. |
| Click to display the text | |
| [8] | KISHORE W C A, DASGUPTA S, RAY G, et al. Control allocation for an over-actuated satellite launch vehicle[J]. Aerospace Science and Technology,2013, 28(1): 56–71. |
| Click to display the text | |
| [9] | XIONG L,CHEN Y,JIN C.A nonlinear control allocation algorithm for DYC in distributed-motor drive electric vehicles using S-SQP[C]//26th Chinese Control and Decision Conference (2014 CCDC).Piscataway,NJ:IEEE Press,2014:1530-1537. |
| Click to display the text | |
| [10] | ALBERDING M B, TJONNAS J, JOHANSEN T A. Integration of vehicle yaw stabilisation and rollover prevention through nonlinear hierarchical control allocation[J]. Vehicle System Dynamics,2014, 52(12): 1607–1621. |
| Click to display the text | |
| [11] | CHEN Y, WANG J. Fast and global optimal energy-efficient control allocation with applications to over-actuated electric ground vehicles[J]. IEEE Transactions on Control Systems Technology,2012, 20(5): 1202–1211. |
| Click to display the text | |
| [12] | CHEN Y,WANG J.A global optimization algorithm for energy-efficient control allocation of over-actuated systems[C]//2011 American Control Conference.Piscataway,NJ:IEEE Press,2011:5300-5305. |
| Click to display the text | |
| [13] | TOL H J, DE VISSER C C, VAN KAMPEN E, et al. Nonlinear multivariate spline-based control allocation for high-performance aircraft[J]. Journal of Guidance,Control,and Dynamics,2014, 37(6): 1840–1862. |
| Click to display the text | |
| [14] | TAN J,ZHOU Z,ZHU X P,et al.Attitude control of flying wing UAV based on active disturbance rejection control and multi-object nonlinear control allocation[C]//Machinery,Materials Science and Engineering Applications 2014.Zurich:Trans Tech Publications,2014:419-422. |
| Click to display the text | |
| [15] | BENETAZZO F,IPPOLITI G,LONGHI S,et al.Dynamic positioning of a marine vessel using DTVSC and robust control allocation[C]//201220th Mediterranean Conference on Control & Automation(MED).Piscataway,NJ: IEEE Press,2012:1211-1216. |
| Click to display the text | |
| [16] | 马建军.过驱动系统控制分配理论及其应用[D].长沙:国防科学技术大学,2009: 71-92. MA J J. Research and application of control allocation theory for overactuated systems[D].Changsha:National University of Defense Technology,2009:71-92(in Chinese).(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [17] | STENFELT G, RINGERTZ U. Yaw control of a tailless aircraft configuration[J]. Journal of Aircraft,2010, 47(5): 1807–1811. |
| Click to display the text | |
| [18] | 屈晓波, 章卫国, 史静平, 等. 一种低速情况下无尾飞翼飞机航向控制方法[J]. 西北工业大学学报,2015, 33(1): 70–75.QU X B, ZHANG W G, SHI J P, et al. A yaw control method for tailles flying wing aircraft under low speed condition[J]. Journal of Northwestern Polytechnical University,2015, 33(1): 70–75.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [19] | 李卫琪, 魏晨, 陈宗基. 受限控制直接分配新算法[J]. 北京航空航天大学学报,2005, 31(11): 1177–1180.LI W Q, WEI C, CHEN Z J. New algorithm for constrained control direct allocation[J]. Journal of Beijing University of Aeronautics and Astronautics,2005, 31(11): 1177–1180.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [20] | 屈晓波.无尾飞翼飞机多操纵面控制分配技术研究[D].西安:西北工业大学,2015:91-92. QU X B.Tailless flying wing aircraft multi-control surfaces control allocation technology research[D]. Xi'an:Northwestern Polytechnical University,2015:91-92(in Chinese).(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
