成形极限是板材成形中判断和评定板材成形性能最直观和有效的方法[4],其获取途径分为理论和试验两大类。理论方法包括Swift分散性失稳理论[5]和Hill集中性失稳理论[6]、MK凹槽理论[7]和损伤准则[8]等,且仍在不断补充和完善。成形极限曲线的试验方法有刚性球头凸模胀形[9]、刚性平底凸模胀形[10]、双轴拉伸[11]和椭圆凹模胀形。
与前3种方法相比,椭圆凹模胀形具有不受板材摩擦影响、试件形状简单、工作量小等优点[12]。李春峰[12]、L?z?rescu[13]和Barata da Rocha[14]等分别采用该方法得到了低碳钢、黄铜、DC04钢板和AA6016-T4铝合金在室温下的成形极限曲线的右半区。Mitukiewicza等[15]以气体为胀形介质确定出AZ31镁合金在高温下的成形极限曲线。上述研究在确定左半区的成形极限时,均应用同一温度下的单拉极限点,与椭圆凹模胀形所得数据点构成完整的成形极限曲线,而未考虑应变率的影响。这既导致左、右半区成形极限曲线在连接时存在误差,无法定量获取影响板材成形性能的因素;也使预测成形极限的理论方法没有准确的试验评判依据。
本文采用改进的Hollomon公式拟合得到2A16-O铝合金在不同温度及应变率下的应力应变曲线;通过有限元分析确定了不同椭圆度的椭圆凹模胀形破裂位置,优化工艺参数从而得到指定应变路径下的成形极限点。为实现恒定应变率加载,建立液体压力与等效应变及应变率的公式,推导出压力变化率与应变率的定量关系。以应变率控制的椭圆凹模胀形试验获得2A16-O铝合金板材在不同温度及应变率下的成形极限图的右半区,结合单拉试验极限点,得到完整的成形极限曲线,对于定量分析应变率的影响规律和评判理论预测方法的准确性提供了依据。
1 椭圆凹模胀形适用性论证 1.1 试验原理 板材在椭圆凹模胀形时,其顶点处微元体如图 1所示。设面内第一、二主应力分别为σ1、σ2,椭圆长、短轴对应主曲率半径为ρ1、ρ2,瞬时厚度及液体压力分别为t、P。为简化解析计算,设材料为各向同性,则顶点处应力为[12]
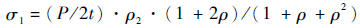 | (1) |
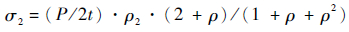 | (2) |
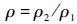 | (3) |
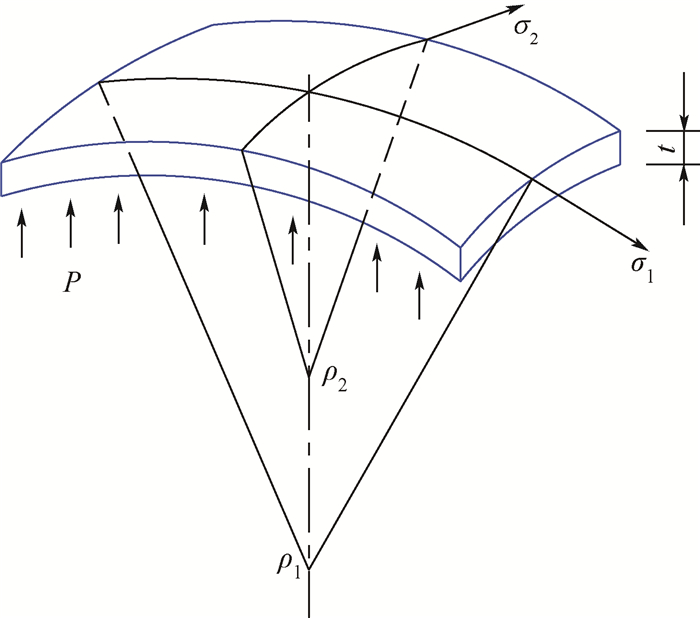 |
| 图 1 胀形顶点处微元体示意图 Fig. 1 Schematic of infinitesimal unit at dome apex |
| 图选项 |
据式(1)~式(3)可知,通过改变液压胀形时的椭圆度χ(χ=b/a,表示椭圆短、长轴直径之比),可以得到不同的应力状态,且能保持线性加载。由于在椭圆凹模胀形时,应变比β=ε2/ε1≥0(ε1、ε2分别为面内第一、二主应变),需结合单拉试验得到完整的成形极限曲线。
1.2 真实应力-应变曲线 本文所用试验材料为2A16-O铝合金板材,厚度为1.0 mm,不同温度T(20、160、210和300℃)和应变率(0.01、0.001和0.000 1 s-1)下的单拉试验在国产CSS-88000电子万能试验机上进行,真实应力-真实应变曲线如图 2所示。图中虚线为基于Hollomon应变幂函数σ=Kεn[16](K为强化系数,n为应变硬化指数,σ为真实应力,ε为真实应变)改进后拟合得到。与传统方法不同,此处只对ε≥0.1的试验数据进行拟合,复合公式为
 | (4) |
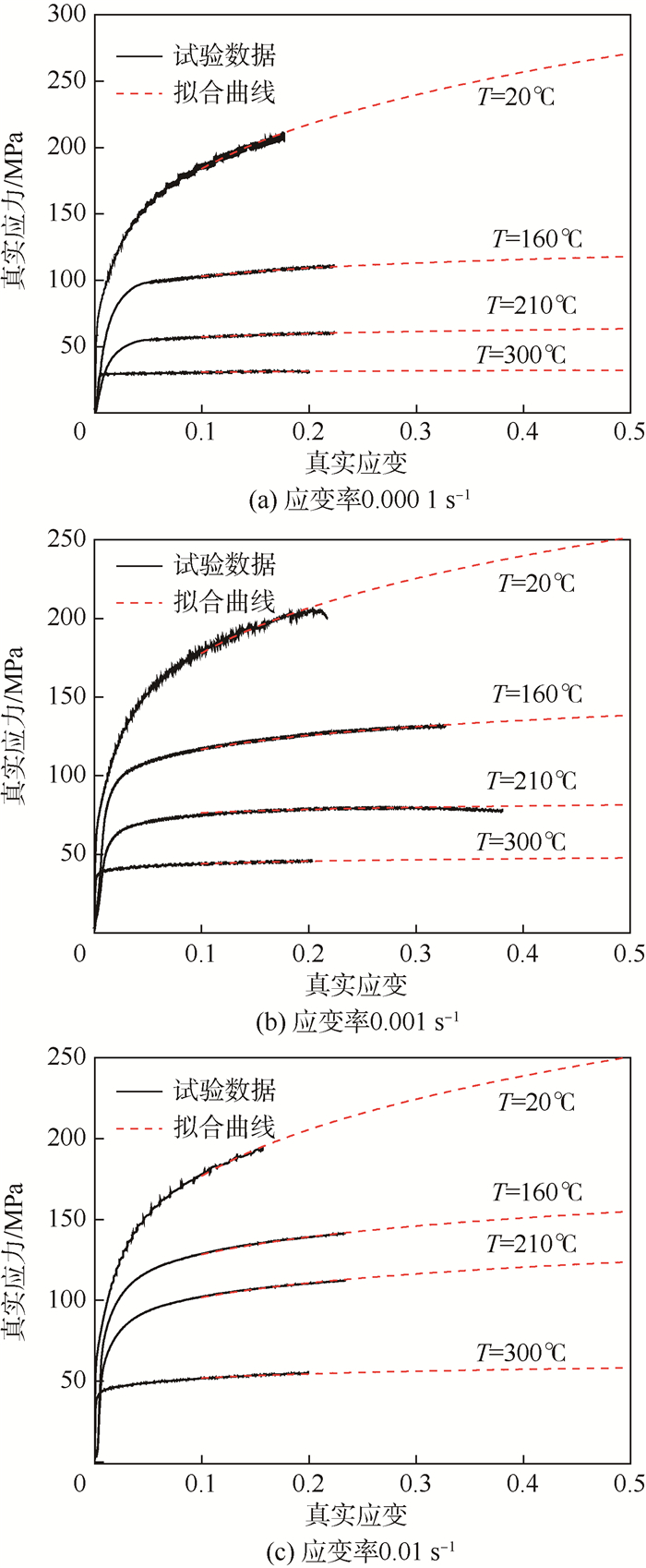 |
| 图 2 不同温度和应变率下真实应力-真实应变曲线 Fig. 2 True stress-true strain curves at different temperatures and strain rates |
| 图选项 |
如图 2所示,式(4)既可以充分利用已有试验数据,又能体现应力-应变曲线的外插延伸的可靠度。
1.3 工艺参数选取 为验证椭圆凹模胀形对2A16-O铝合金板材成形极限测定的适用性,本文建立其1/4的有限元模型如图 3所示。仿真采用板料成形专用软件Dynaform进行分析,坯料与凹模、压边圈间的摩擦系数设置为0.12,并选择适合铝合金板的Barlat89屈服准则,由于2A16-O的面内各向异性不明显,此处仅考虑板材厚向异性。不同T下的厚向异性指数r如表 1所示。
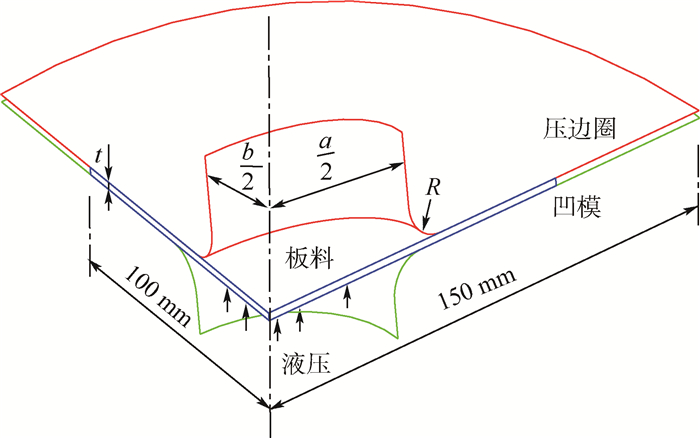 |
| 图 3 1/4椭圆凹模胀形有限元模型示意图 Fig. 3 Schematic of finite element method in 1/4 elliptical hydro-bulging |
| 图选项 |
表 1 不同温度下的厚向异性指数 Table 1 Anisotropic coefficients at different temperatures
| T/℃ | 20 | 160 | 210 | 300 |
| r | 0.69 | 0.77 | 0.85 | 1.04 |
表选项
在椭圆凹模胀形中,影响板材破裂的主要因素为椭圆度χ和凹模圆角半径R。在210℃、应变率0.001 s-1、R=8 mm条件下,分析得到不同椭圆度的等效应变分布趋势如图 4所示,X、Y分别表示椭圆凹模胀形短、长轴对称截面。图 5为X对称截面上的等效应变值分布,H表示瞬时胀形高度。
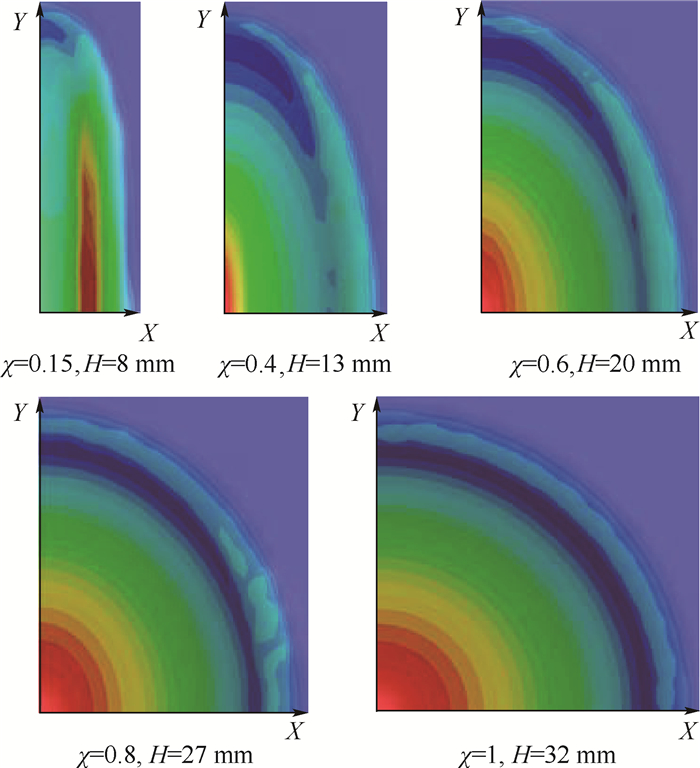 |
| 图 4 等效应变分布趋势 Fig. 4 Distribution trends of equivalent strain |
| 图选项 |
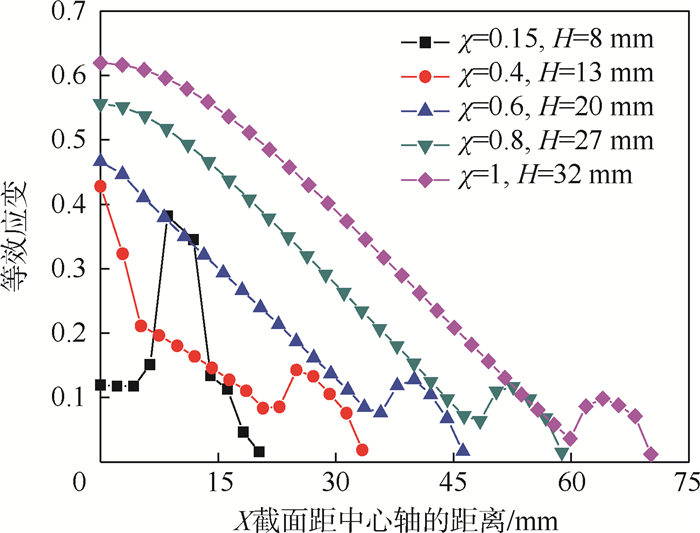 |
| 图 5 不同椭圆度的等效应变分布 Fig. 5 Distribution of equivalent strain with different ovalities |
| 图选项 |
由图 4可知,χ=1,0.8,0.6,0.4时,最大等效应变均出现在胀形顶点处,与理论分析相符;而χ=0.15时,等效应变的最大值出现在椭圆凹模胀形面的侧壁部位,分析中应以此作为危险破裂点进行处理。同时,在凹模圆角处,不同椭圆度下的等效应变均存在一个峰值,并且在胀形前期即达到0.1。经分析,此处应力状态为近平面应变,对于韧性较差的2A16-O铝合金,容易提前破裂而影响成形极限曲线的获取。
在凹模圆角处,板材主要受弯拉作用,以210℃、0.001 s-1、χ=1为例,图 6为通过改变凹模圆角半径进行有限元分析,得到的该位置最大等效应变值,右上角为板材受力示意图,向上的4个箭头表示液体压力。
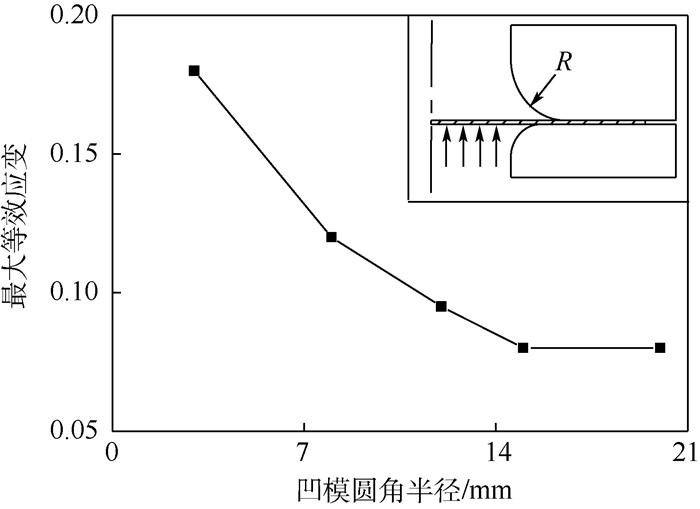 |
| 图 6 凹模圆角半径对最大等效应变的影响 Fig. 6 Influence of die corner radius on maximum equivalent strain |
| 图选项 |
如图 6所示,当R≥15 mm时,等效应变不再随凹模圆角半径的增加而降低。由于本文试验中液体密封采用法兰面密封形式,为增大法兰接触面积,后续将以R=15 mm进行有限元和试验分析。
根据以上分析,分别对χ=1,0.8,0.6,0.4的胀形顶点及χ=0.15的侧壁提取第一、二主应变路径如图 7所示,说明经优化后的椭圆凹模胀形方法可以实现2A16-O铝合金板材在简单加载下的成形极限曲线的测定。
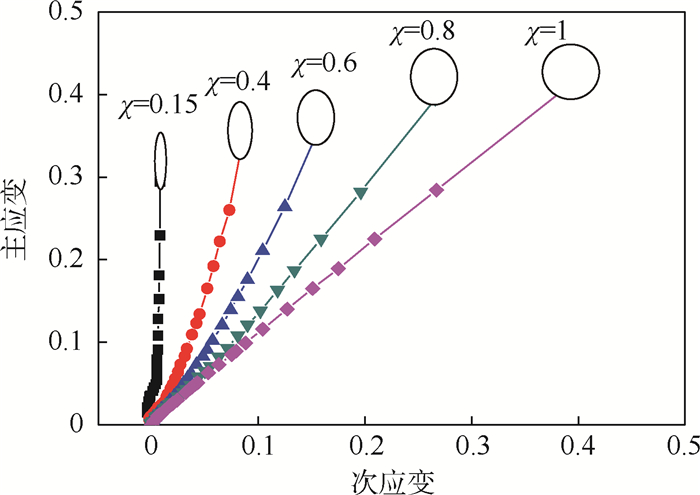 |
| 图 7 不同椭圆度的第一、二主应变路径 Fig. 7 Major and minor strain paths with different ovalities |
| 图选项 |
2 应变率与压力变化率转换 在椭圆凹模胀形试验中,需要确定应变率与压力变化率的关系,通过控制压力变化率,以获得与单拉极限点同一应变率下的成形极限数据,从而绘制不同温度、不同应变率下的成形极限曲线。
以χ=0.6为例,拟合的液体压力-等效应变曲线与模拟结果比较如图 8所示,在胀形过程中,液体压力与等效应变呈单调增函数,且符合幂指数形式。
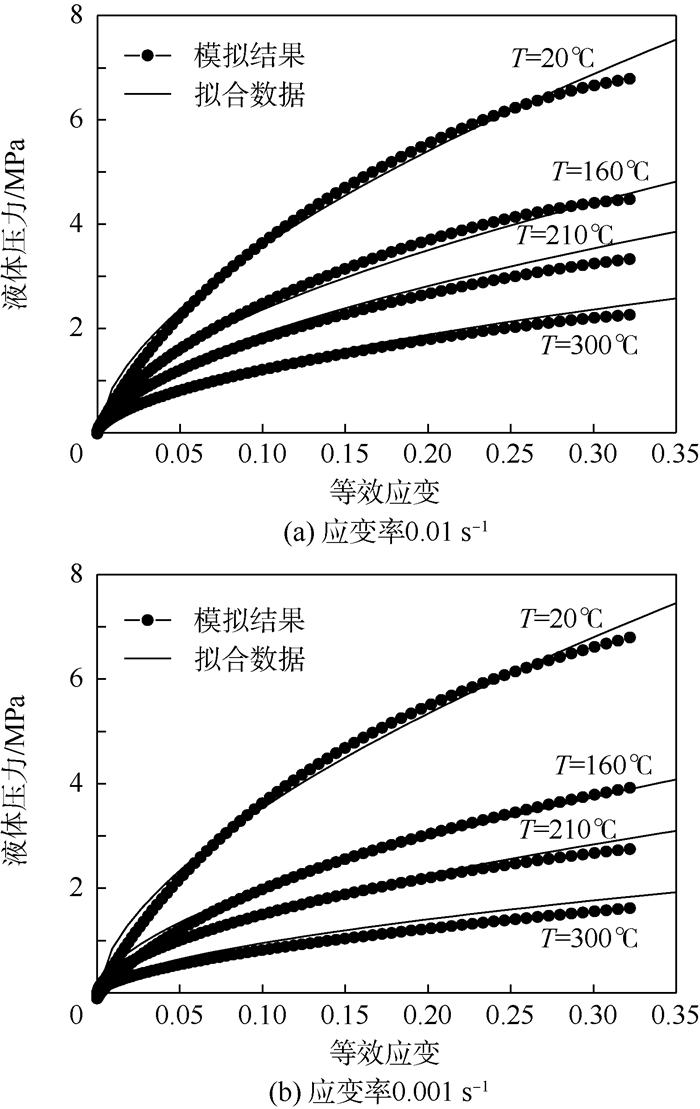 |
| 图 8 拟合的液体压力-等效应变曲线与模拟结果比较 Fig. 8 Comparison of fitted results and simulation results for fluid pressure-equivalent strain |
| 图选项 |
为此,建立液体压力、等效应变及应变率的关系,即
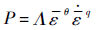 | (5) |
式中:ε为等效应变;
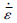
基于图 8所示有限元数据,通过最小二乘法对式(5)在各个T下进行曲面拟合,得到不同温度下Λ、θ和q常数,并将其拟合为温度的函数。则χ=0.6的胀形过程中,液体压力可表示为
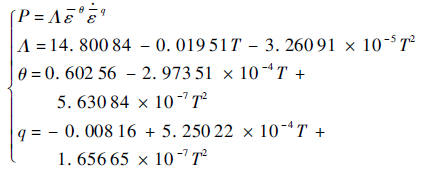 | (6) |
式(6)计算得到的比较结果如图 8所示,可见两者符合程度较高。在胀形过程中设定应变率恒定,式(5)两侧对时间求导,有
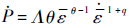 | (7) |
由ε=
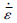
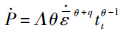 | (8) |
式中:tt为胀形时间。
压力变化率与应变率关系如图 9所示,为保持应变率恒定,在胀形前期,压力变化率迅速降低;随着变形继续,压力变化率趋于平缓。应变率不变情况下,温度越高,压力变化率变化区间相对较小。在同一温度下,应变率越大,胀形前期的压力变化率调整越剧烈,所需的压力变化率明显高于应变率小的情况。
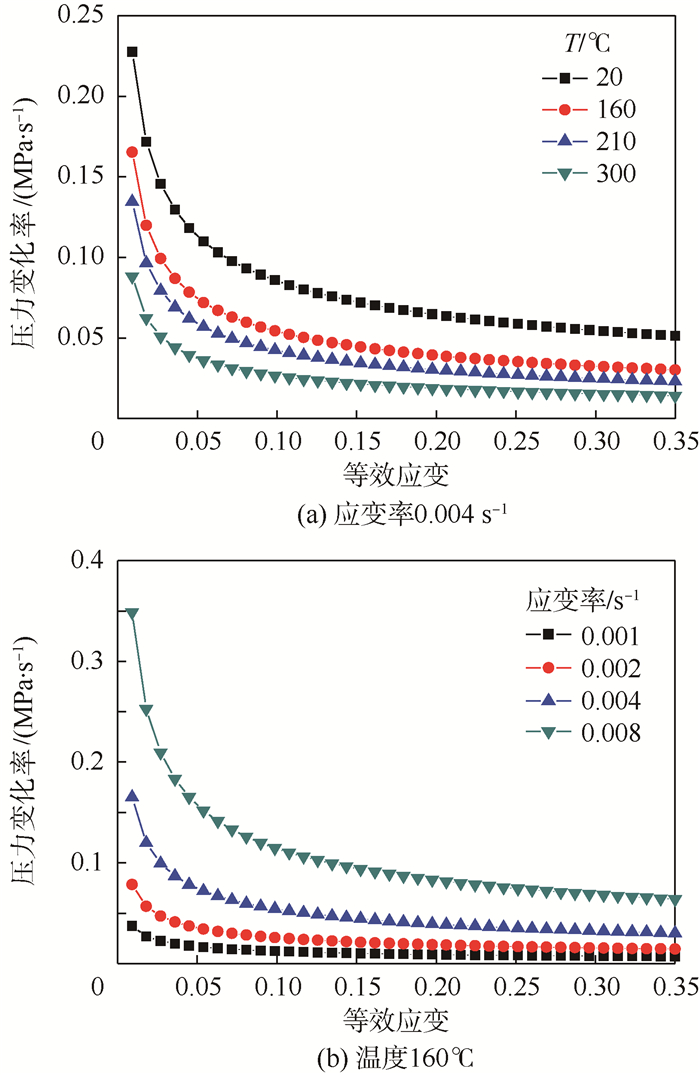 |
| 图 9 压力变化率与应变率关系 Fig. 9 Relation between pressure variation rate and strain rate |
| 图选项 |
3 试验分析 本试验所用液压胀形工装及凹模如图 10所示。通过更换不同椭圆度的凹模,并在胀形过程中控制压力变化率,从而得到不同温度和应变率下的2A16-O铝合金板材的成形极限曲线。
 |
| 图 10 椭圆凹模胀形用试验工装和凹模 Fig. 10 Test setup and die for elliptical hydraulic bulging |
| 图选项 |
图 11为210℃和0.001 s-1时不同椭圆度下的胀形试验件,并在试验件上表面印有网格。χ=1,0.8,0.6,0.4时,破裂点均出现在胀形顶点处;而χ=0.15时,破裂发生在短轴对称面的侧壁位置,破裂处的测量应变与相同高度下的有限元分析结果一致,应变分布与试验结果吻合,验证了有限元模型的正确性及试验方案的可行性。
 |
| 图 11 不同椭圆度下胀形试验件(210℃、应变率0.001 s-1) Fig. 11 Bulged samples with different ovalities (210℃, strain rate 0.001 s-1) |
| 图选项 |
结合椭圆凹模胀形和单拉试验,在20℃、210℃、300℃和应变率0.001 s-1、0.01 s-1下的2A16-O铝合金成形极限曲线如图 12所示。
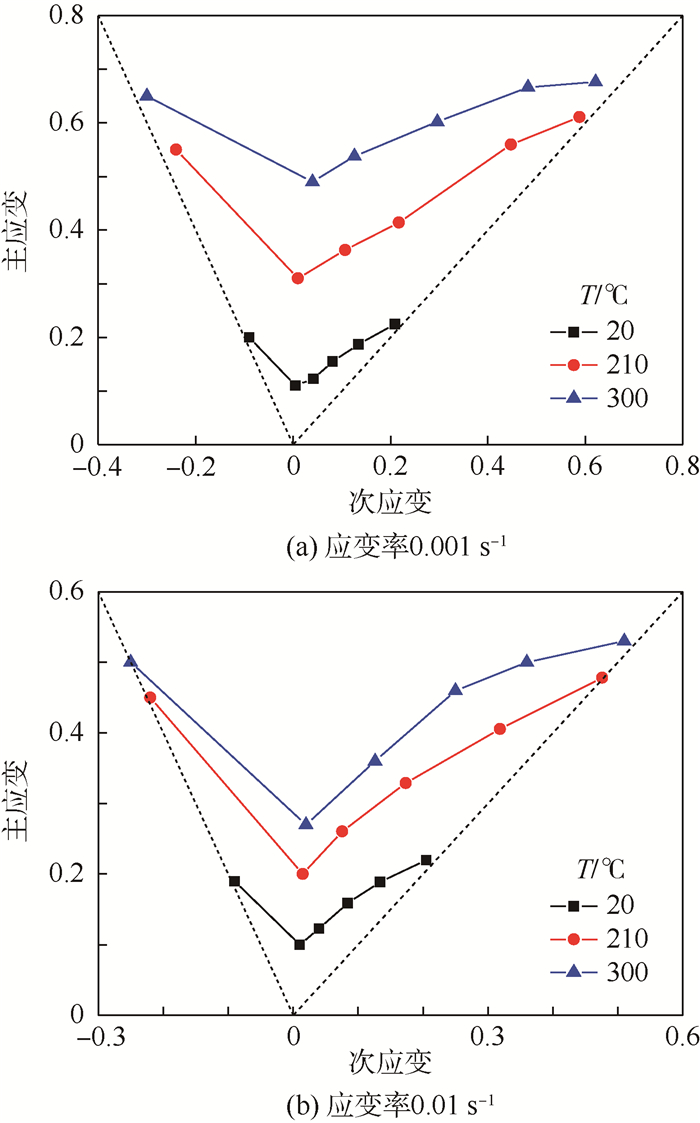 |
| 图 12 不同温度和应变率下的2A16-O铝合金成形极限曲线 Fig. 12 Forming limit curves for 2A16-O aluminum alloy sheet at different temperatures and strain rates |
| 图选项 |
由图 12可知,随着温度的升高,板材的极限应变值增大;对比图 12(a)和图 12(b)可知,在20℃时,应变率对成形极限曲线的影响不大,在210℃和300℃下,随着应变率的降低,成形极限曲线均有所提高;且随着温度的增加,应变率影响作用更大。综上可知,在高温低应变率的情况下,可以得到更高的板材成形性能。
4 结 论 1) 改进Hollomon公式如式(4)所示,该式可获取满足外插可靠度的拟合应力应变,提高有限元分析的精度。
2) χ=1,0.8,0.6,0.4时,最大等效应变均出现在胀形顶点处,与理论分析相符;而χ=0.15时,等效应变的最大值出现在椭圆凹模胀形曲面的侧壁部位。为避免试件提前破裂而影响成形极限获取,椭圆凹模胀形应满足R≥15 mm。
3) 建立了应变率与压力变化率的关系,如式(8)所示,通过控制压力变化以实现板材的恒定应变率加载。同时,结合椭圆凹模胀形和单拉试验,得到不同温度和应变率下的2A16-O铝合金板材成形极限曲线,验证了恒应变率控制的适用性。
参考文献
| [1] | 张珏. 铝合金在航天航空中的应用[J]. 铝加工,2009(3): 50–52.ZHANG Y. The application of aluminum alloy in aerospace field[J]. Aluminum Fabrication,2009(3): 50–52.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [2] | KIM H S, KOC M, NI J, et al. Analysis of warm forming of aluminum alloys-validation through comparisons with experiment and determination of a failure criterion[J]. Journal of Manufacturing Science and Engineering,2006, 128(3): 613–621. |
| Click to display the text | |
| [3] | LI D M, GHOSH A. Tensile deformation behavior of aluminum alloys at warm forming temperature[J]. Materials Science and Engineering A,2003, 352(1-2): 279–286. |
| Click to display the text | |
| [4] | 杨希英, 郎利辉, 刘康宁, 等. 基于修正M-K模型的铝合金板材成形极限图预测[J]. 北京航空航天大学学报,2015, 41(4): 675–679.YANG X Y, LANG L H, LIU K N, et al. Prediction of forming limit diagram of AA7075-O aluminum alloy sheet based on modified M-K model[J]. Journal of Beijing University of Aeronautics and Astronautics,2015, 41(4): 675–679.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [5] | SWIFT H W. Plastic instability under plane stress[J]. Journal of the Mechanics and Physics of Solid,1952, 1(1): 1–18. |
| Click to display the text | |
| [6] | HILL R. On discontinuous plastic states with special reference to localized necking in thin sheets[J]. Journal of Mechanics and Physics of Solids,1952, 1(1): 19–31. |
| Click to display the text | |
| [7] | MARCINIAK Z, KUCZYNSKI K. Limit strains in the processes of stretch-forming sheet metal[J]. International Journal of Mechanical Science,1967, 9(3): 609–620. |
| Click to display the text | |
| [8] | 陈劼实, 周贤宾. 成形极限预测韧性断裂准则及屈服准则的影响[J]. 北京航空航天大学学报,2006, 32(8): 969–973.CHEN J S, ZHOU X B. Suitability of some ductile fracture criteria and yield criteria in forming limit prediction[J]. Journal of Beijing University of Aeronautics and Astronautics,2006, 32(8): 969–973.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [9] | 万敏, 胡运斌, 谢英, 等. 飞机蒙皮铝合金板材成形极限及应用[J]. 中国有色金属学报,2002, 12.WAN M, HU Y B, XIE Y, et al. Forming limit of aircraft skin aluminum alloy sheets and its applications[J]. The Chinese Journal of Nonferrous Metals,2002, 12.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [10] | RAGHAVAN K S. A simple technique to generate in-plane forming limit curve and selected applications[J]. Metallurgical and Materials Transactions A,1995, 26. |
| Click to display the text | |
| [11] | FERRON G, MAKINDE A. Design and development of a biaxial strength testing device[J]. Journal of Testing and Evaluation,1988, 16(3): 253–256. |
| Click to display the text | |
| [12] | 李春峰, 李雪春, 杨玉英. 椭圆凹模液压胀形法制作成形极限图[J]. 材料科学与工艺,1996, 4(2): 101–105.LI C F, LI X C, YANG Y Y. Study on forming limit diagram by bulging with elliptic die[J]. Material Science & Technology,1996, 4(2): 101–105.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [13] | L?Z?RESCU L, COM?A D S, NICODIM I, et al. Characterization of plastic behaviour of sheet metals by hydraulic bulge test[J]. Transactions of Nonferrous Metals Society of China,2012, 22(S2): 275–279. |
| Click to display the text | |
| [14] | BARATA DA ROCHA A, SANTOS A D, TELXEIRA P, et al. Analysis of plastic flow localization under strain paths changes and its coupling with flnite element simulation in sheet metal forming[J]. Journal of Materials Processing Technology,2009, 209(11): 5097–5109. |
| Click to display the text | |
| [15] | MITUKIEWICZA G, ANANTHESHWARA K, ZHOU G, et al. A new method of determining forming limit diagram for sheet materials by gas blow forming[J]. Journal of Materials Processing Technology,2014, 214(12): 2960–2970. |
| Click to display the text | |
| [16] | KOC P, STOK B. Computer-aided identification of the yield curve of a sheet metal after onset of necking[J]. Computational Materials Science,2004, 31(1-2): 155–168. |
| Click to display the text | |
