文献[5]将事件触发控制系统建立为受扰系统模型,并提出了一类基于输入状态稳定性的分析方法。文献[6-7]考虑了基于部分状态的输出反馈事件触发控制系统。文献[8]将事件触发控制与周期采样控制相结合,提出了周期性事件触发控制(periodic event-triggered control),其本质为离散系统事件触发控制[9]的一类特例。文献[10]通过将事件触发控制与基于模型网络化控制(model-based networked control)[11-12]相结合,进一步降低通信频率,并讨论了使用量化信息计算控制律对于闭环系统性能的影响。
虽然近年来事件触发控制受到越来越多的关注,但大部分工作是从理论上对事件触发控制进行讨论与分析。倒立摆作为控制理论研究的典型实验平台,常用于验证新兴的控制策略。因此在倒立摆系统上进行事件触发控制实验有助于说明事件触发控制的工程应用价值。
本文主要研究以一级直线倒立摆为受控对象的事件触发控制系统。首先,根据倒立摆系统的状态空间描述,从理论上给出事件条件中参数的设计范围。其次,搭建Simulink模块,通过仿真计算说明理论结果的可行性。最后,将所设计的事件触发控制策略作用于实际倒立摆对象上,通过得到的实验数据检验事件触发控制的实用性。
1 事件触发控制倒立摆系统 本文主要以由固高科技(深圳)有限公司开发的“倒立摆与自动控制原理实验V2.0”实验平台中的一级直线倒立摆系统为研究对象,其结构如图 1所示。图中:s∈R为直线倒立摆中小车位置,φ∈R为摆杆与竖直向上方向的角度,即φ=0表示摆杆处于上平衡点位置;l∈R为摆杆转动轴心到摆杆质心的距离。
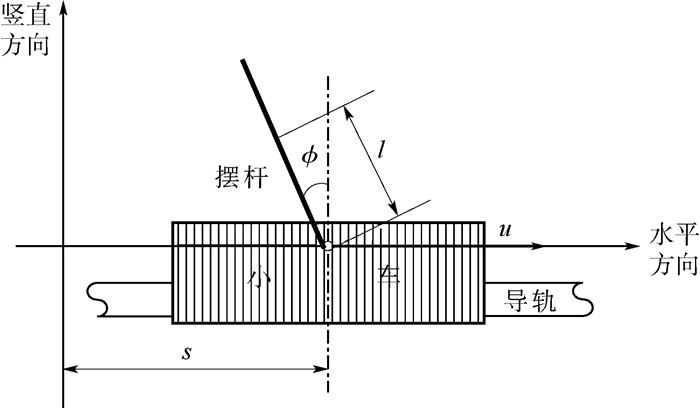 |
| 图 1 一级直线倒立摆示意图 Fig. 1 Sketch map of single linear inverted pendulum |
| 图选项 |
该系统在上平衡点处线性近似的状态空间描述为
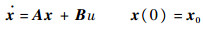 | (1) |
式中:x=
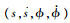
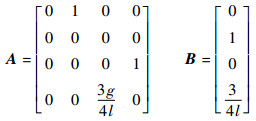 |
式中:g∈R为重力加速度常数。易证,(A, B)是可控的。
由于实际对象通过计算机进行控制,因此系统表现出离散行为。设计算机的采样周期为h∈R>0(R>0表示全体正实数),则离散化后的状态空间描述为
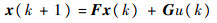 | (2) |
式中:
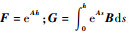
对于位置信号,实验平台采用数字光电编码器进行测量;对于速度信号,实验平台使用编码信号的向后差分值进行近似。因此计算机读入状态值为经过一致量化后的信息,即
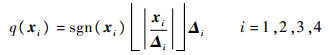 |
式中:xi为状态x的第i个分量; Δi>0表示对xi信号的量化精度;sgn(·)为符号函数;对于任意的非负实数r,
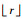
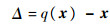 | (3) |
对于一致量化,存在常数M>0使得||Δ||≤M。另外,定义相对量化误差为
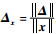
考虑如下两类事件触发控制器:
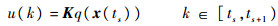 | (4) |
 | (5) |
式中:K∈R1×4为控制器增益矩阵,要求其可使F+GK的特征值位于单位圆内。为保证上述增益阵K存在,引入如下概念。
定义1????[13]采样频率ω(关于方阵A)被称作是病态的(pathological)。如果存在A的两个具有相同实部不同虚部的特征根,其相差的距离为ω的整数倍。否则称为是非病态的(nonpathological)。
由上述定义易得,对于任意的方阵A,总存在足够大的ω,其是关于A非病态的。同时,因为(A, B)可控,由文献[13]可知,若采样频率是非病态的,则(F, G)也是可控的。因此,总可以找到满足上述条件的增益阵K。式(4)采用零阶保持(zero-order-hold)控制方式,即在相邻触发时刻之间控制信号保持常值。而式(5)采用基于模型控制方式,即在相邻采样间隔内,控制信号依据模型的状态计算,其中模型状态由式(6)产生:
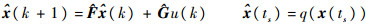 | (6) |
式中:


注1????实际上,零阶保持策略可以被看作基于模型控制的特例,即当模型参数矩阵
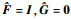
注2 ????在基于模型控制中,虽然模型的作用是对系统的状态进行估计,但它与输出反馈中的观测器有着本质区别。在模型中并未引入模型状态与对象状态差值的反馈项,即模型实际上是开环运行的。考虑到受控对象为开环不稳定的,因此两者初始状态的微小误差会随着时间(以指数速度)迅速发散。
ts∈N≥0(N≥0表示全体非负整数)为事件触发时刻,由如下的事件条件得到。
 | (7) |
式中:e(k)表示误差状态。对于控制器(4),定义e(k)=q(x(ts))-q(x(k)),对于控制器(5),定义e(k)=(k)-q(x(k)),其中k∈[ts, ts+1)。σ∈R>0及σ0∈R≥0(R≥0表示全体非负实数)为待设计参数。对于触发时间序列及采样时间序列,显然有

注3 ????当σ≠0,σ0=0时,事件条件(7)被称为相对型事件条件(relative event condition),若均不为零则被称为混合型事件条件(mixed event condition)[14]。一般而言,若期望系统达到渐近稳定,则使用相对型事件条件;若只需要系统是最终有界的,则使用混合型事件条件。
由上述定义得闭环系统描述为
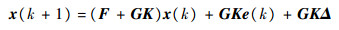 | (8) |
2 理论结果 本节将从理论上对前一部分得到的事件触发控制倒立摆系统进行分析。对于事件条件中待设计参数,有如下结果。
定理1 ????考虑闭环事件触发控制系统(8),若存在正定矩阵P∈R4×4,正常数δ>0及ν>0使得如下的线性矩阵不等式可行:
 | (9) |
式中:
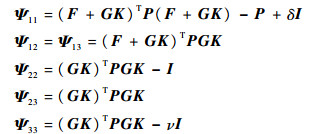 |
则对于任意事件条件参数σ∈(0, δ),σ0>0,闭环系统是最终有界的。特别地,在理想情况下,即量化误差Δ=0且事件条件参数σ0=0时,闭环系统是渐近稳定的。
证明????定义李雅普诺夫函数为V=xTPx,P>0。则V沿闭环系统(8)解的差分为
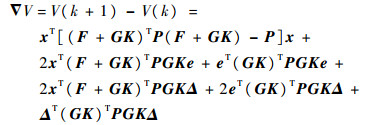 |
进而由式(7)、式(9)及σ∈(0, δ)可得
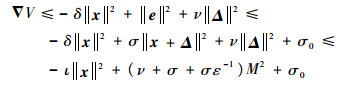 |
式中:ι=δ-σ(1+ε)>0,0 < ε < δσ-1-1。由李雅普诺夫稳定性理论易得,闭环系统是最终有界的。特别地,当Δ=0,σ0=0时,可得ΔV < 0,即系统是渐近稳定的。
注4 ????因为实验平台具有固定的采样周期,所以相邻两次控制律更新时刻的间隔必不小于该采样周期。由此可得,系统一定不会发生芝诺(Zeno)行为[15],即在有限时间内发生无穷次触发的行为。
定理1表明,从稳定性的角度,控制器(4)和控制器(5)具有相同的结果。但不同的控制器会对系统的触发时间序列{ts}s=0∞产生显著的影响。下面的定理讨论了在理想情况下,模型参数矩阵的选取对于触发时间间隔的影响。对于非理想情况,本文将借助仿真及实验结果进行分析。定义参数误差矩阵为
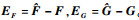
定理2????在理想情况下,事件触发时间间隔的下界可由式(10)估计
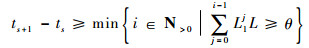 | (10) |
式中:N>0表示全体正整数;
 |
证明????在理想情况下有e=-x及事件条件
 | (11) |
进而有
 | (12) |
其中最后一步应用不等式
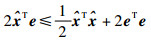 | (13) |
由式(11)及式(12)易得,事件触发时间间隔必大于||e||2从0增长到
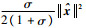
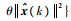
定义
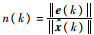
 |
即
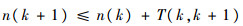 | (14) |
考虑到在理想情况下有如下关系成立:
 | (15) |
则将式(15)代入式(14)可得
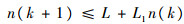 |
由n(ts)=0可得
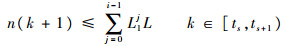 |
进而有
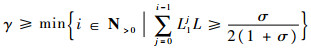 |
即
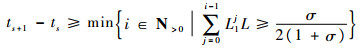 |
注5????由定理2可知,在理想情况下,只要参数误差矩阵EF、EG足够小,则可以得到任意大的事件触发时间间隔。特别地,当模型与对象完全一致时,事件将不再被触发。同时,零阶保持方式显然无法得到充分小的参数误差矩阵,相应地,其触发也会更加频繁。这体现了基于模型控制在理论上的优越性。
3 仿真与实验 3.1 Simulink仿真
3.1.1 Simulink模块搭建 本节通过数值仿真验证理论部分给出结果的有效性。由于实验平台使用Simulink模块进行计算机与硬件的交互,因此通过Simulink完成对系统的数值仿真。基本Simulink仿真框图如图 2所示。
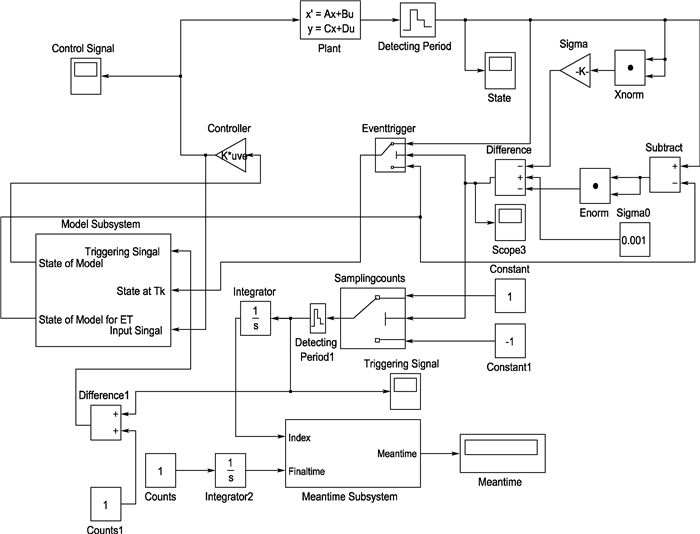 |
| 图 2 Simulink基本仿真框图 Fig. 2 Fundamental Simulink simulation block diagram |
| 图选项 |
图 2中三路选择器模块“Samplingcounts”用于输出事件触发情况,并通过示波器“Triggering Signal”进行观察与记录。若当前时刻为触发时刻,则三路选择器输出为1,反之为-1。子系统“Model Subsystem”以及子系统“Meantime Subsystem”分别用于产生模型状态及计算平均触发时间,其具体框图如图 3所示。
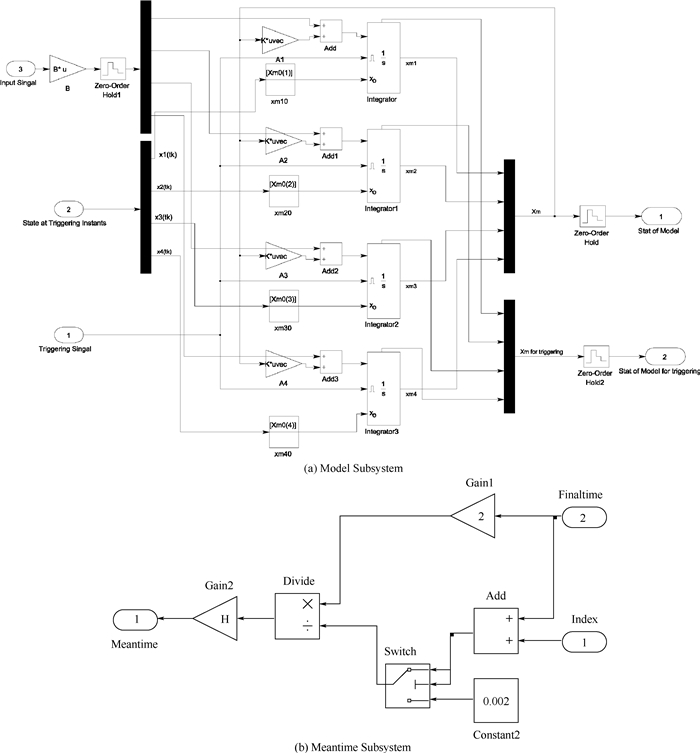 |
| 图 3 Simulink子系统框图 Fig. 3 Simulink block diagrams of subsystems |
| 图选项 |
由事件触发控制的运行机制可知,用于判断事件条件的三路选择模块“Eventtrigger”需要使用当前时刻的模型输出状态进行事件条件的运算与判断,同时若该时刻为触发时刻,则需要使用该时刻状态更新控制律及模型。这就可能出现Model Subsystem子系统中的积分模块以自身输出为输入的情况,进而产生代数环。代数环问题也是使用Simulink仿真事件触发控制系统的主要挑战之一。为了切断代数环,在Model Subsystem子系统中使用高级积分器。高级积分器中的状态端口输出值用于事件条件的判断,输出端口的输出值用于更新控制律。由于二者产生的时间略有不同(但都处于同一仿真步内)[16],可以达到切断代数环的作用。图 3(b)中子系统用于计算平均触发时间,其基本原理为根据在触发时刻“Samplingcounts”模块的输出,统计出触发时刻占总采样时间序列的比例,进而得到平均触发时间。由于图中三路选择器模块的输出作分母,为保证分母不为0,引入小常数模块“Constant2”。
注6????图 2仅给出基本的Simulink框图,可直接用于对理想情况的仿真。对于非理想情况,仅需在其基础上加入对状态信号的量化处理模块即可,具体框图此处略去。
3.1.2 Simulink仿真结果 将实验平台说明书中给出的设备标称参数代入式(1)可得
 |
实验平台内置采样周期为h=0.005 s,则有
 |
将上述(F, G)称为标称参数矩阵。由秩判据可验证标称参数矩阵可控。
仿真初始状态为
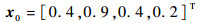 |
取控制器增益矩阵为
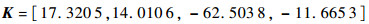 |
则闭环矩阵F+GK的极点为0.940 5, 0.977 2, 0.988 0±0.009 5i,均位于单位圆内。
由于状态空间描述式(1)为倒立摆系统在上平衡点附近的线性近似模型,因此对于基于模型控制器(5), 所构建的模型(6)不可能与受控对象的真实动态完全吻合,为了体现这一差别,在仿真部分,使用如下与标称参数矩阵略有差别的

 |
而在实验部分,将用标称参数矩阵作为

将参数A、B、F和G代入式(9)可得一组可行解为
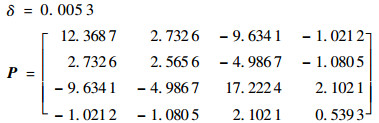 |
本节给出无量化误差时的仿真结果。对于存在量化误差的情况,为了方便将仿真结果与实验结果对比分析,将在实验部分给出。
首先考察相对型的事件条件对于倒立摆系统的影响。图 4及图 5中分别给出了当σ0=0,σ=0.004 9 < δ时,零阶保持控制器(4)及基于模型控制器(5)作用下系统的仿真结果。显然,在所设计的相对型事件条件作用下,两类控制器均可以使系统达到渐近稳定。零阶保持控制器作用下系统的平均触发时间为0.024 9 s,即平均每5个采样周期触发一次,有效地降低了控制信号的更新频率。而在基于模型控制器作用下,系统的平均触发周期为0.133 3 s,几乎为前者的6倍,进一步减少了通信次数。这说明了在理想情况下,基于模型控制器的触发性能确实优于零阶保持控制器。
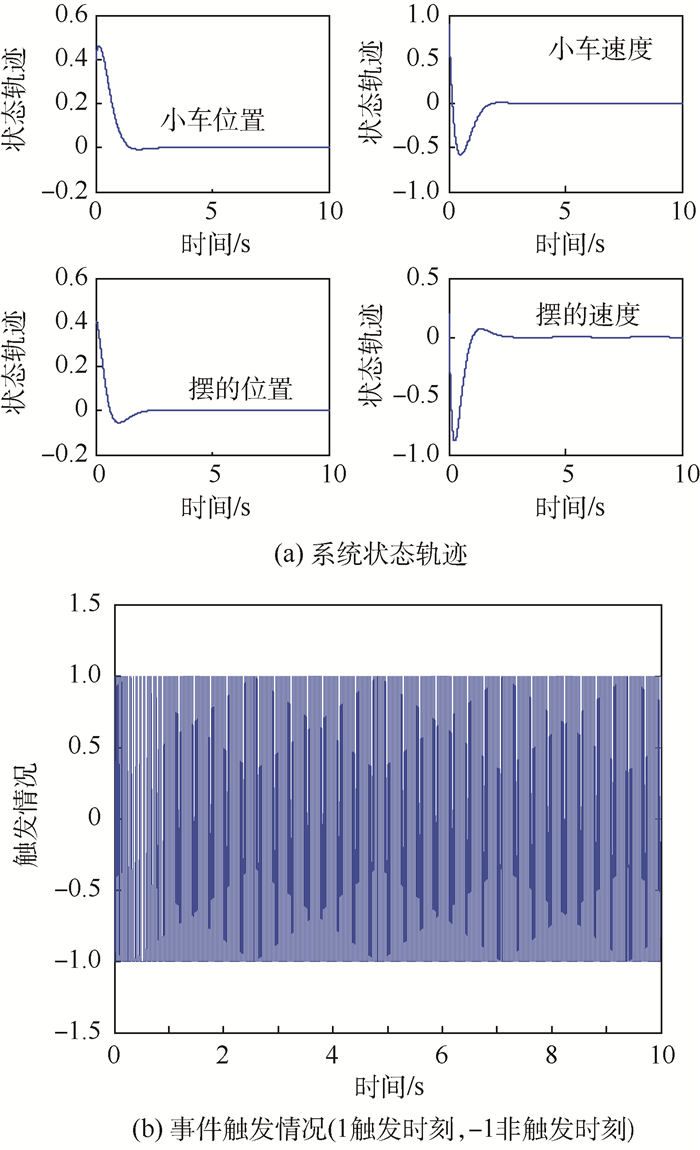 |
| 图 4 相对型事件条件及控制器(4)作用下的仿真结果 Fig. 4 Simulation results of system with relative event condition and controller (4) |
| 图选项 |
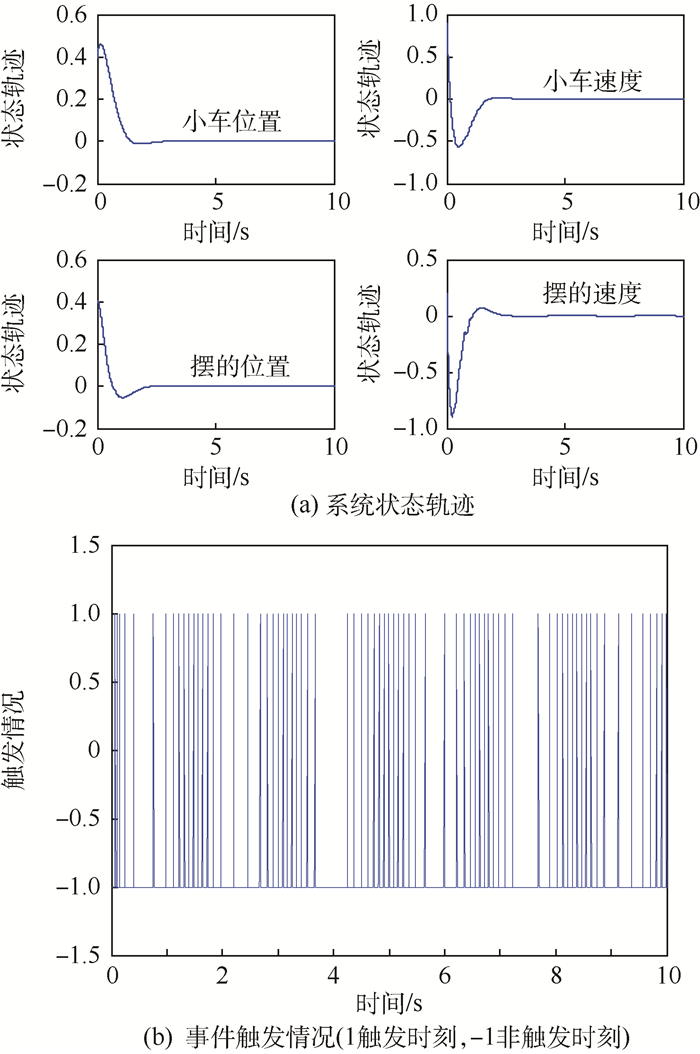 |
| 图 5 相对型事件条件及控制器(5)作用下的仿真结果 Fig. 5 Simulation results of system with relative event condition and controller (5) |
| 图选项 |
另一方面,大量实验表明,倒立摆系统在现实中很难达到渐近稳定性,一般仅能稳定于上平衡点的小邻域内。所以,最终有界性既可以满足工程上对于倒立摆系统稳定性的需求,同时,通过牺牲渐近稳定性,也可以期望得到更好的触发性能。因此,混合型事件条件较相对型事件条件更适合倒立摆系统。图 6给出了当σ0=0.001,σ=0.004 9时,零阶保持控制器(4)作用下系统的仿真结果。虽然图 6(a)说明系统最终只能被稳定于平衡点附近的小邻域内,但图 6(b)中的事件触发情况明显优于图 4(b)中的情况。前者的平均触发时间为0.090 1 s,几乎为后者的4倍。
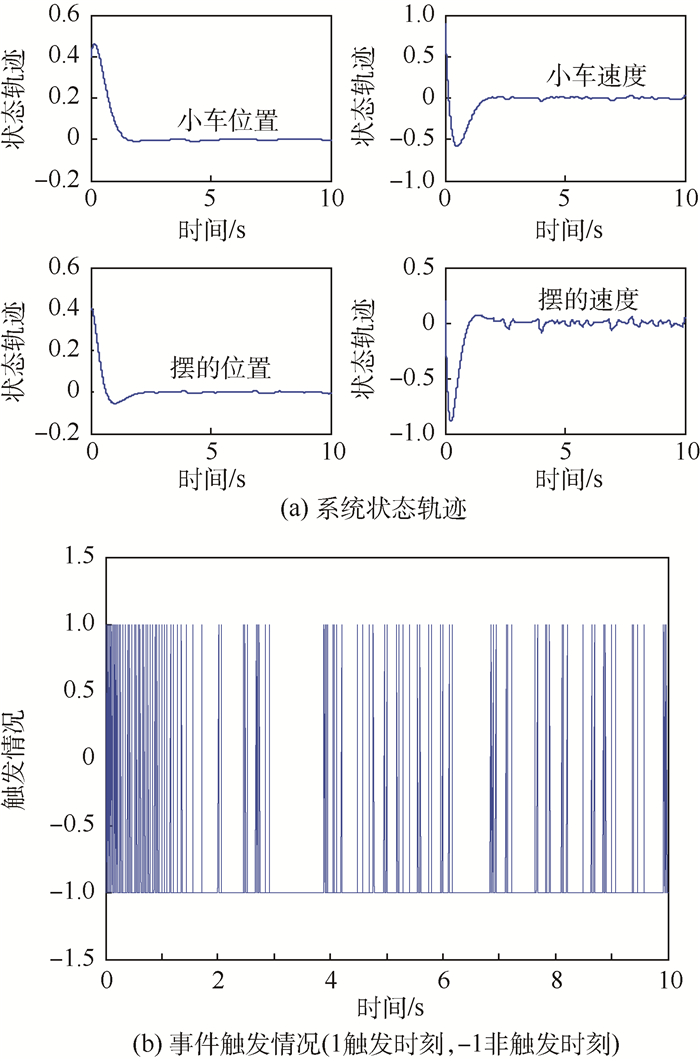 |
| 图 6 混合型事件条件及控制器(4)作用下的仿真结果 Fig. 6 Simulation results of system with mixed event condition and controller (4) |
| 图选项 |
3.2 实验结果 本节将给出对于倒立摆进行事件触发控制实验得到的结果。实验设备实物图如图 7所示。
 |
| 图 7 一级直线倒立摆实物设备 Fig. 7 Equipment of single linear inverted pendulum |
| 图选项 |
首先使用零阶保持控制器(4)对系统进行实验。图 8和图 9分别给出在相对型及混合型事件条件作用下的实验结果,其事件条件参数选取与仿真部分相同。由系统的状态轨迹可以看出,相对型事件条件虽然较混合型事件条件可以得到更小的状态波动范围,但两者均只能使闭环系统是最终有界的。同时,从轨迹中可以明显看出量化对于状态测量的影响,其中对于摆的速度信号的量化精度最低,造成的影响也最大,其轨迹表现为大幅度的跳变。对于事件触发情况,混合型事件条件的平均触发时间为0.037 2 s,优于相对型事件条件的平均触发时间0.009 3 s。这表明对于现实中的倒立摆系统,混合型事件条件更为适用。同时,由上述实验结果可知,两类事件条件对应的平均触发时间均小于(无量化误差情况下)仿真得到的结果。通过对比状态轨迹与触发情况不难发现,量化后摆的速度信号每次发生的跳变都会造成事件的触发。这反映了量化对于系统触发性能的负面影响。
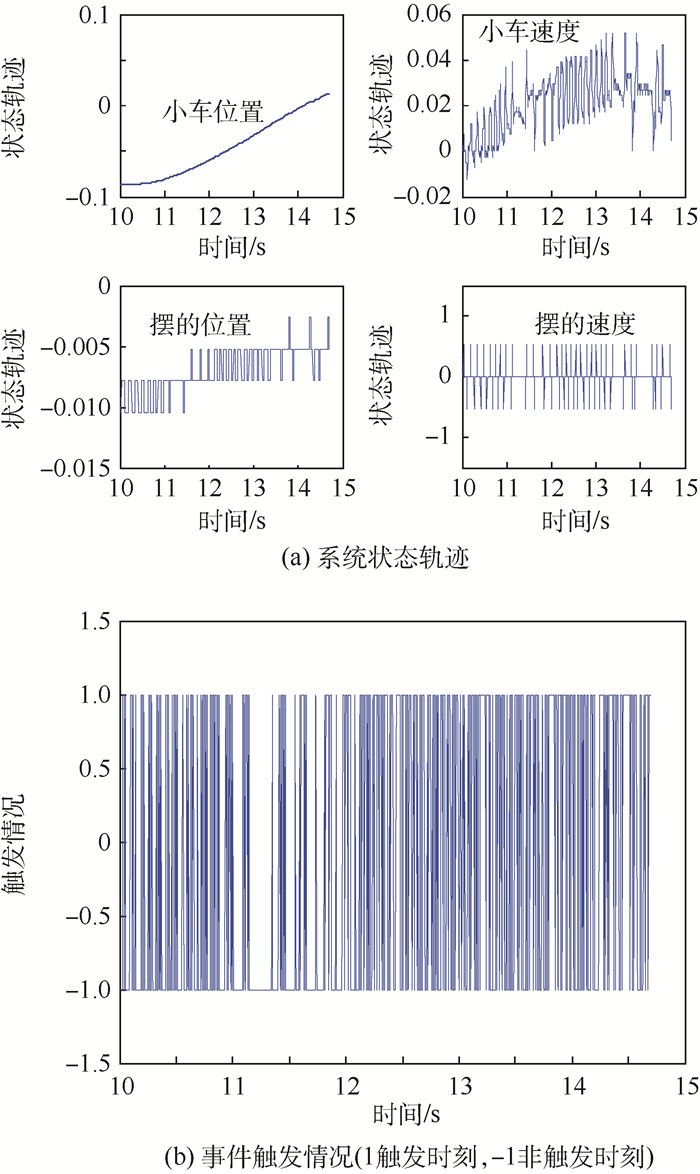 |
| 图 8 相对型事件条件及控制器(4)作用下的实验结果 Fig. 8 Experimental results of system with relative event condition and controller (4) |
| 图选项 |
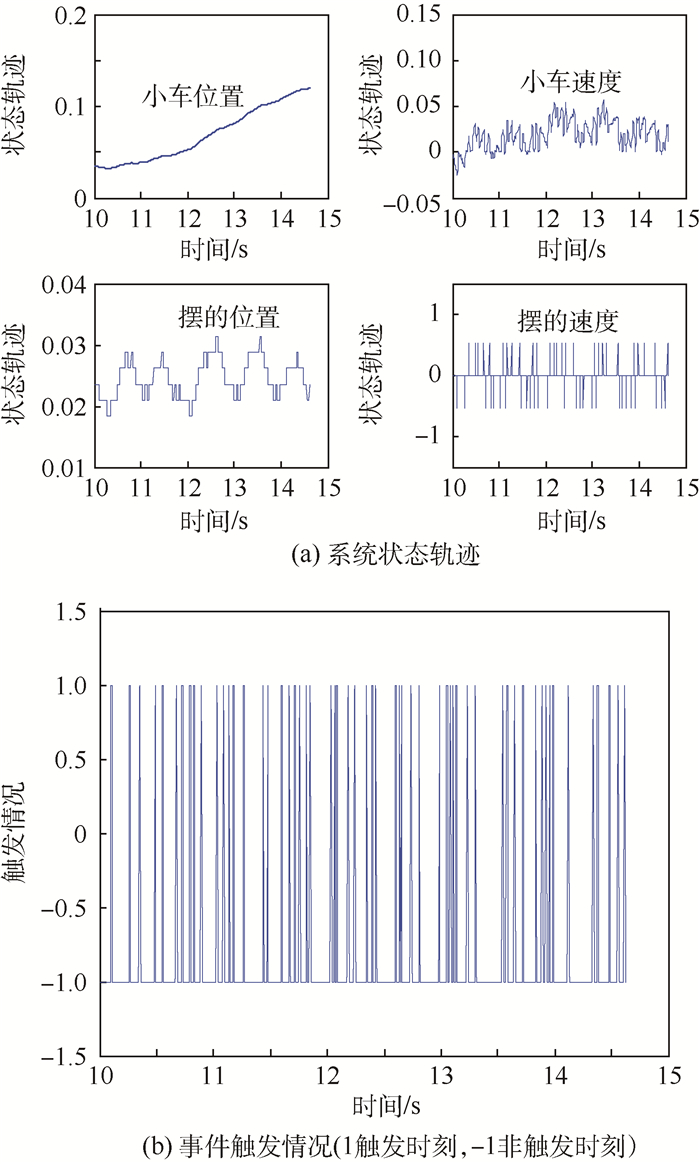 |
| 图 9 混合型事件条件及控制器(4)作用下的实验结果 Fig. 9 Experimental results of system with mixed event condition and controller (4) |
| 图选项 |
图 10中给出了相对型事件条件及基于模型控制器(5)作用下系统的实验结果。图 10(a)说明基于模型控制器可以保证系统满足期望的稳定性。图 10(b)中的事件触发情况相当频繁,其平均触发周期仅为0.009 6 s。这与零阶保持控制器得到的平均触发时间基本相同。可以说基于模型控制器在实验中完全没有体现出理论上预测的应具有的优势。本文将通过数值仿真对这一现象进行分析,找出造成基于模型控制器触发性能衰减的原因。受篇幅所限,本文仅给出相对型事件条件作用下系统的仿真结果。
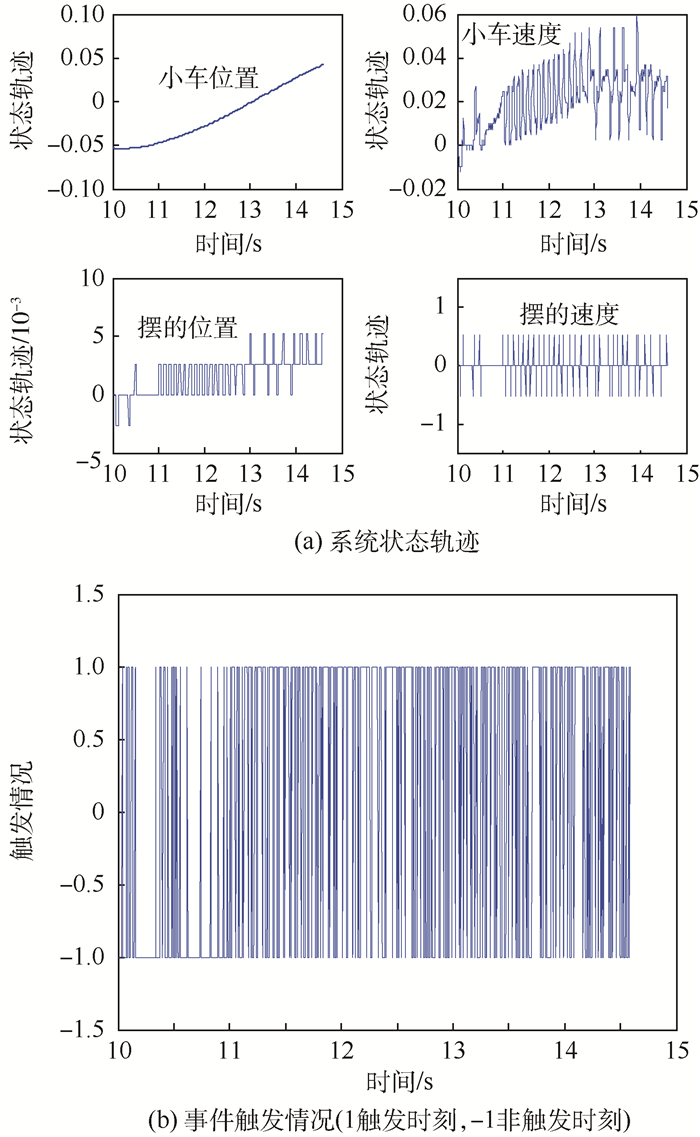 |
| 图 10 相对型事件条件及控制器(5)作用下的实验结果 Fig. 10 Experimental results of system with relative event condition and controller (5) |
| 图选项 |
图 11和图 12分别给出了考虑量化效应后,控制器(4)及控制器(5)作用下系统的仿真结果。两图中的状态曲线表现出与实验结果相类似的量化效果。两系统的平均触发时间分别为0.006 1 s及0.005 7 s,并无明显差别。这与实验所得结果相符。因此,上述仿真结果说明,量化效应对于基于模型控制器(5)的触发性能具有明显的负面影响。一方面,量化导致模型在触发时刻无法获得受控对象的真实状态值,这会大大降低模型状态对系统状态的估计精度(见注2),进而使得事件条件更容易被满足,触发更频繁。另一方面,倒立摆系统一般只在上平衡点的小邻域内运行,因此系统状态变化相对缓慢,其处于同一量化区间的时间也相对较长。计算机读入信息在某些时刻的行为更接近于零阶保持形式。这使得零阶保持控制器在一定程度上也符合计算机读入信息的变化规律,从而拉近了零阶保持控制器与基于模型控制器在触发性能上的差距。为了验证上述分析,给出如下仿真结果,其初始状态为原初始状态的100倍并只考虑系统的调节过程。需要注意的是,上述设定对于实际的倒立摆系统是极不合理的,此处仅用于仿真分析。
 |
| 图 11 带有量化及控制器(4)作用下的仿真结果 Fig. 11 Simulation results of system with quantization and controller (4) |
| 图选项 |
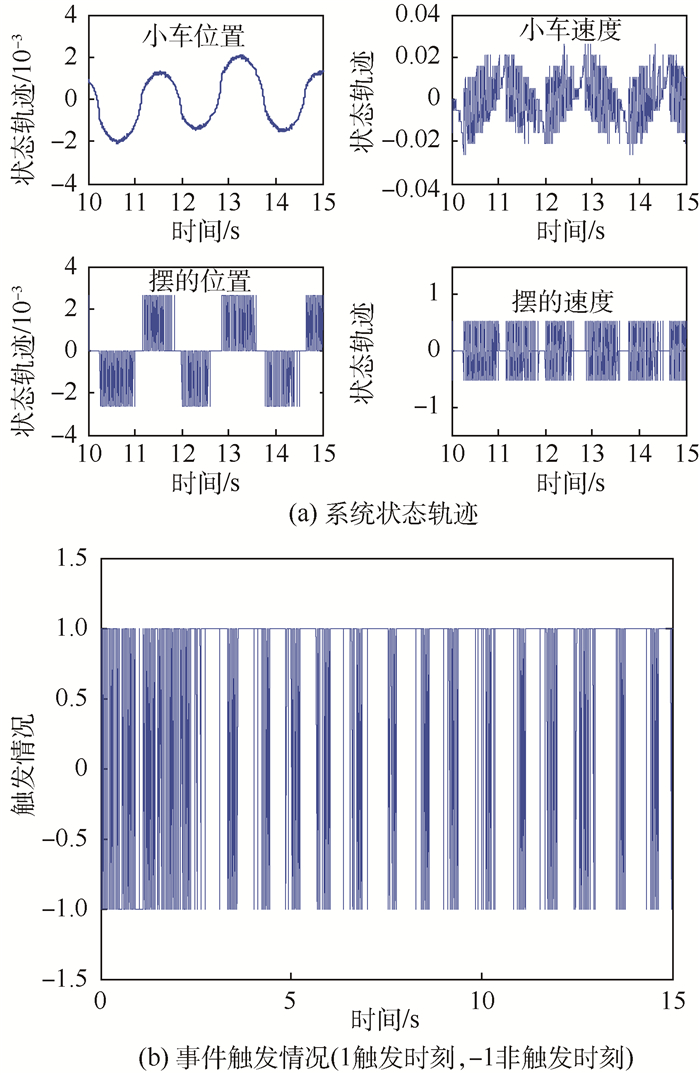 |
| 图 12 带有量化及控制器(5)作用下的仿真结果 Fig. 12 Simulation results of system with quantization and controller (5) |
| 图选项 |
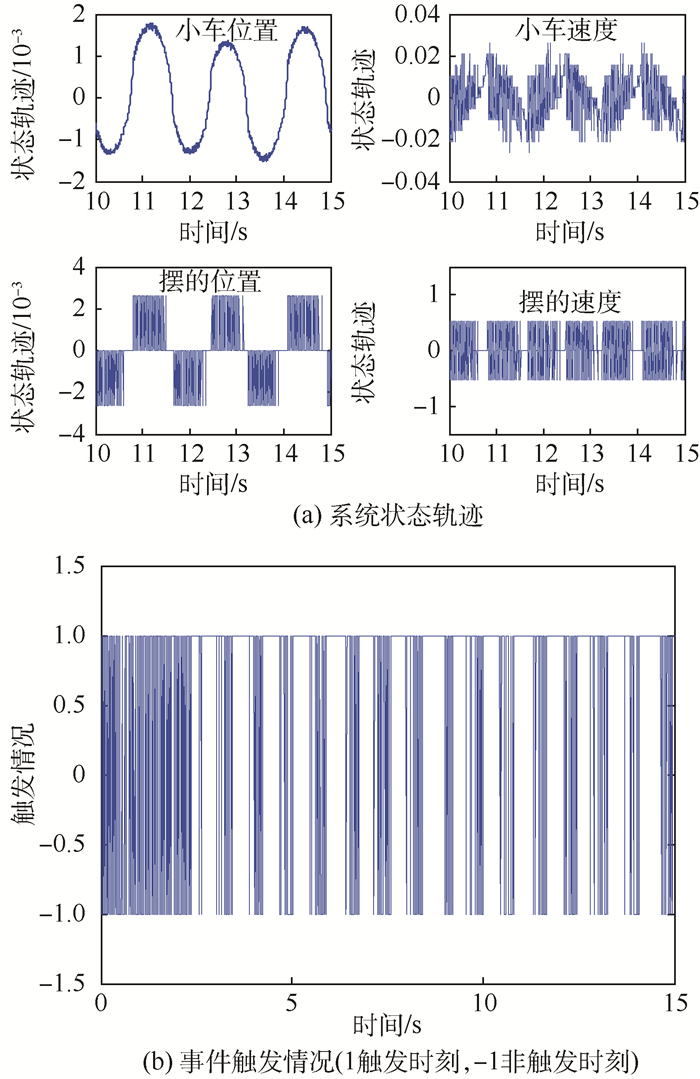
图 13和图 14分别给出了考虑量化效应后,控制器(4)及控制器(5)作用下的带有大初始状态系统的仿真结果。其平均事件触发时间分别为0.019 6 s和0.055 6 s。显然,基于模型控制器具有更优秀的触发性能。这是由于当系统初始状态较大且只考虑调节过程(前2 s内的系统轨迹)时,相对量化误差Δx可以近似忽略。这既提高了模型更新状态
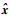
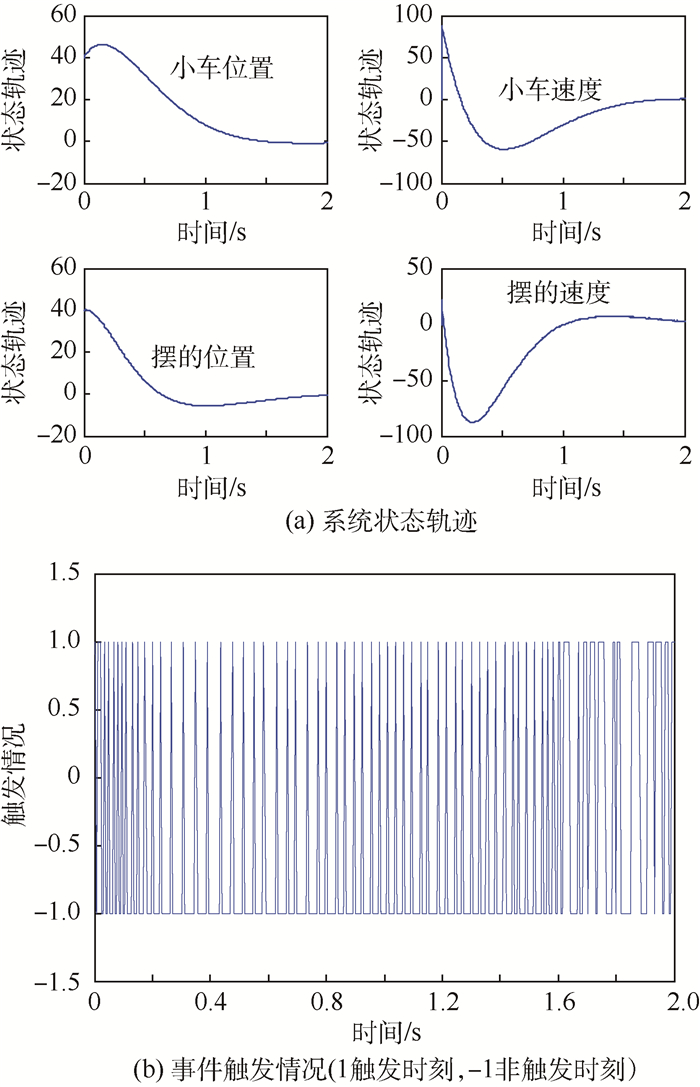 |
| 图 13 带有大初始状态及控制器(4)的系统的仿真结果 Fig. 13 Simulation results of system with large initial state and controller (4) |
| 图选项 |
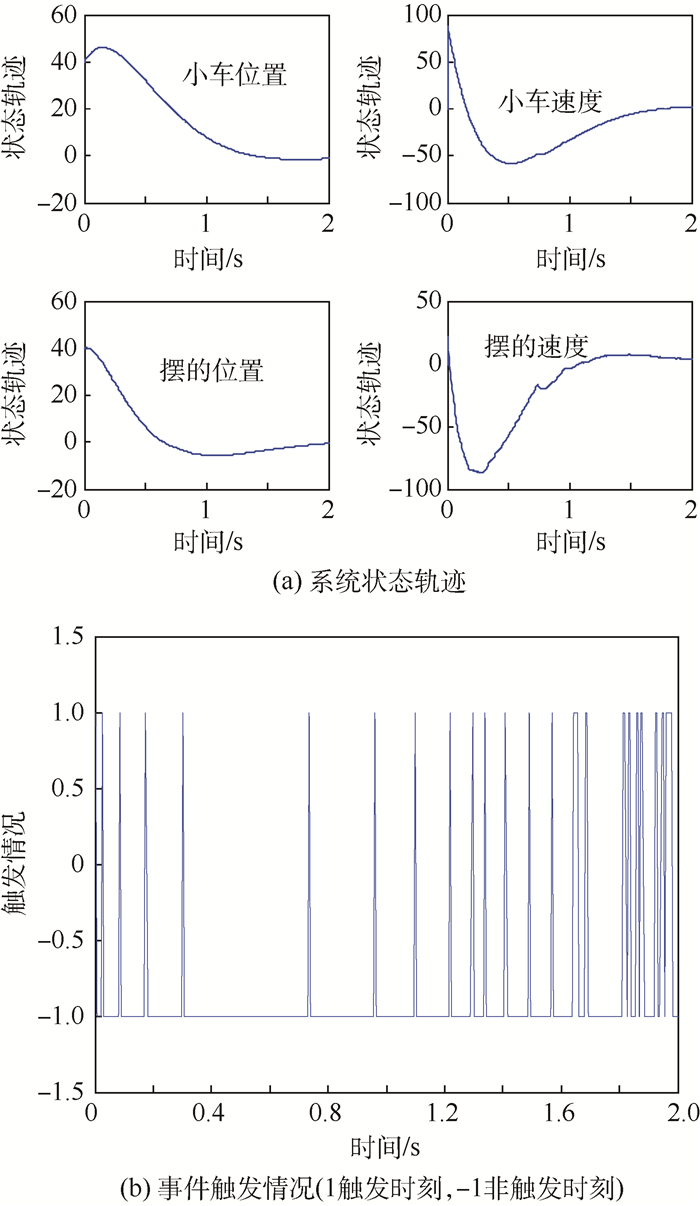 |
| 图 14 带有大初始状态及控制器(5)的系统的仿真结果 Fig. 14 Simulation results of system with large initial state and controller (5) |
| 图选项 |
上述分析表明,对于倒立摆系统,当相对量化精度较低时,基于模型控制器并不比零阶保持控制器优秀。考虑到基于模型控制器需要消耗更多的计算资源来获得模型状态,其总体性能甚至低于结构简单的零阶保持控制器。
4 结论 1) 本文研究了事件触发控制策略在倒立摆系统中的应用。考虑了两类事件触发控制器,即零阶保持控制器及基于模型控制器,在相对型和混合型事件条件作用下对于倒立摆系统稳定性及触发性能的影响。
2) 对于事件条件,只期望保证系统最终有界时,混合型事件条件可以获得更好的触发性能。对于控制器,当可以准确获得系统状态时,基于模型控制器可以得到更好的触发性能。
3) 当量化效应无法被忽略时,两者触发性能无明显差别,但考虑到基于模型控制需要消耗更多的计算资源,则零阶保持控制器更为优秀。因此,对于倒立摆系统,混合型事件条件及零阶保持控制器更为适用。其在保证闭环系统稳定性的前提下可以有效降低控制律的更新频率。
因此,本文从理论、仿真及实验3个角度说明了经过良好设计的事件触发控制系统具有潜在的实用价值。
参考文献
| [1] | LIAN F L, MOYNE J R, TILBURY D M. Performance evaluation of control networks: Ethernet, controlnet, and devicenet[J].Control Systems, 1999, 21(1): 66–83. |
| [2] | ASTROM K J, BERNHARDSSON B M.Comparison of periodic and event based sampling for first order stochastic systems[C]//Proceedings of the 14th IFAC World Congress.Amsterdam:Elsevier Press, 1999:301-306. |
| [3] | SETO D, LEHOCZKY J P, SHA L, et al.On task schedulability in real-time control systems[C]//Proceedings of the 17th Real-time Technology and Applications Symposium.Piscataway, NJ:IEEE Press, 1996:13-21. |
| [4] | TABUADA P, WANG X F.Preliminary results on state-triggered scheduling of stabilizing control tasks[C]//Proceedings of the 45th IEEE Conference on Decision and Control.Piscataway, NJ:IEEE Press, 2006:282-287. |
| [5] | TABUADA P. Event-triggered real-time scheduling of stabilizing control tasks[J].IEEE Transactions on Automatic Control, 2007, 52(9): 1680–1685.DOI:10.1109/TAC.2007.904277 |
| [6] | CHEN X, HAO F. Observer-based event-triggered control for certain and uncertain linear systems[J].IMA Journal of Mathematical Control and Information, 2013, 30(4): 527–542.DOI:10.1093/imamci/dns035 |
| [7] | LIU T F, JIANG Z P. Event-based control of nonlinear systems with partial state and output feedback[J].Automatica, 2015, 53(7): 10–22. |
| [8] | HEEMELS W P M H, DONKERS M C F, TEEL A R. Periodic event-triggered control for linear systems[J].IEEE Transactions on Automatic Control, 2013, 58(4): 847–861.DOI:10.1109/TAC.2012.2220443 |
| [9] | EQTAMI A, DIMAROGONAS D V, KYRIAKOPOULOS K J.Event-triggered control for discrete-time systems[C]//Proceedings of American Control Conference.Piscataway, NJ:IEEE Press, 2010:4719-4724. |
| [10] | GARCIA E, ANTSAKLIS P J. Model-based event-triggered control for systems with quantization and time-varying network delays[J].IEEE Transactions on Automatic Control, 2013, 58(2): 422–434.DOI:10.1109/TAC.2012.2211411 |
| [11] | MONTESTRUQUE L A, ANTSAKLIS P J. On the model-based control of networked systems[J].Automatica, 2003, 39(10): 1837–1843.DOI:10.1016/S0005-1098(03)00186-9 |
| [12] | MONTESTRUQUE L A, ANTSAKLIS P J. Model-based networked control system:Necessary and sufficient conditions for stability[J].IEEE Transactions on Automatic Control, 2004, 49(9): 1562–1572.DOI:10.1109/TAC.2004.834107 |
| [13] | CHEN T, FRANCIS B. Optimal sampled-data control systems[M].London: Springer, 1995: 45-48. |
| [14] | BORGERS D P, HEEMELS W P M H. Event-separation properties of event-triggered control systems[J].IEEE Transactions on Automatic Control, 2014, 59(10): 2644–2656.DOI:10.1109/TAC.2014.2325272 |
| [15] | GOEBEL R, SANFELICE S, TEEL A R. Hybrid dynamical systems[J].IEEE Control Systems, 2009, 29(2): 28–93.DOI:10.1109/MCS.2008.931718 |
| [16] | 姚俊, 马松辉. Simulink建模与仿真[M].西安: 西安电子科技大学出版社, 2002: 142-143.YAO J, MA S H. Modeling and simulation by Simulink[M].Xi'an: Xidian University Press, 2002: 142-143.(in Chinese) |
